ProbKnot: Fast prediction of RNA secondary structure including pseudoknots

Abstract

It is a significant challenge to predict RNA secondary structures including pseudoknots. Here, a new algorithm capable of predicting pseudoknots of any topology, ProbKnot, is reported. ProbKnot assembles maximum expected accuracy structures from computed base-pairing probabilities in O(N²) time, where N is the length of the sequence. The performance of ProbKnot was measured by comparing predicted structures with known structures for a large database of RNA sequences with fewer than 700 nucleotides. The percentage of known pairs correctly predicted was 69.3%. Additionally, the percentage of predicted pairs in the known structure was 61.3%. This performance is the highest of four tested algorithms that are capable of pseudoknot prediction. The program is available for download at: http://rna.urmc.rochester.edu/RNAstructure.html.

INTRODUCTION

There is a diverse world of functional RNA sequences. Originally in the central dogma of biology, RNA was considered to play a transient role in expressing inherited information as proteins. It was later discovered that, besides this role in generating proteins, RNA has a variety of other functions, such as regulating gene expression (Tucker and Breaker 2005; Storz and Gottesman 2006; Wu and Belasco 2008), catalyzing reactions (Nissen et al. 2000; Doudna and Cech 2002), and trafficking proteins (Walter and Blobel 1982). RNA sequences that do not code for proteins are referred to as noncoding RNA, or ncRNA (Eddy 2001). Many of these ncRNA sequences have well-defined structures, and to understand how these ncRNA sequences perform their functions it is important to know their structure.

Determination of RNA structure is challenging. Primary structure is an ordered sequence of nucleotides. Secondary structure consists of canonical base pairs, i.e., AU, GC, and GU pairs. Secondary structure prediction involves predicting the base pairs that occur in a specified sequence of nucleotides. RNA tertiary structure is the three-dimensional arrangement of atoms. Because RNA structure is generally hierarchical, the secondary structure can be largely determined without knowing the tertiary structure (Tinoco and Bustamante 1999).

Many secondary structure prediction methods are available. The most accurate method is comparative sequence analysis (Pace et al. 1999), which determines base pairs conserved among homologous sequences. The method is highly accurate (Gutell et al. 2002) but requires a large number of homologous sequences and significant human insight, and thus is limited in use. When a single sequence is available, the most popular approach for structure prediction is to predict the lowest free energy structure with a dynamic programming algorithm (Zuker 2003; Mathews et al. 2004; Mathews and Turner 2006; Gruber et al. 2008).

A more recent approach to predict RNA secondary structures is called maximum expected accuracy structure prediction (Knudsen and Hein 2003; Do et al. 2006; Hamada et al. 2009; Lu et al. 2009). Roughly, maximum expected accuracy structures are structures composed of pairs that provide the maximal sum of pairing probabilities. The pairing probabilities can be derived by machine learning methods or by thermodynamic methods using partition functions. Maximum expected accuracy structures have improved accuracy compared with free energy minimization because it has been observed that highly probable base pairs are more likely to be correctly predicted pairs (Mathews 2004).

One important topology for RNA secondary structures is a pseudoknot. This is a type of secondary structure that contains nonnested base pairs. Specifically, a pseudoknot is defined by at least two base pairs, i–j and i′–j′, such that nucleotide i appears before i′, i′ before j, and j before j′ in the sequence. Base pairs in pseudoknots represent a small fraction of base pairs in known RNA secondary structures, but pseudoknots occur in a number of functional RNA sequences (van Batenburg et al. 2001; Condon and Jabbari 2009).

The prediction of secondary structures including pseudoknots is a difficult task. For example, the most popular dynamic programming algorithms for finding low free energy structures do not allow pseudoknots. This allows those dynamic programming algorithms to run quickly and scale well, i.e., O(N³) in time where N is the length of the sequence. Including pseudoknots in the structure prediction requires higher-order scaling, the use of heuristics, and/or a compromise on the energy model.

It has been proven that the prediction of lowest free energy secondary structures with pseudoknots is NP-hard (Lyngsø and Pederson 2000). In spite of this, a number of innovative and practical approaches have been developed to predict structures with pseudoknots. These approaches can roughly be summarized in six categories. One approach is to use a dynamic programming algorithm to predict structures with a limited topology (Rivas and Eddy 1999; Uemura et al. 1999; Akutsu 2000; Dirks and Pierce 2003; Reeder and Giegerich 2004). A classification of topologies and an explanation of topologies handled by several dynamic programming algorithms are available (Condon et al. 2004). A second approach to predicting pseudoknots is to construct structures using multiple iterations of algorithms that would otherwise not be capable of predicting pseudoknots (Ruan et al. 2004; Ren et al. 2005; Jabbari et al. 2008). One of these algorithms is also capable of using an alignment of multiple homologous sequences to improve its accuracy by finding a consensus structure (Ruan et al. 2004). A third approach is to either simulate a folding pathway or sample structures with a stepwise addition of helices (Abrahams et al. 1990; Gultyaev et al. 1995; Isambert and Siggia 2000; Dawson et al. 2007; Meyer and Miklos 2007). A fourth approach uses the maximum weight matching algorithm to construct structures composed of pairs that give a maximum score (Tabaska et al. 1998; Witwer et al. 2004). These algorithms use alignments of multiple homologous sequences and scoring functions that summarize free energies associated with pairs and covariation of pairs. Recently, a sixth approach, using constrained integer programming has also been applied to finding lowest free energy structures (Poolsap et al. 2009).

Many of the above algorithms use rules for predicting the free energy change—i.e., stability—of pseudoknots. Significant progress has been reported in this area as well using several approaches. Two sets of empirical rules were designed for use with dynamic programming algorithms (Rivas and Eddy 1999; Dirks and Pierce 2003). A set of parameters was developed using polymer theory and calibrated to experimentally measured stabilities (Wyatt et al. 1990; Nixon and Giedroc 1998; Theimer et al. 1998; Gultyaev et al. 1999; Theimer and Giedroc 1999, 2000). Another set of parameters was developed using lattice models and self-avoidant walks (Cao and Chen 2006, 2009). Additionally, a set of parameters was developed using polymer theory (Aalberts and Hodas 2005). A recent report provides a technique for refining parameters for predicting pseudoknot stability that utilizes experimental data and the database of sequences with known structure (Andronescu et al. 2010).

This contribution reports ProbKnot, a new RNA secondary structure prediction algorithm that is capable of predicting RNA secondary structures of any topology in O(N³) time. Base-pair probabilities are first predicted using a partition function (Mathews 2004), which does not include pseudoknotted structures, in O(N³) time (Xia et al. 1998; Mathews et al. 2004). ProbKnot then assembles a type of maximum expected accuracy structure in O(N²) time from the base-pairing probabilities, but does so without using a dynamic programming algorithm. By assembling structures from base-pair probabilities determined without pseudoknots, ProbKnot does not require a set of rules for predicting the stability of pseudoknots.

The performance of ProbKnot was benchmarked against other freely available programs that predict pseudoknots: pknotsRG-mfe (Reeder and Giegerich 2004), ILM (Ruan et al. 2004), and HotKnots (Ren et al. 2005); and programs that do not predict pseudoknots: MaxExpect, a maximum expected accuracy approach (Lu et al. 2009) and Free Energy Minimization (Mathews et al. 2004). ProbKnot was able to predict the largest fraction of known base pairs.

RESULTS

ProbKnot

ProbKnot is an algorithm that predicts RNA secondary structure by finding the structure with the most probable base pairs. It assembles structures composed of base pairs, i–j, where the probability of the i–j pair is higher than any i–k or j–k base pair, where k is any other nucleotide in the sequence. This is performed in O(N²) time by first calculating and storing the pairing probability of the most probable pair for each nucleotide, P_max(i). Then each base pair is considered for inclusion in the structure. If the probability of the i–j pair is equal to both P_max(i) and P_max(j), that pair is included in the structure. The algorithm is additionally capable of supporting multiple iterations in a similar manner by finding the most probable i–j pair for nucleotides that remained unpaired after previous iterations. For benchmarks shown here, only a single iteration was performed.

As a post-processing step, after the structure is obtained, the algorithm removes helices composed of two or fewer stacked base pairs. For these calculations, single nucleotide bulges are considered stacked and therefore do not interrupt helical stacking. So, for example, two pairs separated by a single bulged nucleotide would be considered stacked.

Structure prediction accuracy

The accuracy of ProbKnot was evaluated by predicting structures for sequences with known structure as determined by comparative sequence analysis. Both sensitivity and positive predictive value (PPV) were determined. Sensitivity is the percent of known pairs correctly predicted and PPV is the percent of predicted pairs in the known structure.

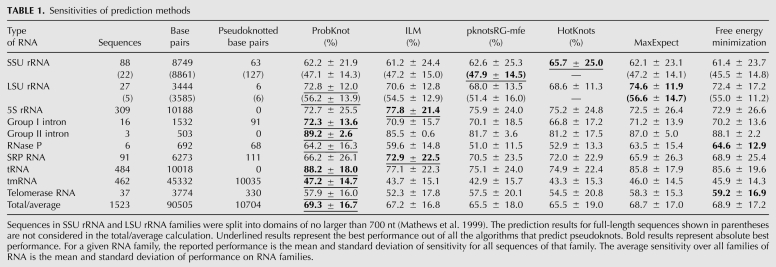
For a diverse set of sequences with known secondary structure, ProbKnot had an average of 69.3% sensitivity (Table 1). The performance was compared against three other programs that are capable of pseudoknot prediction and freely available for download. These programs were demonstrated to be among the top performers in structure prediction accuracy in a previous benchmark (Ren et al. 2005). The programs are ILM version 1.0 (Ruan et al. 2004), HotKnots version 1.2 (Ren et al. 2005), and pknotsRG version 1.3 (Reeder and Giegerich 2004). Each was run using default parameters. Additionally, the performance was compared against two other algorithms from RNAstructure, which predicts structures without pseudoknots, free energy minimization (Mathews et al. 2004), and maximum expected accuracy structure prediction (Lu et al. 2009). Overall, ProbKnot had the highest average sensitivity for all methods and the highest PPV among methods that are capable of predicting pseudoknots.

TABLE 1.

Sensitivities of prediction methods

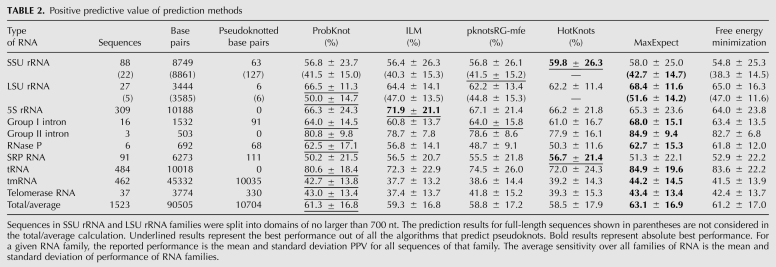
ProbKnot had an average PPV of 61.3% (Table 2), performing best in six out of 10 RNA families including two families with pseudoknots, and performing on the same level with pknotsRG-mfe on the group I intron family that is also known to have pseudoknots. This was the best performance among algorithms that predict pseudoknots, but not as high as MaxExpect, which does not predict pseudoknots. This is consistent with previous observations. Algorithms that predict pseudoknots consider a larger space of possible structures, which leads to a tendency for lower fidelity of structure prediction.

TABLE 2.

Positive predictive value of prediction methods

Pseudoknot prediction

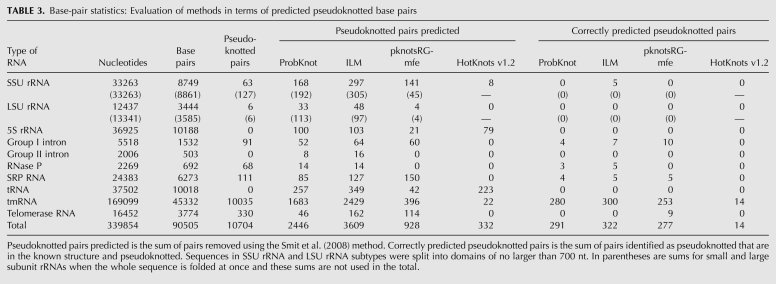
The accuracy of pseudoknot prediction was evaluated separately. First, the number of predicted pseudoknotted pairs was tabulated (Table 3). These pairs were found using the method of Smit et al. (2008) to identify the fewest pairs that need to be removed to remove the pseudoknots from a structure. The number of pseudoknotted pairs reported in Table 3 is the sum of the number of pairs that are removed to remove the pseudoknot. Then, the number of these predicted pseudoknotted pairs that are both in the known structure and pseudoknotted in the known structure was determined and reported as the number of correctly predicted pseudoknotted pairs (Table 3).

TABLE 3.

Base-pair statistics: Evaluation of methods in terms of predicted pseudoknotted base pairs

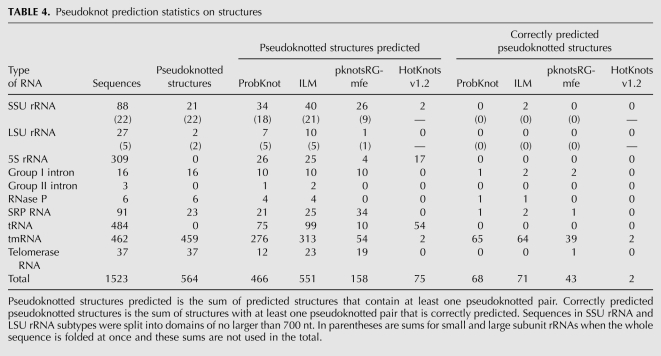
The accuracy of pseudoknot prediction for structures was also tabulated (Table 4). The number of predicted structures with pseudoknotted pairs was determined. The number of the predicted structures with pseudoknots that were correct was then tabulated as correctly predicted pseudoknotted structures. A predicted pseudoknotted structure was considered correct if it contained at least one correctly predicted pseudoknotted pair. For structures with multiple pseudoknots, such as tmRNA sequences, a structure can be considered correctly predicted if only one pseudoknot is correctly predicted.

TABLE 4.

Pseudoknot prediction statistics on structures

ILM has the highest number of correctly predicted pseudoknotted structures and the highest number of correctly predicted pseudoknotted base pairs. Of the predicted pseudoknotted pairs, pknotsRG-mfe has the highest portion of correctly predicted pairs. All algorithms, however, correctly predict only a small fraction of the pseudoknotted base pairs that are in the known structure.

Structure prediction example

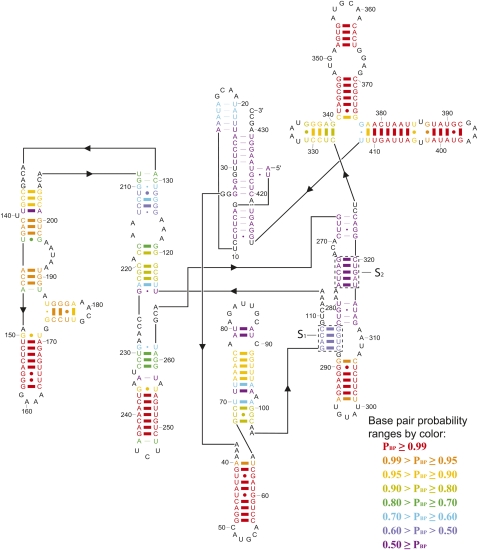
Figure 1 shows an example of predicted structure, the Tetrahymena thermophila group I intron structure predicted by ProbKnot. Thick lines between the base pairs represent correctly predicted pairs. As can be seen from Figure 1, ProbKnot correctly predicts almost all base pairs with probabilities >70%. Helixes S₁ and S₂ that form pseudoknots in the structure are correctly predicted by ProbKnot.

FIGURE 1.

Predicted secondary structure of group I intron from T. thermophila by ProbKnot. Thick lines represent correctly predicted base pairs; thin lines represent incorrectly predicted base pairs. The boxed helices, labeled S₁ and S₂, are the two helices that define the pseudoknot.

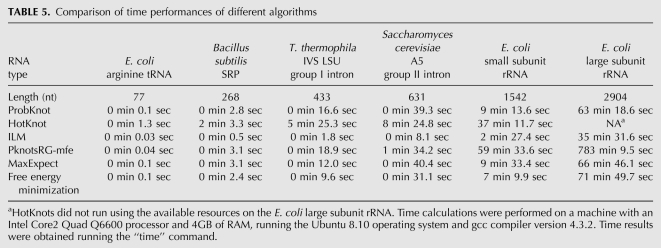
Time benchmarks

Time trials were performed on sequences ranging in length from 77 to 2904 nucleotides (nt) (Table 5). On the longest sequence, ProbKnot showed the second best time performance, requiring 63 min of runtime to predict both the base-pair probabilities and to assemble the predicted structure. ILM had the best time performance and the dynamic programming algorithm (pknotsRG-mfe) had the slowest time performance.

TABLE 5.

Comparison of time performances of different algorithms

DISCUSSION

ProbKnot assembles maximum expected accuracy structures using base-pairing probabilities determined from a partition function calculation. Previous approaches for predicting maximum expected accuracy structures used dynamic programming algorithms that do not allow pseudoknots (Do et al. 2006; Hamada et al. 2009; Lu et al. 2009), but ProbKnot is not limited in the topology of structures it can predict. Although the partition function algorithm does not account for pseudoknotted structures, each of the helices in the pseudoknot can occur in different structures (Mathews 2004). ProbKnot takes advantage of this fact to assemble both helices into a single structure.

ProbKnot has some similarities with the maximum weight matching (MWM) methods previously explored to find secondary structures conserved among multiple sequences (Tabaska et al. 1998; Hofacker et al. 2004). The MWM algorithm takes pairing weights as input, where weights are a function of folding free energy change and covariation, and outputs a structure with the greatest sum of these weights. MWM runs in O(N³) time and is also not limited in topology. It has been noted that MWM methods tend to have poor PPV because the structures are saturated with pairs, but post-processing can remove pairs and improve performance. ProbKnot is distinct because it uses pair probabilities and not folding free energy changes as input. Additionally, the requirement that the pairs included in the structure be the highest pairing probability for pairs possible by either nucleotide provides a stopping rule so that structures are not oversaturated with pairs.

Based on the benchmarks in Tables 1 and 2, ProbKnot has the highest average accuracy for RNA secondary structure prediction among algorithms that predict pseudoknots. It performs on average 2%–4% better in sensitivity and 2%–3% better in PPV. These improvements are considerable, but they leave room for improvement. For example, the average performance for structure prediction on tmRNA, with four pseudoknots, is only 47.2% in sensitivity.

The performance results for ProbKnot were also compared with the performance of two algorithms, MaxExpect (Lu et al. 2009) and free energy minimization (Mathews et al. 2004), which are unable to predict pseudoknots. This comparison was performed to evaluate the benefit for increasing the range of topologies predicted to include pseudoknots. In sensitivity, ProbKnot outperformed both algorithms by ∼0.5%–1%. This was expected because ProbKnot has a wider predicting range of possible topologies, and thus it should predict more correct base pairs than other algorithms. Because of the wider range of possible prediction topologies, however, there is wider latitude for incorrectly predicting base pairs and, because of this, PPV decreases compared with MaxExpect.

Given the poor performance of the methods benchmarked here on tmRNA and telomerase RNA, including ProbKnot, there is a need for continued research in predicting pseudoknotted structures. One possible approach for improving ProbKnot is to use a partition function that explicitly includes pseudoknots to predict the base-pairing probabilities. For example, the algorithm reported by Dirks and Pierce is O(N⁴) in time and includes a restricted set of pseudoknots (Dirks and Pierce 2003, 2004; Condon et al. 2004). These pair probabilities could be used by ProbKnot to assemble structures of any topology and may yield more accurate structures.

ProbKnot is available in the RNAstructure package (Reuter and Mathews 2010). This includes the source code in C++; text interfaces for Linux, Unix, and Windows; a JAVA graphical interface for Linux and Mac OS-X; and a graphical interface for Microsoft Windows.

MATERIALS AND METHODS

Prediction of base-pairing probabilities

Base-pair probabilities were predicted using a partition function algorithm that includes coaxial stacking (Mathews 2004). This program uses the thermodynamic parameters assembled by Xia et al. (1998) and Mathews et al. (2004) to predict the stabilities of secondary structures. Similar to Lu et al. (2009), the multibranch loop parameter bonus for each branching helix was not optimized as done by Mathews et al. (2004) but was kept at −0.6 kcal/mol, the value suggested by optical melting experiments (Diamond et al. 2001; Mathews and Turner 2002).

Accuracy

All algorithms were tested on 1550 RNA sequences from 10 different families: small subunit rRNA (Gutell 1994), large subunit rRNA (Gutell et al. 1993; Schnare et al. 1996), 5S rRNA (Szymanski et al. 1998), group I intron (Waring and Davies 1984; Damberger and Gutell 1994), group II intron (Michel et al. 1989), RNase P RNA (Brown 1998), SRP RNA (Larsen et al. 1998), tRNA (Sprinzl et al. 1998), tmRNA (Zwieb et al. 1999), and telomerase RNA (Chen et al. 2000). This database is an expansion of a database of structures assembled previously (Mathews et al. 1999) to include the telomerase RNA and the tmRNA, which are pseudoknotted RNA structures. Vertebrate telomerase RNA secondary structure alignments were obtained from the Rfam 9.1 database (Griffiths-Jones et al. 2003, 2005; Daub et al. 2008; Gardner et al. 2009). tmRNA secondary structures were obtained from the tmRDB database (Zwieb et al. 2003). Structures with unknown nucleotides were omitted from the full list of structures in the tmRDB database. Small and large subunit rRNA sequences were divided into domains of ≤700 nt as previously reported (Mathews et al. 1999).

The performance of secondary structure prediction algorithms was evaluated by calculating sensitivity and PPV. Sensitivity measures the percent of known base pairs correctly predicted:

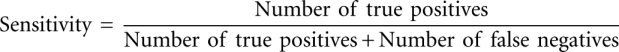PPV measures percent of predicted base pairs that are correctly predicted:

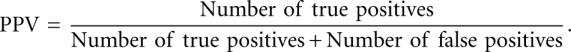Both sensitivity and PPV were evaluated with an allowance for incomplete knowledge of the exact pairing in the known structure. A predicted base pair between nucleotides i and j was considered correctly predicted if i was paired to j, j − 1, or j + 1, or if j was paired to i − 1 or i + 1 (Mathews et al. 1999). Average values were calculated per RNA family and then overall averages were calculated as the mean of the values reported for each family.

Tabulation of pseudoknot content

The number of base pairs in pseudoknots was counted using an implementation of the optimization approach of Smit et al. (2008) as implemented in the RNA class component of RNAstructure (Reuter and Mathews 2010). In this implementation, the scoring function is pairs, so the algorithm counts the fewest number of pairs that would need to be removed to remove the pseudoknot.