Social interactions, information use, and the evolution of collective migration

Abstract

Migration of organisms (or cells) is typically an adaptive response to spatiotemporal variation in resources that requires individuals to detect and respond to long-range and noisy environmental gradients. Many organisms, from wildebeest to bacteria, migrate en masse in a process that can involve a vast number of individuals. Despite the ubiquity of collective migration, and the key function it plays in the ecology of many species, it is still unclear what role social interactions play in the evolution of migratory strategies. Here, we explore the evolution of migratory behavior using an individual-based spatially explicit model that incorporates the costs and benefits of obtaining directional cues from the environment and evolvable social interactions among migrating individuals. We demonstrate that collective migratory strategies evolve under a wide range of ecological scenarios, even when social encounters are rare. Although collective migration appears to be a shared navigational process, populations typically consist of small proportions of individuals actively acquiring directional information from their environment, whereas the majorities use a socially facilitated movement behavior. Because many migratory species face severe threat through anthropogenic influences, we also explore the microevolutionary response of migratory strategies to environmental pressures. We predict a gradual decline of migration due to increasing habitat destruction and argue that much greater restoration is required to recover lost behaviors (i.e., a strong hysteresis effect). Our results provide insights into both the proximate and ultimate factors that underlie evolved migratory behavior in nature.

Migration is often an adaptive response to changes in resource availability, to escape from competition, and/or to reach newer habitats, etc. (1–8). To migrate, both uni- and multicellular organisms have evolved the ability to detect and respond to directional cues in the environment. This ability, in species such as passerine birds and in many groups of vertebrates and insects, may correspond to magnetoreceptivity (9), odor taxis (10), or tracking changes in resource distributions (11). In bacteria and cells, directional information may result from an ability to respond to thermal, chemical, or electromagnetic gradients (12).

It has been suggested that individual organisms can be seen as information processing units (13) and that interactions among organisms can provide collective benefits (14–20). For example, if each individual is error prone in its detection of the migratory direction, grouping may facilitate the spontaneous averaging of individual measurements, leading to improved navigation ability, a property known as the “many wrongs principle” (16). In many navigating groups, however, participants are mixed, such that nearby individuals who may share these potential benefits are of low relatedness. Even in migrating ungulates where family members often maintain cohesion, and can thus be thought of as a functional unit for selection, relatedness between nearby family groups can be low (21). It remains unclear, therefore, how individuals optimize tradeoffs between costs and benefits of migration and thus how, and under what ecological conditions, different migratory strategies evolve.

Here, we develop an individual-based, spatially explicit evolutionary model of organismal movement and social interactions and use this to investigate migratory strategies under a wide range of densities and cost-benefit structures that represent diverse ecological scenarios. We also explore how habitat fragmentation and changes in population density over relatively short ecological time scales, such as those induced by anthropogenic influence (22–24), may be expected to affect migratory behavior.

Model for the Evolution of Migration

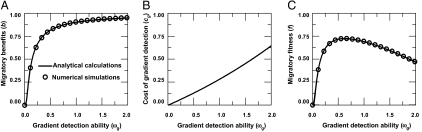
We take into account each individual's ability to obtain information about the appropriate migratory direction by exploiting environmental features such as orienting using geomagnetic field cues (9) or through a gradient detection process (10–12, 14). This is denoted by an evolvable parameter ω_gi (henceforth referred to as “gradient detection ability”), where i refers to the index of the focal individual. A solitary individual in the absence of such an ability, i.e., when ω_gi = 0, performs a random walk. As ω_gi increases, individuals travel probabilistically more accurately along the environmental gradient. Thus they accumulate migratory benefits, defined as the normalized distance traveled (1), or equivalently the velocity, in the migratory direction that asymptotically reaches a maximum value (Fig. 1A and SI Appendices A and B).

Fig. 1.

The optimum, or evolutionary stable, gradient detection strategy ω_gi for a solitary individual. (A) Comparison between numerical simulations and analytical calculations of migratory benefits, b, gained by a solitary individual (SI Appendix B). (B) Cost of gradient detection is given by c_g = p_g(exp(ω_g/ω_gc) − 1) and (C) comparison between numerical simulations and analytical calculations of the individual fitness (f = b − c_g). Parameters: size of population N = 1, p_g = 0.75, ω_gc = 4.0, strength of noise in perception σ_r = 0.1.

We assume that individuals incur costs that increase monotonically with their ω_gi (Fig. 1B) because of properties such as energy expenditure involved (25) and/or associated costs such as reduced predator vigilance during the gradient detection process. In particular, we assume an exponentially increasing cost due to ω_gi, but the specific form of the cost function chosen does not affect the qualitative nature of the results (see SI Appendices A, B, and C for details of model implementation and Appendix D for comments on generality with respect to cost function).

An evolvable “sociality” trait, denoted by ω_si, represents the possibility of social interactions (26), specifically, being attracted toward and aligning direction of travel with nearby individuals (17, 27). This can be facilitated by vision (and/or other sensory modalities) in insects and vertebrates or through more local mechanisms such as adhesion, contact forces, and/or chemical signaling in bacteria or cells (28). We assume that this ability comes at a cost that increases monotonically with ω_si.

Individuals move in a direction determined by the balance of their preference to travel along the migratory gradient and their social tendencies, by weighing them proportionately to the strength of their respective evolvable traits, ω_gi and ω_si (17). Depending on the value of these traits, individuals can exhibit a wide range of motion including random walk (low ω_gi and low ω_si), solitary migration (large ω_gi and low ω_si), formation and maintenance of aggregations (low ω_gi and large ω_si), and fission–fusion dynamics of migrating groups (e.g., large ω_gi and moderate to large ω_si). Consequently, they acquire a fitness corresponding to the migratory benefits minus the costs incurred. Individuals are assumed to reproduce with a probability proportional to their relative fitness and pass on their traits to their offspring with a small mutation rate (29) (SI Appendices A, B, and C).

Evolution of Migratory Strategies

Individuals optimize tradeoffs between the benefits of migration and the costs involved in the migratory gradient detection. For solitary individuals, the fitness does not depend on the strategy of other individuals; hence, the evolutionary stable strategy of the gradient detection ability is same as the value ω_g that optimizes the fitness (Fig. 1C and SI Appendix B).

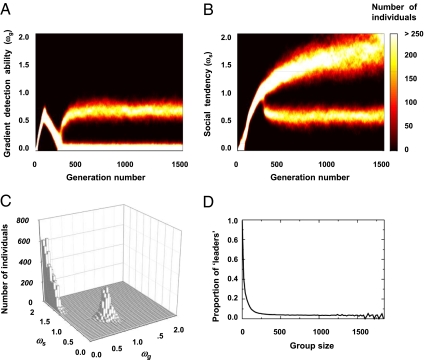
We now consider populations in which individuals may encounter each other. Under a very broad range of parameter conditions, we find that populations evolve two coexisting frequency-dependent strategies, with both the strategies being equivalent in terms of fitness (Fig. 2 A–C and SI Appendix D). In one mode, individuals have a relatively high gradient detection ability with a weak sociality trait (referred to as “leaders”). In the other mode, individuals have an extremely weak or nonexistent gradient detection ability and possess strong social interactions (referred to as “social individuals”) (Fig. 2C).

Fig. 2.

The evolution of collective migration. (A and B) The evolution of the gradient detection ability, ω_g, and sociality trait, ω_s, respectively. This result is largely independent of the initial conditions (SI Appendix C). (C) A 2D histogram of the evolved state at the 1,500th generation demonstrates the relatively small proportion of leaders (high, ω_g; low, ω_s) and a majority of social individuals (low, ω_g; high, ω_s). (D) The group composition is quantified by the proportion of leaders as a function of group size. Parameters: N = 16384, ρ = 7.0 × 10⁻³ individuals per BL², p_g = 0.75, cost of sociality p_s = 0.0 and σ_r = 1.00. The other parameter values are in SI Appendix A.

In this population, social individuals are locally attracted to each other and to leaders, forming groups. Leaders preferentially move in the direction of the gradient and are less influenced by others because of their relatively weak social tendency. Consequently, composite groups consisting of both social individuals and leaders emerge. Leaders tend to occupy frontal or peripheral positions, and the whole group typically acquires a directed motion up the gradient. We note that, to an observer, it would likely appear that all individuals are actively climbing the gradient.

As a consequence of this complex spatiotemporal dynamic, we see a fission–fusion process at the population level where groups constantly merge and split during the collective migration (as seen in many natural populations) (30; Movies S1 and S2). Couzin et al. (17) showed that the proportion of leaders needed to guide a group to the desired destination with a given accuracy decreases with increasing group size (17). Here, we reveal that this leadership principle emerges spontaneously in the evolved population through the dynamics of groups merging and splitting (Fig. 2D).

Density and Cost Structure

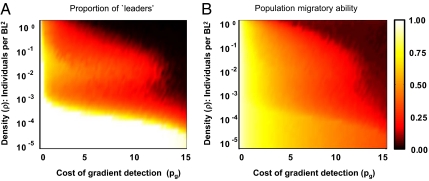
To test the generality of our results, we investigate the evolved states under a wide range of ecological scenarios (Fig. 3 and SI Appendix E). Notably, population density can determine, in large part, how often individuals encounter one another. The costs of gradient detection may be species- and/or environment-specific. Additionally, factors such as group size and/or spatial position in a group can influence the effective cost incurred by individuals. For example, individuals (typically leaders) who either tend to occupy frontal positions or travel alone (due to their weak ω_si and large ω_gi) may be more susceptible to predation (31) or pay higher energetic costs through increased vigilance (32). They might also fail to exploit socially facilitated environmental change, such as moving where others have trampled through vegetation, as in ungulates (33). Within our model, such species-specific details can be approximated by rescaling the effective cost incurred while performing gradient detection.

Fig. 3.

Evolved migratory strategies under different ecological conditions. (A) The proportion of leaders in, and (B) the migratory ability of, evolved populations as a function of density (ρ), and cost of gradient detection (p_g). Note that density is measured in units of individuals per BL⁻². Population migratory ability is defined as the migratory benefits averaged over all individuals in the population. (A) There is a clearly demarcated individual-migration state (bright region), a collective-migration state (yellow-red regions), and a no-migration state (dark region) with sharp changes in the proportion of leaders between these evolved migratory states. (B) Corresponding changes in population migratory ability is relatively gradual. The density is on a log-axis covering nearly five orders of magnitude and the collective migration state occurs for densities where the interactions between individuals are very rare. Parameters: N = 320, p_s = 1.0, and σ_r = 0.10. The other parameter values are in SI Appendix A.

We begin by exploring the evolved migratory strategies as a function of density (ρ) and gradient detection cost (p_g) but for a fixed and relatively small value of social cost (p_s). In extremely low-density populations, where the probability of encountering others is negligible and/or when it is inexpensive to evolve the gradient detection ability, we find that all individuals use a relatively large gradient detection ability (i.e., all are leaders) (bright region in Fig. 3A). Leaders in these evolved populations have extremely weak or no sociality, unlike those in Fig. 2A, because of costs associated with social interactions. As a result, we find solitary migration. At the other extreme, when densities are so high that frequent collisions among individuals inhibit migration and/or when the gradient detection is very expensive, no member of the population evolves to use gradient information leading to resident (i.e., nonmigratory) populations (Fig. 3 A and B, dark regions).

There is, however, a very large intermediate region of parameter space where leaders and social individuals coexist and populations exhibit collective migration (Fig. 3A, yellow-red region). We note that collective migration evolves even at very low densities where individuals rarely interact, such as one individual in 1,000 BL² units, where BL is the typical body length. Thus, even for species that are not considered traditionally to migrate collectively, social interactions may still play an important role.

The costs of social interactions (p_s) may typically be relatively small because they are facilitated by an already necessary machinery, such as vision, or physical forces, such as contact/friction (28). However, larger group sizes can lead to increased competition for resources among group members. These features can be included by rescaling the cost of sociality; for example, p_s is larger when the competition for resources is high. In SI Appendix E, we show evolved migratory strategies for a range of gradient detection (p_g) and social costs (p_s). Depending on the value of these costs relative to the migratory benefits, we find three qualitatively different migratory states of solitary migration (zero to moderate p_g and small to high p_s), resident populations (high p_g), and collective migration (a large intermediate region, as in Fig. 3).

Context-Dependent Interactions

Thus far, we assumed that individuals use the same strategy at all times within a generation. We now consider more intricate and dynamic strategies; individuals might be able to modify their interaction rules either probabilistically or depending on certain local contexts. For instance, to avoid being exploited by social individuals, and/or to exploit others with gradient detection ability, an individual may not perform gradient detection when the local condition is crowded, despite possessing a very high gradient detection ability (ω_gi). This can be facilitated by a quorum sensing ability in cells or microorganisms (34) or, more generally, as a consequence of responding to the state of the local environment. Even under such scenarios, we find that the frequency-dependent coexisting strategies of leaders, who use gradient detection almost all of the time, and social individuals, who very rarely do, remains evolutionarily stable (SI Appendices F and G). In other words, migratory individuals in our model do not evolve context-dependent interactions even when given the possibility to do so.

Impact of Environmental Pressures

Anthropogenic pressures can significantly influence population density, as seen in the steep decline of American bison (Bison bison), and even result in extinction, as occurred with passenger pigeon (Ectopistes migratorius) (1, 22–24). This is despite empirical studies that provide evidence for rapid microevolutionary changes in migratory patterns, for example in birds, within decadal time scales (1, 35, 36). Here we investigate the impact of habitat fragmentation and changes in population density on migratory strategies.

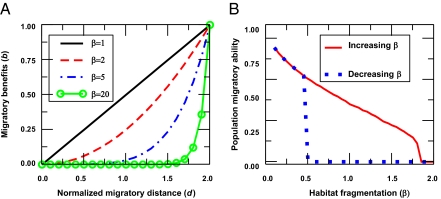
In migratory species, as habitat fragmentation increases, individuals have to travel disproportionately larger distances to reach suitable habitats [because of, for example, a reduced frequency of encountering stop-over or refueling sites (1)] and thus to accumulate migratory benefits. We implement this by assuming that the benefit b is a nonlinear function of the average distance migrated d, i.e., b = d^β (0 ≤ d ≤ 1), where β is a degree of fragmentation with β = 1 corresponding to a contiguous habitat. The larger the value of β, the larger the nonlinearity, and, hence, the organism must cover longer migratory distances to gain benefits (Fig. 4A); a highly nonlinearity, for example, may correspond to the need of some bird species to reach distant, localized breeding grounds. We introduce small changes in the habitat fragmentation (β) and allow adaptation of traits, ω_gi and ω_si, for a small number of generations, n_g, to account for the relatively short ecological time scales. This is in contrast to our previous focus on robust evolutionary stable states that could not be invaded by other mutant strategies and that are often reached only on long evolutionary time scales. We also study how our results are affected by different values of n_g.

Fig. 4.

The microevolutionary response of migratory strategies to habitat fragmentation. (A) Benefits, b, as a function of distance migrated, d, for different degrees of habitat fragmentation (β):b = d^β. (B) The solid line shows response to increasing habitat fragmentation (i.e., increasing β, starting from β = 1). The dotted line shows response to habitat restoration (i.e., decreasing β). Here, N = 320, n_g = 300, p_g = 1.0, p_s = 1.0, ρ = 9.0 × 10⁻⁴ individuals per BL², σ_r = 0.1. The parameter values are in SI Appendices A and H.

We find that, in habitats that fragment, the resulting ability of the population to migrate reduces relatively gradually (Fig. 4B, solid line). At high levels of habitat fragmentation, no individuals evolve to be leaders, and therefore, the population loses its migratory ability. Even after restoring the habitat, however, a population's migratory ability does not recover at the same habitat quality at which it declined; i.e., it shows strong hysteresis, or memory, effects (Fig. 4B, dotted line). In highly fragmented habitats, a small mutation in ω_gi that mildly alters the information use does not improve the individual's fitness; it requires large mutations in ω_gi, exceeding a threshold, to sufficiently enhance the information use and thus migratory benefits that exceed the costs incurred (in ω_gi). Large mutations, however, typically do not occur on relatively short ecological time scales. Upon substantial habitat restoration, the required threshold change in the information use reduces and can be reached by mutations occurring on ecological time scales and hence migratory ability is reestablished (SI Appendix H).

We also find hysteresis effects, although less pronounced, as a function of population density. These results are quantitatively, but not qualitatively, affected by various choices of n_g, representing different rates of change of ecological conditions; more specifically, the faster the rate of change of ecological conditions, the lower the probability of large mutations and thus the stronger the hysteresis effect (SI Appendix H). Note that we do not include an explicit habitat structure where fragmentation is measured, for example, by the extent of patchiness in the resource availability. Instead, we approximated a plausible impact of habitat fragmentation on migratory individuals by assuming that benefits are a nonlinear function of the distance traveled. Also, our focus was on the microevolutionary response of migratory strategies to ecological changes but not the growth and decline/extinction of populations themselves. Our model framework, however, can potentially be useful in investigating combined effects of adaptive migratory strategies together with the density-dependent growth and mortality of populations.

Discussion

Our model predicts that individuals who invest in acquiring information about the migratory direction from environmental cues are readily exploited by others who adopt a socially facilitated movement behavior. For a wide range of biological assumptions, these two coexisting strategies result in collective migration with fission–fusion process. Furthermore, even when interactions among organisms are very sparse and would typically be considered insignificant, we find that social interactions play an important (and perhaps hitherto unknown) role.

Collective migration occurs also when all individuals of a population evolve to use both the migratory directional information and social cues. Migrating groups in these evolved populations preserve their group composition over relatively long time scales. However, this strategy is expected to occur only when the costs of gradient information use and sociality are both negligibly small in comparison with the benefits of migration. We also emphasize general predictions of our model, that the ecology of species, represented by population density, habitat structure, costs, and benefits of migration, determines whether populations will evolve to a resident, a solitary migratory, or a collective migratory strategy.

Although a precise quantification of costs and benefits of information can be difficult, we suggest that evidence for (or the lack of) a bimodal, or other such strongly skewed, population structure in information use, as suggested here, will provide insights to underlying selection forces. The existence of such hierarchical structure among organisms may be deduced through an analysis of individuals’ trajectories during migration such as may be possible by visual tracking of identifiable cells or GPS tracking of higher organisms (37). We note that recently it has been possible to record brain activity in free-flying birds (38), suggesting that the study of the use of specific brain regions during migration may be possible in the future. In addition, recent advances in our understanding of how cells infer, and respond to, the state of its environment and quantification of associated fitness (39, 40) make cellular systems an attractive candidate for testing our model predictions. Other drivers of migration, which are not mutually exclusive with our hypothesis, include predators, competition, and/or disease avoidance (1–8). As we discussed previously, these can be incorporated by rescaling the costs and benefits of gradient climbing in our framework and/or by making species-specific modifications to our model.

Climate change and habitat destruction can dramatically alter the migratory patterns; for example, migratory species may become resident [e.g., blackcaps (Sylvia atricapilla); ref. 36], or lost migration can reappear [e.g., eastern house finch (Carpodacus mexicanus); ref. 41]. Using our model, we predict a gradual decline of migratory behavior because of habitat destruction, but, owing to relatively short time scale of these changes, the reestablishment of lost behaviors will require substantially greater restoration. Our study shows that the time scales of ecological changes play a crucial role in determining the response of migratory species.

At a certain level of description, leaders who migrate by investing in costly directional information, and social individuals who navigate by following others’ motion, can be mapped onto mean-field, discrete-strategy models that exhibit producer–scrounger (PS) dynamics (42, 43), where producers and scroungers are similar to leaders and social individuals, respectively. In contrast to PS models, our approach provides a mechanistic basis for scaling from individual-level description to higher levels of organizations and how it feeds back to local interactions. For example, it allows us to capture the role of nonlinear and emergent collective properties of socially navigating groups, such as the many wrongs principle (SI Appendix D), and that the proportion of leaders needed to guide migratory groups in the desired direction reduces with the group size (Fig. 2D). Additionally, we are able to provide testable predictions regarding the spatiotemporal dynamics and the composition of migratory groups (Movies S1 and S2). Furthermore, our approach allows us to study intricate aspects of fixed vs. context-dependent strategies (SI Appendices F and G) and the implications of environmental structure on the evolution of migratory strategies on both evolutionary and ecological time scales (Figs. 3 and 4).

Here, we focused on the phenomenon of migration with a constant global gradient that leaders could detect with relatively small errors. Would our results continue to hold when gradients/stimuli exhibit complex stochastic spatiotemporal variations? We note that novel collective navigational and search properties may arise depending on the nature of social interactions and the environmental noise (14, 44). Future studies can reveal the role of such emergent collective properties and stochasticity in an evolutionary context.

Linking patterns of aggregation to their function is a question of fundamental importance in biology. Our study offers insights about the adaptive significance of social cues in migratory behavior on both evolutionary and ecological time scales. Our results also have broader implications for studies on the evolution of taxis and/or foraging strategies in complex fluctuating environments. More generally, it provides a useful framework to investigate the evolutionary forces that drive collective behavior over a wide range of spatial and temporal scales.

Materials and Methods

Movies S1 and S2 show spatiotemporal dynamics of the evolved population of Fig. 2. SI Appendix provides further details on the model implementation and generality of our results. It contains the following subsections: SI Appendix A, details of model implementation; SI Appendix B, evolutionary stable strategy, or optimal strategy, for a single individual; SI Appendix C, evolutionary simulations for populations; SI Appendix D, the evolution of bimodal strategies and generality with respect to cost function; SI Appendix E, evolutionary outcome as a function of cost of gradient detection and cost of sociality; SI Appendix F, a model in which individuals can use their strategy probabilistically; SI Appendix G, a model in which individuals can use their strategy in a context-dependent way; SI Appendix H , the microevolutionary response of migration to habitat fragmentation and changes in population density.