Scalable Analysis of Flow Cytometry Data using R/Bioconductor

Abstract

Background

Flow cytometry is one of the fundamental research tools available to the life scientist. The ability to observe multi-dimensional changes in protein expression and activity at single-cell resolution for a large number of cells provides a unique perspective on the behavior of cell populations. However, the analysis of complex multi-dimensional data is one of the obstacles for wider use of polychromatic flow cytometry.

Methods

Recent enhancements to an open-source platform - R/Bioconductor - enable the graphical and data analysis of flow cytometry data. Prior examples have focused on high-throughput applications. To facilitate wider use of this platform for flow cytometry, the analysis of a dataset, obtained following isolation of CD4⁺CD62L⁺ T cells from Balb/c splenocytes using magnetic microbeads, is presented as a form of tutorial.

Results

A common workflow for analyzing flow cytometry data was presented using R/Bioconductor. In addition, density function estimation and principal component analysis are provided as examples of more complex analyses.

Conclusions

The compendium - in the form of text, supplemental R scripts, and supplemental FCS3.0 files - presented here is intended to help illuminate a path for inquisitive readers to explore their own data using R/Bioconductor.

Introduction

Cellular function and phenotype is governed by the expression and activation of intracellular and cell membrane proteins. Flow cytometry is a powerful experimental platform that allows for measuring the abundance and activation state of proteins at single cell resolution [1]. There is an increasing appreciation for how flow cytometry can be used to provide prognostic information by identifying rare cell subsets and to provide greater resolution into protein patterns responsible for heterogeneity in cellular response [2, 3]. In addition, developing low cost flow cytometry equipment for use in developing countries (e.g., [4]) requires low cost software for state-of-the-art analysis of the data. As flow cytometry experiments increase in complexity (i.e., increase the number of parameters measured per cell), more sophisticated tools for data analysis become necessary [5]. In fact, one of the main obstacles for complex multicolor analyses is data processing and proper interpretation [6]. Automated processing algorithms have been proposed to facilitate processing of large complex datasets [7]. However, processing of flow cytometry data is still largely performed manually. To help overcome this obstacle for small-scale flow cytometry experiment, the objective of this document is to illustrate a typical workflow for processing and analyzing flow cytometry data using a new open-source platform for data analysis: Bioconductor.

Bioconductor [8], a free open-source platform built upon the statistical freeware package R [9], provides an economical alternative to other commercial platforms. R is a system comprising a scripting languange and a simulation environment for statistical analysis and data graphics. The R system provides an extensive array of pre-built statistical analysis tools to support applications developed in Bioconductor. Bioconductor was developed as an open source and open development software project for the analysis and comprehension of biological data, with a heavy emphasis to date on genomic data [10]. Applications of the existing algorithms to flow cytometry data is a recent addition to the platform [11, 12, 13]. The novelty of the software and the associated learning curve may present a significant hurdle for wider acceptance of this technology. A tutorial is a common method allowing inquisitive potential users the ability to explore the capabilities of new bioinformatics software. In the following sections, processing of flow cytometry data obtained following isolating a CD4⁺CD62L⁺ T cell population from mouse splenocytes using magnetic microbead sorting provides a concrete example for data analysis using Bioconductor. In the spirit of reproducible research [14], a compendium, including embedded R scripts, is included as supplemental material to encourage readers to explore the dataset themselves.

Methods

Mice

Eight to 12-week old female Balb/c mice were obtained from Hilltop Lab Animals (Scottsdale, PA). Mice were housed in sterilized microisolator cages in the university vivarium, and facility sentinel animals were regularly screened for specific pathogenic agents. These studies were conducted in accordance with all federal and institutional guidelines for animal use and were approved by the West Virginia University Animal Care and Use Committee guidelines.

Antibodies and reagents

BD Phosflow Lyse/Fix buffer and FcBlock were purchased from BD Biosciences (San Diego, CA). The CD4⁺ CD62L⁺ T cell isolation kit was purchased from Miltenyi Biotec (Auburn, CA). FITC-conjugated rat anti-mouse CD4 (GK1.5), PE-conjugated rat anti-mouse CD44 (IM7), and APC-conjugated rat anti-mouse CD62L (MEL-14) were purchased from eBioscience (San Diego, CA). Unless otherwise noted, all cell cultures were maintained at 37° C in 5% CO₂ in RPMI 1640 plus supplements (referred to as complete RPMI or cRPMI). The RPMI supplements were 10% heat-inactivated fetal bovine serum (FBS) (Hyclone, Logan UT), 2 mM of l-glutamine (Medtech Inc., Herndon VA), 50 mM HEPES (Sigma Chemical, St. Louis, MO), 49 μM β-mercaptoethanol (Sigma Chemical) and 100 μg/ml of streptomycin and 100 U/ml penicillin (Hyclone).

Naïve CD4+ T cell isolation

Spleens from Balb/c mice were isolated and a cell suspension was made by mashing the spleens through a nylon screen. Following lysis of red blood cells using tris ammonium chloride, the cells obtained were pooled, and washed twice in cRPMI containing 1.5% FBS. Mouse splenocytes were resuspended at 2.5×10⁸/ml. Unpolarized CD4⁺CD62L⁺ (i.e., naïve) T-cells were subsequently isolated through negative selection by automated magnetic cell sorting, following the manufacturer’s instructions (Miltenyi Biotec, Auburn, CA). Briefly, mouse splenocytes were enriched for CD4+ T cells by negative selection through indirect magnetic labeling of non-CD4+ T cells using a cocktail of biotin-conjugated monoclonal anti-mouse antibodies against CD8a, CD45R, CD11b, CD25, CD49b, TCRγ/δ, and Ter-119 and magnetic microbeads conjugated to monoclonal anti-biotin antibody. CD4⁺ CD62L⁺ T cells were subsequently enriched from CD4⁺ splenocytes by positive selection using magnetic microbeads conjugated to a monoclonal rat anti-mouse CD62L antibody. Enrichment for CD4⁺ CD62L⁺ T cells was confirmed by flow cytometry using anti-CD4, anti-CD62L, and anti-CD44 antibodies.

Flow Cytometry

Unsorted splenocytes and isolated naïve CD4+ T cells were prepared, as describe above, and stained with fluorophore-conjugated antibodies specific for the mouse T cell markers CD4, CD62L, and CD44. For extracellular staining, single cell suspensions were washed with ice-cold PBS containing 1% FBS and 0.2% sodium azide (Sigma-Aldrich Chemical Co) (PBSaz) and then incubated with purified rat immunoglobulin and purified mouse immunoglobulin (BD Biosciences) for 30 min on ice to prevent nonspecific binding. Subsequently, the cells were washed, incubated with buffer containing the appropriate antibody reagent for 30 min on ice. The cycle was repeated for any additional antibodies. Finally, the cells were washed twice in PBSaz, fixed in 0.4% paraformaldehyde, and analyzed using a FACSAria flow cytometer (Becton Dickinson). The fluorescent intensity for each parameter was reported as a pulse area using 18-bit resolution. Single stain controls were used to establish fluorescent compensation parameters. Unstained cells were used as negative controls. Flow cytometry data was analyzed using Bioconductor 2.2, a package implemented in R 2.7.2. The results are representative of three independent experiments.

Results and Discussion

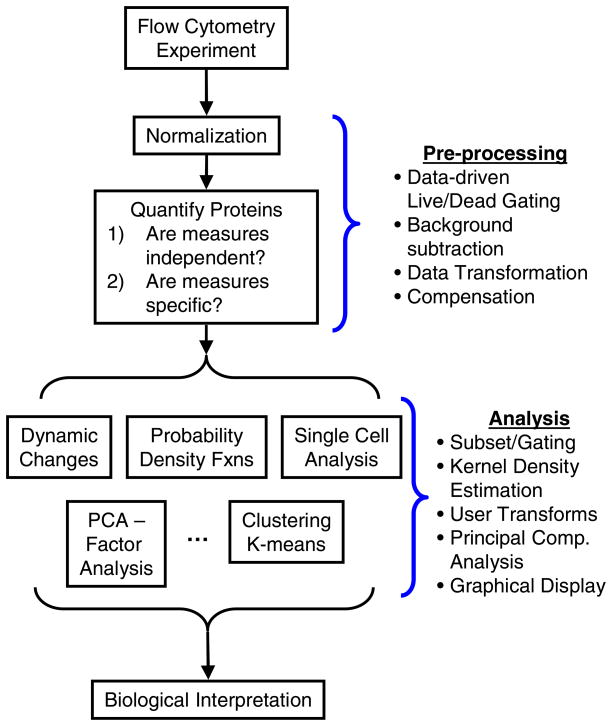
The workflow for data analysis in a typical flow cytometry experiment has evolved with recent technological advances [15] and can be grouped into two key steps, as summarized in Figure 1. First, a pre-processing step was required to ensure that the observed levels of fluorescence were independent and specific measures of the level of expression of the protein of interest, assuming that the antibodies also exhibit specificity. In this study, expression of CD4, CD44, and CD62L were used to characterize the efficiency of CD4⁺CD62L⁺ T cell isolation from Balb/c splenocytes using magnetic microbeads. The second step involved analysis of the cell populations including gating using statistically-based data-driven gates, estimating probability density functions using kernel marginalization, and clustering using principal component analysis.

Figure 1.

Overview of the steps associated with the use of flow cytometry as a tool in biological research. This manuscript will focus on how Bioconductor can be used during pre-processing and analysis steps.

Installation

Following installation of R [9], basic Bioconductor packages and additional packages that are required to process flow cytometry data were downloaded from the web within R using:

>source(“http://www.bioconductor.org/biocLite.R”)
>biocLite(“flowCore”)
>biocLite(“flowViz”)
>biocLite(“flowUtils”)
>biocLite(“geneplotter”)
>openVignette()

Additional Bioconductor packages may also be downloaded directly from the website [8]. Additional R packages can be installed using a menu option in the RGui (see ‘Packages’->‘Install package(s)’). These files need to be downloaded and installed only once. Subsequent sessions can reload the packages using library(“package”).

Pre-processing

Data Entry

The experimental results were exported from the flow cytometer in FCS3.0 format [16] (e.g., foo.fcs) following data acquisition. The default working directory is the installation directory for R. It may be more advantageous to change the directory to a working directory (see ‘File’->‘Change dir’) where the foo.fcs files are stored. Following the definition of an array, fclist, that contains the names of the FCS3.0 files to be analyzed, the data files were loaded into the R workspace using a single command:

>fs <-read.flowSet(fclist, transformation = FALSE)

A summary of the loaded flowSet can be shown by typing the variable name at the command line:

>fs
A flowSet with 9 experiments.
column names:
FSC-A SSC-A FITC-A PE-A APC-A Time

The information contained within a particular experimental data set (i.e., one fcs file) were read and stored in a flowFrame. A flowFrame is the name of a meta-object, a digital construct that collects different types of information (i.e., text and numerical data) into a common identifier. A series of flowFrames can also be collected in a flowSet. Different functions (e.g., phenoData() or exprs()) can be used to extract information from these meta-objects, such as the measured fluorescent intensities of the different parameters for each cell and the time that each cell was observed. As the filenames were not descriptive, a list of title names, shown in Supplemental Tables 1 and 2, was created for use in subsequent figures.

Gating on Forward Scatter and Side Scatter

Non-cellular debris and dead cells exhibit non-specific staining. These potentially confounding observations were eliminated by gating on forward scatter and side scatter to help ensure that the fluorescent measurements exhibit specificity for the target of interest. The gates associated with isolating live splenocytes were initialized as follows. First, cells were retained that had Forward Scatter areas between 50,000 and the maximum intensity using a 1-dimensional gate applied to the Forward Scatter parameter. Second, the Forward Scatter and Side Scatter parameters were used to create a data-driven gate (norm2Filter) that was centered at the median of the specified cell populations in both dimensions and enclosed a region that included 95% of the population (i.e., 2 standard deviations). Additional data-driven gates can also be used (e.g., kmeansFilter, a data-driven filter that performs one-dimensional k-means clustering), especially for the subsequent analysis step. Further refinement of the gates was achieved by combining individual gates using logical arguments. The logical arguments are applied right to left and combined using ! (NOT), — (OR), and & (AND). The gates were applied to the entire flowSet, although they can also be applied to individual flowFrames. The statistics associated with gating were calculated to determine the number of cells retained for subsequent analysis (see Supplemental Table S-1). The results of the gating on the forward and side scatter characteristics of the splenocytes are shown in Supplemental Figure S-1. The live cells are shown in blue using a contour overlay that indicates the density of the spots. A dot plot of the rejected cells were superimposed on the figures and shown in red.

Compensating for Fluorescent Spillover

Given the difficulty of determining appropriate compensation values ‘on-the-fly’, the current generation of flow cytometers incorporate two advancements for the analysis of flow cytometry data. First, contemporary software drivers for flow cytometers include an algorithm for automatically calculating the fluorescent compensation matrix. Second, raw data is uncompensated providing the opportunity to adjust compensation values after data collection. The initial estimate for the compensation matrix was extracted from the text description of MACSPurity_Tube_001.fcs. This initial estimate of the compensation matrix was based upon prior experiments and was used to observe the data during acquisition. To illustrate compensation using R/Bioconductor, it was not optimized.

  FITC-A PE-A APC-A
[1,] 1.000  0.12 0.00
[2,] 0.018  1.00 0.00
[3,] 0.003  0.00 1.00

To illustrate how the compensation matrix can be refined at any time following data acquisition, unstained and single-stained controls were used to estimate the compensation matrix. The adjusted compensation matrix, expressed in terms of a fraction of the primary signal and shown below, was used to modify the fluorescent measurements.

>fij
FITC-A PE-A APC-A
[1,] 1.004  −0.123 −0.014
[2,] −0.032 1.004 0.000
[3,] 0.000  0.000 1.000

This adjusted spillover matrix, fij, was calculated as follows. Fluorescent spillover of the primary parameter into secondary parameters was assumed to be linear function of the primary parameter. The observed parameters (O_ij) were linearly combined using

$$T_{ij}=O_{i1}·f_{1j}+O_{i2}·f_{2j}+O_{i3}·f_{3j}$$ (1)

to estimate the true fluorescent intensity (T_ij) for parameter j in experiment i, where f_kj is the fraction of parameter k that spills over into parameter j. Upon rewriting Equation (1) in matrix notation and re-arranging the terms, the spillover matrix, F, was estimated from the single stain controls using

$$F=O^{-1}·T$$ (2)

by assuming that the observed intensities in the primary parameters provide an estimate of the true fluorescent intensities (i.e., T_ij=O_ij if i=j else T_ij=0). The matrix of the observed intensities (i.e., O) summarized the median values obtained from the single-stain experiments. Prior to calculating the median values, the background fluorescence was subtracted from the raw values. The background fluorescence, corresponding to the median intensity of an unstained parameter, was obtained from the unstained and single-stain experiments (see Supplemental Table S-2).

One of the challenges with single-stained controls is that the cell population used for the experiment may be heterogeneous (e.g., splenocytes) and may bias the estimate of the median. Partitioning the singly-stained cells into high and low expression groups via a kmeansFilter was used to improve the estimate of O.

Linear-Log Data Transformation

A logarithmic transform is a common approach used to cope with the wide dynamic range of the fluorescent measurements obtained by flow cytometry. However, fluorescent compensation and subtraction of background fluorescent creates negative values. Plotting data on logarithmic axes truncate the negative values and can lead to incorrect assessment of the compensation for fluorescence spillover [17]. Various alternative methods for displaying fluorescent values have been proposed [17, 18, 19]. A common theme for these different solutions is to use a transform that is linear around zero and non-linear in other regions. In the following section, a simple data transformation is implemented.

Similar to a recent transform proposed by Battye [19], one of the simplest data transformations is to convert the raw data using a linear relationship at lower values and a logarithmic relationship at higher values:

$$\widehat{Y}=\{\begin{array}{cc}{M}_{\mathit{linear}}·(X_{\mathit{raw}}-b)& if{X}_{\mathit{raw}}<\mathit{transition}\\ {log}_{10}(M_{log}·(X_{\mathit{raw}}-b)& if{X}_{\mathit{raw}}\ge \mathit{transition}\end{array}$$ (3)

where Ŷ is the transformed “parameter intensity” and X_raw is the raw fluorescence value. A smooth transition between these two relationships is ensured by setting the values and the slopes of the linear and logarithmic relationships equal at the transition point. These two constraints provide sufficient information to determine values for the two unknowns: M_linear and M_log. In addition, we can add an additional constraint that the transformed variable must equal zero when the raw variable equals zero. This shifts the transformed variable for both the linear and logarithmic relationships by −b. Prior implementation of this split scale transform required specifying five parameters. Implementing this split scale transform in R/Bioconductor required specifying two values: the median of the untransformed population and the distance (dist) in raw data units between the median adjusted values and the transition point. This relationship was encoded as a function to be reused multiple times within the script:

>linlogTransform = function(transformationId, median = 0, dist = 1, …) {
+  tr <- new(“transform”, .Data = function(x) {
+  idx = which(x <= median + dist)
+  idx2 = which(x > median + dist)
+  if (length(idx2) > 0) {
+   x[idx2] = log10(x[idx2] − median) − log10(dist/exp(1))
+  }
+  if (length(idx) > 0) {
+   x[idx] = 1/dist * log10(exp(1)) * (x[idx] − median)
+  }
+  x
+  })
+  tr@transformationId = transformationId
+  tr
+ }

The transforms were applied to the measured fluorescent values. The transition value was held constant for all of the parameters at a value of 100. The resulting transformed values are deposited within the flowFrame in a new parameter. Finally, confirmation of the appropriate compensation for fluorescence spillover is shown in Supplemental Figure S-2. Together, these pre-processing steps ensured that the parameter intensities were independent and specific measures of the corresponding levels of protein expression, assuming antibody specificity.

Analysis

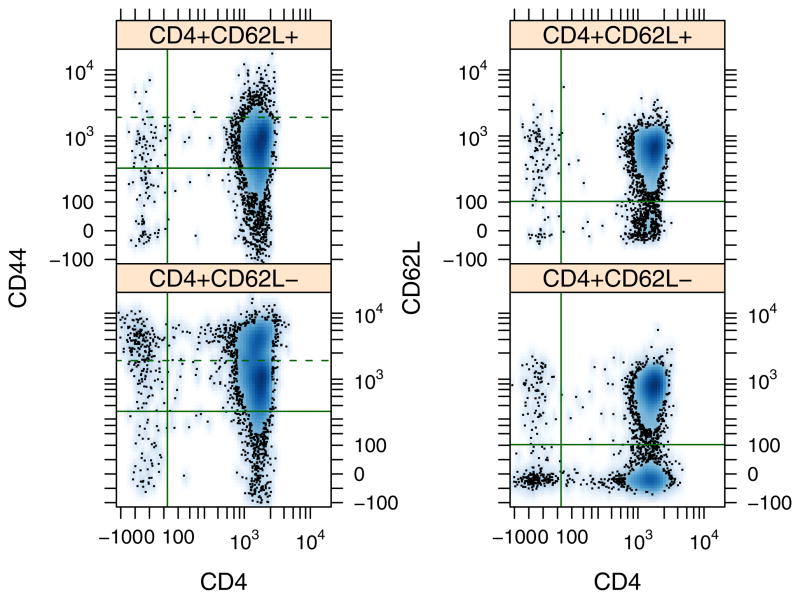
As highlighted in Figure 1, subsequent data analysis can take multiple paths depending on the research question. To illustrate one path using R/Bioconductor, flow cytometry was used to demonstrate the efficiency of cell sorting using magnetic microbeads. Enrichment of a CD4⁺ CD62L⁺ T cell population from mouse splenocytes involve two main steps: enrichment of a CD4⁺ subset using negative selection and subsequent enrichment of a CD4⁺CD62L⁺ subset using positive selection. Five aliquots were obtained from the pre-sort population and after each stage of the isolation protocol: pre-sort, CD4⁺, CD4⁻, CD4⁺CD62L⁺, and CD4⁺CD62L⁻. Expression of CD4, CD62L, and CD44 within these groups is shown in Figure 2 and Supplemental Figure S-3.

Figure 2.

Pairwise density plots for CD4, CD62L, and CD44 expression shown separately for aliquots obtained from CD4⁺CD62L⁺, and CD4⁺CD62L⁻ fractions. Each panel corresponds to a particular pair: CD44 versus CD4 (left panel) and CD62L versus CD4 (right panel). The solid lines indicate the expression threshold for a cell to be associated with positive expression. Ninety five percent of the unstained cell fraction was contained below the threshold. The dotted line indicates the upper limit of CD44 expression for 95% of the CD4⁺CD62L⁺ fraction.

To calculate statistics for the aliquots, a statistically-based data-driven threshold was used define whether a cell was positive for expressing the protein of interest. The threshold was defined as the level of expression for which 95% of the unstained cells exhibited a lower level of expression. As an alternative, a Bayesian framework could be used for gating such that the gate could be refined based upon new data. In practice, classification of a cell into a subset can be obtained by calculating the ratio of the marginalized density of a particular aliquot relative to the marginalized density of a negative control population at a given level of parameter intensity [20]. The disadvantage of this approach is that the particular parameter intensity used for gating would depend on each aliquot.

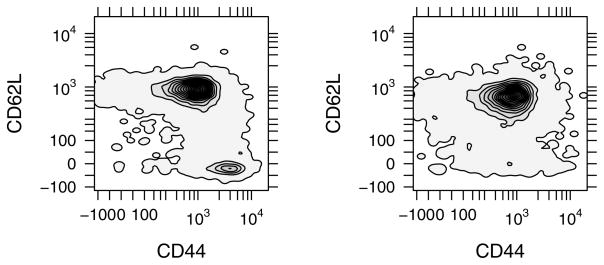
As shown in Table 1, magnetic bead enrichment from the starting population of Balb/c splenocytes was used to obtain a population of cells that were >98% positive for CD4⁺ and >90% positive for both CD4⁺ and CD62L^high (i.e., naïve CD4⁺ T cells). As the population of CD4⁺ CD62L^high splenocytes may contain a mixture of both central memory and naïve T cells, the activation marker CD44 was used assess the contribution of the central memory pool. Greater than 95% of CD4⁺CD62L^high cells were observed by flow cytometry to express intermediate to low levels of CD44, consistent with a naïve T cell population (i.e., CD4⁺CD62L^highCD44^low). The results suggest that contribution of the central memory population (i.e., CD4⁺CD62L^high CD44^high) was minor. In comparison, a high level of CD44 expressions was observed in the CD4⁺ CD62L^low population, consistent with an effector T cell population (i.e., CD4⁺CD62L^low CD44^high). These different T cell subsets can be clearly identified in Figure 3.

Table 1.

Efficiency statistics for naïve CD4⁺CD62L⁺ T cell isolation from Balb/c splenocytes

Fractions	Total Cells	CD4+ (%)	CD4+CD62L+ (%)	CD4+CD62L+ CD44high (%)
Pre-sort Populations	6090	30.46	18.92	3.50
CD4+ Subset	7501	97.77	85.14	6.12
CD4− Subset	6149	21.52	11.21	1.54
CD4+CD62L+ Subset	7141	98.46	90.46	4.08
CD4+CD62L− Subset	7165	96.51	64.98	6.69

Figure 3.

A smoothed contour plot for CD62L versus CD44 expression. The CD4⁺ population (left panel) is comprised of two populations: a CD62L⁺CD44^med subset and a CD62L⁻CD44^high subset. The CD62L⁻CD44^high subset was eliminated from the CD4⁺CD62L⁺ population (right panel) upon sorting using an anti-CD62L antibody. The contours are colored by density estimation.

Marginalized Probability Density Functions

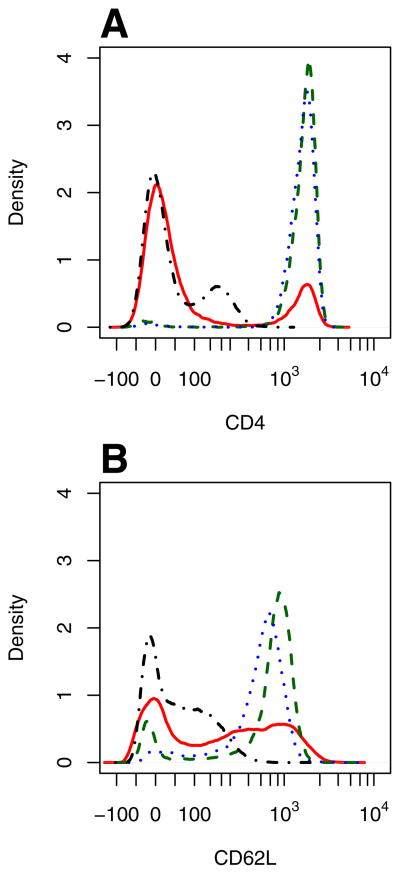
The fluorescent intensities can be presented in the form of a function that describes the probability of observing a particular parameter intensity. This function is referred to as a probability distribution function (PDF). A PDF function is similar to a histogram but is normalized to the total number of observed events, facilitating comparisons among experimental conditions and groups. The PDFs for each time point were obtained by kernel density estimation using the function density [21]. Kernel density estimation is a non-parametric smoothing technique used to estimate probability density functions from independent samples drawn from the population of interest. While it shares some similarity with estimating a density function using a normalized histogram, the kernel method exhibits less bias in estimating the density function. The bias in a histogram estimator with a bin width h is of order h. In contrast, the kernel is centered at each point and, by using a symmetric kernel, yields a leading bias term for the kernel estimate of order h². Improving the resolution of an assay provides a clearer window into fundamental cellular behavior [22]. Default values for the bandwidth were used. Representative PDFs for CD4 and CD62L expression are shown in Figure 4.

Figure 4.

Marginalized probability density functions for CD4 (A) and CD62L (B) expression shown for the different aliquots obtained during MACs cell sorting of Balb/c splenocytes: Unstained fraction (dot-dashed), Pre-sort fraction (solid), CD4⁺ fraction (dashed), and CD4⁺CD62L⁺ fraction (dotted).

More generally, a PDF is a continuous function that summarizes the distribution in protein expression or activity within a population of cells. The presence of a bimodal PDF distribution indicates that multiple subsets exist within a population. Quantifying the relative contribution of a particular subset can be achieved by deconvoluting a bimodal PDF in terms of a series of overlapping probability distributions (e.g., overlapping Gaussians) that have different median parameter intensities. An analogous approach is used to quantify the cell cycle phase distribution of cells following DNA staining [23, 24].

Principal Component Analysis

The CD4⁺ and CD4⁺CD62L⁺ fractions were further characterized using principal component analysis [25]. Principal component analysis (PCA) is a multivariate statistical technique that allows for the discovery of variables that form a coherent subset and are relatively independent of other subsets of variables. Variables that vary in synchrony with other variables are lumped together into independent principal components. The utility of this approach is in creating a lower-dimensional description of the population, such as multi-dimensional scaling or clustering (e.g., [26]).

To illustrate the approach, three principal components (PCs) were created from the three variables - CD44, CD62L, and CD4 - that characterize the cell population using the R function princomp. As principal component analysis is a linear modeling technique, extreme values can influence the quality of the results. Thus the lin-log transformed variables were used in the analysis. The resulting scoring coefficients, shown in Table 2, were used to calculate the principal component values for another cell fraction using:

$$P{C}_{i,p}=C{1_i}^{\ast }v{1}_p+C{2_i}^{\ast }v{2}_p+\dots +{{Cn}_i}^{\ast }v{n}_p,$$ (4)

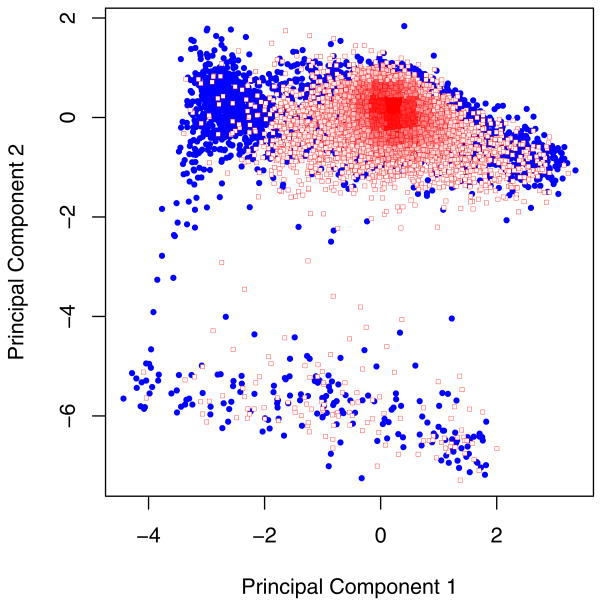
where v’s are variable values for the p cell and C’s are the scoring coefficients for the i^th principal component (PC) and n^th variable. A scoring coefficient is related to a correlation coefficient such that a value for the CD62L scoring coefficient of 0.711 in PC₁ means that 50.6% (100*0.711²) of the variance in CD62L expression is represented in PC₁. The difference in sign between the scoring coefficients for CD44 and CD62L in PC₁ indicates that these two variables are inversely related in the dataset. PC₁ versus PC₂ projections for the CD4⁺ and CD4⁺CD62L⁺ fractions are shown in Figure 5. The difference in the two populations at a low value for PC₁ corresponds to the elimination of the CD44^high subset in the CD4⁺CD62L⁺ fraction, as seen in Figure 3 and inferred from the PC loading coefficients.

Table 2.

Summary statistics for Principal Component Analysis of CD4⁺ Fraction

Parameters	PC1	PC2	PC3
CD4	0.190	0.953	0.235
CD44	−0.677	0.301	−0.671
CD62L	0.711	0.031	−0.703
Std Dev	1.227	1.006	0.695

Figure 5.

Projections of the CD4⁺ (filled circles) and CD4⁺CD62L⁺ (squares) fractions within the subspace defined by principal component 1 and principal component 2.

As mentioned above, PCA identifies linear relationships embedded within high dimensional data. As the number of dimension increases in a flow cytometry experiment, generating and analyzing each pairwise comparison between parameters becomes an onerous task. In addition, a three-way relationship among parameters can be difficult to identify from two-dimensional projections. PCA may be particularly helpful in focusing the analysis to specific combinations of parameters that exhibit interesting relationships, such as the inverse relationship between CD44 and CD62L. Depending on the motivating question, non-linear relationships can be also investigated in R using computationally intensive techniques such as Gaussian Mixture Models (e.g., MCLUST [27]).

In summary, R/Bioconductor is a versatile platform for the analysis of complex data, such as polychromatic flow cytometry data. The value of flow cytometry to inform biological questions requires a multi-step process where the quality of the data can be ensured. As illustrated here, this process for quality control, whether in a high-throughput or low-throughput setting, is aptly suited to R/Bioconductor. A compendium of text, data, and R scripts provides a clear-cube, rather than black box, approach to the analysis and interpretation of flow cytometry data. The additional effort required to learn this new computational tool is rewarded by the ability to apply a large suite of statistical and graphical tools to your dataset. Specifically, processing can be streamlined by establishing a common workflow in the form of R script templates for typical flow cytometry experiments. Subjectivity can be minimized via use of data-driven gates. Scientific judgement can be focused quickly on embedded trends within this high-dimensional data. Ultimately, the existing analysis algorithms within the R platform provide a rich resource for asking complex questions using polychromatic flow cytometry.