Pre-steady state kinetic studies of the fidelity of nucleotide incorporation by yeast DNA polymerase δ

Abstract

Eukaryotic DNA polymerase delta (pol δ) is a member of the B family of polymerases and synthesizes most of the lagging strand during DNA replication. Yeast pol δ is a heterotrimer comprised of three subunits: the catalytic subunit (Pol3) and two accessory subunits (Pol31 and Pol32). Although it is one of the major eukaryotic replicative polymerase, the mechanism by which it incorporates nucleotides is unknown. Here we report both steady state and pre-steady state kinetic studies of the fidelity of pol δ. We found that pol δ incorporates nucleotides with an error frequency of 10⁻⁴ to 10⁻⁵. Furthermore, we showed that for correct versus incorrect nucleotide incorporation, there are significant differences between both pre-steady state kinetic parameters (apparent K_d^dNTP and k_pol). Somewhat surprisingly, we found that pol δ synthesizes DNA at a slow rate with a k_pol of ~1 s⁻¹. We suggest that, unlike its prokaryotic counterparts, pol δ requires replication accessory factors like proliferating cell nuclear antigen to achieve rapid rates of nucleotide incorporation.

Eukaryotic DNA polymerase δ (pol δ), a member of the B family of DNA polymerases, is responsible for synthesizing the bulk of the lagging strand of genomic DNA during normal replication [1–3]. In addition, pol δ participates in nucleotide excision repair, base excision repair, and double strand break repair [4]. It also plays an important role in maintaining genome stability, as mutations in pol δ cause an increased frequency of cancer in mice [5–7] and have been found in cell lines derived from human cancers [8, 9].

Yeast pol δ is a heterotrimer, comprised of three subunits: Pol3 (125 kDa), Pol31 (55 kDa), and Pol32 (40 kDa) [10]. Pol3 is the catalytic subunit and possesses both DNA polymerase and 3′-5′ exonuclease catalytic activities [11, 12]. Pol31 is an accessory subunit that is essential for viability [13]. By contrast, Pol32 is an accessory subunit that is not essential for viability; however, cells lacking this subunit show defects in DNA replication and repair [13]. Pol32 also contains the consensus proliferating cell nuclear antigen (PCNA) binding motif, and interactions with PCNA significantly increase the processivity of pol δ[14, 15].

The structure of the Pol3 catalytic subunit of pol δ bound to both DNA and incoming dNTP substrates has recently been determined [16]. Overall, the structure of the Pol3 subunit resembles that of the bacteriophage RB69 DNA polymerase, another member of the B family of DNA polymerases [17, 18]. The catalytic subunit has three domains: an N-terminal domain, an exonuclease domain, and a polymerase domain, which contains palm, fingers, and thumb sub-domains. The palm sub-domain contains the conserved, acidic residues of the polymerase active site that coordinate the metal ions necessary for catalysis. The fingers sub-domain contacts the nascent base pair, and the thumb subdomain contacts the duplex region of the DNA substrate along the minor groove. The DNA polymerase and exonuclease active sites are ~ 45 Å apart and are located on different domains. In addition, a low-resolution structure of the trimeric form of pol δ shows that the protein has an elongated shape with the Pol31 subunit bridging the Pol3 and Pol32 subunits [19].

The general mechanism of nucleotide incorporation by nearly all DNA polymerases examined to date follows the same overall scheme [20–22]. During non-processive DNA synthesis, this scheme features four events. First, the polymerase binds the DNA substrate to form the polymerase-DNA binary complex in its pre-incorporation state. Second, the polymerase-DNA binary complex binds the incoming dNTP to form the polymerase-DNA-dNTP ternary complex. Third, the incoming nucleotide is then incorporated onto the 3′ end of the primer strand of the DNA substrate followed by release of pyrophosphate. This results in the formation of the polymerase-DNA binary complex in its post-incorporation state. Fourth, the polymerase dissociates from the DNA substrate. During processive DNA synthesis, the polymerase cycles between the nucleotide-binding event, the nucleotide-incorporation event, and an additional event in which the polymerase-DNA binary complex in its post-incorporation state translocates forward one base pair along the DNA to form the binary complex in its pre-incorporation state. We note that these events are likely composites of several elementary steps along the reaction pathway including conformational changes in the polymerase.

Although both the polymerase activity and the proofreading exonuclease activity contribute to the fidelity of DNA synthesis by many DNA polymerases [23–25], we will focus here on the contribution of the polymerase activity. Polymerases generally prefer to incorporate incoming nucleotides that form correct base pairs with the template base compared to those that form mispairs. This preference often leads to significant differences in the apparent dissociation constant for the incoming dNTP (the apparent K_d^dNTP) and in the maximal first-order rate constant for nucleotide incorporation (k_pol) for correct versus incorrect nucleotide incorporation. Some polymerases, such as the Klenow fragment of E. coli pol I, have significant differences in the k_pol, but not in the apparent K_d^dNTP [26, 27]. By contrast, other polymerases, such as the bacteriophage T7 DNA polymerase, have significant differences in both the apparent K_d^dNTP and the k_pol [28, 29].

Despite the importance of pol δ in DNA replication and repair and in maintaining genome stability, the mechanism by which it incorporates nucleotides is unknown. Here we report steady state and pre-steady state kinetic studies of yeast pol δ to measure the fidelity of this enzyme and to understand how the kinetics of nucleotide incorporation differs with correct versus incorrect nucleotides. We find that pol δ incorporates most nucleotides with an error frequency of 10⁻⁴ to 10⁻⁵, and we find that there are significant differences between both the apparent K_d^dNTP and the k_pol for correct versus incorrect nucleotide incorporation. In addition, we find that in the absence of other protein factors, the rate of nucleotide incorporation by pol δ is slower than expected. We suggest that, unlike its prokaryotic counterparts, pol δ requires interactions with other factors like PCNA to achieve the rapid rates of nucleotide incorporation necessary for DNA replication in vivo.

EXPERIMENTAL PROCEDURES

Proteins

S. cerevisiae pol δ was over-expressed in yeast YRP654 cells carrying plasmids pBJ1244 (containing GST-Pol31), pBJ1180 (containing Pol32), and pBJ1581 (containing FLAG-Pol3 exo⁻). The protein, which lacked exonuclease activity because it contained two amino acid substitutions in the exonuclease domain (D321A/E323A), was purified as described previously [30, 31]. Protein concentrations were determined by the BioRad method and by active site titration, and both methods gave similar results (within 10%).

DNA substrates

For steady state and pre-steady state kinetic studies, the primer strand was a 32-mer oligodeoxynucleotide with the sequence: 5′-GGT AGC CAG CCT CGC ACC CGT CCA ACC AAC TC-3′. The four template strands were 52-mer oligodeoxynucleotides with the sequence: 5′-GAC GGC ATT GGA TCG ACC TNG AGT TGG TTG GAC GGG TGC GAG GCT GGC TAC C-3′. In these oligodeoxynucleotides, the N represents G, A, T, or C. The primer strand was 5′-³²P-end-labeled with T4 polynucleotide kinase and [γ-³²P] ATP. The primer and template strands were annealed at 2 μM in 25 mM Tris acetate, pH 7.5 at 90 °C for 2 min followed by slow cooling to room temperature.

Steady state kinetics

Reactions were performed in 25 mM Tris acetate, pH 7.5, 150 mM sodium acetate, 5 mM magnesium acetate, 1 mM DTT, and 10% glycerol at 30 °C. In the case of correct dNTP incorporation, 50 nM of the 5′-³²P-labeled DNA substrate was pre-incubated with various concentrations of the incoming nucleotide (0 to 10 μM), and pol δ (5 nM) was added to the solution to initiate the reaction. Reactions were quenched after one minute with 10 volumes of formamide loading buffer (80% deionized formamide; 10 mM EDTA, pH 8.0; 1 mg/ml xylene cyanol; 1 mg/ml bromophenol blue). The samples were then analyzed on a 15% polyacrylamide sequencing gel containing 8 M urea and formation of DNA products was quantified by measuring the intensities of bands using an Instant Imager (Packard). In the case of incorrect dNTP incorporation, the dNTP concentrations used ranged from 0 to 5 mM, and the reactions were quenched after one hour.

The observed rate of product formation, which was determined by dividing the amount of product formed by the reaction time, was plotted as a function of dNTP concentration. The k_cat and K_m values were determined from the best fit of the data to the Michaelis-Menten equation using SigmaPlot 8.0. The error frequency was determined by calculating the ratio of the catalytic efficiency (k_cat/K_m) for incorporating each incorrect dNTP to the sum of the catalytic efficiencies for incorporating the correct and the three incorrect dNTPs.

Pre-steady state kinetics

Reactions were performed under the same buffer conditions as the steady state studies. For correct base pair formation, the reaction times needed to be very short, and thus the use of a rapid chemical quench flow apparatus (KinTek) was necessary. Pol δ (60 nM final active concentration) and various concentrations of the DNA substrate (0 to 150 nM final concentration) were pre-incubated in one syringe of the quench flow. The reactions were initiated by adding various concentrations of dNTP (0 to 100 μM) from the other syringe. The quenching solution (0.2 M EDTA) was added to each reaction after short time intervals (0 to 20 sec). The synthesized DNA product was then analyzed using polyacrylamide gel electrophoresis as described above. For incorrect base pair formation, longer reaction times (0 to 300 sec) were used, and thus experiments could be performed by hand. For these experiments, 150 nM DNA substrate was pre-incubated with 60 nM pol δ and the reactions were initiated with addition of various concentrations of nucleotide (0 to 5 mM). To ensure reproducibility, each set of DNA and dNTP concentrations was repeated multiple times.

For each experiment involving the formation of a correct base pair, the concentration of product formed (P) was plotted as a function of time (t). The observed first-rate constant of the fast exponential phase (k_obs), the amplitude of the fast exponential phase (A), and the velocity of the slow linear phase (ν) were determined from the best fit of the data to the burst equation:

$$P=A(1-e^{-k_{\text{obs}}t})+\nu t$$

For experiments in which various DNA concentrations were used, the amplitudes of the fast exponential phases (A) were plotted as a function of DNA concentration ([DNA]). The concentration of active pol δ in our protein preparations ([pol δ]) and the dissociation constant for DNA binding (K_d^DNA) were determined from the best fit of the data to the quadratic form of the binding equation:

$$A=0.5({K_{\text{d}}}^{\text{DNA}}+[\mathit{pol}\delta ]+[\mathit{DNA}])-\sqrt{(0.25{({K_{\text{d}}}^{\text{DNA}}+[\mathit{pol}\delta ]+[\mathit{DNA}])}^2-([\mathit{pol}\delta ][\mathit{DNA}])}$$

For experiments in which various dNTP concentrations were used, the observed first-order rate constants of the fast exponential phases (k_obs) were plotted as a function of dNTP concentration ([dNTP]). The apparent dissociation constant for the incoming dNTP (K_d^dNTP) and the maximum first-order rate constant for nucleotide incorporation (k_pol) were determined from the best fit of the data to the rectangular hyperbolic equation:

$$k_{\text{obs}}=\frac{k_{\text{pol}}[\mathit{dNTP}]}{{K_d}^{\mathit{dNTP}}+[\mathit{dNTP}]}$$

For each experiment involving the formation of an incorrect base pair, the concentration of product formed was plotted as a function of time. The k_obs was determined from the slope of the best fit line divided by the concentration of active pol δ. We carried out kinetic simulations to ensure that the k_obs values determined in this manner were valid. The k_obs was then plotted as a function of dNTP concentration, and the apparent K_d^dNTP and the k_pol were determined from the best first of the data to the rectangular hyperbolic equation.

RESULTS

Eukaryotic pol δ synthesizes most of the lagging strand during DNA replication and plays an essential role in several DNA repair pathways. Despite its central role in maintaining genome integrity, the kinetic mechanism of nucleotide incorporation by this enzyme is largely unknown. To understand better the mechanism of this enzyme, we have carried out both steady state kinetic studies and pre-steady state kinetic studies of yeast pol δ. We specifically examined its rate of nucleotide incorporation, its fidelity of nucleotide incorporation, as well as differences between the kinetics of correct and incorrect nucleotide incorporation. To eliminate any complexities arising from the proofreading exonuclease activity of this enzyme, we have used an exonuclease-deficient mutant form of the protein in all of our experiments.

Fidelity of pol δ

The error frequency of a DNA polymerase is measured by taking the ratio of the catalytic efficiency (k_cat/K_m) for incorporating an incorrect dNTP to the sum of the catalytic efficiencies for incorporating the correct and the three incorrect dNTPs. Thus to determine the error frequency of pol δ, we have used steady state kinetics to measure the k_cat and K_m values associated with the formation of all sixteen possible correct and incorrect base pairs (Table 1). For example, the k_cat and K_m for incorporating the correct dCTP opposite a template G were 2.7 min⁻¹ and 1.4 μM, respectively. By contrast, the k_cat and K_m for incorporating the incorrect dGTP opposite a template G were 0.020 min⁻¹ and 630 μM, respectively. Consequently, pol δ misincorporates a dGTP opposite a template G with an error frequency of 1.6 × 10⁻⁵. The highest error frequency occurred with dGTP incorporation opposite a template T (4.5 × 10⁻⁴), which is a wobble base pair. The lowest error frequency occurred with dCTP incorporation opposite a template C (less than 1 × 10⁻⁵), which was beyond the estimated detection limit for our experiments. The error frequency for all of the other incorrect base pairs was in the range of 10⁻⁴ to 10⁻⁵.

Table 1.

Fidelity of pol δ.

Base pair	kcat	Km	kcat/Km	Error frequencya
	min−1	μM	μM−1min−1
dGTP·G	0.020 ± 0.004	630 ± 350	3.2 × 10−5	1.6 × 10−5
dATP·G	0.020 ± 0.002	380 ± 150	5.3 × 10−5	2.7 × 10−5
dTTP·G	0.062 ± 0.001	400 ± 30	1.6 × 10−4	8.0 × 10−5
dCTP·G	2.7 ± 0.4	1.4 ± 0.6	1.9	N/Ab
dGTP·A	0.024 ± 0.006	780 ± 440	3.1 × 10−5	5.2 × 10−5
dATP·A	0.044 ± 0.008	960 ± 360	4.6 × 10−5	7.8 × 10−5
dTTP·A	3.9 ± 1.0	6.6 ± 3.0	0.59	N/Ab
dCTP·A	0.020 ± 0.002	500 ± 170	4.0 × 10−5	6.8 × 10−5
dGTP·T	0.10 ± 0.01	210 ± 20	4.8 × 10−4	4.5 × 10−4
dATP·T	2.2 ± 0.2	2.1 ± 0.6	1.0	N/Ab
dTTP·T	0.022 ± 0.001	410 ± 70	5.4 × 10−5	5.1 × 10−5
dCTP·T	0.045 ± 0.002	410 ± 70	1.1 × 10−4	1.0 × 10−4
dGTP·C	3.8 ± 0.4	2.5 ± 0.8	1.5	N/Ab
dATP·C	0.042 ± 0.004	250 ± 100	1.7 × 10−4	1.1 × 10−4
dTTP·C	0.11 ± 0.01	660 ± 160	1.7 × 10−4	1.1 × 10−4
dCTP·C	N/Dc	N/Dc	< 2 × 10−5	< 1 × 10−5

^aThe error frequency is the ratio of the k_cat/K_m parameter for incorporating the incorrect dNTP to the sum of the k_cat/K_m parameters for incorporating the correct and the three incorrect dNTPs.

^bNot applicable

^cNot detectible.

Pol δ incorporates nucleotides with biphasic kinetics

While steady state kinetics often provides a convenient means of measuring DNA polymerase fidelity, it provides little information regarding the events occurring at the enzyme active site when correct and incorrect nucleotides are incorporated. Thus, we used pre-steady state kinetics to examine the fidelity of nucleotide incorporation by pol δ. To do this, we first needed to determine whether pol δ displayed biphasic kinetics (i.e., burst kinetics) under pre-steady state conditions. We pre-incubated pol δ (60 nM final concentration as determined by active site titration – see below) with the DNA substrate containing a C in the template position (150 nM) in one syringe of a rapid chemical quench flow instrument, and we initiated the reaction by adding dGTP (50 μM) from the second syringe. Fig. 1 shows the kinetics of forming a correct G·C base pair in which two phases of nucleotide incorporation are clearly visible. The fast exponential phase represents nucleotide incorporation during the first enzyme turnover, while the slow linear phase represents incorporation during subsequent, steady state turnovers. The rate of incorporation during subsequent turnovers is limited by a slow step in the reaction pathway that occurs after nucleotide incorporation, and this slow step likely represents DNA dissociation, which is generally the case with DNA polymerases. From the best fit of this data to the burst equation, we determined that the observed first-order rate constant (k_obs) of the fast phase was equal to 0.58 s⁻¹ and the amplitude of the fast phase was equal to 37 nM.

Fig. 1.

Nucleotide incorporation by pol δ displays biphasic kinetics. Pol δ (60 nM) was incubated with the DNA substrate (150 nM), and dGTP (50 μM) for various reaction times up to 20 seconds. The solid line represents the best fit of the data to the burst equation with a k_obs for the fast exponential phase equal to 0.58 ± 0.08 s⁻¹ and an amplitude of the fast exponential phase equal to 37 ± 3 nM.

Active site titration of pol δ and determining the K_d^DNA

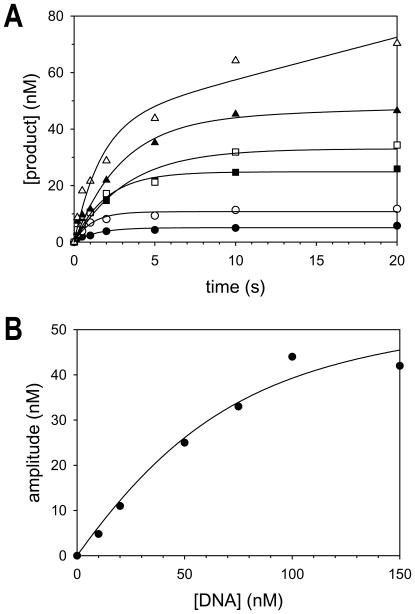
Because pol δ displays biphasic kinetics, we were able to carry out an active site titration to determine the fraction of active pol δ enzyme in our protein preparations and to determine the dissociation constant for DNA binding (K_d^DNA). We pre-incubated pol δ (60 nM) with various concentrations of the DNA substrate containing a template C (0 to 150 nM) and initiated the reactions by adding 50 μM dGTP (Fig. 2A). The data in each plot were fit using the burst equation, and amplitudes of the fast phases were determined from the best fits. These amplitudes are directly proportional to the amount of active pol δ-DNA complex formed during the pre-incubation period. Thus, the concentration of active pol δ and the K_d^DNA could be determined by plotting the amplitudes as a function of DNA concentration (Fig. 2B). From the best fit of these data to the quadratic form of the binding equation, we determined that the concentration of active pol δ enzyme was equal to 60 nM and that the K_d^DNA was equal to 30 nM.

Fig. 2.

Active-site titration of pol δ. (A) Pol δ (60 nM) was incubated with various concentrations of the DNA substrate (●, 10 nM; ○, 20 nM; ■, 50 nM; □, 75 nM; ▲, 100 nM; △, 150 nM) and dGTP (50 μM) for various reaction times up to 20 seconds. The solid lines represent the best fit of the data to the burst equation. (B) The amplitudes of the fast exponential phase were plotted as a function of DNA concentration. The solid line represents the best fit of the data to the quadratic form of the binding equation with a K_d^DNA equal to 30 ± 11 nM and a concentration of active pol δ equal to 58 ± 7 nM.

Kinetics of correct nucleotide incorporation by pol δ

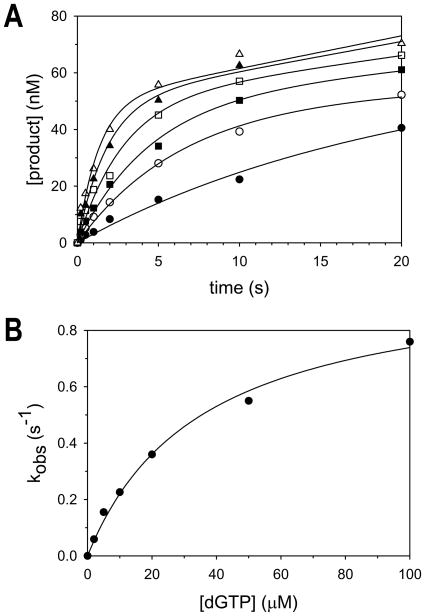
To determine the apparent K_d^dNTP and the k_pol for correct nucleotide incorporation by pol δ, we examined the pre-steady state kinetics of forming a correct G·C base pair. We pre-incubated pol δ (60 nM) and the DNA substrate with a template C (150 nM) and initiated the reaction by addition of various concentrations of dGTP (0 to 100 μM) (Fig. 3A). The data in each plot were fit using the burst equation, and the k_obs values of the fast phases were determined from the best fits. These k_obs values were plotted as a function of dGTP concentration (Fig. 3B). From the best fit of these data to the rectangular hyperbolic equation, we determined that the apparent dissociation constant for nucleotide binding (K_d^dNTP) was equal to 36 μM and the maximal first-order rate constant for nucleotide incorporation (k_pol) was equal to 1.0 s⁻¹. Table 2 provides the mean and standard errors of the apparent K_d^dNTP and the k_pol values obtained from multiple independent experiments.

Fig. 3.

Pre-steady state kinetics of correct base pair formation by pol δ. (A) Pol δ (60 nM) was incubated with the DNA substrate with a template C residue (150 nM) and various concentrations of dGTP (●, 2 μM; ○, 5 μM; ■, 10 μM; □, 20 μM; ▲, 50 μM; △, 100 μM) for various reaction times up to 20 seconds. The solid lines represent the best fit of the data to the burst equation. (B) The k_obs of the fast exponential phases were plotted as a function of dGTP concentration. The solid line represents the best fit of the data to the rectangular hyperbolic equation with an apparent K_d^dNTP equal to 36 ± 5 μM and a k_pol equal to 1.0 ± 0.1 s⁻¹.

Table 2.

Pre-steady state kinetics of pol δ.

Base pair	KddNTPa	kpola	KddNTP/KddNTPb	kpol/kpolc
	μM	sec−1
dGTP·G	620 ± 10	0.0023 ± 0.0003	26	400
dGTP·A	330 ± 110	0.0034 ± 0.0013	14	270
dGTP·T	350 ± 30	0.026 ± 0.007	15	36
dGTP·C	24 ± 9	0.93 ± 0.25	N/A	N/A

^aValue reported here are the mean and standard error from multiple independent experiments.

^bThis is the ratio of the apparent K_d^dNTP for the incorrect base pair to the apparent K_d^dNTP for the correct base pair.

^cThis is the ratio of the k_pol for the correct base pair to the k_pol for the incorrect base pair.

Kinetics of incorrect nucleotide incorporation by pol δ

We next examined the pre-steady state kinetics of forming incorrect G·G, G·A, and G·T base pairs. We pre-incubated pol δ (60 nM) and the DNA substrate with either a template G, template A, or template T (150 nM) and initiated the reaction by addition of various concentrations of dGTP (0 to 2 mM). Fig. 4A shows the kinetics of forming the incorrect G·G base pair. The data in each plot were fit to the linear equation and the k_obs values were determined by dividing the slope of the line by the active enzyme concentration. These k_obs values were plotted as a function of dGTP concentration (Fig. 4B). From the best fit of these data, we determined that the apparent K_d^dNTP was equal to 630 μM and the k_pol was equal to 0.0021 s⁻¹. The mean and standard error values of the apparent K_d^dNTP and k_pol parameters for the formation of all three incorrect base pairs obtained from multiple independent experiments are provided in Table 2. The apparent K_d^dNTP was approximately 15 to 30-fold lower in the context of a correct base pair than an incorrect base pair. With the exception of the unusual G·T wobble base pair, the k_pol was approximately 250 to 400-fold faster in the context of a correct base pair than an incorrect base pair. Therefore, there are significant differences between both the apparent K_d^dNTP and the k_pol for correct versus incorrect nucleotide incorporation.

Fig. 4.

Pre-steady state kinetics of incorrect base pair formation by pol δ. (A) Pol δ (60 nM) was incubated with the DNA substrate with a template G residue (150 nM) and various concentrations of dGTP (●, 0.05 mM; ○, 0.1 mM; ■, 0.2 mM; □, 0.5 mM; ▲, 1 mM; △, 2 mM) for various reaction times up to 300 seconds. The solid line represents the best fit of the data to a linear equation. (B) The k_obs values were plotted as a function of dGTP concentration. The solid line represents the best fit of the data to the rectangular hyperbolic equation with an apparent K_d^dNTP equal to 630 ± 180 μM and a k_pol equal to 0.0021 ± 0.0003 s⁻¹.

DISCUSSION

Pre-steady state kinetic studies have been used to examine the mechanisms of a variety of prokaryotic and eukaryotic DNA polymerases. These include eukaryotic repair polymerases like pol β [32, 33], pol λ [34], and pol μ [35], eukaryotic translesion synthesis polymerases like pol η [36, 37], pol κ [38], pol ι [39], and Rev1 [40], as well as the mitochondrial polymerase pol γ [41]. By contrast, very little is known about the mechanisms of the eukaryotic B-family replicative polymerases, which are responsible for synthesizing the leading and lagging strands during genomic DNA replication. Thus, to better understand the mechanism of eukaryotic pol δ, we examined its fidelity of nucleotide incorporation using steady state and pre-steady state kinetics.

The steady state kinetic analysis reported here shows that the exonuclease-deficient form of yeast pol δ has an error rate of about 10⁻⁴ to 10⁻⁵. This is in close agreement to previous studies of the exonuclease-deficient form of yeast pol δ that determined its error rate either from a more limited steady state kinetic analysis or during DNA synthesis across the lacZ gene [42, 43]. The fidelity of pol δ is similar to the fidelity of the eukaryotic mitochondrial DNA polymerase, pol γ, which has an error rate ranging from 10⁻⁴ to 10⁻⁶ [41]. The fidelity of pol δ is similar to, although in some sequence contexts slightly lower than, the fidelity of the eukaryotic leading strand polymerase, pol ε, which has an error rate of about 10⁻⁴ to 10⁻⁷ [44]. By contrast, the fidelity of pol δ is greater than the fidelity of eukaryotic translesion synthesis polymerases such as pol ζ [45], pol η [46, 47], pol κ [48], and pol ι [45, 49, 50], which have error rates as high as 10¹ for pol ι and as low as 10⁻⁴ for pol ζ and pol κ.

The kinetics of correct base pair formation by pol δ reported here allows for a direct comparison of this enzyme with other DNA polymerases. The apparent K_d^dNTP of pol δ, for example, is ~20 μM, which is similar (i.e., within a factor of 5) to the apparent K_d^dNTP reported for replicative DNA polymerases from bacteriophage, such as the T7 DNA polymerase [28], the T4 polymerase [51], and the RB69 DNA polymerase [52]. By contrast, the k_pol of pol δ is ~1 s⁻¹, which is at least 200-fold slower than those reported for these bacteriophage replicative polymerases [28, 51, 52]. This k_pol value is, in fact, more typical of some of the eukaryotic DNA repair polymerases of the X family, such as pol β [32], pol λ [34], and pol μ [35] and eukaryotic translesion synthesis polymerases of the Y family, such as pol η [36], pol ι [39], and pol κ [38]. It is important to point out that this low k_pol is not due to inactive pol δ in our protein preparations. This low k_pol was observed with multiple protein preparations, and active site titrations showed that nearly all of the pol δ in our preparations was active. This low k_pol value, however, is similar to the k_pol reported for calf thymus pol δ, which was ~6 s⁻¹ [53]. Therefore, it seems that eukaryotic pol δ may be intrinsically slow at nucleotide incorporation in the absence of replication accessory factors when compared to replicative polymerases from simpler bacteriophage systems.

We believe that the interactions with other factors, such as PCNA (the sliding clamp processivity factor), are required for pol δ to achieve the rapid rate of DNA synthesis necessary for DNA replication in vivo. Support for this comes from the fact that PCNA was shown to increase the k_pol of calf thymus pol δ by more than 3-fold [53]. In that study, however, PCNA was inefficiently loaded onto the DNA, because replication factor C (the clamp loader) was not present and the ends of the DNA were not blocked to prevent PCNA from sliding off the substrate. Thus, when loaded onto DNA by RFC, PCNA would enhance the rate of nucleotide incorporation by calf thymus pol δ to a greater degree than has been previously reported. Moreover, we note that data presented by Chen et al [54] show that PCNA dramatically stimulates the nucleotide incorporation activity of S. pombe pol δ and not merely its processivity.

A comparison of the kinetics of correct and incorrect nucleotide incorporation reported here shows that the fidelity of DNA synthesis by pol δ results in significant differences between both the apparent K_d^dNTP and k_pol for correct versus incorrect nucleotide incorporation. For example, the apparent K_d^dNTP is 26-fold tighter when the base pair is correct (G·C) than when it is incorrect (G·G), and the incoming nucleotide is added to the 3′ end of the primer strand 400-fold faster when the base pair is correct than when it is incorrect. One must be careful, however, about interpreting these differences in terms of the elementary steps along the reaction pathway. Recent studies have called into question the assumptions that the apparent K_d^dNTP reflects the ground state binding affinity of the incoming dNTP [55, 56]. Moreover, there is significant debate in the literature regarding the contributions of the chemical step of phosphodiester bond formation and a conformational change step (both in its forward and reverse directions) that precedes the chemical step [57–59]. Thus, proper interpretation of the changes in the apparent K_d^dNTP and k_pol in terms of the elementary steps along the reaction pathway and how these steps contribute to the fidelity of pol δ will require a complete analysis of all steps including any conformational change steps.

Nevertheless, with respect to these significant differences in both the apparent K_d^dNTP and the k_pol for correct versus incorrect nucleotide incorporation, pol δ resembles other replicative DNA polymerases including the bacteriophage T7 DNA polymerase [28, 29], the S. solfactaricus pol B1[60], and human mitochondrial pol γ [41]. This is in contrast to some non-replicative polymerases including repair polymerases like E. coli pol I (Klenow fragment) [26, 27] and translesion synthesis polymerases like S. solfactaricus Dpo4 [61] and eukaryotic pol η [36, 37]. Many of these non-replicative polymerases only have significant changes in the k_pol for correct versus incorrect nucleotide incorporation. This suggests a general trend across both prokaryotes and eukaryotes whereby replicative polymerases tend to have significant differences in both the apparent K_d^dNTP and k_pol and non-replicative (i.e., repair and translesion synthesis) polymerases tend to have significant differences in the k_pol.

The X-ray crystal structure of the catalytic subunit of yeast pol δ has recently been determined [16], which to our knowledge is the only available structure for a eukaryotic, replicative DNA polymerase. Moreover, a low-resolution structure has been determined for the complex containing all three subunits of yeast pol δ [19]. These structures make yeast pol δ the ideal system for examining the structure-function relationship in a eukaryotic B-family polymerase. The kinetics of pol δ reported here provides an excellent platform for these studies. It also provides a basis for understanding the impact of the cancer-causing mutant forms of this protein as well as understanding the role of replication accessory factors, such as PCNA, in promoting its DNA synthesis activity.

ABBREVIATIONS

The abbreviations used are:

dNTP

deoxynucleoside triphosphate

DTT

dithiothreitol

EDTA

ethylenediamine tetraacetic acid

PCNA

proliferating cell nuclear antigen

Pol

polymerase