Molecular basis for the structural stability of an enclosed β barrel loop

Abstract

We present molecular dynamics (MD) simulation studies of the structural stability of an enclosed loop in the β domain of the E. coli O157:H7 autotransporter EspP. Our investigation revealed that in addition to its excellent resistance to thermal perturbations, EspP loop5(L5) also has remarkable mechanical stability against pulling forces along the membrane norm. These findings are consistent with the experimental report that EspP L5 helps to maintain the permeability barrier in the outer membrane(OM). In contrast to major secondary structure elements of globular proteins such as ubiquitin, whose resistance to thermal and mechanical perturbations depend mainly on backbone hydrogen bonds and hydrophobic interactions, the structural stability of EspP L5 can be attributed mainly to geometric constraints and side chain interactions dominated by hydrogen bonds. Examination of the B factors from available high resolution structures of membrane embedded β barrels (MEBBs) indicates that most of the enclosed loops have stable structures. This finding suggests that loops stabilized by geometric constraints and side chain interactions might be used more generally to restrict β barrel channels for various functional purposes.

Introduction

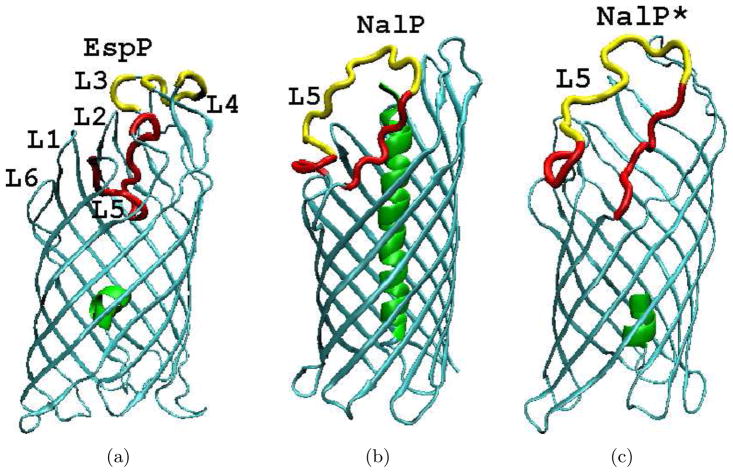
Autotransporters are a superfamily of simple secretion systems in Gram-negative bacteria[1]. Classical autotransporters are single polypeptides comprised of an amino terminal passenger domain and a carboxyl terminal β domain.The β domain integrates into the outer membrane (OM) and promotes the translocation of the passenger domain into the extracellular space by an unknown mechanism. Following their secretion, passenger domains (which encode diverse virulence functions) can be cleaved from β domains or remain on the cell surface[1]. High resolution crystal structures are available for the β domains of two classical autotransporters, NalP from Neisseria meningitidis [2] and EspP from Escherichia coli O157:H7 [3]. Additionally, structure of a full length autotransporter estA was published recently [4]. Both NalP and EspP β domains form a 12-stranded β barrel structure, with the β strands (β 1 through β 12) interconnected by 6 extracellular loops (L1 through L6) and 6 periplasmic turns (T1 through T6). Although their β strand backbone atoms are superimposablewithin 1.7 Å [3], the two structures have significant differences (see Fig. 1). The cleavage of the EspP passenger domain occurs within the β barrel, resulting in a short helix of 5 amino terminal residues remaining inside the periplasmic side of the β barrel (Fig. 47). EspP L5 is tucked into the extracellular side of the β barrel and is clearly identifiable in the crystal structure. In the case of NalP, the cleavage site is located in the extracellular space. Upon cleavage of the passenger domain, a long α helix formed by the first 26 residues of the β domain is positioned at the center of the β barrel and almost completely blocks the channel(Fig. 47). MD simulations of NalP[5] demonstrated that this helix is important in preventing the diffusion of water molecules through the pore, in agreement with visual intuition from examination of the crystal structure. Additionally, most of the NalP L5 residues are not resolved in the crystal structure. In the crystal structure of EspP β domain, residues that constitute L5 (213 through 230) exhibit well-defined positions and extensive side chain hydrogen bonds with other loops and strands. Hydrogen bonds are formed between the following residue pairs: 218–121, 219–30, 219–31, 219–109, 220–105, 220–107, 222–79 224–101, 224–125, 224–127, 226–35. However, given the extreme flexibility of the corresponding L5 in the NalP β domain, it is not immediately clear whether L5 always stays in the same position under thermal fluctuations at physiological conditions. Examination of available high resolution membrane embedded β barrel(MEBB) structures[6] reveals that many of them have an enclosed loop. The prevalence of such loops suggests that they might be of more general importance.

Figure 1.

The β domain structures of a)EspP, b)NalP and c)NalP*. The barrel enclosed α helices are shown in green and L5 is shown in red. Residues that are absent in the crystal structure were built with Modeller[47] and are shown in yellow. The remaining parts of all structures are shown in cyan. Secondary structure elements in EspP with corresponding residues numbers are: α helix (1–6); β 1(16–28); β 2(34–46); β 3(54–69); β 4(74–89); β 5(94–110); β 6(119–134); β 7(142–159); β 8(172–192); β 9(196–212); β 10(231–245); β 11(249–259); β 12(264–277). Secondary structure elements in NalP with corresponding residue numbers are: α helix (1–26); β 1(34–48); β 2(53–70); β 3(73–88); β 4(91–108); β 5(112–130); β 6(136–154); β 7(163–177); β 8(194–210) β 9(215–226); β 10(256–269); β 11(272–283); β 12(286–299).

Both experimental and computational studies have significantly increased our understanding of the stability of various secondary structures in soluble proteins under mechanical and thermal forces[7,8]. Results from many coarse-grained [9,10] and atomistic [11,12,13,14] computational studies of ubiquitin and titin I27 [15,16,17] agree quite well with force spectroscopic investigations [??0,19,20] and non-linear infrared spectroscopy studies [21,22]. However, due to the fact that most protein loops are exposed in solvents and are inherently flexible, studies on the behavior of loops under thermal and mechanical perturbations have been lacking. Significant technological challenges prevent effective force spectroscopic studies of achannel enclosed loop. Based on the good agreement between many of the above computational and experimental studies, we decided to apply computational methods to address the structural stability of loops enclosed in MEBBs under thermal and mechanicalperturbations using EspP as a model protein.

The structural stability of a given part of a protein is determined by three aspects of its underlying free energy landscape (FEL), i) the folding free energy of the complete protein (ΔG = G_unfolded − G_native , representing the free energy difference between its native state ensemble and unfolded state ensembles), which determines the thermodynamic stability; ii) the height of the unfolding energy barrier E_a separating the native state ensemble from many unfolded state ensembles,which determines the kinetic stability; and iii)the breadth of the native FEL basin in molecular coordinate space, which determines the allowed magnitude of molecular motion within the native state ensemble, or the native rigidity. The higher structural stability is associated with a larger folding free energy Δ_G , a higher unfolding barrier E_a and a higher native rigidity. Heat modifiability experiments have demonstrated that EspP β domain, like many other MEBBs, have excellent thermadynamic stability. Its unfolding temperature in 0.01% SDS was found to be higher than 80 °C [3]. By comparison, dispersed vibrational echo (DVE) spectroscopy showed that the well studied globular protein ubiquitin unfolds at approximately 61°C [21]. Additionally, an EspP L5 deletion mutant was found to have essential the same thermal stability as the wild type protein[3], indicating that the interaction between EspP L5 and other parts of the protein does not significantly contribute to the stability of the β barrel.

In this study, we mainly characterize the rigidity (allowed extent of motion) of EspP L5 in its native form and the unfolding energy barrier which confines the EspP L5 within its native free energy basin. We carried out both equilibrium and non-equilibrium MD simulations to explore the behavior of EspP L5 under thermal and mechanical perturbations. Equilibrium MD simulations of NalP were also performed for comparison. Our replica exchange MD (REMD) simulations demonstrated that the magnitude of motion of EspP L5 is quite small on a μ^s time scale. The biased MD simulations of EspP indicate that L5 can withstand strong perturbations without losing structural integrity on a ns time scale. The response of EspP L5 to pulling forces demonstrates its remarkable mechanical stability. Our simulations suggest that EspP L5 has greater resistance to thermal and mechanical perturbations than secondary structure elements in two well studied globular proteins, ubiquitin and titin I27 [16,23,21]. These findings indicate that EspP L5 has rather small native basin in molecular coordinate space and is confined in its native structure by a quite high energy barrier. While the structural integrity ofglobular proteins are mainly maintained by backbone hydrogen bonds that generate secondary structures and by side chain packing (predominantly hydrophobic interactions)[24], it is the geometric constraints and polar side chain interactions that underlie the structural stability of EspP L5. Our analysis of thermal factors and contact orders revealed that EspP L5 and many other enclosed MEBB loops exhibit a much smaller magnitude of thermal motion than exposed loops and form extensive molecular contacts with distant residues in their primary sequences. Based on the absence of backbone hydrogen bonds between enclosed loops and other parts of MEBBs, these observations strongly suggest that enclosed MEBB loop structures are stabilized by extensive side chain interactions and geometric constraints.

Results

The high native rigidity of EspP L5 revealed by equilibrium MD simulations

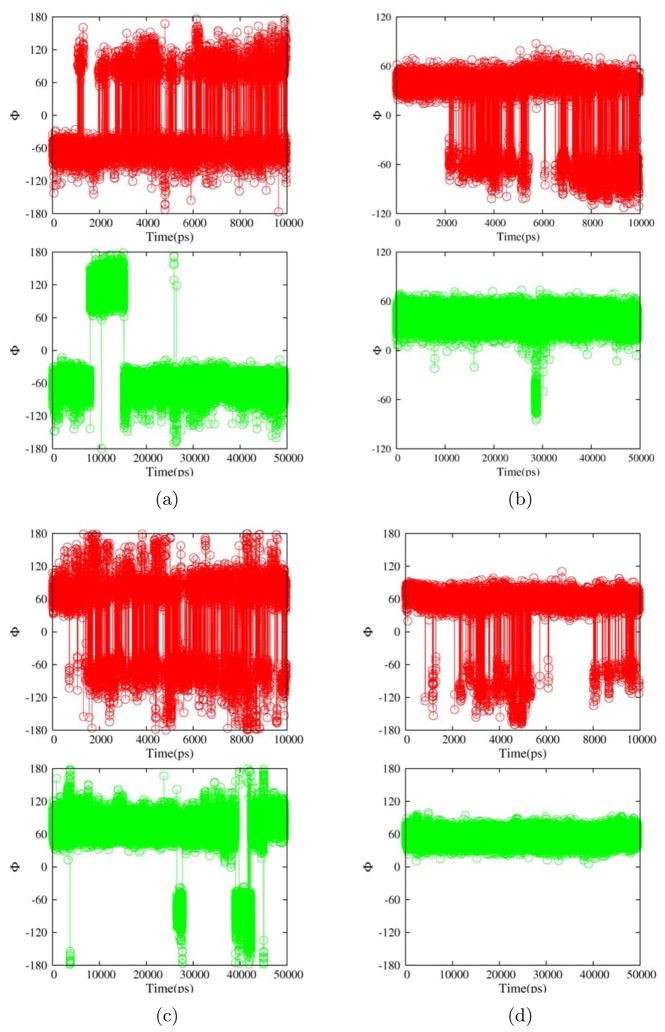
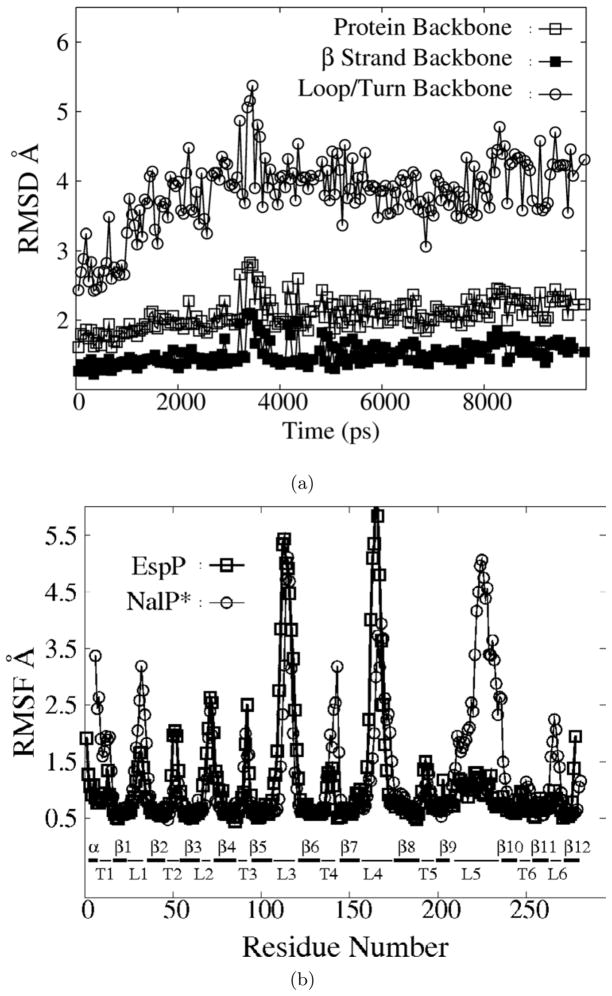
Both regular and replica exchange MD (REMD) simulations were carried out for the β domains of EspP and NalP. To better compare NalP and EspP simulations, REMD simulations of NalP were performed with a derivative in which the 23 amino terminal residues of the α helix were removed (denoted NalP*, Fig. 47) so that both proteins have a similar α helical fragment on the periplasmic side of the barrel. The exposed Ser (the 24th residue for NalP and 1st residue for NalP*) was capped with an NH₂ group. A comparison of simulations conducted with NalP and NalP* showed that removal of the distal portion of the helix did not significantly change the behavior of the β strands and loops. An appreciable increase in the root mean squared fluctuations (RMSF) of the remaining α helical residues was observed, however (data not shown). The root mean squared deviations(RMSD) from the crystal structures for the backbone atoms of the whole protein, the eta strands and loops/turns are plotted in Fig. 1, and the RMSF of each residue is plotted in Fig. 1. EspP L5 was very stable during the whole course of the REMD simulations. The RMSF of residues in L5 was comparable to that of β strand residues embedded in the membrane (Fig. 1). This was in stark contrast to the large-amplitude motion of the corresponding NalP L5 and EspP L3 and L4. As shown in table 1 and Fig. 3, the backbone ϕ dihedral angles of many flexible loop residues in L3, L4 and 4 edge residues in L5 underwent hundreds of transitions among local potential valleys in 10 ns REMD simulations but underwent only a few or no transitions in a 50 nsregular MD simulation. Therefore, we believe that our 10 ns REMD simulations achieved approximately μ^s -level conformational sampling and that the EspP L5 motion is confined within 1.5 Å on the same time scale. These results demonstrate that EspP L5 has rather high native rigidity. It is well established that general ensemble methods perform better for sampling enthalpic barrier limited processes than for entropic barrier limited processes. Cases of both significantly accelerated and decelerated sampling have been reported. Therefore the observed facilitation of backbone dihedral transitions in the flexible EspP loops in this study should not be generalized to other membrane protein simulations (e.g. folding/unfolding of alpha helical membrane proteins).

Table 1.

The number of transitions observed for various backbone ϕ dihedrals in a 50ns regular MD simulation ( N_MD50 ) and 10ns REMD simulation ( N_REMD10 ) of EspP. “ϕ_index” and “SS” are the residue number and thesecondary structure element that the residue resides in.

φindex	SS	NMD50	NREMD10
14	T1	5	613
33	L1	2	233
50	T2	4	429
91	T3	14	528
93	T3	0	386
112	L3	0	206
114	L3	18	318
115	L3	2	504
116	L3	2	24
117	L3	4	599
164	L4	0	205
165	L4	0	232
166	L4	0	380
167	L4	0	314
168	L4	13	374
169	L4	0	572
170	L4	0	105
171	L4	0	210
194	T5	0	239
195	T5	0	23
213	L5	6	210
216	L5	0	318
230	L5	0	146
231	L5	5	446

Figure 3.

Representative backbone dihedral angles ϕ from a 10 ns REMD simulation trajectory (red) and a 50 ns regular MD simulation trajectory (green) for EspP β domain residues 13(a), 91(b), 117(c) and 167(d).

High unfolding energy barrier of EspP L5 revealed by biased MD simulations

To qualitatively characterize the unfolding energy barrier of EspP L5, we carried out biased MD simulations using the HQBM module [25] of the CHARMM program [26]. In this module, the bias potential is applied so as to follow only the thermal motions of a protein away from its reference/native structure. It has the following form:

$$W(r,t)=\{\begin{array}{cc}\frac{\alpha }{2}{(\rho (t)-{\rho }_a(t))}^2& \text{if}\rho (t)<{\rho }_a(t)\\ 0& \text{if}\rho (t)\ge {\rho }_a(t)\end{array}$$

where:

$${\rho }_a(t)=\underset{0<\tau <t}{max}\rho (\tau )$$

and

$$\rho (t)=\frac{1}{N(N-1)}\sum _{i=1}^N\sum _{j\ne i}^N{(r_{ij}(t)-r_{ij}^R)}^2$$

where r_ij = r_i − r_j , $r_{ij}^R$ are the atomic distances from the reference structure, and N is the number of selected atoms experiencing bias potentials. The time needed for the unfolding (t_unfolding ) upon application of bias potentials reflects the height of the energy barrier ( E_a )(including some irreversible work). Different levels of bias potentials [with the force constant α ranging from 20 to 100 kcal./(mol · Å⁴) ] were applied to the backbone atoms of residues 215 to 228, and the response of the protein was monitored after bias forces were turned on. The center of mass of the β strands was harmonically constrained to stay within the lipid bilayer with a force constant of 100 kcal / (mol · Ų) . Five trajectories were generated for each level of applied force. The time needed for a significant deviation (greater than 5 Å on average) of EspP L5 from its native position varied from a few hundred ps when α = 100 kcal / (mol · Å⁴) to a few ns when α =50 kcal / (mol · Å⁴) , as demonstrated by the RMSD plots in Fig. 3. For weaker bias potentials [e.g. α = 20 kcal / (mol · Å⁴) )], no significant movement of L5 wasobserved within 2 ns(data not shown). Snapshots from a typical trajectory of the loop movement under the bias force constant of 100 kcal / (mol · Å⁴) are presented in Fig. 3. Upon the application of bias forces, many new side chain interactions between L5 and other loops/β strands (L1, L3, L4, β 3, β 4, β 5 and β 6) started to form because these loops/β strands geometrically constrain the movement of L5. At some point (e.g. at : 170 ps for the trajectory shown in Fig. 3, see the dashed vertical line), the increased strain caused the constraining loops (L1,L3 and L4) to move and consequently enlarged the extracellular side of the channel, thus providingmore room for L5 to extend itself under the bias potential which was applied to drive L5 away from its native position. The more extended L5 pushed the constraining loops further until it almost became a linear peptide segment (Fig. 3, 500ps time point). The sequence of events is reflected in the RMSD plot (Fig. 3). A major increase in the L5 RMSD was preceded by a small increase in the RMSD of other constraining loops ( : 170 ps in Fig. 3). Although the RMSD and snapshots from only one of the trajectories is presented, qualitatively similar results were obtained for all the trajectories we generated (data not shown). Because EspP L5 does not form significant backbone hydrogen bonds, its native position is maintained by hydrogen bonds between its sidechains and inward pointing side chains of the β barrel. The geometric constraints imposed by β 3 through β 6 and L1, L3 and L4 require that the native interactions between L5 and other parts of the protein, as well as some native interactions within the constraining segments, be eliminated before L5 can be pushed away from its native position. Additionally, the constraining residues easily formed new non-native interactions with L5 due to their physical proximity. Such non-native contacts present further challenges for the complete extension of EspP L5 (Fig. 3,500ps).

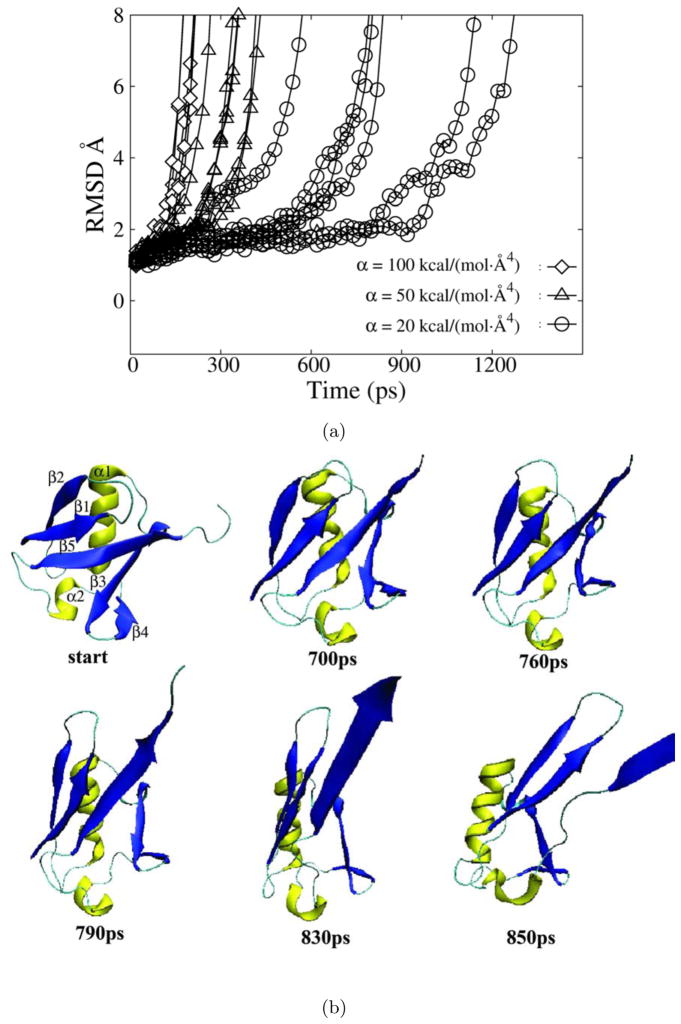
To compare the unfolding energy barrier of EspP L5 to that of a well studied globular protein, we carried out biased MD simulations of ubiquitin. Ubiquitin (pdb code: 1ubq) was fully solvated and the equilibrated structure (from a 2ns equilibrating run) was used as the starting point for HQBM simulations. The bias potential was applied to all C_α atoms and no constraints were applied. Indeed, the unfolding of ubiquitin on a ns time scale required a much smaller bias force constant (α = 20 kcal / (mol · Å⁴) ) than the extension of EspP L5 (Fig. 5). The snapshots from a representative HQBM unfolding simulation of ubiquitin are presented in Fig. 4. Although the sequence in which backbone hydrogen bonds were broken varied from one trajectory to another, in general, the major helix α 1 and β strands β 1 and β 2 exhibited greater stability than β strands β 3, β 4 and β 5 (Fig. 5). These results agree qualitatively with experimental reports[22,21] and other simulations[9,27,28]. Because of the ns time scale limitation in our simulations, significant irreversible work is generated in biased unfolding of both EspP L5 and ubiquitin. Considering the fact that unfolding of ubiquitin involves the displacement of more water molecules and protein residues, the amount of irreversible work resulted from the rapid unfolding of ubiquitin should be no less than that caused by the unfolding of EspP L5. With a bias force constant of α = 20 kcal / (mol · Å⁴) , ubiquitin unfolded within 1 ns for all 5 trajectories. The fact that no unfolding event was observed for EspP L5 in 2 ns in any of the 5 trajectories strongly suggests that the unfolding barrier of EspP L5 is higher than that of ubiquitin.

Figure 5.

HQBM simulations of ubiquitin. a) The RMSD of the ubquitin backbone atoms as a function of time for simulations in which bias potentials with a force constant α of 20 kcal / (mol ·Å⁴) (circles), 50 kcal / (mol ·Å⁴) (triangles) and 100 kcal / (mol ·Å⁴) (diamonds) was applied. b) Snapshots taken at the indicated time points during a HQBM trajectory in which a bias potential with a force constant of 20 kcal / (mol ·Å⁴) was applied. α helices are shown in yellow and β strands are shown in blue. For clarity, some C-terminal residues were omitted from partially unfolded structures.

Figure 4.

HQBM simulations of EspP β domain with bias potentials applied to L5 residues. a)The RMSD of L5 backbone atoms as a function of time for simulations conducted under bias potentials with force constants ha of 100.0 kcal /(mol ·Å⁴) (open squares) and 50.0 kcal /(mol ·Å⁴) (filled circles). b)The RMSD of backbone atoms of various parts of EspP (L5: filled circles; β strands: triangles; other loops/turns: open circles) for a simulation trajectory with a bias force constant of 100 kcal /(mol ·Å⁴) . The vertical dashed line indicates the small RMSD increase of other loops preceding the major RMSD increase of L5. c) Snapshots taken at the indicated time points from a typical trajectory in which a bias potential with a force constant of 100 kcal / (mol ·Å⁴) was applied to L5(shown in red).

High unfolding energy barrier of EspP L5 revealed by pulling simulations

It is well established that mechanical unfolding of a protein generally traverses different pathways than thermal/chemical unfolding [29,30,31,32] and that the mechanical resistance of proteins depends on the direction of the load[33,34,11,35]. To elucidate how EspP L5 responds to mechanical forces, we carried out pulling simulations with different levels of upward constant forces along the membrane norm applied to the tip region of L5 (residues 222 through 224). The center of mass of the β strands was constrained with harmonic forces to stay within the lipid bilayer as in the biased MD simulations described above.

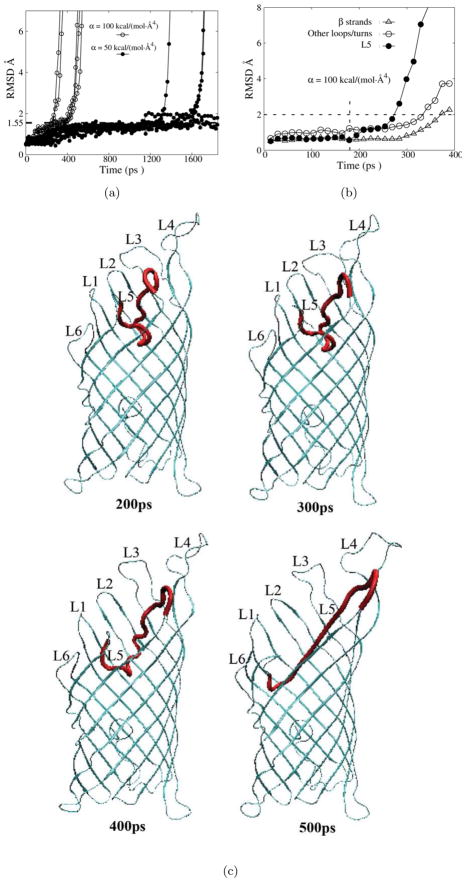
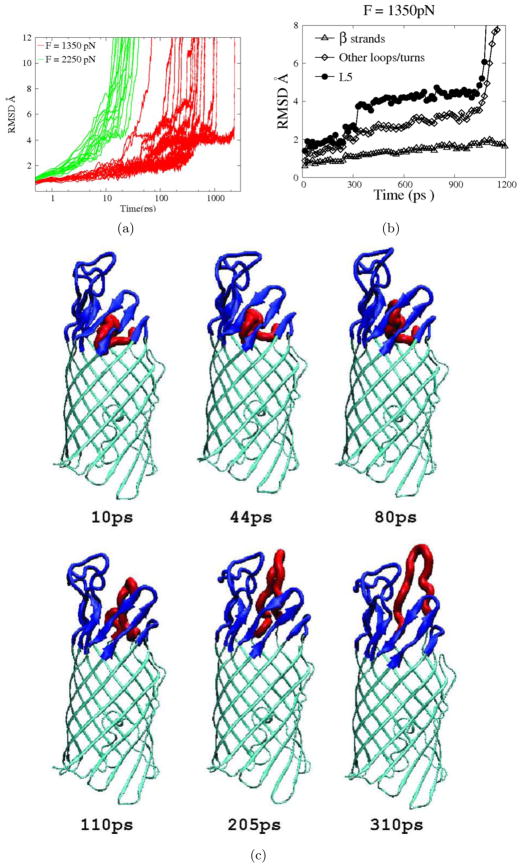
We first generated five 2-ns pulling trajectories with an applied pulling force of 750 pN. Only partial unfolding was observed for 2 trajectories with the largest RMSD of L5 residues from their native position being only : 4 Å, and the RMSD of EspP L5 was limited to 2Å for three other trajectories(data not shown). To observe mechanical unfolding of EspP L5 on a ns time scale, 20 trajectories were generated with applied forces of 1350 pN and 2250 pN, respectively. At a pulling force of 1350 pN, the time needed for complete extraction of L5 from the barrel varied approximately two orders of magnitude from 27 ps to more than 2 ns. At a pulling force of 2250 pN, the unfolding times ranged from 9 ps to 25 ps. For 18 out of the 20 trajectories we generated using a pulling force of 1350 pN, the RMSD of L5 residues paused around 4 Å and formed a shoulder region (Fig. 5) before itsrapid increase, which represents the final stage of the removal of L5 from the barrel. This observation suggests that the structures corresponding to the shoulder region of the RMSD curve represent a rather stable ensemble of intermediate states. At thisstage, some native sidechain hydrogen bonds were lost (residue pairs 215–230, 220–105, 220–107, 222–79), while some non-native sidechain hydrogen bonds (residue pairs 216–159, 220–109, 221–77, 222–109, 222–77, 226–77 and 228–30) formed. A representative structure of this ensemble is presented in Fig. 5(see 80ps timepoint). Other stages of the removal of L5 from the barrel are also shown in Fig. 5.

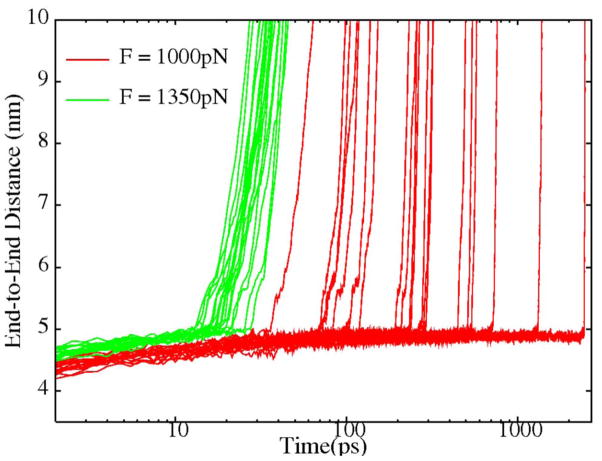
In many AFM studies on the mechanical unfolding of ubiquitin and titin I27, pulling forces of : 100 pN were used[7]. Slightly larger forces were used in many simulation studies utilizing a Go type potential[36,14,27]. However, because the inclusion of explicit water molecules significantly increases the irreversible work required for short time-scale, non-equilibrium unfolding, it was necessary in our pulling simulations ofEspP L5 to apply much larger forces (> 1000 pN) to induce unfolding on a ns time scale. For comparison, we pulled fully solvated ubiquitin from the two termini, available evidence suggest that ubiquitin is especially resistant to mechanical denaturation when pulled in this manner[35]. As shown in Fig. 7, with a pulling force of 1350 pN, ubiquitin exhibited a very narrow distribution of unfolding times ranging from 12 ps to 28 ps.However, at a pulling force of 1000 pN, the unfolding times not only become much longer, but also become more widely distributed from 37 ps to more than 2 ns, a range of almost two orders of magnitude.

Figure 7.

The end-to-end distance of ubiquitin under different pulling forces (red:1000 pN , green: 1350 pN) as a function of time.

In pulling simulations in which increasing forces are applied, the unfolding kinetics of a protein along the pulling direction will gradually change from a barrier crossing scheme to a diffusion limited downhill scheme. Correspondingly, the unfolding times change from a wide exponential distribution to a very narrow distribution. For ubiquitin, this transition happens somewhere between 1000 pN and 1350 pN(Fig. 7), while for EspP L5 it is somewhere between 1350 pN and 2000 pN(Fig. 5). However, it is difficult to determine the exact unfolding barrier because the observed effective barrier includes the irreversible work (which also varies with pulling forces) involved in the non-equilibrium simulations. Due to the limited number of trajectories, we could not calculate the equilibrium free energy along the pulling direction using the rigorous methodologies developed by Hummer and Szabo[37]. Despite these limitations, if similar irreversible work is assumed for the mechanical unfolding of both EspP L5 and ubiquitin, our data show that EspP L5 has a significantly higher unfolding barrier than ubiquitin. Steered MD (SMD) simulations of titin I27 in explicit water[16,23] demonstrated that complete unfolding occurred within 1 ns when a 750 pN pulling force was applied to both termini, while the same level of applied force only resulted in partial unfolding of EspP L5 within 2 emphns in 2 out of 5 pulling trajectories. This observation suggests that EspP L5 also has higher mechanical stability than titin in the respective tested directions.

The overall movement of L5 in response to upward pulling was very different from that observed during biased HQBM simulations. As illustrated in Fig. 4 and Fig. 6, L5 was pulled out of the barrel upon application of upward pulling forces but was extended within the barrel under biased thermal unfolding. In both cases, a major movement of L5 was accompanied by smaller movements of other loops (Fig. 3 and Fig. 5). This is because the geometrical constraints imposed by β 3 through β 6 and L1, L3 and L4 had to be overcome to some extent in both situations. The difference is that before a major movement (RMSD > 5 Å) of L5 occurred, the RMSD of other loops in biased thermal unfolding remained below 1.7 Å (Fig. 3), whereas the RMSD of other loops rose above 2 Å in mechanical unfolding (Fig. 5). This disparity can be explained by the fact that in mechanical unfolding the direction of residue motions was specified by pulling forces to be upward, while in the biased thermal unfolding the residues experiencing bias forces tended to search for the direction of minimum resistance, resulting in less disturbance of the surrounding structure.

Figure 6.

Pulling simulations of EspP β domain with upward pulling forces applied to the tip of L5 (residues 222–224). a)The RMSD of EspP L5 backbone atoms as a function of time for simulations conducted with a pulling force of 1350 pN (red lines) or 2250 pN (green lines). The time axis is shown in log scale. The dashed square highlights a shoulder region of the RMSD curves corresponding to structures of an ensemble of stable intermediates. b) The RMSD of backbone atoms of various parts of EspP β domain (L5: filled circles; β strands: triangles; other loops/turns: diamonds) in a simulation trajectory employing a pulling force of 1350 pN. c)Snapshots taken at the indicated time points from a typical trajectory in which a pulling force of 1350 pN was applied. L5 is shown red, constraining loops/strands are shown in blue and other residues are shown in cyan.

The structural stability of globular proteins is maintained mainly by backbone hydrogen bonds that create helical and strand structures and by sidechain hydrophobic packing interactions[38,24,39]. However, it is the extensive sidechain hydrogen bonds between L5 and the β barrel and the geometrical constraints formed by β 3 through β 6 and loops L1, L3 and L4 that endow EspP L5 with its structural stability against thermal and mechanical perturbations. The sidechain hydrogen bonds directly maintain the native position of EspP L5. The geometrical constraints are also important in that the displacement of the constraining moieties and the disruption of native interactions within them are necessary for L5 to move away from its native position.

B factors and contact orders of enclosed loops in membrane embedded β barrels

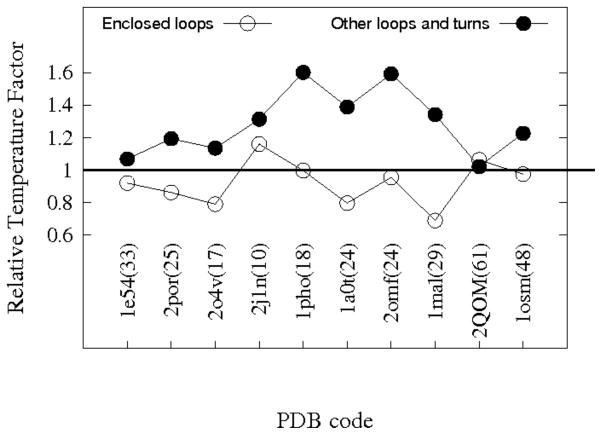
Most MEBBs with high resolution structures have one or two enclosed loops within their barrels. Examination of the B factors obtained from PDB files indicates that the average magnitude of the thermal motion for most of these channel enclosed loop residues is comparable to that of membrane embedded β strand residues and much smaller than that of extracellular exposed loop and periplasmic turn residues (Fig. 8). Thus these loops appear to have little flexibility at their crystallization conditions. The EspP crystal structure (2QOM.PDB) seems to be the only exception, in that thermal factors of its L5 residues are slightly larger than those of other loop/turn residues. However, note that the plotted numbers are averages from residues present in the crystal structures, and extremely flexible residues in exposed EspP loops L3 and L4 are not included. Additionally, the B factors of EspP do not seem to be very informative as even the β strand residues have very large values (61 Ų compared to less that 35 Ų for most other β barrels, see Fig. 8). Strong sidechain interactions between such enclosed loops and β strands are clearly observed in the crystal structures. Therefore, like EspP L5, the structural stability of these loops is likely based on geometric constraints and side chain interactions as relatively few backbone hydrogen bonds are observed.

Figure 8.

The relative temperature factors of enclosed loop residues and exposed loop/turn residues for various MEBBs. The PDB codes are shown for each protein and the numbers inside parentheses besides each PDB code are the average B factors for the β strand residues of that protein. The vertical axis shows the average B factors of enclosed loop residues (open circles) and other loops/turns residues (filled circles) divided by the average B factors of β strand residues. The proteins analyzed were: Anion-selective porin from Comamonas acidovorans(1e54); Porin from Rhodobacter capsulatus(2por); Phosphate specific porin from Pseudomonas aeruginosa(2o4v); Osmotic porin from E.coli(2j1n); Phosphoporin from E. coli(1pho); Sucrose specific porin from Salmonella typhimurium(1a0t); Matrix porin OmpF from E. coli(2omf); Maltoporin from E. coli(1mal); EspP autotransporter β domain from E. coli O157:H7(2qom); Osmoporin from Klebsiella pneumoniae(1osm).

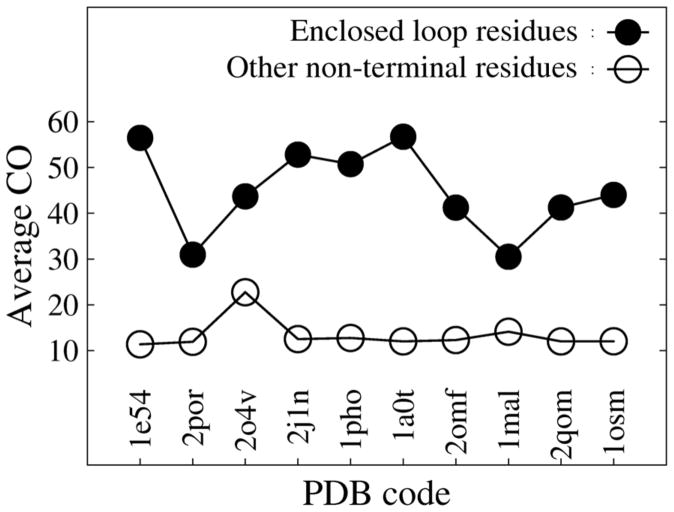
In agreement with the prediction from the Zwanzig kinetic model[40] that larger contact order corresponds to a higher energy barrier of unfolding, the height of unfolding barriers for single domain globular proteins was found to be highly correlated with contact order[41]. The contact order was defined as [EQUATION], where L is the length of a protein, N is the total number of contacts and Δ S_ij for each contact pair is the distance between participating residues i and j in the primary sequence of the protein. Contact is defined by a smaller than 7.5 Å inter-residue C_β distance (C_α is used for Gly), and neighboring residues are excluded from the contact count. Defining contact order for each residue i as ${CO}_i=\frac{1}{N}{\sum }_{k=1}^N\mathrm{\Delta }{S}_{ik}$, the average contact order for enclosed loop residues and other non-terminal residues (excluding residues in the first and last β strands and 5 immediate neighhoring residues of the terminal β strands) are plotted for 10 MEBBs in Fig. 9. The enclosed loop residues have a much higher contact order (ranging from 30 to 56) than other non-terminal residues (ranging from 11 to 22). Without many side chain interactions and geometric constraints, it is hard to imagine that L5 would have high structural stability. Alternatively the structural stability of L5 might be maintained by strong local interactions (in terms of primary sequence) with the barrel, which would correspond to a smaller contact order. However, in that case the effect of geometrical constraints and the structural stability of L5 would be reduced significantly. Therefore the high unfolding barrier of EspP L5 suggests that the correlation of contact order with unfolding barriers might go beyond single domain globular proteins.

Figure 9.

Average contact orders for barrel enclosed loop residues (filled circles) and other nonterminal residues (open circles) from 10 MEBBs (the same set of proteins shown in Fig. 8).

Discussion

Using equilibrium and non-equilibrium simulation studies, we found that EspP L5 has high structural stability. This is reflected by its smaller allowed magnitude of motion when compared with other loops in EspP and NalP, and by its higher unfolding barrier when compared with secondary structure elements of ubiquitin. Interestingly, the structural stability of EspP L5 is maintained by side chain hydrogen bonds and geometric constraint. In contrast, the stability of globular proteins is maintained by backbone hydrogen bonds and hydrophobic packing interactions[14,9,27,42,19,16,24]. An examination of the B factors of the residues in channel enclosed loops of MEBBs indicates that while they serve different biological purposes from that of EspP L5, they seem to share similar structural stability. Additionally, a contact order plot (Fig. 9) indicates that most of the enclosed loops interact with distant residues in the primary sequence. Based on the fact that backbone hydrogen bonds are either absent or very limited in these channel enclosed loops, we speculate that like EspP L5, their structural stability depends mainly on geometric constraints and polar side chain interactions. In many proteins, functionally important flexible/disordered moieties are supported by structural scaffolds which are stabilized by backbone hydrogen bonds and hydrophobic packing[43]. Enclosed loops in MEBBs constitute a different class of stable structures not only in that they have a different molecular basis of structural stability, but also in that they integrate a functional property (i.e. transport modulation) with structural stability.For example, the enclosure of L3 inside barrels of many porins forms a restriction that generates different types of substrate specificity[6]. It has been demonstrated that mutations in the enclosed loops of porins from Rhodopseudomonas blastica and Paracoccus denitrificans significantly change their transport properties[44,45]. From a protein design point of view, this structural feature allows a β barrel scaffold to be decorated internally by different loop arrangements to achieve different transport specificity. Furthermore, for porins, such loop-based decorations restrict only a very small portion of the channel formed by the β barrel, creating a funnel-like internal surface at both sides that minimizes the reduction of transport efficiency.

In force spectroscopic and computational studies of the behavior of globular proteins under thermal and mechanical forces, no constraint is usually applied except for the fixture of one end of tandem proteins for pulling experiments and simulations.In this study, the focus was on the behavior of a loop enclosed within a membrane-embedded barrel. Therefore, constraining the whole protein in a lipid bilayer was necessary. If no constraint was applied, the applied bias forces or pulling forces might have partially or completely driven the protein out of the membrane, thus derailing the goal of understanding the behavior of membrane proteins in their natural environment. While the utilization of an implicit membrane model can greatly extend length of simulation trajectories, explicit representation of lipid bilayers was adopted in this study based on two reasons. Firstly, formulation of many implicit membrane models are solely based on thermodynamics of transferring residues from an aqueous phase to alipid phase, while we are also very interested in the kinetic barrier of the unfolding of L5. It is not known how implicit membrane models influence the relevant kinetics. Secondly, using an implicit membrane model would make a direct comparison of unfolding times of L5 with those of globular proteins in explicit water more difficult.

For a simple two state folder, if diffusive dynamics and a single ensemble of pathways are assumed, the unfolding times from HQBM simulations truthfully reflect the height of the unfolding energy barrier. However, this is not necessarily true if one or more intermediates are involved and a strong bias is applied. For example, if there is one intermediate (I) ensemble of states providing alternative pathways between the native (N) ensemble of states and an ensemble of denatured (D) states for a givenprotein, with energy barriers Δ_NI < Δ_ND < Δ_ID , then N → D will be the dominating folding/unfolding pathway and the energy barrier will be approximately Δ _ND in an unbiased thermal unfolding. However, in a HQBM simulation, because Δ _NI < Δ_ND , a protein starting at a native state will more likely go to an I state. If the bias potential is significantly larger than Δ_ID , a protein will more likely go to a D state from an I state, the resulting dominating unfolding pathway will be N → I → D and the unfolding energy barrier will be approximately Δ _ID . Therefore, HQBM simulations might reflect an unfolding energy barrier higher than the real barrier. Should such alternative pathways exist, it is possible that the observed high resistance of EspP L5 to strong bias potentials is an artifact of strong bias. From our HQBM simulations, it seems that there was at least one intermediate in which the RMSD of L5 backbone atoms remained around 1.55 Å (see Fig. 3) before rapid and complete extention of L5 occurred. However, the fact that all of the trajectories we generated went through this intermediate ensemble suggested that an alternative unfolding pathway, should it exist, probably has a significantly higher energy barrier than that of the pathway to this intermediate. Additionally, the transition of EspP L5 to this intermediate ensemble took more than 200 ps when the bias force constant was 50 kcal /(mol · Å⁴) and did not occur within 2 ns when the bias force constant was 20 kcal / (mol · Å⁴) . Our observations indicate that the energy barrier separating the EspP native ensemble from this intermediate ensemble is higher than the energy barrier of biased ubiquitin unfolding, which occurred within a few hundred ps under a bias potential with a force constant of 20 kcal / (mol · Å⁴) (Fig. 5). Therefore, despite the aforementioned potential caveats of the HQBM method, the conclusion that EspP L5 has higher unfolding barrier than the secondary structure elements of ubiquitin is still valid.

Protein structures are mainly selected to fulfill their biological functions. For NalP, upon the cleavage of the passenger domain, the amino terminal α helix almost completely blocks the central channel. However, for EspP, the remaining amino terminal α helix does not block the whole channel and one would intuitively expect that the enclosure of L5 helps maintain the permeability barrier. Our simulations revealed that EspP L5 has little flexibility in its native state and has a high unfolding barrier and is therefore well suited for the purpose of blocking the channel. This is consistent with an earlier experimental report[3] that L5 helps block the diffusion of antibiotics. Other barrel enclosed loops in various porins mainly restrict the size of their channels to achieve transport specificity or facilitate the translocation of charged species. All of these different functions require a high degree of structural stability, which is likely provided by geometric constraints and polar side chain interactions between enclosed loops and β strands.

Based on the experimental finding that the β barrel gives L5 its structural stability and our results from simulations, we predict that any point mutation in L5 will not significantly influence its structural stability for two reasons. Firstly the large number of contacts between L5 residues and the barrel reduces the relative importance of each residue. Secondly, due to the geometric constraints formed by the barrel, elimination of one interaction may be accompanied by formation of new favorable interactions. For the same reasons, stable loops embedded in β barrels are well suited for the static modulation of substrate transport but not useful for the dynamic control (e.g. opening and closing) of β barrel channels.

The mechanism of autotransporter secretion remains a mystery. Recent experimental evidence increasingly suggests that autotransporters are not self-contained secretion systems in the sense that other factors are required for translocation of the passengerdomain across the OM[1,46]. Our simulation results suggest that if the barrel channel is used for the translocation of the passenger domain, L5 needs to be excluded from the barrel at an early stage of assembly because its displacement requires a large amount of energy. Furthermore, a significant energy source is not likely to be found in the periplasm, which lacks ATP. The simulation data are consistent with a previously proposed model in which L5 folds into the β barrel only after cleavage and release of the passenger domain from the barrel[3].

Methods

All simulations were carried out with the CHARMM program. The particle-mesh-Ewald (PME) technique was used for electrostatics interactions. A switch on distance of 8 Å and a cutoff distance of 12 Å was used for non-bonded interactions. We used an integration time step of 1fs. EspP was solvated with 128 DMPC molecules and 9623 TIP3P water molecules. 22 chloride ions and 27 sodium ions to maintain the charge neutrality and a salt concentration of 0.1M were included. REMD simulations of EspP were carried out in a NVT ensemble with a 67.38 Å × 67.38 Å × 97.18 Å tetragonal box (the box size was obtained from the initial 2.5-ns NPT simulations). 32 replicas with a linear temperature separation of 2 degrees (from 310K to 372K) were simulated. A Hoover thermal piston mass of 10000 kcal / (mol · ps²) was used for maintaining the temperature for each replica. HQBM simulations of EspP were carried out under the same conditions as that ofthe 310K REMD replica except for the addition of bias potentials to either L5 residues or L3 and L4 residues. Regular simulations of EspP were carried out in a NPT ensemble with a piston mass of 500 amu (atomic mass unit). For NalP, the REMD simulations were carried out in a 69 Å × 69 Å × 96.45 Å tetragonal box in a NVT ensemble. The temperature windows used for EspP were also used for NalP. HQBM simulations of ubiquitin were performed in a cubic period box of 50.76 Å, with 4003 explicit TIP3P water molecules in an NVT ensemble. The starting structure was taken from a 2-ns NPT equilibrating run. Temperature factors of each residue were calculated as the average of that for the heavy backbone atoms. In thecontact order calculation, the secondary structure assignment (β strands or loop/turn) was based on information provided in respective PDB files. Since many residues of NalP L5 and some residues of EspP L3 and L4 are missing in the crystal structures (Fig. 1), their starting coordinates were built with Modeller[47]. However, the large magnitude of motion observed duringthe simulations renders the starting configurations of these residues rather unimportant.

Figure 2.

a)The RMSD of various components of EspP backbone atoms as a function of time during a 10-ns REMD simulation. Backbone atoms of the whole protein(open squares), the β strands(filled squares), and the extracellular loops and periplasmic turns (open circles) are shown. b)The RMSF of EspP (squares) and NalP*(circles) during the simulations shown in part a). α α helix; β: β strand; T: periplasmic turn; L: extracellular loop.