Abstract
We have only a vague idea of precisely how protein sequences evolve in the context of protein structure and function. This is primarily because structural and functional contexts are not easily predictable from the primary sequence, and evaluating patterns of evolution at individual residue positions is also difficult. As a result of increasing biodiversity in genomics studies, progress is being made in detecting context-dependent variation in substitution processes, but it remains unclear exactly what context-dependent patterns we should be looking for. To address this, we have been simulating protein evolution in the context of structure and function using lattice models of proteins and ligands (or substrates). These simulations include thermodynamic features of protein stability and population dynamics. We refer to this approach as 'ab initio evolution' to emphasise the fact that the equilibrium details of fitness distributions arise from the physical principles of the system and not from any preconceived notions or arbitrary mathematical distributions. Here, we present results on the retention of functionality in homologous recombinants following population divergence. A central result is that protein structure characteristics can strongly influence recombinant functionality. Exceptional structures with many sequence options evolve quickly and tend to retain functionality -- even in highly diverged recombinants. By contrast, the more common structures with fewer sequence options evolve more slowly, but the fitness of recombinants drops off rapidly as homologous proteins diverge. These results have implications for understanding viral evolution, speciation and directed evolutionary experiments. Our analysis of the divergence process can also guide improved methods for accurately approximating folding probabilities in more complex but realistic systems.
Keywords: lattice models, divergence, recombination, evolution
Introduction
Despite over 30 years of serious effort, the mysteries of protein structure and function are sufficiently complex that it is not possible accurately to predict novel structures from their sequence information and first principles [1-4]. In evolutionary genomics, therefore, people have tended to use extremely simple models of protein evolution for theoretical purposes [5]. These models often have little relation to proteins as thermodynamic molecules and have been further constrained by the limits of computational resources and algorithm development;[6-8] reconstruction of evolutionary processes is itself an extremely difficult and not yet entirely solved problem.
Until recently, evolutionary models used in comparative genomics almost uniformly assumed that substitution probabilities were unchanging and the same at all sites, except for variation in the average rate. A few groups have recently begun to incorporate a broader view of the context dependence of evolutionary rates and, in particular, to incorporate interaction among protein residue positions, or molecular co-evolution, into the evolutionary model [9-11]. A critical component of modern approaches is to observe variance in substitution probabilities and co-evolutionary interactions without presupposing their cause and then relate these observations to structural and functional features.
It is fairly clear (to us, at least) that current concepts of how proteins evolve are not sufficiently robust to build good reality-based evolutionary models and are likely to be misleading in many aspects -- for example, when trying to differentiate selection and adaptation from neutral or random processes. Due to the large numbers of sequences and genomes from diverse organisms which are rapidly accumulating in worldwide databases, however, the potential for evolutionary analysis to inform genomics studies on molecular structure, function and interaction is enormous. We are beginning to obtain more detailed and densely sampled taxonomic datasets that are allowing much more sophisticated deconstruction of site-specific and variable rates and are developing methodology to take these datasets into account [12-19]. In spite of this progress, the lack of reasonable expectations for precisely how structural and functional contexts affect evolutionary processes hinders the development of realistic models.
As a consequence of this situation, we have embarked on a long-term series of studies to utilise thermodynamic models of proteins and protein function, in conjunction with population simulations, to improve our understanding of protein evolutionary dynamics and make better predictions of the effects to test for in real proteins. What happens in evolution that allows variation to exist with no apparent effect in some species, but causes disease in others? How do we expect ligand binding, catalysis and protein-protein interaction to affect evolution -- and how far across a protein should the effects of these interactions spread? Do different types of proteins behave differently (and what defines a 'type')? How does the strength of selection (or the importance of a function) affect evolution, and how does population size modulate this effect? It is our experience that intuition is not necessarily a good guide, and that proteins evolved in semi-natural populations can have very different properties to random proteins or proteins evolved in an ad hoc fashion [20,21].
We use the term 'ab initio evolution' to describe our approach, to emphasise the fact that the distributions of selective effects in these models arise naturally from the system, rather than as a consequence of artificially constructed distributions of selective effects or from artificial and overly simplistic adaptive landscapes. This approach owes a great deal to a long history of work on energy-based landscapes, both for RNA and for proteins. In our work, we particularly focus on protein-like structures (ie the energy landscape is not solely limited to pairwise interactions, as in nucleic acid structure), 'proteins' evolved to equilibrium in reasonably large populations and also on reasonably complex interaction energies (ie we use empirically based interaction potentials that are different for every pair of amino acids, not simplified to a basic two-state hydrophobic potential).
We also focus on patterns of evolution that can emerge from the interaction between structure, function and selection in a thermodynamic system, rather than focusing on a perfectly accurate representation of protein energy or on protein structure prediction. For example, we introduced one of the first, and up to this time one of the few, models that allowed a diverse and manipulable protein function criterion that was separate from the simple criterion that a protein need only fold in order to function [22]. We have also been interested in the effect that the details of protein structure may have on the evolutionary process. The size of the sequence space that will fold to a particular structure, also known as the structural designability,[20,23-25] has a particularly important influence. For example, a small number of structures are what is called 'highly designable', but, because (by definition) many more sequences are compatible with these structures than with other structures, they are more often compatible with random mutations and thus evolve more quickly.
We present here an analysis of the process of divergence with regard to structural designability and thermodynamic competition with adjacent structures. We consider how the context changes as divergence proceeds, as measured by the fitness of recombinants that result from homologous recombination between divergent proteins. We use the common genetic definition of 'homologous'; Cui et al.[26] previously studied the functionality of recombinants under a hydrophobic and polar (HP) model, but used a novel definition of 'homologous' that did not involve divergence and did not involve a naturally evolved and selected population. Aside from the 'Materials and methods' section, we avoid extensive discussion of the biophysical details in order to present the evolutionary motivations of the research clearly to a broad genomics audience. These details are available in numerous previous publications by ourselves and others [27-29]. Since a central focus of our work is to infer biologically realistic models that may be useful for predictive application in evolutionary genomics, we provide detailed consideration of various choices with regard to aspects of the models that might be simplified or made more complex, and suggest new approaches for future modelling.
Materials and methods
Modelling protein evolution on a lattice
The main biophysical considerations in modelling proteins on a lattice have been given in detail previously [22,30,31]. In brief, however, for each sequence we consider its energetic compatibility with the entire ensemble of maximally compact two-dimensional arrangements that are possible on a regular lattice. We analyse sequences of length 25 or 36, which thus have maximally compact arrangements that are perfect squares, with side lengths of five or six. The two-dimensional approximation allows us to consider all possible structures in reasonable computational time and also has a more realistic ratio of internal to surface residue positions. Compatibility of a sequence with a two-dimensional arrangement, called a 'structure' or 'fold', is calculated by considering the residues that are adjacent to one another on the lattice, but not connected along the sequence. Thus, the energy, , of a protein sequence k in fold f is calculated as the sum of all such interactions in the fold. The energy of each specific amino acid interaction is given by the empirical Miyazawa-Jernigan potential, which is based on the frequencies of observed contacts in known crystal structures [32]. We do not directly address folding kinetics in this study, but include a folding approximation in our fitness equation (below). Assuming thermodynamic equilibrium among the structures, and using standard Boltzmann statistics, the probability that sequence k will be in fold f is given by:
| (1) |
where RT is the universal gas constant multiplied by temperature (here, room temperature in degrees Kelvin). Z is the canonical partition function, which is simply the sum of the numerator in Equation 1 over all possible structures.
Sequence evolution in populations
We modelled evolution in constant-size haploid populations of 1,000 individuals with a mutation rate of 0.05 mutations per protein per generation (ie for each generation, five mutants are expected to arise in the population). Fitness was based primarily on the probability of folding into a specific 'native' structure, fN, which is presumed to be required for protein function and which was prespecified for any given simulation. The ability of a sequence to achieve a fold kinetically is also an important consideration that is often modelled,[23] but we considered kinetic folding to be more realistic as a minimum requirement, and thus included foldability as a step function such that proteins estimated to fold slower than a critical cutoff had extremely low fitness. For any sequences remotely close to evolutionary equilibrium, foldability was always far above the minimum cut-off and the fitness of a sequence k, was thus:
| (2) |
Each generation consisted of mutation followed by selection of sequences according to their fitness, followed by random multinomial sampling to create the subsequent generation. We also evaluated the potential for two structures (i and j) to be 'co-selected' by using a modified fitness function:
| (3) |
with the division by one-quarter introduced because the sum of both folding probabilities must be less than one, hence their multiple is, at most, 0.25.
In preliminary simulations, the time for populations of sequences to reach equilibrium (as measured by the autocorrelation of the fitness between well-separated generations) depended on the native structure chosen. We therefore ran all simulations conservatively to 5,000 generations prior to any analysis, a cut-off that suffices for all structures. To study the divergence of sequences, equilibrium populations were duplicated and allowed to evolve independently under identical conditions. After duplication, the most frequent sequences in each population were sampled every 500 generations. At each sampling point, the two sequences were recombined at all possible sites and the probability of folding into each structure was evaluated for each reciprocal recombinant. To summarise this information over a sample of size S, and all possible recombinants, we generalised Taverna and Goldstein's occupancy measure for a sequence of length 25 [33] as:
| (4) |
in which case there are 48 different reciprocal recombinants. For comparison, we also considered the occupancy of each structure in the entire parent population over the entire course of evolution. We present the difference between the natural logarithms of these two measures as the 'Δ(ln occupancy)' measure for each structure. We also, of course, considered the fitness of the recombinant sequences.
Structural comparison
We considered the results of our simulations in terms of two structural features. First, we classified alternative structures by their distance from the native structure. Since contact energy between residue pairs solely determines compatibility of a sequence with a particular structure, we measured the distance between two structures by the number of contact pairs that the structures had in common. A compact structure for sequences of length 25 has 16 contact pairs, and for a sequence of length 25 this distance measure varies between 0 and 14. The other structural feature we considered was the 'designability' of a structure, which is defined as the proportion of random sequences that 'fold' to that structure [23]. Here, we considered that a sequence 'folds' to a particular structure if the probability of folding (Equation 1) was greater than 98 per cent. We use this definition because it closely matches the average probability of folding at evolutionary equilibrium in our fitness-based population simulations. We divided sequence space into three levels, according to the designability criterion, which we designate 'low-', 'medium-' and 'high-designable' structures. About 50 per cent of the sequences in foldable sequence space fold to the 10 per cent most designable structures. The medium-designable structures, accounting for another 20 per cent of structures, account for 40 per cent of the designable sequence space, and the remaining 70 per cent -- the low-designable structures --account for only about 10 per cent of the designable sequence space.
Approximating the probability of folding with fewer structures
As a result of the analyses presented here, it is apparent that not all structures play an equal role in determining the evolutionary trajectory through sequence space. We therefore considered whether we might carry out an efficient approximation of the probability of folding to the native structure, based on our results and a carefully considered sampling of the structural ensemble. This may allow much more efficient simulation of longer sequences in two or three dimensions. For a structure space of F folds, the partition function can be split into two parts:
| (5) |
where the first part is summed over the C folds closest to the native fold (based on shared contact pairs) and the second part is summed over the remaining folds. We approximate the partition function by calculating the energies of all C folds, but taking a small random sample of the F - C folds that are more distant from the native structure. To reduce variance, we also tried breaking the F - C more distant folds into categories according to their distance from the native fold and then randomly sampling to estimate the partial Z score for each distance category separately.
Results
Considerations on model complexity
The simplicity of the model used in protein evolutionary simulations can have a large influence on what questions can be asked and answered with these systems. Relatively more accurate models (for example, all-atom models that incorporate van der Waals effects, electrostatic interactions, amino acid rotamer information and other important physical principles) will give more precise and realistic energies for a single structure than simpler models, but the computational time spent calculating each variant is much longer, meaning that the evolutionary time span that can be simulated is severely limited. Neither is there as much potential for thorough consideration of a large sample of structural alternatives, nor is it feasible to evolve a large population. This means that, although the individual energies are more accurate, the entropic contributions to energy are much less accurate and the consequences of long-term evolution are ignored. We sometimes utilise such models to link our results more closely to real proteins (Xu, Y. and Pollock, D., unpublished data), but in this paper we present results from simple lattice models because we are concerned here with long-term processes of divergent evolution. The simplicity of the function allows us to sample the energy function over many types of structures, and to replicate results.
There are numerous alternatives and choices for simplification, even in simpler lattice-based models [27,28]. Some of these may depend simply on choice, while others depend heavily on what questions are being addressed. We usually use a simple contact potential from Miyazawa and Jernigan (MJ),[32] but we avoid further simplification to the HP model [27] because we are interested in the effect of the more numerous and subtle interactions in the full MJ potential and there is little computational cost compared with the HP model. Furthermore, with the MJ potential, it is extremely rare to find a sequence that folds equally well to two structures, whereas this is common with the HP model.
Other choices with regard to simplification are the length of sequence, the dimensionality, limiting the analysis to compact structures and the consideration of the folding process. The choices we have made in the current study have mostly been made to allow more thorough long-term evolutionary analysis. Three dimensions allow much more conformational flexibility than two dimensions, meaning that there are many more structures to consider. For the lengths of sequence that can be managed, three-dimensional structures have unrealistically few 'core' sites due to their small size. Likewise, there are far more non-compact structures than compact structures, but most of these structures are much less stable than the compact structures (because they necessarily make fewer contacts). Structure or fold space also increases exponentially with sequence length, and so the choice of sequence length is simply a matter of how much computational power is available and how many variants must be calculated in the study. Further specifics on some of these trade-offs are given later in the results, where we consider the potential for approximations that could restrict the impact of some of these computational limitations. The folding process itself is even more complex and we do not generally consider it in great detail. It appears that, for the most part, however, equilibrium sequences produced by evolution based on a thermodynamic fitness function are also predicted to fold well (data not shown).
A further benefit of simple models over more complex models is that simple models allow clear sufficiency proofs. In other words, if we can find evidence for a particular behaviour in a simple model, this can provide a simple and comprehensible explanation, whereas a more complex model can be more difficult to parse and reduce to its meaningful components. Also, we can test more variables in a simple model to ascertain the most important model details, rather than having only one or a few enigmatic examples, as is often the case for more complex models.
Divergence, recombination and designability
As proteins diverge from one another, we can reasonably expect that recombinants formed between these proteins may eventually cease to function because of accumulated co-evolutionary incompatibilities between the divergent halves of the proteins. We can also expect that the specifics of this process are difficult to predict. An important initial question is whether this process varies between different kinds of proteins (as measured by designability, the number of sequences that can fold into a particular structure) and whether competition with specific alternative misfolded structures is responsible for poor folding in recombinants. We measure this competition by considering the probability of folding to alternative misfolded structures (the occupancy of the alternate folds) during normal evolution and after recombination between divergent proteins.
Visually, the occupancy of misfolded structures had a log-linear relationship in both the parental and recombinant populations, with no clear differences between proteins with different designability levels (data not shown). This means that there is not a large difference in how target structures with different designabilities mutate to deleterious sequences. There is, however, a large difference between low-, medium- and high-designable structures in terms of the extent to which the recombinants are worse than their parents (Figure 1).
Figure 1.
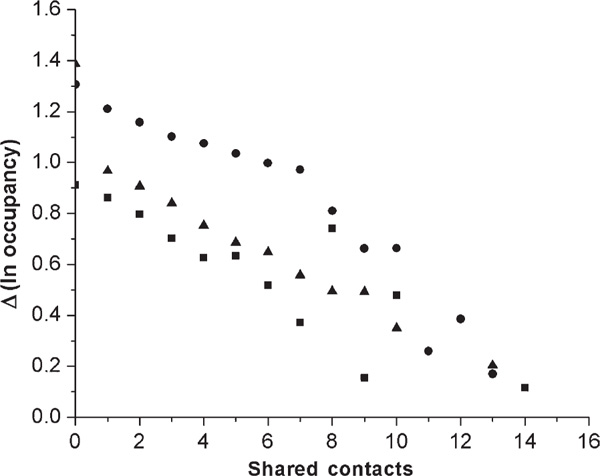
Differences between alternative structure log occupancies in parental and recombinant proteins. The average differences after one million generations for eight high-, 24 medium-, and 32 low-designable target (native) structures are represented with squares, triangles and circles, respectively, with results for each structure replicated four times. The differences in the natural log occupancies decrease linearly with the number of shared contact pairs, although there are many fewer alternative structures with large rather than small numbers of shared contacts -- and thus much more variable results. The difference in log occupancies between low-designable and medium- and high-designable structures is consistent, meaning that the occupancy of alternative (non-native) folds in low-designable recombinants is about one- to two-fold higher.
The difference in the misfolding of alternative structures in recombinants is necessarily reflected in a similar difference in the probability of folding to the native structure -- that is, the fitness of recombinants. This is seen in a rapid and continuing decrease in the fitness of low-designable recombinants over the course of evolution (Figure 2). High- and medium-designable structures have a much slower rate of decrease. We observe here that there is apparently considerable asymmetry in the fitness of reciprocal recombinants. For high- and medium-designable proteins, the more fit of the two reciprocal recombinants is on average only slightly less fit than the parental type, even after one million generations of evolution. By contrast, even the better of the two reciprocal recombinants is substantially less fit than the parents in low-designable proteins, and the worse of the two is dramatically poorer than any other recombinants. Although it is in some ways surprising that the various levels of fitness of recombinants are not worse than they are, the drops in fitness for the recombinants are such that they would be removed from the population by natural selection. According to standard population genetics theory,[34] for a population of 1,000, fitness differences of 1/1,000 are considered selectable, and fitness differences greater than 1/100 (Ns > 10, where N is the population size and s is the selective effect) are considered to be strong selective differences.
Figure 2.
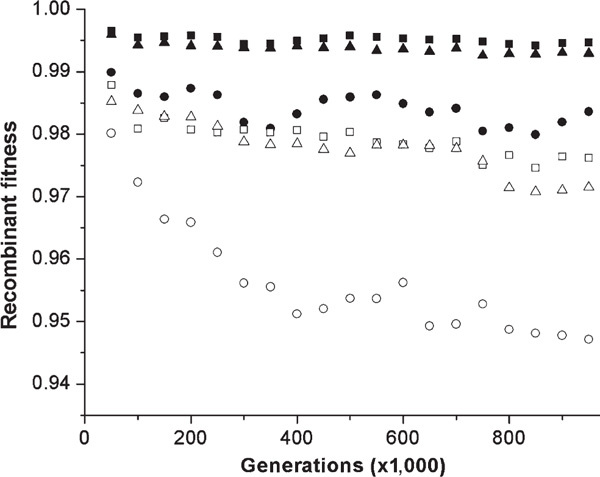
Average fitness of recombinants between proteins from two diverging populations over the course of evolution. Averages of the same number of high-, medium- and low-designable structures are represented as in Figure 1, except that the average of the better of the two reciprocal recombinants is shown with a solid symbol, while the average of the worse reciprocal recombinant is shown with a hollow symbol. Populations of size 1,000 were equilibrated for 10,000 generations prior to duplication and divergence for a further one million generations and sequences were recombined at the midpoint.
It should also be noted that our fitness function, by contrast with many studies, does not increase linearly with increasing energy, nor do we use an arbitrary flat fitness cut-off to produce a neutral network artificially. Thus, the benefit of increasing stability decreases as the protein approaches the evolutionary/thermodynamic equilibrium. With every mutation, the fraction of space that is approximately neutral changes, as does the distribution of selective effects in probable future mutants.
The differences shown are averages over all sites of recombination. It is expected that recombination sites closer to the centre of the protein might lead to greater effects, since at such sites there is a greater amount of disruption in contact pairs in the recombinants. Indeed, our own simulations agree with previous results [35] in demonstrating a strong correlation between the recombination site with lowest fitness for any pair of structures and the number of contact pairs that are disrupted by recombination at that site (data not shown). Not surprisingly, the site of lowest fitness tends on average to be near the middle of the protein (Figure 3). The variation in fitness reduction versus the site of recombination was much more notable and dramatic in low-designable structures, and there was also more variation among low-designable structures in the location of the worst recombinant (Figure 3).
Figure 3.
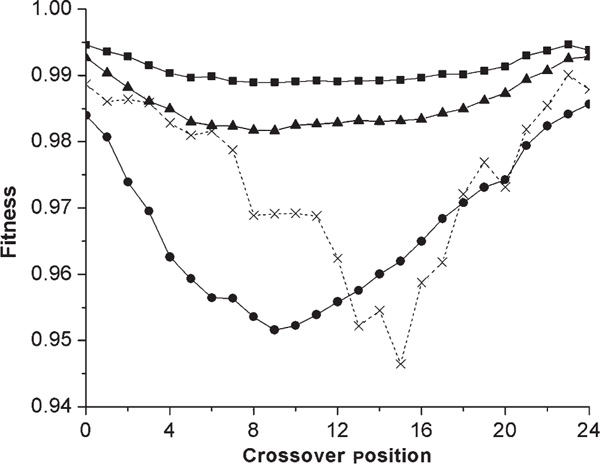
Average fitness of recombinants from diverged populations as a function of crossover position. Recombinants at all possible positions were tested from the equilibrated and diverged populations from Figure 2. Averages of the same number of high-, medium- and low-designable structures are represented with solid lines and the same symbols as in Figure 1. In addition, results for a particular low-designable structure are shown with a dashed line and an 'X' to demonstrate that there is considerable variation among low-designable structures in the crossover position of the lowest-fitness recombinants (this was also replicated four times).
Competition between structures in sequence space
The preceding results illustrate an interesting difference in how structures diverge according to their designability. It has previously been shown [36,37]--and our own simulations agree -- that compared with high-designable structures, structures with low designability tend to have more 'adjacent' structures with many shared contact pairs. We see here that the difference in designability must be solely due to the number of adjacent structures, since there is no difference between high- and low-designable structures in their tendency to mutate to adjacent structures with the same number of contact pairs.
By contrast, low-designable recombinants have a greater tendency to fold into alternative structures at all distances. Thus, the lower fitness of low-designable recombinants is a combination of both the number of adjacent structures and an increased propensity to fold to adjacent structures. To determine how well this result is upheld on a structure by structure basis, it is necessary to evaluate the sequence space where pairs of structures are in direct conflict. In other words, one should evaluate the sequence space that is most ambivalent about which structure is preferred. This sequence space is so small a proportion of the overall sequence space that it is not feasible to identify it through random sampling (unless the structure space is very simple [38]); instead, we therefore used co-selection for two structures at the same time. This approach allowed us to locate this space efficiently through the evolutionary process.
We do not have a direct measure of the size of the overlapping space using this method, but the average fitness of these co-selected populations can serve as a surrogate. We found a surprisingly linear relationship between the average equilibrium fitness of co-selected populations and the number of contact pairs shared between the two co-selected structures (Figure 4). We did not find any relationship between equilibrium fitness and the designability of either structure in the pair. It is also interesting that we did not find any asymmetry in the tendency of equilibrium sequences to fold to one structure in the pair or the other, regardless of whether one structure was high designable and the other was low designable (data not shown).
Figure 4.
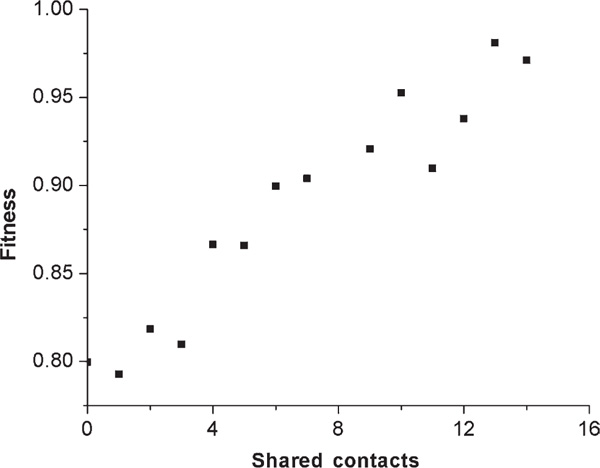
The average fitness of co-selected protein pairs as a function of the number of shared contacts between the pairs. Populations of size 1,000 were equilibrated for N generations under a co-selection regime (see methods). The fitness values were averaged across all structure pairs with the same number of shared contacts. Since there was no correlation between fitness of co-selected pairs and the designabilities of the structures in the pair, the fitnesses shown here were averaged over all possible structure pairs regardless of designability.
Increased computational efficiency for energy calculations
In ab initio evolutionary studies, complete analysis of longer and more complex proteins is precluded by the immense size of conformation space as sequence lengths increase, when non-compact structures are considered and when moving to three dimensions. For example, there are 1,081 structures possible for the square 5 × 5 lattices used in most of this study, but a 6 × 6 lattice has 57,337 structures and there are nearly 5.77 billion non-compact structures for sequences of length 25 [39]. For a sequence of length 27, there are over 103,000 compact structures in a three-dimensional 3 × 3 × 3 lattice [39].
To further consider the potential use of the previous results, we ran simulations to test how many structures were necessary to approximate the partition function and whether targeted sampling of these structures might lead to more accurate results. We first tried sampling a set of the closest structures (those with the most shared contact pairs), plus an equal-sized set of randomly sampled structures for a sequence of length 36 on a 6 × 6 lattice, to estimate the remainder of the partition function. Comparing set sizes of 50 and 50; 500 and 500; and 5,000 and 5,000, we found that set sizes of 5,000 were necessary to obtain a reasonably good approximation of the probability of folding to the native structure (Figure 5A). The important region of sequence space is not random, however, but is the region closest to the well-folded and relatively fit sequences achieved at equilibrium. To evaluate this region, we ran evolutionary simulations as described earlier and considered the accuracy of our approximation for all the sequences, including mutants, that were generated in 800 generations after reaching equilibrium (Figure 5B). In this region, the results were not as accurate as we might have hoped, and so we tested another approximation in which the partition function was divided according to structural distance from the target structure and the partial partition function for each structural distance category was sampled and estimated separately. This resulted in a dramatic increase in accuracy (Figure 5C). For comparison, we evaluated a structurally divided estimator using only 500 random structures and found that it was a more accurate estimator than the entirely random sampling of 5,000 structures (Figure 5D).
Figure 5.
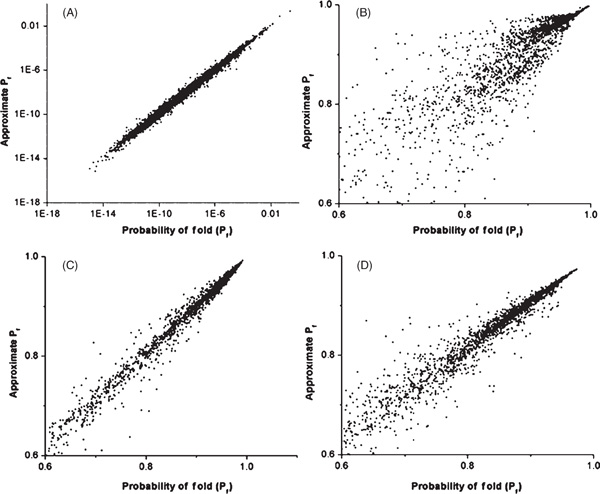
Relationship between the true probability of folding to the target sequence and the approximate probability of folding estimated from a limited sample of structures. Sequences were sampled either randomly (A) or else all mutants were sampled for 800 generations of the evolutionary process subsequent to equilibrium (B-D). The approximate probability of folding was estimated from a sample of random structures plus the same number of structures closest to the native structure in terms of shared contact pairs (B). The random sample was treated as a representative of the remaining unsampled structural ensemble and thus multiplied by the inverse of its proportional representation of this ensemble (see Materials and methods). In (C) and (D), each category of structural distance from the native or target structure was sampled separately, and the contribution of each distance category to the overall partition function was also estimated separately. The number of random and adjacent structures used in the approximations was 5,000 in all cases except (D), for which 500 distance-based random structures and 500 adjacent structures were used.
Discussion
We have described here the overall motivation of our work in ab initio evolution and how it relates to evolutionary genomics. In general, we are trying to use realistic thermodynamic and evolutionary simulations make better predictions of the kinds of evolutionary features that we might expect from real proteins with realistic functional requirements. This is done in order that we might then develop models to detect the presence of such features in real proteins using comparative genomics. Here, to illustrate our approach, we present a study that was designed specifically to achieve a better understanding of the process of divergence with respect to protein function and fitness. To what extent does molecular co-evolution between residues as proteins evolve lead to reduced fitness in recombinants between diverged proteins?
Our primary result is that the answer to this question is highly dependent on the type of structure being considered. High-designable structures are infrequent and evolve quickly due to the larger number of sequences that fold to them; however, they produce highly fit homologous recombinants, even after long periods of divergence. Structures that are compatible with fewer sequences, the much more common and slow-evolving low-designable structures, are much less likely to produce fit recombinants.
Thus, it should be expected that in low-designable structures, recombination is a less efficient method to explore sequence space for novel variants because many recombinants will be structurally unfit. This has obvious implications for protein engineering, in which in vitro evolution and recombination are important methods for generating variation. It is also important for understanding how to use observations of sequence evolution to predict the effect of sequence variants in the human genome and to identify those variants that are most likely to cause disease. Since there is more co-evolution and incompatibility between diverged low-designable proteins, divergence in low-designable proteins is probably a worse predictor of variant effects than in medium- and high-designable proteins.
Another interesting aspect that arises from our simulations is the high degree of asymmetry in fitness between reciprocal recombinants, particularly in low-designable structures. This effect is sufficiently strong that the worse reciprocal recombinant would generally be quickly eliminated by selection, whereas for high- and medium-designable structures, the better of the two reciprocal recombinants might not be eliminated in this way, even after long periods of divergence. The potential benefits of recombinant diversity, such as those that a recombinant immunodeficiency virus might be expected to incur by presenting novel epitopes to the human immune system, were not modelled in this study. They would have to be rather strong, however, to overcome the deleterious effect of recombination in low-designable protein structures. Interestingly, we have observed this effect even more clearly in binding studies that do not involve competition between structures (to be described more thoroughly elsewhere). Thus, the asymmetry appears to arise mostly from evolution on an energy landscape, and may even be somewhat ameliorated by the force of structural competition in high- and medium-designable structures.
Previously, it has been observed that evolution can drive sequences towards high-designable structures [23,29] -- and presumably recombination can drive it even faster [26]. Our detailed analysis of the process of divergence and recombination based on occupancy of alternative structures provides no evidence of a bias or tendency for low-designable structures to mutate or recombine towards high-designable structures. Furthermore, our use of co-selection to analyse the boundary in sequence space between structures indicates that there is no bias towards the more designable structure at these boundaries. Together, these data indicate that populations evolving without recombination tend towards high-designable structures solely because of the larger size of the high-designable sequence space. Recombining populations tend even more towards high-designable structures because of the greater tendency for recombinants to move out of low-designable sequence space in any direction. With a greater number of structures close to low-designable structures, there are a greater number of sequence pair boundaries, which provide high-fitness openings to other structures and thus a faster approach to local equilibrium.
Our analysis of the processes of divergence and co-evolution also clarifies the extent to which it is necessary to incorporate alternative structures when trying to understand evolutionary trajectories of real proteins. It is well known that the energetic compatibility of sequences with target structures alone is an insufficient description of thermodynamic constraints, but it is not always easy to know what aspects of entropy are important. Here, we have seen that for evolutionarily equilibrated proteins, the importance of different structures in evolutionary competition is a simple (log linear) function of their distance from a target (ie presumably functional) structure.
Empirical testing of inclusion of both random and adjacent 'decoy' structures has already been used to improve predictions of protein structures [1,40-43]. Our results might be used to improve the distribution of decoy structures that ought to be included. One must make choices when trying to reproduce essential biological features in the face of immense computational burdens. Our conclusion is that these modified fitness functions could be used to analyse more complicated structural scenarios with a much lower computational burden then would otherwise be the case. It also seems likely that sampling from known protein database structures to estimate energy functions [44] is probably insufficient to understand the evolution of sequences in structure space because adjacent structures are far more important in determining the evolutionary trajectory of stable sequences.
Estimating the number of sequences that will fold to a naturally occurring protein structure is not feasible, since the number of folds is so high and determining whether a sequence achieves a particular fold is so difficult. Nevertheless, natural proteins are evolved thermodynamic objects and approximate methods of predicting designability indicate that it is an important property of real proteins [37,45-47]. The designability principle, postulated from simple models, is believed to hold in real proteins [46]. Designability affects rates of sequence evolution (issues of function and selective importance aside), here we show that, counter to intuition, it affects neutral rates of co-evolution and functional divergence in an exactly opposite manner. This means that different proteins will be more or less amenable to in vitro redesign using mutation and recombination, and that the course of viral evolution through mutation and recombination may be affected by the designability of their component proteins. It also means that the use of comparative genomics to predict the function of possible disease-related variants may need to rely on an understanding of the type of protein structures involved, since the degree of epistatic interaction between variants is highly dependent on designability.
Acknowledgements
This work was supported by grants to D. D. P. from the National Institutes of Health (GM065612-01 and GM065580-01); the National Science Foundation through Louisiana EPSCOR and the Center for Biomodular Multi-scale Systems; and the State of Louisiana Board of Regents (Research Competitiveness Subprogram LEQSF (2001-04)-RD-A-08 and the Millennium Research Program's Biological Computation and Visualization Center) and Governor's Biotechnology Initiative. In addition to our own Linux-based Beowulf cluster, we also made extensive use of supercomputers at Louisiana State University, which were purchased by the Biological Computation and Visualization Center and the Louisiana Biotechnology Research Network.
References
- Vendruscolo M, Najmanovich R, Domany E. Can a pairwise contact potential stabilize native protein folds decoys obtained by threading? Proteins. 2000;38:134–148. doi: 10.1002/(SICI)1097-0134(20000201)38:2<134::AID-PROT3>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Bonneau R, Baker D. Ab initio protein structure prediction: Progress and prospects. Annu Rev Biophys Biomol Struct. 2001;30:173–189. doi: 10.1146/annurev.biophys.30.1.173. [DOI] [PubMed] [Google Scholar]
- Rost B. Review: Protein secondary structure prediction continues to rise. J Struct Biol. 2001;134:204–218. doi: 10.1006/jsbi.2001.4336. [DOI] [PubMed] [Google Scholar]
- Hardin C, Pogorelov TV, Luthey-Schulten Z. Ab initio protein structure prediction. Curr Opin Struct Biol. 2002;12:176–181. doi: 10.1016/S0959-440X(02)00306-8. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Shakhnovich EI. Protein structure prediction by threading. Why it works and why it does not. J Mol Biol. 1998;283:507–526. doi: 10.1006/jmbi.1998.2092. [DOI] [PubMed] [Google Scholar]
- Lio P, Goldman N. Models of molecular evolution and phylogeny. Genome Res. 1998;8:1233–1244. doi: 10.1101/gr.8.12.1233. [DOI] [PubMed] [Google Scholar]
- Pollock DD. Genomic biodiversity, phylogenetics and coevolution in proteins. Appl Bioinformatics. 2002;1:81–92. [PMC free article] [PubMed] [Google Scholar]
- Ouzounis CA, Valencia A. Early bioinformatics: The birth of a discipline -- A personal view. Bioinformatics. 2003;19:2176–2190. doi: 10.1093/bioinformatics/btg309. [DOI] [PubMed] [Google Scholar]
- Koshi JM, Goldstein RA. Models of natural mutations including site heterogeneity. Proteins. 1998;32:289–295. doi: 10.1002/(SICI)1097-0134(19980815)32:3<289::AID-PROT4>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Krishnan NM, Raina SZ, Pollock DD. Analysis of among-site variation in substitution patterns. Biol Proced Online. 2004;6:180–188. doi: 10.1251/bpo88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siepel A, Haussler D. Phylogenetic estimation of context-dependent substitution rates by likelihood. Mol Biol Evol. 2004;21:468–488. doi: 10.1093/molbev/msh039. [DOI] [PubMed] [Google Scholar]
- Pollock DD, Bruno WJ. Assessing an unknown evolutionary process: Effect of increasing site-specific knowledge through taxon addition. Mol Biol Evol. 2000;17:1854–1858. doi: 10.1093/oxfordjournals.molbev.a026286. [DOI] [PubMed] [Google Scholar]
- Pollock DD, Eisen JA, Doggett NA, Cummings MP. A case for evolutionary genomics and the comprehensive examination of sequence biodiversity. Mol Biol Evol. 2000;17:1776–1788. doi: 10.1093/oxfordjournals.molbev.a026278. [DOI] [PubMed] [Google Scholar]
- Pollock DD, Zwickl DJ, McGuire JA, Hillis DM. Increased taxon sampling is advantageous for phylogenetic inference. Syst Biol. 2002;51:664–671. doi: 10.1080/10635150290102357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faith JJ, Pollock DD. Likelihood analysis of asymmetrical mutation bias gradients in vertebrate mitochondrial genomes. Genetics. 2003;165:735–745. doi: 10.1093/genetics/165.2.735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillis DM, Pollock DD, McGuire JA, Zwickl DJ. Is sparse taxon sampling a problem for phylogenetic inference? Syst Biol. 2003;52:124–126. doi: 10.1080/10635150390132911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan NM, Seligmann H, Raina SZ, Pollock DD. Detecting gradients of asymmetry in site-specific substitutions in mitochondrial genomes. DNA Cell Biol. 2004;23:707–714. doi: 10.1089/dna.2004.23.707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan NM, Seligmann H, Stewart CB. et al. Ancestral sequence reconstruction in primate mitochondrial DNA: Compositional bias and effect on functional inference. Mol Biol Evol. 2004;21:1871–1883. doi: 10.1093/molbev/msh198. [DOI] [PubMed] [Google Scholar]
- Wang ZO, Pollock DD. Context dependence and coevolution among amino acid residues in proteins. Methods Enzymol. 2005;395:779–790. doi: 10.1016/S0076-6879(05)95040-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchler NEG, Goldstein RA. Surveying determinants of protein structure designability across different energy models and amino-acid alphabets: A consensus. J Chem Phys. 2000;112:2533. doi: 10.1063/1.480893. [DOI] [Google Scholar]
- Buchler NEG, Goldstein RA. Effect of alphabet size and foldability requirements on protein structure designability. Proteins. 1999;34:113. doi: 10.1002/(SICI)1097-0134(19990101)34:1<113::AID-PROT9>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Williams PD, Pollock DD, Goldstein RA. Evolution of functionality in lattice proteins. J Mol Graph Model. 2001;19:150. doi: 10.1016/S1093-3263(00)00125-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Govindarajan S, Goldstein RA. Evolution of model proteins on a foldability landscape. Proteins. 1997;29:461. doi: 10.1002/(SICI)1097-0134(199712)29:4<461::AID-PROT6>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- Govindarajan S, Goldstein RA. On the thermodynamic hypothesis of protein folding. Proc Natl Acad Sci USA. 1998;95:5545. doi: 10.1073/pnas.95.10.5545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Govindarajan S, Recabarren R, Goldstein RA. Estimating the total number of protein folds. Proteins. 1999;35:408–414. doi: 10.1002/(SICI)1097-0134(19990601)35:4<408::AID-PROT4>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Cui Y, Wong WH, Bornberg-Bauer E, Chan HS. Recombinatoric exploration of novel folded structures: A heteropolymer-based model of protein evolutionary landscapes. Proc Natl Acad Sci USA. 2002;99:809. doi: 10.1073/pnas.022240299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill KA, Bromberg S, Yue K. et al. Principles of protein folding -- A perspective from simple exact models. Protein Sci. 1995;4:561. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan HS, Bornberg-Bauer E. Perspectives on protein evolution from simple exact models. Appl Bioinformatics. 2002;1:121–144. [PubMed] [Google Scholar]
- Goldstein RA. Evolutionary perspectives on protein folding, structure, and thermodynamics. American Chemical Society, Washington, DC, USA; 2003. Abstracts of papers, 226th ACS National Meeting, New York, NY, USA, 7-11th September, 2003. [Google Scholar]
- Buchler NEG, Goldstein RA. Universal correlation between energy gap and foldability for the random energy model and lattice proteins. J Chem Phys. 1999;111:6599. doi: 10.1063/1.479951. [DOI] [Google Scholar]
- Taverna DM, Goldstein RA. Why are proteins so robust to site mutations? J Mol Biol. 2002;315:479. doi: 10.1006/jmbi.2001.5226. [DOI] [PubMed] [Google Scholar]
- Miyazawa S, Jernigan RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol. 1996;256:623. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- Taverna DM, Goldstein RA. The distribution of structures in evolving protein populations. Biopolymers. 2000;53:1. doi: 10.1002/(SICI)1097-0282(200001)53:1<1::AID-BIP1>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- James PC, Peter S. Evolution Dynamics: Exploring the Interplay of Selection, Accident, Neutrality, and Function. Oxford University Press, Oxford, UK; 2003. p. 3. [Google Scholar]
- Voigt CA, Martinez C, Wang ZG. et al. Protein building blocks preserved by recombination. Nat Struct Biol. 2002;9:553. doi: 10.1038/nsb805. [DOI] [PubMed] [Google Scholar]
- Dokholyan NV, Li L, Ding F, Shakhnovich EI. Topological determinants of protein folding. Proc Natl Acad Sci USA. 2002;99:8637–8641. doi: 10.1073/pnas.122076099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakhnovich BE, Deeds E, Delisi C, Shakhnovich E. Protein structure and evolutionary history determine sequence space topology. Genome Res. 2005;15:385–392. doi: 10.1101/gr.3133605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bornberg-Bauer E. How are model protein structures distributed in sequence space? Biophys J. 1997;73:2393. doi: 10.1016/S0006-3495(97)78268-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan DC, Aynechi T, Voelz VA, Kuntz ID. Information content of molecular structures. Biophys J. 2003;85:174. doi: 10.1016/S0006-3495(03)74464-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H, Skolnick J. A distance-dependent atomic knowledge-based potential for improved structure selection. Proteins. 2001;44:223–232. doi: 10.1002/prot.1087. [DOI] [PubMed] [Google Scholar]
- Keasar C, Levitt M. A novel approach to decoy set generation: Designing a physical energy function having local minima with native structure characteristics. J Mol Biol. 2003;329:159–174. doi: 10.1016/S0022-2836(03)00323-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seok C, Rosen JB, Chodera JD, Dill KA. MOPED: Method for optimizing physical energy parameters using decoys. J Comput Chem. 2003;24:89–97. doi: 10.1002/jcc.10124. [DOI] [PubMed] [Google Scholar]
- Tsai J, Bonneau R, Morozov AV. et al. An improved protein decoy set for testing energy functions for protein structure prediction. Proteins. 2003;53:76–87. doi: 10.1002/prot.10454. [DOI] [PubMed] [Google Scholar]
- McConkey BJ, Sobolev V, Edelman M. Discrimination of native protein structures using atom-atom contact scoring. Proc Natl Acad Sci USA. 2003;100:3215–3220. doi: 10.1073/pnas.0535768100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emberly EG, Miller J, Zeng C. et al. Identifying proteins of high designability via surface-exposure patterns. Proteins. 2002;47:295–304. doi: 10.1002/prot.10067. [DOI] [PubMed] [Google Scholar]
- Larson SM, England JL, Desjarlais JR, Pande VS. Thoroughly sampling sequence space: Large-scale protein design of structural ensembles. Protein Sci. 2002;11:2804. doi: 10.1110/ps.0203902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu C, Li X, Liang J. Developing optimal non-linear scoring function for protein design. Bioinformatics. 2004;20:3080–3098. doi: 10.1093/bioinformatics/bth369. [DOI] [PubMed] [Google Scholar]


