Evolution of functionality in lattice proteins

Abstract

We study the evolution of protein functionality using a two-dimensional lattice model. The characteristics particular to evolution, such as population dynamics and early evolutionary trajectories, have a large effect on the distribution of observed structures. Only subtle differences are observed between the distribution of structures evolved for function and those evolved for their ability to form compact structures.

INTRODUCTION

There has been increased interest in understanding the observed properties of proteins in terms of their evolutionary history. One of the more active approaches involves deciphering evolutionary histories to obtain information regarding the biochemistry of specific proteins. A parallel effort involves developing simplified theoretical and computational models to address the broader biophysics of proteins, examining such areas as how the need for foldability, stability, and functionality can explain some of the properties common to all (or a large number of) proteins. These analyses have shown that the topography of the fitness landscape can have a strong influence on the course of evolution as well as on the properties of the resultant organisms. One central concept that has emerged from this work is the notion of “sequence entropy” or “designability,” the relative number of genotypes corresponding to a given phenotype. This concern has led us (and others) to look at how many sequences correspond to different possible structures and how this number could affect their relative distribution among biological proteins^1–6 as well as their thermodynamic properties.^3,5,7–13

Studies such as these (with a few exceptions) have had two major limitations. Most of these studies on protein models examine the nature of the mapping of sequence to structure and how this is affected by the details of the model. The dynamics of evolution are often neglected. We have demonstrated, for instance, that population dynamics can strongly influence the frequency of the variously observed structures.¹² In addition, the majority of such studies have focused on the infinite-time distribution of properties under steady-state conditions. In reality, it is likely that many properties of proteins were “frozen in” during the initial stages of evolution in much the same way that the genetic code has been fixed. Any analysis should deal explicitly with the freezing-in process. Secondly, again with few exceptions,^14,15 previous studies have tended to concentrate on the structural aspects of proteins rather than their functional aspects, even though functional concerns represent a major source of selective pressure. We consider these two additional aspects of protein evolution, using lattice models to simulate the evolution of populations of proteins as they change from poorly suited random sequences to proteins adapted for a simple function, the binding of a small prespecified peptide ligand. We find that modeling the early stages of evolution results in significant differences between the distribution of structures observed in evolutionarily-derived proteins and what would be expected based on their steady-state properties. In contrast, we find that incorporating this form of selective pressure for simple functionality does not appreciably change the resulting distribution.

METHODS

The Model

Our protein model consists of a chain of 16 monomers on a two-dimensional square lattice, with each monomer located at one lattice point. All self-avoiding lattice walks were enumerated, resulting in 802,075 possible conformations not related by rotations, reflections, or inversions, of which 69 were maximally compact (i.e., fitting on a 4 × 4 lattice). A contact is assumed to exist between two residues if they are not covalently connected but are on adjacent lattice points. There are important limitations of a two-dimensional model concerning whether the conformation space is ergodic.^16,17 While these limitations are critical in folding simulations, the thermodynamical properties described below involve sums over states and should be less affected. For the following thermodynamic analysis, we assume that all structures are at equilibrium. We should therefore consider the 802,075 conformations as representing the ensemble of kinetically accessible states.

We evaluate the energy of the protein in structure 𝒮_k according to the formula

$$E({𝒮}_k){\displaystyle \sum _{\mu <\nu }^{16}\gamma ({{𝒜}_{\mu }}^P,{{𝒜}_{\nu }}^P){U_{\mu \nu }}^k}$$ (1)

where γ(𝒜_μ^P, 𝒜_ν^P) is the contact potential between amino acids 𝒜_μ^P and 𝒜_ν^P at the μth and νth position on the protein chain, respectively, and U_μν^k is equal to 1 if residues μ and ν come into contact in structure 𝒮_k, and 0 otherwise. There are between 0 and 9 intra-protein contacts, with the maximum number formed only in the 69 maximally-compact structures. The contact potentials used are a modified set of potentials statistically determined from real proteins by Miyazawa and Jernigan (MJ).¹⁸ We multiply the interaction potentials by 2 to compensate for the reduced number of contacts available to residues on a two-dimensional lattice compared with the three-dimensional proteins used to construct the potentials. In addition, as the pairwise contact potential is inappropriate for cystine– cystine covalent bonds, we replace the C–C potential with the value of the S–S potential.

Due to our ability to enumerate the energy of all possible conformations, we can calculate thermodynamic properties exactly. For instance, the probability that a protein is in structure 𝒮_k is

$$P({𝒮}_k)=\frac{\text{exp[}-E({𝒮}_k)/\mathit{\text{kT}}]}{Z_{\text{fold}}},$$ (2)

and the ΔG for folding into that structure is

$$\mathrm{\Delta }{G}_{\text{folding}}({𝒮}_k)=-\mathit{\text{kT}}\text{ln}\left[\frac{\text{exp}[-E({𝒮}_k)/\mathit{\text{kT}}]}{Z_{\text{fold}}-\text{exp}[-E({𝒮}_k)/\mathit{\text{kT}}]}\right],$$ (3)

where Z_fold is the partition function, given by

$$Z_{\text{fold}}={\displaystyle \sum _k\text{exp}[-E({𝒮}_k)/\mathit{\text{kT}}]}$$ (4)

and kT is 0.6 kcal mol⁻¹ (corresponding to room temperature). We can also calculate the total probability that the protein is compact by summing the respective probability of being in any of the 69 compact conformations.

Although protein function can be very complex and influenced by many different factors, one common aspect of functionality involves binding ligands. To model the binding of a ligand to a protein, we use a tetra-peptide as the ligand and allow it to contact any side of a compact protein with each residue of the peptide in contact with one residue on the protein, as shown in Figure 1. For simplicity we assume that the protein must be in a compact conformation to bind a ligand. There are eight binding sites per compact conformation (each conformation has four sides, and there are two directions the ligand can face), so there are 69 × 4 × 2 = 552 possible combinations of protein conformation and binding site. The energy of a protein in structure 𝒮_k with the peptide bound at binding site ℬ_l is modeled as

$$E({𝒮}_k,{ℬ}_l)={\displaystyle \sum _{\mu <\nu }^{16}\gamma ({{𝒜}_{\mu }}^P,{{𝒜}_{\nu }}^P){U_{\mu \nu }}^k+{\displaystyle \sum _{\mu =1}^{16}{\displaystyle \sum _{\lambda =1}^4\gamma ({{𝒜}_{\mu }}^P,{{𝒜}_{\lambda }}^L){U_{\mu \lambda }}^{k,l},}}}$$ (5)

where the first sum is the energy of the protein in its conformation (identical to Equation 1) and the second sum represents the interaction between amino acids 𝒜_μ^P in the protein and 𝒜_λ^L in the ligand; U_μλ^k,l = 1 if these two amino acids are in contact. The modified Miyazawa-Jernigan potential is used for both the intraprotein and protein–ligand interactions. Note that because we consider the total energy of the ligand–protein combination, it is possible that binding of the ligand can alter the stability of the protein in its folded state.

Figure 1.

Model of a 16-residue two-dimensional lattice protein in a maximally compact conformation binding a tetra-peptide ligand. Four intermolecular contacts are formed ({H,Q}, {G,I}, {L,F}, {M,W}).

Assuming that the protein is dilute, the equilibrium probability of the protein binding the peptide is

$$P_{\text{binding}}=\frac{\text{exp}[\mathrm{\Delta }{S}_{\text{ligand}}/k]{\displaystyle {\sum }_{k,l}\text{exp}[-E({𝒮}_k,{ℬ}_l)/\mathit{\text{kT}}]}}{{\displaystyle {\sum }_l\text{exp}[-E({𝒮}_k)/\mathit{\text{kT}}]+\text{exp}[\mathrm{\Delta }{S}_{\text{ligand}}/k]{\displaystyle {\sum }_{k,l}\text{exp}[-E({𝒮}_k,{ℬ}_l)/\mathit{\text{kT}}}]}},$$ (6)

where Σ_k,l exp[−E(𝒮_k, ℬ_l)/kT] includes the sum over all possible structures with bound ligand calculated with Equation 5; Σ_l exp[−E(𝒮_k)/kT] involves the sum over all structures of the protein with no bound ligand calculated with Equation 1; and ΔS_ligand is the concentration-dependent change in the entropy of the ligand upon binding. In the weak-binding limit we can neglect the second term in the denominator and calculate the concentration-independent relative probability of a protein binding a ligand. In this limit, the relative probability of a bound peptide is given by

$$P_{\text{binding}}\propto \frac{{\displaystyle {\sum }_{k,l}\text{exp}[-E({𝒮}_k,{ℬ}_l)/\mathit{\text{kT}}]}}{{\displaystyle {\sum }_l\text{exp}[-E({𝒮}_k)/\mathit{\text{kT}}]}},$$ (7)

where the proportionality constant is just exp[ΔS_ligand/k].

Calculating Protein Designabilities

As described in the introduction, an important parameter for each structure 𝒮_k is the designability, 𝒟(𝒮_k), defined as the relative fraction of viable sequences that will successfully fold into that particular conformation. We define as viable any sequence with positive stability, that is, ΔG_folding(𝒮_k) < 0. Designabilities were calculated by choosing approximately 20 billion sequences at random, finding their ground-state structures, and evaluating ΔG_folding(𝒮_k). There are a number of pairs of compact structures that can be interconverted by switching the N and C termini of the protein chain; these structures should have the same designabilities. To provide better statistics, the designabilities of these states (as well as the occupancies, defined below) were averaged over both members of the pair. In spite of this generous viability requirement, the large number of noncompact conformations and the resulting entropy of the unfolded state results in only 0.00003% of all sequences being sufficiently stable, with 5,765 viable protein sequences found.

Evolution for Compactness

As emphasized above, it is important to consider explicitly the evolution of populations during the different stages of evolution. Our first evolutionary run involves investigating the effect of such population adaptation for a specifically structural fitness criterion. One aspect of protein viability is that proteins must be able to form a well-ordered compact state to resist such processes as proteolysis and aggregation. For our first evolutionary run, we ignore protein functionality and only consider the ability of the protein to form such a compact state. We start with a population of 1,000 random protein sequences. At each generation, a given number of random mutations are made to these sequences; the total number of mutations is chosen from a Poisson distribution so that there are an average of 20 mutations in the population per generation. We then calculate the total probability of each of the various sequences forming a compact structure (P_compactness) by taking the sum of P(𝒮_k) over all compact states. This probability is treated as the fitness of that sequence. To implement the evolutionary procedure, the 1,000 proteins in the next generation are randomly selected (with replacement) from the current generation of proteins so that the probability of any sequence being chosen is proportional to that protein’s P_compactness value. 10,000 runs were made with different initial sequences, with each simulation lasting 1,000 generations. We then computed the occupancy, 𝒪_folding(𝒮_k), defined as the average fraction of all of the protein sequences resulting from these simulations that fold into structure 𝒮_k.

Evolution for Ligand Binding

To study how the requirements for functionality affect the evolutionary process, we evolve a protein population to bind a prespecified ligand. As before, we start with a population of 1,000 random proteins. The same process of random mutation and random selection is implemented, but this time the relative probability of any sequence being selected for the next generation corresponds to the value of P_binding calculated with Equation 7. We perform 10,000 runs, each with a different ligand selected at random; in addition, we perform an additional 10,000 runs with each of three particular ligands: QIFW, TSGL, and GKSV. We again compute the occupancy 𝒪_binding^X (𝒮_k) (X = random, QIFW, TSGL, or GKSV), defined as the fraction of all of the protein sequences resulting from each of these simulations that fold into structure 𝒮_k.

RESULTS AND DISCUSSION

Structures Freeze-in Quickly

Figure 2 shows the time-course of various parameters for a typical simulation when P_compactness is used as the fitness criterion; Figure 3 shows a corresponding plot for a typical simulation where P_binding^TSGL represents the fitness. One of the quantities included in these graphs is η, the effective number of compact states, given by

$$\eta ={\left({\displaystyle \sum _{{𝒮}_k}\frac{1}{{\left(\frac{P({𝒮}_k)}{{\displaystyle {\sum }_{{𝒮}_{k\prime }}P({𝒮}_{k\prime }})}\right)}^2}}\right)}^{-1},$$ (8)

where P(𝒮_k) is averaged over all of the proteins in the population and both sums are over all compact conformations. η = 1 if only one compact state is occupied, and is equal to the total number of compact states if all are equally occupied. η generally decreases to approximately 1 within the first tens of generations, indicating that the population quickly decides on a native state that is preserved for the remainder of the simulation. This represents the freezing-in effect described above. There are two possible reasons for this effect in the evolution of natural biomolecules. One reason is that the rest of the organism becomes adapted for the current characteristics of this particular biomolecule, so changes in these characteristics result in misadaptation of the rest of the organism. While this is likely the reason for the stability of the genetic code, this effect is obviously absent from the current simulations. The second effect is based on our previous work, which showed that as selective pressure increases, changes in structure greatly slow down.^8,9 In the beginning stages of the simulation, each protein sequence is competing against other poorly adapted sequences. As the simulation progresses, the other members of the population become increasingly adapted, so that the selective pressure is stronger. As a result, it becomes more difficult to form the less-fit sequences that are in-between structures, and structural change ceases. Comparison of the changes in η with tendency for compaction and binding ability demonstrate that relatively little adaptation is necessary before the structure is frozen in.

Figure 2.

Time-course of various parameters for a typical simulation with Fitness equal to P_compactness: (—) the average probability that the protein is in some compact conformation; (⋯) the average probability that the protein is in the compact conformation of lowest energy; and (- - -) η, the effective number of compact states present in the population.

Figure 3.

Time-course of various parameters for a typical simulation with Fitness equal to P_binding^TSGL. Top graph: (—) the average relative probability of the peptide being bound by the protein (P_binding^TSGL) in arbitrary units; (⋯) the contribution to P_binding^TSGL of the current most likely binding site and conformation. Bottom graph: (—) the average probability that the protein in its unbound state is in a compact conformation; (- - -) η, the effective number of compact states present in the population.

While population-wide structural changes in later generations are rare, this is not to say that such changes are nonexistent. In the simulation shown in Figure 2, an ensemble of sequences that fold into one compact structure is replaced with an ensemble of sequences that fold into a new structure, approximately at generation 575.

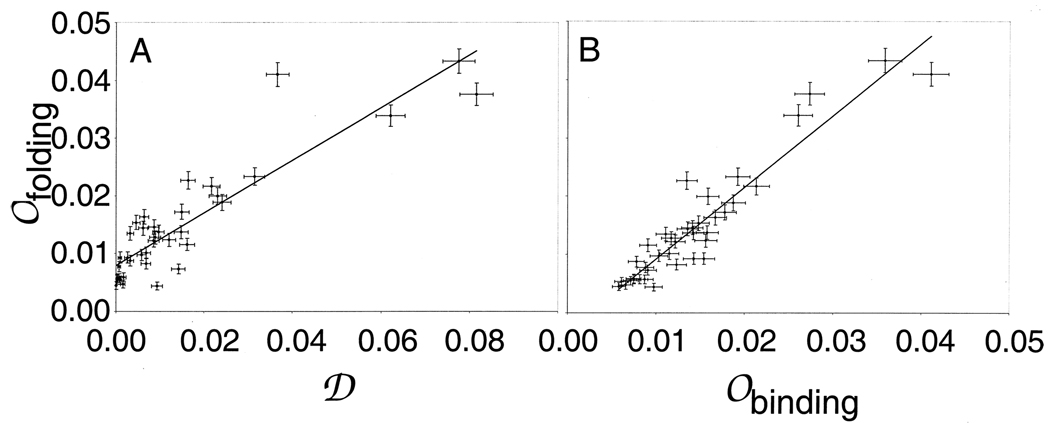
Occupancies are Highly Correlated with Designabilities

On the left side of Figure 4 we compare the relationship between the occupancies 𝒪_folding(𝒮_k) observed with simulations of a population adapted to folding into a compact state with the designability 𝒟(𝒮_k). 𝒪_folding(𝒮_k) is highly (but imperfectly) correlated with designability, with a correlation coefficient of 0.90. This suggests, similarly to our earlier conclusions,¹² that while designability is an important element in understanding the distribution of observed protein structures, this distribution can be modified by the interaction of population effects with the underlying topology of the fitness landscape.

Figure 4.

A: Correlation between occupancy for evolutionary trajectories with compaction as the fitness criterion (𝒪_folding) and designability (𝒟). B: Correlation between 𝒪_folding and 𝒪_binding^random, the occupancy when fitness is given by the ability to bind a random ligand. Error bars represent expected statistical errors.

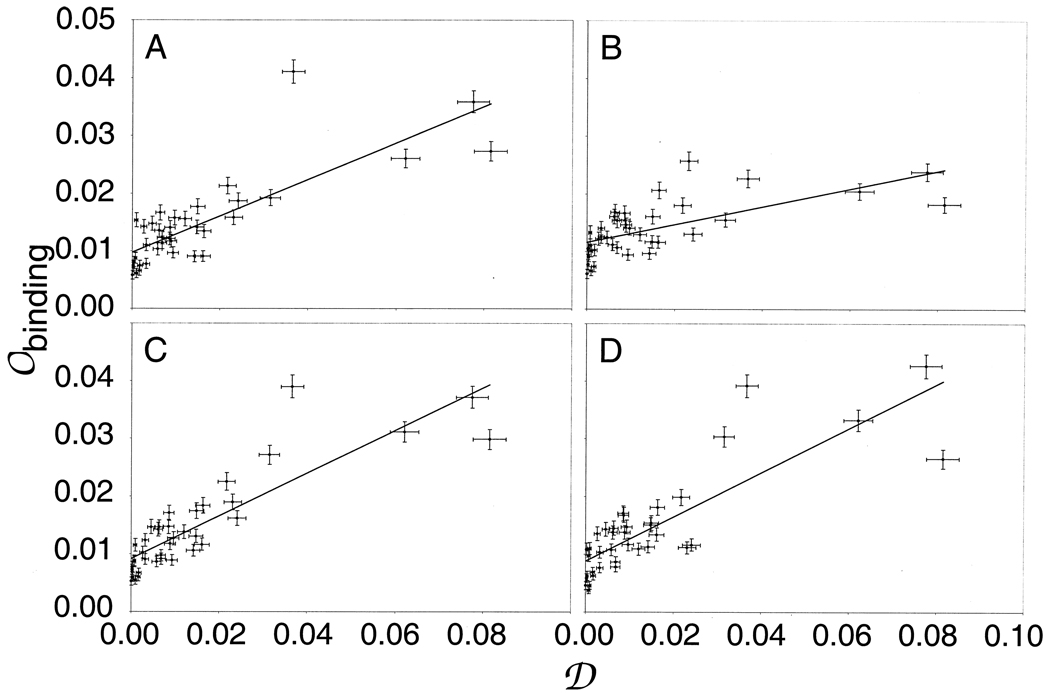
Values of 𝒪_binding(𝒮_k) for the random and specified ligands are compared with 𝒪_folding(𝒮_k) in Figure 4 and with designability 𝒟(𝒮_k) in Figure 5. The correlation coefficient between 𝒪_binding^random(𝒮_k) for proteins evolved for binding random ligands and designabilities 𝒟(𝒮_k) is 0.81; correlations between 𝒪_binding(𝒮_k) and 𝒟(𝒮_k) for specific ligands have correlation coefficients 0.66, 0.87, and 0.84 for QIFW, TSGL, and GKSV, respectively. These values are all comparable with the correlation between 𝒪_folding(𝒮_k) and 𝒟(𝒮_k). As shown in Figure 4, 𝒪_binding^random(𝒮_k) for the random ligands and 𝒪_folding(𝒮_k) are extremely well correlated, with a correlation coefficient of 0.95. This shows that in this model the distribution of structures is not greatly affected by the need for functionality, and that the need for compactness combined with the designability most influence the distribution of structures.

Figure 5.

Correlation between occupancy 𝒪_binding for evolutionary trajectories with ligand binding as the fitness criterion for (A) random ligands, (B) QIFW, (C) TSGL, and (D) GKSV, compared with designability 𝒟. Error bars represent expected statistical errors.

Distribution of Designabilities Affected by Freezing-in of Structures

Figure 6 shows the distribution of designabilities of the various compact structures. In previous results, we showed that the distribution of designabilities becomes increasingly uneven as the criterion for viability becomes more stringent.¹⁹ In the current model, with only 0.00003% of all sequences viable, we expect a highly uneven distribution with most structures of extremely small designability and with a few highly-designable structures. This is exactly what is observed. In particular, six structures account for more than 44% of all of the designable sequences. The distribution of occupancies [both 𝒪_folding(𝒮_k) and 𝒪_binding(𝒮_k)] is also shown in Figure 6. In spite of these high correlation coefficients between designability and occupancy, the distribution of designabilities and occupancies are quite different, with both 𝒪_folding(𝒮_k) and 𝒪_binding(𝒮_k) more evenly distributed among the structures than 𝒟(𝒮_k). This is somewhat surprising, as our earlier results with steady-state population dynamics showed that population dynamics make the distribution of occupancies more uneven than the distribution of designabilities.¹² The difference between these two simulations can be explained by considering Figure 2 and Figure 3. In the previous study, we allowed the protein population to equilibrate among all of the various possible structures. Sequences that folded into structures that had smaller designabilities would be less resistant to mutations, and would be correspondingly less frequent. In the current simulations, we started with a set of sequences with low fitness. As the simulation proceeded, the average level of the fitness increased, so that the fitness required for reproducing continually increased. As a result, the volume of the sequence space available to each structure continually decreased as each sequence had to compete with more and more fit members of the evolving population. As described above, the folded structure is decided quite early in the simulation. As a result, the probability of each of the folded states was decided when the overall fitness required for reproduction was quite low, and a larger fraction of all sequences was viable. Low required values of fitness generally result in a more equitable distribution of proteins among the various structures.¹⁹

Figure 6.

Zipf’s Law plot. The logarithms of the designabilities and occupancies ranked in descending order. 𝒟(𝒮_k) (—); 𝒪_folding (𝒮_k) (· · · ·); 𝒪_binding^random (𝒮_k) (- - -); 𝒪_binding^QIFW (𝒮_k) (·–·–); 𝒪_binding^TSGL (𝒮_k) (–··–··); 𝒪_binding^GKSV (𝒮_k) (– –· – –·).

CONCLUSION

Proteins are the result of a long evolutionary process. We can gain much insight into the nature of proteins by explicitly modeling the manner in which these proteins originated. We have described preliminary work in this direction, where we model the evolution of populations of proteins as they evolve from random, nonadapted biopolymers to compact, functional proteins. While the functionality used in this model (as well as the protein model itself) is highly abstracted and simplified, the results are highly suggestive. In previous work, we assumed that selective pressure for functionality and for stability and foldability were somewhat unrelated, so that a protein that successfully folded into one structure would be as likely to be functional as a protein that successfully folded into an alternative structure. We find that including functionality in this model does not greatly alter the distribution of observed structures. We do, however, observe that the distribution is affected by the population aspects. We also demonstrate that it is important to consider the evolutionary epoch at which nature chose properties such as the distribution of structures, and to recognize that this situation may be poorly represented by the current circumstances. This also suggests that while sequences are rather accommodating to change, structures have been largely determined and are far less mutable.