Economy of Operon Formation: Cotranscription Minimizes Shortfall in Protein Complexes

Abstract

Genes of prokaryotes and Archaea are often organized in cotranscribed groups, or operons. In contrast, eukaryotic genes are generally transcribed independently. Here we show that there is a substantial economic gain for the cell to cotranscribe genes encoding protein complexes because it synchronizes the fluctuations, or noise, in the levels of the different components. This correlation substantially reduces the shortfall in production of the complex. This benefit is relatively large in small cells such as bacterial cells, in which there are few mRNAs and proteins per cell, and is diminished in larger cells such as eukaryotic cells.

Introduction

What are the evolutionary forces that drive operon formation in prokaryotes but not in eukaryotes? One idea is that stronger genome size constraints in prokaryotes provide a large benefit to reducing the number of promoters. Another idea is that the high rate of horizontal gene transfer in prokaryotes provides an advantage for functionally related genes to be grouped together to increase their probability of cotransfer (1–3). Another benefit of operon formation is that it decreases the fluctuations between the concentrations of the coexpressed proteins (4). Fluctuations in relative protein concentrations can be wasteful, for example, when multiple proteins form a tight complex or act in concert (4–7). Translational coupling, in which ribosomes translating an upstream gene aid the translation of the downstream gene on the same mRNA molecule, has been emphasized as a way in which operon formation can reduce such fluctuations (6, 7). But strong translational coupling is not a general feature of operons (6). Here we show that cotranscription by itself can provide a substantial cost reduction in the production of protein complexes. This benefit decreases as the number of complexes increases, as required in larger cells. Thus, reduction in the shortfall of protein complexes provides an additional explanation for the abundance of operons in prokaryotes and Archaea compared to the lack of that in eukaryotes.

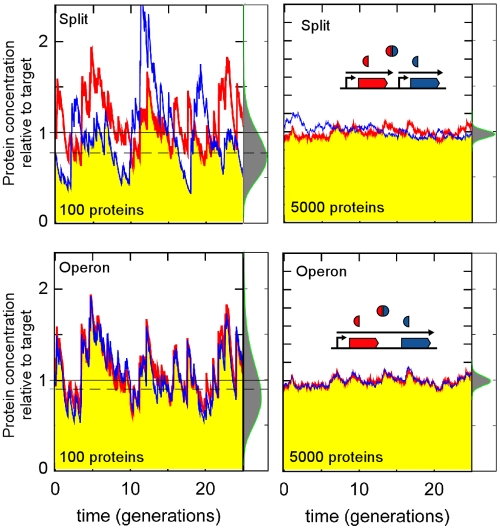
Considering a functional 1:1 complex of two different proteins, we compare a system in which the two genes are cotranscribed but not translationally coupled to a system in which the two genes are transcribed independently from promoters of equal strength (split). If 100 copies of the complex are required, then in the absence of noise (and assuming a tight complex), it would be sufficient to produce 100 copies of each protein. In a living cell, both systems would fall short of the 100-complex target because the number of each protein will fluctuate around 100, and the number of complexes is determined by the minimum level of the two proteins. However, in the operon arrangement, the levels of the two proteins tend to fluctuate in synchrony, and thus, the shortfall is substantially less; in this example, the average number of complexes produced by the operon is ~20% higher than that produced with the split arrangement (Fig. 1). Another way of looking at this is that in order to ensure that at least 100 complexes are present in the cell for at least 95% (50%) of the time, then the cell must make on average 180 (110) copies of each protein in the operon arrangement, while it needs to make 190 (126) copies of each in the split case.

FIG 1 .

The cost of protein complex formation is improved by operon organization. The red and blue traces show fluctuations in the numbers of two proteins produced stochastically in equimolar amounts from two separate promoters (top) or a single promoter (bottom). The yellow areas show the concentration of a 1:1 complex of the proteins (minimum of two proteins for a tight complex). Individual RNA production, degradation, and translation events were random, with rates such that per generation, an average of 5 (left) or 250 (right) mRNAs were made, each producing 20 proteins on average. Proteins were stable and randomly distributed upon cell division. The distributions of the number of complexes are shown on the side of the traces. Mean values (dashed lines) for the left panels are 78 (top) and 93 (bottom) and for the right panels are 4,851 (top) and 4,958 (bottom). The average complex levels fall short of the target, but the shortfall is larger when proteins are transcribed separately and when mRNA numbers are smaller. Conversely, fluctuations in complex numbers (i.e., the widths of the distributions) are larger when the two proteins are cotranscribed.

Other factors being equal, this avoidance of a shortfall should thus provide an evolutionary pressure for genes encoding complex-forming proteins to be cotranscribed. This prediction is supported by comparisons of metabolic genes conserved in diverse eubacterial and archaebacterial genomes (Table 1). Genes encoding components of a strong complex (e.g., trpA-trpB) are more likely to be cotranscribed than genes encoding noncomplex-forming proteins acting in the same pathway (e.g., trpE-trpD).

TABLE 1 .

Conserved cotranscription of genes for complex-forming proteins

Genes	Complexa	Cotranscription (% of genera)b		No. of genera
		Likelyc	Unlikelyd
trpB-trpA	+	69	21	204
malF-malG	+	100	0	9
carA-carB	+	58	29	226
nrdA-nrdB	+	63	18	68
trpE-trpD	–	6	42	178
malE-malF	–	43	43	7
thrA-thrB	–	41	43	58
thrB-thrC	–	20	80	164

^a +E. coli: trpB-trpA, tryptophan synthase; malF-malG, maltose ABC transporter; carA-carB, carbamoyl phosphate synthetase; nrdA-nrdB, ribonucleoside diphosphate reductase. –, pairs cotranscribed in E. coli and used for the same pathway but are not complex forming (15).

^b Data shown for one representative member of each genus obtained from the JVCI-CMR database (bacterial and archaeal genomes) (16). Some gene pairs were absent in some genera.

^c Genes were judged likely to be cotranscribed when they were in the same orientation and the end of the upstream gene is <150 bp from the start of the other.

^d Genes were judged unlikely to be cotranscribed when the intergenic distance was larger than 5,000 bp or when the genes were in opposite orientations. Some gene pairs could not be placed into either of these categories.

This economic advantage of operons is lessened when fluctuations in protein numbers are smaller. The size of fluctuations decreases when the number of mRNAs or proteins is larger (Fig. 1), which can be achieved by increasing the transcription rate, the translation rate, or the lifetime of the mRNA (see Materials and Methods). In eukaryotic cells, noise generated in the production of complex-forming proteins is kept at a minimum by longer-lived mRNAs and higher transcription rates (5). In Escherichia coli, because the number of transcripts is generally low, it is the variation in these numbers (8, 9) that makes the largest contribution to noise. In Fig. 1 and elsewhere, we have examined fluctuations when an average of 20 proteins is produced per mRNA. However, recent measurements suggest that an average E. coli mRNA produces ~100 proteins (9). This suggests that the noise benefit of operons may be ~2-fold greater than our estimates, since the number of mRNAs needed to produce a given number of proteins would be smaller, and thus more noise sensitive, than what we assumed.

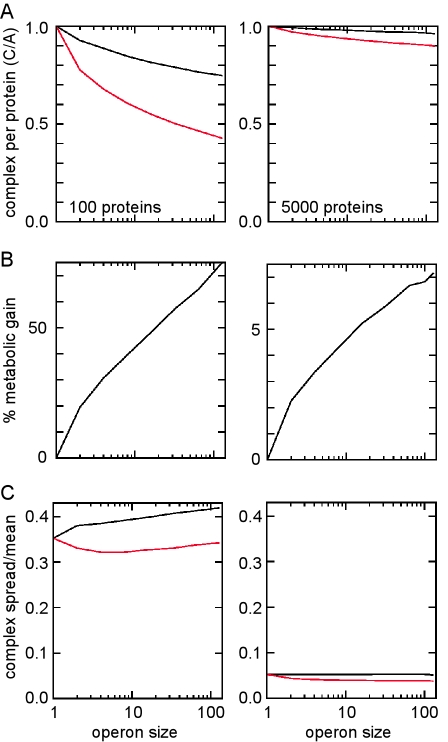
The metabolic benefit of operon organization increases when the number of different proteins in the complex is larger (Fig. 2). This is because having more proteins in the complex means that there are more chances for the level of one protein to fall below those of the others and thus to become limiting. The ~20% gain for a 2-protein operon increases to ~30% for a 4-protein complex and to more than 50% for a 30-protein complex (e.g., a bacteriophage particle). Thus, for E. coli, in which one-third of the transcription units are polycistronic (10), we estimate an overall lowering of the cell’s metabolic cost by at least 0.2% due to this effect of cotranscription (Table 2).

FIG 2 .

Effect of the number of genes carried by the operon. The number of different proteins in the complex (genes carried by the operon) affects the average number of complexes formed in the operon (black) and split (red) arrangements (〈C_O〉 and 〈C_S〉) in units of average production of each protein (A) (A), the percent gain due to the operon arrangement $\left[100\times \left(\langle C_O\text{〉−〈}{C}_S\rangle \right)/\langle C_S\rangle \right]$ (B), and the coefficient of variance (σ/〈x〉) of the number of complexes formed for the operon and split arrangements (C). Stochastic simulations were performed as shown for Fig. 1, with an average of 100 (left) or 5,000 (right) of each protein produced per cell generation.

TABLE 2 .

Calculations of metabolic gain due to cotranscription

Abundance	Complex	No. of complexes per cell	% contribution to dry cell mass	Avg operon size	% gain per operon	Mass × gain (%)
High	Translation apparatus heat shock proteins	20,000	10	4	2	0.2
Medium	RNA polymerase β, β′	4,000	1	2	3	0.03
Lowa	Other	(~500)	(2.5 to 5)	(4)	(~10)	(~0.25 to 0.5)

^a Numbers are estimates of average values or ranges for these complexes.

Conversely, operon organization has the potential disadvantage of increasing fluctuations in the level of the complex (Fig. 1) because the fluctuations in the components occur in synchrony and thus do not cancel each other out. Although this effect is small, roughly 20%, it does not diminish with increasing protein numbers (Fig. 2). Thus, it may be significant in larger systems which require complex regulation. This effect and the reduced regulatory flexibility of cotranscription may favor independent transcription units in eukaryotes. In bacteria and archaea, the metabolic savings in the production of protein complexes seem to dominate, promoting operon formation.

MATERIALS AND METHODS

Computer simulations.

In our simulations, the individual RNA production, degradation, and translation events occur randomly, with rates which secure a preset average protein number in a cell. Throughout the paper, we assume that each ribosome binding site initiates an average of 20 proteins before the mRNA is inactivated by degradation factors. We assume that mRNA has a much shorter lifetime than the encoded proteins and, accordingly, simulate protein production as an instant event happening immediately after the production of each mRNA. We implement this by assigning each newly synthesized mRNA a protein production capacity c drawn from an exponential distribution with a mean number of 20. Subsequently, we increase the concentration of each protein encoded by the mRNA by an amount drawn from a Poisson distribution with mean c. In this way, protein production by subsequent genes carried by a given polycistronic mRNA will vary to an extent, given by the variations in the number of random translation initiations. Finally, protein dilution upon cell division was taken into account by randomly distributing each protein between the daughter cells.

Assumption of equal production for proteins consecutively encoded by the same mRNA.

In our simulations, we assign identical protein production capacity to each ribosome binding site on a polycistronic mRNA. In this way, the intrinsic noise between two proteins (A and B) encoded by the same mRNA is calculated $\langle {\left(\mathit{A}/\mathit{\langle A\rangle }\mathit{-B/}\mathit{\langle B\rangle }\right)}^2\rangle$, proportional to $\langle {\left(\mathit{A-B}\right)}^2\rangle /\mathit{\langle A\rangle }\mathit{\langle B\rangle }$, which decays inversely with the protein concentration. Assuming equal protein production capacity from different parts of the same mRNA seems appropriate to estimate the gain of cotranscription, because a different average protein production capacity would obviously lead to systematic wastage if the proteins are required in equimolar amounts in a functional complex. Such a systematic difference in production capacity was present in a previous study (7) and resulted in the underestimation of the noise reduction due to cotranscription alone. Any systematic differences in protein production caused by a time delay in transcription or the directionality of mRNA decay (7) can easily be compensated by altering the translation initiation sites of the genes without affecting the advantage of the operon arrangement.

Premature termination of an RNA polymerase within an operon can produce systematic decreases in protein production from distal genes (11) and can be compensated for in the same way to maintain equal numbers of the components of the complex. However, this kind of polarity reduces the transcriptional coupling between the genes and reduces the noise benefits of operon organization.

Factors that control fluctuations in intracellular protein numbers.

In our paper, we focus on the amount of protein complex formed relative to the amount that would be produced if protein production and degradation were noise free. In our simulations, we assume that noise is independent of the mRNA lifetime. This is true when the mRNA lifetime is much shorter than the protein lifetime. Even in a more general case, where we do not make such an assumption, we can calculate noise in the protein number as follows:

$${\displaystyle \frac{{\text{σ}}_P^2}{{\mathit{\langle P\rangle }}^2}=\frac{{\gamma }_p{\gamma }_m}{k_c{k}_l}+\frac{{\gamma }_p{\gamma }_m}{k_c\left({\gamma }_p+{\gamma }_m\right)}}$$

where 〈P〉 and ${\text{σ}}_P^2$ are the average and the variance of the protein number, respectively, γ_m and γ_p are the degradation rates for mRNA and protein, respectively, and k_c and k_l are transcription and translation rates, respectively (12).

Thus, the protein noise indeed approaches a constant for large γ_m and k_c, provided that the average number of protein copies produced per mRNA, k_l/γ_m (in our simulations, 20 copies), is kept fixed.

Calculations of metabolic gain.

The estimate of overall synthetic gain of at least 0.23% for protein complex formation due to the use of operons in E. coli (Table 2) uses the measurements of Pedersen et al. (13), with later identifications of protein spots for high- and medium-abundance proteins, and an estimate of 50% protein for the dry cell mass (14). This gain is a minimum estimate, as it ignores the fraction of the protein mass comprising numerous different complex-forming proteins with lower expression levels whose encoding genes are cotranscribed. These could make a large contribution to the gain (Table 2).