Skip to main content
PMC home page
Springer logoLink to Springer
. 2010 Jun 26;8(3):171–182. doi: 10.1007/s12021-010-9074-x

Anatomical Global Spatial Normalization

Jack L Lancaster 1,✉, Matthew D Cykowski 1, David Reese McKay 1, Peter V Kochunov 1, Peter T Fox 1, William Rogers 1, Arthur W Toga 2, Karl Zilles 3,4, Katrin Amunts 3,5, John Mazziotta 6
PMCID: PMC2945458  PMID: 20582489

Abstract

Anatomical global spatial normalization (aGSN) is presented as a method to scale high-resolution brain images to control for variability in brain size without altering the mean size of other brain structures. Two types of mean preserving scaling methods were investigated, “shape preserving” and “shape standardizing”. aGSN was tested by examining 56 brain structures from an adult brain atlas of 40 individuals (LPBA40) before and after normalization, with detailed analyses of cerebral hemispheres, all gyri collectively, cerebellum, brainstem, and left and right caudate, putamen, and hippocampus. Mean sizes of brain structures as measured by volume, distance, and area were preserved and variance reduced for both types of scale factors. An interesting finding was that scale factors derived from each of the ten brain structures were also mean preserving. However, variance was best reduced using whole brain hemispheres as the reference structure, and this reduction was related to its high average correlation with other brain structures. The fractional reduction in variance of structure volumes was directly related to ρ 2, the square of the reference-to-structure correlation coefficient. The average reduction in variance in volumes by aGSN with whole brain hemispheres as the reference structure was approximately 32%. An analytical method was provided to directly convert between conventional and aGSN scale factors to support adaptation of aGSN to popular spatial normalization software packages.

Keywords: Size preservation, Linear distance, Area, Mean volume, aGSN, GSN, Variance

Introduction

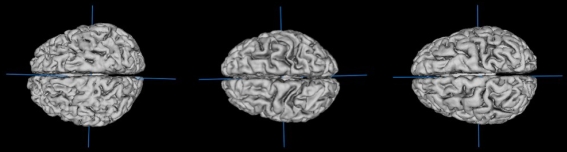
In this study we evaluated 40 brain images from the LPBA40 brain atlas of a young adult population where brain development was assumed to have reached an adult plateau level (20 males; 29.2 ± 6.3 years from 19.3 to 39.5 years). Even so, brain size and shape varied considerably ranging from 986,143 mm3 to 1,472,377 mm3 with mean value ±SD of 1,179,978 ± 112,537 mm3 (Fig. 1). Global spatial normalization (GSN) can be used to eliminate much of this variability by scaling each brain image to a standard template brain image, such as the ICBM-152. Though conventional GSN works well to register and standardize brains, it does not preserve size, which is important in studies of anatomical differences between groups (Clark et al. 2001; Allen et al. 2008; Shattuck et al. 2008). Group-wise size is considered preserved when the “average size” of each brain structure is not altered by spatial normalization, and this is one goal of anatomical global spatial normalization (aGSN).

Fig. 1.

Fig. 1

Open in a new tab

Surface views of three brains from the LPBA40 database illustrating variation in size and shape. Surfaces extracted and views generated using Mango

While the main focus in controlling size variability has been on volume, there are other measures of size that should be considered; linear distance such as cortical thickness (Luders et al. 2006; Lerch et al. 2006; Sowell et al. 2007) and area such as cortical surface area (Le Goualher et al. 1999; Lancaster et al. 2003; Rogers et al. 2007). For example, cortical thickness remains relatively unchanged among all orders of mammals (Zhang and Sejnowski 2000), in contrast to cortical volume, which scales approximately according to brain volume across many species including humans (Prothero and Sundsten 1984; Prothero 1997; Hoffman 1988). This dissociation between the relationships of cortical thickness/brain size and cortical volume/brain size is presumably driven by an increase in cortical surface area in larger brains, rather than thickness (Pakkenberg and Gundersen 1997; Im et al. 2008). Additionally, it has been shown that conventional GSN can falsely alter mean relationships in cortical thickness (Luders et al. 2006; Lerch et al. 2006; Sowell et al. 2007).

Anatomical spatial normalization is based on the assumption that when a brain structure’s size varies with brain size, this variability can be reduced by controlling for brain size. In aGSN we apply mean preserving scale factors to individual brains to match a group-wise mean standard with dual goals of controlling for brain size and preserving mean sizes. We formulate and test two classes of mean preserving scale factors for aGSN; shape preserving and shape standardizing scale factors. Shape preserving scale factors remove variability in brain volume without altering brain shape, mimicking non-imaging methods. Shape standardizing scale factors adjust size in the x-, y- and z-axis directions to group mean values, mimicking conventional GSN, and this is achieved without fitting to a standard brain template.

Materials and Methods

Test Data

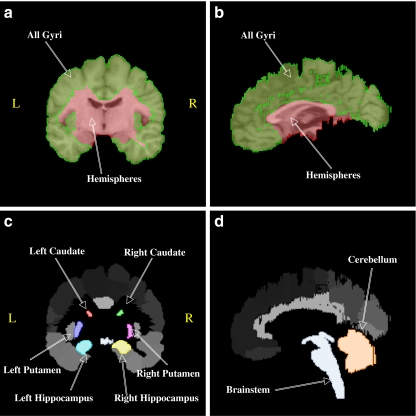
The Probabilistic Brain Atlas (LPBA40) distributed by UCLA’s Laboratory of Neuro Imaging (LONI) includes 56 individually labeled structures from 40 healthy adult volunteers. An important feature of this data is that images are consistently oriented and positioned, but no scaling had been applied (Fig. 1). Images and structures analyzed were from the “delineation” subset with 1-mm spacing. Ten structures were selected for detailed analysis: cerebral hemispheres (“hemispheres”), all cerebral gyri (“all gyri”), cerebellum, brainstem, caudate, putamen, and hippocampus (for the latter three structures left/right homologues were treated separately). 3-D regions of interest (ROIs) were formulated for each structure using Mango image processing software (Lancaster, Martinez; www.ric.uthscsa.edu/mango) (Fig. 2). The hemispheres ROIs were formulated from skull-stripped T1-weighted 3-D MR images with brainstem and cerebellum removed. The hemispheres regions served as the reference structures for brain size control since whole brain images were not present in the atlas. The all-gyri ROI was formulated as a chiefly cortical structure from the union of all gyral labeled regions in the cerebrum (LPBA40 codes 21-122). Cerebellum and brainstem ROIs were used for testing non-cerebral structures, and the hippocampus, caudate, and putamen ROIs were used for testing deep brain structures.

Fig. 2.

Fig. 2

Open in a new tab

Examples of ROIs formulated from the LPBA40 database for one brain. Hemispheres and All Gyri in a & b are overlaid transparently onto the grey scale brain image

Principal Axis Analysis

Principal axes analysis was used to provide bias free measures of size of each brain structure. Principal axes analysis has been used for brain image registration (Alpert et al. 1990; Toga and Banerjee 1993; Schormann and Zilles 1997) and as a tool to support brain structure classification (Mangin et al. 2004a). The principal axes analysis software is available as a plug-in application for Mango (Lancaster, Martinez; www.ric.uthscsa.edu/Mango/plugins.html). This plug-in application tabulates volume, geometric center, eigenvectors, and eigenvalues for Mango defined ROIs. Three linear distances were formulated as the square root of eigenvalues, one for each principal axis. Linear distances calculated in this manner are average distances from the center of an ROI to its surface for each of the three principal directions.

Structure Correlation

Structure-to-structure volume correlations for the ten structures of interest from the LPBA40 atlas were quite variable (Table 1) with Pearson correlation coefficients (ρ) near zero for caudate-to-putamen correlation. The hemispheres-to-structure correlation was of particular interest since the hemispheres ROI was used as our brain reference. Hemispheres-to-structure volume correlation was highest for the all-gyri structure (ρ = 0.99). The hippocampus, cerebellum, and brainstem followed with intermediate correlations ranging from 0.65 to 0.76. Finally the caudate and putamen had the lowest brain-to-structure correlation ranging from 0.45 to 0.51. Though not tabulated, the hemispheres-to-structure correlations for all 56 structures showed that 10% of structures had ρ > 0.75, 50% had ρ > 0.50 and 90% had ρ > 0.25. Left-to-right correlations for caudate, putamen, and hippocampus were all high (ρ > 0.80). These correlation data served to guide analyses in the study of mean preserving scaling.

Table 1.

Correlation of volumes for ten brain structures from the LPBA40 database (non-scaled)

Hemispheres All Gyri L Cau R Cau L Put R Put L Hcp R Hcp Cbm Bstm
Hemispheres 1.000
All Gyri 0.990 1.000
L Caudate 0.483 0.467 1.000
R Caudate 0.448 0.425 0.931 1.000
L Putamen 0.469 0.468 0.028 −0.016 1.000
R Putamen 0.513 0.529 0.128 0.053 0.804 1.000
L Hippocampus 0.758 0.751 0.169 0.098 0.482 0.523 1.000
R Hippocampus 0.653 0.631 0.231 0.175 0.323 0.425 0.839 1.000
Cerebellum 0.686 0.712 0.354 0.358 0.261 0.349 0.602 0.443 1.000
Brainstem 0.714 0.686 0.303 0.252 0.428 0.497 0.644 0.574 0.660 1.000
Open in a new tab

Scale Factors

Shape preserving scale factors were formulated as sxi = syi = szi = (<V>/Vi)1/3, where Vi is the hemispheres volume in subject “i” and <V> the group mean hemispheres volume. By design these scale factors were isotropic and adjusted individual hemispheres’ ROIs to the same volume, thereby providing full control for variability in hemispheres volume.

Shape standardizing scale factors were formulated from the three principal axes linear distance measures in hemispheres (Xi, Yi, and Zi) as sxi = <X>/Xi, syi = <Y>/Yi, and szi = <Z>/Zi, where <X> is the mean value of X, and so forth. These scale factors are generally non-isotropic but produce scaled hemispheres with identical X, Y, and Z linear distances, so the method was loosely termed shape standardizing. Shape standardizing scale factors were derived from measures along principal axes of hemispheres rather than the x-y-z axes; however, the principal axes of hemispheres were virtually aligned with x-y-z axes for the brain images supporting their use for x-y-z scaling.

Volume Analysis

The objective of this analysis was to determine if mean preserving scale factors, formulated using hemispheres as the standard, would preserve mean volumes of the other brain structures, and whether this could be done with both classes of scale factors. Since 40 volume measures were available for each ROI, volume scaling was done by simply multiplying these measures by volume scale factors. This approach avoids issues with scaling and interpolation of the ROI images, providing more precision. Volume scale factors were formulated for each brain as the product of x-, y- and z-scale factors for both classes of mean scale factors.

Distance Analysis

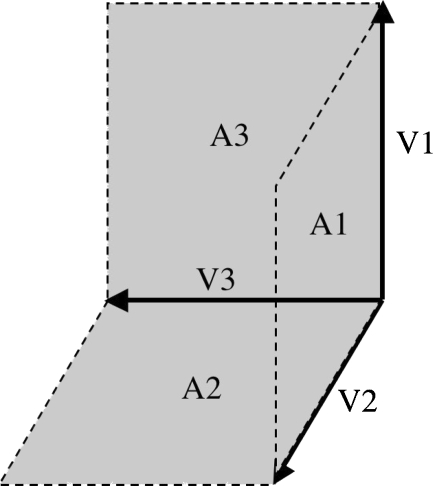
The purpose of this analysis was to determine the effect of shape preserving and shape standardizing scale factors on linear distances. To avoid bias in selecting points needed to define distances we formulated three linear distances from principal axes analysis. The three distances were derived from the three eigenvectors for the right hippocampus (Fig. 3). Since these vectors are not necessarily aligned with the x-y-z axes, post-scaled linear distances were calculated using Eq. (A.2.2). The right hippocampus was used as the test structure, because its three directed distances varied sufficiently from subject to subject in both magnitude and orientation, providing natural variability and its moderately high correlation with hemispheres (Table 1). While there is variability in how the hippocampus is defined (see Discussion) the method used by Shattuck et al. 2008 served well as a test structure for our analyses.

Fig. 3.

Fig. 3

Open in a new tab

Examples of three eigenvectors and three planar areas (dashed grey) used for analysis of scaling of linear distances and planar areas for right hippocampus

Area Analysis

The purpose of this analysis was to determine the effect of shape preserving and shape standardizing scale factors on surface areas. Well-defined 3-D surface areas are difficult to obtain since surface areas depend on image resolution and structure detail. To overcome this potential limitation we formulated areas for testing using the three eigenvectors from the right hippocampus. Three rectangular plane surfaces (A1–A3) were formulated in each brain, with pairs of eigenvectors determining a rectangle’s dimensions (Fig. 3). Since planar surfaces were not necessarily aligned with the x-y-z axes, post-scaled plane areas were calculated using Eq. (A.3.3). Lastly, we examined the effect of scaling on a non-planar surface with a surface mesh formulated about the exterior surface of the cerebellum using BrainVisa (http://brainvisa.info/) (Mangin et al. 2004b).

Image Based Analysis

In the volume, distance, and area analyses scale factors were applied either directly to measured volumes, distances and areas formulated from principal axes analysis of the right hippocampus, or a surface model of the cerebellum. However, pre- and post-scaled brain images were not directly evaluated, so we performed an additional test on one structure (hemispheres) by applying shape standardizing scaling to its ROIs in the 40 brain images.

Results

Volume Analysis

No disparities in pre-scaled measured volumes were found compared with those reported by Shattuck et al. (2008) verifying accurate conversion from the LPBA40 images to Mango ROIs. Both shape preserving and shape standardizing scale factors derived from hemispheres as the reference structure preserved volumes of all structures (Table 2) with mean volumes within ∼0.1% of pre-scaled values. As designed shape preserving scaling resulted in hemispheres volumes that were identical in all subjects. Though shape standardizing scaling was designed from distance measures alone, it also resulted in mean volumes within ∼0.1% of pre-scaled values. In addition to preserving mean volumes both scaling methods reduced variability in all ten structures (Table 2). The largest reductions in variance were seen for hemispheres and all-gyri regions. This was expected for hemispheres since scale factors were derived from analysis of this region.

Table 2.

Volumes of brain structures before and after shape preserving and shape standardizing scaling (mean ± SD (CV))

Structure Non-scaled (mm3) Shape preserving (mm3) Shape standardizing (mm3)
Hemispheres 1,179,978 ± 112,537 (0.095) 1,179,978 ± 0 (0.000) 1,178,307 ± 9,819 (0.008)
All Gyri 882,398 ± 87,371 (0.099) 882,185 ± 12,261 (0.014) 880,950 ± 15,115 (0.017)
L Caudate 2,972 ± 558 (0.188) 2,972 ± 475 (0.160) 2,968 ± 477 (0.161)
R Caudate 2,856 ± 623 (0.218) 2,854 ± 546 (0.191) 2,850 ± 544 (0.191)
L Putamen 4,249 ± 531 (0.125) 4,263 ± 479 (0.112) 4,257 ± 480 (0.112)
R Putamen 4,206 ± 504 (0.120) 4,219 ± 444 (0.105) 4,213 ± 447 (0.106)
L Hippocampus 3,907 ± 528 (0.135) 3,905 ± 347 (0.089) 3,899 ± 350 (0.090)
R Hippocampus 4,120 ± 527 (0.128) 4,125 ± 413 (0.100) 4,119 ± 415 (0.101)
Cerebellum 134,585 ± 17,519 (0.130) 134,647 ± 12,988 (0.096) 134,423 ± 12,643 (0.094)
Brainstem 29,590 ± 3,365 (0.114) 29,627 ± 2,371 (0.080) 29,581 ± 2,320 (0.078)
Open in a new tab

Consistent with other studies on naturally developed brains (Stephan et al. 1981; Prothero and Sundsten 1984; Prothero 1997; Hoffman 1988), a high positive correlation was seen between all-gyri and hemispheres’ volumes (0.99 from Table 1). This strong correlation indicates that total gyral volume scales closely with brain volume. This is further supported by the large reduction in variance for all-gyri for the two scaling methods, which used hemispheres as the controlling structure (Table 2). Left-right volume asymmetry of the caudate and hippocampus was not altered by either scaling method, consistent with observations by Filipek et al. 1994 and Goncalves-Pereira et al. 2006.

To further test volume preserving capabilities we applied both scaling methods to all 56 structures from the LPBA40 database. The post-scaled mean volumes ranged from −0.33% to +0.34% of their pre-scaled values, indicating that mean volumes were preserved for all structures. As shown in Appendix A.1 two properties are necessary for scale factors to be mean preserving: 1) they should be near unity mean and 2) correlation between scale factors and the size measure should be near zero. These conditions were met for scaling factors derived from hemispheres volumes.

The question arose as to whether structure volumes could be preserved using scale factors derived using volumes of other brain structures as the reference. This was tested with shape preserving scale factors derived from each of the ten brain structures as the reference. Notably, each of the ten reference structures preserved volumes. The reference structure with the smallest mean volume error (0.08%) and variance (mean CV = 9.5%) was hemispheres. Most other structures led to mean volume errors of about 1% with mean CV of 13%, which was approximately the CV of non-scaled brains, so volume was preserved but variance was not always reduced. The reference structure with the largest mean error and variance was right caudate with mean volume error of 3.7% and mean CV of 21%, so it noticeably increased variance. This study clearly shows that whole brain standards such as hemispheres used in this study are best for preserving mean volumes of internal brain structures while reducing variance.

Distance Analysis

For both scaling methods mean linear distances were within 0.2% of pre-scaled values (Table 3), and orientation was also preserved. However, variance reduction for linear distance varied by orientation, with the largest reduction in CVs seen in x and z directions, with little or no reduction in the y direction. Shape standardizing scaling usually produced slightly lower CVs than shape preserving scaling, especially for the y direction. In Appendix A.2 we present mathematical support for the preservation of mean distances and orientation using mean preserving scale factors. These results together with those from volume testing show that both distances and volumes can be preserved and variance reduced using a common set of x-y-z scale factors.

Table 3.

Effects of x-y-z scaling on linear distances and plane areas derived from right hippocampus (mean ± SD (CV))

Scaling method Linear distance (mm)a Area (mm2)a
x-dir y-dir z-dir x-y plane x-z plane y-z plane
Non-scaled 4.87 ± 0.33 (0.068) 8.70 ± 0.62 (0.071) 2.82 ± 0.20 (0.070) 42.42 ± 4.59 (0.110) 13.76 ± 1.65 (0.120) 24.46 ± 2.09 (0.086)
Shape Preserving 4.88 ± 0.27 (0.055) 8.71 ± 0.65 (0.075) 2.82 ± 0.16 (0.058) 42.50 ± 4.09 (0.096) 13.76 ± 1.25 (0.091) 24.65 ± 2.58 (0.105)
Shape Standardizing 4.88 ± 0.28 (0.056) 8.69 ± 0.62 (0.071) 2.82 ± 0.16 (0.057) 42.45 ± 4.23 (0.100) 13.79 ± 1.20 (0.087) 24.46 ± 1.74 (0.071)
FLIRT 5.40 ± 0.31 (0.057) 9.48 ± 0.68 (0.072) 3.23 ± 0.18 (0.056) 51.21 ± 5.15 (0.101) 17.46 ± 1.50 (0.086) 30.55 ± 2.21 (0.073)
aFLIRT 4.89 ± 0.27 (0.055) 8.69 ± 0.62 (0.072) 2.82 ± 0.16 (0.057) 42.44 ± 4.25 (0.100) 13.79 ± 1.19 (0.086) 24.46 ± 1.77 (0.073)
Open in a new tab

adirections are for nearest image axis or image plane

A comparison was performed between aGSN’s mean preserving scaling and conventional GSN scaling using the ICBM152 brain template. Conventional GSN scaling used x-y-z scale factors extracted from the transform matrix files provided at the LPBA40 web site based on fitting with FSL’s FLIRT (Jenkinson and Smith 2001). Mean right hippocampal distances for FLIRT scaling varied significantly from non-scaled values, but fractional variance reductions (CVs) were similar. Importantly, distance errors varied by orientation (+10.9% the x-direction, +9.0% for the y-direction, and +14.5% for z-direction). These findings highlight the potential for orientation and size problems when using a conventional brain template to control for size in anatomical studies. The larger values for FLIRT are not an indication of its quality of fit but rather of the design of the ICBM152 brain template which naturally leads to larger brains (Lancaster et al. 2007).

Area Analysis

Mean planar areas were preserved for both shape preserving (within 0.8%) and shape standardizing (within 0.5%) scaling (Table 3). The trend in variance reduction in plane areas followed that seen for linear distance, with the largest reduction in CVs for the x-z plane and smallest reduction for the x-y plane. Shape preserving scaling increased variance for the y-z plane, and this was assumed to be due to the poor performance in the y-direction seen for the distance study. These results along with those for volume and distance testing show that distance, areas and volumes can be preserved using the same set of x-y-z scale factors. In Appendix A.3 we present mathematical support for the preservation of mean area using mean preserving scale factors. For FLIRT using the ICBM152 template brain areas were larger and varied by orientation, ranging from 20.7% above natural values for the x-y plane to 26.9% above for the x-z plane. However, relative variance reduction was similar to the mean preserving methods.

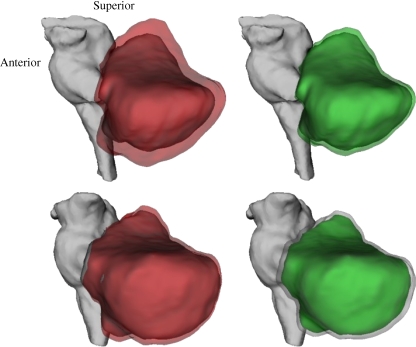
Testing the surface area of the cerebellum yielded similar accuracy results. The mean non-scaled surface area of the cerebellum was 16,665 ± 1,504 mm2. Scaling using the shape standardizing scale method minimally altered this mean surface area (16,749 ± 1,214 mm2) while reducing variance. For comparison FLIRT using the ICBM152 template increased mean surface area by 17.9% (19,649 ± 1,269 mm2). Interestingly the relative variance in surface area of the cerebellum was smaller for FLIRT scaling (CV = 0.077 vs. 0.086), most likely because FLIRT includes the cerebellum during fitting while the shape standardizing method used only cerebral hemispheres. The mean volume of the non-scaled 3-D surface mesh was calculated for size verification yielding 133,394 ± 17,246 mm3, which corresponded well with values calculated directly from cerebellum ROI volumes (Table 2). Scaling of the cerebellum by FLIRT using the ICBM152 template is compared with shape preserving scaling in Fig. 4 for a small and large brain to illustrate these effects.

Fig. 4.

Fig. 4

Open in a new tab

Two scaling methods are illustrated for cerebellum: ICBM152 template using FLIRT (red) and aGSNs mean shape preserving (green). Natural cerebellum and brainstem are grey. Upper row is for a smaller than average size brain and lower row for a larger than average size brain. Note that aGSN scaling increased smaller and decreased larger cerebellum, while fitting using ICBM152 enlarged both

Image Based Analysis

The mean volume of the hemispheres ROIs (1,179,970 ± 10,064 mm3) following shape standardizing scaling applied directly to the forty images was almost identical to that for volume scaling (Table 2), and standard deviation reduced to approximately 10% of its non-scaled value. The standard deviation was ∼2% larger than non-image shape standardizing scaling (SD = 9,819 mm3). This was attributed to random errors that occur when reformulating ROIs after scaling (Collins et al. 1994). Linear distances and plane areas were also preserved, with difference of less than 1% in each. Standard deviations in the distance and area measures were reduced to less than 1% of mean values; similar to what was seen for non-image scaling (Table 3). This large reduction in variance was expected since shape standardizing scale factors were derived from the hemispheres ROIs.

These analyses show that when mean preserving scaling is not used that natural sizes are not preserved globally. Moreover, nonlinear scaling has the potential to change natural sizes locally. For processing applications such as FreeSurfer that use nonlinear registration of surface meshes, we recommend providing a 1:1 map from post-warped to pre-warped meshes. Regions of interest that are defined on nonlinearly registered surfaces can then be mapped back to native brain surfaces for distance, area, and volume analyses.

Discussion

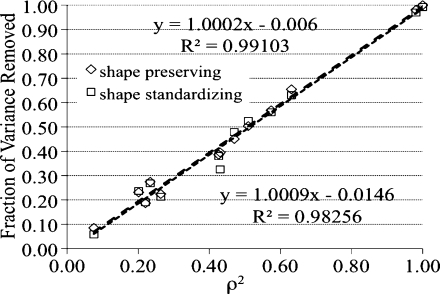
To better understand the reduction in volumetric variance by aGSN the variance of a brain structure can be parceled into two components, one associated with variability in native brain size and the second from other sources. Other sources of variability include boundary definition variability, natural structure variability, and variability due to interactions with other structures. Shape preserving scaling removes variance due to brain size, since each brain’s volume is rendered identical. The reduction to near zero correlation between native brain (hemispheres) and native structure volumes following mean preserving scaling confirms this (left column, Table 1 vs. Table 4). Linear regression of brain structure volumes with native brain volume as the regressor was done to obtain R 2 values, which indicate the fraction of variance explained by the model. Brain-to-structure correlations were also determined using a Pearson correlation coefficient (ρ), and ρ 2 values were identical to R 2 values. More importantly, the fractional variance reduction following mean preserving scaling was nearly identical to that predicted by regression analysis, suggesting equivalence regarding variance reduction (Fig. 5). This equivalence held up for shape standardizing as well as shape preserving scaling. However, mean preserving scaling provides variance reduction for all brain structures, while regression analysis has to be done for each structure to estimate the reduced variance (Fig. 5).

Table 4.

Correlation of volumes for ten brain structures from the LPBA40 database after shape preserving scaling

Hemispheres All Gyri L Cau R Cau L Put R Put L Hcp R Hcp Cbm Bstm
Hemispheres 1.000
All Gyri −0.014 1.000
L Caudate −0.013 −0.016 1.000
R Caudate −0.008 −0.063 0.906 1.000
L Putamen −0.020 −0.038 −0.230 −0.263 1.000
R Putamen −0.012 0.105 −0.129 −0.210 0.760 1.000
L Hippocampus −0.013 −0.006 −0.313 −0.379 0.124 0.150 1.000
R Hippocampus −0.008 −0.199 −0.138 −0.196 0.043 0.146 0.703 1.000
Cerebellum 0.017 0.280 0.046 0.110 −0.083 −0.011 0.190 0.013 1.000
Brainstem 0.005 −0.284 −0.060 −0.102 0.185 0.237 0.195 0.211 0.301 1.000
Open in a new tab

Fig. 5.

Fig. 5

Open in a new tab

The fraction of variance removed by mean preserving scaling is shown to be equivalent to that explained by regression analysis using brain structure as the regressor where the modeled R 2 = ρ 2

It is important to assess the lower limit on brain-to-structure correlation for aGSN to successfully reduce variance. The mean reduction of variance in volumes for all 56 structures was 32%. The lower limit on ρ 2 for reducing volume variance was estimated to be ∼7%, a level of correlation that indicates a very weak relationship between brain size and structure size. This level was set to divide the group into structures that reduced variance and those that did not. All but four structures reduced variance (the left orbital frontal gyrus, left angular gyrus, and left & right cingulate gyrus though increases were small (CV change <0.02). Visual inspection by two authors (JLL, MDC) determined that some internal boundaries of these structures were not consistently defined, so it appears that the boundary definition component of variance masked that due to brain size. While boundary definition variance was present in other structures, its fractional contribution was apparently smaller since shape preserving scaling successfully reduced total variance in all other structures. It appears that if boundary definition variance is well managed then aGSN will reduce volumetric variance.

An important finding concerning mean preserving scaling was that, when used as the reference volume, each of the ten structures preserved the volume of the other nine structures. Strikingly, even when mean preserving scale factors determined from hemispheres were randomly applied rather than matched to individual brains the mean volumes were minimally changed (∼1%); however, variance was increased as much as 37%. The practical significance of this observation is that researchers should be very cautious when tabulating scaled volumes to ensure that scale factors are properly paired with brains.

Though volume was preserved for all reference volumes, average variance was only reduced when whole brain (hemispheres) was used as the reference, which was predictable based on its high structure-to-structure correlation (Table 1). Additionally, as can be seen from Table 4 left-to-right correlations remained high for caudate, putamen and hippocampus after mean preserving scaling. Finally, by removing hemispheres size effect an interesting relationship was revealed between caudate and left hippocampus as a moderate negative correlation. This relationship was assumed to fall into the other component of variance category where one structure influences another independent of brain size. The nature of this relationship is unclear and suggests the need for further investigation.

Distances and areas were preserved for both classes of scale factors, and this was achieved regardless of orientation. This finding supports making measures of mean cortical thickness and surface areas of brain structures while controlling for brain size with aGSN’s scaling. Shape preserving scale factors were applied isotropically, so they naturally preserved shape. Unlike shape preserving scale factors, shape standardizing scale factors are usually non-isotropic, but as formulated each x-, y-, and z-scale factor met the conditions for mean preserving scaling. Finally, for both classes of scale factors their area scale factors (paired products of scale factors) and volume scale factors (triple products) also met the conditions for mean preserving scaling. Correlation between the three distances for hemispheres and three distances for right hippocampus lead to nine possible first order interactions, so simple correlation analysis was not done. However, analysis of hemispheres x and z distances revealed negative correlations with the y distance in hippocampus, supporting the poor reductions in variance for distances and areas in hippocampus involving the y direction.

Template-based aGSN

To support conversion between conventional GSN and aGSN we developed an analytical method to adjust conventional GSN x-y-z scale factors to mean preserving x-y-z scale factors (Appendix A.4). FLIRT scale factors that fit each brain to the ICBM152 template served as the basis for testing. A new set of mean preserving aFLIRT scale factors was calculated from the FLIRT scale factors using Eq. (A.4.4). Both sets of scale factors were applied to each subject’s 10 volumes of interest. The FLIRT scaled volumes (Table 5) were similar to those published by Shattuck et al. 2008, verifying proper application of the scale factors. As predicted, the aFLIRT scale factors preserved mean volumes and decreased variability. Equivalent mean volumes were seen for aFLIRT (Table 5) and shape standardizing scaling (Table 2), with differences <1%.

Table 5.

Volumes using FLIRT and mean preserving aFLIRT scaling (mean ± SD (CV))

Structure Non-scaled (mm3) FLIRT (mm3) aFLIRT (mm3)
Hemispheres 1,179,978 ± 112,537 (0.095) 1,625,494 ± 33,227 (0.020) 1,180,826 ± 24,138 (0.020)
All Gyri 882,398 ± 87,371 (0.099) 1,215,227 ± 28,311 (0.023) 882,791 ± 20,566 (0.023)
L Caudate 2,972 ± 558 (0.188) 4,093 ± 658 (0.161) 2,974 ± 478 (0.161)
R Caudate 2,856 ± 623 (0.218) 3,929 ± 748 (0.190) 2,854 ± 543 (0.190)
L Putamen 4,249 ± 531 (0.125) 5,875 ± 695 (0.118) 4,268 ± 505 (0.118)
R Putamen 4,206 ± 504 (0.120) 5,813 ± 640 (0.110) 4,223 ± 465 (0.110)
L Hippocampus 3,907 ± 528 (0.135) 5,378 ± 484 (0.090) 3,907 ± 352 (0.090)
R Hippocampus 4,120 ± 527 (0.128) 5,682 ± 585 (0.103) 4,128 ± 425 (0.103)
Cerebellum 134,585 ± 17,519 (0.130) 185,271 ± 16,005 (0.086) 134,589 ± 11,627 (0.086)
Brainstem 29,590 ± 3,365 (0.114) 40,796 ± 3,124 (0.077) 29,636 ± 2,270 (0.077)
Open in a new tab

Variance in most structures was similar; however, there were several significant differences, with the shape standardizing method having lower CVs for hemispheres and all-gyri regions and the aFLIRT method having a lower CV for cerebellum. These differences were assumed to arise from differences in reference structures, where the shape standardizing method used hemispheres and the aFLIRT method used whole brain. To test this assumption we formulated a whole brain ROI by adding brainstem and cerebellum ROIs to the hemispheres’ ROI. When using this whole brain ROI as the reference structure the variance differences between shape standardizing and aFLIRT methods were practically eliminated. The CVs in hemispheres and all gyri for the shape standardizing scaling increased but remained smaller than those for aFLIRT (0.014 vs. 0.020 for hemispheres and 0.018 vs 0.023 for all gyri). Linear distance and plane area were also preserved using aFLIRT (Table 3). These data indicate that the shape standardizing method based on principal axes analysis provides control of volume variability equivalent to that achievable using FLIRT.

Shape preserving scale factors can be approximated from shape standardizing scale factors as si = (sx·sy·sz)1/3, where sx, sy, and sz are the shape standardizing scale factors and si the resulting isotropic scale factor. While calculation of volumes using these scale factors can be done in a spreadsheet, corrections for distances and areas require more complex manipulations, as indicated in “Appendices A.2 and A.3”, since these don’t naturally align with the image’s x-y-z scale directions. Additionally, surface areas of individual structures must be determined from surface models such as that used in this study.

Between Group Anatomical Studies

When performing between group anatomical studies it is important to preserve mean measurements of “each” group while reducing variance, and aGSN does that for high-resolution brain imaging studies. This leads to improved power in between-group anatomical studies. Using the methods described above for conversion from template based GSN one can break large groups into subgroups and each independently normalized by aGSN, a strategy useful in formulating post hoc analyses for a variety of subgroups. The use of aGSN in this manner supports comparisons of distances, areas, and volumes of brain structures with transformed images.

Boundary Definition Variability

The component of variability due to boundary definition appears to vary by structure and by laboratory. For example, wide ranges of volumes have been reported for the hippocampus. Amunts et al. 2005 reported left and right hippocampus volumes as 4,713 ± 1,007 and 4,884 ± 1,087 mm3 (N = 10, 5 males), while Kronmuller et al. 2009 reported 3.09 ± 0.25 and 3.30 ± 0.29 cm3 (N = 11 males), and for LPBA40 data (Shattuck et al. 2008) the values were 3,907 ± 528 and 4,120 ± 527 mm3. Amunts used post mortem sectioned images with excellent hippocampal definition, and may have included subregions that were not possible in MR images, so this might explain why their mean values were largest. Both Kronmuller and Shattuck used MR images, but Kronmuller used a sagittal tracing method devised by Pantel et al. 2000, and Shattuck used a coronal delineation method based on their lab’s published rules (Supplementary material from their paper). The right hippocampus was larger than left for all three groups, but standard deviations varied tremendously, covering a four-fold range from Kronmuller to Amunts. Shattuck’s mean values were closer to those of Amunts than were Kronmuller’s. While aGSN cannot resolve variability due to differences in delineation methods, we have shown that it will reduce group-wise structure variability associated with brain size, so would be useful with a consistent method of boundary definition.

Conclusions

Anatomical GSN was shown to preserve distances, areas and volumes in a group of 40 adult brains while reducing variance. The mean preserving capabilities of aGSN scaling methods were also presented mathematically. The level of reduction in volumetric variance of brain structures was shown to be predictable from the correlation between the reference structure and individual brain structures. Conventional template based GSN scaling was successfully converted analytically to mean preserving aGSN scaling, supporting incorporation of this feature into popular software.

Acknowledgments

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

Appendix

A.1 Mean Preserving Scale Factors

The scaled volume 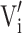Inline graphic of a brain structure’s pre-scaled value Vi in brain “i” is

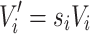graphic file with name M2.gif A.1.1

where si is the mean preserving scale factor calculated as <Vref>/Vrefi. Here <Vref> is the mean of a reference brain measure and Vrefi the measure in brain “i”. Equation (A.1.1) can be rewritten where si and Vi are expressed as their mean values <s> and <V> plus a zero-mean deviation term.

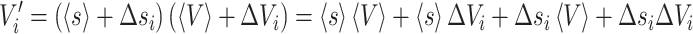graphic file with name M3.gif A.1.2

Since the mean value of the two middle terms on the right side of Eq. (A.1.2) is zero, the group mean scaled volume of a structure is

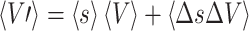graphic file with name M4.gif A.1.3

According to (A.1.3) two conditions regarding si are sufficient to preserve mean volumes of brain structures: 1) that <s> = 1 and 2) that covariance between s and V be zero, i.e. that <ΔsΔV> = 0. The value of <s> was near unity (1.0088) for the 40 brains when using hemispheres as the reference volume. The value of <ΔsΔV> was less than 0.3% of <V> for each of the other major brain structures so condition two was met as well. Similar values were seen for shape standardizing scale factors so both classes were classified as mean preserving.

A.2 Distance Scaling

Distances calculated by principal axes analyses are the magnitude of vectors originating from the centroid of a structure. These can be described as a vector (A) of arbitrary direction and length for brain “i” as

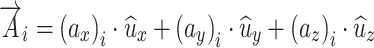graphic file with name M5.gif A.2.1

where a’s are the vector components the x-y-z directions. The length or magnitude of this vector is calculated as the square root of the sum of the squares of the three components. After x-y-z scaling the vector is

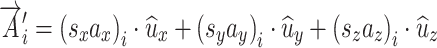graphic file with name M6.gif A.2.2

and the length of the scaled vector is just the magnitude of (A.2.2). For “length” and “orientation” to be preserved the average of each component of (A.2.2) must match the average of each component in (A.2.1). The difference with and without mean preserving x-y-z scale factors for the ten tested structures in 40 brains was less than 1%, supporting the preservation of vector length and orientation.

A.3 Area Scaling

The area of a plane surface by can be modeled as a rectangle. Pairs of orthogonal eigenvectors from brain “i” were used to formulate three rectangles using a vector cross product as follows:

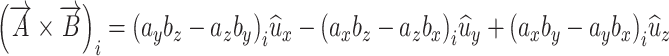graphic file with name M7.gif A.3.1

where A and B are the eigenvectors. Pairs of eigenvectors were derived by principal axes analysis of the right hippocampus. The area of a rectangle is the magnitude of the vector in (A.3.1). For brain “i” the vector area changes due to the three x-y-z scale factors as follows:

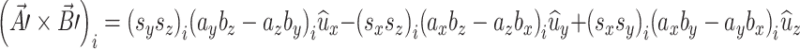graphic file with name M8.gif A.3.2

The post-scaling area of the rectangle is just the magnitude of this scaled vector. The average of this vector product for a group of brains is

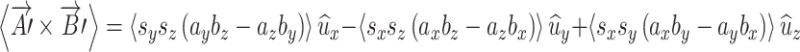graphic file with name M9.gif A.3.3

For area and “orientation” to be preserved the average of each of the three components following scaling must be equal to their pre-scaled average values. This was tested using mean preserving scaling applied to the set of unit area vectors derived from right hippocampus ROIs. The resulting mean value for each vector component in (A.3.3) was found to be within 1% of non-scaled values, so mean area and orientation was preserved.

A.4 Calculating Mean Preserving Scale Factors

Given that mi is an x-, y- or z-directed size measure in each brain and its target measure is mt, then a conventional scale factor si is

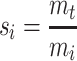graphic file with name M10.gif A.4.1

Multiplication by the ratio of the mean directed distance M to mt will adjust si to be a mean preserving scale factor (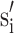Inline graphic):

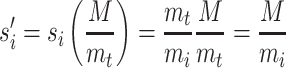graphic file with name M12.gif A.4.2

The correction factor (M/mt) can be formulated from the original set of the scale factors as

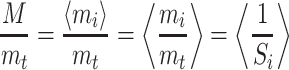graphic file with name M13.gif A.4.3

so that a mean preserving scale factor can be calculated as

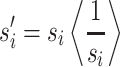graphic file with name M14.gif A.4.4

for each of the x-, y- and z-scale directions. The scaling term in (A.4.4) is just the average of the inverse of GSN scale factors. The importance of (A.4.4) is that is shows that conventional GSN scale factors (si) can be converted to mean preserving scale factors (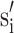Inline graphic) using only the original set of scale factors, i.e. without mt or M. Therefore, this rescaling approach can potentially work for any brain template and any brain grouping. If si is already mean preserving then the scaling term in (A.4.3) will be exactly unity.

Information and Sharing Agreement

The Mango software and add-in described in this publication are usable and accessible from www.nitrc.org as well as www.ric.uthscsa.edu/mango.

Footnotes

Research supported by grants from the Human Brain Mapping Project jointly funded by NIMH and NIDA (P20 MH/DA52176), the General Clinical Research Core (HSC19940074H), and NIBIB (K01 EB006395). Additional support was provided through the NIH/National Center for Research Resources through grants P41 RR013642 and U54 RR021813 (Center for Computational Biology (CCB)). Also, support for Cykowski was from F32-DC009116 to MDC (NIH/ NIDCD). This work was partly supported by the Initiative and Networking Fund of the Helmholtz Association within the Helmholtz Alliance on Systems Biology (KZ). KA was partly supported by the Bundesministerium für Bildung und Forschung (01 GW0613, 01GW0771, 01GW0623), and the Deutsche Forschungsgemeinschaft (AM 118/1-2).

References

  1. Allen JS, Bruss J, Mehta S, Grabowski T, Brown CK, Damasio H. Effects of spatial transformation on regional brain volume estimates. Neuroimage. 2008;42:535–547. doi: 10.1016/j.neuroimage.2008.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alpert NM, Bradshaw JF, Kennedy D, Correia JA. The principal axis transformation—A method for image registration. Journal of Nuclear Medicine. 1990;31:1717–1722. [PubMed] [Google Scholar]
  3. Amunts K, Kedo O, Kindler M, Pieperhoff P, Mohlberg H, Shah NJ, et al. Cytoarchitectonic mapping of the human amygdala, hippocampal region and entorhinal cortex: intersubject variability and probability maps. Anatomy and Embryology. 2005;210:343–352. doi: 10.1007/s00429-005-0025-5. [DOI] [PubMed] [Google Scholar]
  4. Clark DA, Mitra PP, S-H WS. Scalable architecture in mammalian brains. Nature. 2001;411:189–193. doi: 10.1038/35075564. [DOI] [PubMed] [Google Scholar]
  5. Collins DL, Neelin P, Peters TM, Evans AC. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. Journal of Computer Assisted Tomography. 1994;18:192–205. doi: 10.1097/00004728-199403000-00005. [DOI] [PubMed] [Google Scholar]
  6. Filipek PA, Richelme C, Kennedy DN, Caviness VS., Jr The young adult brain: an MRI based morphometric analysis. Cerebral Cortex. 1994;4:344–360. doi: 10.1093/cercor/4.4.344. [DOI] [PubMed] [Google Scholar]
  7. Goncalves-Pereira PM, Oliveira E, Insausti R. Quantitative volumetric analysis of the hippocampus, amygdala and entorhinal cortex: normative database for the adult Portuguese population. Revista de Neurologia. 2006;42:713–722. [PubMed] [Google Scholar]
  8. Hoffman MA. Size and shape of the cerebral cortex in mammals. II. The cortical volume. Brain, Behavior and Evolution. 1988;32:17–26. doi: 10.1159/000116529. [DOI] [PubMed] [Google Scholar]
  9. Im K, Lii J-M, Lyttelton O, Kim SH, Evans AE, Kim SI. Brain size and cortical structure in the adult human brain. Cerebral Cortex. 2008;18:2181–2191. doi: 10.1093/cercor/bhm244. [DOI] [PubMed] [Google Scholar]
  10. Jenkinson M, Smith S. A global optimization method for robust affine registration brain images. Medical Image Analysis. 2001;5:143–156. doi: 10.1016/S1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
  11. Kronmuller K-T, Schroder J, Kohler S, Gotz B, Victor D, Unger J, et al. Hippocampal volume in first episode and recurrent depression. Psychiatry Research: Neuroimaging. 2009;174:62–66. doi: 10.1016/j.pscychresns.2008.08.001. [DOI] [PubMed] [Google Scholar]
  12. Lancaster JL, Kochunov PV, Thompson PM, Toga AW, Fox PT. Asymmetry of the brain surface from deformation field analysis. Human Brain Mapping. 2003;19(2):79–89. doi: 10.1002/hbm.10105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lancaster JL, Tordesillas-Guiterriz D, Martinez M, Salineas F, Evans A, Zilles K, et al. Bias between MNI and Talairach coordinates analyzed using the ICBM-152 brain template. Human Brain Mapping. 2007;28:1194–1205. doi: 10.1002/hbm.20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Le Goualher G, Procyk E, Collins DL, Venugopal R, Barillot C, Evans AC. Automated extraction and variability analysis of sulcal neuroanatomy. IEEE Transactions on Medical Imaging. 1999;18(3):206–217. doi: 10.1109/42.764891. [DOI] [PubMed] [Google Scholar]
  15. Lerch JP, Worsley K, Shaw WP, Greenstein DK, Lenroot RK, Giedd J, et al. Mapping anatomical correlations across cerebral cortex (MACACC) using cortical thickness from MRI. Neuroimage. 2006;31:993–1003. doi: 10.1016/j.neuroimage.2006.01.042. [DOI] [PubMed] [Google Scholar]
  16. Luders F, Narr KL, Thompson PM, Rex DE, Woods RP, Deluca H, et al. Gender effects on cortical thickness and the influence of scaling. Human Brain Mapping. 2006;27:314–324. doi: 10.1002/hbm.20187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mangin J-F, Poupon F, Duchesnay E, Riviere D, Cachia A, Collins DL, et al. Brain morphometry using 3D moment invariants. Medical Image Analysis. 2004;8:187–196. doi: 10.1016/j.media.2004.06.016. [DOI] [PubMed] [Google Scholar]
  18. Mangin J-F, Riviere D, Cachia A, Duchesnay E, Cointepas Y, Papadopoulos-Orfanos D, et al. A framework to study the cortical folding patterns. Neuroimage. 2004;23:S129–S138. doi: 10.1016/j.neuroimage.2004.07.019. [DOI] [PubMed] [Google Scholar]
  19. Pakkenberg B, Gundersen HJG. Neocortical neuron number in humans: effect of sex and age. The Journal of Comparative Neurology. 1997;384:312–320. doi: 10.1002/(SICI)1096-9861(19970728)384:2&#x0003c;312::AID-CNE10&#x0003e;3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
  20. Pantel J, O’Leary DS, Crestsinger K, Bockholt HJ, Keefe H, Magnotta VA, et al. A new method for the in vivo volumetric measurement of the human hippocampus with high neuroanatomical accuracy. Hippocampus. 2000;10:752–758. doi: 10.1002/1098-1063(2000)10:6&#x0003c;752::AID-HIPO1012&#x0003e;3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
  21. Prothero J. Scaling of cortical neuron density and white matter volume in mammals. Journal für Hirnforschung. 1997;38:513–524. [PubMed] [Google Scholar]
  22. Prothero JW, Sundsten JW. Folding of the cerebral cortex in mammals. A scaling model. Brain, Behavior and Evolution. 1984;24:152–167. doi: 10.1159/000121313. [DOI] [PubMed] [Google Scholar]
  23. Rogers J, Kochunov P, Lancaster J, Shelledy W, Glahn D, Blangero J, et al. Heritability of brain volume, surface area, and shape: an MRI study in an extended pedigree of baboons. Human Brain Mapping. 2007;28:576–583. doi: 10.1002/hbm.20407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schormann T, Zilles K. Limitations of the principal-axes theory. IEEE Transactions on Medical Imaging. 1997;16(6):942–947. doi: 10.1109/42.650891. [DOI] [PubMed] [Google Scholar]
  25. Shattuck DW, Mirza M, Adisetiyo V, Hojatkashani C, Salamon G, Narr KL, et al. Construction of a 3D probabilistic atlas of human cortical structures. Neuroimage. 2008;39:1064–1080. doi: 10.1016/j.neuroimage.2007.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sowell ER, Peterson BS, Kan E, Woods RP, Yoshii J, Bansal R, et al. Sex differences in cortical thickness mapped in 176 healthy individuals between 7 and 87 years of age. Cerebral Cortex. 2007;17:1550–1560. doi: 10.1093/cercor/bhl066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Stephan H, Framm H, Baron G. New and revised data on volumes of brains structures in insectivores and primates. Folia Primatologica (Basel) 1981;35:1–29. doi: 10.1159/000155963. [DOI] [PubMed] [Google Scholar]
  28. Toga AW, Banerjee OK. Registration revisited. Journal of Neuroscience Methods. 1993;48:1–13. doi: 10.1016/S0165-0270(05)80002-0. [DOI] [PubMed] [Google Scholar]
  29. Zhang K, Sejnowski TJ. A universal scaling law between gray matter and white matter of cerebral cortex. PNAS. 2000;97:5621–5626. doi: 10.1073/pnas.090504197. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Neuroinformatics are provided here courtesy of Springer

RESOURCES