Role of symmetric and asymmetric division of stem cells in developing drug resistance

Abstract

Often, resistance to drugs is an obstacle to a successful treatment of cancer. In spite of the importance of the problem, the actual mechanisms that control the evolution of drug resistance are not fully understood. Many attempts to study drug resistance have been made in the mathematical modeling literature. Clearly, in order to understand drug resistance, it is imperative to have a good model of the underlying dynamics of cancer cells. One of the main ingredients that has been recently introduced into the rapidly growing pool of mathematical cancer models is stem cells. Surprisingly, this all-so-important subset of cells has not been fully integrated into existing mathematical models of drug resistance. In this work we incorporate the various possible ways in which a stem cell may divide into the study of drug resistance. We derive a previously undescribed estimate of the probability of developing drug resistance by the time a tumor is detected and calculate the expected number of resistant cancer stem cells at the time of tumor detection. To demonstrate the significance of this approach, we combine our previously undescribed mathematical estimates with clinical data that are taken from a recent six-year follow-up of patients receiving imatinib for the first-line treatment of chronic myelogenous leukemia. Based on our analysis we conclude that leukemia stem cells must tend to renew symmetrically as opposed to their healthy counterparts that predominantly divide asymmetrically.

Drug resistance is a fundamental problem in the treatment of cancer, strongly limiting the effects of the drugs used in therapy, and therefore considerably reducing the probability of treatment success and survival of the patient. There are multiple mechanisms by which drug resistance may develop. It appears to be both a stochastic phenomenon caused by random genetic mutations, as well as a drug-induced one (in which using the drug increases the chances of developing resistance to it). There is clear experimental evidence that at least in the case of certain drugs, known as “mutagenic drugs,” the drug can induce resistance to itself (see refs. 1 and 2).

In this work we focus on genetic mutations, mutations that are genetic changes that occur during cell division. The best example is that of “point mutations,” i.e., mutations that cause the replacement of a single base nucleotide or pair, with another nucleotide or pair in the DNA or RNA. Such an event may modify the cellular phenotype, making any of its daughter cells resistant to the drug. Other examples of genetic mutations are frameshift and missense mutations.

The cause for genetic mutations is not completely clear. Is it a mainly random phenomenon, or rather a drug-induced, directed one, perhaps both? Such a fundamental question has been the focus of the Nobel Prize winning work of Luria and Delbrück (3). Using fluctuation analysis, Luria and Delbrück showed that drug resistance in in vitro bacterial cultures seems to have an important random component. Many further in vitro experiments with tumor cell lines confirmed this result.

In the following, we focus only on resistance due to genetic mutations and, because of the results of Luria and Delbrück, we assume that such resistance is caused by a random mutation mechanism. Furthermore, we consider the case of absolute resistance, i.e., resistance that is not relative to the dosage of the drug administered. A cancer cell is either resistant to the drug or not, once the dosage of the drug is prescribed.

Drug resistance has been the focus of many studies in the mathematical modeling community. The first model of drug resistance in cancer due to point mutations is the celebrated model by Goldie and Coldman (see refs. 4 and 5). This work was followed by extensive literature (see, for example, refs. 6–9, and the references therein).

In a recent work (8), Iwasa et al. have shown that the probability that resistance to a drug develops by the detection time is given by

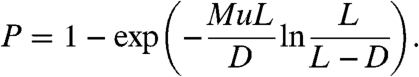[1]

Here, M is the total number of cancer cells found at detection; u is the probability of mutation per cell division, and L and D are the birth and death rates, respectively. This result was obtained using Markov chains and continuous-time branching processes. Furthermore, in the case where Mu ≪ 1, the expected number of resistant cancer cells found at detection, conditional on the presence of resistance, is

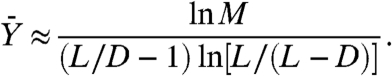[2]

It is important to emphasize that the study in ref. 8 is based on assuming that cancer cells are a homogeneous population, which is why M is taken to be the total number of cells. Yet, recent experimental evidence suggests that tumors should not be thought of as homogeneous. Indeed, it appears that tissues are maintained by a small subset of slowly replicating cells. These so-called “stem cells” have the capacity of both self-renewal and differentiation into more mature cells. Stem cells are very long-lived, while mature, fully differentiated cells have a variable life span, which, depending on the tissue of origin, can typically range from a few days to several months.

From the point of view of drug resistance, the heterogeneity hypothesis implies that only the cells that have the capacity for self-renewal can propagate drug resistance. Therefore, these cells should be taken into account in any model of drug resistance in cancer. In fact, these are the only cells that should be taken into account.

The rest of the paper is devoted to deriving, presenting, and applying the results we obtained while calculating the probability of developing resistance to drugs by the time a tumor is diagnosed, this time taking into account the heterogeneity of the population.

To demonstrate the significance of our result, we focus on chronic myelogenous leukemia (CML) for which a recent study has been published on a six-year follow-up of patients that receive imatinib as the first line of treatment (10). The clinical study provides us with a concrete estimate of the percentage of patients that shift from the chronic phase to the acute phase (or enter into a blast crisis). We use this estimate as an upper bound on the number of patients that have developed resistance to the drug by the time CML was diagnosed. By integrating the mathematical estimates with clinical and experimental data, we are able to infer the preferred mode of division of the hematopoietic cancer stem cells, predicting a large shift from asymmetric division to symmetric renewal. Such a division is required in order to explain the clinical data.

Results

We assume that a stem cell may divide in the following three ways:

1. asymmetric division: a stem cell divides into one progenitor cell and one stem cell (with probability a)

2. symmetric differentiation: a stem cell divides into two progenitor cells (with probability b)

3. symmetric renewal: a stem cell divides into two stem cells (with probability c = 1 - a - b)

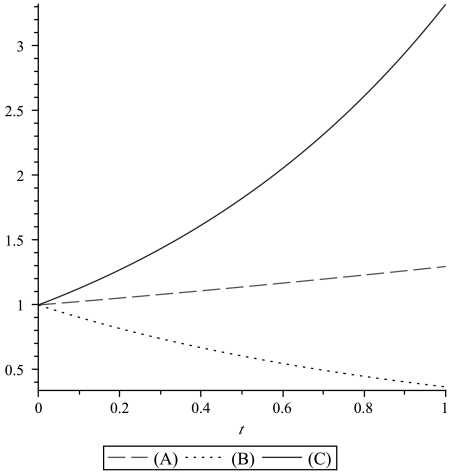
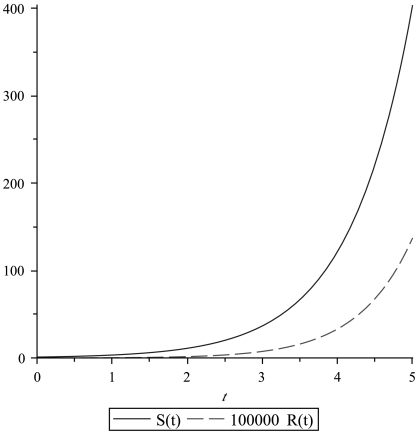
All three possibilities have been experimentally observed (see refs. 11–14). Generally, these three modes of division coexist. Growth curves for different choices of parameters are illustrated in Fig. 1. We recall that the division rate is denoted by L, the death rate by D, and the mutation probability per cell division by u. When a tumor is detected, the number of cancer stem cells is assumed to be M. Note that this M is different from the M that was used in Eq. 1, where it denoted the total number of cancer cells. An example of the time course of the growth of the drug-resistant population versus the sensitive one is shown in Fig. 2.

Fig. 1.

Growth curves for the stem cell population. (A) Predominantly asymmetric division: a = 0.75 and b = 0.01. (B) Predominantly symmetric differentiation: a = 0.2 and b = 0.6. (C) Predominantly symmetric renewal: a = 0.2 and b = 0.05. In all plots D = 0.2 and L = 2.

Fig. 2.

An example of the growth of drug-resistant cancer stem cells R(t) versus the sensitive ones S(t). The parameters are a = 0.2, b = 0.05, D = 0.2, L = 2, and u = 4·10^-7.

First, we compute the expected number of mutations occurring when there are exactly x wild-type (drug-sensitive) cancer stem cells in the population. This expected number of mutations, which we denote by m_x, is given by

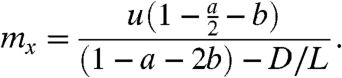[3]

Note that m_x is independent of x, a result that is not surprising because when the population is large there are many more cells that may divide but also substantially less time for them to do so before the population increases to x + 1. A result similar to Eq. 3 was obtained using Markov chains in ref. 8.

Our next result is the calculation of the probability, P_R, that at the time of detection, there are cancer stem cells that developed resistance to the drug. If the death rate D is assumed to be zero, then this probability is given by

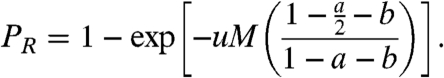[4]

Otherwise, when D ≠ 0, we obtain

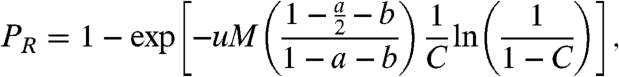[5]

where 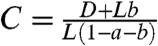. We note that Eq. 5 is an extension of Eq. 1 (which can be recovered by setting a = b = 0, and setting M as the total population size).

Given Eq. 5, we calculate the expected value of the number of resistant cells that are found at detection, assuming that resistance has indeed developed by the time of detection. This conditional expectation of resistant cells is given by

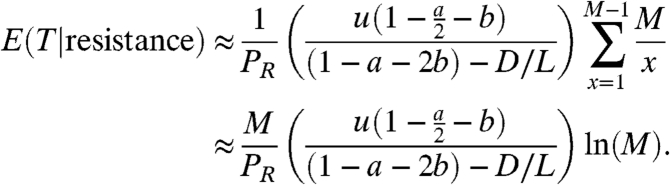[6]

Eq. 6 is obtained noting that 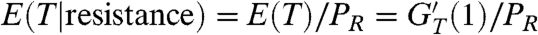. Here, P_R is given by Eq. 5, and G_T is the generating function of the random variable T, which is the total number of resistant cancer stem cells that are present when the cancer is detected.

Having obtained these results, we demonstrate their significance by considering a concrete problem. Our goal is to study the division pattern of hematopoietic leukemic stem cells in CML. This can be accomplished by estimating the probabilities a, b, and c in CML.

It is estimated that in CML, the leukemic stem cell population at early detection is of the order of M ≈ 2.5·10⁵ cells (15, 16). It is also estimated that the probability of a random point-mutation conferring resistance to imatinib is u ≈ 4·10^-7 (16). The turnover rate D/L is estimated to be in the range 0.1–0.5 (17). The model parameters are summarized in Table 1.

Table 1.

Model parameters

Parameter	Description	Estimate
M	Cancer stem cell population at detection	2.5·105
u	Mutation rate	4·10-7
D/L	Turnover rate	0.1–0.5

A recent clinical study (10) follows CML patients that have been treated with imatinib over a period of 6 years. It is shown that no more than 15% of the patients stop responding to the drug at some point during this time period. Interestingly, after 5 years, patients seem to stop relapsing, at least during the time frame of the study. Because it has been recognized that imatinib has a positive effect on eliminating differentiated leukemic cells, the cases of observed relapses must be traced back to the subpopulation of leukemic stem cells that developed resistance to imatinib. This implies that the probability that cancer stem cells mutated and developed resistance to imatinib by the time of detection cannot exceed 15%, a figure that can be used as an upper bound on the probability of developing resistance by the time the disease is detected, P_R.

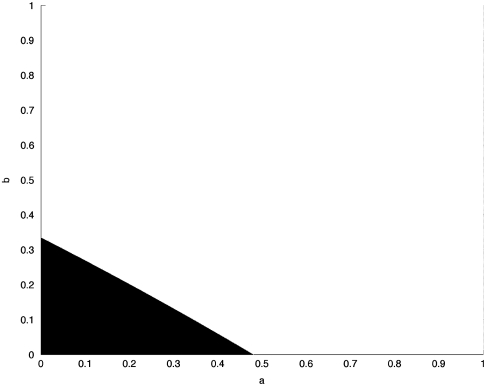
Using these estimated parameters, we use Eq. 5 to fit the parameters a and b; c is then given by 1 - a - b. In Fig. 3 we plot the range of a and b for which P_R < 0.15. In this case we set the turnover rate D/L = 0.1. Clearly, the figure indicates that in order for P_R < 0.15, a and b must be relatively small. For example, if a = 0.87 and b = 0.01, then P_R = 0.71. However, if a = 0.2 and b = 0.05, then P_R = 0.12, which is in the desirable range. Similar results are obtained for other values of the turnover rate. The larger D/L is, the smaller the admissible region is.

Fig. 3.

The range of a and b for which P_R < 0.15. The turnover rate is D/L = 0.5.

This result is not surprising for the probability of a symmetric differentiation, b, which is typically estimated to be very small. However, the estimated value of the asymmetric division probability a is interesting, because it has been observed that for healthy hematopoietic stem cells, a should be close to 1, and generally above 0.9 (18, 19).

These estimates suggest that leukemic hematopoietic stem cells should have a much lower than normal tendency to divide asymmetrically (i.e., a low a), hence making a substantial shift toward an increased symmetric renewal.

Discussion

The main result of Iwasa et al. (8) is given by Eq. 1. How should this equation be understood given actual estimates of the parameters? We recall that in Eq. 1, the parameter M is the total number of cells in the tumor. At present, an approximation of the lower limit of clinical detection of solid tumors is M ≈ 10⁹; see, e.g., ref. 20, page 31). For the mutation rate, a common estimate is on the order of u≥10^-8 (see refs. 21 and 22). Hence, according to the results of Iwasa et al., because (L/D) ln[L/(L - D)] > 1 if D < L, the probability that resistance develops by the time a tumor is detected must always be greater than .9999.

Another quantity of interest is the expected number of resistant cancer cells found at detection 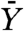, assuming that resistance developed. An estimation of 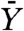is given in ref. 8 by Eq. 2. Unfortunately Eq. 2 is valid only when Mu ≪ 1, which is not the case when M = 10⁹ and u = 10^-8. Hence, we estimate 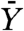for M = 10⁶ and u = 10^-8, which according to Eq. 2 is 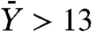. Consequently, for M = 10⁹ we could expect thousands of mutated, drug-resistant cancer cells. Such a result implies that resistance should always be present in large numbers at the detection time. Therefore, clones that are generated by such resistant cells are invulnerable to the treatment. They will expand, and no patient will be able to survive the disease in the long run. This result is in contradiction with clinical data. It turns out that, e.g., among CML patients that are treated with imatinib in the chronic phase, only in less than 15% of the patients the drug is unable to keep the disease under control, which results in a relapse (10, 16). The apparent contradiction between the mathematical analysis and the experimental data suggests that something may be missing from the modeling assumptions of Iwasa et al. Alternatively, the experimental estimates of the mutation rates might have to be adjusted.

This dichotomy has been addressed in recent works, e.g., refs. 16 and 23, in which the modeling assumptions include a heterogeneous tumor population, comprising from stem cells and other cells that are at various stages of maturation. For example, Michor et al. focus only on the stem cell compartment and accordingly use a much smaller value as an estimate for M (16). Hence, they effectively think of M as the number of cancer stem cells found at cancer detection, and not as the total number of cells in the tumor. As already mentioned in Results, it is estimated that in the case of CML in the early chronic phase, the stem cell population at detection is approximately 2.5·10⁵ cells, and the mutation probability u is approximately 4·10^-7. With such values in mind, Michor et al. obtain an estimate (using Eq. 1 with D/L = 0.5) for the probability of resistance mutations present at the time of diagnosis. This probability is calculated in ref. 16 to be approximately 13%, an estimate that is in agreement with the data (16, Table 1). Unfortunately, the methodology of ref. 16 is based on applying the results of ref. 8 to small cell populations in order to consider only stem cells. The problem with this approach is that Eq. 1 was derived assuming a homogeneous tumor population. It is not valid for describing the dynamics of stem cells and should not be applied directly to heterogeneous populations as done in ref. 16.

In contrast, the model that we study in this work is based on the “stem cell hypothesis.” It incorporates the different ways a stem cell may divide and studies the dynamics that emerges due to these division paths. We emphasize once again that from the point of view of drug resistance, the heterogeneity in the tumor cell population implies that it is only the stem-like long-lived cells, those cells that have the ability of self-renewal, that propagate the drug resistance. Any model of drug resistance in cancer must therefore take into account the cancer stem cells. Cancer cells that do not have self-renewal capabilities cannot propagate the resistance in the long run and should be disregarded.

In order to address the heterogeneity of the tumor cell population we chose to simplify the mathematical tools. In modeling the wild-type cancer stem cell population we replace the Markov chains that were used in ref. 8 by ordinary differential equations. Our approach amounts to using a deterministic model that considers the averaged behavior of such a population. Intriguingly, notwithstanding such simplification, our approach provides identical results to those found in Iwasa et al. if we also assume a homogeneous cell population. This can be immediately obtained by setting a = 0, and b = 0 in Eqs. 4–6. Thus, in the context of the specific questions we are studying, nothing is lost by using a partially deterministic approach. On the contrary, our simplified approach enables us to extend the results of ref. 8.

The prediction of a large shift from asymmetric division to symmetric renewal of hematopoietic stem cells in CML is an important example of what the mathematical modeling of drug resistance can tell us about cancer. Our estimates were based on a resistance probability of approximately 15%. If instead we use a less conservative estimate that the probability of resistance is less than 10% (as could be interpreted from the data in ref. 10), then the conclusion of our study is that cancer stem cells must generally renew symmetrically.

In order to discuss the confidence level at which the conclusions were obtained, we make the following observations on the sensitivity to the parameter estimates and on certain extensions of the model.

It is important to comment on the sensitivity of the result on the shift from asymmetric division to symmetric renewal to the parameter estimates. It is easy to check that reasonable variations in the turnover rate do not affect our conclusion. With respect to the dependence on the estimates of M and u, it seems unlikely that the estimate for M, the cancer stem cell population size present at the time of detection, would be much smaller than what is estimated in the literature (15). Rather, it appears reasonable to assume that for many patients, M will actually be larger (depending on the detection time). In this case, there must be an even more substantial shift toward symmetric renewal. The same is true for the mutation probability u. If u is larger than the estimated value, then there will have to be an even stronger shift to symmetric renewal in order to explain the clinical data.

Our calculations did not include the possibility of recruitment of progenitor cells (and their offsprings) into the cancer stem cell compartment. It is possible that progenitor cells whose normal function has been perturbed will acquire stem-like self-renewal properties (24). However, we note that if such a recruitment takes place, this would only strengthen our result. The total amount of drug resistance that is found at detection and is due to the original compartment of cancer stem cells would have to be smaller than our original estimates due to the recruitment of progenitors. In this case, the probability of asymmetric division would be even smaller than our current estimates. Our model also did not take into account gene amplification, a cellular process that amplifies the phenotype that the gene confers on the cell, preventing the absorption of the drug by the cell. However, a similar reasoning to the case of recruitment of progenitor cells shows that the inclusion of this kind of resistance would again only strengthen our conclusions.

Our results do not contradict the somewhat sparse experimental data. On the contrary, there is some experimental evidence to support the hypothesis that cancer stem cells change their mode of division. For example, it has been observed that when the mechanism regulating asymmetric divisions is disrupted, Drosophila neuroblasts begin dividing symmetrically and form tumors (25). It is also known that some gene products can both induce symmetric cell divisions and function as oncogenes in mammalian cells (25, 26). Thus there seems to be a link between symmetric divisions and cancer progression.

It could be of great interest if our model could be tested experimentally, at least in vitro, on cancer cell lines. Ideally, a direct experimental method would require us to isolate cancer stem cells and healthy stem cells and compare the growth of both stem cell populations.

From a methodological perspective, the mathematical analysis allows us to use indirect information about the mechanisms that control the dynamics of the disease evolution to reach specific conclusions that go beyond the present reach of experiments. Although we have applied our mathematical results to the available clinical data on CML, the approach is not limited to this specific disease, and we expect similar conclusions about the division of cancer stem cells in other types of cancer as well. Specifically, our model should apply to any cancer for which stem cells are known to be the driving force of the progression of the disease and for which point mutations are a source of drug resistance.

Materials and Methods

We derive the mathematical model using ordinary differential equations (ODEs) for the wild-type cancer population and branching processes for the mutant cells. In Iwasa et al. (8) both the wild-type and the mutant cancer populations are modeled as stochastic processes. Our deterministic approach in modeling the total number of drug-sensitive CSCs is equivalent to considering their averaged behavior. For completeness we derive in SI Text the corresponding model in which both populations are represented by branching processes. The standard theory for these multitype branching processes can be found in refs. 27 and 28 and especially in the book by Mode (29). Thus the methodology we used in the paper may be seen as a simplified version of the stochastic approach, and in this sense it has the advantage of easily allowing modifications. For example, an exponential cancer growth may be a good assumption only when the cancer population is small. To replace it by any other growth model, while straightforward with the ODEs approach, would be a somewhat more complex undertaking when dealing directly with stochastic methods. Furthermore, we note that arguably our modeling methodology may be seen as more general, in the sense that at least for the wild-type population we make assumptions only on their averaged behavior (no Markov property, for example). Finally, we note that if the cells are assumed to be a homogeneous population, then our results, obtained through a partially deterministic methodology, match exactly the results of Durrett et al. obtained by the completely stochastic approach (30).

Ordinary Differential Equations.

As was already mentioned in Results, we consider the different ways in which a stem cell may divide (shown in Fig. 3): (i) asymmetric division in which a stem cell divides into one progenitor cell and one stem cell, (ii) symmetric differentiation in which a stem cell divides into two progenitor cells, and (iii) symmetric renewal in which a stem cell divides into two stem cells. All three types of division have been observed experimentally (see refs. 11–14). We can therefore assign probabilities to the three division paths of stem cells as follows: We denote by a the probability of an asymmetric division, by b the probability of a symmetric differentiation, and by c = 1 - a - b the probability of a faithful symmetric renewal. Clearly, 0 ≤ a,b,c ≤ 1 and a + b + c = 1.

Because we are interested in the dynamics of drug resistance in cancer, from now on we focus on cancer stem cells. In addition we focus on the case of a single drug therapy. We denote the total number of wild-type, i.e., drug-sensitive, cancer stem cells at time t by S(t). This population is assumed to grow exponentially. The second group of cells, the mutated cancer stem cells that developed resistance to the drug, are denoted by R(t). The dynamics of the averaged behavior of the two cell populations can be described using the following system:

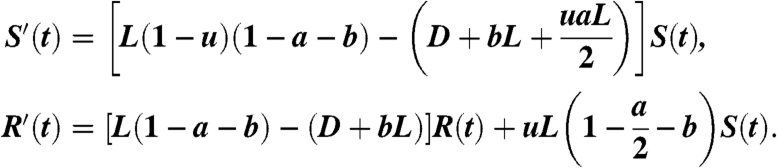[7]

We assume that at time t = 0, we start with a single wild-type cancer stem cell, and no mutated stem cells. Consequently, the initial conditions for Eq. 7 are given by S(0) = 1 and R(0) = 0. As previously stated, u is the mutation probability per cell division, whereas L and D are the birth and death rates, respectively. To be precise, from now on, we refer to L as the division rate, because a division may not result in the birth of a stem cell. In addition, because the mutation probability is usually extremely small, system 7 is written under the assumption that mutations may occur in the division process only to one of the two daughter cells. This is a standard assumption; see, e.g., refs. 7 and 8.

In the first equation in Eq. 7, the size of the wild-type cell population can increase only as a result of a symmetric renewal, where no mutation occurs. The probability of such an event is (1 - u)(1 - a - b). Multiplying this probability by the division rate L provides the birth rate of S(t). On the other hand, a decrease in the wild-type population will occur in the following cases: a cell death (D), a symmetric differentiation into two progenitors (bL), and if there is an asymmetric division (aL) in which the stem cell daughter is the mutant. The stem cell daughter will be the mutant with probability u/2, because u is the probability of mutations, and in this scenario only one of the two daughter cells is a stem cell.

For the second equation in Eq. 7, the size of the mutant population can once again increase only due to a symmetric renewal. Only that this time, we assume that mutated cells can no longer mutate back to the wild-type state (due the rarity of this event for point mutations). A decrease in the mutant population will be the result of cell death and of a symmetric differentiation into two progenitors. The last term of the equation is the wild-type cells that mutated. They come either from a symmetric renewal, uL(1 - a - b), or from an asymmetric division in which a mutation hits the daughter stem cell, uLa/2. The sum of these two terms is uL(1 - a/2 - b).

Given that u is very small, it can be eliminated from the first equation. However, it cannot be removed from the second equation because S(t) is much larger than R(t). System 7 can be thus reduced to the following:

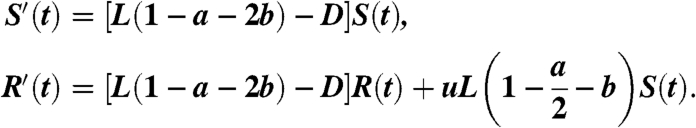[8]

We make the following remarks:

1. Because we are modeling a cancer stem cell population that is assumed to grow from one cell to a large number, it must be that [L(1 - a - 2b) - D] > 0, which implies that (1 - a - 2b) > 0 and therefore .

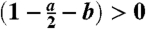2. Because the mutant population is always considered to be very small, we are actually not going to use the equation for R(t) from Eq. 8. This equation will be replaced with a stochastic approach. It is still instructive to keep this equation as part of system 8 because it can be used to understand the meaning of the final formulas.

3. In this model we assume that both the wild-type and the resistant stem cells have the same division and death rates and the same division events’ probabilities a, b. This assumption is made in order to simplify the presentation and can be easily modified to model situations where the mutant cancer cells R(t) have a relative fitness advantage or disadvantage with respect to the wild-type cancer cells S(t) (as done in ref. 8).

4. Because of the simplicity of our approach, the assumption regarding the exponential growth of cancer can be easily replaced by any other growth model. Such a modification is more complex when dealing directly with stochastic methods.

5. We assume that mutations happen only in one direction, i.e., wild-type cells mutate and become resistant but not vice versa, and thus (1 - u) is not multiplying L in the second equation. This seems to be a reasonable assumption in the case in which the focus is on point-mutation resistance and not on resistance that is caused by gene amplification. Indeed, the probability of reversal of a point mutation is much smaller than the probability of the point mutation itself and can therefore be neglected.

6. By modeling the cancer stem cell population growth in a deterministic way instead of as a random process, we lose the sensitivity to events that can happen for small populations, such as a population going extinct. Our focus in this study is on modeling the case where the wild-type cancer stem cell population reaches a detection size, M, and on its impact on drug resistance. Such a deterministic approach cannot provide the probability distribution of how long it takes for the tumor to reach detection size. However, our study provides the average behavior of such time. Interestingly, the formulas that we obtain using our mixed approach are in exact agreement with the results that were derived with the full-blown stochastic approach [in the simple case where only symmetric renewal is considered, the only case that was previously studied with stochastic methods (8)].

The Expected Number of Mutations when the Size of the Wild-Type Population Is x.

At this stage we can use system 8 to estimate the expected number of mutations, m_x, that occur once the wild-type population is of size x.

Consider the first equation of system 8. As first step, we are interested in finding the expected lengths of time for which the total number of wild-type cancer stem cells S(t) is equal to 1,2,…,M - 1. Here, M is the number of wild-type cancer stem cells at detection time. Note that, given the very small probability of a mutation, M is also a good approximation of the total number of cancer stem cells found at detection, i.e., both wild-type and mutated ones. Because the solution of Eq. 8 for S(t) is given by

[9]

then the “average” time at which the wild-type cancer stem cell population reaches size x, defined as t_(x), is given by

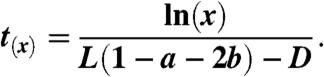[10]

Thus the average length of time for which the population will consist of exactly x stem cells is

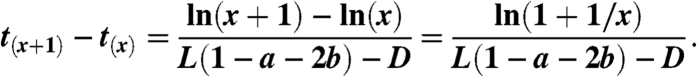[11]

Hence, the “expected number” of mutations occurring when there are exactly x wild-type cancer stem cells, m_x, is given by

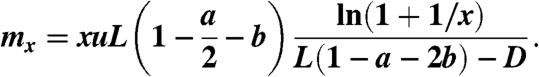[12]

This expression is obtained by multiplying the number of wild-type stem cells present at that time, x, by the mutation rate 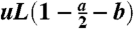, and by the length of time for which the total stem cell population equals x.

Finally, note that φ≔x ln(1 + 1/x) ∼ 1 (e.g., φ ≈ .9 for x = 4 and φ ≈ .98 for x = 20). Hence, because we are ultimately interested in large values of x, Eq. 12 can be reduced to

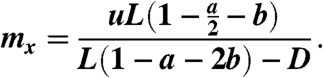[13]

Note that if the cancer stem cell population is growing, L(1 - a - 2b) - D must be greater than zero and hence the expression in Eq. 13 is well defined.

Branching Processes.

We are ultimately interested in calculating the probability of developing drug resistance by the time a tumor is detected. At this stage of the analysis, it is proper to take advantage of stochastic methods.

Assume that the tumor population grows exponentially starting from one wild-type stem cell. Let r_x be the actual number of mutations produced when there are x = 1,2,…,M - 1 wild-type cancer stem cells. Assume that all the random variables, r_x, follow a Poisson distribution with mean m_x, given by Eq. 13 and that they are independent. Note that the Poisson distribution seems to be a good choice given the very small probability of a mutation u.

Consider the clone initiated by a mutant cancer stem cell that originated when there were x wild-type cancer stem cells. Assume that the population size of such clone follows a continuous-time branching process where in each time step of length Δt, a stem cell divides with probability LΔt and dies with probability DΔt.

Let g_x(ξ) be the generating function of such clone for which the original mutation happened when S(t) = x. To calculate this generating function we proceed as follows:

To simplify the notation we let 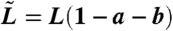and 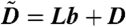. Then by the Kolmogorov backward equation we have

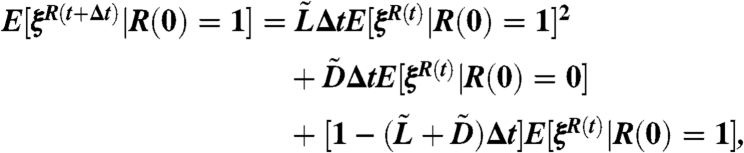[14]

because E[ξ^R(t)|R(0) = 2] = E[ξ^R(t)|R(0) = 1]², by independence. The time t = 0 in Eq. 14 is the time of occurrence of the original mutation that generates the clone, i.e., when the wild-type population is of size x. The time t in Eq. 14 measures time starting from this t = 0.

Let g(ξ,t) = E[ξ^R(t)|R(0) = 1]. As Δt → 0 we get

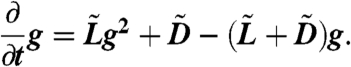[15]

Solving Eq. 15 with the initial condition g(ξ,0) = ξ gives

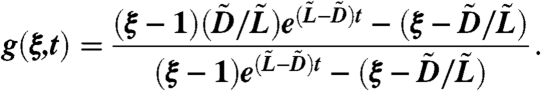[16]

Because 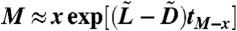, where t_M-x is the time it takes for the cancer stem cells to go from x to M, we obtain the generating function

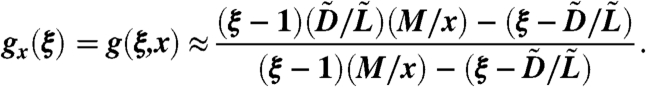[17]

We now denote by T the total number of drug-resistant cancer stem cells that are present when the cancer is detected, i.e., when the total stem cell population is M. We let G_T(ξ) be its generating function. To calculate G_T(ξ), we let K_x be the total amount of resistant cells found at detection whose originating mutation occurred when there were x sensitive cancer stem cells. Then

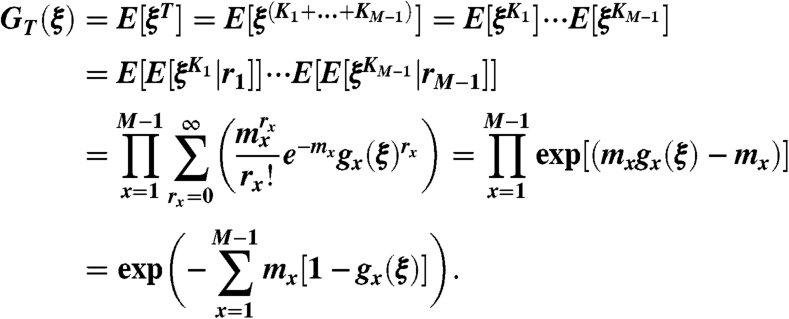[18]

Note that, on line four of Eq. 18, we used the fact that 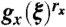is the generating function of all the r_x clones for which the original mutations happened when S(t) = x, that is the product of r_x generating functions g_x(ξ).

The Probability of Having Resistant Cancer Stem Cells at the Time of Detection.

By Eqs. 18, 13, and 17, we have that the probability of having resistant cancer stem cells at the time of detection is

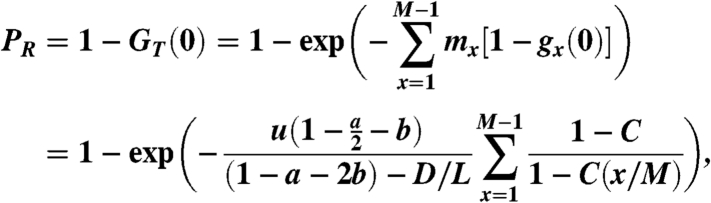[19]

where 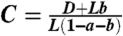. By replacing the summation with an integral, and with a change of variable, we get

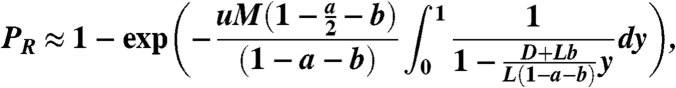[20]

from which we obtain the desired expressions.