A Comparison of the Statistical Power of Different Methods for the Analysis of Repeated Cross-Sectional Cluster Randomization Trials with Binary Outcomes

Abstract

Repeated cross-sectional cluster randomization trials are cluster randomization trials in which the response variable is measured on a sample of subjects from each cluster at baseline and on a different sample of subjects from each cluster at follow-up. One can estimate the effect of the intervention on the follow-up response alone, on the follow-up responses after adjusting for baseline responses, or on the change in the follow-up response from the baseline response. We used Monte Carlo simulations to determine the relative statistical power of different methods of analysis. We examined methods of analysis based on generalized estimating equations (GEE) and a random effects model to account for within-cluster homogeneity. We also examined cluster-level analyses that treated the cluster as the unit of analysis. We found that the use of random effects models to estimate the effect of the intervention on the change in the follow-up response from the baseline response had lower statistical power compared to the other competing methods across a wide range of scenarios. The other methods tended to have similar statistical power in many settings. However, in some scenarios, those analyses that adjusted for the baseline response tended to have marginally greater power than did methods that did not account for the baseline response.

1. Introduction

Cluster randomization trials are randomized controlled trials in which intact clusters of subjects are randomized to either the intervention or to the control arms (Klar and Donner, 2005; Donner and Klar, 2000). Examples of clusters include families, physicians’ practices, schools, communities, and hospitals. Cluster randomization trials are particularly suited for the evaluation of educational interventions, lifestyle modifications, and non-therapeutic interventions (Klar and Donner, 2005; Donner and Klar, 2000). In cluster randomization trials the cluster is the unit of randomization. However, the responses are measured at the subject level. Responses from subjects within the same cluster can exhibit a greater degree of homogeneity compared to responses from subjects in different clusters. Due to the possible existence of within-cluster homogeneity, traditional statistical methods for randomized controlled trials (RCTs) cannot be directly applied to cluster randomization trials.

The simplest design for cluster randomization trials is the completely randomized cross-sectional trial with two treatment arms. Using this design, the response is measured on a sample of subjects from each cluster following the treatment intervention. Several authors have described statistical methods for the analysis of these trials (Donner and Klar, 2000; Donner and Klar, 1994; Donner and Donald, 1988; Klar et al., 1995; Bellamy et al., 2000; Klar and Donner, 2001; Donner, 1999; Feng et al., 2001; Omar and Thompson, 2000). A recent study compared the relative statistical power of different methods for the analysis of completely randomized cross-sectional cluster randomization trials with binary outcomes (Austin, 2007). Alternative designs for cluster randomization trials include the cohort and repeated cross-sectional design (Feldman and McKinlay, 1994). In both these designs, measurement of the outcome is made on subjects in each cluster both prior to the intervention (baseline responses) as well as after the intervention (follow-up responses). Furthermore, in both of these designs, the same clusters are included at both time periods. However, in the cohort design, each cluster contains the same subjects both prior to and subsequent to the intervention, while in the repeated cross-sectional design, each cluster contains different subjects prior to the intervention compared to after the intervention. Examples of the first may include community intervention trials, in which communities are randomized to an intervention. Examples of the latter include trials of obstetrical practices, in which women giving birth are only in the pre-intervention time period or the post-intervention time period, but not both (Ukoumunne and Thompson, 2001).

Ukoumunne and Thompson (2001) describe different statistical methods for the analysis of cluster randomization trials with repeated cross-sectional binary measurements. In an empirical comparison of these methods, they applied these methods to the analysis of a cluster randomization trial in which the clusters were hospital obstetric units. They obtained qualitatively different conclusions depending on the method of analysis employed. While the relative statistical power of different methods for the analysis of cross-sectional completely randomized cluster randomization trials with binary outcomes has been examined (Austin, 2007), there is no comparable information on the relative statistical power of different statistical methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. Donner and Klar (1994) have suggested that more research is needed on the relative statistical efficiencies of different analytic methods for cluster randomization trials.

Accordingly, the objective of the current study was to compare the relative statistical power of different statistical methods for the analysis of repeated cross-sectional cluster randomization trials. This will permit researchers employing repeated cross-sectional cluster randomization trials to optimize statistical power within the given design. The paper is organized as follows: In Section 2, we review statistical methods for the analysis of these trials. In Section 3, we briefly describe a conceptual model for repeated cross-sectional cluster randomization trials that has been proposed in the literature. This conceptual model is then used as the basis for a data-generating process used in Monte Carlo simulations that were conducted to examine the relative statistical power of different statistical methods. In Section 4, we report the results of our Monte Carlo simulations. Finally, in Section 5, we summarize our findings and place them in the context of the existing literature.

2. Statistical methods for repeated cross-sectional cluster randomization trials with binary outcomes

In this section, we describe different statistical methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. These methods have been described in greater detail by Ukoumunne and Thompson (2001). The reader is referred to their article for further detail and discussion of these methods. Ukoumunne and Thompson empirically compared the inferences obtained using these methods when analyzing a repeated cross-sectional cluster randomization trial in which the clusters were hospital obstetrical units. In the current study we focus on repeated cross-sectional cluster randomization trials with binary outcomes in which there are two arms: an intervention arm and a control arm. We further restrict our attention to trials employing a completely randomized design. Within each method, Okoumunne and Thompson describe three different ways of evaluating the effect of the intervention: the effect of the intervention on the follow-up binary response alone, the effect of the intervention on the follow-up binary response after adjusting for the baseline log-odds of the response, and the effect of the intervention on the change from baseline.

2.1. Notation

We use the notation proposed by Ukoumunne and Thompson (2001) throughout this section. Let y_ijkt ∼ Bin(π_jkt,1) denote the response for the i^th subject in the j^th cluster, in the k^th treatment arm, and at the t^th time point, where π_jkt denotes the probability of success for this patient. Let G_k denote the treatment arm (this denotes the arm of the trial to which the cluster was randomized: control = 0, intervention = 1) and let T_t denote time (baseline = 0, follow-up = 1). (GT)_kt =G_k T_t denotes the interaction between group and time. Let π̂_jkt denote the observed probability of the outcome for subjects in the j^th cluster in the k^th group at the t^th time point ( ${\widehat{\pi }}_{jkt}=\frac{1}{N_{jkt}}\sum _{i=1}^{N_{jkt}}{y}_{ijkt}$, where N_jkt denotes the number of subjects in the j^th cluster in the k^th group at the t^th time point). Finally, let C_jkt denote the observed log-odds of the outcome for subjects in the j^th cluster in the k^th group at the t^th time point $(C_{jkt}=\text{log}\left(\frac{{\widehat{\pi }}_{jkt}}{1-{\widehat{\pi }}_{jkt}}\right))$.

2.2. Statistical methods for individual-level analyses

In this section, we describe two methods of analysis that use the subject as the unit of analysis. Both of these methods are based on logistic regression models. Two different families of models are used. The first consists of marginal models estimated using Generalized Estimating Equation (GEE) methods, while the second consists of conditional models that incorporate cluster-specific random effects. We will refer to the second family of models as random effect models (they have also been described as multilevel models, hierarchical models, or mixed effects models in the literature).

2.2.1. Generalized estimating equation methods

A model-based method for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes is the use of a logistic regression model estimated using generalized estimating equations (GEE) methods developed by Liang and Zeger (1986). For estimating the effect of the intervention on the follow-up binary response alone, the following logistic regression model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jk}}1})=\mu +{\alpha G}_k$$ (1)

The intervention effect is the exponential of the group coefficient (α). When estimating the effect of the intervention on the follow-up binary response after adjusting for the baseline log-odds of the response, the following model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jk}}1})=\mu +{\alpha G}_k+{\beta C}_{\mathit{\text{jk}}0}$$ (2)

The intervention effect is the exponential of the treatment-arm coefficient (α). Finally, when estimating the effect of the intervention on the change in the follow-up response from the baseline response, the following model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jkt}}})=\mu +{\alpha G}_k+{\gamma T}_t+{\delta (\mathit{\text{GT}})}_{\mathit{\text{kt}}}$$ (3)

The intervention effect is the group-time interaction term (δ). Each of the above models assumes an exchangeable (or compound-symmetry) correlation structure for the correlations of outcomes within a cluster. Robust estimates of standard errors can be obtained to account for the clustering of subjects within clusters.

In the current setting, the regression model only included a term for the treatment exposure. However, in practice, one could also include subject characteristics in the regression model to account for residual differences in subject characteristics between the arms of the trial.

2.2.2. Random effects regression methods

Random effects logistic regression models may be used for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. For estimating the effect of the intervention on the follow-up binary response, the following logistic regression model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jk}}1})=\mu +{\alpha G}_k+u_{\mathit{\text{jk}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{\mathit{\text{jk}}}\hspace{0.17em}\sim \hspace{0.17em}N(0,{\sigma }_u^2)$$ (4)

The intervention effect is the exponential of the treatment arm coefficient (α). When estimating the effect of the intervention on the follow-up binary response after adjusting for the baseline log-odds of the response, the following model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jk}}1})=\mu +{\alpha G}_k+{\beta C}_{\mathit{\text{jk}}0}+u_{\mathit{\text{jk}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}_{\mathit{\text{jk}}}\hspace{0.17em}\sim \hspace{0.17em}N(0,{\sigma }_u^2)$$ (5)

The intervention effect is the exponential of the treatment arm coefficient (α). Finally, when estimating the effect of the intervention on the change in the follow-up response from the baseline response, the following model can be used:

$$\text{logit}\hspace{0.17em}({\pi }_{\mathit{\text{jkt}}})=\mu +{\alpha G}_k+{\gamma T}_t+{\delta (\mathit{\text{GT}})}_{\mathit{\text{kt}}}+u_{\mathit{\text{jk}},}\hspace{0.17em}\hspace{0.17em}{u}_{\mathit{\text{jk}}}\hspace{0.17em}\sim \hspace{0.17em}N(0,{\sigma }_u^2)$$ (6)

The intervention effect is the treatment arm-time interaction term (δ). In the current setting, the regression model only included a term for the treatment exposure. However, in practice, one could also include subject characteristics in the regression model to account for residual differences in subject characteristics between the arms of the trial.

The above methods were proposed by Ukoumunne and Thompson (2001). They also proposed extensions of the above methods, in which the variance of the random effects was allowed to differ between the two arms of the trial. However, due to the computationally intensive nature of our simulations, we restricted our attention to the three methods described above.

2.3. Statistical methods for cluster-level analyses

Cluster-level analyses treat the cluster as both the unit of randomization and the unit of analysis. An aggregated response is computed at the cluster level at each time point. When estimating the effect of the intervention on the follow-up response, a two-sample t-test can be used to compare the difference in the follow-up probability of success, π_jk1, between the two treatment arms of the trial. This is equivalent to fitting the following regression model:

$${\pi }_{\mathit{\text{jk}}1}=\mu +{\alpha G}_k$$ (7)

π_jk1 is replaced by its sample estimate, which, since the outcome is binary, is the observed proportion of successes in the given cluster. Therefore, this method is testing whether the mean cluster-specific proportion of successes is different between the two arms of the trial. The effect of the intervention on the follow-up probability of success, after adjusting for the baseline probability of success can be estimated using the following regression model:

$${\pi }_{\mathit{\text{jk}}1}=\mu +{\alpha G}_k+{\beta \pi }_{\mathit{\text{jk}}0}$$ (8)

Once the random variables in (8) are replaced by their sample quantities, one is testing whether the mean cluster-specific probability of success is different between the two arms of the trial, after adjusting for potential between-cluster differences in the baseline probability of success. Finally, the effect of the intervention on the change from baseline can be estimated using the following regression model:

$${\pi }_{\mathit{\text{jk}}1}-{\pi }_{\mathit{\text{jk}}0}=\mu +{\alpha G}_k$$ (9)

which is equivalent to using a two-sample t-test to compare the change in the probability of success between the two treatment arms of the trial. It should be noted that the methods described in formulas (7) – (9) involve fitting a linear regression model. This in contrast to the methods described in Sections 2.1 and 2.2, which involve fitting logistic regression models. In each of the above three methods, the probability of success could be replaced by the log-odds of success, as was done by Ukoumunne and Thompson (2001). This was done by Ukoumunne and Thompson since they were comparing estimated effect sizes across different methods, and wanted all estimates to be on the odds ratio scale. In the current study, we have elected to conduct the analyses on the probability scale, since, in practice it allows for a more natural metric in which to interpret the results. Furthermore, our focus was on statistical power, rather than on the comparability of estimated treatment effects. Thus, it was less important for the estimated treatment effect to be on the odds ratio scale.

3. Monte Carlo simulations: Methods

In this section, we describe the Monte Carlo simulations that were used to compare the relative statistical power of different statistical methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. First, we present a conceptual model for repeated cross-section cluster randomization trials. This conceptual model will be used as the basis for the data-generating process in the subsequent Monte Carlo simulations.

3.1. Conceptual model for repeated cross-sectional cluster randomization trials

In designing the Monte Carlo simulations that will be used for examining the relative power of different statistical methods we used a conceptual framework for repeated cross-sectional cluster randomization trials that was proposed by Feldman and McKinlay (1994). In this section, we use the notation of Feldman and McKinlay. We assume that a dichotomous response variable has been measured on each subject. Let y_ijkt denote the response of the i^th subject, in the j^th cluster, in the k^th treatment arm, and at the t^th time point (t= 0 for baseline and t = 1 for follow-up), with y_ijkt =1 denoting a success and y_ijkt =0 denoting a failure. Let π_jkt denote the probability of success for a subject in the j^th cluster, in the k^th treatment arm, at the t^th time point. Then, we assume the following model:

$$\text{logit}({\pi }_{\mathit{\text{jkt}}})=\mu +{\mathit{\text{TAE}}}_k+{\mathit{\text{STE}}}_t+{(\mathit{\text{GT}})}_{\mathit{\text{kt}}}+C_{\mathit{\text{jk}}}+{(\mathit{\text{CT}})}_{\mathit{\text{jkt}}}$$ (10)

In (10), there are four fixed effects: μ, which denotes the grand mean (on the log-odds scale), TAE_k which denotes the treatment-arm effect (this denotes the systematic baseline difference in outcomes between the intervention arm and the control arm of the trial), STE_t which denotes the secular time effect, and (GT)_kt which denotes the time × treatment-arm interaction, with (GT)_kt =0 for both t = 0 and for the control arm of the trial. This final effect denotes the effect of the intervention on outcomes after adjusting for baseline differences in the outcome between treatment arms – it denotes the different in the log-odds of the outcome between the two groups that is due to treatment. One can exponentiate this effect to obtain a treatment odds ratio - the relative change in the odds of the outcome between the two groups that is due to treatment. The treatment arm effect, TAE_k, allows one to account for systematic baseline difference in outcomes between the intervention arm and the control arm of the trial. On average, across all randomizations, this effect will be zero. Randomization will ensure that, in expectation, there are no systematic differences in baseline characteristics between the arms of the trial. However, in a given trial, there may be systematic differences in the baseline value of the response variable between treatment groups. The inclusion of the treatment-arm effect (TAE) allows one to account for this possibility. In (10), the random effects are $C_{\mathit{\text{jk}}}\sim N(0,\hspace{0.17em}{\rho }_C{\sigma }_C^2)$, 1 ≤ j ≤ J, and ${(\mathit{\text{CT}})}_{\mathit{\text{jkt}}}\sim N(0,\hspace{0.17em}(1-{\rho }_C){\sigma }_C^2)$. C_jk denotes the cluster effect, nested in treatment group, while (CT)_jkt denotes the cluster × time interaction. Therefore, cluster-to-cluster variation is modelled as the sum of two independent random effects, the first time-invariant (C_jk) and the second time-varying (CT)_jkt. Feldman and McKinlay refer to ρ_C as the cluster autocorrelation, as it refers to correlation between the log-odds of success for the same cluster at different points in time. Similarly, we refer to σ_C and ${\sigma }_C^2$ as the cluster standard deviation and the cluster variance, respectively. The above model is derived from a broader, unifying model for cluster randomization trials comprising both cohort designs and repeated cross-sectional designs. We have presented the component that is applicable to repeated cross-sectional trials and have not presented the components of the model that incorporate cohort designs (repeated measurements on the same individuals).

3.2. Data-generating process

We randomly generated data using the theoretical model proposed by Feldman and McKinlay (1994) which was described in the previous section. This allowed us to generate data from simulated repeated cross-sectional cluster randomization trials with specific designs. We assumed a completely randomized design with two arms: an intervention arm and a control arm. Furthermore, we simulated cluster randomization trials that had a balanced design: there were an equal number of subjects per cluster and there were an equal number of clusters in each of the two arms of the trial. In the Monte Carlo simulations we allowed the following factors (using the terminology of Section 3.1) to vary: the cluster standard deviation (σ_c), the cluster autocorrelation (ρ_c), the secular time effect (STE), and the treatment effect (GT). The treatment-arm effect (TAE) (the systematic difference in outcomes between the treatment arms at baseline) was fixed at zero. The reason for this is that in RCTs, randomization will result in the treatment groups being, on average, similar at baseline. While systematic differences in baseline responses may exist in individual trials, one would not expect differences between arms to occur to occur systematically across trials.

We chose some of the parameters for our Monte Carlo simulations to be similar to cluster randomization trials of interventions to change professional practice, as has been done in an earlier study of the power of different methods for the analysis of simple cross-sectional cluster randomization trials (Austin, 2007). From an existing database of such trials, we examined 146 binary outcomes for which the average number of clusters and the average number of subjects per cluster were reported (http://www.abdn.ac.uk/hsru/epp/iccs-web.xls - site accessed February 15, 2006). We computed the quartiles of each of these two factors. Across the 146 binary outcomes, the 25^th percentile, median, and 75^th percentile of the average number of subjects per cluster were 6, 7, and 39, respectively (thus, in a typical cluster randomized trial, the average number of subjects per clusters was 7). The 25^th percentile, median, and 75^th percentile of the number of clusters were 25, 54, and 60, respectively. Since we are basing our design upon a two-armed trial, this would result in 12, 27, and 30 clusters per arm. Accordingly, we chose to simulate cluster randomization trials with either 7 or 39 subjects per cluster and with either 12 or 27 clusters per arm. Therefore, depending on the scenario, each randomly generated datasets would consist of 336, 756, 1872, or 4212 subjects (2 time periods x 2 treatment arms x Number of clusters/treatment arm x Number of subjects/cluster). The grand mean (μ) was allowed to take on the value −1 (thus, at baseline, the probability of success for an average cluster in the control arm is 0.27). The treatment-arm effect (TAE) was fixed at zero (0 indicating no systematic difference in outcomes between treatment arms prior to the exposure), while the secular time effect (STE) was also allowed to take on the values 0 and 0.1. The intervention effect, (GT), was allowed to take on the values from −0.50 to 0.50, in increments of 0.05. We chose two values for the cluster standard deviation (σ_c) : 0.10 and 0.50, two values for the cluster autocorrelation (ρ_c) : 0.5 and 0.8. The values for the cluster variance and cluster autocorrelation were a subset of values that Feldman and McKinlay (1994) used in a series of Monte Carlo simulations that they conducted. Having σ_c =0.10 implies that the cluster-specific probability of success at baseline will range between 0.23 and 0.31 for 95% of clusters in the control arm. Similarly, having σ_c =0.50 implies that the cluster-specific probability of success at baseline will range between 0.12 and 0.50 for 95% of clusters in the control arm. We thus examined 672 scenarios (2 cluster sizes × 2 number of clusters per treatment arm × 2 cluster variances × 2 cluster autocorrelations × 1 treatment-group effect × 2 secular time effects × 21 treatment effects). Computational considerations restricted the number of levels of the different factors that could be examined in the current study. Within a given scenario, the values of the above parameters were fixed. For each of the clusters, cluster specific random effects were drawn from normal distributions as described above. This allowed the logit of the probability of success (π_jkt) (see formula (10)) to be determined for each of the subjects. Using this time-period and cluster-specific probability of success, dichotomous outcomes were randomly generated from a Bernoulli distribution with parameter π_jkt.

3.3. Monte Carlo simulations

We used a full factorial design for the Monte Carlo simulations. In each of the 672 scenarios, we generated 1,000 random datasets each consisting of the appropriate number of subjects (336, 756, 1872, or 4212 subjects per simulated dataset), using the data-generating process described in Section 3.2 (the use of 1,000 replicates for each scenario is justified in the paragraph below). Each statistical method described in Section 2 was used to assess the statistical significance of the intervention in each of the 1,000 random datasets. A significance level of 0.05 was used to determine statistical significance of the intervention effect. We examined 640 scenarios in which the treatment effect was non-zero. Within each of these 640 scenarios, statistical power was defined as the proportion of the 1,000 simulated trials in which the intervention effect was determined to be significantly different than zero.

In 32 of our 672 scenarios the treatment effect was null. In each of these scenarios we determined the Type I error rate of each of the different statistical methods. The empirical Type I error rate was estimated as the proportion of simulated trials in which the intervention effect was determined to be significantly different than zero, when in fact the null hypothesis of a null intervention effect was true. Given our use of 1,000 iterations per scenario, a Type I error rate smaller than 0.0365 or greater than 0.0635 is significantly different than 0.05, using a 5% significance level (based on the normal-theory method for a test of a binomial proportion).

The data were randomly generated using the R statistical programming language (version 2.2.0) and the statistical analyses were conducted using SAS version 9.1.3 (SAS Institute Inc, Cary NC). The logistic regression models estimated using GEE methods were fit using PROC GENMOD. Each model assumed an exchangeable (or compound-symmetry) correlation structure for the working correlation matrices, and robust estimates of standard errors were obtained to account for the clustering of subjects within clusters. The cluster-specific analyses were conducted using PROC GLM. The logistic regression models incorporating random effects were fit using the glmer function in the lme4 package for R. The glmer function fits generalized linear mixed models using the adaptive Gauss-Hermite approximation to the likelihood. The default number of points per axis for evaluating this approximation is one, in which case the approximation corresponds to the Laplacian approximation.

Two of the statistical methods that we considered adjusted for the log-odds of the cluster-specific baseline success rate. When the observed cluster-specific probability of success is 0 or 1, then the log-odds of this probability is not defined. In our simulations, if the observed cluster-specific probability of success was equal to either 0 or 1, then this quantity was replaced by 0.01 or 0.99, respectively. This allowed all clusters to be included in all nine statistical analyses.

4. Monte Carlo simulations: Results

4.1. Type I error rate of the different statistical methods

The type I error rate for each analytic method and for each scenario is reported in Table 1. For each statistical method, the empirical type I error rate was reported for 32 different scenarios. Given a type I error rate of 5%, one would expect that, on average, 1.6 of the 32 scenarios would have an empirical type I error rate that was statistically significantly different from 0.05 for each statistical method. Instead, the number of scenarios in which the empirical type I error rate was significantly different from 0.05 (lower than 0.0365 or higher than 0.0635) ranged from a low of 10 to a high of 18. The median type I error rate across the 32 scenarios for the random effects approach was 0.034, 0.0385, 0.0395 when the follow-up response was analyzed alone, when the model adjusted for the baseline response rate, and when analyzing the change from baseline method was used, respectively. The median type I error rate for the 32 scenarios when the GEE approach was used were 0.0435, 0.0515, and 0.057 for the three different approaches, respectively. The median type I error rate for the 32 scenarios when the cluster-level analyses were used were 0.034, 0.0365, and 0.0445 when the response rate was analyzed, when adjustment was made for the baseline response rate, and when the change from baseline method was used, respectively. Overall, 131 of the 288 (45.5%) different empirical type I error rates were significantly different from 0.05. For the random effects approaches and the cluster-level analyses, in those settings in which the empirical type I error rate was statistically significantly different than 0.05, the empirical type I error rate was always low (P < 0.0365), as opposed to high (P > 0.0636). The Wilcoxon signed rank test was used to compare empirical type I error rates between the random effects approach and the two other statistical methods of analysis. The median empirical type I error rates were significantly different between the GEE analyses and the random effects analyses (P < 0.0001 for follow-up response analyzed alone; P < 0.0001 when adjusting for the baseline response rate; P < 0.0001 when analyzing the change from baseline). The median empirical type I error rates were significantly different between the random effects approach and the cluster-level analyses for two sets of analyses (P = 0.0487 when the adjusting for the baseline response rate; P < 0.0001 when analyzing the change from baseline). However, the empirical type I error rates were not significantly different between the two approaches when analyzing the follow-up response alone (P = 0.4301).

Table 1.

Type I error rates of different statistical methods for the analysis of repeated cross-sectional cluster randomization trials.

Number of clusters/arm	Number of subjects/cluster	ρC	σC	Random effects model			GEE model			Cluster-level analysis
				Follow-up response	Adjust for baseline	Change from baseline	Follow-up response	Adjust for baseline	Change from baseline	Follow-up response	Adjust for baseline	Change from baseline
STE = 0
12	7	0.5	0.1	0.038	0.039	0.040	0.064	0.065	0.059	0.050	0.054	0.044
12	7	0.5	0.5	0.029	0.042	0.029	0.042	0.051	0.056	0.025	0.030	0.031
12	7	0.8	0.1	0.039	0.041	0.045	0.067	0.071	0.062	0.048	0.051	0.047
12	7	0.8	0.5	0.029	0.033	0.035	0.042	0.051	0.057	0.028	0.030	0.040
12	39	0.5	0.1	0.041	0.038	0.048	0.060	0.074	0.079	0.041	0.041	0.052
12	39	0.5	0.5	0.005	0.018	0.004	0.004	0.019	0.021	0.003	0.008	0.009
12	39	0.8	0.1	0.038	0.038	0.053	0.066	0.072	0.086	0.040	0.040	0.057
12	39	0.8	0.5	0.007	0.039	0.007	0.005	0.042	0.047	0.003	0.017	0.031
27	7	0.5	0.1	0.054	0.057	0.048	0.061	0.061	0.058	0.051	0.052	0.055
27	7	0.5	0.5	0.031	0.033	0.041	0.031	0.037	0.055	0.025	0.030	0.046
27	7	0.8	0.1	0.048	0.051	0.042	0.057	0.060	0.057	0.050	0.051	0.052
27	7	0.8	0.5	0.035	0.045	0.028	0.035	0.049	0.048	0.025	0.036	0.043
27	39	0.5	0.1	0.040	0.046	0.044	0.050	0.052	0.053	0.038	0.039	0.044
27	39	0.5	0.5	0.002	0.006	0.000	0.001	0.005	0.008	0.001	0.004	0.006
27	39	0.8	0.1	0.045	0.047	0.041	0.048	0.052	0.058	0.044	0.042	0.047
27	39	0.8	0.5	0.006	0.018	0.003	0.004	0.015	0.028	0.004	0.010	0.019
STE = 0.1
12	7	0.5	0.1	0.034	0.035	0.041	0.062	0.067	0.059	0.042	0.040	0.039
12	7	0.5	0.5	0.023	0.030	0.034	0.043	0.049	0.051	0.032	0.029	0.033
12	7	0.8	0.1	0.038	0.037	0.039	0.067	0.067	0.060	0.046	0.043	0.045
12	7	0.8	0.5	0.028	0.034	0.038	0.038	0.052	0.057	0.024	0.032	0.041
12	39	0.5	0.1	0.032	0.035	0.047	0.059	0.069	0.066	0.042	0.045	0.047
12	39	0.5	0.5	0.006	0.017	0.004	0.004	0.015	0.020	0.002	0.006	0.012
12	39	0.8	0.1	0.040	0.039	0.051	0.062	0.068	0.080	0.042	0.042	0.058
12	39	0.8	0.5	0.006	0.038	0.006	0.006	0.040	0.051	0.003	0.022	0.027
27	7	0.5	0.1	0.051	0.055	0.048	0.063	0.068	0.060	0.052	0.059	0.051
27	7	0.5	0.5	0.034	0.039	0.032	0.033	0.036	0.058	0.025	0.031	0.046
27	7	0.8	0.1	0.051	0.059	0.040	0.065	0.068	0.057	0.055	0.059	0.049
27	7	0.8	0.5	0.034	0.041	0.026	0.035	0.039	0.060	0.028	0.034	0.046
27	39	0.5	0.1	0.040	0.040	0.043	0.044	0.050	0.058	0.039	0.037	0.047
27	39	0.5	0.5	0.004	0.005	0.001	0.001	0.003	0.007	0.001	0.003	0.005
27	39	0.8	0.1	0.041	0.045	0.042	0.045	0.053	0.054	0.036	0.042	0.047
27	39	0.8	0.5	0.005	0.013	0.000	0.002	0.011	0.022	0.002	0.010	0.018

Note: Each cell reports the empirical Type I error over the 1,000 simulated datasets for the given scenario.

Thus, it appears that when analyzing change from baseline, the random effects analysis had lower type I error rates than the GEE approach or the cluster-level analysis.

4.2. Statistical power of different statistical methods for cluster randomization trials

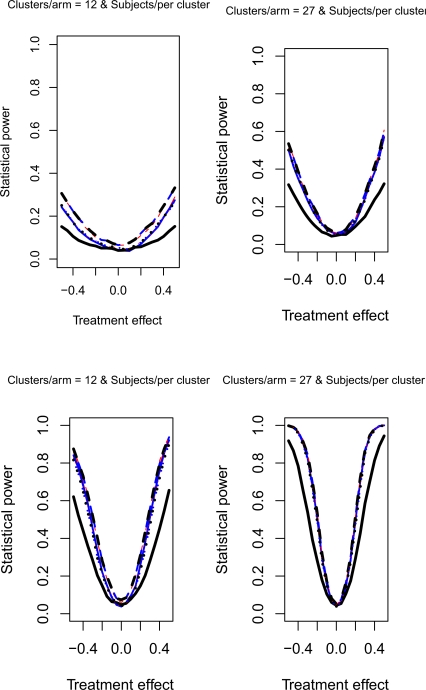
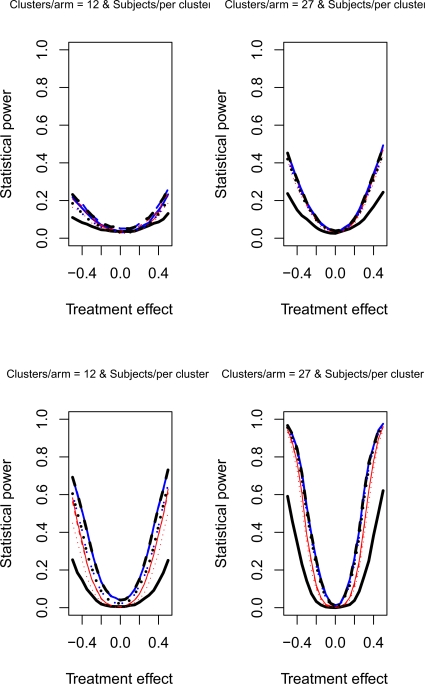
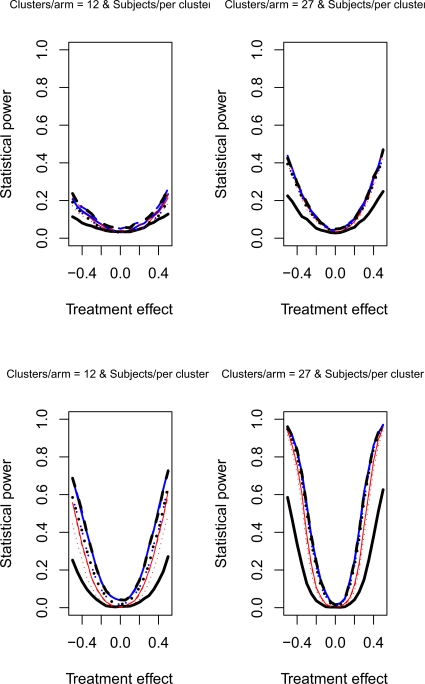
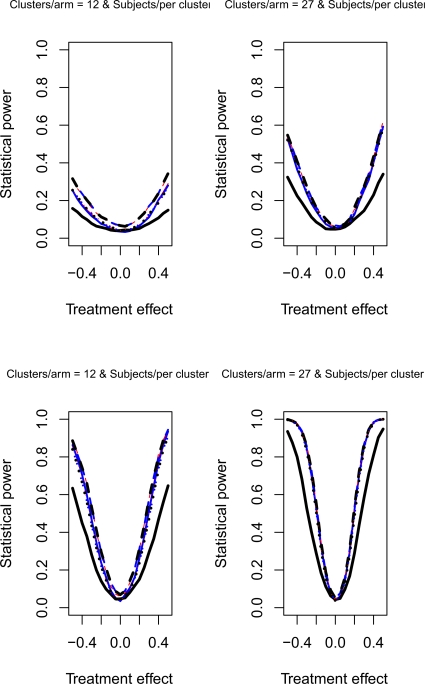
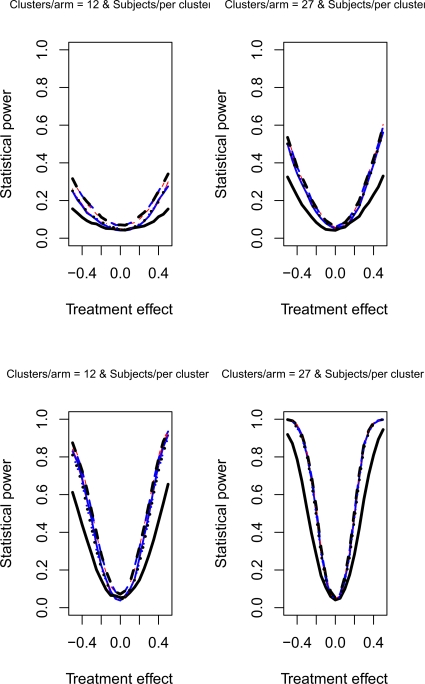
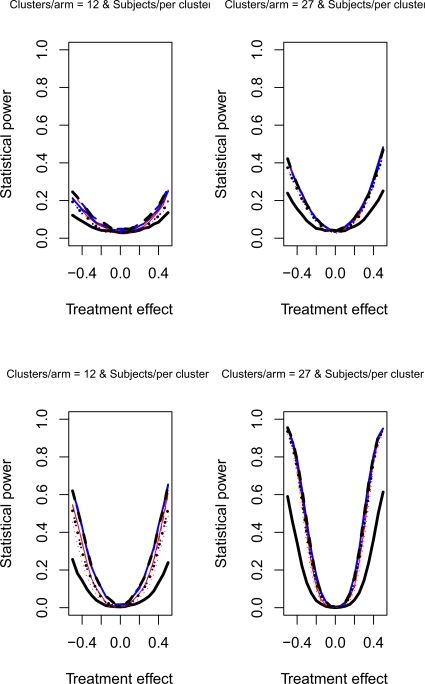
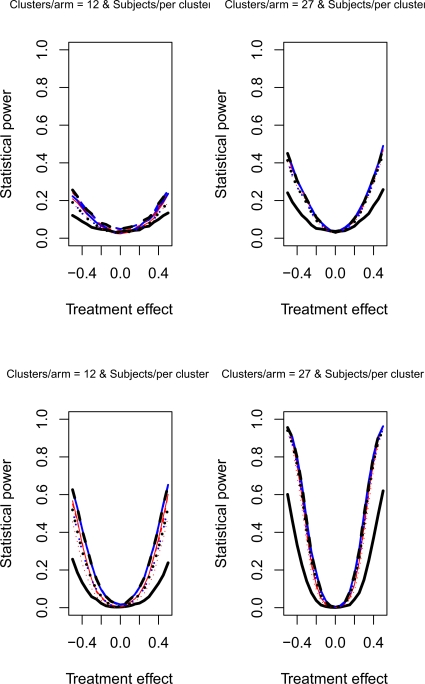
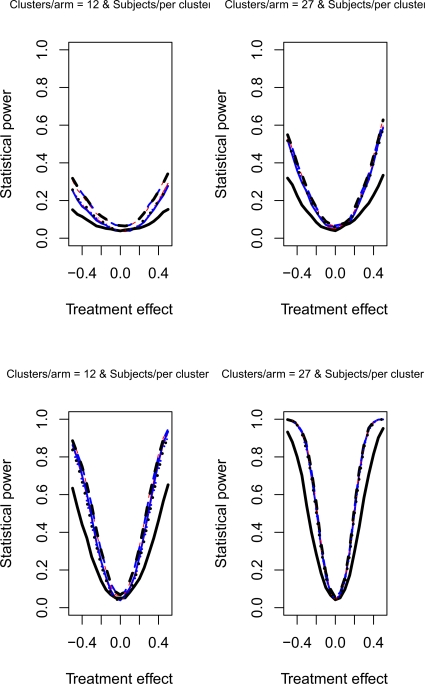
The relative statistical power of different methods of analysis for repeated cross-sectional cluster randomization trials with binary outcomes are described in Figures 1 through 8. Figures 1 through 4 describe results for scenarios in which there was a null secular time effect (STE = 0), while figures 5 through 8 describe results for scenarios in which there was a non-null secular time effect. Each figure consists of four panels, each describing power curves for scenarios with different numbers of clusters per arm and different numbers of subjects per cluster.

Figure 1.

Null STE & ρ_C = 0.5 & σ_C = 0.1

Figure 8.

Non-null STE & ρ_C = 0.8 & σ_C = 0.5

Figure 4.

Null STE & ρ_C = 0.8 & σ_C = 0.5

Figure 5.

Non-null STE & ρ_C = 0.5 & σ_C = 0.1

4.2.1. Null secular time effect

In examining Figure 1, one observes several results. First, the use of a random effects model that modeled change from baseline had the lowest statistical power in the four scenarios described in Figure 1. Second, the difference in power between this method and the other approaches was amplified as the number of clusters per arm or the number of subjects per cluster increased. Third, differences between the remaining eight methods were negligible. Fourth, minor differences in statistical power between the remaining eight methods diminished as the number of clusters per arm or the subjects per cluster increased. Fifth, for a given statistical method, power increased as the number of clusters per arm or the number of subjects per cluster increased. Similar observations can be made in Figure 3. Thus, these observations appear to hold when there was a null secular time effect and the cluster standard deviation was small (σ_c = 0.1).

Figure 3.

Null STE & ρ_C = 0.8 & σ_C = 0.1

Figures 2 and 4 report the results when there was a null secular time effect and the cluster standard deviation was large (σ_c = 0.5). As above, we observe that the use of a random effects model to model change from baseline resulted in lower statistical power compared to the other eight approaches. Furthermore, as above, the difference in power between this method and the other eight approaches was amplified as the number of clusters per arm or the number of subjects per cluster increased. The power of each method increased as the number of clusters per arm or the number of subjects per cluster increased. Finally, the three methods that did not account for baseline response tended to have marginally lower statistical power when the number of subjects per cluster was large. This observation was more evident when the cluster autocorrelation was high (ρ_c = 0.8) compared to when the cluster autocorrelation was low (ρ_c = 0.5).

Figure 2.

Null STE & ρ_C = 0.5 & σ_C = 0.5

4.2.2. Non-null secular time effect

If one compares the results for a given scenario with a non-null secular time effect with the similar scenario with a null secular time effect, one observes that the results are essentially identical (a given figure in Figures 5 through 8 is essentially identical to the corresponding figure in Figure 1 through 4). Therefore, the observations made above for the setting of a null secular time effect would hold in the presence of a non-null secular time effect.

4.3. Supplemental analyses

We conducted a series of supplemental analyses to further examine the relative performance of the two regression-based methods of analysis. For each scenario, we computed the mean standard error of the estimated treatment effect (on the log-odds scale) for each of the two regression-based methods. For each scenario, we then compared the ratio of the mean standard error from a given random effect-based method to that of the comparable GEE-based method. In all 672 scenarios, the ratio was positive (range of ratio: 1.02 to 1.52). However, the range of the ratio of the standard errors depended on the particular regression-based method. When no adjustment was made for the baseline response, the ratio ranged from 1.03 to 1.09; when adjustment was made for the baseline response, the ratio ranged from 1.02 to 1.11. However, when the change from baseline was analyzed, the ratio ranged from 1.04 to 1.52. Furthermore, when modeling the change from baseline, the ratio tended to be large when the cluster standard deviation was high (σ_c = 0.5) (range of ratio: 1.10 to 1.52). Finally, when the cluster standard deviation was high, the ratio was larger when the number of subjects per cluster was high (range of ratio: 1.25 to 1.52, compared to when the number of subjects per cluster was low (range of ratio: 1.10 to 1.17).

It is likely that the increased standard error when a random effects model was used to analyze change from baseline compared to the standard error when a GEE model was used when the cluster standard deviation was high explains, at least in part, the greater difference in statistical power between these two methods in certain scenarios. As noted in Section 4.1, it appeared that when analyzing change from baseline, the random effects analysis had lower type I error rates than the GEE approach or the cluster-level analysis. The observation that analyzing change from baseline using a random effects model had more conservative significance levels compared to the other two approaches may also contribute to the reduced statistical power of the random effects approach compared to that of the two competing methods.

5. Discussion

The objective of the current study was to compare the relative power of different statistical methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. Our primary finding was that the use of random effects model to model change from baseline consistently had lower statistical power compared to the other statistical methods that were considered. The remaining eight statistical methods tended to have comparable statistical power; however, in certain scenarios, methods that did not account for the baseline response had marginally lower statistical power compared to methods that accounted for baseline responses.

There is currently a paucity of research into the power of different statistical methods for the analysis of cluster randomization trials with binary outcomes. To the best of our knowledge, only two studies have examined the relative statistical power of different methods for the analysis of simple cross-sectional cluster randomization trials (no measurements of the outcome at baseline – only follow-up measurements) (Austin, 2007; Bellamy et al. 2000). Lewsey (2004) examined the relative power between a completely randomized and a stratified randomized design for cross-sectional cluster randomization trials, and described certain settings in which stratification resulted in superior power. Donner and Klar (1994) have suggested that more research is needed on the relative statistical efficiencies of different analytic methods for cluster randomization trials. While a few studies have compared different methods of analysis for repeated cross-sectional cluster randomization trials with binary outcomes, none have examined the relative statistical power of these methods. Thus, the current study fills a void in the methodological literature for cluster randomization trials.

There is a large literature that discusses adjusting for baseline covariates in conventional RCTs in which the subject is both the unit of randomization and the unit on which responses are measured (Senn, 1989; Senn, 1994; Rothman, 1977). In conventional RCTs, adjusting for baseline covariates can allow for more precise estimates of the treatment effect, and allows for adjusting for chance imbalance in baseline covariates between treatment arms. Prior studies have examined conventional RCTs in which both baseline and follow-up responses are available for all subjects. Vickers and Altman (2001) recommend adjusting for baseline responses over the use of analyzing change from baseline, as it generally has higher statistical power. In the context of cohort cluster randomization trials (repeated measurements of the outcome variable made on the same subjects both at baseline and at follow-up) with continuous outcomes, Klar and Darlington (2004) describe methods to model change when measurements of the response are made both at baseline and at follow-up. Similarly, Nixon and Thompson (2003) discuss baseline adjustment for repeated cross-sectional cluster randomization trials with binary outcomes. They found that adjusting for baseline responses resulted in improved precision only when both the number of subjects per cluster was large and there was substantial heterogeneity between clusters at baseline. In the current study, we examined scenarios with a low number of subjects per cluster, as is typical in cluster randomization trials to change professional practice (http://www.abdn.ac.uk/hsru/epp/iccs-web.xls - site accessed February 15, 2006). In some scenarios when the number of subjects per cluster was equal to 39, we found that the methods that did not account for baseline response had modestly lower power compared to those methods that accounted for baseline (apart from the use of random effects model to model change from baseline). Thus, some of our observations mirror the findings of Nixon and Thompson (2003).

It may appear surprising that, in many scenarios, we did not observe an advantage to accounting for baseline responses. One must remember that in the simulations the data were generated such that there were no systematic differences in outcomes between treatment groups at baseline. This was done to reflect the fact that randomization will, on average, result in the two treatment groups being comparable at baseline. In any particular randomization (as in any particular simulated dataset) it is possible that the groups may be imbalanced at baseline; however, on average, the treatment groups will be comparable at baseline. Our findings suggest that in many settings, one will not, on average, observe substantial differences in power between cluster-level analyses and GEE-based methods of analyses. However, in specific cluster randomization trials, one may observe meaningful differences in baseline response between treatment groups. For this reason, there are strong arguments for using statistical methods that account for baseline responses. In several of the scenarios that we examined, the three methods that adjusted for baseline response had good statistical power relative to the competing methods.

Apart from statistical power, there are other advantages and disadvantages to the different statistical methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes which are more fully described elsewhere (Donner and Klar, 2000; Ukoumunne and Thompson, 2001). However, we briefly highlight a few of these. An advantage of the regression based approaches (GEE and random effects methods) is the ability to adjust for subject characteristics. It is possible that the two treatment groups may be imbalanced on measured baseline characteristics during the second measurement period. Regression-based approaches allow one to adjust for residual differences between treatment groups. A drawback to these methods is that measure of treatment effect is the odds ratio. The use of the odds ratio as a measure of treatment effect in RCTs has been criticized by clinical commentators (Sackett et al., 1996; Jaeschke et al., 1995). Clinical commentators have suggested that the relative risks, the absolute risk reduction, and the number needed to treat are more informative for clinical decision making (Laupacis et al., 1988; Cook and Sackett, 1995; Sinclair and Bracken, 1994). An advantage to the use of cluster-level analyses is that one can report absolute measures of treatment effect. In particular, one can report the absolute change in the probability of the outcome at the cluster level.

There are certain limitations to the current study. First, we only examined power in the setting of the completely randomized design. Other designs such as the matched pairs design and the stratified randomized design are also used for cluster randomization trials (Donner and Klar, 2000; Donner, 1999). However, the completely randomized design is both the simplest design as well as allowing for a wide number of different statistical methods of analysis. Thus, it is important that the relative power of different statistical methods be examined for this design. Second, we examined a limited number of scenarios defined by different values for the number of clusters per arm, the number of subjects per cluster, the cluster variance, the cluster auto-correlation, and the secular time effect. The number of clusters and number of subjects per cluster were selected from an analysis of a database of cluster randomization trials that were designed to change professional practice in health care. Thus, our data-generation processes resulted in simulated trials that were similar to cluster randomization trials that were designed to examine interventions to change professional practice in health care, an area in which cluster randomization is frequently employed. Furthermore, our findings were consistent across a large number of different scenarios within this framework. The time intensive nature of the simulations restricted the number of different scenarios that could feasibly be examined. A final limitation was that our study was limited to an examination of statistical power, and did not examine estimation issues such as bias and precision. We did not examine bias, since the different methods used different metrics to estimate the treatment effect. The cluster-level analyses used either the follow-up probability of a response or the change in the probability of a response as the metric, while the other methods used the odds ratio as the measure of treatment response. Furthermore, the GEE approach estimates marginal (or population-average) odds ratios, while the random effects approach estimates conditional (or subject-specific) odds ratios. The current study focused on statistical power alone, since this aspect of the design of cross-sectional cluster randomization trials has not been well explored. Furthermore, cluster randomization trials are often small, and therefore using the analytic method that will maximize statistical power will allow for an efficient use of resources.

In conclusion, the current study is the only study to date to examine the relative statistical power of different methods for the analysis of repeated cross-sectional cluster randomization trials with binary outcomes. The use of random effects models to estimate the effect of the intervention on the change from baseline had lower power compared to the other methods across a wide range of scenarios. Apart from this, the remaining competing methods tended to have comparable statistical power.

Figure legend

Random effects (no adjustment)

Random effects (adjust for baseline)

Random effects (change from baseline)

GEE method (no adjustment)

GEE method (adjust for baseline)

GEE method (change from baseline)

Cluster analysis (no adjustment)

Cluster analysis (adjust for baseline)

Cluster analysis (change from baseline)

Figure 6.

Non-null STE & ρ_C = 0.5 & σ_C = 0.5

Figure 7.

Non-null STE & ρ_C = 0.8 & σ_C = 0.1