Dependence of Glycine CH₂ Stretching Frequencies on Conformation, Ionization State, and Hydrogen Bonding

Abstract

We experimentally and theoretically examined the conformation, pH and temperature dependence of the CH₂ stretching frequencies of glycine (gly) in solution and in the crystalline state. To separate the effects of the amine and carboxyl groups on the CH₂ stretching frequencies we examined the Raman spectra of 2,2,2-d₃-ethylamine (CD₃-CH₂-NH₂) and 3,3,3-d₃-propionic acid (CD₃-CH₂-COOH) in D₂O. The symmetric (ν_sCH₂) and asymmetric (ν_asCH₂) stretching frequencies show a significant dependence on gly conformation. We quantified the relation between the frequency splitting (Δ = ν_asCH₂ − ν_sCH₂) and the ξ angle which determines the gly conformational geometry. This relation allows us to determine the conformation of gly directly from the Raman spectral frequencies. We observe a large dependence of the ν_sCH₂ and ν_asCH₂ frequencies on the ionization state of the amine group, which we demonstrate theoretically results from a negative hyperconjugation between the nitrogen lone pair and the C-H anti-bonding orbitals. The magnitude of this effect is maximized for C-H bonds trans to the nitrogen lone pair. In contrast, a small dependence of the CH₂ stretching frequencies on the carboxyl group ionization state arises from delocalization of electron density from carboxyl oxygen to C-H bonding orbitals. According to our experimental observations and theoretical calculations the temperature dependence of the ν_sCH₂ and ν_asCH₂ of gly is due to the change in the hydrogen bonding strength of the amine/carboxyl groups to water.

Introduction

Vibrational spectroscopy is a powerful technique to study the conformations of peptides and proteins. Vibrational spectroscopy provides a unique opportunities to study fast protein folding dynamics^1–4 and unordered states of polypeptides chains.⁵ Vibrational spectra are highly informative on molecular structure due to the extreme sensitivity of certain vibrational bands or so-called “conformational markers”, to the small structural alterations such as bond lengths, dihedral angles, and hydrogen bonding patterns.

The most commonly used markers for the polypeptide backbone conformation analysis are the amide bands. The Amide I band (primarily C=O stretching of the peptide bond) is used for the IR spectroscopy secondary structure elucidation.^1,6 The Amide II, Amide III and C_αH bending vibrations, observed in Raman spectra, have been shown to be even more valuable for peptide secondary structure analysis.^3,4,7,8 There should be other conformationally sensitive vibrations which can be used to expand the informational context of vibrational spectroscopy.

The CH (or deuterated CD) stretch is a potential candidate for use as a conformational marker to study the secondary structure of polypeptide chains. It has recently been shown theoretically^9,10 that the C_αH (C_αD) bond stretching frequency depends on the ψ and φ Ramachandran angles.

CH stretching vibrations have previously been used to determine the structure of small organic molecules. Isolated C-D stretching frequencies have also been used in the conformational analysis of alkylamino chains,¹³ and monosaccharides.¹⁴ Good correlations have been experimentally found between isolated methyl CH stretching frequencies and HCH angles.¹¹

The origin of the CH conformational sensitivity is not well understood. It is generally agreed that the CH stretching frequencies depend almost solely on the C-H bond lengths because these vibrations are essentially decoupled from other vibrations. Previous work has quantified the relationship between CH stretching frequencies and C-H bond lengths in various organic compounds^12,15 This work includes McKean, Bellamy and others^16,17 extensive IR spectroscopy studies in 60’s and 70’s which examined the factors influencing CH stretching frequencies

In the present study we focus our attention on gly, the smallest amino acid, which has a hydrogen atom instead of a side chain. There is no coupling or overlap of the gly CH₂ stretches in proteins and peptides with the CH stretches of the adjacent amino acid residue side chains. In addition, the CH₂ stretches of gly are unaffected by Fermi resonances because of the significant downshift of the CH₂ scissoring vibration. The two CH stretches of the gly CH₂ group couple with each other to form a high-frequency asymmetric and a low-frequency symmetric CH₂ stretching components, which appear as a doublet in the Raman spectra. The magnitude of the frequency splitting of this doublet depends on the extent of vibrational coupling which in turn is determined by the C-H bond length difference.

The unique flexibility of gly makes it an essential structural element of many proteins, determining protein folding pathways, tertiary structure and biological function. Gly is frequently found in the turn and loop structures, which play an important role in polypeptide chain collapse during the early stages of folding. Gly accelerates loop formation compared to other amino acids.¹⁸ Gly rich flexible motifs are often impossible to characterize by x-ray crystallography and 2D NMR.¹⁹ Thus, there is a great need to develop new structural methods to determine the gly residue conformations.

In this paper we investigate the gly CH₂ stretching frequency dependence on amino acid conformation and ionization state in order to develop methodologies for the conformational analysis of gly residues in polypeptides and proteins.

Experimental methods

Sample Preparation

For the pD measurements anhydrous gly (Sigma Chemicals) was dissolved in D₂O (Cambride Isotope Laboratories Inc). Low and high pD samples were prepared by addition of DCl or NaOD solutions (Sigma Chemicals). 2,2,2-d₃-ethylamine hydrochloride was obtained from Medical Isotopes Inc. and 3,3,3-d₃-propionic acid from Cambride Isotope Laboratories Inc. Crystals of Gly•HCl, Gly•HNO₃, 3Gly•H₂SO₄ (TGS) were obtained by slow evaporation of water solutions of stoichiometric mixtures of gly and the corresponding acid. All acids were purchased from J. T. Baker Inc. Crystal structures were determined by using x-ray crystallography.

Raman measurements

All Raman measurements were performed using 488 nm Ar-ion Laser (Coherent Inc.) excitation. Scattered light was collected using a back-scattering geometry, dispersed by a single monochromator and collected using a Princeton Instruments Spec-10:400B CCD camera (Roper Scientific). A 488 nm holographic notch filter (Kaiser Optical Systems Inc.) was used for Raleigh rejection. Typical accumulation times were ~ 2 min. A temperature controlled fused silica cell (20 mm path length, Starna Cell Inc.) was used for solutions. A custom made, rotating metal cell was used for solid powder samples to avoid light-induced degradation under continuous irradiation. The powder was pressed into a circular groove cut in the rotating metal cylinder.

Computational methods

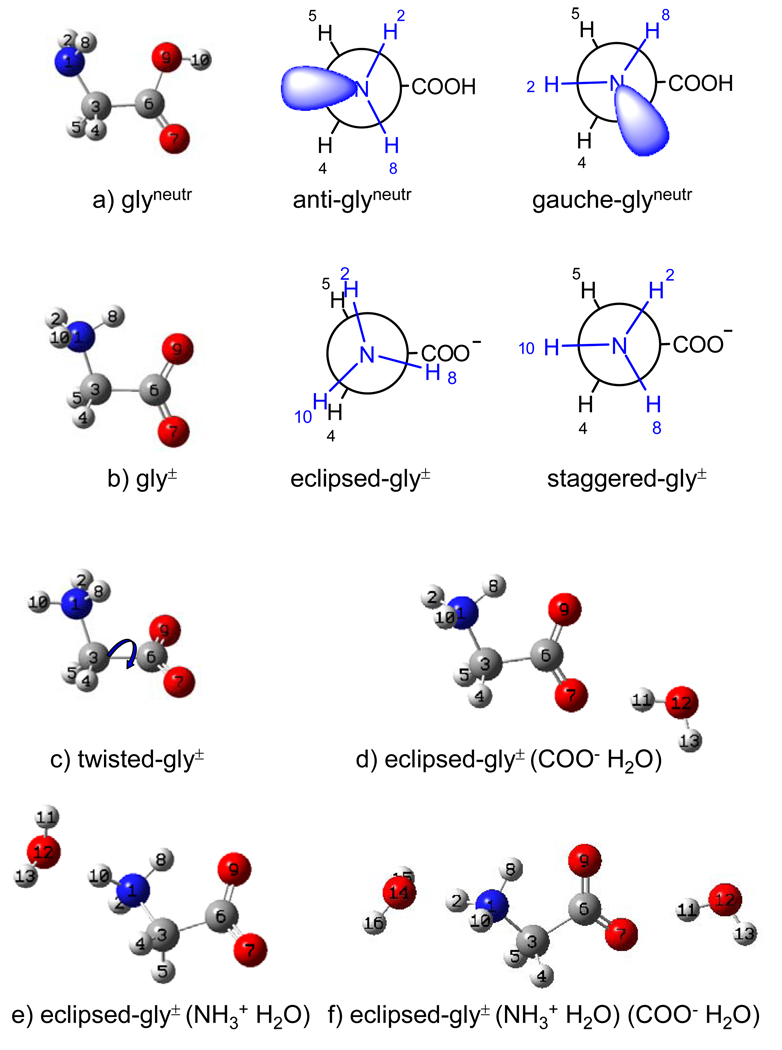
We optimized the geometries and calculated the vibrational frequencies, normal mode compositions, molecular orbital analysis, and charge distributions of a series of gly conformers in neutral and zwitterionic forms. We also performed the calculations for zwitterionic gly hydrogen bonded to one or two water molecules (Fig.1).

Figure 1.

Calculated conformers of gly: a) anti and gauche rotamers of neutral gly; b) eclipsed and staggered rotamers of zwitterionic gly; c) non-planar conformer (ξ = 60°) of zwitterionic gly; d) eclipsed zwitterionic gly hydrogen bonded to the acceptor water molecule, e) eclipsed zwitterionic gly hydrogen bonded to the donor water molecule, f) eclipsed zwitterionic gly hydrogen bonded simultaneously to the acceptor and donor water molecules. All conformers except c) are planar ξ = 0°.

All calculations were carried out at the DFT level of theory^20–22 employing the B3LYP exchange functional^23–25 and 6-311+G(d,p) basis set. All frequencies were calculated at the harmonic approximation and scaled by 0.98.^26,27 The presence of the solvent water was modeled using the Polarizable Continuum Model (PCM) initially devised by Tomasi and coworkers.^28–30 The PCM calculations were performed using the integral equation formalism model³⁰ (IEFPCM) and the Bondii’s atomic radii. Atomic charges were calculated using the Atoms in Molecule (AIM) algorithm^31–33 as implemented in Gaussian’98. Orbital occupancies and hybridization analysis of Natural Local Molecular Orbitals were obtained through the Natural Bond Orbital (NBO) Analysis. All calculations except the AIM charge calculations were performed with the Gaussian’03 calculational package.³⁴ Normal mode compositions for the calculated vibrational frequencies were obtained from the Gaussian output files employing the GAR2PED program.³⁵

Experimental Results

The conformational dependence of the CH₂ stretching frequencies on carboxyl group orientation of gly in the solid state

We investigated the structures of gly found in the Cambridge Structural Database (CSD):

1. Gly hydrochloride (Gly•HCl). In this crystal all heavy atoms lie almost in the same plane.³⁶

2. Gly nitrate (Gly•HNO₃). Here gly is bent.³⁷

3. Triglycine sulphate (3Gly•H₂SO₄), TGS. In this crystal structure two gly molecules have geometries close to planar while one gly molecule is bent.³⁸

In these structures the amine groups are protonated (-NH₃⁺). Thus, rotation about the N-C bond should not significantly affect the CH₂ stretching frequencies.

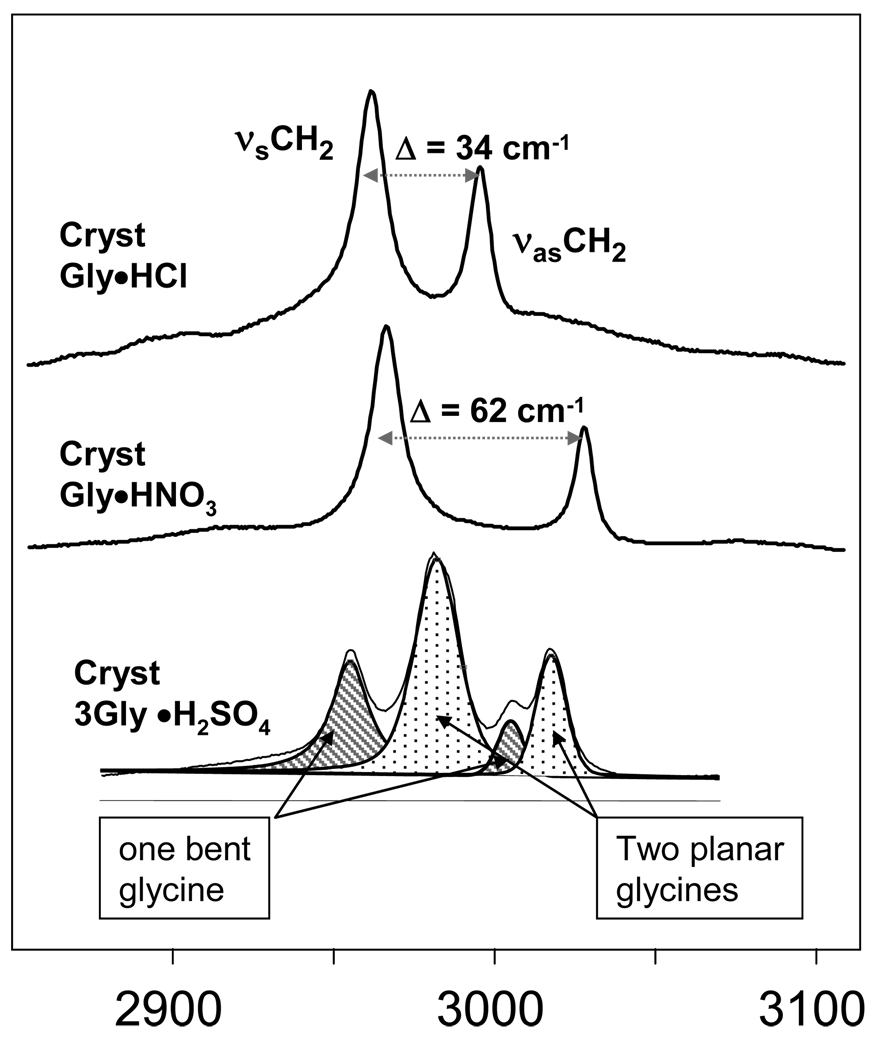
There is a remarkable difference in the frequencies and the frequency splitting between the CH₂ symmetric (ν_sCH₂) and asymmetric (ν_asCH₂) stretching frequencies for these three samples. The Raman spectrum of crystalline Gly•HCl shows the symmetric and asymmetric stretching bands at ν_sCH₂ = 2962 cm⁻¹ and ν_asCH₂ = 2996 cm⁻¹, with a splitting Δ of ~ 34 cm⁻¹. Crystalline Gly•HNO₃ has a much larger splitting, Δ ~ 62 cm⁻¹ between the ν_sCH₂ = 2966 cm⁻¹ and ν_asCH₂ = 3028 cm⁻¹ bands, mainly due to the upshift of the ν_asCH₂. TGS has 3 nonequivalent gly in the crystal unit cell. In TGS we observe two different doublets of ν_sCH₂ and ν_asCH₂.

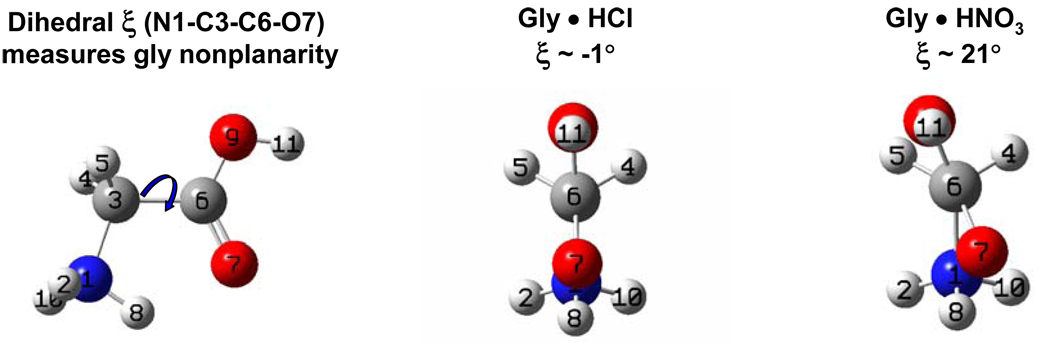
X-ray crystallographic data shows (Fig. 3) that in Gly•HCl crystals all heavy atoms (N-C-COO) lie almost in the same plane and the two C-H bonds are symmetrically disposed about this plane. The dihedral angel ξ, defined by atoms N-C-C-O_{cis to N} (since carboxyl group has two oxygens, ξ is defined by the one which is the closest (cis) to the nitrogen). The ξ angle indicates the deviation of gly from the planar conformation through rotation around the C-C bond. When ξ = 0° all heavy atoms in the gly molecule lie in the same plane (Figure 3). In contrast, the -COOH group of the Gly•HNO₃ crystal is rotated such that ξ ~ 21°. In this case the C-H bonds are not symmetrically disposed on both sides of the COO plane, which results in greater splitting between the ν_sCH₂ and ν_asCH₂ frequencies.

Figure 3.

Dihedral angle ξ measures planarity of gly molecule. If ξ ~ 0°, the molecule is planar and the C-H bonds are symmetric with respect to the carboxyl group plane, as in case of Gly•HCl. In Gly•HNO₃ the carboxyl is rotated ~ 21° with respect to the N1-C3 bond making the C-H bonds nonequivalent.

In TGS crystals, two of the gly molecules are almost planar (ξ = 4° and = 5°), while the third one is bent ξ ~ 21°. Thus, we assign the more intense, less split doublet (2982 cm⁻¹ and 3017 cm⁻¹) to the two planar gly molecules and the less intense more split doublet (2956 cm⁻¹ and 3005 cm⁻¹) to the third gly.

pD and temperature dependences of the CH₂ stretching frequencies of gly in solution

We investigated the influence of the ionization state of the carboxyl and amine groups on the CH₂ stretching vibrations. Deuteration of the amine in gly molecule significantly downshifts the N-D stretches which removes overlap or coupling between C-H and N-D stretches and simplifies the interpretation of the Raman spectra.

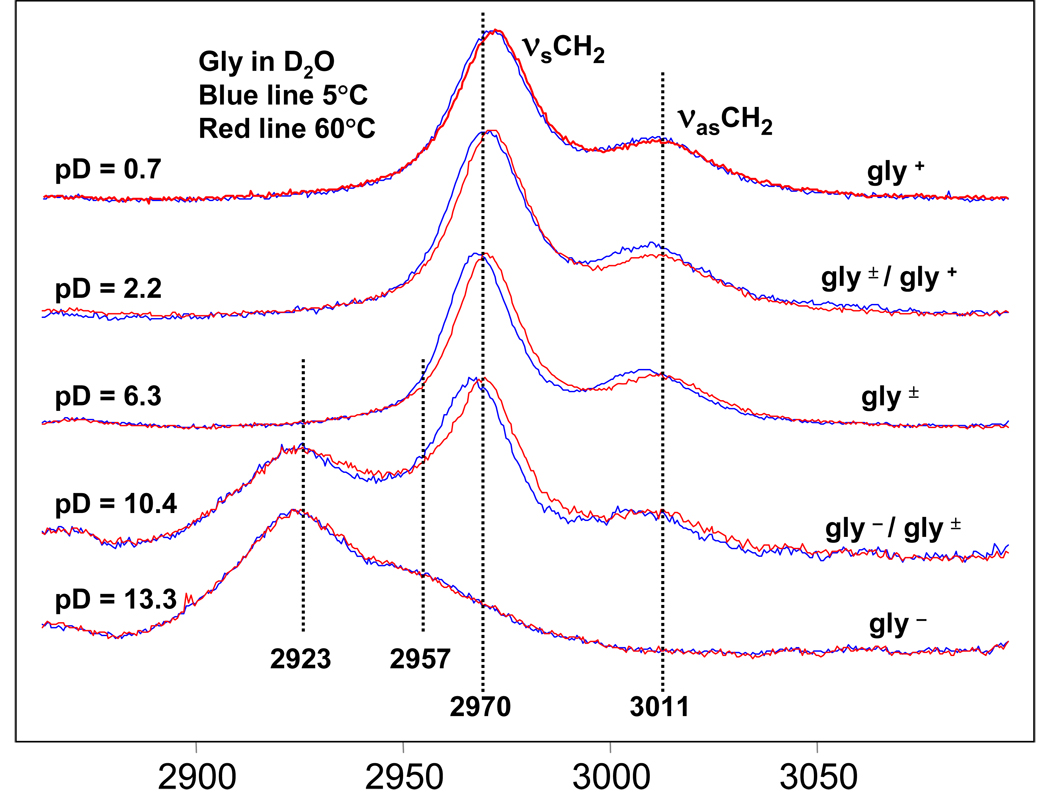
Figure 4 shows the 488 nm Raman spectra of gly in D₂O at various pD values at 5°C and 60°C. At low pD values gly is cationic D₃N⁺-CH₂-COOD (gly⁺), while at pD values close to neutral gly is zwitterionic D₃N⁺-CH₂-COO⁻ (gly^±), and at high pD values gly is anionic D₂N-CH₂-COO⁻ (gly⁻).

Figure 4.

488 nm excitation Raman spectra of gly solution in D₂O at pD= 0.7, 2.2, 6.3, 10.4, 13.3. For each solution spectra were accumulated at two temperatures 5°C and 60°C.

pD Dependence

For the low pD (gly⁺) and neutral pD values (gly^±) the CH₂ stretching region Raman spectra are very similar, indicating that the ionization state of the carboxyl group has little effect on the CH₂ group stretching frequencies. The CH₂ symmetric stretch is at ~ 2970 cm⁻¹ and is ~ 4 times more intense than the CH₂ asymmetric stretch at ~ 3010 cm⁻¹.

For pD values close to or above the pK_a value of the gly amine group (pD = 9.8) a peak appears at lower frequency ~ 2920 cm⁻¹, which must be due to C-H bond weakening due to interaction with the lone pair of the unprotonated amine group (-ND₂), as discussed in detail below.

The frequency splitting between ν_sCH₂ and ν_asCH₂ is ~ 41 cm⁻¹ for gly⁺ and gly^±, while for gly⁻ it is smaller (Δ ~ 34 cm⁻¹).

Thus, the C-H bonds stretching frequencies depend only on the ionization state of the terminal amine with a little influence of the ionization state of the carboxyl.

Temperature dependence

Figure 4 and Table 1 indicate the temperature dependence of the CH₂ stretching frequencies of gly in D₂O.

Table 1.

Temperature dependence of the Raman CH₂ stretching frequencies of gly in D₂O

Solution	T°C	νsCH2 / cm−1	Δν/ΔT sym	νasCH2 / cm−1	Δν/ΔT asym
D2O pD = 0.7	5	2971.2	0.016	3011.2	0.025
	60	2972.1		3012.6
D2O pD = 2.2	5	2969.9	0.027	3009.3	0.055
	60	2971.4		3012.3
D2O pD = 6.3	5	2968.1	0.038	3008.6	0.064
	60	2970.2		3012.1
D2O pD = 13.3	5	2923.1	0	2956.8	0
	60

There is a significant temperature dependence of the symmetric and asymmetric CH₂ stretching frequencies on pD. Temperature induced frequency shifts are larger at neutral pD than at high or low pD values. At pD = 13.3 the broad low frequency doublet is essentially temperature independent.

The stretching frequencies of gly methylene are affected by both the amine and carboxyl groups. In order to characterize the impact of the amine and carboxylic groups separately we investigated the CH₂ stretching frequencies of 2,2,2-d₃-ethylamine (CD₃-CH₂-NH₂) and 3,3,3-d₃-propionic acid (CD₃-CH₂-COOH) in D₂O at different pD values and temperatures.

pD And temperature dependence of the CH₂ stretching vibrations of CD₃-CH₂-COOD and CD₃-CH₂-ND₂

pD Dependence

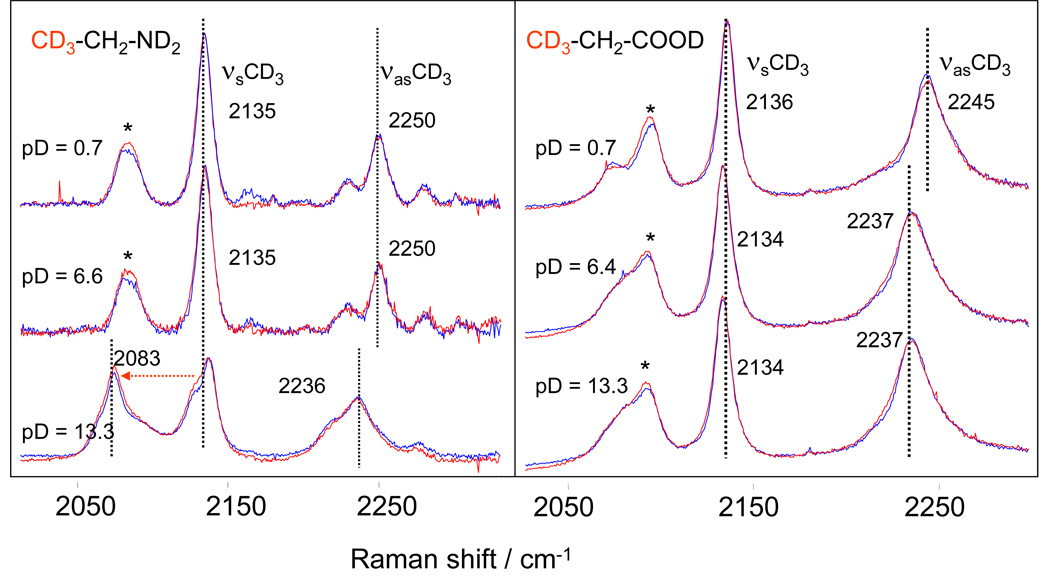
In CD₃-CH₂-ND₂ and CD₃-CH₂-COOD, the CH₂ is affected by changes in the ionization state of either the amine or carboxylic groups.

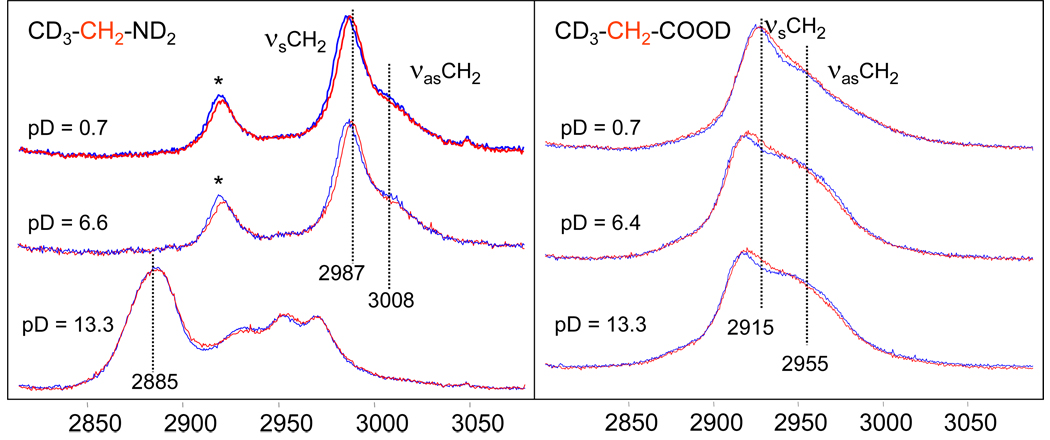
Figure 5 shows the CH₂ stretching region of the Raman spectra of CD₃-CH₂-ND₂ and CD₃-CH₂-COOD in D₂O. At low and neutral pD values 2,2,2-d₃-ethylamine is in its cationic form (CD₃-CH₂-ND₃⁺). The ν_sCH₂ and ν_asCH₂ frequencies are 2987 cm⁻¹ and 3008 cm⁻¹, respectively. At high pD values 2,2,2-d₃-ethylamine is in its neutral form (CD₃-CH₂-ND₂) where the nitrogen possesses a lone pair of electrons. As in gly, the adjacent ND₂ group significantly downshifts the CH₂ stretching vibrations.

Figure 5.

CH₂ stretching region of the Raman spectra of the 2,2,2-d₃-ethyl amine and 3,3,3-d₃-propionic acid in D₂O at different pD values at 5°C (blue curve) and 60°C (red curve). Band marked with (*) at 2918 cm⁻¹ in 2,2,2-d₃-ethylamine is most likely due to Fermi resonance of the ν_sCH₂ with the overtone of the CH₂ scissoring. The splitting between symmetric and asymmetric CH₂ stretches in CD₃-CH₂-ND₃⁺ at pD = 0.7 and 6.6 is unusually small, ~ 19 cm⁻¹ (an additional indication that ν_sCH₂ is up-shifted due to Fermi resonance) In gly and propionic acid CH₂ scissoring is at a significantly lower frequency than in ethylamine which removes the condition for Fermi resonance.

The Raman spectrum of the 2,2,2-d₃-ethylamine at pD = 13.3 consists of four bands in the CH₂ stretching region which are due to the free rotation about the C-N bond and presence of both gauche- and ant-i rotamers. The gauche form is slightly more stable (~ 0.3 kcal/mol) and gauche-anti rotational barrier is about 2 kcal/mol for the vapor phase.³⁹ The assignment of the high pD spectrum will be given late in the discussion after getting additional information from theoretical calculations.

The 3,3,3-d₃-propionic acid CH₂ stretching vibrations (ν_sCH₂ ~ 2915 cm⁻¹ and ν_asCH₂ ~ 2955 cm⁻¹) show a weak frequency dependence on solution pD. At neutral and high pD, the anionic CD₃-CH₂-COO⁻ CH₂ stretching bands are somewhat broader than are those of the protonated species at low pD.

Temperature dependence

High pD neutral 2,2,2-d3-ethylamine (CD₃-CH₂-ND₂) shows no CH₂ stretching temperature dependence (figure 5). In the cationic form (at low and neutral pD values) the CH₂ symmetric stretches upshift with temperature similar to that of the CH₂ symmetric stretch of gly^±, while the temperature shift of the CH₂ asymmetric stretch is 2-fold smaller. Table 2 shows the CH₂ stretching frequencies and their temperature dependence.

Table 2.

Temperature dependence of the CH₂ ν_s and ν_as of 2,2,2-d₃-ethylamine in D₂O

pD	T°C	νsCH2 / cm−1	Δν/ΔT sym	νasCH2 / cm−1	dν/dT asym
0.7	5	2985.7	0.033	3006.3	0.033
	60	2987.5		3008.3
6.6	5	2986.1	0.033	3007.5	0.022
	60	2987.9		3008.7

The temperature induced CH₂ stretching frequency shifts in 2,2,2-d₃-ethylamine are similar to those of zwitterionic gly (compare Table 1 and Table 2). 3,3,3-d₃-propionic acid, in contrast, shows little temperature dependence of the CH₂ stretching frequencies for any solution pD values. Thus, we can conclude that the amine group dominates the temperature dependence of the CH₂ stretching frequencies in gly.

pD and temperature dependence of the CD₃ stretching frequency in CD₃-CH₂-COOD and CD₃-CH₂-ND₂

Deuteration of the methyl group in CD₃-CH₂-ND₂ and CD₃-CH₂-COOD separates the originally overlapping methylene and methyl stretching vibrations, allowing us to unambiguously observe these vibrations in different solution conditions.

Figure 6 shows the CD₃ stretching region for 2,2,2-d₃-ethylamine and 3,3,3-d₃-propionic acid at different pD values and temperatures. For both compounds, the CD₃ stretching frequencies depend on the carboxyl or amine ionization states.

Figure 6.

CD₃ stretching region of the 2,2,2-d₃-ethyl amine and 3,3,3-d₃-propionic acid in D₂O at different pD values at 5°C (blue curve) and 60°C (red curve). CD₃ stretches show a clear dependence on the ionization state of the amine and carboxylic group even though the CD₃ group is not directly linked to the carboxyl or amine groups. Frequencies of the ν_sCD₃ and ν_asCD₃ for both 2,2,2-d₃-ethylamine and 3,3,3-d₃-propionic acid do not show any temperature dependence at any pD values. Band marked by (*) is an overtone of CD₃ asymmetric bending (2δ_asym CD₃) enhanced due to Fermi resonance with intense CD₃ symmetric stretch.⁴⁰

At pD = 0.7 and pD = 6.6 the 2,2,2-d₃-ethylamine cation (CD₃-CH₂-NH₃⁺) shows ν_sCD₃ frequencies of 2135 cm⁻¹ and ν_asCD₃ frequencies of 2250 cm⁻¹ (Fig. 6). In contrast, at pD = 13.3 the ν_sCD₃ vibration of neutral CD₃-CH₂-NH₂ splits in two bands. One remains near ~ 2135 cm⁻¹ while the other downshifts 52 cm⁻¹ to 2083 cm⁻¹. The ν_asCD₃ of the neutral form downshifts ~ 14 cm⁻¹ to 2236 cm⁻¹ and broadens. For 3,3,3-d₃-propionic acid the ν_asCD₃ downshifts ~ 8 cm⁻¹ (from 2245 cm⁻¹ to 2237 cm⁻¹) as the carboxylic acid (pD = 0.7) becomes a carboxylate anion (pD = 6.4 and 13.3).

From these data we conclude that the CD₃ stretches in CD₃-CH₂-NH₂ and CD₃-CH₂-COOD show the pD-induced frequency shifts of about the same magnitude as do the CH₂ stretches, despite the fact that the CD₃ group is not directly attached to the NH₂ or COOH groups. It should be noted, however, that although the CD₃ group is not directly bound to the amine or carboxyl group, it is very close to them; in their equilibrium conformations. The CD₃ deuterium atoms are closer to the carbonyl oxygen or nitrogen lone pairs than are the CH₂ group hydrogens.

In contrast to CH₂ stretching vibrations the CD₃ stretches show no temperature dependence for any pD value for both 2,2,2-d₃-ethylamine and 3,3,3-d₃-propionic acid. In both these compounds the CH₂ group is directly linked to amine or carboxyl groups by a σ-bond while the CD₃ group is only spatially close. This indicates that in order to show a CH₂ stretching frequency temperature dependence the CH₂ group must be directly linked to the amine or carboxyl group.

Theoretical calculations

The effect of carboxyl group orientation on the CH₂ stretching frequencies

The experimental results indicate a dependence of the CH₂ stretching frequencies on carboxyl group orientations. Although in real crystals the range of available conformations is limited because gly prefer to be in planar conformations where ξ is small,⁴¹ theoretical calculations allow us to explore a much broader range of conformations. Thus, we theoretically modeled the conformational dependence of CH₂ vibrations frequencies upon the ξ angle for neutral gly. We fixed the orientation of the nitrogen lone pair with respect to the CH₂ group to rule out any possible impact of the nitrogen lone pair orientation.

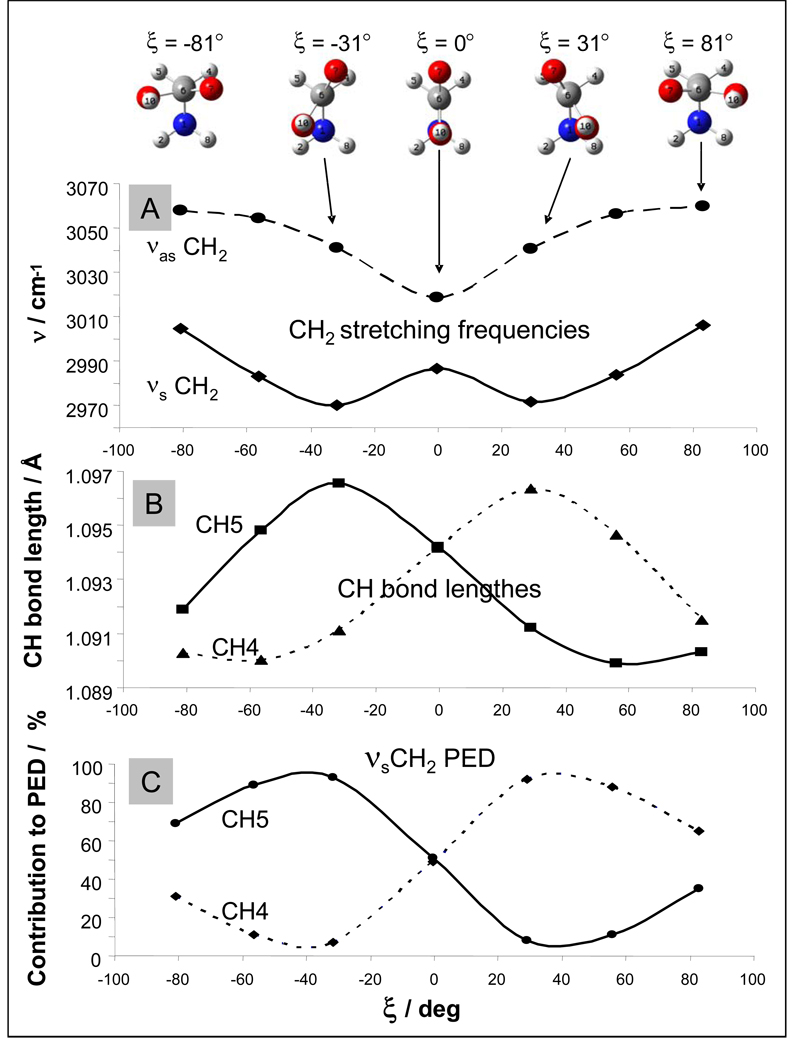
As expected from experiments, our theoretical results show that the ν_asCH₂ and ν_sCH₂ frequencies significantly depend on ξ (Fig. 7A), and these frequencies correlate with the C-H bond lengths (Fig 7B).

Figure 7.

Calculated ξ angular dependence of (A) gly CH₂ stretching frequencies, (B) C-H bond lengths, and (C) normal mode composition (%) of CH₂ symmetric stretch. Frequencies are scaled to 0.98.

For ξ = 0°the C-H bonds symmetrically arrange with respect to the carboxyl group plane and have identical bond lengths (Fig. 7B). This results in the minimum calculated frequency splitting between the ν_asCH₂ and ν_sCH₂ vibrations (Δ_{0°, calc} = 33 cm⁻¹). At ξ = ± 31° one of the C-H bonds is almost perpendicular to the carboxyl plane, while the other lies within the COO plane. These conformations have the maximal frequency splitting between the ν_s and ν_as CH₂ stretching frequencies and the largest differences in C-H bond lengths. At ξ = ± 81° the ν_sCH₂ and ν_asCH₂ frequencies are at their maximum values, both C3-H4 and C3-H5 bonds have their shortest bond lengths and both lie almost within the COO plane (Fig. 7, top).

The normal mode composition indicates that the extent of coupling between the two C-H stretching vibrations depends on the difference in C-H bond lengths. For planar gly (ξ = 0°) with equivalent C-H bonds, both C-H stretching vibrations contribute equally to symmetrical and asymmetrical components of CH₂ stretching (Fig. 7C). At ξ = ± 31°, where the C-H bond length difference is the largest, the coupling is smallest, and each calculated C-H stretching mode is an almost local vibration. The longer the C-H bond length, the more it contributes to the low-frequency symmetric vibration and vice versa.

Our experimental data and our theoretical modeling show that the proximity of the C-H bond to the carboxyl group oxygen results in significant upshift of the corresponding CH stretching frequencies due to C-H bond shortening.

As shown above, the carboxyl group orientation affects the C-H bond length. To study the carboxyl group orientation effect on the gly electronic structure, we calculated the AIM charge distributions for the ξ = 0°, ξ = 31°, ξ = 81° gly conformers. The calculated charge distributions indicate that the C-H bond length decrease results from transfer of electronic density from the carboxyl group oxygen to the nearest methylene hydrogen which decreases the oxygen negative charge and decreases the hydrogen positive charge. The magnitude of this effect depends on the distance between the C=O and C-H bonds. At ξ = 0°, where both hydrogens are equidistant from the COOH plane, the two methylene hydrogens have equal charge (Table 3). At ξ = 81° both hydrogens are closer to the COOH plane than in the ξ = 0° conformer.

Table 3.

AIM charge distributions for selected ξ conformations

	ξ = 0°	ξ = 81°	ξ = 31°
N1	−1.014	−1.001	−1.012
H2	0.366	0.368	0.369
C3	0.365	0.367	0.366
H4	0.052	0.044	0.047
H5	0.052	0.041	0.051
C6	1.503	1.493	1.501
O7	−1.208	−1.199	−1.203
H8	0.366	0.370	0.365
O9	−1.122	−1.121	−1.124
H10	0.641	0.064	0.641

Consequently, the hydrogens will have similar, less positive charges than for the ξ = 0° conformer. In addition, the negative charges on both oxygens are decreased compared to the ξ = 0° conformer. In the ξ = 31° conformer, the hydrogen atom of the C-H bond closest to the COOH plane has less positive charge than does the other, while the negative charge on the oxygen decreases.

Theoretical modeling of the pD dependence of CH₂ stretching frequency. Effect of the amine and carboxyl ionization states and orientations

We calculated the geometry, electronic structure properties, vibrational frequencies and normal mode compositions for a series of gly conformers in neutral and zwitterionic forms in solution. Both neutral and zwitterionic forms were calculated in an implicit solvent with the dielectric constant of water modeled by PCM. PCM was employed to both stabilize the zwitterion which is unstable in gas phase calculations, and to account for the macroscopic effects of water. We calculated neutral gly.

Amine group effect

The nitrogen lone pair impact on the C-H stretching frequencies of organic compounds has been referred to as either the "trans effect of lone pair", “negative hyperconjugation” or “the Bohlmann effect”.^16,42 C-H bonds within the same CH₃ or CH₂ linked to an atom carrying a lone pair of electrons often have different lengths.⁴³ Some C-H bonds are substantially longer which results in large frequency downshifts (up to 150 cm⁻¹). This phenomenon is especially prominent in cases with nitrogen or oxygen lone pair electrons. The specific influence of the lone pair is confirmed by the disappearance of C-H bond lengthening when the lone pair was removed.

It is generally agreed that the trans-C-H bond weakening occurs because of partial transfer of the lone pair electrons to the vacant σ* orbital of the C-H bond.⁴⁴ The stretching frequency of the C-H bond trans to the lone pair is significantly decreased compared to that of the gauche C-H bond.^45,46 It should be noted that “lone pair trans effect” is quite general, also occurring for OH, NH, etc.⁴⁶

Transfer of electronic density to a σ^* orbital is expected to be particularly favored when the acceptor orbital presents a smooth, nodeless character in the region of the donor orbital as do σ^*C-H orbitals. The best donor orbital for such interaction would be a diffuse lone pair nonbonding orbital, such as the nitrogen lone pair. From the shapes of these orbitals, simple consideration suggests that the n-σ^* interaction is optimized in a linear “end-on” arrangement. Thus, the strongest n-σ^* interactions would occur for the C-H bond trans to the lone pair, since this particular orientation gives a linear arrangement of the nitrogen lone pair relative to the C-H antibonding orbital (Fig. 1).

We examined the effect of the nitrogen lone pair on two conformations of neutral gly with different orientations of the CH₂ group relative to the NH₂ group (Fig. 1a). In anti-gly^neut the nitrogen lone pair is gauche to both C-H bonds, where both C-H bonds are approximately equidistant from the lone pair. In contrast, in gauche-gly^neut one of C-H bond (C3-H4) is gauche to the nitrogen lone pair, while the other (C3-H5) is trans. In zwitterionic gly such orientations are not differentiated because of the lack of the nitrogen lone pair.

For neutral gly our calculations show that anti-gly^neut has equivalent C-H bonds, while in gauche-gly^neut the C3-H5 bond trans to the nitrogen sp³ lone pair orbital is significantly elongated, while the other bond is slightly contracted compared to anti-gly^neut (Table 4). In zwitterionic gly both C-H bonds have equal length. The zwitterionic C-H bonds shorten because of the proximity of the positively charged NH₃⁺ group.

Table 4.

Calculated C-H bond lengths, C-H stretching frequencies^†, normal mode compositions, and AIM charge distributions for neutral, zwitterionic gly conformer, and the hydrogen bonded zwitterionic gly-water conformers

		glyneut		gly±			gly±-Water Complexes
		anti-glyneut	gauche-glyneut	eclipsed-gly±	staggered-gly±	twisted-gly±	eclipsed-gly±	eclipsed-gly±	eclipsed-gly±
l(C-H), Å	C-H4	1.096	1.095	1.090	1.091	1.089	1.091	1.090	1.090
	C-H5	1.096	1.101	1.090	1.091	1.091	1.090	1.090	1.091
Freq, cm−1*	νsCH2	2962	2902	3015	3007	3008	3011	3017	3012
	νasCH2	2995	2983	3069	3063	3074	3063	3073	3065
PED, %	νsCH2	C-H5 s (51) C-H4 s (48)	C-H5 s (97) C-H4 s (3)	C-H4 s (50) C-H5 s (48)	C-H5 s (50) C-H4 s (49)	C-H5 s (67) C-H4 s (33)	C-H4 s (55) C-H5 s (44)	C-H4 s (52) C-H5 s (47)	C-H4 s (56) C-H5 s (44)
	νasCH2	C-H4 s (51) C-H5 s (48)	C-H4 s (97) C-H5 s (3)	C-H5 s (51) C-H4 s (49)	C-H4 s (50) C-H5 s (49)	C-H4 s (66) C-H5 s (33)	C-H5 s(55) C-H4 s (44)	C-H5 s(52) C-H4 s (48)	C-H5 s(56) C-H4 s (44)
AIM Charges	N1	−1.013	−1.003	−0.980	−0.962	−0.959	−1.010	−0.979	−1.010
	H2	0.364	0.364	0.468	0.473	0.473	0.455	0.469	0.504
	C3	0.359	0.348	0.244	0.249	0.261	0.250	0.247	0.253
	H4	0.052	0.055	0.083	0.080	0.070	0.073	0.086	0.079
	H5	0.052	0.034	0.083	0.080	0.076	0.076	0.086	0.076
	C6	1.508	1.523	1.654	1.660	1.647	1.648	1.655	1.649
	O7	−1.204	−1.204	−1.257	−1.263	−1.254	−1.261	−1.235	−1.239
	H8	0.364	0.361	0.482	0.472	0.473	0.469	0.481	0.468
	O9	−1.134	−1.128	−1.241	−1.256	−1.257	−1.246	−1.231	−1.236
	H10	0.642	0.641	0.468	0.469	0.473	0.502	0.470	0.456

^†Frequencies are scaled by 0.98

The C-H stretching frequencies differ between anti-gly^neut and gauche-gly^neut. In anti-gly^neut the ν_sCH₂ is calculated at 2962 cm⁻¹, while in gauche-gly^neut this vibration downshifts by 60 cm⁻¹ compared to that in anti-gly^neut. The frequency splitting between the symmetrical and asymmetrical components of CH₂ also differs in these structures. In anti-gly^neut, where both C-H bonds are equal, the split is 33 cm⁻¹, while in gauche-gly^neut the split is a much larger 81 cm⁻¹ (Table 4). Our Raman spectra of gly at pD=13.3 shows a 34 cm⁻¹ spliting between the two CH₂ stretching peaks which agrees well with the frequencies calculated for anti-gly^neut. This suggests that at high pH gly exists mainly in the anti-gly^neut conformation. However, the breadth of both CH₂ stretching bands indicates the existence of additional conformations in solution.

C-H bond length changes impact the coupling between the CH₂ stretching vibrations (Table 4). In anti-gly^neut both C-H bonds contribute equally to the asymmetric and symmetric components. In contrast, in gauche-gly^neut the two C-H vibrations are uncoupled. The high frequency vibration is almost a pure stretch of the shorter C-H bond, while the low-frequency band is almost a pure stretch of the longer C-H bond.

In zwitterion gly the C-H bonds have the same length, but are shorter than in anti-gly^neut. Consequently, both symmetric and asymmetric stretches of CH₂ occur at higher frequencies (Table 4) The zwitterion calculated CH₂ 54 cm⁻¹ frequency splitting is larger than for the anti-gly^neut conformer. We also observe a larger frequency splitting of the CH₂ stretching vibrations at lower pD than at higher pD.

The charge distribution on the CH₂ group (Table 4) indicates that in the zwitterion each C-H bond is more polar than in the neutral form. This increased bond polarity results from the nitrogen negative inductive effect, which shortens the zwitterionic C-H bonds. In anti-gly^neut, the C-H bond lengths and charges on both methylene hydrogens are equal. In gauche-gly^neut, different bond lengths and charge distributions occur. The longest C-H bond hydrogen atom is less positive than the other, whereas the positive charge is almost equal to that in anti-gly^neut. In gauche-gly^neut the decreased hydrogen positive charge indicates an increased electronic density transferred from the nitrogen lone pair, since the nitrogen negative charge is decreased compared to that in anti-gly^neut. The correlation of an increased electronic density with a bond length elongation indicates that the electronic density was accepted by an orbital with non- or anti-bonding character; the NBO analysis shows an increased occupancy of the C-H σ* MO (Table 5). This interaction elongates the corresponding C-H bond resulting in a downshift of the C-H stretching frequency in the gly anion compared to the zwitterion or cation, where the lone pair is removed by protonation. This explains the strong dependence of C-H stretching frequencies on the ionization state of the gly amino group.

Table 5.

NBO calculated occupancies of selected molecular orbitals of methylene, amino, and carboxyl groups in neutral and zwitterionic gly conformers

			glyneut		gly±			gly±-Water Complexes
			anti-glyneut	gauche- glyneut	eclipsed-gly±	staggered- gly±	twisted-gly± ξ=60°	eclipsed-gly± NH3 H2O	eclipsed-gly± COO− H2O	eclipsed gly± NH3 H2O, COO− H2O
MO Occupancy	σ	C-H4	1.964	1.963	1.978	1.976	1.985	1.978	1.978	1.978
		C-H5	1.964	1.969	1.978	1.976	1.979	1.978	1.978	1.978
	σ*	C-H4	0.0157	0.0139	0.0083	0.0096	0.0107	0.0094	0.0083	0.0084
		C-H5	0.0157	0.0287	0.0083	0.0096	0.0096	0.0085	0.0083	0.0094
	LP N		1.950	1.958	N/A
	COO−	LP2 O7	1.863	1.864	1.884	1.885	1.897	1.886	1.874	1.875
		LP3 O9	N/A		1.631	1.616	1.613	1.629	1.825	1.612
		LP2 O9	1.799	1.797	1.872	1.892	1.893	1.876	1.869	1.873
		BD CO7	1.996	1.996	1.996	1.996	1.988	1.996	1.832	1.993
	NH3+	BD N-H2	N/A		1.994	1.993	1.993	1.994	1.994	1.993
		BD N-H8	N/A		1.993	1.994	1.994	1.993	1.993	1.993
		BD N-H10	N/A		1.994	1.994	1.993	1.993	1.994	1.994

The effect of carboxyl group in zwitterionic gly

Comparison of the solution gly Raman spectra measured at pD = 0.7 (cationic form) and pD = 6.3 (zwitterionic form) show that the carboxyl group ionization does not significantly affect the CH stretching vibrations. The frequency shift of both C-H stretching vibrations does not exceed 3 cm⁻¹ (see Table 1). The charge distribution calculated for the ξ = 0° (staggered) and ξ = − 60° (twisted) conformations of gly zwitterion (Table 4) indicates that the C-H bond length decrease is caused by redistribution of electronic density from the C=O bond lying in the same plane with the C-H bond. Analysis of the molecular orbital occupancy (Table 5) shows a significantly increased occupancy of the bonding orbital of the short C3-H4 bond and a decreased O7 lone pair molecular orbital occupancy. The 0.002 Ǻ bond length difference between the C-H bonds of twisted-gly^± prevents coupling between the two CH stretches. PED indicates that two CH stretching frequencies calculated for twisted-gly^± result from almost pure vibrations of the individual C-H bonds, while in staggered-gly^± the CH stretching motions are coupled into symmetric and asymmetric vibrations (Table 4). In twisted-gly^± the C-H bond contraction results in an 11 cm⁻¹ upshift of the high-frequency CH stretch, while the low-frequency CH stretch is equal to that in staggered-gly^±.

Temperature dependence of the CH₂ and CD₃ stretches

As shown above the electronic configuration of the nitrogen atom and spatial orientation of the carboxyl group have a large impact on the neighboring CH₂ bond lengths and stretching frequencies. Hydrogen bonding to -NH₃⁺/-NH₂ and -COOH/-COO⁻ of gly affects the electronic configurations of these groups which, in turn, change the CH₂ bond strengths, which shift the CH₂ stretching frequencies.

To examine the effect of water hydrogen bonding on the C-H frequencies, we calculated the geometries and electronic properties of gly zwitterion (ξ = 0°), the zwitterion with water attached to the NH₃⁺ group and the zwitterion with water attached to the COO⁻ site. We also examined gly zwitterion with waters attached to both NH₃⁺ and COO⁻.

Water hydrogen bonding to the gly -COO⁻ terminus does not change the C-H bond lengths significantly. However, it does result in a slight frequency increase of both the symmetric (2 cm⁻¹) and asymmetric (4 cm⁻¹) C-H stretching vibrations (Table 4). Hydrogen bonding to the NH₃⁺ site elongates both C-H bonds more significantly. As a result, the frequencies of the symmetric and asymmetric C-H stretching vibrations downshift by 4 and 6 cm⁻¹ respectively. Two waters added to COO⁻ and NH₃⁺ groups results in an increase in C-H bond lengths and frequency downshifts of the symmetric (4 cm⁻¹) and asymmetric (6 cm⁻¹) stretches.

The MO occupancy listed in Table 5 shows that the water hydrogen bonded to -NH₃⁺ decreases the electronic density of the N-H bonding orbitals and increases the electronic density of the C-H σ^* orbitals. In contrast, water hydrogen bonding to COO⁻ did not significantly change the C-H bond electronic density (Table 4).

An additional important insight into the origin of the CH₂ stretching temperature induced frequency shifts is evident from the CD₃ stretching frequencies of CD₃-CH₂-ND₂ and CD₃-CH₂-COOD. As shown above, the CD₃ group, which is not directly connected to the amine or carboxyl, does not show any temperature induced frequency shifts but does show a significant dependence on the amine and carboxyl group ionization state. Thus, we conclude that the temperature dependence results from some inductive interaction through σ-bonds.

Our calculations show that water hydrogen bonding to the donor (-NH₃⁺) group downshifts CH₂ stretching frequencies while water hydrogen bonding to the acceptor group (-COO⁻) upshifts CH₂ stretches. The deprotonated amine (-NH₂) and the protonated carboxyl (-COOH) can serve as both hydrogen bond donors and acceptors. Thus, the temperature induced frequency shift of the CH₂ stretches of gly in solution depends on interplay of different hydrogen bonding patterns. However, our experimental and theoretical results show that at the pH values close to neutral, hydrogen bonding to the gly -NH₃⁺ group has dominant effect on the CH₂ stretching frequencies.

CH₂ stretching frequency splitting monitors gly non-planarity

The splitting between ν_sCH₂ and ν_asCH₂ stretching vibrational frequencies should depend less on environment than the frequencies themselves because the splitting depends mostly on C-H bond nonequivalence which depends upon the gly conformation. The actual doublet frequency can depend on the dielectric constant of the medium, hydrogen bonding to the amine/carboxyl groups etc. Such environmental factors will likely shift the frequencies of the symmetric and asymmetric stretches in the same direction without significantly changing the splitting between them. This makes the splitting a more reliable criterion for gly conformational analysis.

For the planar Gly•HCl molecules the calculated and observed splittings between the ν_asCH₂ and ν_sCH₂ vibrations are essentially identical at Δ ~ 33 cm⁻¹. For gly nitrate, Gly•HNO₃, the ξ ~ 21° deviation from planarity results in Δ_{Gly•HNO3 cryst} = 62 cm⁻¹ (Fig. 3), while the calculated ξ = 21° splitting is Δ_{21°, calc} ~ 56 cm⁻¹. For TGS, the splitting between ν_asCH₂ and ν_sCH₂ of the more intense doublet (2982 cm⁻¹ and 3017 cm⁻¹) corresponding to almost planar gly pair is Δ_{TGS, planar} ~ 35 cm⁻¹, which again is very close to the calculated value. In contrast for bent gly the observed value is Δ_{TGS, bent} ~ 45 cm⁻¹ compared to a calculated Δ_{ξ = 19°, calculated} = 53 cm⁻¹. Thus, the splitting between the ν_asCH₂ and ν_sCH₂ stretching frequencies definitely depends upon the relative orientations of the CH₂ and carboxylic groups. The small deviations between calculated and measured CH₂ frequency splitting values in crystals may result from crystal packing forces which distort the gly molecules.

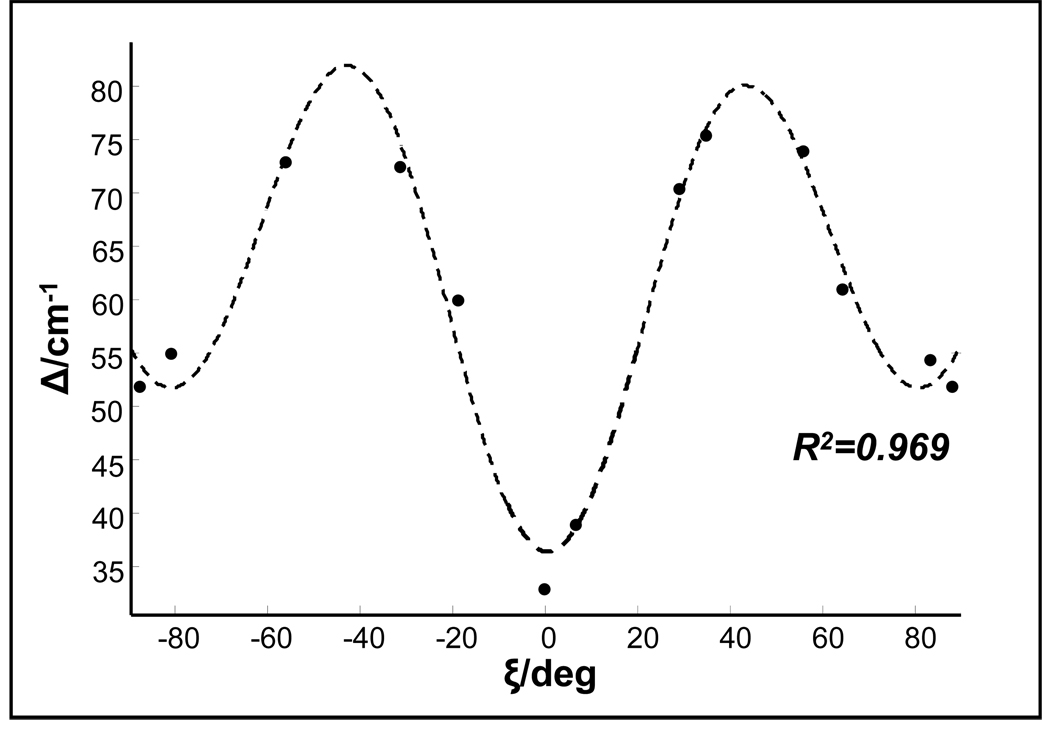
As we have shown both experimentally (Fig. 2) and theoretically (Fig. 7A), the frequency splitting between symmetrical and asymmetrical components of CH₂ stretching depends on the value of ξ angle. Therefore, the frequency splitting (Δ) measured experimentally can be used to determine the ξ angle defined by the gly conformation. Figure 8 shows the frequency splitting calculated for gly conformers versus the ξ angle.

Figure 2.

Raman spectra of the CH stretching region of the crystalline gly hydrochloride (Gly•HCl), crystalline gly nitrate (Gly•HNO₃), crystalline trigly sulphate or TGS (3Gly•H₂SO₄).

Figure 8.

Calculated ξ angular dependence of frequency splitting of the gly CH₂ stretching. The dots represent calculated data points, the dashed line is the Fourier fit to the calculated results. Δ(ξ) = 60 − 10.6cos(0.04ξ) − 4.3sin(0.04ξ) − 21.3cos(0.08ξ) − 3.6sin(0.08ξ)

This correlation describes the frequency splitting change which results from the non-planarity of gly molecule, when the amide group is protonated and the nitrogen lone pair does not affect the CH₂ stretching frequencies.

Conformational preferences of gly in solution

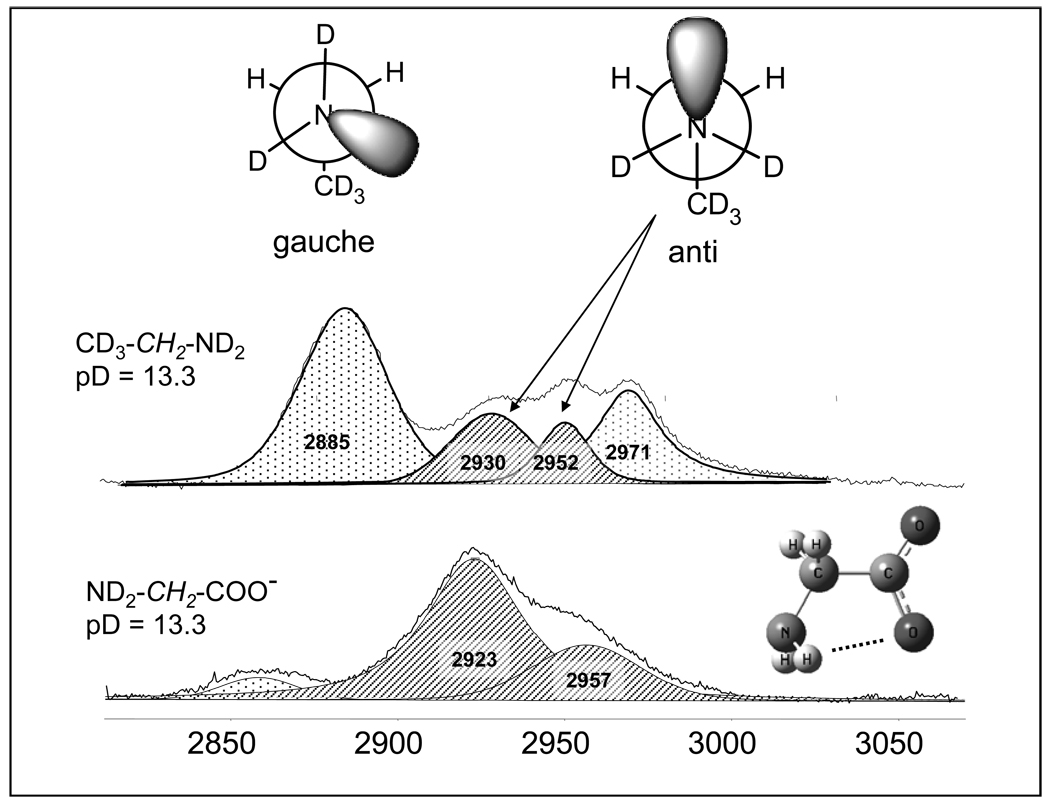
Figure 9 shows Raman spectra of 2,2,2-d₃-ethylamine and gly in solution at pD = 13.3. Two staggered conformations – gauche and anti are populated in solution at room temperature which differ by a rotation about the C-N bond in ethylamine. In the gauche conformation the nitrogen lone pair is trans to a C-H bond which results in elongation of the trans C-H bond due to electron delocalization from the nitrogen lone pair to the C-H anti-bonding σ* orbital which significantly downshifts the C-H stretching frequency by ~ 100 cm⁻¹ to ~2885 cm⁻¹. The other C-H bond is slightly upshifted. Thus, the two most intense, most separated bands at ~2885 cm⁻¹ and ~2971 cm⁻¹ correspond to the uncoupled CH stretches of the gauche conformation of ethylamine. Interaction of the C-H bonds with the lone pair in the anti conformer modestly downshifts both CH stretching vibrations without increasing the frequency splitting between the symmetric and asymmetric components at ~ 2930 cm⁻¹ and 2952 cm⁻¹ are ν_sCH₂ and ν_asCH₂ of anti-ethylamine. Assuming that the areas of the bands are proportional to the population of the ethylamine rotamers in D₂O allows us to calculate that the population of gauche conformers is ~ 71 % and the anti conformer is ~ 29 %. This distribution agrees well with that for n-propylamine in the gas phase as determined from the NH₂ wagging and torsion bands in the IR spectra.⁴⁷

Figure 9.

Fitted Raman spectrum (CH₂ stretching region) of the CD₃-CH₂-ND₂ and ND₂-CH₂-COO⁻ solutions in D₂O at pD = 13.3. Also shown are the two conformations of the ethylamine and for gly⁻ in solution.

In contrast to ethylamine, gly⁻ shows only two bands at ~ 2923 cm⁻¹ (ν_sCH₂) and 2957 cm⁻¹ (ν_asCH₂), with frequencies similar to those for the anti conformation of 2,2,2-d₃-ethylamine. This indicates that the anti-gly⁻ conformer dominates high pD solutions. This anti-conformational preference of gly⁻ in solution may result from bifurcated intramolecular hydrogen bonding between the amine group hydrogens and the carboxylic group oxygen (Fig. 9) Such a hydrogen bond was shown to stabilize gas phase gly conformations^48,49 and gly molecules in inert gas matrices at low temperatures.⁵⁰ Hyperconjugation could also contribute to the increased stability of the gly anti- conformation.⁵¹

Conclusions

We examined the dependence of the CH₂ stretching frequencies of glycine, 2,2,2-d₃-ethylamine and 3,3,3-d₃-propionic acid on conformation, pD and temperature by means of Raman spectroscopy (488 nm excitation) and DFT calculations.

Experimental data show a large dependence of the CH₂ stretching frequencies on the ionization state of the amine group. We theoretically demonstrate that the high sensitivity of the ν_sCH₂ and ν_asCH₂ frequencies on the orientation and ionization state of the amine group results from a negative hyperconjugation between the nitrogen lone pair and anti-bonding C-H orbitals. This effect is maximal when a C-H bond is trans to the lone pair.

The C-H stretching frequency dependence on the carboxyl group ionization state is small, however carboxyl group orientation affects the CH₂ symmetric and asymmetric stretching frequencies as well as their frequency splitting. The magnitude of frequency splitting between the ν_sCH₂ and ν_asCH₂ depends on the relative orientation of the CH₂ and COOH/COO⁻ groups. The calculated conformational dependence of the CH₂ stretches frequency splitting (ν_asCH₂ − ν_sCH₂) agrees well with the experimental data obtained from gly crystals.

According to our experimental observations and theoretical calculations, the temperature dependence of the ν_sCH₂ and ν_asCH₂ of gly in solution is due to the change in hydrogen bonding strength of the amine and carboxyl groups to water. This effect has an inductive mechanism and occurs only for the CH₂ directly connected to amine/carboxyl groups by a σ-bond. The magnitude of the frequency shifts varies with the ionization states of amine/carboxyl groups. At pD values close to neutral, hydrogen bonding to the protonated amine group (-NH₃⁺) is likely to dominate temperature dependence of the CH₂ stretches of gly.

CD₃ stretching of the deuterated methyl of 2,2,2-d₃-ethylamine and 3,3,3-d₃-propionic acid show a significant dependence on the ionization state of the amine and carboxylic groups even though the CD₃ group is separated by a CH₂ group. It appears that the delocalization of the electron density from the amine and carboxyl groups to the CH/CD bonds occurs “through space” and requires interacting groups to be spatially close, but not necessarily linked by a covalent bond. Our results indicate that in D₂O at high pD gly is predominantly in an anti conformation in contrast to 2,2,2-d₃-ethylamine which exists in both anti and gauche conformers.