Conformational diversity and computational enzyme design

Abstract

The application of computational protein design methods to the design of enzyme active sites offers potential routes to new catalysts and new reaction specificities. Computational design methods have typically treated the protein backbone as a rigid structure for the sake of computational tractability. However, this fixed-backbone approximation introduces its own special challenges for enzyme design and it contrasts with an emerging picture of natural enzymes as dynamic ensembles with multiple conformations and motions throughout a reaction cycle. This review considers the impact of conformational variation and dynamics on computational enzyme design and it highlights new approaches to addressing protein conformational diversity in enzyme design including recent advances in multistate design, backbone flexibility, and computational library design.

Introduction

The quest to design enzymatic activity tests both our understanding of the physical origins of catalysis and our ability to find creative strategies to confront the enormous size of protein sequence space. The application of computational protein design technology represents a compelling approach because it offers the benefit of surveying astronomically large numbers of possible amino acid sequences in silico and because it suggests the possibility of a predictive framework for relating protein sequence to catalytic function.

However, the requirement for reasonable calculation time imposes limitations on the accuracy of prediction. Computational protein design methods have typically employed two key conformational approximations to reduce calculation time: the conformation of the protein backbone is fixed and the amino acid side chains are modeled by a set of discrete rotameric configurations[1-5]. The use of fast energy functions to calculate pairwise interaction energies represents a further tradeoff between accuracy and speed [6-9], but the use of pairwise potentials allows search algorithms to efficiently identify optimal amino acid sequences with respect to these energy functions[10,11]. These procedures have proven successful for designing stable proteins[2-5], and they have been extended for enzyme design through incorporation of geometry-based interaction requirements[12-18].

The conformational limitations of the fixed-backbone and rotamer approximations can lead to unpredictable results from oversensitivity to small geometric changes, a problem that has been reduced for the general protein design problem through empirical adjustments to the energy function[19-21]. However, natural enzymes feature numerous interactions with precise geometry and tuned electrostatics, and a balance of conformational sampling and energetic terms chosen for protein stability may not be optimal for stabilization of reaction transition states. While computational enzyme design approaches have used additional constraints to enforce predefined catalytic interaction geometries[12-18], these constraints may contribute to, rather than alleviate, the problems of conformational discretization[14].

This themed issue on conformational diversity and catalytic mechanisms highlights an additional, fundamental limitation of the fixed-backbone approximation in computational enzyme design: evidence continues to emerge that natural enzymes do not behave as single static structures. Kinetic and single-molecule studies have suggested that some enzymes may have multiple long-lived, catalytically-competent conformational states[22-24]. Multiple motions and conformational states may be involved during a reaction cycle to allow substrates to enter, to position substrates and side chains for different reaction steps, and to release products[25,26]. A key element of enzymatic catalysis is the use of binding energy to limit the motions of enzymes and substrates to orientations and conformations where reaction transition states are stabilized[27], and discussion continues over the circumstances and extent to which dynamic motions play additional roles in the catalysis of individual reaction steps[28-30]. Variation of substrate specificity and allostery provide additional important motivations for considering conformational variation[31-33].

This review highlights recent efforts to understand how conformational diversity and dynamics impact computational enzyme design as well as new developments that offer promise for introducing conformational diversity into enzyme design calculations.

Conformation and dynamics of computationally designed proteins

Studies of the structural and dynamic properties of computationally designed proteins have revealed conformational variations—both intended and unintended—that illustrate current issues for control of conformation in protein design.

In cases where x-ray or NMR structures have been obtained for full-sequence computationally designed proteins, there has typically been good overall agreement between design and model, but some variation in side chain placement and local backbone structure[2,34-37]. Dynamic properties of designed proteins have been investigated with NMR methods. Two studies concluded that wild-type and designed proteins displayed similar side-chain and backbone dynamics[35,38], while two other studies attributed differences to imperfect core packing and rotameric strain[39,40]. A recent NMR study of a designed protein G variant concluded that backbone motions on the μs-ms timescale were increased in the designed sequence relative to the natural sequence as a result of overpacking of the hydrophobic core[41].

Large-scale changes in conformation of computationally designed proteins have also been observed. Design methods were used to produce a single protein sequence that could switch between a zinc-binding motif and a helical bundle with changes in pH and Zn²⁺ concentration[42]. This example represents a successful use of simultaneous design for multiple conformational states (see Multi-state computational design) on the scale of the full three-dimensional fold.

In another case, unintended large-scale switching in three-dimensional fold may also have been observed. In this work, two similar thermostable variations of a full-sequence protein redesign were tested experimentally and the solution NMR structure of one showed the intended fold[37]. The other variant was crystallized and surprisingly showed a different fold, a tetrameric four-helix bundle[43]. The crystallization conditions contained 25% dioxane, which was found to increase both helicity and molecular weight[43]. While it remains untested whether a full switch of three-dimensional fold occurred as a result of crystallization solvent, this example illustrates a key complexity of protein design energy functions: they must optimize for fold specificity in addition to thermal stability. As design efforts move toward functional interactions including enzymatic activity, additional energetic and conformational complexities arise.

Conformation and dynamics in de novo designed enzymes

Efforts to use computational design to produce new catalytic sites in previously inactive protein scaffolds have yielded a few successes. Ester hydrolysis, Kemp elimination, and retroaldol cleavage reactions catalyzed by computationally designed active sites have been reported[13,16,17]. Most recently, catalysis of a Diels-Alder reaction has been reported[18]. These enzymes show the potential of computational design, but they also illustrate how much remains unknown. Second-order rate constants (k_cat/K_M) for these enzymes range from about 0.01 to 100 M^-1s^-1, much lower than those of natural enzymes (10⁵ to 10⁹ M^-1s^-1) (Figure 1).

Figure 1.

Activities for computationally designed active sites catalyzing ester hydrolysis[13], retroaldol cleavage[16], Kemp elimination[17], and Diels-Alder cycloaddition (a bimolecular reaction; reported pseudo-second order rate constants for diene with apparent saturation of dienophile are shown)[18]. Kemp eliminases were improved through directed evolution[17,44]; the highest resulting activity is indicated with an asterisk.

Four recent studies have investigated these designed enzymes experimentally[44,45] and computationally[46,47]. For the Kemp elimination designs, directed evolution was used to further improve activity [17,44] (Figure 1), and crystallographic structures were determined for improved variants [44]. These unliganded structures showed changes to the network of interactions that surround the designed catalytic residues as well as some rearrangement of an active site loop relative to the original design, suggesting possible structural origins for the overall 200-fold improvement in k_cat/K_M. A QM/MM computational analysis of the Kemp eliminase design models also suggested possible structural explanations for differences in reactivity among the designs[46]. Both studies of the Kemp eliminases identified that a key area for improvement lies in optimizing the network of side chains that surround and properly position the designed catalytic base.

A computational study performed molecular dynamics simulations of a designed retroaldolase and concluded that the dynamic motions of the enzyme were insufficiently constrained to optimally promote the intended reactive geometries of the proposed catalytic residues and bound substrate[47].

An experimental mechanistic study of the designed retroaldolases compared the designs to related small molecule catalysts in solution[45]. This work suggested that most of the rate acceleration by the best designed enzyme could be accounted for through a combination of shifting the lysine pK_a and hydrophobic binding of the substrate[45]. Specific side-chain contacts intended to stabilize a bound water molecule were found not to contribute to catalysis, and in accord with the molecular dynamics study, investigation of regio- and enantio-selectivity suggested a lack of precision and specificity in binding interactions[45].

These analyses suggest that a major current challenge for computational enzyme design is in limiting conformational diversity of the enzyme-substrate complex. In other words, achieving specificity and precision in binding small-molecule ligands is a preliminary step to design of efficient enzymatic activity that has not yet been established. While an earlier work raised high expectations for computational design of new ligand binding sites, the results from that study have been called into question[48,49]. Rigorous structural and biochemical evaluation of the capabilities of computational design methods to produce specific new ligand-binding sites is needed.

The challenge of designing specific, precise ligand-binding sites is likely to require that design calculations improve upon the fixed-backbone methods used in enzyme designs to date. New methods that seek to introduce conformational diversity into design calculations have great potential to improve the success and reliability of active site and ligand-binding site design.

Multi-state computational design

Multi-state computational design methods allow selection of a single amino acid sequence that simultaneously satisfies multiple design objectives. A typical application of multi-state design has been the variation of interaction specificity through a combination of positive design for the desired state and negative design against an undesired state. A few examples include computational alteration of specificity for coiled-coil dimers[50], protein-ligand binding interactions[51], and protein-protein interfaces[52]. Multi-state computational design methods are well suited to designing substrate specificity, stereospecificity, or even catalytic specificity through the combination of positive and negative design.

New directions for treating conformational diversity have been opened up by the recent development of search algorithms for efficient optimization with respect to large numbers of objective states (Figure 2). A multi-state design algorithm based on the efficient FASTER method[11,53] was tested in experiments that designed sequences with respect to ensembles of 128 different target backbone templates[54]. In this work, the use of multi-state design in conjunction with a template backbone ensemble constructed from constrained molecular dynamics simulations yielded improved results in a large-scale experimental test of protein stabilities. In a different approach, a cluster-expansion method[55] was used for simultaneous design with many states to introduce backbone conformational diversity[56] and to perform negative design for specificity[57], although de novo active site design may be a more difficult application of this approach. By allowing simultaneous design for large ensembles of backbone conformations, these new methods offer promising routes to relieving problems of the fixed-backbone approximation and they may enable new strategies, such as designing sequences consistent with moveable active-site loops for substrate entry.

Figure 2.

Approaches for computational protein design. Multi-state design methods allow design of a single optimized sequence with respect to multiple backbone conformations. Iterative approaches to backbone flexibility alternate between design steps, where side chain identities are allowed to vary, and backbone optimization steps, where conformation is optimized for a given amino acid sequence.

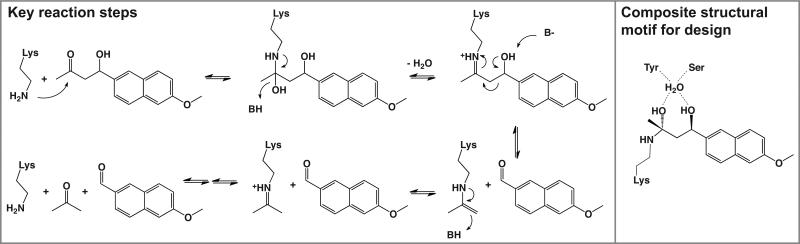
Multi-state design methods offer additional potential for addressing conformational variation in enzyme design through improved modeling of multistep reaction mechanisms. To date, reported successes in de novo computational enzyme design have used only single-state design with composite structural motifs representing all transition states and ground states during multistep reaction pathways[13,16-18] (Figure 3) In the future, the use of multistate design to simultaneously model transition states for key individual reaction steps may allow for greater precision in defining specific interactions. A multi-state approach with negative design could offer additional benefit for relieving tight product inhibition as has been observed in computationally designed retroaldolase enzymes[16,45].

Figure 3.

Example of the use of a single structural motif to represent key ground states and transition states. The multistep reaction pathway is catalyzed by retroaldolase enzymes that were designed using the composite structural motif shown[16].

Incorporation of backbone flexibility

Flexible-backbone methods have also been developed to introduce conformational complexity into protein design calculations. These include the use of iterative cycles of backbone relaxation and side-chain design (Figure 2) as well as generation of local backbone perturbations. These approaches can add improved reliability to modeling and they allow utilization of backbone conformation for enhanced binding specificity[58,59]. Computational de novo active site design examples to date have not made use of flexible-backbone methods[13,16-18], but flexibility has been included in efforts to vary substrate specificity in existing natural enzymes. Flexible-backbone methods have recently been reviewed[58,59], so only the most recent applications to enzyme specificity are highlighted here.

Computational design methods were used to alter the substrate specificity of gramicidin S synthetase A phenylalanine adenylation domain, yielding a 2200-fold increase in specificity for the target Leu substrate[60]. About 5-fold of this specificity increase arose from steps to vary selected residues beyond the active site in the context of backbone flexibility. In another approach, an iterative process including backbone perturbation was used to identify mutations to three amino acid positions of a xylose reductase to increase specificity for NADH over NADPH by 10⁴-fold[61].

Two new approaches were described for handling backbone loop remodeling in the context of the types of geometrical restrictions needed for binding and catalytic interactions. One approach defines a library of specific, favorable ligand-sidechain interaction motifs, and then performs cycles of backbone loop variation and motif incorporation to find compatible combinations of backbone loop structures and interaction motifs[62]. A related approach defines required interaction geometries between sidechains and ligands[63]. A series of loop-building steps are performed to find backbone conformations compatible with these contacting side chains, and then fixed-backbone design is used to populate the loop with side chains. This latter procedure was used to produce a change in specificity of 10⁶-fold in a guanine deaminase for ammelide over guanine[63].

Multi-state design and flexible-backbone methods offer complementary routes for incorporation of conformational diversity into enzyme design calculations (Figure 2). These methods show potential for improved active site design through better sampling of conformational space, and they allow new strategies for increased binding specificity. In the future, these methods might enable more dramatic approaches to enzyme design, including consideration of protein motions, explicit design for catalytic promiscuity, or designed catalysis of multiple individual reaction steps.

Computational library design: Reducing the impact of limitations

Given the current limitations imposed by both limited conformational sampling and energy functions, a reasonable question is the extent to which present design methods can quantitatively predict energetic changes. This question was recently highlighted in a comparison of experimental and calculated free energy changes for folding upon mutation (ΔΔG) with several energy functions[64]. Comparing the effects of 2156 single mutations, the study found that the general trend of the data could be predicted, but correlation between experimental and calculated energies with design energy functions was poor, with correlation coefficients as low as 0.26. While there are necessary differences between energy functions for protein design and for energetic calculations[6-9,19-21], the reality is that there is little expectation of strong quantitative correlation between design energies and catalytic activities with current enzyme design methods.

Acknowledging these limitations in quantitative predictive power, design groups have developed procedures to use the sequence and energetic information from protein design to produce libraries of designed sequences for screening and selection[54,65-69]. This approach takes the view that computational design can efficiently enrich sequence space for functional variants even when quantitative energetic prediction is limited. In recent work, a computational library design algorithm was described that optimizes the extent to which the library reflects the list of energetically ranked sequences, allowing a more direct linkage between calculated energies and the output library[54]. The procedure was used in a large-scale test of stabilities of proteins designed using multi-state methods.

Given the special challenges of conformational sampling and energetic modeling for active site design, computational library design may prove especially valuable in future computational enzyme design efforts.

Conclusions

Many crucial questions remain unanswered in computational protein design, including the optimal balances of computational speed and accuracy in energetics and conformational sampling. Recent successes in de novo design of enzymatic activity show the potential of computational enzyme design methods, but these successes do not indicate that the methods have reached a high level of quantitative predictive capability for enzymatic activity. Investigations of computationally designed proteins and enzymes suggest that a critical challenge is in imparting specificity and precision in binding interactions with substrate, as well as in the network of interactions that position catalytic side chains.

New methods that incorporate conformational diversity are likely to help in achieving this goal, first, by relieving problems associated with fixed-backbone protein design, and second, by allowing more precise definition of interactions with transition states relative to products and substrates. Negative design and backbone flexibility can allow better design for substrate specificity or promiscuity. Methods for computational design of targeted protein libraries can help to reduce the impact of existing limitations. Along with energy function improvements, these new developments are important steps toward the long-term goal of reliable enzyme design.