Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Oct 13.
Published in final edited form as: J Am Chem Soc. 2010 Oct 13;132(40):14092–14103. doi: 10.1021/ja1036644

Bimetallic Reductive Elimination from Dinuclear Pd(III) Complexes

David C Powers 1, Diego Benitez 1, Ekaterina Tkatchouk 1, William A Goddard III 1, Tobias Ritter 1,✉
PMCID: PMC2954233  NIHMSID: NIHMS238678  PMID: 20858006

Abstract

In 2009, we reported C–halogen reductive elimination reactions from dinuclear Pd(III) complexes and implicated dinuclear intermediates in Pd(OAc)2-catalyzed C–H oxidation chemistry. Herein, we report results of a thorough experimental and theoretical investigation of the mechanism of reductive elimination from such dinuclear Pd(III) complexes, which establish the role of each metal during reductive elimination. Our results implicate reductive elimination from a complex in which the dinuclear core is intact and suggest that redox synergy between both metals is responsible for the facile reductive elimination reactions observed.

Introduction

Metal-metal redox cooperation during catalysis can potentially lower activation barriers of chemical transformations and thus allow access to reaction pathways that are difficult to access with mononuclear catalysts.1 Redox chemistry of multinuclear complexes has been intensely studied, in part due to potential advantages in catalysis; however, metal-metal cooperation during redox chemistry has been difficult to establish. Mononuclear Pd(IV) complexes have been suggested as intermediates in palladium-catalyzed C–H oxidation reactions since 1971.2 In 2009, we proposed dinuclear Pd(III) intermediates in catalysis as an alternative to Pd(II)/Pd(IV) redox cycles.3 In a preliminary study of C– Cl reductive elimination from the dinuclear Pd(III) complex 1 (eq 1), we were unable to establish whether reductive elimination proceeded with simultaneous, co-operative redox participation of both metals, or via one-centered redox chemistry. Herein, we report a detailed investigation of the mechanism of C–Cl reductive elimination from 1 and present a tool for evaluating metal-metal synergy during redox transformations of multinuclear complexes. Our results implicate synergistic redox chemistry of both metals during reductive elimination, which leads to an energetic advantage as compared to related monometallic reductive elimination reactions. This analysis is the first detailed evaluation of reductive elimination from Pd(III) and, more importantly, gives insight into evaluating and understanding metal-metal redox synergy in general.

graphic file with name nihms238678f18.jpg (1)

Redox catalysis in synthesis is often accomplished by homogeneous, mononuclear catalysts.4 Oxidative addition and reductive elimination, two of the fundamental redox transformations of organometallic chemistry, have been well studied for mononuclear complexes. Oxidative additions are reactions in which the oxidation state and coordination number of a transition metal center increase by two upon addition of a small molecule.5 Oxidative addition can proceed via concerted,6 SN2-like,7 and radical8 mechanisms. Reductive elimination – formally the reverse of oxidative addition – describes a transformation in which the oxidation state and coordination number of a metal are reduced by two with concurrent formation of a small molecule. Like oxidative addition, reductive elimination can proceed via various mechanisms.9 In a catalytic cycle, the mechanisms of oxidative addition and reductive elimination need not be the microscopic reverse of one another.

Redox chemistry in biology10 and heterogeneous catalysis11 often occurs at multinuclear sites. For example, biologically relevant redox catalysis, such as the reduction of dinitrogen by nitrogenase10a,b and the oxidation of methane by methane monooxygenase,10c,d,e is frequently accomplished by multinuclear active sites. While redox catalysis involving more than one metal is frequently encountered, it is difficult to ascertain the specific role of each individual metal center during a redox transformation.

The mechanisms of redox transformations at multinuclear complexes are less understood than the corresponding reactions of mononuclear complexes.12 Stoichiometric oxidative addition13 to, and reductive elimination14 from dinuclear complexes has been observed, and dinuclear intermediates have been proposed as intermediates in catalysis.3,15 The potential of utilizing metal-metal redox synergy to accomplish challenging transformations has long been recognized and while mechanism proposals involving metal-metal cooperation have been posited,16 identification of the intimate role of each metal center during redox transformations at dinuclear complexes is difficult to establish experimentally.14i,j,k,17 Understanding how metal-metal redox synergy can be used in catalysis requires insight into the role of each metal during redox chemistry.

During our efforts to utilize metal-metal redox synergy in catalysis, we found it useful to employ a two-tiered nomenclature scheme in which organometallic redox transformations are classified by both the nuclearity of the complex undergoing the redox transformation as well as the metallicity of the transformation. Nuclearity is a descriptor of structure and refers to the number of metal centers present in the complex undergoing the redox transformation. Metallicity is a descriptor of the mechanism of a redox transformation and refers to the number of metal centers that undergo redox chemistry coupled to substrate oxidation or reduction. The presence of multiple metal centers (nuclearity) in a redox transformation does not necessitate redox participation (metallicity) of all metal centers.

  • Nuclearity – descriptor of structure; the number of metal centers in a complex undergoing a redox transformation.

  • Metallicity – descriptor of mechanism; the number of metal centers that participate in redox chemistry during a redox transformation.

One can, in principle, determine the nuclearity of a redox transformation using the tools of reaction kinetics. For example, fragmentation of a dinuclear complex into two identical mononuclear complexes prior to reductive elimination can afford a half-order rate law with respect to the dinuclear transition metal complex.18 While redox transformations that take place at mononuclear complexes are by definition monometallic,19 redox transformations at dinuclear complexes can be either mono- or bimetallic depending on whether one or both metals change their oxidation state in the redox transformation. Differentiating between mono- and bimetallic mechanisms is experimentally challenging.

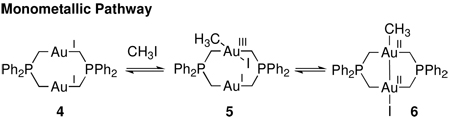
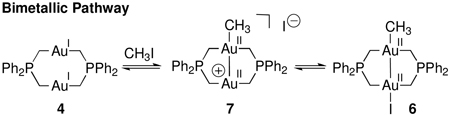
Mono- and bimetallic transformations are kinetically indistinguishable, because the transition states do not differ in chemical composition but only in specific roles of the metal center in the dinuclear core. Further, the identity of the transition metal fragment produced by a redox transformation is not sufficient to assign the metallicity of a given reaction. For example, the oxidative addition of MeI to dinuclear Au(I) complex 4 to afford dinuclear Au(II) complex 6 illustrates the difficulty in assigning the metallicity of a redox transformation.13d,f,h If oxidative addition proceeds initially at a single Au site to afford the Au(I)/Au(III) mixed valence species 5, before comproportionative isomerization to complex 6, the oxidative addition to 5 is monometallic (eq. 2). Alternatively, if oxidative addition proceeds with Au–Au bond formation concurrent with Au–C bond formation to form 6 via 7 (eq. 3), the redox transformation is bimetallic.

graphic file with name nihms238678f19.jpg (2)
graphic file with name nihms238678f20.jpg (3)

Development of catalysis concepts that rely on metal-metal synergy during redox transformations requires fundamental understanding of the role of each metal involved in the redox transformation. Potentially, metal-metal cooperation during catalysis could allow development of reactions that are difficult to accomplish with monometallic systems. We have sought to evaluate the potential advantage of utilizing two metals during redox chemistry in desirable – but currently challenging – transformations. Transition metal-mediated halogenation reactions are difficult and only a few methods are available.21 Reductive elimination from dinuclear Pd(III) complexes is facile and provides a venue to better understand and characterize reductive elimination from dinuclear complexes.3 Herein, we provide evidence for synergistic redox participation of both palladium centers during reductive elimination and show that bimetallic reductive elimination is more facile than related monometallic processes. The observed facility of redox transformations at bimetallic Pd(III) complexes challenges the previously proposed generality of Pd(II)/Pd(IV) redox cycles.22

Results

Two fundamental questions are addressed in this manuscript. First, does C–Cl reductive elimination from 1 proceed from a mono- or dinuclear complex? Second, do both metals participate in the redox chemistry of reductive elimination? The redox activity of each metal is difficult to evaluate experimentally; no experimental observable can be directly correlated with reaction metallicity. We have thus pursued a computational investigation of reaction metallicity. The computational model used to assay metallicity was benchmarked by comparing the computed mechanism with three experimental observables: 1) the ground state structure of 1, 2) the activation parameters for C–Cl reductive elimination from 1, and 3) the ability of computed charge distributions to correlate with experimentally obtained ρ-values from Hammett analysis.

Synthesis and Structure of Pd(III) Dichloride 1

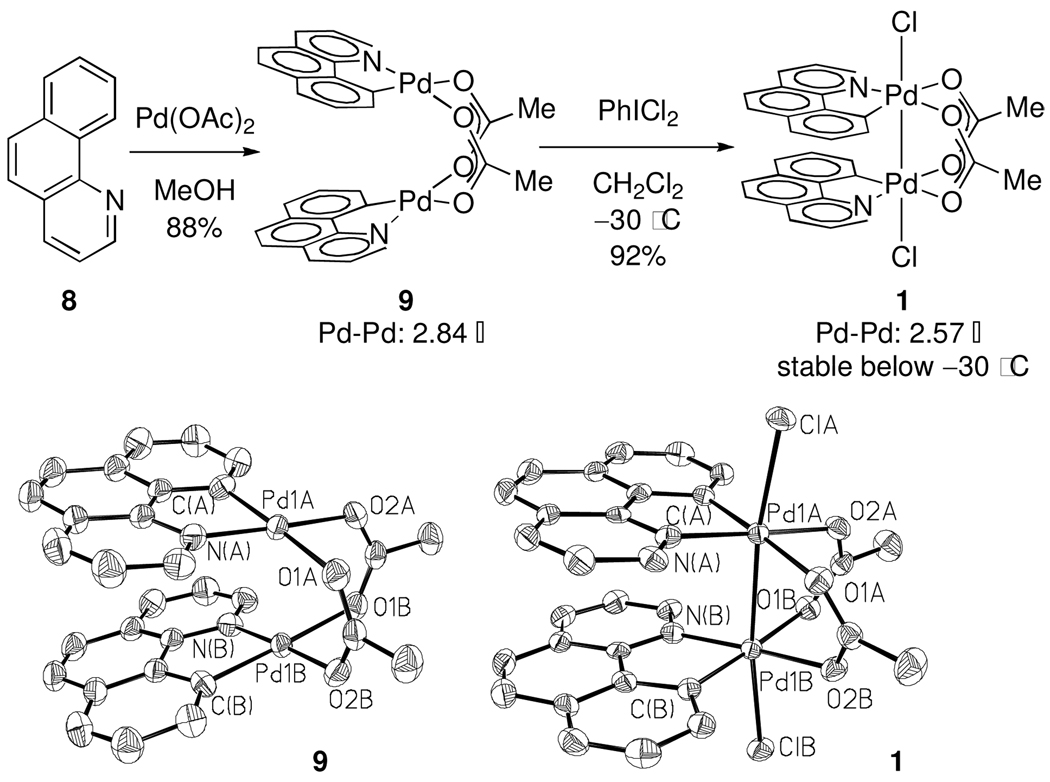
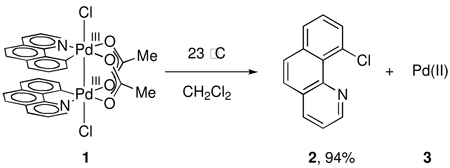
Dinuclear Pd(III) complex 1 was chosen as a suitable substrate to investigate reductive elimination from dinuclear Pd complexes for two reasons. First, Pd(OAc)2 is frequently used as a catalyst in directed C–H oxidations. Second, the bridging acetate ligands hold the two palladium centers in proximity, and therefore allow for metal-metal interaction.23 Treatment of complex 9, derived from cyclometallation of benzo[h]quinoline (8) with Pd(OAc)2, with PhICl2 resulted in the formation of dinuclear Pd(III) dichloride 1 in 92% yield (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Synthesis of 1. ORTEP drawing of 9 and 1 with ellipsoids drawn at 50% probability (hydrogen atoms omitted for clarity). Selected bond lengths in 1 [Å]: Pd(1A)–Pd(1B), 2.5672(5); Pd(1A)–Cl(A), 2.4167(10); Pd(1A)–C(A), 2.000(4); Pd(1A)–O(1A), 2.133(3); Pd(1A)–O(2A), 2.042(3); Pd(1A)–N(A), 2.016(3). For comparison, the Pd–Pd distance in 9 is: 2.8419(8) Å.

By 1H NMR spectroscopy, complex 1 is diamagnetic, consistent with a Pd–Pd single bond. At −50 °C, the 1H NMR spectrum displays eight non-equivalent aromatic resonances and a single resonance for the bridging acetate ligand at 2.69 ppm. In the solid-state, the Pd–Pd distance in 1 is 2.5672(5) Å, 0.27 Å shorter than the corresponding distance in 9, consistent with the formation of a Pd–Pd bond upon oxidation.24 The Pd–O bonds are nonequivalent; the Pd–O bond trans to the carbon ligand is 2.133(3) Å and the Pd–O trans to the nitrogen ligand is 2.042(3) Å, consistent with the stronger structural trans effect of the aryl ligand as compared to the substituted pyridine ligand.25

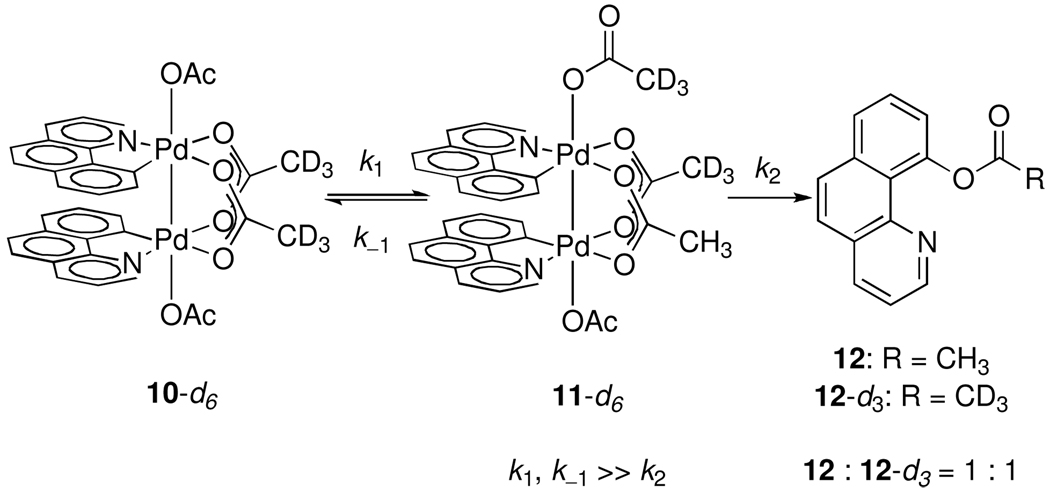
Potential ligand fluxionality, in which the apical and bridging ligands might exchange with one another, was probed by variable temperature NMR of dinuclear Pd(III) tetraacetate 10-d6, in which the bridging acetate ligands were perdeuterated. At −60 °C, the 1H NMR spectrum of 10-d6 displayed a single 1H NMR resonance at 1.48 ppm (apical acetate). Upon warming to −30 °C, the integration of the signal at 1.48 ppm (apical acetate) decreased with concurrent development of a new resonance at 2.71 ppm (bridging acetate). Acetate scrambling was determined to be fast relative to reductive elimination; warming a sample of 10-d6 to 23 °C afforded a 1:1 mixture of 12 and 12-d3 (Scheme 1).26

Scheme 1.

Scheme 1

Open in a new tab

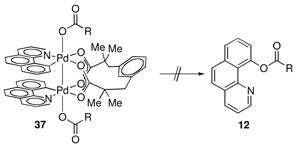
Rapid exchange between bridging and apical acetate ligands leads to a 1:1 mixture of 12 and 12-d3 upon thermolysis of 10-d6.

C–Cl Reductive Elimination from 1

Upon warming complex 1 to 23 °C, 10-chlorobenzo[h]quinoline (2) was isolated in 94% yield based on 1 (eq 1). Monitoring the thermolysis of 1 by 1H NMR spectroscopy established that both decomposition of 1 as well as formation of 2 obey first-order rate laws. The activation parameters of C–Cl reductive elimination were determined to be ΔH‡ = 17.2 ± 2.7 kcal·mol−1, ΔS‡ = −11.2 ± 9.4 cal·K−1, ΔG‡298 = 20.5 ± 0.1 kcal·mol−1 by monitoring the evolution of 2 as a function of temperature (between 5–35 °C). The rate of reductive elimination was unaffected by exogenous chloride (up to 17.1 mM in n-Bu4NCl; 1.17 equivalents with respect to 1) and acetate (up to 11.8 mM in n-Bu4NOAc; 0.81 equivalents with respect to 1).

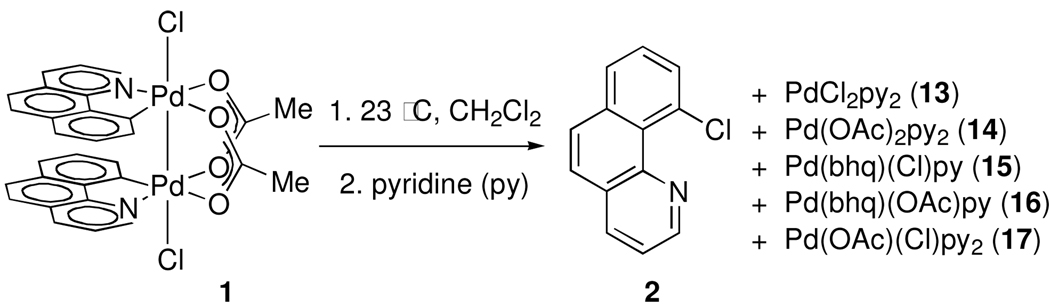
Reductive elimination of 2 from 1 is accompanied by the formation of a mixture of Pd-containing products (3). Treatment of the crude reaction mixture after reductive elimination with excess pyridine provided a mixture of 2 and five palladium-containing species, identified as Pd(II) complexes 13, 14, 15, 16, and 17 based on comparison of the 1H NMR spectrum of the mixture with the 1H NMR spectra of authentic samples (Scheme 2). By 1H NMR, the combined yield of complexes 13, 14, 15, 16, and 17 was determined to be 99%. The observed products of reaction with pyridine establish that the oxidation state of Pd in 3 is +(II). The exact structure of the Pd(II) complex immediately after reductive elimination is unknown (see Supporting Information for further discussion of the identity of the Pd-containing byproducts of reductive elimination).

Scheme 2.

Scheme 2

Open in a new tab

Treatment of the reaction mixture after reductive elimination with excess pyridine affords a mixture of 2, 13, 14, 15, 16 and 17 which establishes the +(II) oxidation state for palladium.

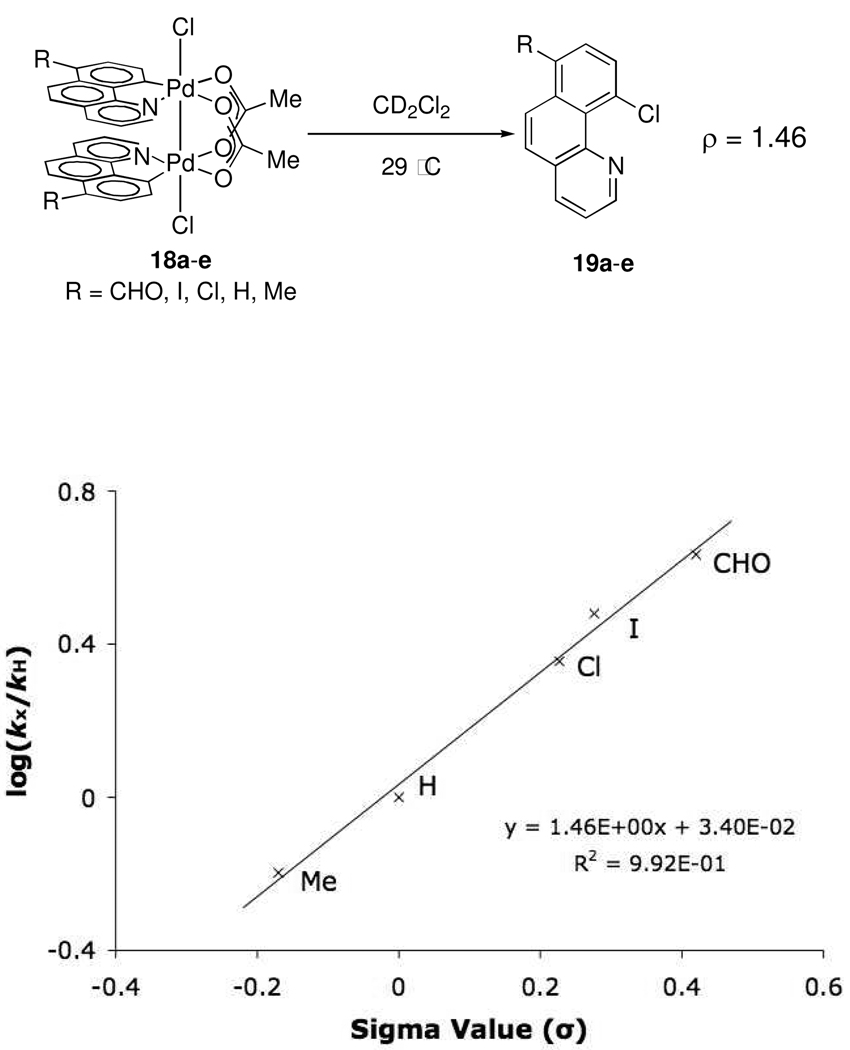
Effect of 7-substitution of the benzo[h]quinolinyl ligand on the rate of C–Cl reductive elimination

Dinuclear Pd(III) dichloride complexes 18a–e with 7-substituted benzo[h]quinolinyl ligands were prepared by cyclometallation of 7-substituted benzo[h]quinolines with Pd(OAc)2 followed by oxidation with PhICl2. Dinuclear Pd(III) complexes with NO2 (18f) and CN (18g) substituents were not sufficiently soluble to be used in kinetics experiments. Thermolysis of 18a–e at 29 °C afforded 7-substituted-10-chlorobenzo[h]quinolines 19a–e in 84–95% yield. Reaction yields did not correlate with the σ values of the substituents. In all cases, C–Cl bond formation was observed exclusively; C–O reductive elimination to afford 7-substituted-10-acetoxybenezo[h]quinolines was not detected. The rate of C–Cl bond formation was measured by monitoring the formation of 19a–e by 1H NMR spectroscopy. The Hammett plot27 generated from this data (Figure 2) shows that C–Cl reductive elimination from dinuclear Pd(III) complexes is accelerated by electron withdrawing 7-substituents on the benzo[h]quinolinyl ligand (ρ=1.46).

Figure 2.

Figure 2

Open in a new tab

Hammett plot based on 7-benzo[h]quinolinyl substitution.

Effect of Bridging Carboxylate Ligand on the Rate of C–Cl Reductive Elimination

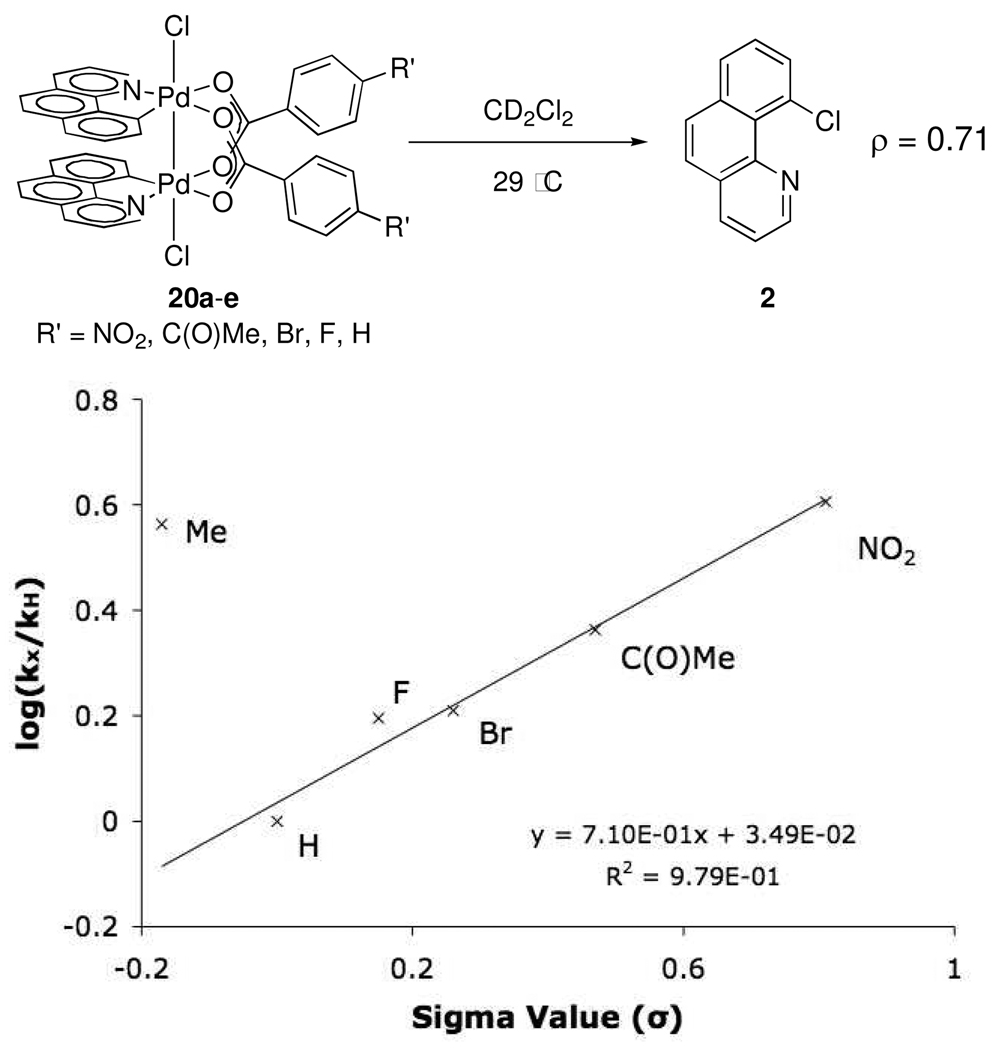
Benzoate-bridged dinuclear Pd(III) complexes 20a–e were prepared by treatment of 9 with 4-substituted benzoic acids at reduced pressure followed by oxidation with PhICl2. Decomposition of 20a–e at 29 °C afforded compound 2 in 91–96% yield with no C–O reductive elimination observed in any case. The Hammett plot27 (Figure 3) generated from this data shows that reductive elimination is accelerated by electron-withdrawing substituents on the bridging carboxylate ligands (ρ = +0.71). For complexes 20f (R = Me) and 20g (R = OMe), bearing electron-donating substituents, log(kx/kH) was not linearly correlated with the substituent σ-values.

Figure 3.

Figure 3

Open in a new tab

Hammett plot based on bridging benzoate substitution.

Competitive Reductive Elimination of Substituted Benzoate Ligands

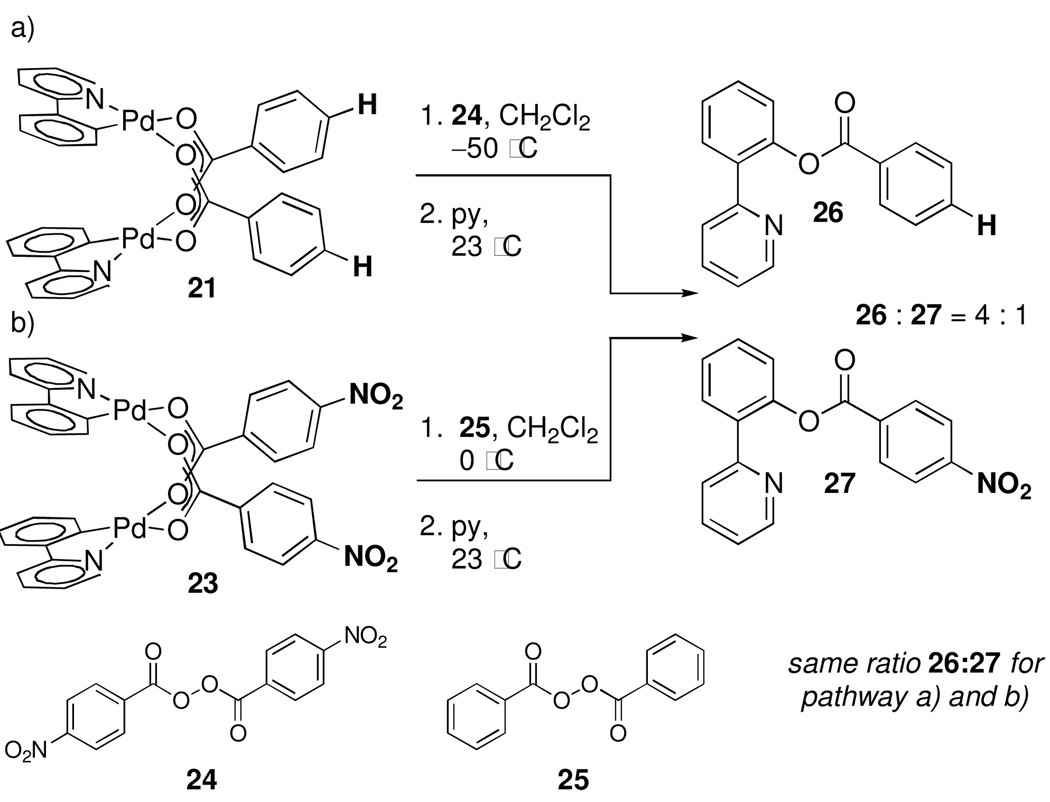
Because the electronic properties of chloride cannot be altered, the electronic demand of the apical ligand during reductive elimination from 1 cannot be investigated. Dinuclear Pd(III) tetrabenzoates were selected as substrates to probe the electronic demand of the apical ligand during reductive elimination because the electronic properties of benzoate ligands can be modified (Scheme 3).26 In the following experiments, the 2-phenylpyridyl ligand was used in lieu of the benzo[h]quinolinyl ligand because 2-(pyridin-2-yl)phenyl benzoate is more stable towards hydrolysis than benzo[h]quinolin-10-yl benzoate, which simplified product isolation and analysis. Further, pyridine is added to the dinuclear Pd(III) complexes prior to thermolysis because we have previously observed that in the absence of pyridine, the products of C–O reductive elimination can react with the palladium-containing byproducts of reductive elimination.3b

Scheme 3.

Scheme 3

Open in a new tab

Carboxylate scrambling on Pd(III) complexes is fast relative to C–O reductive elimination.

Oxidation of Pd(II) benzoate 21 with p-nitrobenzoyl peroxide (24) afforded Pd(III) complex 22, which, after subsequent warming to 23 °C in the presence of 20.0 equivalents of pyridine, afforded a 4:1 mixture of 26 and 27 as determined by both 1H NMR spectroscopy as well as isolated yields of 26 and 27 (Scheme 3a). Oxidation of para-nitrobenzoate bridged complex 23 with benzoyl peroxide (25) also afforded a 4:1 mixture of 26 and 27 (Scheme 3b), which confirmed that carboxylate exchange is fast relative to C–O reductive elimination.

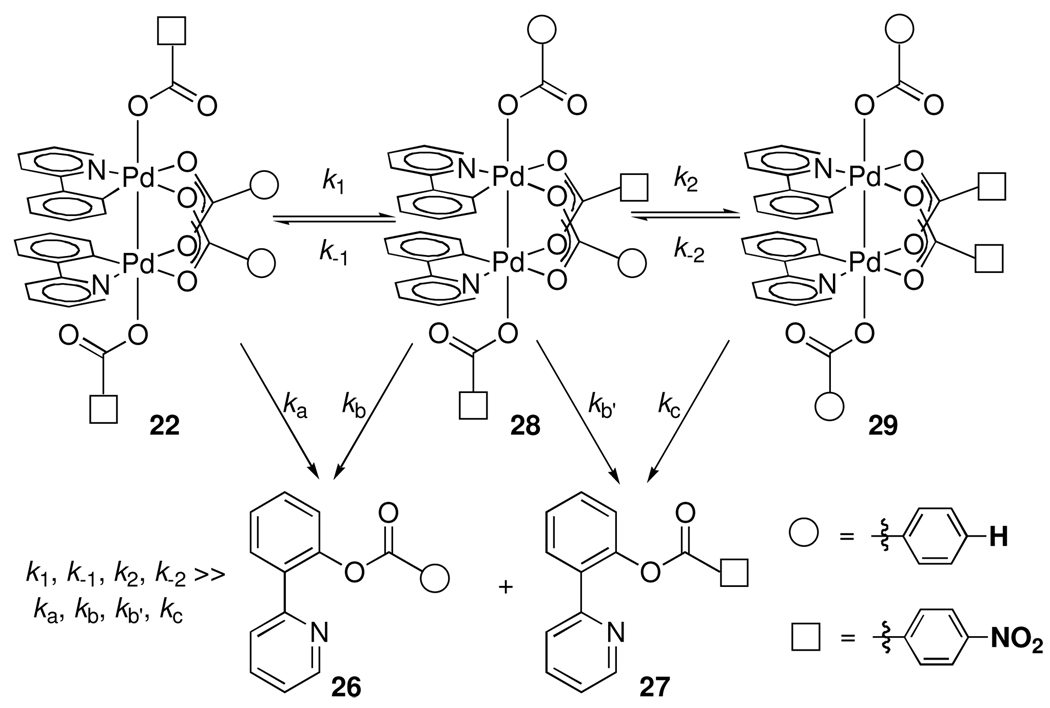
Intramolecular carboxylate exchange in tetrabenzoate dipalladium(III) complex 22 could generate an equilibrium mixture of three isomers (Scheme 4).26 Reductive elimination from isomer 28 can afford either 26 or 27, while reductive elimination from 22 or 29 can afford only 26 or 27, respectively. Without knowledge of all four product-forming rate constants, the ratio of 26 and 27 cannot be deconvoluted to provide kb/kb’, the relative rate of benzoate over 4-nitrobenzoate reductive elimination.28

Scheme 4.

Scheme 4

Open in a new tab

Carboxylate scrambling on Pd(III) complexes prevents Hammett analysis of electronic demand of apical ligands.

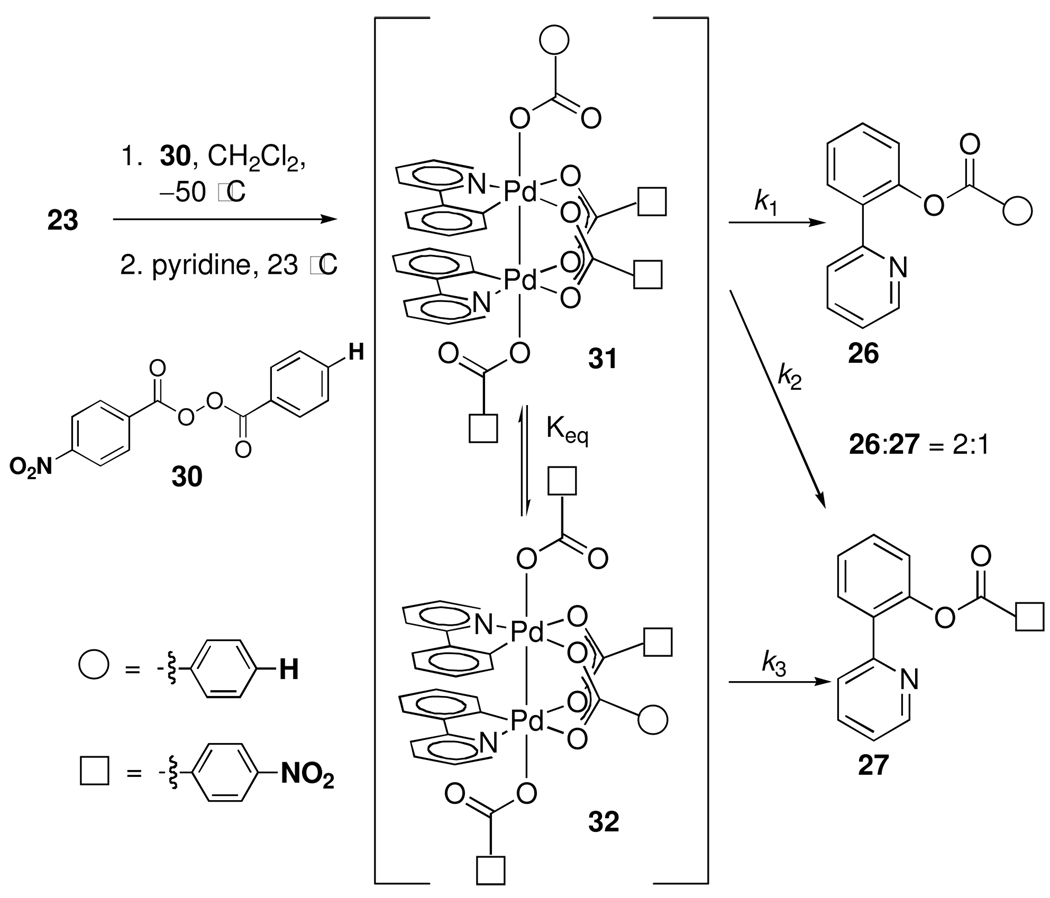
Oxidation of 23 with unsymmetrical peroxide 30 at −50 °C followed by treatment with pyridine at 23 °C afforded a 2:1 mixture of 26 and 27 (Scheme 5).26 Intramolecular carboxylate exchange in dinuclear Pd(III) complex 31, which features three 4-nitrobenzoate and one benzoate ligand, could generate either one of two isomers (31 or 32). Reductive elimination from 32 can afford only 27 (k3) while reductive elimination from 31 can afford 26 (k1) and 27 (k2). The observed 2:1 ratio of 26 and 27 shows that k1 > k2 + k3·Keq and that benzoate undergoes reductive elimination faster than 4-nitrobenzoate.

Scheme 5.

Scheme 5

Open in a new tab

Oxidation of 23 with unsymmetrical peroxide 30 affords a 2:1 mixture of 26 and 27, which establishes the kinetic preference for reductive elimination of more electron-rich benzoate ligands.

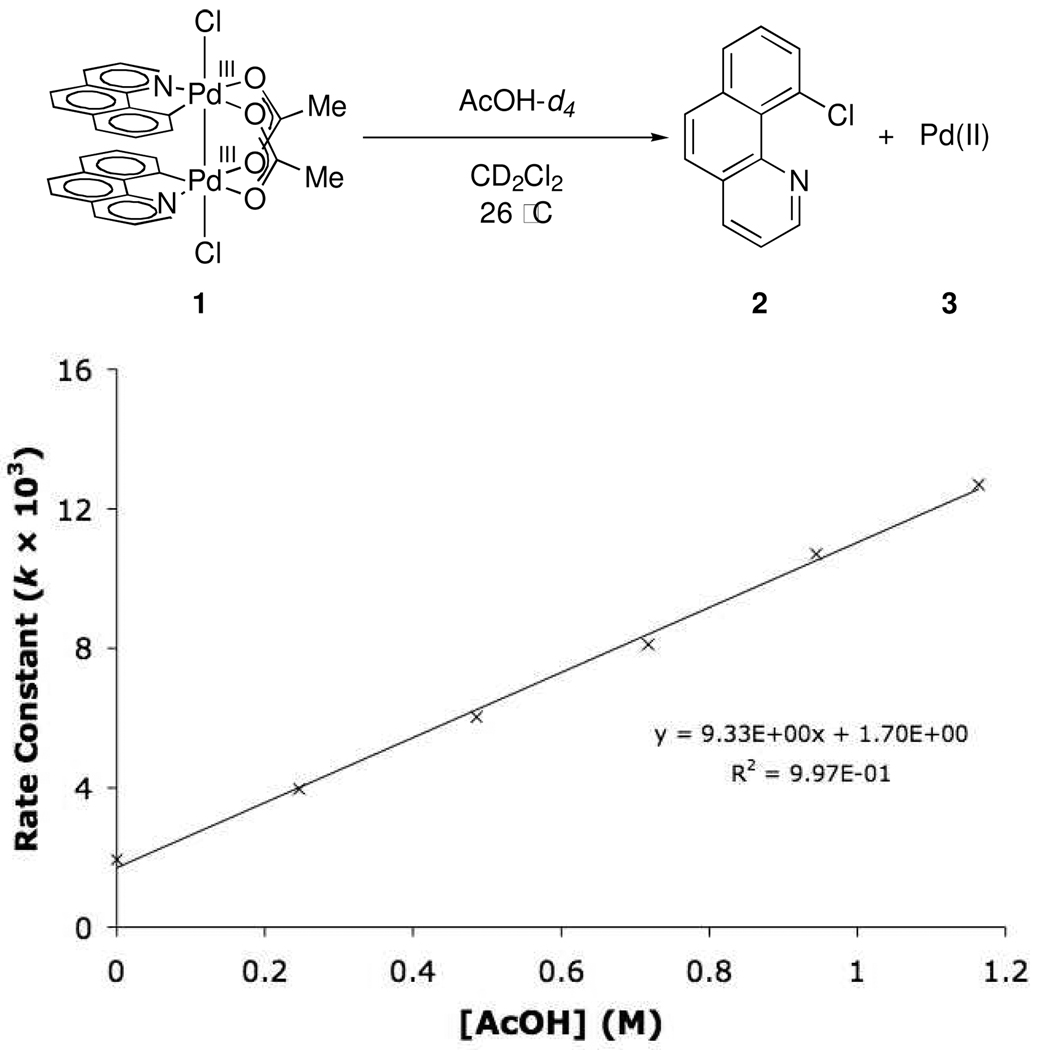
Reductive Elimination in the Presence of Exogenous AcOH

We have proposed that reductive elimination from dinuclear Pd(III) complexes similar in structure to 1 is the product-forming step of a variety of Pd-catalyzed C–H functionalizations.3 During catalysis, substrate is present in large excess relative to Pd and thus we investigated C–Cl reductive elimination in the presence of exogenous benzo[h]quinoline (8). By 1H NMR and UV-vis spectroscopy, no interaction between complex 1 and 8 was observed between −50 °C and 23 °C. We have observed a reproducible acceleration of C–Cl bond formation in the presence of exogenous benzo[h]quinoline (8) at 23 °C.3a We now report a reexamination of the observed rate enhancement for the formation of 2 from 1 upon addition of 8, which indicates that the observed acceleration is due to acid generated by palladation of added 8, not N-coordination of 8 to 1, as we previously proposed. 3a

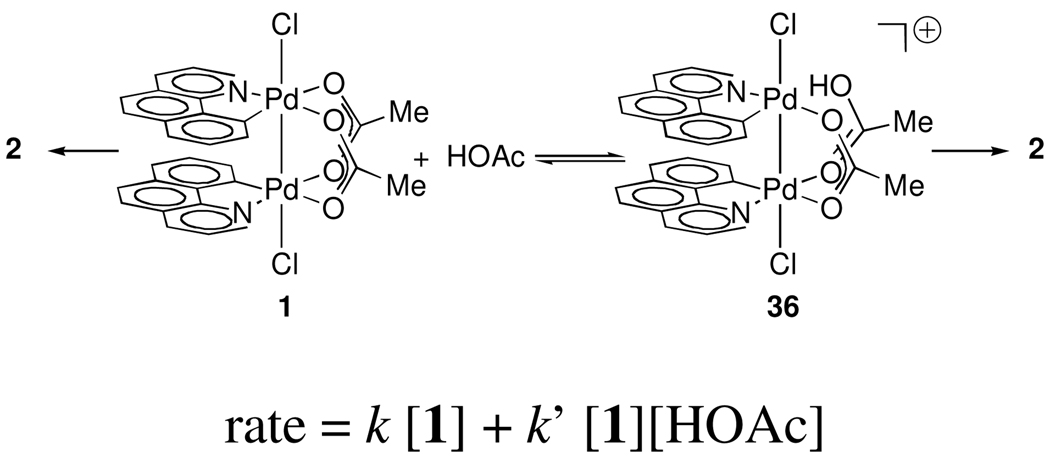
Examination of the thermolysis of 1 in the presence of exogenous benzo[h]quinoline (8) revealed that the concentration of 8 decreased during the evolution of 2 (for quantitative kinetic data regarding the rate of reductive elimination from 1 as a function of initial benzo[h]quinoline concentration, see Supporting Information). Cyclometallation of 8 (for example 8→9 shown in Figure 1) by the Pd(II)-containing byproducts of reductive elimination (3) generates an equivalent of acid, as a result of C–H bond cleavage during metallation. We therefore examined the potential effect of acid on the rate of reductive elimination from 1 by monitoring the formation of 2 as a function of AcOH concentration ([AcOH]). AcOH was selected because potential exchange of the conjugate base – acetate – with the acetate ligands of 1 is a degenerate process. The rate of formation of 2 was monitored at AcOH concentrations up to 1.16 M in CD2Cl2 by 1H NMR spectroscopy. The rate of formation of 2 is accelerated in the presence of AcOH (Figure 4). The plot of first-order rate constant vs. [AcOH] has a non-zero intercept, reflective of the background rate of C–Cl reductive elimination in the absence of AcOH, and shows that at least two pathways are available for C–Cl reductive elimination: one pathway independent and one pathway linearly dependent on the concentration of AcOH.

Figure 4.

Figure 4

Open in a new tab

First order rate constant of C–Cl reductive elimination as a function of [AcOH].

Computational Studies

Structure of 1

Description of the halogen–metal–metal–halogen tetrad present in 1 was anticipated to be computationally challenging using DFT. The combination of high oxidation state metal centers, metal-metal bonding, and the coupling of the metal-metal bond to the electronegative chloride ligands are demanding for exchange-correlation hybrid density functionals.29 In addition, the lack of accurate consideration of attractive medium-range interactions such as π–π stacking in orthodox hybrid DFT functionals30 (e.g. B3LYP, PBE0) was expected to overestimate Pd–Pd bond distances. The M06 functional31 has been shown to accurately describe both transition metal-based complexes containing Au, Ru, and Pd,32 as well as non-covalent interactions between proximal aromatic groups.33 The M06 functional with a triple-ζ basis set for Pd and Cl predicted a Pd–Pd distance of 2.62 Å (compared to 2.57 Å determined experimentally) and accurately described the relative spacing of the benzo[h]quinolinyl ligands (see Supporting Information for evaluation of other functionals). In addition, the computed structure of 1, which we will denote A, reflects the experimentally observed nonequivalence of the two oxygen-based ligands on each palladium atom (Figure 1). The M06 functional also accurately described the Pd-Pd distance in 9, which does not contain a formal Pd–Pd bond23 (experimental: 2.84 Å; computed: 2.87 Å). In the ensuing discussion, computed structures will be designated by compound letters, not numbers.

Activation Parameters for C–Cl Reductive Elimination from 1

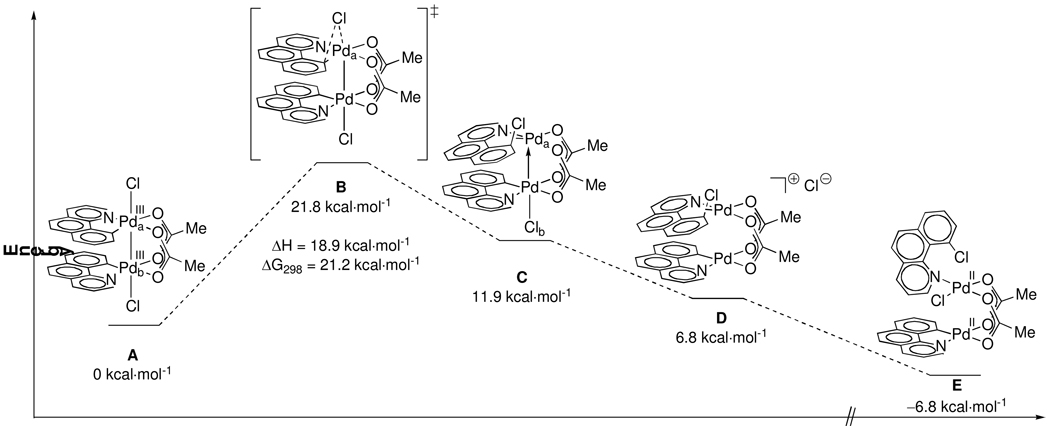
Transition state B has been located at ΔG‡298 = 21.2 kcal·mol−1 (ΔH‡= 18.9 kcal·mol−1) higher in energy than structure A (Figure 5). This agrees well with the experimentally determined activation parameters (ΔG‡298 = 20.5 ± 0.1 kcal·mol−1, ΔH‡= 17.2 ± 2.7 kcal·mol−1; Table 1).

Figure 5.

Figure 5

Open in a new tab

Calculated gas-phase stationary points in the mechanism of C–Cl reductive elimination from A. Energies are solvent-corrected electronic energies at 0K (E0K); ΔH‡ and ΔG‡ (transition state B) for the reductive elimination are at 298K.

Table 1.

Comparison of experimental and computational activation parameters for reductive elimination from 1.

ΔH‡(kcal·mol−1) ΔS‡(cal·K−1) ΔG‡298(kcal·mol−1)
Experiment 17.2 ± 2.7 −11.2 ± 9.4 20.5 ± 0.1
Computation 18.9 −7.5 21.2
Open in a new tab

Unlike in structure A, the Pd nuclei in B are non-equivalent because C–Cl bond formation proceeds at Pda while ionization of Cl− proceeds at Pdb. The Pd–Pd distance is longer in B (2.65 Å) than in A (2.62 Å) by 0.03 Å. The bond lengths between Pda and the carbon (Ca) and chlorine (Cla) ligands that participate in reductive elimination are longer by 0.20 Å and 0.12 Å in the transition state, respectively. The Pd–O bond trans to Ca is 0.16 Å longer in B than it is in A.

Structure C has been located as a local energy minimum in the gas-phase; C is not an energy minimum when a CH2Cl2 solvent model is applied but is depicted in Figure 6 to better illustrate the path of reductive elimination. In C, the C–Cl bond is 1.76 Å long, indicating that bond formation is nearly complete (for comparison, the C–Cl bond in E is 1.75 Å). Ionization of Clb from C affords ion pair D, which is 6.8 kcal·mol−1 higher in energy than A. Experimentally, the structure of the Pd(II) complex immediately following reductive elimination has not been determined. Computationally, the ion pair D evolves to Pd(II) structure E. Several other Pd(II) complexes could form by ligand rearrangement and structure E was only chosen as a stationary point in Figure 6 to illustrate that, as observed by experiment, reductive elimination from a dinuclear Pd(III) complex to form a Pd(II) complex, such as E, is energetically favorable.

Figure 6.

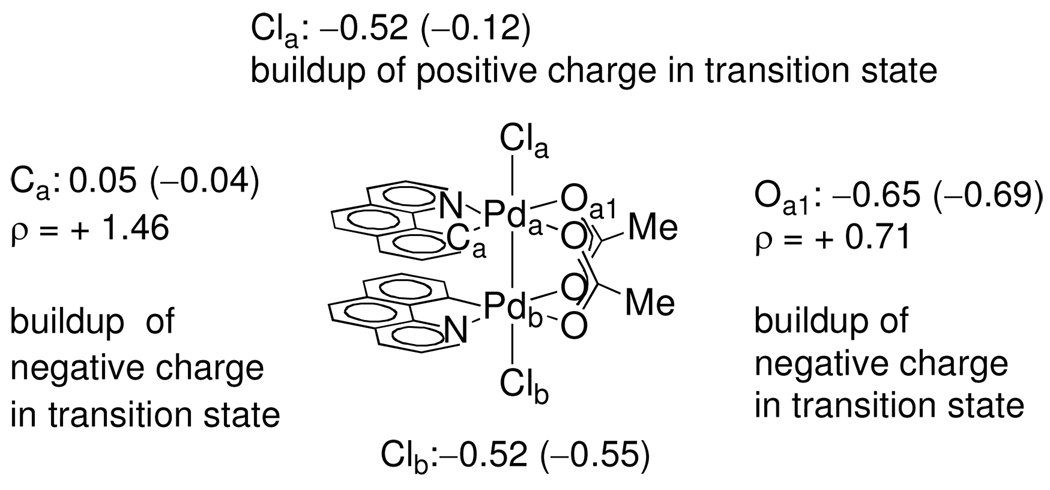
Figure 6

Open in a new tab

Partial charge distribution in structure A and transition state B (numbers in parentheses). Hammett analyses of benzo[h]quinolinyl, bridging carboxylate, and apical ligands are consistent with the computed charge distributions.

Comparison of Computed Transition State with Hammett Analyses

We have computed natural charge distributions of structure A and transition state B (Figure 6) from natural population analyses.34 The difference in computed charge distribution in the transition state B and structure A was compared with the experimentally determined ρ-values from the Hammett analyses. The relative charge distributions in A and B are in qualitative agreement with the experimentally determined ρ-values. For example, the increased anionic charge in the transition state of carbon Ca atom bound to Pda (0.05 for A; −0.04 for B) is consistent with the positive ρ-value (+1.46) that was experimentally determined for benzo[h]quinolinyl ligand substitution.

Discussion

In the following discussion we will first analyze experimental and computational evidence consistent with reductive elimination proceeding from a dinuclear palladium complex. Subsequently, we will evaluate the redox participation of both metals during reductive elimination (metallicity). Because metallicity cannot be probed experimentally, we have pursued a computational description of metallicity.

Nuclearity of Pd Complex During Redox Transformation

C–Cl bond formation from complex 1 could proceed via reductive elimination from a mono- (after dissociation of 1) or a dinuclear complex (Figure 7).

Figure 7.

Figure 7

Open in a new tab

C–Cl reductive elimination could, in principle, proceed from mononuclear or dinuclear complexes.

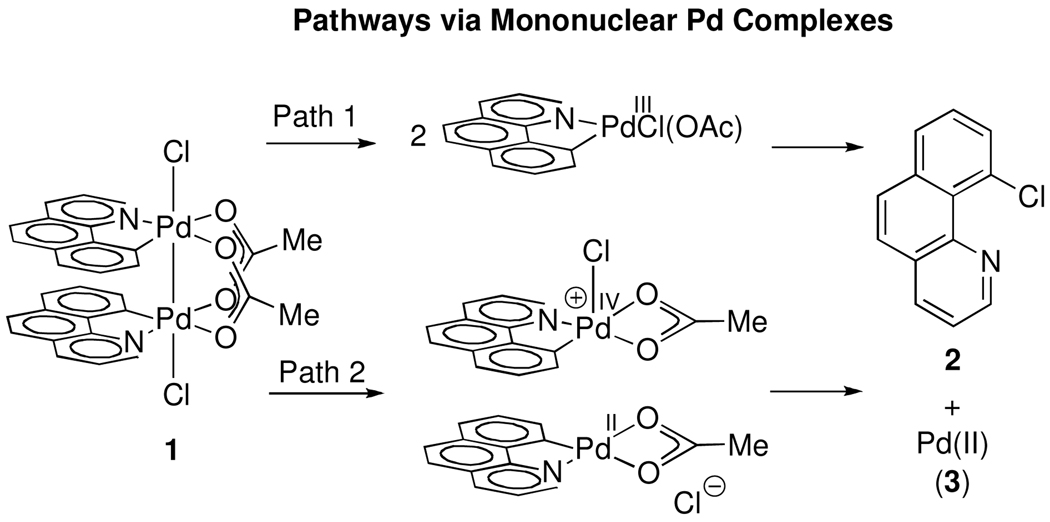
Reductive elimination from a mononuclear complex following initial Pd–Pd bond cleavage could, in principle, afford observed product 2.35 We have considered two processes by which the dinuclear core could fragment into mononuclear palladium complexes prior to reductive elimination: 1) homolytic Pd–Pd bond cleavage to afford two mononuclear Pd(III) complexes, and 2) heterolytic Pd–Pd bond cleavage to afford one Pd(IV) complex and one Pd(II) complex (Figure 8). For each pathway, either Pd–Pd bond cleavage or subsequent reductive elimination from mononuclear Pd complexes could be rate determining.

Figure 8.

Figure 8

Open in a new tab

Potential pathways via mononuclear Pd complexes. Path 1: Dissociation into two Pd(III) monomers followed by reductive elimination from mononuclear Pd(III). Path 2: Disproportionation to Pd(II) and Pd(IV) followed by reductive elimination from Pd(IV).

Fast homolytic Pd–Pd bond cleavage to afford two identical Pd(III) monomers followed by rate-determining reductive elimination would proceed with a reaction order of 0.5 with respect to 1, and was excluded by the observed first-order rate law for decomposition of 1 and formation of 2.18

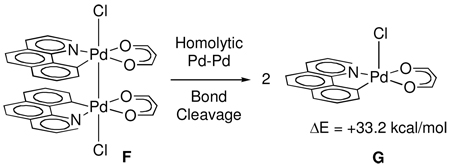
Rate-determining homolytic Pd–Pd bond cleavage followed by fast reductive elimination was excluded by comparison of the activation parameters for C–Cl reductive elimination (ΔH‡ = 17.2 ± 2.7 kcal·mol−1, ΔS‡ = −11.2 ± 9.4 cal K−1, ΔG‡298 = 20.5 ± 0.1 kcal· mol−1) with the calculated Pd–Pd bond strength. The Pd–Pd bond in A was calculated to be 35.3 kcal·mol−1 by calculating the energy required to separate the palladium nuclei to 3.65 Å. Stretching of the Pd–Pd bond led to geometrical distortions of the bridging acetate ligands. Therefore, the Pd–Pd bond energy was also calculated for structure F, in which the bridging acetate ligands have been replaced by chelating propanedialato ligands (33.2 kcal·mol−1) (eq. 4). The computed value of 35.3 kcal·mol−1 is likely an underestimate of the energy required to cleave the dinuclear core because cleavage requires breaking of the Pd–Pd bond in addition to two Pd–O bonds. The effect of solvent polarization (Poission-Boltzmann Model) in CH2Cl2 was included while calculating the Pd–Pd bond strength in F to account for solvent stabilization of the complexes generated after bond cleavage.

graphic file with name nihms238678f21.jpg (4)

Reductive elimination could potentially proceed by disproportionation of 1 into a Pd(II) and a Pd(IV) complex, with subsequent monometallic reductive elimination from a mononuclear Pd(IV) complex (Path 2, Figure 9). Such disproportionative metal-metal bond cleavage has been reported for dinuclear Pt(III) intermediates during the oxidation of Pt(II) to Pt(IV).36 As with homolytic Pd–Pd bond cleavage, either heterolytic cleavage or subsequent reductive elimination could be rate limiting.

Figure 9.

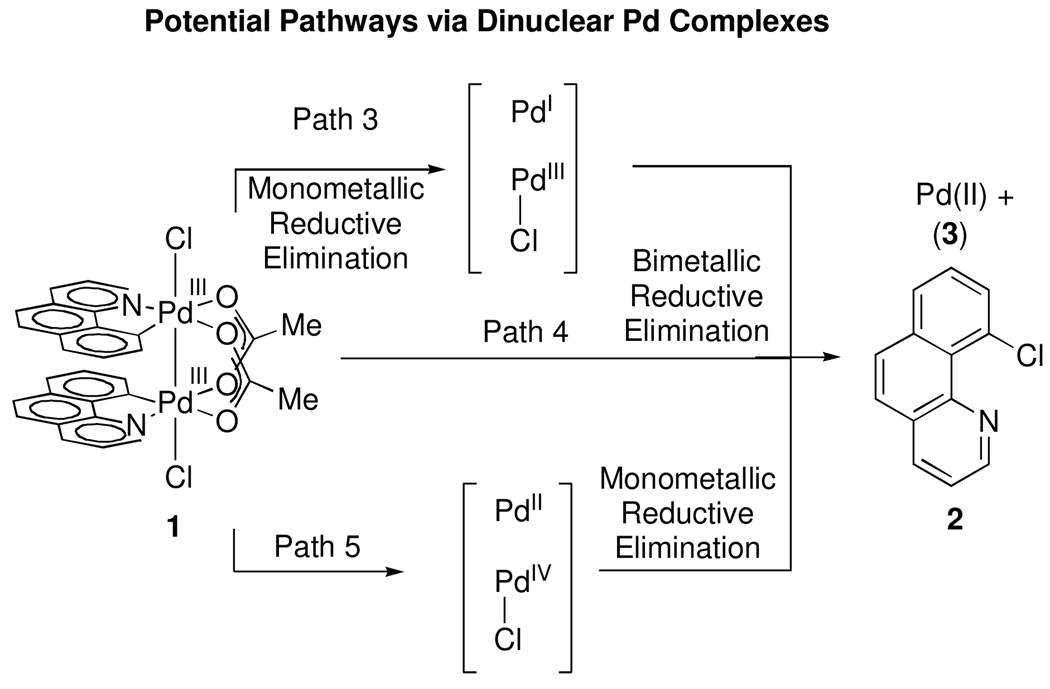
Figure 9

Open in a new tab

Potential pathways from dinuclear Pd complexes. Path 3: Monometallic reductive elimination to form a Pd(I)/Pd(III) mixed valence complex and 2 followed by comproportionation to afford Pd(II). Path 4: Computed low-energy pathway for reductive elimination (Figure 6). Path 5: Disproportionation to a Pd(II)/Pd(IV) mixed valence complex followed by monometallic reductive elimination.

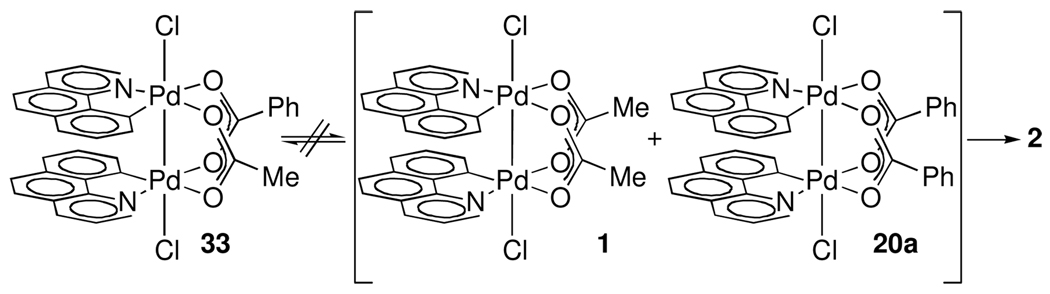
Possible pre-equilibrium dimer cleavage followed by rate-determining reductive elimination was evaluated by a crossover experiment between acetate-bridged complex 1 and benzoate-bridged complex 20a (Scheme 6). Complex 33, the product of crossover between 1 and 20a, was not observed during C–Cl reductive elimination, precluding pre-equilibrium dimer cleavage. Addition of 1.0 equivalents of benzo[h]quinoline (8), a potentially coordinating ligand, did not lead to observed exchange either.

Scheme 6.

Scheme 6

Open in a new tab

Exchange between 1 and 20a is not observed on the time scale of formation of 2, precluding pre-equilibrium dissociation of 1 during reductive elimination.

To evaluate the possibility of rate-determining heterolytic Pd–Pd cleavage prior to C–Cl reductive elimination, the relative rates of reductive elimination from acetate-bridged complex 1 and esp-bridged complex 35 (eq 5) were measured at 35 °C. Reductive elimination from esp-bridged Pd(III) complex 35 proceeds 16 times more slowly than from acetate-bridged Pd(III) complex 1. However, the esp-bridged Pd(II) complex 34 dissociates at least 1500 times more slowly than acetate-bridged Pd(II) complex 9 (see Supporting Information). The relative rates of reductive elimination from 1 and 35 are therefore most consistent with reductive elimination proceeding from a dinuclear complex. In addition to the experimental data, we computed the barrier for heterolytic cleavage of the dinuclear core to generate a Pd(II) and Pd(IV) complex to be at least 29.5 kcal·mol−1 (see Supporting Information); the experimentally determined activation enthalpy for reductive elimination from 1 is H‡ = 17.2 ± 2.7 kcal·mol−1.

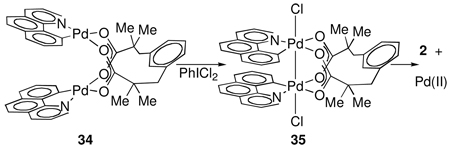graphic file with name nihms238678f22.jpg (5)

The combination of the observed first-order disappearance of 1 and formation of 2, the measured activation parameters which show that reductive elimination from 1 is more facile than homolytic Pd–Pd bond cleavage, and the lack of crossover between 1 and 20a are all consistent with reductive elimination from a dinuclear complex. Further, the computed reaction pathway agrees with experimental observations of ground state structure, Arrhenius parameters for C–Cl reductive elimination, and Hammett ρ-values, and also implicates dinuclear complexes in every step of reductive elimination.

Metallicity of Reductive Elimination

Knowledge of the nuclearity of the complex from which reductive elimination proceeds provides no information about the role of each metal center during reductive elimination. Depending on the extent of metal–metal cooperation during reductive elimination from a dinuclear complex, either monometallic or bimetallic redox pathways are possible (Figure 9).

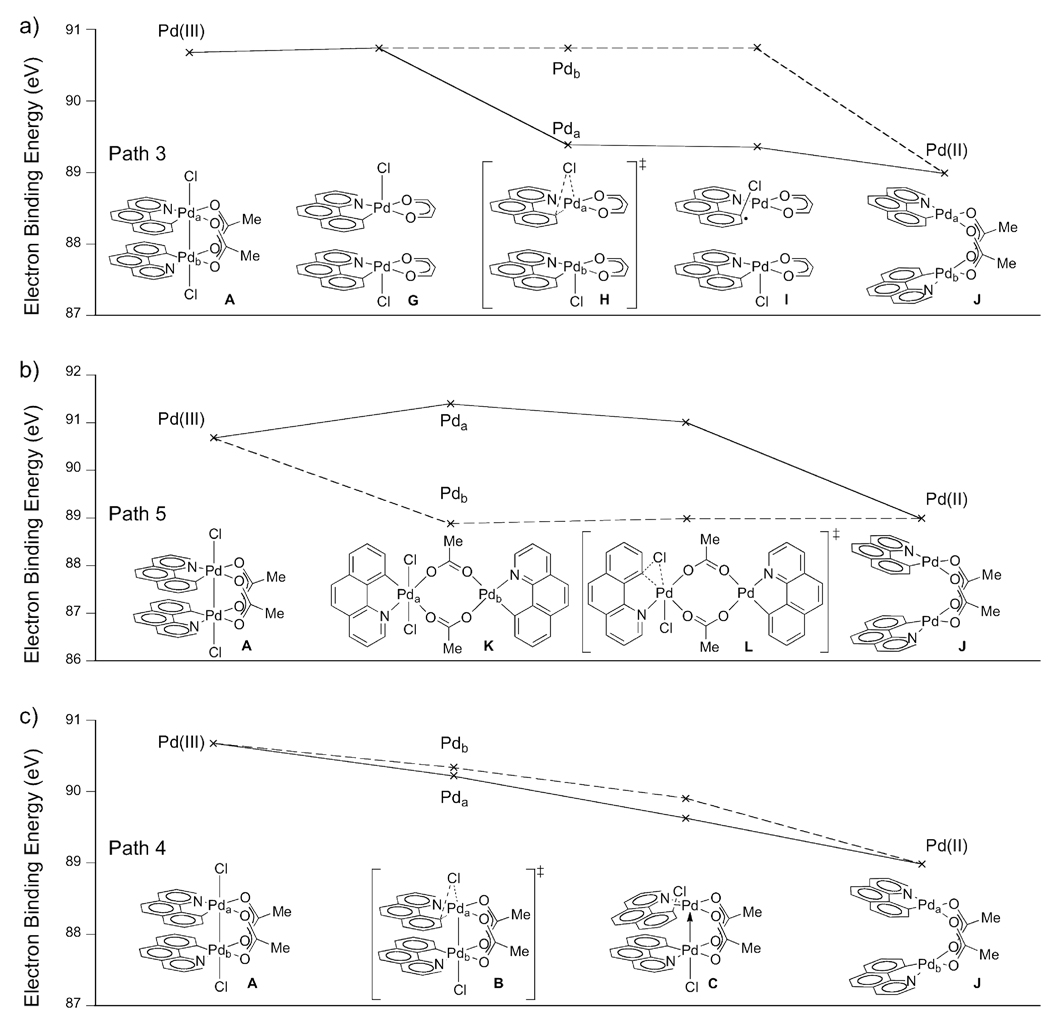
To probe the electronic contribution of each metal center during reductive elimination the electron binding energy37 of the 4s core electrons of both Pda and Pdb were calculated as a function of reaction progress for pathways 3–5 shown in Figure 10. The electron binding energy38 of a 4s electron is the energy required to remove an electron from the 4s orbital42 to infinite separation, without allowing any relaxation of the remaining electrons. For metal centers with similar ligand environments, electron binding energy is well correlated with formal oxidation state.43 The electron binding energy decreases during reduction of a metal center because the metal becomes more electron rich and the electron is more effectively shielded from the nuclear charge. Conversely, the electron binding energy increases during oxidation because the electron is less effectively shielded from the nuclear charge. When comparing the electron binding energies in metal centers with similar ligand sets, higher electron binding energies correlate with higher oxidation states. We suggest that the electron binding energies, which correlate with oxidation state, are suitable to ascertain the redox participation of the metals.44

Figure 10.

Figure 10

Open in a new tab

a) Plot of the 4s core electron binding energy of Pda (solid) and Pdb (dashed) as a function of reaction progress for monometallic reductive elimination via a Pd(I)/Pd(III) mixed valence species (Figure 9, path 3). b) Plot of electron binding energy of Pda and Pdb as a function of reaction progress for monometallic reductive elimination from a Pd(II) / Pd(IV) mixed valence species (Figure 9, path 5). c) Plot of electron binding energy of Pda and Pdb as a function of reaction progress for calculated bimetallic reductive elimination (Figure 5).

We selected two hypothetical but well-defined limiting cases for monometallic reductive elimination (paths 3 and 5; Figure 9), and computed the pathways of reductive elimination, repectively. Subsequently, the electron binding energies of electrons in the 4s orbitals of both palladium centers, Pda and Pdb, have been calculated for each of the two pathways.45

Hypothetical reductive elimination from Pda with Pdb as a non-redox-active spectator ligand on Pda would proceed through a dinuclear Pd(I)/Pd(III) mixed valence complex (Figure 10a, path 3). We investigated path 3 by computationally cleaving A into two mononuclear Pd(III) complexes (G). Computed intermediate G serves as model for dinuclear compound A, in which potential metal-metal cooperation is eliminated. The electron binding energies were determined computationally to describe the redox chemistry of each Pd center during hypothetical path 3 (Figure 10a). The cleavage from A to G is redox-neutral and does not significantly effect the computed electron binding energy of either Pda or Pdb. Monometallic reductive elimination from Pda proceeds through transition state H to afford structure I. Redox chemistry is only occurring at Pda during the transformation of G to I and thus the electron binding energy of Pdb does not change. At the same time, the electron binding energy of Pda decreases as G is transformed to I, consistent with redox contribution at Pda. We selected the Pd(II) complex J as the endpoint, because complex J has well-defined oxidation states on palladium. Further, the ligand sphere of palladium in J is closely related to the ligand sphere of palladium in A, allowing for meaningful comparison of electron binding energies. Formal comproportionation of the mixed valence structure I to J results in the electron binding energies of Pda and Pdb converging. Pda in structure I is most accurately described as a Pd(II) with a ligand-centered radical and thus the electron binding energy of Pda during comproportionation does not increase as would be expected for oxidation of Pd(I) to Pd(II). The diagram in Figure 11a shows that only Pda participates in redox chemistry during reductive elimination; hypothetical path 3 is therefore monometallic.

Figure 11.

Figure 11

Open in a new tab

Reductive elimination from 1 in the presence of AcOH proceeds via at least two pathways, one linearly dependent on and one independent of [AcOH].

Alternatively, C–Cl bond formation could proceed by initial disproportionation of complex 1 to a mixed valence Pd(II)/Pd(IV) complex prior to reductive elimination from Pd(IV) as shown in Figure 9, path 5. Previously, it was speculated that reductive elimination from dinuclear Pd(III) complexes may proceed via Pd(II)/Pd(IV) mixed valence species.46,47 As shown in Figure 10b, the electron binding energy diagram computed for disproportionation from A to K shows increased electron binding energy of Pda because Pda is more oxidized in K than it is in A. Reductive elimination proceeds through transition state L, in which redox chemistry is occurring at Pda. The electron binding energies of Pda and Pdb converge as reductive elimination affords two Pd(II) centers (J). During reductive elimination from Pda, the electron binding energy of Pdb is constant because Pdb is not redox-active according to path 5. Hypothetical path 5 is therefore monometallic.

Both path 3 and path 5 were selected to illustrate and benchmark the electron binding energies in two limiting cases of monometallic reductive elimination. Path 4 is derived from the computed low-energy pathway shown in Figure 5. Both electron binding energies of Pda and Pdb monotonically decrease while A is converted to C via transition state B. The electron binding energies continue to monotonically decrease until Pd(II) structure J. Neither metal center becomes oxidized beyond Pd(III) during the course of reductive elimination.

The calculated electron binding energies implicate simultaneous redox participation of both metals during reductive elimination. Monotonic reduction in electron binding energy at both metals is inconsistent with initial disproportionation to a Pd(II)/Pd(IV) complex prior to monometallic reductive elimination. Simultaneous change in the electron binding energies of both Pda and Pdb is also inconsistent with initial monometallic reductive elimination to a Pd(I)/Pd(III) mixed valence complex. Therefore, we conclude that reductive elimination from 1 is bimetallic.

Kinetic Advantage of Bimetallic Reductive Elimination

Based on the HOMO and LUMO calculated for structure A and transition state B (see Supporting Information), metal-metal bonding during reductive elimination is accomplished primarily by overlap of the palladium dz2 orbitals. We have calculated the activation barrier for reductive elimination as a function of Pd–Pd distance. Computationally forced elongation of the Pd–Pd bond attenuates the overlap of the dz2 orbitals and thus decreases electronic communication between the metals as compared to low-energy structure A (eq. 6). By preventing electronic communication between the metals, bimetallic reductive elimination is forced to become increasingly monometallic.

graphic file with name nihms238678f23.jpg (6)

The activation barrier for reductive elimination when the Pd–Pd distance is fixed at 2.62 Å (the Pd–Pd distance in A) is 17.1 kcal·mol−1. Computational elongation of the Pd–Pd distance to 2.95 Å (Table 2, entry 2) increased the activation barrier to 21.8 kcal·mol−1. Further elongation to 3.30 Å and 3.65 Å led to activation barriers of 33.3 kcal·mol−1 and 46.0 kcal·mol−1, respectively (entries 3 and 4). Pd–Pd distances beyond 3.65 Å, which is greater than the sum of the two van der Waals radii of the palladium atoms, could not be accommodated while maintaining the bridging geometry of the acetate ligands. Comparison of the activation barriers for bimetallic reductive elimination (entry 1) and monometallic reductive elimination (entry 4) indicates that metal–metal cooperation during reductive elimination lowers the energy barrier by ~30 kcal·mol−1 as compared to monometallic reductive elimination, which approximately corresponds to the Pd–Pd bond dissociation energy in 1.

Table 2.

Computed reference ground state and activation energies of reductive elimination as a function of restricted Pd–Pd distance. Energies are gas-phase electronic energies at 0K (E0K).

Pd–Pd Distance [Å] Ground State Energy [kcal·mol−1] Activation Energy [kcal·mol−1] relative to A
2.62 0.0 (A) 17.1
2.95 6.2 21.8
3.30 20.5 33.3
3.65 35.3 46.0
Open in a new tab

Reductive Elimination in the Presence of AcOH

Previously, based on the observation of C–C,48 C–O,2d,e C–Cl,49 and C–F50 reductive elimination from isolated Pd(IV) complexes, Pd(II)/Pd(IV) redox cycles have been invoked as mechanistic rationale for Pd-catalyzed C–H oxidation reactions.51 We have proposed that reductive elimination from dinuclear Pd(III) complexes, similar to 1, is the product-forming step in a variety of Pd catalyzed C–H oxidation reactions based on the observation of dinuclear complexes during chlorination3a and acetoxylation3b of 2-phenylpyridine derivatives.52

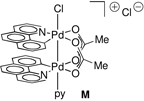
During catalysis, C–H metallation by Pd(II) generates an equivalent of acid. We have found that the rate of reductive elimination is linearly correlated with [AcOH]. We propose that the observed C–Cl reductive elimination rate enhancement is due to protonation of one of the bridging acetate ligands of 1 to afford 36 (Figure 11). In the presence of acid, protonation of the acetate ligand would result in a pentacoordinate Pd center of a dinuclear complex, in which one Pd–O bond is cleaved. We suggest that reductive elimination from 36, in which one bridging acetate ligand is protonated, is faster than from 1. A dinuclear transition state for reductive elimination from cationic complex 36, similar in structure to the transition state for reductive elimination from 1 (B), has been located computationally. The barrier to reductive elimination from 1 was computed to be 21.8 kcal·mol−1 whereas the barrier to reductive elimination from 36 was computed to be 20.1 kcal·mol−1, consistent with the observed rate enhancement in the presence of AcOH.45 Computed electron binding energies for both palladium atoms in A + H+ and in B + H+ indicate that, similar to reductive elimination from A, reductive elimination from a protonated dinuclear core is bimetallic as well. During Pd-catalyzed C–H functionalization, C–H metallation generates acid, and thus acid-catalyzed reductive elimination may be relevant during catalysis. Based on the presented data, we cannot distinguish between pre-equilibrium and rate-determining protonation in the acid-catalyzed pathway for reductive elimination from 1 (k’, Figure 11).

Conclusions

In this manuscript we sought to address the following questions: Does the core of dinuclear Pd(III) complex 1 stay intact during reductive elimination? Do both metal centers participate in the redox transformation and is there an energetic benefit to having two metals as opposed to a single metal? How closely related are previously proposed mononuclear Pd(IV) to the dinuclear Pd(III) complexes reported here with respect to the mechanism of reductive elimination?

Experimental and theoretical analysis of C–Cl reductive elimination from complex 1 has implicated reductive elimination from a dinuclear core with synergistic, bimetallic redox participation of both metals during reductive elimination. The presence of the second metal in dinuclear complex 1 lowers the activation barrier of reductive elimination. If reductive elimination is artificially forced to proceed via a monometallic pathway by eliminating metal-metal communication, the barrier to reductive elimination increased by approximately 30 kcal·mol−1.

Transition metal-mediated C–heteroatom bond construction remains a synthetically challenging goal. We have shown that C–heteroatom bonds can be efficiently formed by bimetallic reductive elimination from dinuclear Pd(III) complexes. In this manuscript we have provided a theoretical framework for bimetallic redox catalysis. Redox synergy between metal centers, as is seen for C–Cl reductive elimination here, also has the potential to lower the activation barriers for other redox processes. We anticipate that our findings may serve as a foundation for future reaction development.

Supplementary Material

1_si_001
2_si_002
3_si_003
4_si_004
5_si_005

Acknowledgment

We thank Douglas M. Ho, Jessica Y. Wu and Takeru Furuya for X-ray crystallographic analysis, Robert Nielsen and David Ford for insightful discussions, Sanofi Aventis for a graduate fellowship for DCP, the reviewers of this manuscript for comments, which improved the quality of the manuscript, and the NSF (CHE-0952753) and NIH-NIGMS (GM088237) for funding. Computational facilities were funded by grants from ARO-DURIP and ONR-DURIP.

Footnotes

Supporting Information Available: Detailed experimental procedures and spectroscopic data for all new compounds. Detailed computational methods and XYZ coordinates. This material is available free of charge via the Internet at http://pubs.acs.org.

REFERENCES

  • 1.a Fackler JP. Inorg. Chem. 2002;41:6959–6972. doi: 10.1021/ic025734m. [DOI] [PubMed] [Google Scholar]; b Gray TG, Veige AS, Nocera DG. J. Am. Chem. Soc. 2004;126:9760–9768. doi: 10.1021/ja0491432. [DOI] [PubMed] [Google Scholar]
  • 2.a Henry PM. J. Org. Chem. 1971;36:1886–1890. [Google Scholar]; b Stock LM, Tse K-T, Vorvick LJ, Walstrum SA. J. Org. Chem. 1981;46:1757–1759. [Google Scholar]; c Yoneyama T, Crabtree RH. J. Mol. Cat. A: Chem. 1996;108:35–40. [Google Scholar]; d Dick AR, Kampf JW, Sanford MS. J. Am. Chem. Soc. 2005;127:12790–12791. doi: 10.1021/ja0541940. [DOI] [PubMed] [Google Scholar]; e Racowski JM, Dick AR, Sanford MS. J. Am. Chem. Soc. 2009;131:10974–10983. doi: 10.1021/ja9014474. [DOI] [PubMed] [Google Scholar]
  • 3.a Powers DC, Ritter T. Nat. Chem. 2009;1:302–309. doi: 10.1038/nchem.246. [DOI] [PubMed] [Google Scholar]; b Powers DC, Geibel MAL, Klein JEMN, Ritter T. J. Am. Chem. Soc. 2009;131:17050–17051. doi: 10.1021/ja906935c. [DOI] [PubMed] [Google Scholar]
  • 4.a Masters C. Homogeneous Transition-Metal Catalysis. London: University Press; 1981. [Google Scholar]; b van Leeuwen P. Homogeneous Catalysis. Boston: Kluwer Academic Publishers; 2004. [Google Scholar]
  • 5.a Heck RF. Organotransition Metal Chemistry: A Mechanistic Approach. New York: Academic Press; 1974. p. 49. [Google Scholar]; b Miessler GL, Tarr DA. Inorganic Chemistry. Third ed. Upper Saddle River, New Jersey: Pearson Education, Inc; 2004. pp. 525–526. [Google Scholar]; c Anslyn EV, Dougherty DA. Modern Physical Organic Chemistry. Sausalito, California: University Science Books; 2006. pp. 724–726. [Google Scholar]
  • 6.Hartwig JF, Paul F. J. Am. Chem. Soc. 1995;117:5373–5374. [Google Scholar]
  • 7.a Chock PB, Halpern J. J. Am. Chem. Soc. 1966;88:3511–3514. [Google Scholar]; b Lau KSY, Wong PK, Stille JK. J. Am. Chem. Soc. 1976;98:5832–5840. [Google Scholar]; c Ellis PR, Pearson JM, Haynes A, Adams H, Bailey NA, Maitlis PM. Organometallics. 1994;13:3215–3226. [Google Scholar]
  • 8.a Tsou TT, Kochi JK. J. Am. Chem. Soc. 1979;101:6319–6332. [Google Scholar]; b Hall TL, Lappert MF, Lednor PW. J. Chem. Soc., Dalton Trans. 1980:1448–1456. [Google Scholar]
  • 9.a Brown MP, Puddephatt RJ, Upton CEE. J. Chem. Soc., Dalton Trans. 1974:2457–2465. [Google Scholar]; b Brown JM, Cooley NA. Chem. Rev. 1988;88:1031–1046. [Google Scholar]; c Mann G, Baranano D, Hartwig JF, Rheingold AL, Guzei IA. J. Am. Chem. Soc. 1998;120:9205–9219. [Google Scholar]; d Widenhoefer RA, Buchwald SL. J. Am. Chem. Soc. 1998;120:6504–6511. [Google Scholar]; e Hartwig JF. Acc. Chem. Res. 1998;31:852–860. [Google Scholar]; f Williams BS, Holland AW, Goldberg KI. J. Am. Chem. Soc. 1999;121:252–253. [Google Scholar]; g Williams BS, Goldberg KI. J. Am. Chem. Soc. 2001;123:2576–2587. doi: 10.1021/ja003366k. [DOI] [PubMed] [Google Scholar]
  • 10.a Shilov AE. J. Mol. Catal. 1987;41:221–234. [Google Scholar]; b Ericson A, Hedman B, Hodgson KO, Green J, Dalton H, Bentsen JG, Beer RH, Lippard SJ. J. Am. Chem. Soc. 1988;110:2330–2332. [Google Scholar]; c Holm RH, Kennepohl P, Solomon EI. Chem. Rev. 1996;96:2239–2314. doi: 10.1021/cr9500390. [DOI] [PubMed] [Google Scholar]; d van den Beuken EK, Feringa BL. Tetrahedron. 1998;54:12985–13011. [Google Scholar]; e Reedijk J, Bouwman E, editors. Bioinorganic Catalysis. Second ed. New York: Marcel Dekker, Inc; 1999. [Google Scholar]; f Meunier B, editor. Biomimetic Oxidations Catalyzed by Transition Metal Complexes. London: Imperial College Press; 2000. [Google Scholar]
  • 11.a Araki M, Ponec V. J. Catal. 1976;44:439–448. [Google Scholar]; b Muetterties EL. Science. 1977;196:839–848. doi: 10.1126/science.196.4292.839. [DOI] [PubMed] [Google Scholar]; c Muetterties EL, Rhodin TN, Band E, Brucker CF, Pretzer WR. Chem. Rev. 1979;79:91–137. [Google Scholar]; d Shriver DF, Sailor MJ. Acc. Chem. Res. 1988;21:374–379. [Google Scholar]; e Wiegand BC, Friend CM. Chem. Rev. 1992;92:491–504. [Google Scholar]; f Adams RD. J. Organomet. Chem. 2000;600:1–6. [Google Scholar]
  • 12.Adams RD, Cotton FA, editors. Catalysis by di- and polynuclear metal cluster complexes. New York: Wiley-VCH; 1998. [Google Scholar]
  • 13.a Schmidbaur H, Franke R. Inorg. Chim. Acta. 1975;13:85–89. [Google Scholar]; b Fackler JP, Basil JD. Organometallics. 1982;1:871–873. [Google Scholar]; c Fackler JP, Murray HH, Basil JD. Organometallics. 1984;3:821–823. [Google Scholar]; d Basil JD, Murray HH, Fackler JP, Tocher J, Mazany AM, Trzcinska-Bancroft B, Knachel H, Dudis D, Delord TJ, Marler DO. J. Am. Chem. Soc. 1985;107:6908–6915. [Google Scholar]; e Elduque A, Aguilera F, Lahoz FJ, López JA, Oro LA, Pinillos MT. Inorg. Chim. Acta. 1998;274:15–23. [Google Scholar]; f Jamali S, Nabavizadeh SM, Rashidi M. Inorg. Chem. 2005;44:8594–8601. doi: 10.1021/ic0511064. [DOI] [PubMed] [Google Scholar]; g Abdou HE, Mohamed AA, Fackler JP. Inorg. Chem. 2007;46:9692–9699. doi: 10.1021/ic700929e. [DOI] [PubMed] [Google Scholar]; h Bonnington KJ, Jennings MC, Puddephatt RJ. Organometallics. 2008;27:6521–6530. [Google Scholar]
  • 14.a Wegman RW, Brown TL. J. Am. Chem. Soc. 1980;102:2494–2495. [Google Scholar]; b Brown MP, Fisher JR, Hill RH, Puddephatt RJ, Seddon KR. Inorg. Chem. 1981;20:3516–3521. [Google Scholar]; c Hill RH, Puddephatt RJ. Inorg. Chim. Acta. 1981;54:L277–L278. [Google Scholar]; d Hill RH, de Mayo P, Puddephatt RJ. Inorg. Chem. 1982;21:3642–3646. [Google Scholar]; e Davies SG, Hibberd J, Simpson SJ, Watts O. J. Organomet. Chem. 1982;238:C7–C8. [Google Scholar]; f Sundararajan G, San Filippo J. Organometallics. 1985;4:606–608. [Google Scholar]; g Sundararajan G. Organometallics. 1991;10:1377–1382. [Google Scholar]; h Stockland RA, Anderson GK, Rath NP. J. Am. Chem. Soc. 1999;121:7945–7946. [Google Scholar]; i Stockland RA, Janka M, Hoel GR, Rath NP, Anderson GK. Organometallics. 2001;20:5212–5219. [Google Scholar]; j Chaouche N, Forniés J, Fortuño C, Kribii A, Martín A, Karipidis P, Tsipis AC, Tsipis CA. Organometallics. 2004;23:1797–1810. [Google Scholar]; k Ara I, Chaouche N, Forniés J, Fortuño C, Kribii A, Tsipis AC. Organometallics. 2006;25:1084–1091. [Google Scholar]
  • 15.a Misumi Y, Ishii Y, Hidai M. J. Mol. Catal. 1993;78:1–8. [Google Scholar]; b Broussard ME, Juma B, Train SG, Peng W-J, Laneman SA, Stanley GG. Science. 1993;260:1784–1788. doi: 10.1126/science.260.5115.1784. [DOI] [PubMed] [Google Scholar]; c Li C, Widjaja E, Garland M. J. Am. Chem. Soc. 2003;125:5540–5548. doi: 10.1021/ja029499i. [DOI] [PubMed] [Google Scholar]; d Li C, Widjaja E, Garland M. Organometallics. 2004;23:4131–4138. [Google Scholar]; e Li C, Chen L, Garland M. Adv. Synth. Catal. 2008;350:679–690. [Google Scholar]
  • 16.Nappa MJ, Santi R, Halpern J. Organometallics. 1985;4:34–41. [Google Scholar]
  • 17.a Halpern J. Inorg. Chim. Acta. 1982;62:31–37. [Google Scholar]; b Trinquier G, Hoffmann R. Organometallics. 1984;3:370–380. [Google Scholar]
  • 18.a Chan YNC, Osborn JA. J. Am. Chem. Soc. 1990;112:9400–9401. [Google Scholar]; b Louie J, Hartwig JF. J. Am. Chem. Soc. 1995;117:11598–11599. [Google Scholar]; c Driver MS, Hartwig JF. J. Am. Chem. Soc. 1997;119:8232–8245. [Google Scholar]; d Vazquez-Serrano LD, Owens BT, Buriak JM. Inorg. Chim. Acta. 2006;359:2786–2797. [Google Scholar]; e Fulmer GR, Muller RP, Kemp RA, Goldberg KI. J. Am. Chem. Soc. 2009;131:1346–1347. doi: 10.1021/ja807936q. [DOI] [PubMed] [Google Scholar]
  • 19.In this conversation, we are excluding transition metal complexes in which significant redox participation of the ligand is involved. For discussion: (a) Holm RH, Balch AL, Davison A, Maki AH, Berry TE. J. Am. Chem. Soc. 1967;89:2866–2874. Pierpont CG. Coord. Chem. Rev. 2001;216–217:99–125. Blackmore KJ, Ziller JW, Heyduk AF. Inorg. Chem. 2005;44:5559–5561. doi: 10.1021/ic050997c. Bart SC, Chłopek K, Bill E, Bouwkamp MW, Lobkovsky E, Neese F, Wieghardt K, Chirik PJ. J. Am. Chem. Soc. 2006;128:13901–13912. doi: 10.1021/ja064557b. Haneline MR, Heyduk AF. J. Am. Chem. Soc. 2006;128:8410–8411. doi: 10.1021/ja061107a. Zarkesh RA, Ziller JW, Heyduk AF. Angew. Chem. Int. Ed. 2008;47:4715–4718. doi: 10.1002/anie.200800812. Radosevich AT, Melnick JG, Stoian SA, Bacciu D, Chen C-H, Foxman BM, Ozerov OV, Nocera DG. Inorg. Chem. 2009;48:9214–9221. doi: 10.1021/ic9010218.
  • 20.Tolman CA, Meakin PZ, Lindner DL, Jesson JP. J. Am. Chem. Soc. 1974;96:2762–2774. [Google Scholar]
  • 21.Vigalok A. Chem. Eur. J. 2008;14:5102–5108. doi: 10.1002/chem.200701738. [DOI] [PubMed] [Google Scholar]
  • 22.a Kalyani D, Dick AR, Anani WQ, Sanford MS. Tetrahedron. 2006;62:11483–11498. [Google Scholar]; b Muñiz K. Angew. Chem. Int. Ed. 2009;48:9412–9423. doi: 10.1002/anie.200903671. [DOI] [PubMed] [Google Scholar]; c Xu L-M, Li B-J, Yang Z, Shi Z-J. Chem. Soc. Rev. 2010;39:712–733. doi: 10.1039/b809912j. [DOI] [PubMed] [Google Scholar]; d Sehnal P, Taylor RJK, Fairlamb IJS. Chem. Rev. 2010;110:824–889. doi: 10.1021/cr9003242. [DOI] [PubMed] [Google Scholar]; e Lyons TW, Sanford MS. Chem. Rev. 2010;110:1147–1169. doi: 10.1021/cr900184e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Bercaw JE, Durrell AC, Gray HB, Green JC, Hazari N, Labinger JA, Winkler JR. Inorg. Chem. 2010;49:1801–1810. doi: 10.1021/ic902189g. [DOI] [PubMed] [Google Scholar]
  • 24.a Cotton FA, Gu J, Murillo CA, Timmons DJ. J. Am. Chem. Soc. 1998;120:13280–13281. [Google Scholar]; b Cotton FA, Koshevoy IO, Lahuerta P, Murillo CA, Sanaú M, Ubeda MA, Zhao QL. J. Am. Chem. Soc. 2006;128:13674–13675. doi: 10.1021/ja0656595. [DOI] [PubMed] [Google Scholar]; c Berry JF, Bill E, Bothe E, Cotton FA, Dalal NS, Ibragimov SA, Kaur N, Liu CY, Murillo CA, Nellutla S, North JM, Villagrán D. J. Am. Chem. Soc. 2007;129:1393–1401. doi: 10.1021/ja067328y. [DOI] [PubMed] [Google Scholar]
  • 25.Coe BJ, Glenwright SJ. Coord. Chem. Rev. 2000;203:5–80. [Google Scholar]
  • 26.Exchange of carboxylate ligands can proceed intermolecularly (see Supporting Information). For simplicity, here we depict only those complexes arising from intramolecular exchange; intermolecular exchange does not change our conclusions based on these experiments because exchange, whether intra- or intermolecular, is fast relative to reductive elimination.
  • 27.Hammett LP. Chem. Rev. 1935;17:125–136. [Google Scholar]
  • 28.Attempts to accomplish Hammett analysis using esp-bridged complex 37, anticipated to prevent carboxylate exchange were unsuccessful because, unlike C–Cl reductive elimination from 35, C–O reductive elimination does not proceed from esp-bridged complex 37.graphic file with name nihms238678f24.jpg
  • 29.a Petrie S, Stranger R. Inorg. Chem. 2004;43:2597–2610. doi: 10.1021/ic034525e. [DOI] [PubMed] [Google Scholar]; b Cramer CJ, Truhlar DG. Phys. Chem. Chem. Phys. 2009;11:10757–10816. doi: 10.1039/b907148b. [DOI] [PubMed] [Google Scholar]
  • 30.Zhao Y, Truhlar DG. Org. Lett. 2007;9:1967–1970. doi: 10.1021/ol0705548. [DOI] [PubMed] [Google Scholar]
  • 31.a Zhao Y, Truhlar DG. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]; b Zhao Y, Truhlar DG. Acc. Chem. Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  • 32.a Benitez D, Tkatchouk E, Goddard WA., III Organometallics. 2009;28:2643–2645. [Google Scholar]; b Benitez D, Tkatchouk E, Gonzalez AZ, Goddard WA, III, Toste FD. Org. Lett. 2009;11:4798–4801. doi: 10.1021/ol9018002. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Benitez D, Shapiro ND, Tkatchouk E, Wang YM, Goddard WA, III, Toste FD. Nat. Chem. 2009;1:482–486. doi: 10.1038/nchem.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Benitez D, Tkatchouk E, Yoon I, Stoddart JF, Goddard WA., III J. Am. Chem. Soc. 2008;130:14928–14929. doi: 10.1021/ja805953u. [DOI] [PubMed] [Google Scholar]
  • 34.a Landis CR, Weinhold F. J. Comput. Chem. 2007;28:198–203. doi: 10.1002/jcc.20492. [DOI] [PubMed] [Google Scholar]; b Reed AE, Weinstock RB, Weinhold F. J. Chem. Phys. 1985;83:735–746. [Google Scholar]
  • 35.Schore NE, Ilenda C, Bergman RG. J. Am. Chem. Soc. 1976;98:7436–7438. [Google Scholar]
  • 36.a Bandoli G, Caputo PA, Intini FP, Sivo MF, Natile G. J. Am. Chem. Soc. 1997;119:10370–10376. [Google Scholar]; b Canty AJ, Gardiner MG, Jones RC, Rodemann T, Sharma M. J. Am. Chem. Soc. 2009;131:7236–7237. doi: 10.1021/ja902799u. [DOI] [PubMed] [Google Scholar]
  • 37.The core and valence (available in the LACV3P++**(2f) basis set) natural atomic orbital energies of both Pda and Pdb were obtained and plotted as a function of reaction progress. According to Janak's theorem, the relative orbital energies are estimates of the relative vertical electron binding energies. The relative natural atomic orbital energies can be regarded as approximations of the vertical ionization potential or the negative of the electron affinity.
  • 38.Energies were obtained from Natural Bond Orbital (NBO) (ref. 39) analyses of the M06 wavefunction using the NBO 5.0 module (ref. 40) in Jaguar. The NBO analysis method is a popular mathematical treatment of wavefunctions to study bonding effects such as hybridization and covalency (refs 32c, 41).
  • 39.a Reed AE, Curtiss LA, Weinhold F. Chem. Rev. 1988;88:899–926. [Google Scholar]; b Weinhold F, Landis CR. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge University Press; 2005. [Google Scholar]
  • 40.Glendening ED, Badenhoop JK, Reed AE, Carpenter JE, Bohmann JA, Morales CM, Weinhold F. Theoretical Chemistry Institute. Madison: University of Wisconsin; 2001. [Google Scholar]
  • 41.a Kim CK, Lee KA, Kim CK, Lee B-S, Lee HW. Chem. Phys. Lett. 2004;391:321–324. [Google Scholar]; b Nori-Shargh D, Roohi F, Deyhimi F, Naeem-Abyaneh R. J. Mol. Struct. 2006;763:21–28. [Google Scholar]; c Leyssens T, Peeters D, Orpen AG, Harvey JN. Organometallics. 2007;26:2637–2645. [Google Scholar]
  • 42.The 4s orbital was selected because it is spherically symmetrical and more sensitive to perturbations in the electron density of the metal center than energetically lower lying s orbitals.
  • 43.a Riggs WM. Anal. Chem. 1972;44:830–832. doi: 10.1021/ac60312a041. [DOI] [PubMed] [Google Scholar]; b Leigh GJ. Inorg. Chim. Acta. 1975;14:L35–L36. [Google Scholar]; c Chatt J, Elson CM, Hooper NE, Leigh GJ. J. Chem. Soc., Dalton Trans. 1975:2392–2401. [Google Scholar]; d Cisar A, Corbett JD, Daake RL. Inorg. Chem. 1979;18:836–843. [Google Scholar]; e Corbett JD. Inorg. Chem. 1983;22:2669–2672. [Google Scholar]
  • 44.Similarly analysis of the carbon 1s orbitals of CH3 bound to transition metals has been shown to correlate well with the electrophilicity or nucleophilicity of the methyl groups. Nielsen RJ, Goddard WA., III J. Phys. Chem. manuscript in preparation.
  • 45.In addition to calculating the electron binding energy from A, we have also computed the electron binding energies of both Pd centers during C–Cl reductive elimination from cationic structure M, in which one of the apical chloride ligands is replaced by a pyridyl ligand. The results of these calculations are in the Supporting Information and the conclusions drawn from this structure mirror those from complex A.graphic file with name nihms238678f25.jpg
  • 46.Deprez NR, Sanford MS. J. Am. Chem. Soc. 2009;131:11234–11241. doi: 10.1021/ja904116k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.The relative energy of acetate-bridged Pd(II) dimers in which either the Pd centers are held in proximity (as in 9) or the palladium centers are in a planar arrangement (as in K)was investigated (see Jack, T. R.; Powell, J. Can. J. Chem. 1975, 53, 2558–2574.). It was concluded that a planar complex is greater than 12 kcal·mol−1 higher in energy than a structure in which the palladium centers are held in proximity. We have been unable to locate a local minimum for a planar complex with two Pd(II) centers; all attempts to calculate such a species result in the structure folding to bridged structure 9. Structure K is calculated to be 12.4 kcal·mol−1 higher in energy than A.
  • 48.Byers PK, Canty AJ, Skelton BW, White AH. J. Chem. Soc., Chem. Commun. 1986:1722–1724. [Google Scholar]
  • 49.Whitfield SR, Sanford MS. J. Am. Chem. Soc. 2007;129:15142–15143. doi: 10.1021/ja077866q. [DOI] [PubMed] [Google Scholar]
  • 50.a Furuya T, Ritter T. J. Am. Chem. Soc. 2008;130:10060–10061. doi: 10.1021/ja803187x. [DOI] [PubMed] [Google Scholar]; b Furuya T, Benitez D, Tkatchouk E, Strom AE, Tang P, Goddard WA, III, Ritter T. J. Am. Chem. Soc. 2010;132:3793–3807. doi: 10.1021/ja909371t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.a Giri R, Chen X, Yu J-Q. Angew. Chem. Int. Ed. 2005;44:2112–2115. doi: 10.1002/anie.200462884. [DOI] [PubMed] [Google Scholar]; b Jordan-Hore JA, Johansson CCC, Gulias M, Beck EM, Gaunt MJ. J. Am. Chem. Soc. 2008;130:16184–16186. doi: 10.1021/ja806543s. [DOI] [PubMed] [Google Scholar]; c Qin C, Lu W. J. Org. Chem. 2008;73:7424–7427. doi: 10.1021/jo801345b. [DOI] [PubMed] [Google Scholar]; d Neumann JJ, Rakshit S, Dröge T, Glorius F. Angew. Chem. Int. Ed. 2009;48:6892–6895. doi: 10.1002/anie.200903035. [DOI] [PubMed] [Google Scholar]; e Wang X, Mei T-S, Yu J-Q. J. Am. Chem. Soc. 2009;131:7520–7521. doi: 10.1021/ja901352k. [DOI] [PubMed] [Google Scholar]; f Zhang Y-H, Shi B-F, Yu J-Q. Angew. Chem. Int. Ed. 2009;48:6097–6100. doi: 10.1002/anie.200902262. [DOI] [PMC free article] [PubMed] [Google Scholar]; g Wang G-W, Yuan T-T. J. Org. Chem. 2010;75:476–479. doi: 10.1021/jo902139b. [DOI] [PubMed] [Google Scholar]
  • 52.For detailed investigation of the relevance of dinuclear Pd(III) complexes in catalysis, see: Powers DC, Xiao DY, Geibel MAL, Ritter T. manuscript submitted.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1_si_001
NIHMS238678-supplement-1_si_001.pdf (5.2MB, pdf)
2_si_002
NIHMS238678-supplement-2_si_002.cif (30.9KB, cif)
3_si_003
NIHMS238678-supplement-3_si_003.cif (32.5KB, cif)
4_si_004
NIHMS238678-supplement-4_si_004.cif (23.8KB, cif)
5_si_005
NIHMS238678-supplement-5_si_005.cif (39.3KB, cif)

RESOURCES