Protein Flexibility and Conformational Entropy in Ligand Design Targeting the Carbohydrate Recognition Domain of Galectin-3

Abstract

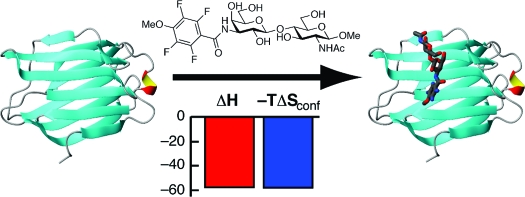
Rational drug design is predicated on knowledge of the three-dimensional structure of the protein−ligand complex and the thermodynamics of ligand binding. Despite the fundamental importance of both enthalpy and entropy in driving ligand binding, the role of conformational entropy is rarely addressed in drug design. In this work, we have probed the conformational entropy and its relative contribution to the free energy of ligand binding to the carbohydrate recognition domain of galectin-3. Using a combination of NMR spectroscopy, isothermal titration calorimetry, and X-ray crystallography, we characterized the binding of three ligands with dissociation constants ranging over 2 orders of magnitude. ¹⁵N and ²H spin relaxation measurements showed that the protein backbone and side chains respond to ligand binding by increased conformational fluctuations, on average, that differ among the three ligand-bound states. Variability in the response to ligand binding is prominent in the hydrophobic core, where a distal cluster of methyl groups becomes more rigid, whereas methyl groups closer to the binding site become more flexible. The results reveal an intricate interplay between structure and conformational fluctuations in the different complexes that fine-tunes the affinity. The estimated change in conformational entropy is comparable in magnitude to the binding enthalpy, demonstrating that it contributes favorably and significantly to ligand binding. We speculate that the relatively weak inherent protein−carbohydrate interactions and limited hydrophobic effect associated with oligosaccharide binding might have exerted evolutionary pressure on carbohydrate-binding proteins to increase the affinity by means of conformational entropy.

Introduction

Structure-based ligand design is an established tool in drug discovery research. Nonetheless, designing ligands on the basis of knowledge of the target protein structure alone represents a formidable challenge.(1) Ligand design benefits from detailed knowledge of the thermodynamics of ligand binding, which can be broken down into separate contributions from enthalpy and entropy,(2) which in turn should ideally be further partitioned into contributions from separate interactions or degrees of freedom.(3) Ligand design efforts typically concentrate on optimizing drug−target interactions, which essentially relate to enthalpy. Entropy is primarily considered in the context of the hydrophobic effect and solvation, which are believed to govern this term.^1,4 However, this view has been questioned on the basis of analyses of a database covering thermodynamics of ligand binding to proteins as measured by isothermal titration calorimetry (ITC), which suggest that conformational entropy might contribute significantly to binding affinity.(5) Indeed, recent advances in computational and experimental approaches support this notion. Changes in conformational entropy of the ligand upon binding have been investigated, underlining the advantage of designing conformationally restricted ligands.^6,7 Similarly, several studies have indicated that protein conformational entropy can contribute significantly to the free energy of ligand binding.⁸⁻¹⁶ Despite these observations, protein flexibility has been considered in drug design mainly in the context of improved docking methods to predict ligand−protein complexes,^7,17−19 although the need to account explicitly for protein conformational entropy has recently become recognized in this field.^14,20

Nuclear spin relaxation is the only experimental method available to date that enables site-specific investigations of conformational entropy.^9,21,22 It has been recognized for some time that NMR order parameters report on the entropy of bond-vector fluctuations.^9,23,24 More recently, molecular dynamics simulations in combination with NMR relaxation studies have demonstrated that order parameters provide estimates of the conformational entropy of the protein backbone^25,26 and side-chain dihedral angles.^26,27 Applications of this approach have revealed details of conformational entropy changes upon ligand binding in a number of systems.^{9−11,16,25,28−37}

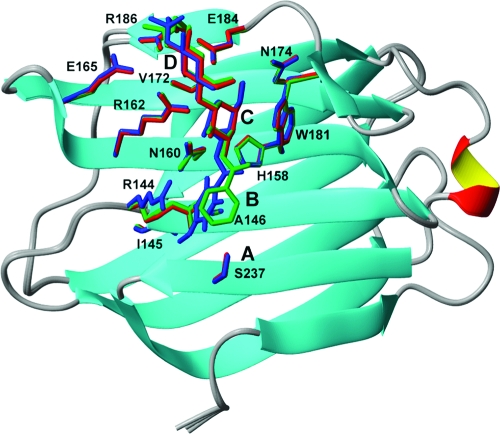
In an ongoing effort, we have designed a series of synthetic ligands that bind to the carbohydrate recognition domain of galectin-3 (Gal3C),³⁸⁻⁴⁷ a protein that plays an important role in cell growth, cell differentiation, cell-cycle regulation, and apoptosis, making it a potential target for therapeutic intervention in inflammation and cancer.⁴⁸⁻⁵³ Galectins represent a family of proteins defined by a 135 amino acid carbohydrate recognition domain (CRD) with affinity for β-galactoside-containing glycans.(54) The galectin CRD is folded into two slightly bent antiparallel β-sheets, and the concave surface of the ligand-binding sheet forms a groove that is long enough to accommodate a tetrasaccharide and therefore may be divided into subsites A, B, C, and D (Figure 1).(54) Subsite C is the galectin-defining β-galactoside binding site, and it is formed by a conserved amino acid sequence motif involving residues H158, N160, R162, N174, and E184 (numbered according to the galectin-3 sequence), which make specific hydrogen bonds to the ligand, and W181, which stacks against the galactose moiety.(55) Galectins bind galactose with affinities of 5−20 mM, and additional interactions in the more variable adjacent subsites yield affinities in the low micromolar range for natural oligosaccharides.^54,56,57 Galectin-3 preferentially binds Galβ1−4GlcNAc (LacNAc) in subsites C and D with K_d ≈ 60 μM; again, higher affinities can be achieved with suitable additional ligand substituents targeting subsites A and B.

Figure 1.

Crystal structures of Gal3C complexed with lactose (red; PDB entry 2nn8(96)), ligand L2 (green; PDB entry 2xg3), and ligand L3 (blue; PDB entry 1kjr(39)). Side chains of residues that are within 5 Å of the ligands are shown in the stick representation using the same color code as for the ligands. Ligand-binding subsites A, B, C, and D are indicated (see the text for details).

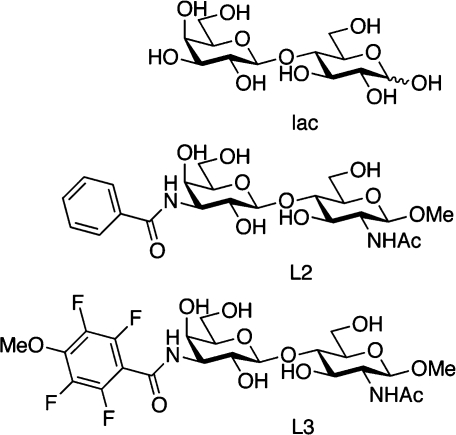
Galectins typically cross-link glycoprotein LacNAc-containing glycans to form galectin−glycoprotein lattices that serve to increase the residence time of glycoproteins at cell surfaces and hence prolong/enhance their activity⁵⁸⁻⁶⁰ or prevent protein−protein interactions (e.g., in CD8−TCR colocalization), resulting in anergy of tumor-infiltrating lymphocytes.(61) Such multivalent binding has been suggested to increase affinity,(62) but it remains unknown how this binding mode compares to monovalent binding mediated by additional interactions throughout the extended region encompassing subsites A−D.(57) The binding free energy for small saccharide ligands is generally dominated by enthalpic contributions and has an unfavorable entropic contribution.^39,62,63 The low affinity reflects inherent properties of saccharides, such as their lack of charge and lack of extended hydrophobic surfaces, which limit the potential of tight binding to proteins. Instead, protein binding is based on relatively weak van der Waals contacts and hydrogen bonds involving the carbohydrate hydroxyl groups and acetamides as well as ring and glycosidic oxygens. As a result, the design of high-affinity inhibitors originally posed a significant challenge, although recent advances have resulted in compounds with submicromolar affinities through the introduction of additional chemical groups projecting into subsites B and D.^39,40,43,47 The set of ligands characterized in the present work comprises lactose (lac) and the first-generation low-micromolar inhibitors 3′-benzamido-N-acetyllactosamine (L2) and 3′-(4-methoxy-2,3,5,6-tetrafluorobenzamido)-N-acetyllactosamine (L3), which have been described previously(39) (see Chart 1). The canonical interactions of natural ligands are largely mirrored in complexes between Gal3C and designed ligands based on LacNAc,^39,55 which are further stabilized by interactions involving arginine side chains and hydrophobic moieties, including the side chains of A146 and V172 (Figure 1).

Chart 1. Chemical Structures of the Three Ligands: Lactose (lac), 3′-Benzamido-N-acetyllactosamine (L2), and 3′-(4-Methoxy-2,3,5,6-tetrafluorobenzamido)-N-acetyllactosamine (L3).

Here we investigated the role of protein conformational entropy in ligand binding to Gal3C using a combination of NMR spectroscopy, ITC, and X-ray crystallography. Our results demonstrate that protein conformational entropy makes significant favorable contributions to the free energy of ligand binding and that it varies significantly among the complexes as a result of an intricate interplay between structure and conformational fluctuations.

Experimental Section

Protein Expression and Purification

The galectin-3 CRD (Gal3C; amino acid residues 113−250) was expressed and purified as either a thioredoxin fusion construct(25) or isolated Gal3C. The expression protocol was identical for the two constructs and has been reported elsewhere.(25) The purification protocol for isolated Gal3C was very similar to that reported previously,^25,64 except that the final steps including and following cleavage were omitted. ¹⁵N/¹³C/²H-labeled Gal3C was expressed in 60% D₂O using published protocols.(65) To obtain stereospecific methyl assignments, one culture was grown on a mixture of 10% uniformly ¹³C-labeled and 90% unlabeled glucose.(66) Typical yields of isolated Gal3C were 100−150 mg/L of culture.

X-ray Crystallography

Gal3C (1.2 mM) was prepared in 10 mM phosphate-buffered saline (PBS) (pH 7.5, 100 mM NaCl, 10 mM β-mercaptoethanol, and 0.02% NaN₃). A 9.5 μL sample was mixed with 0.5 μL of 100 mM L2 and incubated for 2 h on ice, after which the mixture was centrifuged at 7000 rpm and 4 °C for 10 min prior to crystallization. Crystals were obtained from drops containing 2 μL of protein solution + 2 μL of reservoir solution [30 % (w/v) poly(ethylene glygol) (PEG) 4000, 0.1 M Tris-HCl (pH 7.5), 0.1 M MgCl₂, 0.4 M NaSCN, 8 mM β-mercaptoethanol] in NeXtal plates (QIAGEN). The drops were streak-seeded immediately after setup using apo-Gal3C crystals grown under the same conditions without ligand. Crystals appeared overnight and grew within a few days to 0.2 mm × 0.2 mm × 0.3 mm. The largest crystals had visible cracks and did not diffract well.

A crystal with dimensions of 0.1 mm × 0.1 mm × 0.1 mm was flash-cooled to 100 K in the cold gas stream of an Oxford Diffraction Cryojet using a cryo solution consisting of 4 mM L2, 15% glycerol, 25.5% (w/v) PEG 4000, 0.255 M NaSCN, 85 mM Tris-HCl (pH 7.5), 85 mM MgCl₂, and 7 mM β-mercaptoethanol. Diffraction data were collected at MAX-lab beamline I911-5 (Lund University), processed using XDS,(67) and scaled using XSCALE(67) and SHELXL.(68)

The structure of the L2−Gal3C complex was determined using molecular replacement starting from another Gal3C complex (1.08 Å resolution) with the ligand omitted. The calculation of the free R factor employed 5% of the reflections. Refinement was performed using SHELXL.(68) Because of the similarities in the unit cell dimensions, the refinement could be started at 1.5 Å resolution. The initial R factor was 0.144 (R_free = 0.231) following conjugate-gradient least-squares refinement to 1.5 Å using anisotropic B factors. Gradually the resolution was increased to 1.2 Å, and then the L2 molecule was fitted into the electron density maps, leading to a decrease in R_free to 0.212 (R = 0.145). The structure of L2 was generated using the CCP4 program Monomer Library Sketcher and Libcheck,(69) as were restraints used in the graphic program Coot.(70) Riding hydrogen atoms were included in the later rebuilding and refinement cycles to yield a final R factor of 0.138 (R_free = 0.193).

NMR Sample Preparation

Lactose-bound Gal3C and apo-Gal3C samples were prepared as reported previously.(25) Ligands L2 and L3 were dissolved in dimethyl sulfoxide (DMSO) stock solutions to concentrations of 120 and 60 mM, respectively. Ligand complexes were prepared by titrating the ligand into apo-Gal3C samples while monitoring the Gal3C chemical shifts in the ¹⁵N heteronuclear single-quantum correlation (HSQC) spectra. At the end of each titration, the total amount of added DMSO was 2% (v/v). The concentration of ¹⁵N-labeled Gal3C complexed with ligand was 0.4 mM in both cases, while that of the ¹⁵N/¹³C-labeled samples was 0.7 mM. The ¹⁵N/¹³C/²H-labeled samples were 0.9 mM (apo), 0.8 mM (lac), and 0.4 mM (L2 and L3). All of the NMR samples included small amounts of NaN₃, DSS, and ²H₂O.

Chemical Shift Assignments

Backbone chemical shifts of apo-Gal3C and lac-bound Gal3C have been reported previously for the present construct (residues 113−250)(25) as well as for a longer construct comprising residues 107−250.^71,72 Backbone chemical shifts of L2- and L3-bound Gal3C were assigned using HNCACB spectra.(73) Arginine side-chains were assigned using CCC-TOCSY-NEHE(74) and CCONH.(75) Methyl groups were assigned using a combination of CCONH,(76) HCCONH,(76) HCCH-TOCSY,(77) and CCmHm-TOCSY experiments.(78) Methyl groups of valines and leucines were stereospecifically assigned on the basis of a constant-time ¹H−¹³C HSQC spectrum acquired on the 10% ¹³C-labeled sample, as described elsewhere.^66,79

Spectra were processed using NMRPipe.(80) The processing protocol involved a solvent filter, cosine apodization functions, zero filling to twice the number of increments in all dimensions, and baseline correction in the ¹H dimension. Resonance assignments were carried out using the CcpNmr suite.(81) Chemical shift differences between the apo and ligand-bound states of Gal3C were evaluated as the weighted chemical shift differences for backbone amides, {[Δδ(¹H)]² + [0.1Δδ(¹⁵N)]²}^1/2, and for methyl groups {[Δδ(¹H)]² + [0.25Δδ(¹³C)]²}^1/2.(82) The root-mean-square deviation (RMSD) of the chemical shift between states was calculated as RMSD = [∑_i(δ_A,i − δ_B,i)²/N]^1/2, where the sum runs over the N resonances i that are available in both states A and B.

Relaxation Experiments and Data Analysis

R₁, R₂, and {¹H}−¹⁵N nuclear Overhauser effect (NOE) experiments^83,84 targeting the ¹⁵N spins of the backbone and tryptophan side chain indole were performed on apo and ligand-bound Gal3C at static magnetic field strengths of 11.7 and 14.1 T. Typically, 8−12 data points were acquired, interleaved with relaxation delays in the range 0−1 s for R₁ or 0−0.192 s for R₂, using a delay between experiments of 2.0 s. R₂ was measured using a 0.6 ms delay between refocusing pulses in the CPMG train. {¹H}−¹⁵N heteronuclear NOEs were measured in an interleaved manner using a ¹H saturation time of 7 s and a recycle delay of 10 s between acquisition and the first ¹⁵N pulse in both the NOE and control experiments. For the saturation of the proton magnetization, 180° pulses were used.(85) The spectral widths were 8013 and 1835 Hz in the ¹H and ¹⁵N dimensions, respectively, covering 1024 and 128 points. The carrier frequencies of ¹H and ¹⁵N were placed on the water frequency and in the center of the backbone amide region, respectively. Experiments targeting the arginine side-chain guanidino groups were performed essentially as described for the backbone except that the ¹⁵N carrier was placed at 72 ppm and the spectral widths were 8013 Hz (1024 points) and 2880 Hz (128 points). The recycle delay in the NOE experiment was 15 s in order to allow full relaxation of flexible side chains.

R₁(2N_zH_z), R₂(2N_xH_z), R₂(2N_zH_x), and R₂(2N_xH_x) relaxation experiments^86,87 were acquired for apo-Gal3C at 11.7 T using a sample with 60% ²H incorporation. Relaxation decays were sampled by nine data points covering delays of 2−30 ms using a recycle delay of 2 s and spin-lock field strengths of 13.1 kHz (¹H) and 2.1 kHz (¹⁵N). The ¹H carrier frequency was placed at 9.5 ppm during the spin-lock. The exchange-free transverse relaxation rate was obtained as the linear combination R_2dd = [R₂(¹⁵N_x¹H_z) + R₂(¹⁵N_z¹H_x) − R₂(¹⁵N_x¹H_x) − R₁(¹⁵N_z¹H_z)]/2.

R(D_z), R(3D_z² − 2), R(D₊), and R(D₊D_z + D_zD₊) relaxation experiments(88) were performed on the ²H-labeled methyl groups of apo and ligand-bound Gal3C at a static magnetic field strength of 14.1 T. The spectral widths were 8012 and 3000 Hz in the ¹H and ¹³C dimensions, respectively, covering 1024 and 84 points. The B₁ field strength of the ²H channel was 1.05 kHz. Relaxation data were acquired using interleaved delays in the range 0−40 ms for R(D_z) and R(3D_z² − 2) or 0−20 ms for R(D₊) and R(D₊D_z + D_zD₊) and were sampled by 8−12 data points. A recycle delay of 2.0 s was used in all of the experiments.

All of the experiments were acquired at a temperature of 301 ± 0.1 K, which was calibrated using a methanol sample prior to each series of experiments.

All of the spectra were processed using two different apodization schemes. Most peaks were resolved using squared cosine window functions in both dimensions, while a subset of peaks benefited from a cosine window function in the indirect dimension. In the case of the arginine side chains in lac−Gal3C, the high-resolution apodization scheme involved Lorentzian-to-Gaussian window functions in both dimensions with an inverse exponential width of 5.0 Hz and a Gaussian width of 5.0 Hz. Peak intensities were measured as the summed signal in windows of 5 × 3 (¹H × ¹⁵N/¹³C) points centered on the peak. The signal-to-noise ratio (S/N) was estimated by calculating the standard deviation of 200 samples of integrated 5 × 3-point windows in empty regions of each spectrum. Monoexponential functions were fitted to the R₁ and R₂ decays using the Levenberg−Marquardt minimization routine(89) as implemented in C programs developed in-house. Errors in the fitted parameters were estimated from 1000 synthetic data sets created using Monte Carlo simulations.^89,90 Each NOE was calculated as the ratio of the peak intensities in the saturated and unsaturated experiments. The S/N was estimated as described above, and the errors in the NOEs were determined by error propagation. The trimmed mean and standard deviation were calculated for each data set of R₁, R₂ and NOE, where residues outside of two standard deviations were excluded in a single pass.

Model-Free Optimization

The global correlation time was initially estimated by fitting the iteratively trimmed R₂/R₁ ratio to an isotropic tensor using in-house routines implemented in MATLAB (The Mathworks, Inc., Natick, MA). The model-free analysis used an N−H bond length of 1.02 Å and a chemical shift anisotropy (CSA) of −172 ppm for the ¹⁵N backbone spins.(91) Backbone model-free parameters were fitted using the program suite relax(92) with scripts modified in-house. Four different diffusion tensors (spherical, oblate, prolate, and asymmetric) were considered. In each case, the optimization was performed iteratively by fixing the diffusion tensor and optimizing five different models of the local motion for each residue, as described elsewhere.^90,92 Next, the parameters describing the diffusion tensor and local motion were optimized simultaneously. The optimized parameters were taken as input for the next round of optimization. This procedure was iterated until the diffusion tensor and model-free parameters converged. Following convergence of the diffusion tensor parameters, the Akaike information criterion(93) (AIC) was used to select models. Errors in the fitted model-free parameters were estimated using the Monte Carlo approach with 1000 synthetic data sets and a fixed diffusion tensor.(90)

R_2dd rates were back-calculated from the optimized model-free parameters and compared to the experimental data to verify that the former accurately represent conformational fluctuations on time scales faster than overall rotational diffusion.

In the case of the arginine and tryptophan side-chain N^ε−H^ε groups, only the local motional models were fitted to each residue, while the diffusion tensor parameters were fixed at those obtained in the model-free analysis of the backbone relaxation data. The CSA values of the N^ε spins were set to −114 ppm for arginine(27) and 89 ppm for tryptophan.(94)

Model-free parameters for the side-chain methyl groups were optimized against the experimental relaxation rates using in-house routines implemented in MATLAB. Two different models containing two (O², τ_f) or three (O², τ_f, τ_eff) parameters were considered, assuming an isotropic diffusion tensor.(95) Enforcing an isotropic diffusion model resulted in systematic errors of <3% in the back-calculated ²H relaxation rates; this value was much less than the typical variation between states. Model selection was based on the F test by accepting the three-parameter model on the level p < 0.1. The global correlation times were determined by ¹⁵N relaxation as described above.

Calculation of Entropy from Order Parameters

We estimated the change in backbone conformational entropy from the backbone order parameters using the previously described relationship^9,26

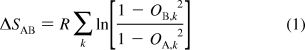where ΔS_AB is the change in entropy upon going from state A to state B, O_X,k is the order parameter for residue k in state X, and the sum runs over all of the residues. Similarly, the change in side-chain entropy was evaluated following Li and Brüschweiler:(26)

where C_m is a function of the number of side-chain dihedral angles in a given residue type and a fit parameter and the sums run over all residues n of types m. C_m = 1.32 for V and T, 3.1 for I and L, and 2.31 for M. For tryptophan, C_m was set to 3.02 on the basis of the value reported for F, Y, and H.(26) The side-chain entropy of alanine was evaluated using eq 1. Arginines were not included because the N^ε−H^ε bond vector alone does not provide a reliable probe of side-chain entropy;^26,27 also, there were no major differences in the arginine O² values for the various states (see below).

Isothermal Titration Calorimetry

Samples for ITC were prepared by extensive dialysis against 5 mM HEPES (pH 7.4) to remove lactose. ITC titrations were performed using a MicroCal VP-ITC system at 301 K with 30 injections of 10 μL (first injection 5 μL) of ligand in 5 mM HEPES (pH 7.4) and a delay of 300 s between injections. The concentration of Gal3C was 10−100 μM. Reference injections of ligand into buffer were performed to measure the heat of dilution for each ligand, which was subtracted from the integrated data prior to curve fitting. L2 and L3 were dissolved in a stock solution of DMSO. In order to avoid heating effects due to differing concentrations of DMSO in the injectant and protein solutions, DMSO was added to the protein and reference solutions. Less than 1% (v/v) DMSO was used for titrations. Origin software (Microcal) was used to fit the titration curve to a one-site model given by

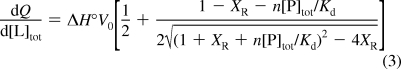where dQ/d[L]_tot is the incremental heat of binding with respect to the change in total concentration of the ligand, ΔH° is the standard enthalpy of binding, V₀ is the effective volume of the calorimeter cell, X_R is the ratio of the total ligand and receptor concentrations at any given point during the titration, n = 1 is the number of binding sites, K_d is the dissociation constant, and [P]_tot is the total protein concentration. Errors in ΔH° and K_d were estimated from the asymptotic covariance matrix of the regression coefficients and propagated to ΔG° and TΔS°.

Results and Discussion

We used a combination of NMR spectroscopy, ITC, and X-ray crystallography to investigate the binding of three ligands to Gal3C. ITC provided the thermodynamic fingerprint of the binding process, which served as a starting point for unraveling the different contributions to the free energy of ligand binding. High-resolution crystal structures of protein−ligand complexes were a prerequisite for interpreting binding affinity in terms of detailed molecular interactions. NMR relaxation provided information on the conformational flexibility of the protein complexes and the associated entropic contributions to the free energy of binding. ¹⁵N spin relaxation probed the backbone as well as the arginine and tryptophan side chains via the secondary amines (N^ε−H^ε) in the tryptophan indole and arginine guanidino groups, enabling us to investigate detailed interactions in the ligand-binding site. Methyl groups partially labeled with ²H probed the hydrophobic core between the two β-sheets as well as contacts with the designed ligands in the extended binding site. Thus, the combination of ¹⁵N and ²H relaxation experiments provided information on conformational entropy changes throughout the protein upon ligand binding.

Ligand Coordination Differs among the Complexes

We based our investigations on high-resolution X-ray crystal structures of Gal3C complexed with each ligand. Here we report the X-ray crystal structure of Gal3C complexed with the designed ligand L2 (Chart 1) at a resolution of 1.20 Å and an R_free value of 19.3%. The final model (PDB entry 2xg3) includes 138 amino acids, 232 water molecules, and 1 chloride ion. Ligand L2 could be traced unambiguously in the electron density. Table S1 in the Supporting Information summarizes the quality statistics of the L2−Gal3C structure. Together with the previously reported structures of lac−Gal3C (PDB entry 2nn8)(96) and L3−Gal3C (PDB entry 1kjr),(39) which were determined at 1.35 and 1.55 Å resolution, respectively, the L2−Gal3C structure formed a solid structural basis for the present work (Figure 1).

Comparisons of the various ligand-bound structures revealed variations in binding mode. Gal3C generally showed very minor differences among the ligand-bound states, with RMSDs of <0.15 Å between C^α atoms in all pairwise comparisons. Significant conformational changes occur for a limited number of hydrophilic side chains, while the hydrophobic core is virtually identical in all four states. The side chains of K176, R183, and R186 exhibit minor conformational changes among the various ligand-bound states. R183 adopts conformations that point away from the protein surface in all cases, whereas the orientations of K176 and R186 reflect slight differences in ligand orientation in subsite D (Figure 1). As observed previously, the R144 side chain is oriented differently in lac−Gal3C and L3−Gal3C, forming a cation−π interaction in the latter complex.(39) In L2−Gal3C, the R144 side chain has the same orientation as in lac−Gal3C, but the aryl group of the ligand, located in subsite B, is nearly orthogonal to the orientation observed in L3−Gal3C (Figure 1). This arrangement largely maintains the cation−π interaction, even though the guanidino group is shifted slightly to the side of the aromatic ring. Potentially, this conformational change might be driven by the different solvation and electrostatic properties expected for the fluorinated aryl ring in L3 in comparison with the nonfluorinated one in L2.(97) The fluorine substituents on the C6 and C7 atoms of the aryl ring interact with the side chain of N160 in a geometry typical for this type of recognition mode.(97)

Taken together, our results demonstrate that the flexibilities of both the ligand and the protein play significant roles in modulating the binding interactions in the complex, underlining the advantage of determining the structure of each complex rather than relying solely on computational approaches such as docking.

Chemical Shift Mapping Confirms Ligand Binding in Solution

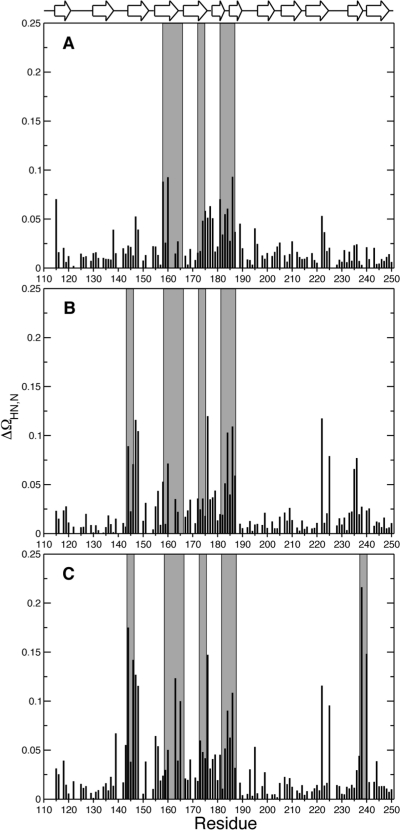
We verified that the ligand binding in solution agreed with that observed in the crystal structures. The NMR chemical shift is an exquisitely sensitive probe of the local magnetic field, which depends on the molecular structure. The chemical shifts of apo-Gal3C and lac−Gal3C have been reported previously.(25) Backbone chemical shift assignments for L2−Gal3C and L3−Gal3C were obtained by transferring the assignments from lac−Gal3C based on the HNCACB experiment.(73) The chemical shift changes observed for L2− and L3−Gal3C relative to apo-Gal3C are more extensive than those for lac−Gal3C, as expected from the larger size and the aromatic moieties of the designed ligands, but are still relatively small in magnitude (Figure 2). The chemical shift RMSDs between the apo and ligand-bound states are 0.02 and 0.14 ppm (lac), 0.03 and 0.19 ppm (L2), and 0.05 and 0.24 ppm (L3) in the ¹H and ¹⁵N dimensions, respectively. The backbone amide ¹H−¹⁵N chemical shift differences between apo-Gal3C and each of the three complexes were primarily observed for residues in proximity of the bound ligand (Figure 2a−c), and the same areas generally showed the greatest coordinate RMSD between the apo and ligand-bound states (Figure S1 in the Supporting Information). The affected residues are primarily located across the ligand-binding β-sheet and adjacent loops. Notable exceptions include N222 and V225 (Figure 2), which are situated in a distal loop between strands in the β-sheet that does not bind the ligand.

Figure 2.

Chemical shift differences between apo-Gal3C and the ligand-bound complexes. Δδ is plotted vs residue number for (A) Δδ(lac−apo), (B) Δδ(L2−apo), and (C) Δδ(L3−apo). Secondary structure elements are indicated at the top of the graph. Residues within 5 Å of the ligand are highlighted by gray bars.

The chemical shifts of the methyl region in Gal3C are largely unaffected by ligand binding, as expected from the high structural similarity of the four states. RMSD values between the apo and bound states were 0.002 and 0.013 ppm (lac−apo), 0.007 and 0.036 ppm (L2−apo), and 0.016 and 0.052 ppm (L3−apo) in the ¹H and ¹³C dimensions, respectively. There were only two cases of weighted ¹H/¹³C chemical shift differences greater than 0.05 ppm, which were observed for I145δ1 and V172γ1 in L3−Gal3C. The methyl groups of V172 are in close contact with the lactose scaffold of the ligands. In contrast, the chemical shift change for I145δ1 methyl is noteworthy in view of the fact that the methyl group is located >5 Å from the ligand and points away from the binding site into the hydrophobic core. It is possible that this shift is a relayed effect due to the conformational change of R144 described above.

There were no contiguous residues outside of the confirmed binding site (identified by crystallography) with significant backbone or side-chain chemical shift perturbations (Δδ > 0.05 ppm) that might indicate secondary binding in solution. Thus, the chemical shift mapping demonstrates that all of the ligands bind to the same site with a stoichiometry of 1:1.

Ligand Binding is Enthalpically Favored but Entropically Disfavored

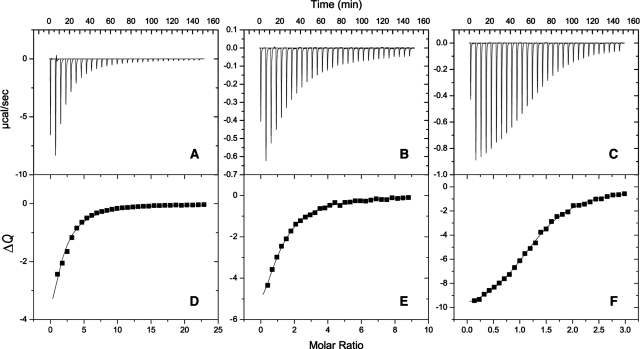
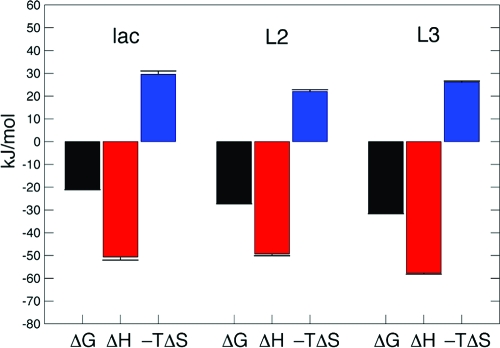
We characterized the thermodynamics of ligand binding by ITC measurements. The dissociation constant of each ligand falls in the micromolar range amenable to determination by ITC, as demonstrated by the binding isotherms in Figure 3. Thus, we analyzed the ITC data to determine ΔH°, ΔG°, and ΔS° for the binding process. The ITC data were adequately fit to a single-site model for the binding of each ligand to Gal3C, as expected from the NMR and X-ray data. The resulting dissociation constants span a range of nearly 2 orders of magnitude: K_d = 231 μM for lactose, 18 μM for L2, and 3 μM for L3 (Table 1). The K_d values measured by ITC are consistently higher by a factor of 4 than those determined previously using a fluorescence polarization assay,^39,98 but the relative affinities remain essentially unchanged. For all three ligands, binding is driven by a large enthalpic contribution but is entropically disfavored (Figure 4, Table 1), in keeping with previous results for other ligands.^39,43,99 In the case of lactose binding to Gal3C, ITC measurements were performed using different buffers to examine whether ligand binding affects the protonation equilibria.(100) Experiments performed using phosphate or Tris buffers yielded identical results (data not shown), indicating that ligand binding does not involve ionization of titrating groups in the protein.

Figure 3.

Enthalpy of ligand binding to Gal3C. ITC data characterizing complex formation between Gal3C and (A, D) lactose, (B, E) L2, and (C, F) L3 are shown. Panels (A−C) present the experimental ITC data and panels (D−F) the extracted heats of binding, ΔQ, as a function of added ligand together with the fitted binding curves. The temperature was 301 K.

Table 1. Thermodynamics of Ligand Binding to Gal3C.

ligand	Kd (μM)	ΔG° (kJ/mol)	ΔH° (kJ/mol)	−TΔS° (kJ/mol)a
lactose	231 ± 15	−21.0 ± 0.2	−50.6 ± 1.4	30 ± 1
L2	18.2 ± 0.2	−27.3 ± 0.1	−49.3 ± 0.8	22.0 ± 0.8
L3	3.3 ± 0.1	−31.6 ± 0.1	−57.7 ± 0.5	26.1 ± 0.5

^aT = 301 K.

Figure 4.

Comparison of the binding thermodynamics of Gal3C complexes at T = 301 K: (left) lac−Gal3C, (center) L2−Gal3C, and (right) L3−Gal3C. The free energies of binding, ΔG°, were determined using K_d values from the titration curves (see Figure 3), after which the equation −TΔS° = ΔG° − ΔH° was used. Legend: black, ΔG°; red, ΔH°; blue, −TΔS°. Error bars indicate one standard deviation.

Notably, the present series of ligands does not exhibit enthalpy−entropy compensation; rather, the lowest-affinity binder (lactose) has the least negative (least favorable) ΔH° value and the most positive (most unfavorable) value of −TΔS°, while L2 shows a ΔH° value comparable to that of lactose but a significantly lower ΔS°; the highest-affinity binder (L3) shows the most favorable ΔH° and an intermediate value of ΔS° (Figure 4, Table 1). These trends might be expected on the basis of the chemical nature of the ligands. In particular, the less unfavorable ΔS° values observed for the designed ligands can be rationalized by their increased hydrophobicity, which tends to favor binding through the hydrophobic effect. In qualitative terms, the unfavorable ΔS° values can be rationalized in terms of the expected entropic penalties associated with the translational, rotational, and vibrational degrees of freedom of the ligands upon binding. Given the differences in the overall entropies of complex formation for the various ligands, we next asked whether ΔS° is governed solely by solvation and ligand entropy or whether the conformational entropy of the target protein plays a role in modulating the affinity and specificity.

NMR Relaxation Data

To obtain residue-specific information on the conformational entropy, we characterized the protein backbone and side-chain fluctuations using ¹⁵N and ²H spin relaxation experiments and interpreted these within the model-free framework.^101−103 We have previously published ¹⁵N R₁ and R₂ relaxation rates acquired at static magnetic field strengths of 11.7 and 14.1 T, together with {¹H}−¹⁵N NOEs acquired at 14.1 T, for the backbone amides, tryptophan indoles, and arginine guanidino groups of Gal3C in the apo and lac-bound states.(25) The present work is based on ¹⁵N relaxation data (R₁, R₂, and NOEs) acquired at 11.7 and 14.1 T together with ²H relaxation data [R(D_z), R(3D_z² − 2), R(D₊), and R(D₊D_z + D_zD₊)] acquired at 14.1 T for methyl groups in the apo state and lac-, L2-, and L3-bound states. In addition, the exchange-free transverse relaxation rate R_2dd was obtained for apo-Gal3C from a series of four ¹⁵N−¹H relaxation rates acquired at 11.7 T following Hansen and co-workers^86,87 in order to assess the extent of conformational exchange contributions to R₂.

Relaxation rates were measured for 111 backbone amides in apo-Gal3C, 116 in lac−Gal3C, 115 in L2−Gal3C, and 106 in L3−Gal3C. The lower number of observations in L3−Gal3C is due to a greater degree of spectral overlap in this state than in the other three states. The relaxation data are relatively uniform throughout the sequence for all four states (Figure S2 in the Supporting Information; see Table S2 in the Supporting Information for a summary of the relaxation rates). The mean values and standard deviations of the relaxation data for the ligand-bound states indicate that they are highly similar on average, although significant differences occur for individual residues. These differences are further analyzed in the following sections in terms of order parameters and conformational entropies.

¹⁵N relaxation rates were measured for seven side chains in L2−Gal3C and six in apo-, lac−, and L3−Gal3C. Five residues (R129, R162, R168, W181, and R224) could be characterized in all four states. As expected, the side-chain data exhibited a greater degree of variation among sites than the backbone data (Figure S2), but the variations among states were relatively minor. Two weak cross-peaks in L2−Gal3C arising from N^ε−H^ε in R144 yielded identical relaxation rates within the experimental error and exhibited rates similar to those of R162 and R186, which also coordinate the ligand. Thus, there was no indication that either of the two conformations of R144 is more flexible than the other, and they were treated together in the ensuing model-free analysis.

²H relaxation rates were measured for 67 (apo), 66 (lac), 65 (L2), and 63 (L3) methyl groups out of a total of 85. There were 61 methyl groups that could be characterized in all four states, including A146 and V172, which are in contact with ligands L2 and L3. The ²H methyls showed highly variable relaxation rates throughout the sequence as well as significant variation between states, as summarized in Figure S2 and Table S2.

Model-Free Parameters Reveal Changes in Fluctuations upon Ligand Binding

The model-free order parameters report on the amplitudes of conformational fluctuations on time scales faster than overall rotational diffusion.^101−103 Model-free parameters were optimized for the four different states (apo-Gal3C, lac−Gal3C, L2−Gal3C, and L3−Gal3C) using directly comparable experimental data and a common protocol. The diffusion tensors obtained from the model-free optimization were nearly isotropic for each state. The best fits for the apo and lac- and L2-bound states yielded axially symmetric tensors with global correlation times and anisotropies of 7.3 ns and 0.93, 8.0 ns and 1.10, and 7.6 ns and 1.14, respectively. The correlation times for apo-Gal3C and lac−Gal3C were within 2% of those reported previously.(25) lac−Gal3C had a significantly longer correlation time than the other states because the sample contained ∼200 mM lactose (7% by weight), resulting in increased viscosity. For comparison, a pure 7% solution of lactose in water (without protein and buffer) yielded an increase of ∼20% in viscosity at 303 K.(104) Hence, the observed increase in correlation time (6%) is readily explained by the increase in viscosity. The relaxation data for L3−Gal3C were best fit to an ellipsoidal diffusion tensor with a global correlation time of 7.5 ns, an anistropy of 1.12, and a rhombicity of 0.62. Forcing the tensor to be axially symmetric yielded internal model-free parameters identical within experimental error to those obtained with the optimal model. The correlation times obtained here are slightly less than those predicted by hydrodynamics model calculations(105) [7.9 ns (apo), 8.1 ns (lac), 7.8 ns (L2), and 8.2 ns (L3)], indicating that Gal3C is monomeric in solution, in keeping with previous reports based on mass spectrometry and analytical ultracentrifugation.^106,107

We previously reported that the backbone order parameters for apo-Gal3C are slightly higher than those for lac−Gal3C.(25) Here we included additional {¹H}−¹⁵N NOE data obtained at 11.7 T and refitted the model-free parameters to the extended data set. The inclusion of the 11.7 T NOE data set for apo- and lac−Gal3C produced only small changes in the order parameters in comparison with those reported previously(25) [RMSD =0.0083 (lac) and 0.0084 (apo)]. The previous conclusion holds true, as gauged from a paired t test of the difference in order parameters between the two states (p = 1.6 × 10⁻¹⁰).

Prior evidence indicates that proteins may experience pervasive conformational fluctuations on time scales of ∼10 μs and shorter that lead to enhanced R₂ rates,^87,108 which might translate into artificially high order parameters if the problem is not recognized.(109) We verified that the higher order parameters observed for apo-Gal3C did not result from exchange contributions to the transverse relaxation rate by comparing the measured exchange-free R_2dd rates with those back-calculated from the model-free parameters (excluding R_ex) (Figure S3 in the Supporting Information). The mean difference between the experimental and back-calculated values was 0.3 ± 0.4, showing that they agree within experimental error. We conclude that the order parameters determined for apo-Gal3C were not significantly inflated by exchange contributions to R₂.

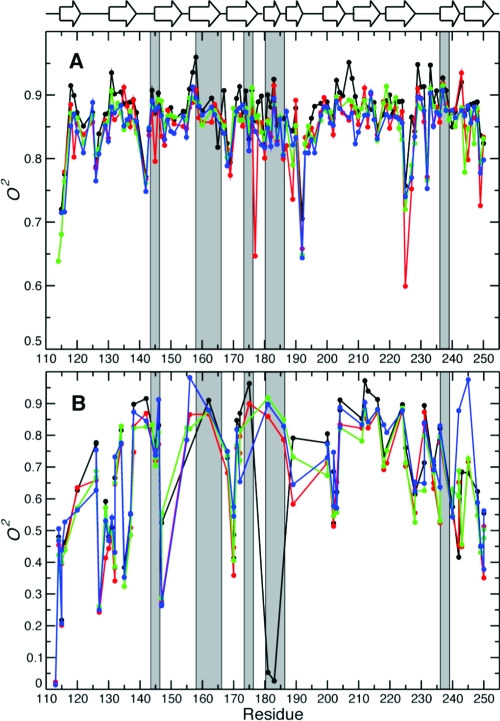
The backbone order parameters of the four states are compared in Figure 5a. Overall, the variation of order parameters along the sequence is highly similar in all four states, although distinct differences are readily apparent, as further discussed below. Comparing the order parameters of L2- and L3-bound Gal3C with those of apo-Gal3C, we find a similar decrease in the order parameters upon binding, with p = 2.5 × 10⁻¹⁵ (L2−Gal3C) and 1.9 × 10⁻²⁰ (L3-Gal2) as determined by a paired t test. Furthermore, the order parameters of L2−Gal3C differ significantly from those of both lac−Gal3C and L3−Gal3C (p = 0.025 and 0.0085, respectively), while the lac−Gal3C and L3−Gal3C states have indistinguishable distributions (p = 0.34). The mean order parameters are 0.87 ± 0.04 for all available backbone amides (N = 111) in the apo state and 0.82 ± 0.14 (N = 114), 0.85 ± 0.05 (N = 114), and 0.85 ± 0.04 (N = 106) for the lac-, L2-, and L3-bound states, respectively. For residues in β-sheets, the mean values are 0.89 ± 0.03 (apo, N = 69), 0.86 ± 0.04 (lac, N = 69), 0.87 ± 0.02 (L2, N = 71), and 0.86 ± 0.03 (L3, N = 70). For residues outside of secondary structure elements, the mean values are 0.85 ± 0.06 (apo, N = 42), 0.77 ± 0.21 (lac, N = 45), 0.82 ± 0.06 (L2, N = 43), and 0.82 ± 0.06 (L3, N = 36).

Figure 5.

Order parameters describing the probability distribution of bond-vector orientations in Gal3C: (A) backbone amide order parameters; (B) side-chain order parameters for arginine and tryptophan ¹⁵N and methyl ²H. Legend: black, apo-Gal3C; red, lac−Gal3C; green, L2−Gal3C; blue, L3−Gal3C. Secondary structure elements are indicated at the top of the graph. Residues within 5 Å of any of the ligands are highlighted by gray bars. For clarity, error bars are not shown. The average error (one standard deviation) was ±0.07 and was relatively uniform throughout the protein. See Table S3 in the Supporting Information for a complete list of fitted model-free parameters and estimated errors.

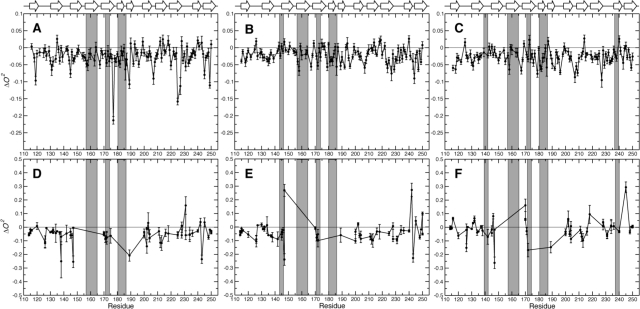
The differences between the backbone order parameters for the apo state and each of the ligand-bound states are shown in Figure 6. Comparing Figures 2 and 6, we find that a subset of residues shows significant changes in both order parameter and chemical shifts, suggesting that changes in motional amplitudes are accompanied by subtle structural adjustments in these cases. Residues with significant changes in both O² and chemical shift are 147, 158, 176−178, 181, and 186 in lac−Gal3C; 144, 158, 183, 186, 225, and 235 in L2−Gal3C; and 144, 146, 148, 155, 176, 183−184, 186, 195, 222, 238, and 240 in L3−Gal3C. Overall, apo-Gal3C appears to be more rigid than the ligand-bound states, with exceptions observed for certain residues (Figure 6). The weighted mean pairwise difference in O² between lac−Gal3C and apo-Gal3C is ⟨ΔO²⟩ = −0.028 ± 0.003 (mean ± standard error of the mean), indicating a significant decrease in order parameter upon binding. The corresponding values for L2−Gal3C and L3−Gal3C are −0.021 ± 0.002 and −0.027 ± 0.002, indicating slightly different responses in the order parameters upon binding. Notably, the observed differences are not localized to the galactoside binding site but occur throughout the protein. Comparing the order parameters for residues in β-sheets, we observe significant differences between the apo state and each of the ligand-bound states as well as between lac−Gal3C and L2−Gal3C (p < 10⁻⁷) and possibly also between L2−Gal3C and L3−Gal3C (p = 0.034), whereas there is no difference between lac−Gal3C and L3−Gal3C (p = 0.29). In the case of residues outside of secondary structure elements, the differences between the O² values for apo-Gal3C and each of the ligand-bound states are significant (p < 10⁻³), while there is no significant difference among the ligand-bound states (p > 0.15). These results indicate that the entire protein backbone responds to ligand binding but that the loop regions do not sense the differences among the various ligands. In contrast, the backbone fluctuations of residues in β-sheets depend to some extent on the nature of the ligand.

Figure 6.

Difference between the order parameters of the ligand-bound states and apo-Gal3C plotted vs residue number: (A−C) backbone H−N order parameters, (D−F) side-chain methyl axis order parameters; (A, D) ΔO²(lac−apo), (B, E) ΔO²(L2−apo), (C, F) ΔO²(L3−apo). Secondary structure elements are indicated at the top of the graph. Residues within 5 Å of the ligand are highlighted by gray bars. Error bars indicate one standard deviation.

Focusing next on residue-specific differences in backbone order parameters between states, we observe patterns of concerted changes across neighboring β-strands. While ligand binding predominantly leads to decreased O² values, stretches of residues show increased values. In lac−Gal3C, this is observed for residues in the nonbinding β-sheet (i.e., A212 and L218) as well as for L135, K199, N214, and T243 (Figure 7a). These residues have identical hydrogen-bonding patterns in all four states. While A212 and L135 have regular hydrogen-bonding patterns typical of antiparallel β-sheets, only the amides (but not the carbonyls) of K199, N214, L218, and T243 are hydrogen-bonded. L218 is located in a kink, and its HN forms an irregular hydrogen bond to V211 CO. N214 is located in the β-hairpin between strands 8 and 9, and its N−H is hydrogen-bonded to the CO of K199. The K199 N−H is hydrogen bonded to the side chain of N214. The T243 N−H forms an irregular hydrogen bond to L135 CO. A212 and L135 are located opposite L218 and K199, respectively, but hydrogen bond to the distal strand in each case (to Q201 and S244, respectively). The neighboring residue pairs (V211−L219 and I134−I200, respectively) form regular antiparallel hydrogen bonds. Thus, A212 and L135 are located in similar positions with respect to the noncanonical regions of the strands, possibly explaining their parallel response to ligand binding. The identified network of hydrogen bonds apparently relays the dampening of fluctuations caused by lactose binding.

Figure 7.

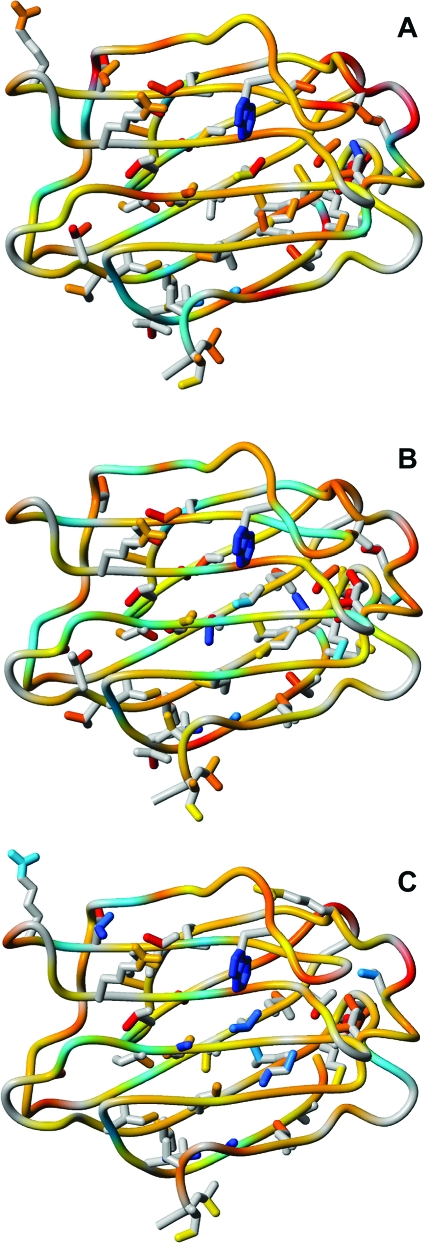
Difference between the order parameters of the ligand-bound states and apo-Gal3C color-coded onto the corresponding ligand-bound structures: (A) ΔO²(lac−apo); (B) ΔO²(L2−apo); (C) ΔO²(L3−apo). The color code ranges from cyan to blue (0 < ΔO² ≤ +1; increase in O² upon binding) and yellow to red (0 > ΔO² ≥ −1; decrease in O² upon binding). Side chains are shown only for those residues with |ΔO²| > 1 standard deviation.

Similar effects are observed for the designed ligands. Of particular interest is the observation that I236, L147, and F159 form a groove along the ligand-binding sheet that has higher O² values in L2−Gal3C than in the apo state (Figure 7b). Each of these residues forms regular antiparallel hydrogen bonds: L147 and F159 interact with one another, while I236 is hydrogen-bonded to Y118. An analogous pattern is observed in L3−Gal3C, but it is shifted in register toward the galactose-binding region (Figure 7c) and involves instead residues F159 and C173.

The side-chain ¹⁵N order parameters reveal motional restrictions due to interactions with the bound ligands or water molecules or within the protein. The O² values exhibit high site-to-site variability (Figure 5b) but generally small differences between states (Figures 6d−f and 7a−c), except for R129 and W181. R144 and R183 were detected only in L2−Gal3C and apo-Gal3C, respectively, and R186 was not observed in apo-Gal3C, while the remaining side chains were detected in all four states. R144 has a high order parameter (O² = 0.83) but shows duplicate cross-peaks arising from two alternative conformations. This evidence of conformational heterogeneity in the L2 complex might suggest that the side-chain resonance is broadened by exchange between alternative conformations in the other states, thereby making it undetectable. The flexibility of the R144 side chain is echoed by its different orientation in the crystal structures of L3−Gal3C and the other two ligand-bound states (see above). Previous work has demonstrated that R144 forms cation−π interactions between its guanidino group and aromatic moieties of designed inhibitors, as verified by the L3−Gal3C crystal structure.(39) The present results demonstrate that in solution R144 samples alternative, well-ordered conformations. Future work should address the role of these conformations in determining ligand affinity.

R162, R186 (not observed in apo-Gal3C), and R224 have high order parameters (⟨O²⟩ = 0.87 ± 0.03) that reflect a motional restriction of the guanidino group similar to that observed for the backbone. The high order parameters of these residues indicate that the binding site is preorganized in the apo state. Indeed, the crystal structure shows that these side chains are involved in a network of hydrogen bonds and electrostatic interactions.(96) In apo-Gal3C, the R162 side chain interacts with the side chains of N160 and E165 as well as with two water molecules. The interactions with N160 and E165 are maintained in the ligand-bound states, but the water molecules are replaced by ligand oxygens. The R186 side chain coordinates the carboxylates of E184 and E165 as well as to one or two water molecules in all four states. The side chain of R224 has the same interactions in all four states, involving the E165 carboxylate, the backbone carbonyl of R183, and three water molecules. R183 is detectable only in the apo state, where it is highly disordered. Common to all four crystal structures, the R183 guanidino group forms hydrogen bonds to water molecules only. R129 and R168 have intermediate order parameters ⟨O²⟩ = 0.53 ± 0.08 and 0.72 ± 0.03, respectively. In all four states, the R129 side chain interacts with the terminal carboxylate of I250, while R168 coordinates waters only. Altogether, the order parameters of arginine side chains report sensitively on the extent and persistence of interactions of the guanidino groups.

The order parameter for W181 is very low in apo-Gal3C (O² = 0.05 ± 0.05) but high in the ligand-bound states (⟨O²⟩ = 0.89 ± 0.03), indicating a significant reduction in motional amplitude as a result of ligand binding. In essence, this side chain changes from having virtually unrestricted rotational dynamics on the subnanosecond time scale in the apo state to highly restricted librations in the ligand-bound states. This dramatic rigidification upon ligand binding reflects the CH−π interactions between the ligand and W181 indole that are highly conserved throughout the galectin family.

The methyl order parameters report on the amplitudes of C−C axis fluctuations (Figure 5b). The fact that the methyl chemical shifts are virtually identical in the different states indicates that the side-chain rotamers are also highly similar.(110) In general, the O² values vary significantly throughout the protein (Figures 5b and 8) and show intricate differences between states (Figures 6e−f and 7a−c), in sharp contrast to the very high similarity of the structures. In apo-Gal3C, high O² values (≥0.7) were generally found for the hydrophobic core close to the binding site, whereas low O² values (<0.7) were observed for two clusters of methyl groups distal from the binding site (Figure 8). One cluster comprises methyl groups L114, I115, V116γ2, L120δ1, I240δ1, L242δ1, and A245 (cluster 1), and the other involves V127γ1, M130, L131δ1, I132δ1, V202γ2, M249, and I250 (cluster 2). Here and in the following, we do not specify the stereochemical identity of the methyl groups when we refer to both methyl groups of a given residue.

Figure 8.

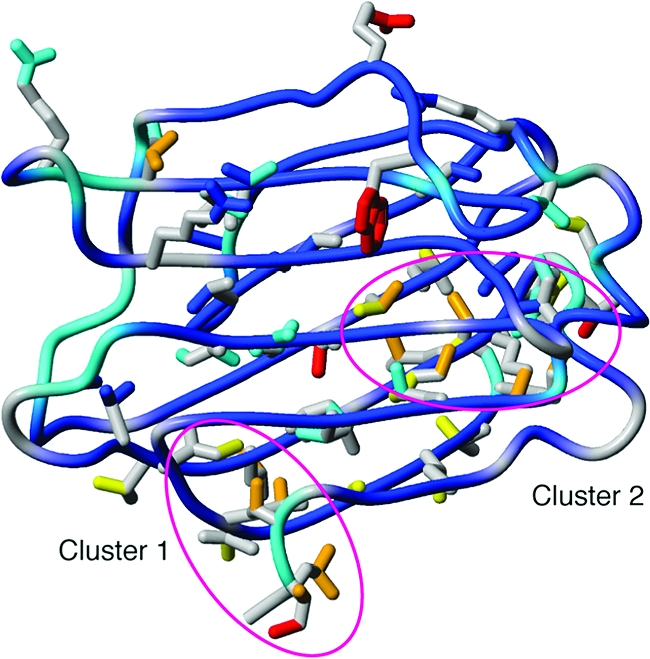
Backbone and side-chain order parameters of apo-Gal3C color-coded onto the structure. O² values for methyl ²H and arginine and tryptophan ¹⁵N are color coded as follows: blue (1 ≤ O² < 0.85); cyan (0.85 < O² ≤ 0.7); yellow (0.7 < O² ≤ 0.55); orange (0.55 < O² ≤ 0.4); red (O² < 0.4). Side chains are shown only for residues for which O² could be measured. Magenta ellipsoids indicate methyl clusters 1 and 2 (see the text for details).

Notably, ligand binding affects the rigidity of the hydrophobic core in a differential manner (Figure 7a−c). The central methyl groups in cluster 1 (L242δ2 and A245) are significantly more rigid in all of the ligand-bound states than in the apo state. In response to lactose binding, all of the methyl groups in cluster 2 and essentially all of the ones proximal to the galactose binding site experience decreased or unaltered order parameters (Figure 7a). L2−Gal3C shows increased rigidity for residue L147δ2, which extends cluster 2 toward the region underneath the phenyl group of L2 (Figure 7b). Cluster 2 shows a mixed response, with increased O² values for V127γ2, M130, I250δ1, and also V202γ2 but otherwise reduced or unaffected O² values. L3−Gal3C shows yet another pattern of changes in O². Increased O² values were found for A146, which packs against L3, and a number of more peripheral methyl groups, including V170, L218δ1, L228δ2, and L131δ1 (Figure 7c). As in the case of L2−Gal3C, cluster 2 exhibits variability, but a different set of methyl groups becomes more rigid: L131δ1, I132, and V202. We note that several of the residues that become less flexible in response to ligand binding are located in regions previously identified as being required for nuclear−cytoplasmic shuttling: I240, L242, and T243 form the IXLT nuclear import motif, while L228, I231, L234, and I236 correspond to the nuclear export signal.(111) This observation suggests that carbohydrate binding might modulate the accessibility of these interior residues and hence their recognition by the transport receptors importin-α and exportin-1.

Taken together, the present results demonstrate that molecular recognition by Gal3C is associated with variable changes in conformational fluctuations that depend on the nature of the ligand. In many cases, contiguous residues exhibit concerted changes in motional amplitudes that apparently are communicated within structurally connected networks. The variability among and within the ligand-bound states reveals that ligand binding modulates the energy landscape of Gal3C in a complex fashion without any significant changes in the protein structure.

Conformational Entropy Favors Ligand Binding and Differs Significantly among the Complexes

NMR relaxation provides a unique means of estimating conformational entropy at the level of atomic resolution.^9,23,24,26 We calculated the difference in conformational entropy between pairs of states from the order parameters using previously described relationships (eqs 1 and 2).^9,26 The resulting values are listed in Table 2. As reported previously, the NMR relaxation data indicate that Gal3C responds to lactose binding by a favorable increase in conformational entropy of the backbone (ΔS_bb = 187 ± 11 J mol⁻¹ K⁻¹ or TΔS_bb = 56 ± 3 kJ/mol at 301 K).(25) Interestingly, similar results have been obtained for the homologous protein galectin-1,(37) although ΔS_bb in that case was lower by a factor of 2. Furthermore, the arabinose-binding protein also shows a favorable change in conformational entropy upon binding (ΔS_bb = 170 J mol⁻¹ K⁻¹).(11) In addition to these two specific examples of carbohydrate-binding proteins, there are several other cases that provide precedent for the observed effect (see ref (112) for a review). Carbohydrate binding is based on relatively weak interactions such as hydrogen bonds involving the carbohydrate hydroxyl groups, van der Waals contacts, and CH−π interactions. Since carbohydrates are well-solvated in the free state, there is rarely any entropic gain upon binding due to changes in solvation. We speculate that these inherent limitations might have exerted evolutionary pressure on carbohydrate binding proteins to increase their binding affinities by means of changes in conformational entropy.

Table 2. Changes in Conformational Entropy of Gal3C in Response to Ligand Binding^a.

state	ΔSbb (J mol−1 K−1)b	ΔSsc (J mol−1 K−1)c	−TΔSconf (kJ/mol)d
lactose	187 ± 11	44 ± 6	−70 ± 4
L2−Gal3C	153 ± 9	35 ± 5	−57 ± 3
L3−Gal3C	185 ± 9	−7 ± 5	−54 ± 3

^aAll entropies are relative to that for the apo state. Data include only those residues for which order parameters were determined in all four states (104 residues for the backbone and 50 residues for side chains).

^bDifference in backbone entropy obtained from experimental order parameters.

^cDifference in side-chain entropy obtained from experimental order parameters.

^dContribution to the free energy of binding from conformational entropy obtained from experimental order parameters. T = 301 K.

Binding of the designed ligands also leads to an increase in backbone entropy (ΔS_bb = 153 ± 9 and 185 ± 9 J mol⁻¹ K⁻¹ for L2 and L3, respectively; Table 2). Similarly, changes in side-chain entropy contribute favorably to ligand binding in the case of lactose and L2 (ΔS_sc = 44 ± 4 and 35 ± 5 J mol⁻¹ K⁻¹, respectively), whereas the effect is neutral within experimental error in the case of L3 (ΔS_sc = −7 ± 5 J mol⁻¹ K⁻¹). The sum ΔS_conf = ΔS_bb + ΔS_sc provides an estimate of the total change in conformational entropy of Gal3C based on the experimental NMR order parameters, which sample a subset of all dihedral angles. While ΔS_conf is identical for L2 and L3, the partitioning into backbone and side-chain entropy is quite different in the two complexes (Table 2). ΔS_conf is more favorable for lac−Gal3C than for either L2− or L3−Gal3C, possibly reflecting enthalpy−entropy compensation due to improved interactions between Gal3C and the designed ligands in comparison with lactose.

We next compared the conformational entropy of ligand binding with the overall thermodynamics determined by ITC. First, −TΔS_conf is on par with ΔH°, indicating that conformational entropy might be as important for ligand binding as enthalpy in absolute terms (see Tables 1 and 2). Second, we note that an evaluation of the relative binding thermodynamics of the designed ligands versus lactose shows that TΔΔS_conf and ΔΔH° have comparable magnitudes, indicating that conformational entropy contributes as much as enthalpy does to the difference among the three complexes with respect to binding free energy. Overall, our results demonstrate that changes in the conformational entropy of Gal3C contribute significantly and favorably to ligand binding.

Discussion of Possible Caveats

The NMR order parameter captures bond-vector fluctuations on time scales shorter than overall rotational tumbling. Thus, the present method does not account for the entropy associated with motional modes on longer time scales, which might conceivably differ between states.

The conformational entropy determined from NMR order parameters is based on the assumption that the fluctuations of individual residues are uncorrelated.(9) To this extent, the results represent an upper limit of the conformational entropy of those degrees of freedom that have been probed here. Conversely, only a subset of all dihedral angles are sampled by the ¹⁵N and ²H relaxation data, implying that the conformational entropy is underestimated. We are primarily concerned with entropy differences between states, which should suffer less from these caveats provided that the extent of motional correlations is similar in the different states and that the average response of the sampled residues is representative of the entire protein.

Conclusions

Ligand binding significantly affects the conformational entropy of Gal3C. Correspondingly, conformational entropy contributes significantly and favorably to the free energy of ligand binding to Gal3C. The protein shows complex changes in its backbone and side-chain fluctuations that depend on the structure of the designed ligands and their interactions with the binding site. Importantly, extensive dynamical effects are observed, despite the absence of any major structural changes in crystal structure in going from the free state to the ligand-bound states. In particular, the hydrophobic core is essentially identical in all four states but shows a rich diversity in its dynamical response to ligand binding. These results reveal a delicate fine-tuning of affinity arising from variable differences in conformational entropy between the free and ligand-bound states. In conclusion, it appears that information on conformational entropy is critical for a deep understanding of protein−ligand recognition.

Supporting Information Available

Summary of the quality statistics for the X-ray crystal structure of L2−Gal3C (Table S1), summary of relaxation rates for each state (Table S2), model-free parameters for each state (Table S3), atom-coordinate RMSDs between each ligand-bound state and the apo state plotted vs residue number (Figure S1), relaxation rates for each state plotted vs residue number (Figure S2), and experimental and theoretical exchange-free relaxation rates for apo-Gal3C (Figure S3). This material is available free of charge via the Internet at http://pubs.acs.org.