Changes in the force–velocity relationship of fatigued muscle: implications for power production and possible causes

Abstract

Slowing of the contractile properties of skeletal muscle is one of the characteristic features of fatigue. First studied as a slowing of relaxation from an isometric contraction, it has become apparent that this slowing is indicative of functional changes in muscle responsible for a major loss of power with all its functional repercussions. There are three factors contributing to the loss of power in mammalian muscle at physiological temperatures, a decrease in isometric force, which mainly indicates a reduction in the number of active cross bridges, a slowing of the maximum velocity of unloaded shortening and an increased curvature of the force–velocity relationship. This latter change is a major cause of loss of power but is poorly understood. It is probably associated with an increase in the proportion of cross bridges in the low force state but there are no clear candidates for the metabolic changes that are responsible for this shift in cross bridge states. The possibility is discussed that the reduction in activating calcium that occurs with metabolically depleted muscle, alters the distribution of cross bridge states, affecting both shortening velocity and curvature.

David Jones graduated in Medical Biochemistry from the University of Birmingham and completed his PhD in Neurochemistry at the Institute of Psychiatry in London. With a family and house to support he changed fields and went to work at the Royal Postgraduate Medical School on basic muscle physiology and studies of patients with muscle problems. He continued these interests at UCL and in 1993 returned to Birmingham as Professor of Sport and Exercise Sciences; he is currently Emeritus Professor of Muscle Physiology at Manchester Metropolitan University. He has wide interests in muscle and exercise physiology but his abiding concern has been the changes in contractile function that occur with acute fatigue.

Muscle function in the body depends on a long chain of command starting from motivation, and even within the muscle fibres there are many steps between electrical activity in the surface and T tubular membranes and the molecular interaction of actin and myosin (Edwards, 1981). It would be wasteful of energy and resources to have certain parts of the chain ‘over-engineered’ so the different links in the chain are all likely to fail at about the same time when the system is stressed. It is unlikely, therefore, that there is any one site or mechanism of fatigue that applies to every situation. Thus the precise link which fails will vary depending on a range of factors including the type of activity, the type of muscle and the temperature, and when discussing fatigue it is important to specify the preparation and conditions under which the muscle is working. This short review will be concerned with mammalian, mainly human, muscle, undertaking metabolically demanding exercise at physiological temperatures of around 37°C. There have been a number of recent detailed reviews of muscle fatigue mainly from Allen, Lannergren, Westerblad and colleagues (e.g. Allen et al. 2008) which have concentrated largely on the processes of excitation–contraction coupling and loss of force. Consequently the present review will take a slightly different angle, concentrating on the slowing of contractile properties.

In 1971 Richard Edwards was working in the Respiratory Unit at Hammersmith Hospital after a sabbatical in Scandinavia where he had acquired the needle biopsy technique that he was to introduce into the UK. He had a grant from the Muscular Dystrophy Group of Great Britain to set up a muscle testing laboratory in which he was greatly helped by David (D.K.) Hill who was head of the Medical Physics Department at the Royal Postgraduate Medical School. Although the MDGB grant was to look at muscle disease, Richard had yet to establish himself as an authority on muscle disease and patients were slow to be referred in the first year or so. During that time, at David Hill's suggestion, Richard began a study of muscle fatigue in healthy subjects and, in particular, the characteristic slowing of relaxation which at that time had hardly been documented, let alone explained.

Changes in contractile properties with fatigue

The slowing of relaxation is illustrated in Fig. 1 showing the effect of fatigue in one subject (R.H.T.E.) during a prolonged voluntary contraction of the quadriceps, interrupted at intervals to measure the rate of relaxation. EMG activity was recorded to demonstrate that the relaxation phase was electrically silent and that the slowing was a function of changes in the contractile apparatus of the muscle rather than a slow decline in voluntary activation. The observation has since been repeated many times on a wide range of human muscles, generally using electrical stimulation which avoids any suspicion of continued voluntary effort, with animal muscle both in situ and in vitro and with all fibre types, including the slow soleus muscle (Edwards et al. 1975). Typical of these results are the brief tetani shown in Fig. 2 (Cady et al. 1989) where the isometric force is reduced and the relaxation phase is prolonged in the fatigued muscle. In isolated single fibre preparations (Fig. 3; Westerblad & Allen, 1993), the loss of force occurs in two phases: a relatively small initial loss that is associated with a small increase in intracellular Ca²⁺ and is probably due to an inhibition of force production by inorganic phosphate (P_i), and then a second more rapid loss of force that is accompanied by a reduction in calcium release. The same combination of events is almost certainly responsible for the loss of isometric force in Fig. 2 although how much of the force loss is due to a direct effect of P_i on cross bridge function is not known; see below.

Figure 1. Relaxation rate, sampled during and after contraction at 50% MVC in one subject.

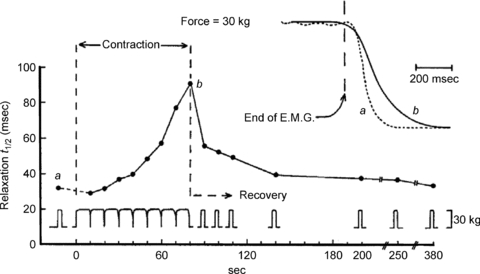
The short breaks for testing t_1/2 (the half-time of the relaxation phase) as fatigue progresses and short (3 s) test contractions during recovery are indicated below. Inset: two records of relaxation to show prolongation with fatigue (from Edwards et al. 1972).

Figure 2. Brief tetanic contractions of the human first dorsal interosseous in the fresh state and after a fatiguing 45 s ischaemic voluntary contraction.

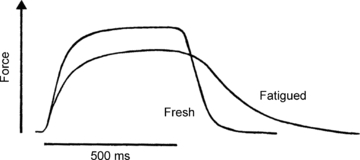
Horizontal bar indicates the duration of stimulation at 50 Hz (from Cady et al. 1989).

Figure 3. Records of tension and [Ca²⁺]_i from a single mouse muscle fibre (flexor brevis) during a fatiguing run.

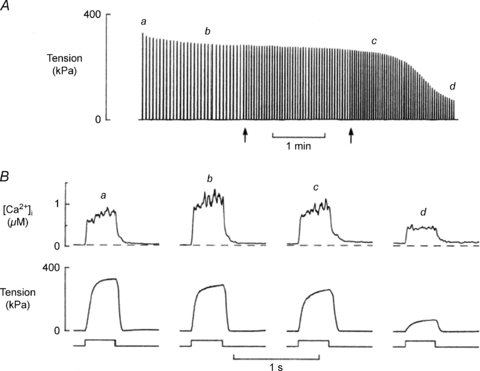
A shows the continuous tension record where each tetanus appears as a vertical line. Arrows indicate times when the intervals between tetani were changed. B shows [Ca²⁺]_i and tension of tetani produced at times (a, b, c, d) indicated above the continuous tension record (from Westerblad & Allen, 1993).

The cause of the decrease in calcium release is still uncertain but interest focuses on the possibility that P_i enters the sarcoplasmic reticulum where it binds with the stored calcium thus reducing the quantity available for release. A possible slow diffusion of P_i into the SR or regulation by ATP might explain why there is a poor temporal relationship between changes in P_i and force with P_i rising rapidly at the start of the contraction when force is well maintained and increasing only marginally late in the contraction when force is falling rapidly (see Allen & Westerblad, 2001, for discussion).

Causes of slow relaxation

The causes of the slow relaxation can, broadly, be either a slow removal of activating calcium or a change in cross bridge kinetics, possibly a slowing of cross bridge detachment, as suggested by Edwards et al. (1975). Evidence to support the idea that cross bridge function is altered as a result of high intensity metabolically demanding exercise first came from observations of the force–velocity relationship of rat gastrocnemius muscle (de Haan et al. 1989) where the slowing of relaxation was found to be accompanied by a reduction in shortening velocity and a considerable loss of power. What was true for rat gastrocnemius muscle was subsequently shown to be true for human muscle in situ with experiments on the adductor pollicis muscle (de Ruiter et al. 1999a; Fig. 4) fatigued under ischaemic conditions with repeated tetanic contractions. While these findings clearly show that there are changes in cross bridge function they do not actually explain the slow relaxation or rule out a slowing of calcium re-accumulation into the sarcoplasmic reticulum. However, direct observation of the intracellular free calcium in mouse muscle fibres at room temperature during slow relaxation showed only small changes in calcium reuptake in the fatigued muscle fibres, the effects of which were offset by a decrease in the affinity of the actin filaments for calcium (Westerblad & Allen, 1993).

Figure 4. Force–velocity relationships of fresh and fatigued human adductor pollicis muscle, together with power.

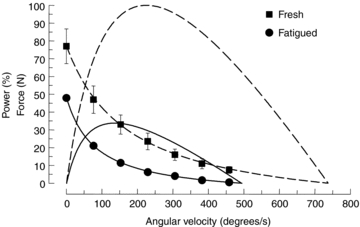
Force is given in absolute units (fresh, square symbols; fatigued, circles) while power is expressed as a percentage of the peak power of the fresh muscle (fresh, dashed line; fatigued continuous line) (from de Ruiter et al. 1999a).

A further feature of fatigued muscle is that it becomes more resistant to stretch. Figure 5 shows how fatigue leads to lower force when the muscle is allowed to shorten but when it is stretched the fatigued muscle offers more resistance and this behaviour may explain the slow relaxation from an isometric contraction. Relaxation from an isometric contraction in a single fibre is characterised by an initial relatively slow linear phase of force decline, then a shoulder followed by a more rapid exponential decay of force. The shoulder, and subsequent loss of force, is associated with relative movements of different segments of the fibre, generally with the ends being stretched (Huxley & Simmons, 1970). Curtin & Edman (1989) showed that these differential movements are reduced in the fatigued state and are associated with an increased resistance of the fibre to stretch which may act to stabilise the fibre and prolong the relaxation phase (Curtin & Edman, 1994). Human muscle working in situ does not show the two phases of relaxation but it does become more resistant to stretch. The shift in the force–velocity relationship (Fig. 5) shows how a fatigued muscle may become more stable and sustain force for longer once stimulation stops since segments that begin to shorten and stretch other regions will develop less force, while those that are initially lengthened will be more resistant to stretch than would be the case for a fresh muscle.

Figure 5. Force–velocity relationships for fresh and fatigued human adductor pollicis muscle both for shortening and lengthening contractions.

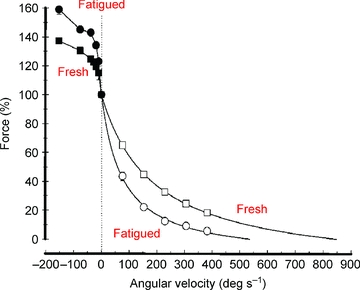
Fresh muscle, square symbols; fatigued muscle, circles. Data for shortening contractions, open symbols; during lengthening, filled symbols. The vertical dotted line indicates the isometric condition to which the data were normalised (from de Ruiter et al. 2000).

Loss of power with fatigue

The data in Fig. 4 draw attention to the fact that while there may be relatively modest decrements in both force and maximum velocity of unloaded shortening (V_max) of between 20 and 30%, when combined to generate power, the loss is considerable, reducing peak power to about one-third of the fresh value, largely explaining the often dramatic and painful slowing seen as runners struggle to maintain their speed in the home straight of a 400 m sprint, or the rapid loss of power in a standard Wingate test.

What was not commented on at the time of the experiments illustrated in Fig. 4 is that the shape of the force–velocity relationship changes with fatigue, becoming more concave with a lower value of a/P_o, as specified in the Hill (1938) equation. The more concave the relationship the less force is exerted at intermediate velocities of shortening thereby reducing the peak power. The curvature also determines the force or velocity at which the maximum power is generated setting, for instance, the cadence at which professional cyclists aim to ride and, as the curvature increases with fatigue, the optimum velocity decreases. A subsequent examination of the factors determining power during a fatiguing series of contractions and recovery (Jones et al. 2006; Fig. 6) showed that the decrease in V_max (Fig. 6C), which had been the focus in earlier work, made the smallest contribution to the loss of power (about 20%) while loss of force (Fig. 6B) and increased curvature (Fig. 6D) both contributed about 40%. The contribution that changes in curvature make to the loss of function with fatigue raises a number of interesting questions about the aspects of cross bridge interaction that determine curvature and what may induce a change in fatigued muscle. The fact that loss of power and change in curvature are closely related to the slowing of relaxation initially suggested that the underlying change in cross bridge kinetics might be a slowing of cross bridge detachment (Edwards et al. 1975) and this was the hypothesis underlying much of our subsequent work on slowing and fatigue.

Figure 6. Changes in contractile function during fatigue and recovery.

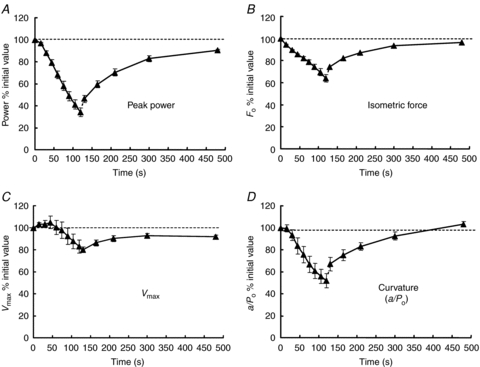
Human adductor pollicis fatigued with a series of ischaemic contractions and then allowed to recover. A, changes in peak power; B, isometric force; C, maximum velocity of unloaded shortening (V_max); D, curvature of the force–velocity relationship (a/P_o). In each case the values are expressed as a percentage of those of the fresh muscle, also indicated by the dotted horizontal line (from Jones et al. 2006).

Cross bridge mechanisms and possible changes in kinetics with fatigue

In the Huxley (1957) model of cross bridge function the curvature of the force–velocity relationship is given by the ratio (f + g₁)/g₂, where f is the rate constant for attachment, g₁ that for detachment in the region where cross bridges develop active force, and g₂ the rate constant for detachment of negatively strained cross bridges. The constant g₂ determines V_max and the ratio (f+g₁)/g₂ is the equivalent of a/P_o in the Hill equation. In the experiment shown in Fig. 6D, a/P_o fell from 0.22 to 0.11 with fatigue. To achieve this change in the ratio (f+g₁)/g₂, either g₂ would have to double or the sum of the rate constants (f+g₁) would need to halve. In fact V_max, and thus g₂, fell by about 20% so it is (f + g₁) that must have changed and would have had to decrease to less than half the fresh value. The rate constant f is generally thought to be several times higher than g₁ to ensure a reasonably high proportion of attached cross bridges during an isometric contraction. In this case it is impossible to make much change in the ratio (f + g₁)/g₂ by just changing g₁, the conclusion being that, contrary to the original hypothesis, the slowing of cross bridge function must involve a substantial decrease in f, the rate constant for attachment (Jones et al. 2006).

The proposition that it is the rate of attachment rather than the rate of detachment which changes with fatigue can be tested by measuring the economy of the muscle; more precisely, what is tested is whether the rate of detachment, g₁, changes. The economy of a muscle is the rate of energy utilisation per unit of force in the isometric state. In a two-state model where cross bridges are either detached and not generating force, or are attached and generating force, the proportion of available cross bridges that are attached in the isometric state is given by the ratio f/(f+g₁). Assuming that one ATP is used per cycle, as is likely to be the case in the isometric state or during slow shortening (e.g. Piazzesi & Lombardi, 1995), then the ATP turnover is g₁ times the number of attached cross bridges i.e. g₁fn/(f + g₁), where n is the number of available cross bridges. Assuming that force per cross bridge remains constant, the total force is proportional to the number of attached cross bridges, fn/(f + g₁), so if ATP turnover is divided by force to give the economy of the muscle this is proportional to g₁ alone, the rate constant for detachment. Dawson et al. (1980) found no change in the economy of frog muscle as it fatigued and, likewise, Hultman & Sjöstrom (1983) found no change in a biopsy study of human muscle. These findings have been confirmed more recently by a study using magnetic resonance spectroscopy (MRS) of the human anterior tibialis and, again, no change in economy was observed even though the muscle became appreciably slower as it fatigued (Jones et al. 2009). The metabolite changes in the muscle are shown in Fig. 7A and the isometric force sustained in Fig. 7B, while in Fig. 8A the ATP turnover has been calculated. The economy (Fig. 8B) remained constant throughout the duration of the contraction. Although power output and the force–velocity relationship were not measured in this experiment the close relationship between slowing of relaxation and increased curvature (Jones et al. 2006) shows that relaxation is a good indicator of changes in the force–velocity relationship. The inference from this, and previous studies measuring economy, is that it is the rate constant for attachment, f, rather than g₁, which decreases with fatigue, giving rise to the change in curvature and being a major factor in the loss of power.

Figure 7. Changes in muscle metabolites and isometric force with fatigue.

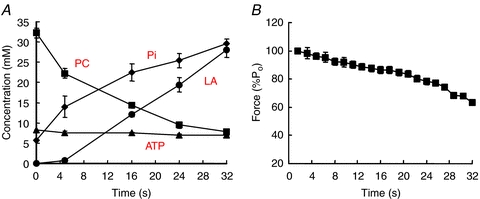
Human anterior tibialis muscle fatigued by a series of tetani under ischaemic conditions. A, muscle metabolite concentrations estimated by magnetic resonance spectroscopy. PC, phosphocreatine; P_i, inorganic phosphate; LA, lactate, estimated from changes in pH and likely values of muscle buffering capacity. B, changes in isometric force (from Jones et al. 2009).

Figure 8. ATP turnover and economy during a series of fatiguing contractions.

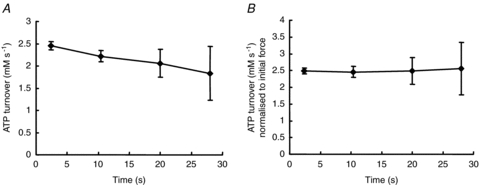
A, ATP turnover derived from the data in Fig. 7A. B, economy of the muscle calculated as turnover in Fig. 8A divided by the force in Fig. 7B. The data have been normalized to the value of the fresh muscle (from Jones et al. 2009).

The rate constant for attachment

In the two-state model of cross bridge action all the attached cross bridges exert force and the Huxley rate constant f determines the rate of both attachment and the generation of force. However, in reality there may be a number of intermediate cross bridge states between the attachment of myosin to actin and generation of force (e.g. Regnier et al. 1995) and the rate constant f must encompass all the individual steps. The changes in the force–velocity relationship with fatigue, both for shortening and stretching as shown in Fig. 5, are very similar to the differences seen between fast and slow fibres (Linari et al. 2003). While slow fibres have lower V_max and greater curvature of the force–velocity relationship than fast fibres during shortening, they sustain greater forces during lengthening. The force sustained by the slow fibres was greater than that for the fast fibres when expressed relative to isometric although the absolute forces were very similar. To explain this behaviour, Linari et al. concluded that during stretch of slow fibres there is a greater recruitment of new force-generating cross bridges. These additional cross bridges could either be new attachments or cross bridges that were already attached but in a low force state where they do not contribute to the instantaneous stiffness of the fibre. The rapidity with which the new force-generating cross bridges were recruited at the start of a steady stretch argues in favour of the latter mechanism (Linari et al. 2003). It is an attractive idea, therefore, that fatigue may result in a redistribution of cross bridges with a greater proportion in the low force state. Consequently the next question is what metabolic change can cause an accumulation of low force cross bridges?

Muscle metabolites and fatigue

The metabolic changes in fatiguing muscle are shown in Fig. 7A and there are clearly a number of possible candidates that may affect force or the speed of contraction. Acidosis is often blamed for muscle fatigue and apart from an initial alkalosis as phosphocreatine is broken down, the relationship shown in Fig. 8A might suggest this is, indeed, the case. However, there is ample evidence now that pH changes play a relatively small part in the fatigue of mammalian muscle at normal physiological temperatures (see Allen et al. 2008). A direct demonstration that acidosis is not required for fatigue comes from Cady et al. (1989) who found that a patient with McArdle's disease, who produced no H⁺ in her muscle during contraction, still showed the characteristic loss of force and slow relaxation.

Accumulation of ADP has been suggested to slow V_max (Westerblad et al. 1998) and ADP release from the bound cross bridge is generally regarded as the rate limiting step in the full cross bridge cycle (Nyitrail et al. 2006). Although it cannot be measured directly by MRS, ADP concentrations can be estimated from the observed changes in phosphocreatine, ATP and H⁺. However, the changes in concentration bear little or no temporal relationship to the slowing of the muscle (Fig. 9C). The difficulty with ADP playing a major role is that myokinase and AMP deaminase are very active enzymes in muscle and it is unlikely that ADP will remain at a high level for any length of time. Westerblad et al. (1998) found that in the fatigued state the velocity of shortening was slower immediately after a longer tetanus compared to a short contraction, which they ascribed to a transient ADP accumulation. There was then a partial recovery in a matter of a few seconds, presumably as the ADP was removed by enzyme action or diffusion. In the type of experiment discussed here in which the muscles are fatigued whilst ischaemic, the slowing is not a transient phenomenon but remains until the blood returns and only then recovers over several minutes (Fig. 6D), much more slowly than would be expected if ADP were the cause of the problem. It is also notable that patients suffering from myoadenylate deficiency, in whom high levels of ADP would be expected during muscle activity, do not show any obvious abnormalities in muscle function either at rest or when fatigued (de Ruiter et al. 1999b) and muscle fatigue in adenylate kinase-deficient mice is also reported to be little different to that of the wild-type (Hancock et al. 2005).

Figure 9. The relationship between relaxation rate and muscle metabolite concentrations during a series of fatiguing contractions.

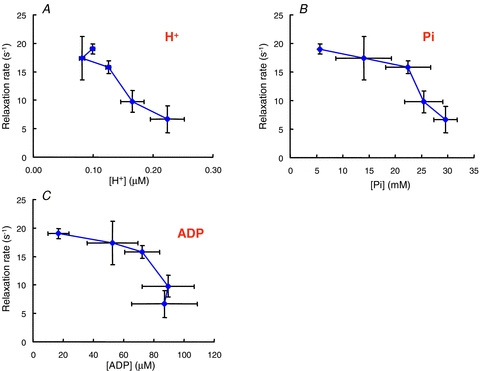
Data from the experiment shown in Fig. 6. A, hydrogen ion concentration; B, inorganic phosphate (P_i); C, ADP (from Jones et al. 2009).

There is considerable interest in the possibility that accumulation of P_i may affect cross bridge function in fatigue. The release of P_i from the A.M.ADP.P_i complex (where A.M. is actomyosin) is closely associated with the generation of force and is a reversible process. High levels of P_i in skinned fibre preparations decrease force and change the distribution of cross bridge states so there is a greater proportion in a low force state, much as discussed above in relation to the differences between fast and slow fibres (see, for example, Coupland et al. 2001; Caremani et al. 2008). There are, however, a number of problems with P_i being a major cause of fatigue by acting directly on cross bridges. The first is the observation, evident in Fig. 9B, that the changes in P_i do not correlate at all well with changes in relaxation. The major change in P_i occurs relatively early in the contraction when phosphocreatine is being broken down and the muscle is functioning fairly well, yet when the muscle begins to fail there is relatively little further change in P_i concentration. The effects of P_i on force in skinned fibres are also very temperature dependent, being appreciable at low temperature and minimal at higher temperatures which approach the physiological levels of the human experiments discussed here (e.g. Coupland et al. 2001). The third problem is that P_i appears to be most effective in influencing cross bridge function in the range of about 0–10 mm, but human muscle, even at rest, has an appreciable concentration of P_i of 5–8 mm (Fig. 7A) so there may be little scope for further effects as the muscle fatigues.

There are many reasons why the metabolite concentration measured in biopsy samples or by MRS may not reflect the concentrations of metabolites actually interacting with the cross bridges. There may, for instance, be different concentrations in the various fibre types or compartmentation within the fibre. Equally, there need not necessarily be a linear relationship between metabolite concentration and function. Nevertheless the lack of clear relationships suggests it may be instructive to look at other mechanisms that could affect curvature.

Calcium and cross bridge kinetics

Cross bridge kinetics and the rate of shortening have traditionally been thought to be independent of the activating calcium, but this may not be the case. The sum (f + g₁) in the Huxley model is equivalent to the rate at which tension will redevelop following rapid shortening and re-stretch (ktr, Brenner, 1988) and is known to be sensitive to the activating calcium concentration, with f decreasing at low calcium. Likewise, the velocity of unloaded shortening is also known to be affected by the level of activation (Moss, 1986; McDonald, 2000; Morris et al. 2003). The mechanism of the slowing at low levels of activation was suggested by Moss to be due to an accumulation of long-lasting cross bridges which provide an internal resistance slowing the maximum rate of shortening. However, McDonald (2000) and Morris et al. (2003) both concluded that slower recruitment of high force cross bridges during shortening leads to lower force so that in isotonic contractions a reduction in speed is necessary to maintain the target force. In the Huxley analysis this slowing would be apparent as a reduction in the rate constant g₂. If, therefore, both f and g₂ are affected by calcium then it is possible that the slowing of V_max and the decrease in curvature could both be explained by a decline in activating calcium that occurs with fatigue (Fig. 3). Thus it is possible that a reduction of intracellular calcium as a result of some metabolic event, such as the accumulation of P_i in the sarcoplasmic reticulum, could play a part in all three of the characteristic features of fatigue that determine the power output of a muscle, the reduced isometric force, slowing of V_max and change in curvature. The emphasis here is on the word ‘could’ since with intact fibres Westerblad et al. (1998) tested the idea that low calcium was responsible for a reduction in V_max by exposing the fibres to dantrolene which reduced force but had no effect on shortening velocity.

Another caveat is that there is a marked slowing of relaxation during moderate fatigue of frog muscle fibres at 1–2°C (Curtin & Edman, 1989) but, in contrast to results shown in Figs 4 and 5, Curtin & Edman (1994) found a decrease in the curvature of the force–velocity relationship as a result of fatigue, with a/P_o increasing by about 30%. De Ruiter & de Haan (2000) likewise found that the force–velocity relationship became less curved when human muscle was fatigued at low temperatures although V_max decreased and the muscle relaxed more slowly. The two components of the Huxley ratio that determine curvature, (f + g₁) and g₂, must have different temperature coefficients since curvature, and thus the ratio of (f + g₁)/g₂, changes nearly threefold in the range 22–37°C (de Ruiter & de Haan, 2000). Consequently f and g₂ may respond differently to the metabolic changes of fatigue at high and low temperatures.

In summary, there are some things we can say with certainty. Firstly, a loss of power is a major consequence of muscle fatigue and that in mammalian muscle at normal physiological temperatures this is due to changes in three properties of the muscle: a decrease in isometric force, a slowing of V_max and an increase in curvature of the force–velocity relationship, this latter factor being appreciated only relatively recently. Secondly, fatigued muscles are more resistant to stretch which suggests there may be an increase in the proportion of cross bridges in a state from which they can be rapidly recruited to generate force. Metabolic causes for these changes are hard to identify and it is speculated that a decrease in activating calcium might affect force, curvature and V_max and, consequently, make a contribution to all three of the changes giving rise to the loss of power with fatigue.