Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2010 Aug 26;26(21):2737–2743. doi: 10.1093/bioinformatics/btq474

Measuring the physical cohesiveness of proteins using physical interaction enrichment

Iziah Edwin Sama 1,*, Martijn A Huynen 1,*
PMCID: PMC2958743  PMID: 20798171

Abstract

Motivation: Protein–protein interaction (PPI) networks are a valuable resource for the interpretation of genomics data. However, such networks have interaction enrichment biases for proteins that are often studied. These biases skew quantitative results from comparing PPI networks with genomics data. Here, we introduce an approach named physical interaction enrichment (PIE) to eliminate these biases.

Methodology: PIE employs a normalization that ensures equal node degree (edge) distribution of a test set and of the random networks it is compared with. It quantifies whether a set of proteins have more interactions between themselves than proteins in random networks, and can therewith be regarded as physically cohesive.

Results: Among other datasets, we applied PIE to genetic morbid disease (GMD) genes and to genes whose expression is induced upon infection with human-metapneumovirus (HMPV). Both sets contain proteins that are often studied and that have relatively many interactions in the PPI network. Although interactions between proteins of both sets are found to be overrepresented in PPI networks, the GMD proteins are not more likely to interact with each other than random proteins when this overrepresentation is taken into account. In contrast the HMPV-induced genes, representing a biologically more coherent set, encode proteins that do tend to interact with each other and can be used to predict new HMPV-induced genes. By handling biases in PPI networks, PIE can be a valuable tool to quantify the degree to which a set of genes are involved in the same biological process.

Contact: i.sama@cmbi.ru.nl; m.huynen@cmbi.ru.nl

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Physical interactions between proteins explain how proteins function together in protein complexes or functional modules (Dittrich et al., 2008; Ideker and Sharan, 2008; Tucker et al., 2001; Vidal, 2001). Discovery of all protein–protein interactions (PPIs) has therefore been a priority in systems biology and there have been several efforts to elucidate PPIs both in low- and in high-throughput platforms (Collins et al., 2007; Rual et al., 2005; Stelzl et al., 2005), as well as by evolutionary inference (Brown and Jurisica, 2007; Huang et al., 2007; Yu et al., 2004).

The resulting PPI networks are invaluable for the interpretation of other genomics data. In a number of studies, specific emphasis has been placed on quantifying aspects of network topology to identify proteins that are specifically relevant to a biological process or for evolution. For instance Wachi and coworkers identified a high network centrality for genes that are upregulated during lung cancer as a distinguishing topological feature to enable placement of cancer genes into the global and systematic context of the cell (Wachi et al., 2005). In a similar study, essential genes in yeast have been found to be well connected and globally centered in the PPI network (Jeong et al., 2001; Wuchty and Almaas, 2005).

Notwithstanding the success of such approaches, there are some experimental biases in the determination of PPIs. For instance, the Yeast-2-Hybrid (Y2H) approach is known to detect interactions among proteins that may not be likely because the proteins naturally do not occur in the same subcellular compartment (von Mering et al., 2002). Tandem Affinity Purification followed by mass spectrometry is known to favor highly abundant proteins (Bjorklund et al., 2008; von Mering et al., 2002). In addition, evolutionary inference of PPIs as ‘interologs’ has placed highly conserved proteins as hubs in general PPI networks (Brown and Jurisica, 2007). Even manual curation of PPIs in scientific literature has caveats. One main caveat being that the discovery of such interactions is driven by existing knowledge and hypotheses (Cusick et al., 2009). The latter has led to an overrepresentation of interactions between proteins encoded by disease genes in the Human Protein Reference Database (HPRD) (Oti et al., 2006).

Several measures have been developed to improve the reliability of PPI networks (Sharan et al., 2007), like the integration of general PPI networks with networks based on other data (Karni et al., 2009; Tornow and Mewes, 2003; Yosef et al., 2008). Although such comparative genomic approaches increase the reliability of the PPI network, they do not specifically remove systematic biases, like the overrepresentation of well-studied proteins, from general PPI networks. This is of pertinent concern because function information derived from such networks would be skewed towards well-studied genes that are often evolutionarily conserved nodes, immune-related nodes or disease-associated nodes in PPI networks. Moreover, such biases can cloud quantitative assessments of whether a set of proteins of interest tend to interact with each other, and are therewith ‘physically cohesive’. For example, when genes that are upregulated under a specific condition encode proteins that physically interact with each other, this can be because they truly interact more with each other than a random set of proteins, or simply because there are just more interactions known for these proteins than for those whose genes are not highly expressed (von Mering et al., 2002).

To handle the bias that arises from the overrepresentation of certain proteins (e.g. well-studied proteins) in PPI networks, we present an approach called physical interaction enrichment (PIE). PIE extracts ‘random’ sets of proteins from a general PPI network that have the same node (protein) and edge (interaction) biases in the general PPI network as a set of proteins of interest. Secondly, it assesses whether the average degree of interaction among the proteins of interest is higher than that among the proteins from the random sets and thus quantifies how physically cohesive the proteins are.

To illustrate the usefulness of PIE, we first show how general human PPI networks have higher node degrees (i.e. number of interactions) for proteins encoded by morbid genetic disease genes. We also reveal biases in these networks for proteins encoded by genes that are stimulated by human metapneumovirus (HMPV) infection, a virus recently discovered to cause morbidity in very young and elderly people (van den Hoogen et al., 2001; van Diepen et al., 2010). The HMPV-induced genes are used here to represent a scientifically new and likely more focused context than the morbid genetic disease genes. Secondly, we demonstrate how PIE compensates for the enrichment biases in both the morbid genetic disease gene set and the sets of HMPV-induced genes. Thirdly, we assess physical cohesiveness of genes that are upregulated or downregulated to examine the biological coherence in such context. Furthermore, we apply PIE to other datasets in which the gene expression response of epithelial cells to a cytokine, interferon gamma (INFG) or other airway pathogens like Chlamydia pneumoniae, uv-irradiated Pseudomonas aeruginosa, UV-irradiated respiratory syncytial virus (RSV) have been measured. Finally, we use PIE to assess whether the propagation of interactions through PPI networks is biologically relevant. For the cases where it is relevant, we propagate these networks to larger networks and demonstrate the predictability of future expressed genes therein, thus showing exploratory potential in general PPI networks using PIE.

2 METHODS

2.1 General PPI networks

The PPI network used were built from an accumulation of human-curated PPIs obtained from the Biomolecular Interaction Network Database (BIND; Bader et al., 2003) (data downloaded in October 2006), the HPRD (Peri et al., 2003) (data of release 6 of January 2007), the IntAct database (Kerrien et al., 2007) (downloaded in May 2007), the Molecular Interactions Database (MINT; Chatr-aryamontri et al., 2007) (downloaded in May 2007) and the PDZBase database (Beuming et al., 2005) (downloaded in May 2007). For the scope of this study, only direct PPIs within the same species were used. We refer to the network composed of all interactions between human proteins as HsapiensPPI. Furthermore, interologous PPIs were built using the orthologues datasets from the Ensembl genome browser (Hubbard et al., 2007) (Ensembl release 44, downloaded on May 2007). These were combined with the HsapiensPPI dataset. We refer to this comprehensive dataset as AllspeciesPPI. The HsapiensPPI contains 53 807 interactions between 10 826 proteins. The AllspeciesPPI network contains 205 050 interactions among 13 920 proteins. Unique to AllspeciesPPI are 151 243 interactions, among 3094 proteins. The main difference between the HsapiensPPI and AllspeciesPPI is that the former has fewer interactions per node than the latter. The high average degree in the AllspeciesPPI is in agreement with other studies that posit that preferential conservation of proteins with higher degree (hubs) leads to enrichment in protein complexes when interactions are transferred between organisms using interologs (Brown and Jurisica, 2007; Wuchty and Almaas, 2005). All the nodes in the HsapiensPPI and AllspeciesPPI networks represent the Entrez gene IDs of interacting proteins, and are not redundant in the networks. These PPI networks are large enough for the scope of our study. Unless otherwise stated, the HsapiensPPI is used in this article as the general PPI network.

2.2 Disease and immune-related data

All human disease genes were obtained from the Morbid Omim database (downloaded February 10, 2009 from ftp://ftp.ncbi.nih.gov/repository/OMIM/morbidmap) (Sayers et al., 2009). The HMPV infection data was obtained from (Bao et al., 2008), as deposited in the NCBI Gene Expression Omnibus database with reference as GSE8961. Other data included that of human lung epithelial cell treatment with the cytokine INFG (GSE1815) (Pawliczak et al., 2005). Expression data of bronchial epithelial cells infected with respiratory pathogens like Chlamydia pneumonia (GSE7246) (Alvesalo et al., 2008) and UV-irradiated airway-pathogens (for P.aeruginosa and RSV; GSE6802; Mayer et al., 2007).

A geometric average of all probes for a gene was used to represent the fold change (FC) of a gene due to infection or treatment. A FC threshold of ≥1.5 was used to select genes induced by the inert pathogens (UV irradiated), and this low threshold was necessary to yield adequately testable sample sizes. In all other cases, upregulated or downregulated genes used were those that showed a FC ≥3.0 after infection or treatment.

2.3 Enrichment of PPIs for disease genes and immune-related genes in general PPI networks

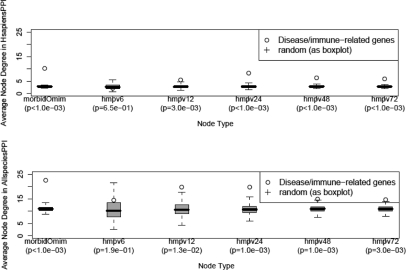
To measure the biased enrichment in interactions for proteins of genetic disease genes in general PPI networks, the morbid Omim gene set (n = 1996) was used as the genetic disease test set. Its enrichment was assessed as follows: the average node degree (nodes of degree zero inclusive) in the general PPI network for proteins encoded by the disease genes was compared with those of sets of 1996 genes that were randomly selected from all human genes (n = 36 456) that were available in NCBI Entrez gene database in 2008. The P-value of enrichment in interactions for proteins of disease genes was estimated as a fraction of the frequency (out of 1000 simulations) of the sets of random genes having an average degree that was equal or greater than that of the disease genes. As shown in Figure 1, disease genes have significantly (P < 0.001) high node degrees in the general PPI networks HsapiensPPI and AllspeciesPPI.

Fig. 1.

Fig. 1.

Open in a new tab

Proteins of disease genes and immune-related genes have higher node degree in general PPI networks than do proteins of randomly sampled genes. The average node-degree of disease genes (represented by morbid Omim genes) and immune-related genes (represented by genes upregulated at least 3-fold in expression at various time points after HMPV infection) is observed in the HsapiensPPI (top panel) and the AllspeciesPPI (bottom panel) networks to be generally higher than randomly sampled genes from the genome. In the top and lower panels, hmpv6, hmpv12, etc. refer to gene sets upregulated in expression after 6 and 12 h of HMPV infection. In brackets are the P-value estimates of higher node degree (compared with random) of disease and immune-related genes in the general PPI networks.

To measure the biased enrichment in interactions for proteins of immune-related genes in the general PPI networks, genes that were upregulated at a FC threshold of 3.0 at various time points after HMPV infection were used as an example. The enrichment procedure for these representative immune-response genes was similar to that carried out for the morbid disease gene set. Apart from the gene set at the earliest infection time point (6 h), these immune-related sets of genes have significantly (P < 0.01) high node degrees in general PPI networks (Fig. 1).

Overall, these results indicate that proteins of disease genes and immune-related genes have, on average, more interactions in general PPI networks than do proteins of randomly chosen genes.

2.4 PIE procedure

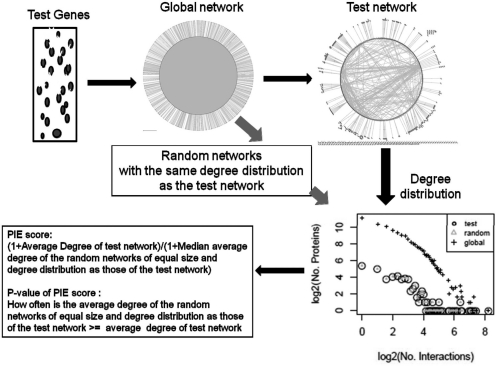
Proteins of disease genes or of genes involved in immune response have relatively more interactions than random sets of genes in general PPI networks (Fig. 1). This can lead to a bias when measuring whether genes whose expression is e.g. triggered by a viral infection or involved in genetic disease tend to interact with each other. As such, one cannot simply compare the extent to which proteins of these genes interact with each other relative to randomly chosen proteins from the PPI network, thus dictating the need for appropriate random models (Koyuturk et al., 2007). In order to circumvent these biases in the number of proteins that are present in the PPI network and also in the number of interactions per protein in the PPI network, the PIE procedure is presented as depicted in Figure 2. PIE measures the physical cohesiveness of interacting proteins via the strict randomization procedure described in detail below.

Fig. 2.

Fig. 2.

Open in a new tab

Summary of the PIE procedure. In the PIE procedure, a test set of genes of interest, e.g. those upregulated by a virus, are used to extract a specific PPI network from the general PPI network that consists of proteins encoded by genes in that test set. The number of interactions of each protein of the test set in the general PPI network (i.e. degree) is calculated. A number of proteins equal to the test set and with the same degree distribution as the test proteins in the general PPI network are then randomly selected from the set of all proteins in the general PPI network. As such the test set and the randomly selected set have the same degree distribution in the general PPI network. The average degree within the test set itself (i.e. total number of edges divided by total number of nodes in the test set) is then obtained and compared with that within the randomly selected set. The fraction of cases in which the average degree within a randomly selected set surpasses or equalizes that of the test network is recorded as the P-value for the physical cohesiveness of proteins of the genes of interest. The PIE score is the ratio of the average degree within the test network to the median average degree within the random networks.

2.4.1 Derivation of test and random PPI networks from a general PPI network for PIE

A test PPI network is derived from a set of test genes by selecting all the interactions from the general PPI network occurring between proteins encoded by the genes in that test set (Equation 1). An example of a test set is a set of genes that are upregulated in expression due to a viral infection. Next, for each node in the general PPI network, the degree (i.e. number of interactions the node has in the network) is obtained. Thus, a degree distribution for the nodes in the general PPI network is derived. We call this the global degree distribution. From the global degree distribution, a test degree distribution consisting only of the test network nodes (and their associated degree in the general PPI network) is extracted. Subsequently, proteins that have the same degree as those in the test network are randomly selected from the global degree distribution. This is done such that for every degree in the test degree distribution, the number of randomly chosen nodes for that degree is the same as that of the test nodes for that degree. Moreover, the total number of nodes in the test set is ideally much smaller than the total number of nodes in the general PPI network (Equations 2 and 3). As such the total number of randomly chosen nodes is the same as that of the test nodes. Thus, both random and test have been normalized in the context of the general PPI network.

Essentially, the PIE randomization involves selection of nodes from the general PPI network that have the same node degrees as those of the test nodes in the general PPI network prior to constructing an induced subgraph by selecting all the interactions from the general PPI network that occur between the random nodes.

This randomization procedure presents a caveat regarding saturation of network sampling space. In the random sampling procedure, many random protein sets with identical degree distribution as the test set are extracted from the global network. When the test network becomes large and therewith largely identical to the global network, randomly sampled networks will largely overlap with the test network, and it will become meaningless to try to measure an increase in the number of interactions in the test network relative to the random networks. We measured the overlap of nodes between the test and random networks and also the overlap of interactions. In practice, the sets of proteins that we tested for physical cohesiveness contained <16% of the nodes of the random networks, while the overlap in the number of interactions was <13%. Only propagated test networks (see Section 3 below and Supplementary Material) contain a substantial fraction of the global network.

2.4.2 Measuring physical cohesiveness

First, the average degree of the test network is calculated as the average number of interactions per node (Equation 4). Also, for the random network the average degree is calculated by dividing the number of interactions by the number of nodes. Next, the ratio of the average degree of the test network relative to the median average degree of the corresponding random networks (i.e. those obtained after PIE randomization) is calculated (Equation 5). This is the measure of physical cohesiveness or ‘PIE score’ for the set of test genes. Finally, the fraction of instances whereby the average degree of the random networks is larger or equal to the test network is calculated (Equation 6). This strict empirical value represents the P-value for the physical cohesiveness for the test set of genes.

2.5 Algorithm

All calculations and graphs were obtained using Python scripting and R. Network graphs and Gene Ontology enrichment analyses were obtained using Cytoscape (Shannon et al., 2003) and the Cytoscape plugin BINGO version 2.3 (Maere et al., 2005), respectively. P-values reported for the gene enrichment analyses were gotten after Benjamini and Hochberg false discovery rate correction.

All network P-values indicate how often the average degree of a test network is less than that of random networks of equal size and equal global degree distribution as the test set.

All calculations of correlations and associated P-values are Pearson moment correlations as implemented in the statistical package R. Other specific calculations are as described below.

2.5.1 Test PPI network

Given a general PPI network, G = (V, E) such that V is a set comprising NV vertices (nodes) and E is a set comprising NE edges (links, degrees). A PPI network, Gt = (Vt, Et) of a given test set of genes is constructed such that:

graphic file with name btq474m1.jpg (1)

That is, Vtare the vertices in G that are proteins encoded by the test genes and Et are the edges from G that connect all the Vt vertices. For clarity, each gene is represented by only one protein node.

2.5.2 Random PPI network for PIE

The appropriate nodes used to construct the random networks used for comparison with the test network are obtained as follows. Let global degree, g be the number of edges (interaction partners) a node has in a general PPI network, and αg be a vector of all existing g. Given the general network G = (V, E) comprising a set V of NV vertices, with a set E of NE edges: we create another vector βg comprising Ng number-of-nodes for each distinct global node degree g in αg.

Next, given a test network Gt = (Vt, Et), we create a vector βt comprising Ngt number-of-nodes from Vt such that, Gt ⊆ G and αt ⊆ αg.

Finally, a corresponding (i.e. to the test network) random induced subgraph, Gr = (Vr, Er) is deduced from G such that Gr ⊆ G and βr = βt and also αr = αt, whereby Vr is randomly selected from V.

Resulting in:

graphic file with name btq474m2.jpg (2)

i.e. total number of nodes of the test network and for a random network is the same, and have the same degree distribution.

Furthermore, for adequate sampling space of Vr from V;

graphic file with name btq474m3.jpg (3)

2.5.3 Average Degree of PPI network

The average degree ω of a network G = (V, E) is the average number of interaction per node. This is calculated as follows:

graphic file with name btq474m4.jpg (4)

Where NE is the total number of edges linking nodes and NV is the total number of distinct vertices (nodes) in the PPI network.

2.5.4 Physical cohesiveness

The score of physical cohesiveness ρ is calculated as follows:

graphic file with name btq474m5.jpg (5)

Where ωt and ωr are as derived in (Equation 4) for a test network, and N random networks of identical global node-degree distribution (as derived in Equations 2 and 3), respectively. The denominator is the median of N random networks. Unless otherwise indicated, this N is 1000. To avoid division by zero error, 1 is added to both numerator and denominator.

2.5.5 P-value of physical cohesiveness

The P-value of physical cohesiveness, Pvalue ρ, is calculated as follows:

graphic file with name btq474m6.jpg (6)

3 RESULTS

3.1 Assessment of enrichment of disease or immune-related protein interactions in general PPI networks

As expected, when assessing the presence of genes involved in disease or in the immune system we observed a significant overrepresentation of interactions for the proteins of these genes. Morbid disease genes have a higher node degree than random (P < 0.001). Likewise were the proteins of HMPV-induced genes (P < 0.01) (Fig. 1).

3.2 Physical cohesiveness of disease and immune-related genes

The PIE approach was tested on morbid genetic disease genes and genes that were upregulated in expression due to HMPV infection. The first set of genes represents the general context of genes relevant to human health and disease. The second set serves as an example of a more focused context and is selected using a more objective criterion, i.e. gene expression perturbations upon HMPV infection. Both sets of genes encode proteins with overrepresented interactions in general PPI networks (Fig. 1).

3.2.1 Morbid disease genes

Proteins of morbid disease genes have more interactions with each other than do proteins of randomly chosen genes. The average number of interactions between morbid disease genes is 2.29 while that of the same number of randomly chosen genes is 1.15 (P < 0.001). Nevertheless, the PIE procedure indicates that the morbid disease gene set has no physical cohesiveness (PIE score = 1), and this is not because the morbid disease gene network is quantitatively similar to the general network as it contains only 11% of the nodes, and 5% of the interactions in the general network. The morbid disease gene set has only 15% of its nodes, and 12% of its interactions in common with those of the random networks used in the PIE randomization approach.

Thus, the proteins encoded by morbid disease genes are not more likely to interact with each other than random proteins with the same degree distribution. Overall, the absence of physical cohesiveness for morbid disease genes using PIE might be expected because disease genes are involved in many different diseases and likely many different processes, and it is encouraging to see that PIE effectively corrects for such biases.

3.2.2 HMPV-induced genes

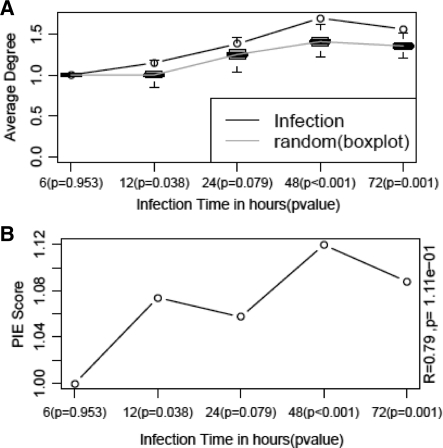
Like the morbid disease genes, proteins of genes whose expression are induced after 12 h of HMPV infection also have a higher number of interaction with each other (average degree = 1.148) than the same number of randomly chosen genes (median average degree = 1.0). Unlike the case of morbid disease genes, however, the 12 h HMPV-induced genes do display significant physical cohesiveness (PIE score = 1.1, P = 0.04) when the latter is measured using PIE. The physical cohesiveness of the nodes of the HMPV-induced genes therefore does not depend on their overrepresentation in general PPI networks (Fig. 1) in which it contains only 0.5% of the general network nodes and 0.12% of the interactions. Furthermore, both average degree and physical cohesiveness depend on some criteria of severity of HMPV infection. For instance at a gene expression FC threshold of 3.0, physical cohesiveness increases with longevity of the infection (Fig. 3). In line with the changes in physical cohesiveness, the immune response might become more specific in the time course of infection. For example, apoptosis starts to play a more prominent role later in infection as reflected by the enrichment of the GO term ‘apoptosis’ for genes that are upregulated at a FC threshold of 3.0. At various time points of infection, the process apoptosis is observed to change in significance as follows: 6 h (absent), 12 h (P = 2.58e-2), 24 h (P = 1.94e-2), 48 h (P = 2.68e-4) and 72 h (P = 7.39e-4). In addition, key apoptosis marker genes like MDA-5 and RIG-1 were found using western blotting to increase over time of HMPV infection as seen in the data of Bao and others (i.e. the HMPV data used in this article) (Bao et al., 2008). In addition to the temporal cohesiveness of upregulated genes, it is interesting to examine the cohesiveness of infection and immune system related genes in other regulatory contexts.

Fig. 3.

Fig. 3.

Open in a new tab

Timewise variation in physical cohesiveness of HMPV infection induced genes. (A) Changes in average degree for the infection (circles with black line) and random (boxplots with grey line). (B) Changes in physical cohesiveness measured as PIE scores with P-values of cohesiveness in brackets.

3.2.3 Other infection related datasets

The 12 h HMPV perturbed genes were cohesive, not only for upregulated genes (PIE score = 1.1, P = 0.04) but also for downregulated genes (PIE score = 1.4, P < 0.001), indicating the ability of PIE to effectively reveal physical cohesiveness in different regulatory settings. We further explored the physical cohesiveness of infection and immune system related genes by analyzing the upregulated and downregulated genes in a number of relevant datasets: (i) genes that are affected in expression after 24 h treatment of bronchial epithelial cells with IFNG (Pawliczak et al., 2005), (ii) genes affected by cells infected for 4 h with UV-irradiated RSV or pseudomonas (Mayer et al., 2007) and (iii) genes that are affected after 24 h infection by Chlamydia pneumonia (Alvesalo et al., 2008). Both the IFNG and the UV-irradiated pathogens led to a significant PIE score for upregulated genes [PIE score = 1.14, P = 0.02 (IFNG), PIE score = 1.35, P < 0.001 (RSV) and PIE score = 1.19, P = 0.022 (Pseudomonas)], while only for IFNG did the downregulated genes display physical cohesiveness (PIE score = 1.17, P = 0.032). In contrast, PIE indicates no physical cohesiveness for genes that were upregulated or downregulated after Chlamydia infection of human lung epithelial cells. The absence of physical cohesiveness of genes perturbed by Chlamydia might be partly explained by the ability of this intracellular parasite to de-modulate host-cell responses, e.g. its abrogation of apoptosis in epithelial cells (Airenne et al., 2002; Hacker et al., 2006), thus resulting in PPI networks that are less or equally dense as random networks. In this light, the significant physical cohesiveness of the upregulated genes after infection with UV-irradiated pathogens is particularly interesting, as these cannot be the result of the direct interference of the pathogen with the gene regulation, but, in contrast point to the cellular program that appears to be triggered by the infection.

3.3 Correlation of physical cohesiveness with prediction of downstream pathway genes in propagated networks

We also examined to what extent proteins that interact with the proteins of upregulated genes are physically cohesive (Supplementary Material). We observed that a one step propagation of networks of genes upregulated in expression by HMPV or IFNG led to physically cohesive networks (Supplementary Fig. 1). Nevertheless, the overlap between random networks with the same degree distribution and the propagated network becomes substantial (25%). At higher levels of propagation, this overlap becomes too large to assess a significance value for the PIE score. Comparison between the one step propagated networks of genes induced by the HMPV virus at time points 12, 24 and 48 h and the genes overexpressed at the next time point indicated a significant overlap (P < 1.0e-3), showing some predictive capacity of such propagation (Supplementary Table 1). Overall, the sensitivity of prediction is 5–41% and the positive predictive value is 5–11%. There is a positive, albeit insignificant correlation between the PIE score of precursor networks and the predictability of genes in their propagated networks. For instance, the correlation between the PIE score and sensitivity of predictions is 0.93 (P = 0.066). These results demonstrate the usefulness of the PIE approach to assess the biological coherence of a set of genes and the potential to use general PPI networks in an exploratory manner to predict genes of relevance to a process being studied.

4 DISCUSSION

In order to explore PPIs in a quantitative manner, we have developed a method called PIE, to circumvent interaction enrichment biases in context-specific networks derived from general PPI networks. PIE employs a randomization procedure that appropriately considers the global degrees (in a general PPI network) of the extant nodes in a context-specific test network, prior to assigning physical cohesiveness to the test network.

We have focused on the context of disease and immunity because many proteins have been studied in this area. We observe that there are significantly (P < 0.01) more interactions for proteins of morbid disease genes and HMPV-induced genes than random expectation in general PPI networks. This observed enrichment for PPI of morbid disease genes and HMPV-induced genes is in agreement with other studies indicating that disease-based inquisitional biases have an influence on the topology of general PPI networks (Oti et al., 2006; Wachi et al., 2005). The basis for this enrichment can be biological, in the sense that disease genes or genes that are triggered upon infection are simply more likely to have physical interactions. Nevertheless, it is not unlikely that this enrichment is at least partly caused by an experimental bias in research efforts. Based on these premises, we investigated the physical cohesiveness of the proteins of these sets of genes using the PIE approach.

The PIE approach reveals no physical cohesiveness among the morbid disease genes, by taking into account that these genes are significantly enriched in general PPI networks. Other studies examining global topological properties of protein encoded by disease genes have focused on cancer genes. In this light, greater degrees and centralities of cancer genes in comparison to non-cancer genes within the interactome have been observed (Jonsson and Bates, 2006; Wachi et al., 2005). In contradiction to the previous observation, Goh et al. (2007) have shown that the majority of disease genes do not actually show a tendency to code for highly interacting proteins but instead the apparent correlation between high degrees and disease genes is entirely due to the ∼22% overlap between disease genes and essential genes, the latter set of genes being mainly hubs (Goh et al., 2007). The methods used by the previous authors were not similar to the PIE approach. Nevertheless, PIE further clarifies this discrepancy in the literature by indicating that globally, there is no physical cohesiveness between the proteins of morbid disease genes, when taking into account their high degrees in PPI networks. This suggests that genes that are not associated with similar disorders, even if their protein products have many interactions in PPI networks, show negligible biological coherence and advocates the existence of distinct, disease-specific functional modules.

On the other hand, the PIE approach reveals significant physical cohesiveness for HMPV-induced genes. In general, both average degree and the physical cohesiveness increased in the time course of infection. The observed increase in physical cohesiveness in the course of HMPV infection suggests the existence of biologically coherent functional modules, like those for apoptosis (van Diepen et al., 2010), being elicited in response to the infection. This observation is in agreement with other interactome–transcriptome studies that posit that there is a correlation between transcription pattern similarities of a pair of genes and there being an interaction between their protein products (Ge et al., 2001; Hahn et al., 2005; Wachi et al., 2005).

Moreover, the biologically coherent information observed so far using PIE sets the premise to predict genes that might be relevant to HMPV-infection biology but not yet expressed at the particular time point of infection being studied. We observe that the propagation of a physically cohesive network rapidly leads to a less cohesive network; a phenomenon that is likely due to the change in context from which the genes in the original network were chosen to the global context of the general PPI network. This observation is in agreement with other studies indicating that there is a correlation between network distance (distance apart in a PPI network) and functional distance (semantic similarity in functional category) between proteins in a PPI network. That is, the closer two proteins are in a PPI network, the more similar are their function annotations (Sharan et al., 2007). In this light, we could predict 5–41% of the genes that would be overexpressed at future time points of the infection. Although the positive predictive values for these predictions are low (<11%), mainly due to the rapid growth of the propagated networks, they are significant (P ≤ 0.001, Supplementary Table 1) even after randomizations based on networks of the same sizes and degree distributions as those of the test networks (i.e. the PIE approach).

PIE is different from general methods designed to derive functional insights from a set of genes by integrating gene lists with general PPI networks mainly in the sense that most of these methods are aimed at decomposing the network into smaller clusters or functional modules (Sharan et al., 2007). As such it is difficult to directly compare PIE with other methods. Notwithstanding, PIE is a very strict and globally unbiased approach. Even though PIE scores are in general not very high (the increase in the average number of interactions relative to the random networks is about 5–10%) they can nevertheless be deemed significant or not (i.e. they are informative). Moreover, the PIE procedure is very reliable, in the sense that it mimics the degree distribution of the network that is being tested exactly. A disadvantage of this approach is that it limits the number of alternative, independent networks that can be extracted from the global network for comparison with the network under investigation. An alternative would be to relax this constraint slightly by either modeling or binning the degree distribution and extracting networks with that modeled or binned distribution. This would also have the advantage that the physical cohesiveness of networks with many high degree nodes could be assessed (Koyuturk et al., 2007).

Contingencies with respect to the interactions, like inhibition or stimulation, are not available at a scale that allows systematic comparisons of networks. Such information would of course make the networks more specific, allowing more meaningful comparisons with respect to their biological cohesiveness. Nevertheless, regardless of the source of experimental or inquisitional bias, PIE circumvents gene enrichment biases in a global manner as has been shown here using data of morbid genetic disease genes, virus-perturbed genes (HMPV), cytokine-perturbed genes (IFNG), bacteria-perturbed genes (C.pneumoniae), and even genes perturbed by inert pathogen material (UV-irradiated RSV and P.aeruginosa). PIE can in principle be applied to any given set of genes to estimate the overrepresentation of protein interactions as a proxy for their biological cohesiveness.

Supplementary Material

Supplementary Data
supp_26_21_2737__index.html (734B, html)

ACKNOWLEDGEMENTS

We are grateful to the reviewers for their constructive remarks.

Funding: This work was supported by the VIRGO consortium, an Innovative Cluster approved by the Netherlands Genomics Initiative and partially funded by the Dutch Government (BSIK 03012), The Netherlands.

Conflict of Interest: none declared.

REFERENCES

  1. Airenne S, et al. Chlamydia pneumoniae inhibits apoptosis in human epithelial and monocyte cell lines. Scand. J. Immunol. 2002;55:390–398. doi: 10.1046/j.1365-3083.2002.01075.x. [DOI] [PubMed] [Google Scholar]
  2. Alvesalo J, et al. Microarray analysis of a Chlamydia pneumoniae-infected human epithelial cell line by use of gene ontology hierarchy. J. Infect. Dis. 2008;197:156–162. doi: 10.1086/524142. [DOI] [PubMed] [Google Scholar]
  3. Bader GD, et al. BIND: the biomolecular interaction network database. Nucleic Acids Res. 2003;31:248–250. doi: 10.1093/nar/gkg056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bao X, et al. Identification of human metapneumovirus-induced gene networks in airway epithelial cells by microarray analysis. Virology. 2008;374:114–127. doi: 10.1016/j.virol.2007.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beuming T, et al. PDZBase: a protein-protein interaction database for PDZ-domains. Bioinformatics. 2005;21:827–828. doi: 10.1093/bioinformatics/bti098. [DOI] [PubMed] [Google Scholar]
  6. Bjorklund AK, et al. Quantitative assessment of the structural bias in protein-protein interaction assays. Proteomics. 2008;8:4657–4667. doi: 10.1002/pmic.200800150. [DOI] [PubMed] [Google Scholar]
  7. Brown KR, Jurisica I. Unequal evolutionary conservation of human protein interactions in interologous networks. Genome Biol. 2007;8:R95. doi: 10.1186/gb-2007-8-5-r95. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chatr-aryamontri A, et al. MINT: the Molecular INTeraction database. Nucleic Acids Res. 2007;35:D572–D574. doi: 10.1093/nar/gkl950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Collins SR, et al. Toward a comprehensive atlas of the physical interactome of Saccharomyces cerevisiae. Mol. Cell Proteomics. 2007;6:439–450. doi: 10.1074/mcp.M600381-MCP200. [DOI] [PubMed] [Google Scholar]
  10. Cusick ME, et al. Literature-curated protein interaction datasets. Nat. Methods. 2009;6:39–46. doi: 10.1038/nmeth.1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dittrich MT, et al. Identifying functional modules in protein-protein interaction networks: an integrated exact approach. Bioinformatics. 2008;24:i223–i231. doi: 10.1093/bioinformatics/btn161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ge H, et al. Correlation between transcriptome and interactome mapping data from Saccharomyces cerevisiae. Nat. Genet. 2001;29:482–486. doi: 10.1038/ng776. [DOI] [PubMed] [Google Scholar]
  13. Goh KI, et al. The human disease network. Proc. Natl Acad. Sci. USA. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hacker G, et al. Apoptosis in infectious disease: how bacteria interfere with the apoptotic apparatus. Med. Microbiol. Immunol. 2006;195:11–19. doi: 10.1007/s00430-005-0239-4. [DOI] [PubMed] [Google Scholar]
  15. Hahn A, et al. Confirmation of human protein interaction data by human expression data. BMC Bioinformatics. 2005;6:112. doi: 10.1186/1471-2105-6-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Huang TW, et al. Reconstruction of human protein interolog network using evolutionary conserved network. BMC Bioinformatics. 2007;8:152. doi: 10.1186/1471-2105-8-152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hubbard TJ, et al. Ensembl 2007. Nucleic Acids Res. 2007;35:D610–D617. doi: 10.1093/nar/gkl996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ideker T, Sharan R. Protein networks in disease. Genome Res. 2008;18:644–652. doi: 10.1101/gr.071852.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jeong H, et al. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
  20. Jonsson PF, Bates PA. Global topological features of cancer proteins in the human interactome. Bioinformatics. 2006;22:2291–2297. doi: 10.1093/bioinformatics/btl390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Karni S, et al. A network-based method for predicting disease-causing genes. J. Comput. Biol. 2009;16:181–189. doi: 10.1089/cmb.2008.05TT. [DOI] [PubMed] [Google Scholar]
  22. Kerrien S, et al. IntAct–open source resource for molecular interaction data. Nucleic Acids Res. 2007;35:D561–D565. doi: 10.1093/nar/gkl958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Koyuturk M, et al. Assessing significance of connectivity and conservation in protein interaction networks. J. Comput. Biol. 2007;14:747–764. doi: 10.1089/cmb.2007.R014. [DOI] [PubMed] [Google Scholar]
  24. Maere S, et al. BiNGO: a Cytoscape plugin to assess overrepresentation of gene ontology categories in biological networks. Bioinformatics. 2005;21:3448–3449. doi: 10.1093/bioinformatics/bti551. [DOI] [PubMed] [Google Scholar]
  25. Mayer AK, et al. Differential recognition of TLR-dependent microbial ligands in human bronchial epithelial cells. J. Immunol. 2007;178:3134–3142. doi: 10.4049/jimmunol.178.5.3134. [DOI] [PubMed] [Google Scholar]
  26. Oti M, et al. Predicting disease genes using protein-protein interactions. J. Med. Genet. 2006;43:691–698. doi: 10.1136/jmg.2006.041376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pawliczak R, et al. Influence of IFN-gamma on gene expression in normal human bronchial epithelial cells: modulation of IFN-gamma effects by dexamethasone. Physiol. Genomics. 2005;23:28–45. doi: 10.1152/physiolgenomics.00011.2005. [DOI] [PubMed] [Google Scholar]
  28. Peri S, et al. Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res. 2003;13:2363–2371. doi: 10.1101/gr.1680803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rual JF, et al. Towards a proteome-scale map of the human protein-protein interaction network. Nature. 2005;437:1173–1178. doi: 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
  30. Sayers EW, et al. Database resources of the National Center for Biotechnology Information. Nucleic Acids Res. 2009;37:D5–D15. doi: 10.1093/nar/gkn741. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Shannon P, et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sharan R, et al. Network-based prediction of protein function. Mol. Syst. Biol. 2007;3:88. doi: 10.1038/msb4100129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Stelzl U, et al. A human protein-protein interaction network: a resource for annotating the proteome. Cell. 2005;122:957–968. doi: 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
  34. Tornow S, Mewes HW. Functional modules by relating protein interaction networks and gene expression. Nucleic Acids Res. 2003;31:6283–6289. doi: 10.1093/nar/gkg838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tucker CL, et al. Towards an understanding of complex protein networks. Trends Cell Biol. 2001;11:102–106. doi: 10.1016/s0962-8924(00)01902-4. [DOI] [PubMed] [Google Scholar]
  36. van den Hoogen BG, et al. A newly discovered human pneumovirus isolated from young children with respiratory tract disease. Nat. Med. 2001;7:719–724. doi: 10.1038/89098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. van Diepen A, et al. Quantitative proteome profiling of respiratory virus-infected lung epithelial cells. J. Proteomics. 2010;73:1680–1693. doi: 10.1016/j.jprot.2010.04.008. [DOI] [PubMed] [Google Scholar]
  38. Vidal M. A biological atlas of functional maps. Cell. 2001;104:333–339. doi: 10.1016/s0092-8674(01)00221-5. [DOI] [PubMed] [Google Scholar]
  39. von Mering C, et al. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
  40. Wachi S, et al. Interactome-transcriptome analysis reveals the high centrality of genes differentially expressed in lung cancer tissues. Bioinformatics. 2005;21:4205–4208. doi: 10.1093/bioinformatics/bti688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wuchty S, Almaas E. Peeling the yeast protein network. Proteomics. 2005;5:444–449. doi: 10.1002/pmic.200400962. [DOI] [PubMed] [Google Scholar]
  42. Yosef N, et al. Improved network-based identification of protein orthologs. Bioinformatics. 2008;24:i200–i206. doi: 10.1093/bioinformatics/btn277. [DOI] [PubMed] [Google Scholar]
  43. Yu H, et al. Annotation transfer between genomes: protein-protein interologs and protein-DNA regulogs. Genome Res. 2004;14:1107–1118. doi: 10.1101/gr.1774904. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_26_21_2737__index.html (734B, html)
supp_btq474_SupplementaryMaterialPIE_bioinformatics.doc (384.5KB, doc)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES