Abstract
In this paper, thermal mixing characteristics of two miscible fluids in a T-shaped microchannel are investigated theoretically, experimentally, and numerically. Thermal mixing processes in a T-shaped microchannel are divided into two zones, consisting of a T-junction and a mixing channel. An analytical two-dimensional model was first built to describe the heat transfer processes in the mixing channel. In the experiments, de-ionized water was employed as the working fluid. Laser induced fluorescence method was used to measure the fluid temperature field in the microchannel. Different combinations of flow rate ratios were studied to investigate the thermal mixing characteristics in the microchannel. At the T-junction, thermal diffusion is found to be dominant in this area due to the striation in the temperature contours. In the mixing channel, heat transfer processes are found to be controlled by thermal diffusion and convection. Measured temperature profiles at the T-junction and mixing channel are compared with analytical model and numerical simulation, respectively.
INTRODUCTION
Microfluidics has been receiving great attention over the past decades. An increasing number of researchers focus on this area because of its compatibility and high performance with (bio) chemical analysis.1, 2, 3 Microfluidics shows immense potentials in enhancing mass and heat transfer by the large surface-to-volume ratio and the short transport path.4 Based on the enhanced mass and heat transfer, fast mixing can be achieved more efficiently. Therefore, it is necessary to have a fundamental understanding of mass and heat transfer phenomena in microfluidics.
Micromixers based on different working principles have been proposed and investigated systematically. Generally speaking, micromixers are divided into passive micromixers and active micromixers.5, 6 Passive micromixers only rely on diffusion or chaotic advection, while active micromixers relying on external disturbance.
Parallel lamination micromixer is one of the most commonly used passive micromixer. It is based on the decrease of molecular diffusion path by splitting the inlet streams into n substreams and then recombining them into a single stream. A basic design with two inlets is called as T-mixer or Y-mixer,5 which is an ideal configuration for the investigation of transport phenomena on the microscale. Many experimental and numerical studies were conducted for mixing of miscible fluids in the T-shaped microchannels. Bokenkamp et al.7 achieved better mixing efficiency by connecting two T-shaped micromixers with a commercially available quench-flow instrument. Jacobson et al.8 fabricated devices for parallel mixing, which consists of a series of independent T-shaped intersections. Gobby et al.9 studied the mixing characteristics of gaseous flow in a T-shaped micromixer by using numerical simulation. T-shaped microchannels have also been employed to measure the molecular diffusion coefficient for chemical analysis.10, 11, 12 Wong et al.13 fabricated and tested a micro-T-mixer as a rapid mixing micromixer. Kockmann and co-workers14, 15 carried out numerical simulations and experimental studies on mixing in a T-shaped micromixer. Three flow regimes were distinguished, which were named as strictly laminar flow, symmetrical vortex flow, and engulfment flow depending on the Reynolds number. Zhao et al.4 investigated the mass transfer process in the T-junction microchannels of immiscible fluids. Empirical correlations were proposed to predict the mass transfer coefficient in the microchannel. The diffusion coefficient and flow rate ratios were also studied in a sandwich T-shaped micromixer.16
The limitation of the previous experimental and numerical studies on the T-shaped micromixer was that they all focused on mass mixing of two miscible fluids. Little work has been carried out to study the thermal mixing characteristics in T-shaped microchannels. Kockmann et al.17 utilized the thermal mixing of a hot vapor-gas mixture with a cold gas to generate aerosols with nanoscale droplets. Glawdel et al.18 proposed a simple and effective technique, which employed photobleaching method to remove the fluorescent signal from absorbed Rhodamine B dye. This new technique was demonstrated by measuring the temperature field at the Y-junction where hot and cold stream merged. However, this paper did not analyze the thermal mixing process. To the best knowledge of the author, theoretical analysis related to thermal mixing processes in the microchannel is yet to be reported. In this paper, the main objective is to qualitatively study the thermal mixing characteristics of the two miscible fluids in a T-shaped microchannel with different combination of flow rates. Two heat transfer zones (at the T-junction and the mixing channel) are analyzed and investigated. An analytical model is proposed for the thermal mixing process in the mixing channel. Experiments are carried out to validate the analytical model. Laser induced fluorescence (LIF) method is employed to measure the internal fluid temperature field in microchannel, which is based on the temperature-dependent fluorescence. In this method, the temperature-dependent fluorescence Rhodamine B was added into the working fluid. The intensity of the fluorescence was imaged using a fluorescence microscope and a CCD camera. The internal fluid temperature field can be obtained by measuring the intensity of fluid through a calibration curve. A three-dimensional numerical simulation is subsequently carried out to give a better understanding of the thermal mixing processes on the microscale.
ANALYTICAL MODEL
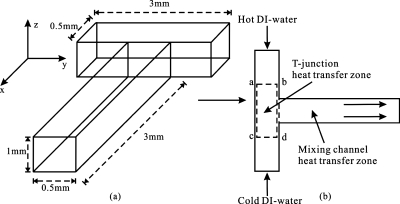
The configuration of an opposed T-shaped microchannel is shown in Fig. 1. The microchannel through which the two opposing inlet streams flow horizontally along the y-direction is a rectangle (3.0 mm×0.5 mm). A vertical rectangle bisects the horizontal channel and forms two short rectangular inlet arms, each with a length of 1.25 mm and a width of 0.5 mm.
Figure 1.
(a) Schematic illustration of T-shaped microchannel. (b) The opposed T-shaped microchannel.
To accurately describe the heat transfer processes in the opposed T-junction micromixer, the thermal mixing processes in the T-shaped microchannel are divided into T-junction (a-b-d-c) and mixing channel as shown in Fig. 1b. In the T-junction, hot and cold de-ionized (DI) water flows coaxially into the two inlet arms. Thermal mixing occurs as soon as they contact each other. Thermal diffusion is dominant in the T-junction. Meanwhile, low energy dissipation arises due to that the kinetic energy is converted into a motion through collision and redirection of the fluid flow at the T-junction. In our study, Reynolds number is less than 1. The flow is laminar, and the streamlines are scarcely bent and follow the channel walls.14 In the mixing channel heat transfer zone, thermal diffusion and convection dominate in the thermal mixing processes. The thermal mixing is greatly enhanced due to the enough residence time provided by the long mixing channel. The fluid flow in the mixing channel will continue to be laminar flow.
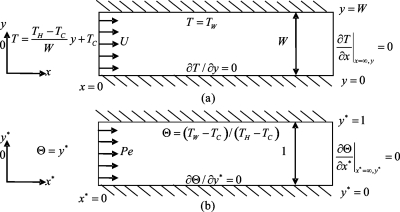
An analytical model is developed to describe the heat transfer processes in the mixing channel heat transfer zone [Fig. 1b]. Figure 2 illustrates the two-dimensional model for the thermal mixing processes in the mixing channel. The microchannel is a long channel with a width of W. The flow in the rectangular channel is assumed to have a constant velocity of U. For low Reynolds number flow (Re<1),19 due to the strong thermal diffusion occurs at the T-junction heat transfer zone, a linear temperature distribution is specified at the inlet of the mixing channel (x*=0). At the upper wall (y*=1), constant surface temperature is specified due to the thermal conduction from the thermal electric module. This is due to that under an applied voltage, the thermal electric module will provide a constant heating temperature continuously. At the steady state, the upper wall temperature, which is adjacent to the thermal electric module, will becomes a constant surface temperature. At the bottom wall (y*=0), adiabatic condition is specified due to the negligible heat loss to the ambient environment. For a very long channel, in particular as x*→∞, fully thermal mixing will be achieved, so there will be no temperature gradient in the flow direction in the mixing channel.
Figure 2.
Two-dimensional model of thermal mixing in the mixing channel: (a) the actual model and (b) the dimensionless model.
In the analytical model, the following assumptions are made:
-
(1)
laminar, incompressible, Newtonian fluid, steady flow is assumed;
-
(2)
two fluids with same the property, viscosity, and thermal diffusivity are independent of temperature;
-
(3)
convection is assumed to occur in one direction, axially along the mixing channel; and
-
(4)
decoupled convection and diffusion processes.
The governing equation can be formulated in the dimensional form as
| (1) |
where α is the thermal diffusivity of the fluid [α=k∕(ρcp)]. By introducing the dimensionless coordinate system x*=x∕W,y*=y∕W, the normalized temperature Θ=(T−TC)∕(TH−TC) and the Péclet number,
| (2) |
where TH, TC, U, W, and α are the temperature of hot fluid, temperature of cold fluid, uniform velocity, mixing channel width, and thermal diffusivity, respectively. Energy equation 1 can be formulated in dimensionless form as
| (3) |
The inlet and outlet boundary conditions for Eq. 3 are
| 4 |
The boundary condition for the wall was set as follows:
| 5 |
Using the finite Fourier transform method20 and applying corresponding boundary conditions Eqs. 4, 5, the dimensionless temperature distribution in the microchannel can be obtained,
| (6) |
where , c=(TW−TC)∕(TH−TC), and .
EXPERIMENT
Fluorescence imaging setup
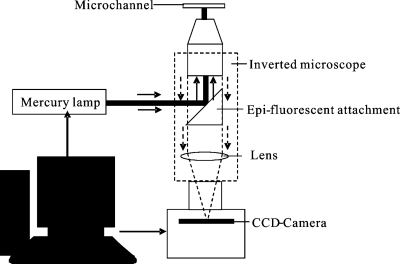
The schematic illustration of the fluorescence imaging setup is shown in Fig. 3, consisting of four main components: an illumination system, an optical system, a coupled charge device (CCD) camera, and a personal computer based control system. A mercury lamp with the wavelength of 540 nm was employed as the illumination source for the fluorescence imaging setup.
Figure 3.
Schematic illustration of experimental setup for fluorescence imaging.
The Nikon inverted microscope (Model ECLIPSE TE2000-S) with a set of epifluorescent attachments was used as the optical system. Excitation filter, dichroic mirror, and emission filter constitute the filter cube. Emission filters were used in the measurements to select the specific emission wavelength of the sample and to remove traces of excitation light.
An interline transfer CCD camera (Sony ICX 084) was used for recording the images. The resolution of the camera is 1324×1024 pixels with 16 bits grayscale. The active area of the CCD sensor is 4 mm×3 mm. The exposure time for recording the image is 70 ms.
Calibration of temperature measurement
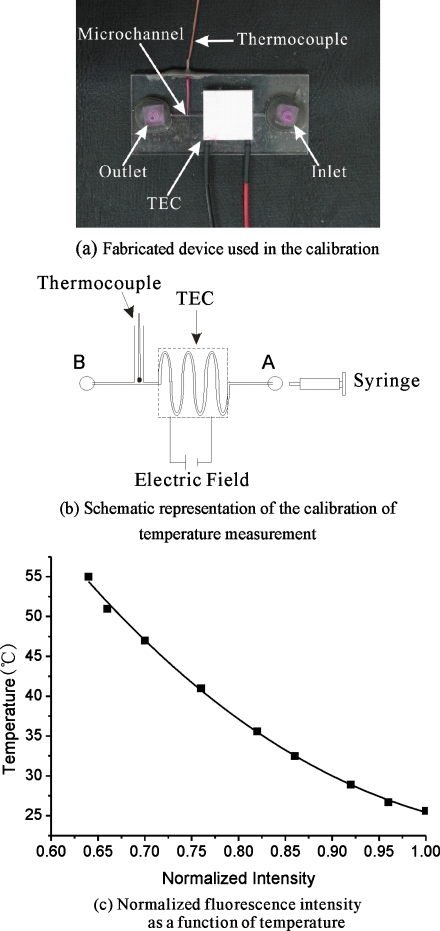
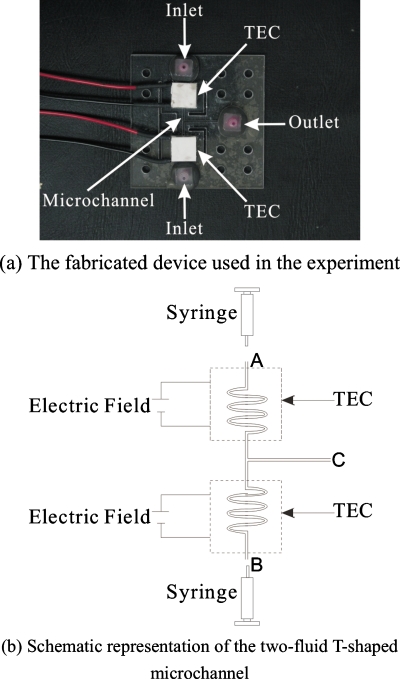
The schematic of the experimental setup for the calibration of temperature measurement is shown in Fig. 4a, 4b. The calibration was used to determine the relationship between the fluorescence intensity and temperature. The microchannel has a cross section of 1000 μm×500 μm. Rhodamine B solution (0.025 g∕100 ml) is introduced into the inlet port A by a single syringe pump (74900-05, Cole-Parmer; 0.2 μl∕h to 5001∕h, accuracy of 0.5%). A low voltage power supply (GW Model GPC-30300) was used to supply voltage to a thermoelectric module to heat up the Rhodamine B solution in the microchannel. A thermoelectric module is a solid-state method of heat transfer by means of different semiconductor materials, which is also commonly known as the Peltier effect. The voltage was supplied to enable heating∕cooling in the microchannel.
Figure 4.
Calibration of temperature measurement.
The thermoelectric module was placed on the square slot on the top PMMA plate to heat the Rhodamine B solution by varying the voltages. The temperature of the solution increases with increasing the voltage. The image of the Rhodamine B solution in the microchannel for different temperature was captured with the microscope. Each captured image was generated by 30 sequential video frames. For the calibration curve, the fluorescence intensity for the image at each temperature was determined by averaging the intensity value (after background subtraction) of all the pixels of the corresponding image. A calibration curve is generated to accurately describe the dependence of Rhodamine B fluorescence on temperature. The resulting intensity (normalized by the intensity at 25 °C) versus temperature is plotted in Fig. 4c.
Experiment on thermal mixing
The T-shaped microchannel used in the experiment is shown in Fig. 5. The fabrication is based on the lamination thermal bonding technique.21, 22 In this method, three polymethylmethacrylate (PMMA) plates (50 mm×50 mm) were bonded together to form a closed microfluidic channel with inlet and outlet holes. Thus, the middle PMMA defines the depth of the channel. The two fluids flow side by side in the T-shaped straight microchannel in the direction from left to right by two identical syringe pumps. In this experiment, the straight portion of the T-shaped channel has a cross section of 1000 μm×500 μm and the length of 2 cm. Hot DI water with Rhodamine B solution (0.025 g∕100 ml) enters the upper inlet arm, and cold DI water with Rhodamine B solution enters the lower inlet arm. Two low voltage power supplies are used to supply voltage to the thermoelectric module to enable heating∕cooling of the working fluids. The images of the Rhodamine B solution at the inlet arms and the main channel for different flow rates (QH∕QC) were captured by the CCD camera and microscope.
Figure 5.
Schematic illustration of experimental setup for thermal mixing.
RESULTS AND DISCUSSION
Experimental results and discussion
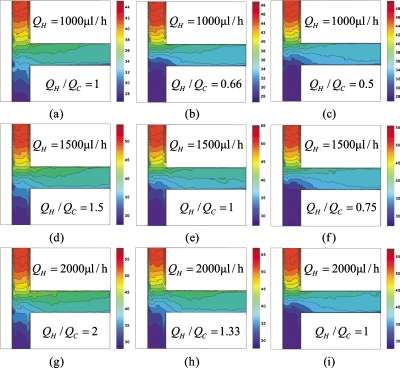
Figures 6a, 6b, 6c show the measured temperature profiles for three flow rate ratios (QH∕QC): 1, 0.66 and 0.5 respectively, of which QH was maintained at 1000 μl∕h. Hot and cold DI water with flow rates QH and QC flow coaxially into the respective inlet arms. The formation of temperature contours was observed, indicating that extensive thermal mixing had already taken place in the inlet arms. The striation in the temperature contours indicated that diffusion was dominant in this area. This phenomenon is due to the fact that the thermal diffusivity is three orders larger than the mass diffusivity, which corresponds to a Lewis number Le=α∕D=1000. As a result, the efficiency of thermal mixing was much larger than the mass mixing in laminar flow. At the inlet of the mixing channel (x*=0), a linear temperature distribution was observed due to thermal diffusion in the inlet arms. The two injected streams flowed into the mixing channel which was perpendicular to the inlet arms. Two streams flowed side by side down the mixing channel. Thermal mixing occurred during the parallel flow through the combined diffusion-convection mechanism. The number of striations in the temperature contours decreased in the mixing channel. A more uniformity of temperature distribution was observed in the mixing channel. When QH∕QC=1, each stream occupied half of the cross section in the mixing channel. At flow rate ratios of 0.66 [Fig. 6b] and 0.5 [Fig. 6c], the cold stream occupies a larger fraction of the channel as QC increases.
Figure 6.
Experimental temperature contours plot of thermal mixing in the T-shaped microchannel.
Figures 6d, 6e, 6f show the measured temperature profiles for three flow rate ratios (QH∕QC): 1.5, 1 and 0.75 respectively, of which QH was maintained at 1500 μl∕h, while Figs. 6g, 6h, 6i show the measure temperature profiles for three flow rate ratios (QH∕QC): 2, 1.33 and 1 respectively, of which QH was maintained at 2000 μl∕h. These figures show the same trend as Figs. 6a, 6b, 6c.
Comparison between analytical analysis and experimental results
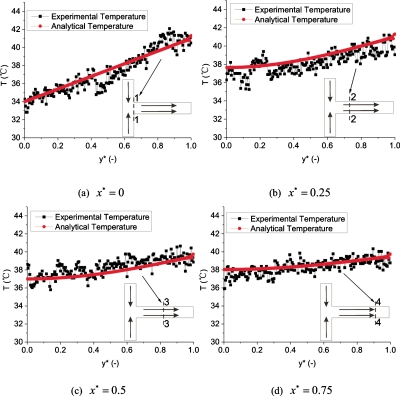
A comparison between theoretical analysis and experimental results is shown in Fig. 7. The analytical model agrees well with the experimental results, which demonstrate the usability of the boundary conditions setting for the heat transfer processes in the mixing channel heat transfer zone. At the entrance region (x*=0) of the mixing channel, a linear temperature distribution boundary condition confirms the thermal mixing processes in the inlet arms. Striation in the temperature contours formed due to the thermal diffusion in the inlet arms. The evolution of temperature profiles at four different sections (x*=0, x*=0.25, x*=0.5, x*=0.75) along the axial direction can be clearly seen in Fig. 7. As the mixing channel length increases, a more uniform temperature distribution is observed due the combined convection and diffusion. Thermal mixing is found to be proportional to the mixing channel length.
Figure 7.
Comparison between analytical and experimental temperature profiles at four different sections in the mixing channel (QH=1500 μl∕h, QH∕QC=1).
THREE-DIMENSIONAL NUMERICAL SIMULATION
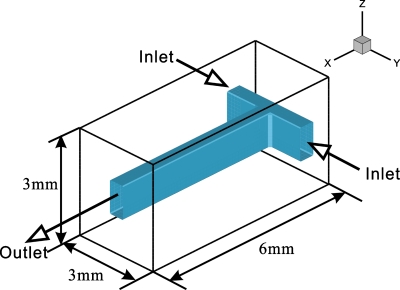
Thermal mixing within the T-shaped microchannel depends on the transport phenomena in the T-junction and the mixing channel. The proposed analytical model describes heat transfer within the mixing channel only. Therefore, a 3D numerical simulation to integrate the two heat transfer zones is needed. Furthermore, the flow fields obtained from the numerical simulation can be used to confirm the analytical model. The schematic of the computational domain is shown in Fig. 8. The temperature and transverse velocity along the y direction at the inlet are specified. Both the temperature and velocity at the inlet are assumed to be uniform. The nonslip and adiabatic boundary conditions are used for the walls. At the outlet, zero gradient conditions are imposed on the transverse velocity and temperature. Axial velocity at the outlet is calculated to ensure mass conservation over the whole computational domain. The density, specific heat, thermal conductivity, and viscosity of DI water are allowed to vary with temperature.23
Figure 8.
Computational domain.
Governing equations
The fluid flow and heat transfer are assumed to be in steady state, incompressible, and laminar. The continuity, momentum, and energy equations can be written in the Cartesian tensor notation as follows: continuity equation
| (7) |
momentum equation,
| (8) |
and energy equation,
| (9) |
where ρ, μ, cp, and k are the fluid density, viscosity, specific heat, and thermal conductivity, respectively, whose dependence on temperature are given as follows:
| (10) |
| (11) |
| (12) |
| (13) |
Numerical procedure
The finite volume method is employed to solve the continuity, momentum, and energy equations. A stagger grid is used to store the scalar and velocities at the nodes and faces of each control volume, respectively. The convection-diffusion effect is manipulated by using power-law scheme. SIMPLER algorithm is used to treat the velocity-pressure coupled problem.24
A grid independence test was conducted by using different numbers of unstructured grid. Three different grid numbers—41×18×21, 62×27×32, and 93×41×48—are employed. The differences in u, v, w, and T at all grid points are less than 1%, which means the numerical solution is grid independent. Therefore, the numerical method is considered to be appropriate for the simulation of our conjugate convection-conduction heat transfer problem.
Comparison between numerical simulation and experimental results
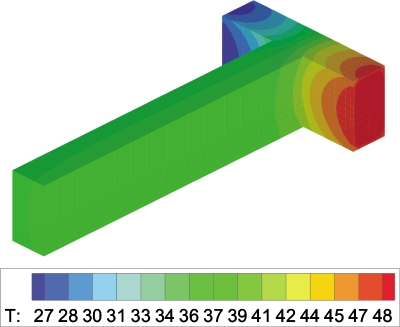
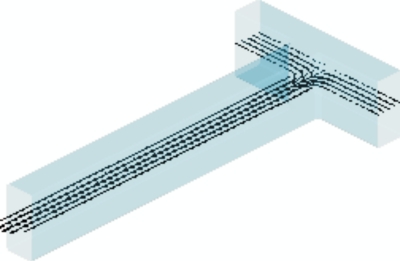
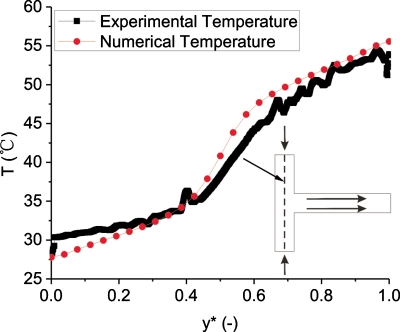
Three-dimensional temperature and velocity distributions in the T-shaped microchannel are shown in Fig. 910, respectively. In order to compare the numerical simulation result with the experimental result, depth-wise averaging approach is employed to average the temperature distributions along the z direction. Based on this method, the three-dimensional temperature distribution is converted to a two-dimensional temperature distribution. The comparison between numerical and experimental temperature profiles in the T-junction heat transfer zone is shown in Fig. 11. The numerical model agrees well with the experimental results. Striation temperature contours in the T-junction are confirmed by the numerical simulation.
Figure 9.
Temperature distribution in the T-shaped microchannel (QH=1500 μl∕h, QH∕QC=1).
Figure 10.
Velocity distribution in the T-shaped microchannel (QH=1500 μl∕h, QH∕QC=1).
Figure 11.
Comparison between experimental and numerical temperature profiles in the T-junction heat transfer zone (QH=1500 μl∕h, QH∕QC=1).
CONCLUSIONS
In this paper, LIF microscopy allows the measurement of the temperature field in microchannels. This measurement would be impossible with conventional techniques using thermocouple. Thermal mixing characteristics of two fluids in the T-shaped microchannel are investigated theoretically, experimentally, and numerically. Some significant results obtained are listed as follows:
-
(1)
the heat transfer process in the T-shaped microchannel can be divided into two heat transfer zones: the T-junction and the mixing channel;
-
(2)
striations in the temperature contours in the T-junction are experimentally and numerically revealed; and
-
(3)
flow rate ratio plays an important role in the thermal mixing process.
References
- Auroux P.-A., Iossifidis D., Reyes D. R., and Manz A., Anal. Chem. 74, 2637 (2002). 10.1021/ac020239t [DOI] [PubMed] [Google Scholar]
- Reyes D. R., Iossifidis D., Auroux P.-A., and Manz A., Anal. Chem. 74, 2623 (2002). 10.1021/ac0202435 [DOI] [PubMed] [Google Scholar]
- Wang J., Chen G., Chatrathi M. P., and Musameh M., Anal. Chem. 76, 298 (2004). 10.1021/ac035130f [DOI] [PubMed] [Google Scholar]
- Zhao Y., Chen G., and Yuan Q., AIChE J. 53, 3042 (2007). 10.1002/aic.11333 [DOI] [Google Scholar]
- Nguyen N. T. and Wu Z., J. Micromech. Microeng. 15, R1 (2005). 10.1088/0960-1317/15/2/R01 [DOI] [Google Scholar]
- Wu Z. and Nguyen N. T., Biomed. Microdevices 7, 13 (2005). 10.1007/s10544-005-6167-7 [DOI] [PubMed] [Google Scholar]
- Bökenkamp D., Desai A., Yang X., Tai Y. C., Marzluff E. M., and Mayo S. L., Anal. Chem. 70, 232 (1998). 10.1021/ac9708250 [DOI] [Google Scholar]
- Jacobson S. C., McKnight T. E., and Ramsey J. M., Anal. Chem. 71, 4455 (1999). 10.1021/ac990576a [DOI] [Google Scholar]
- Gobby D., Angeli P., and Gavriilidis A., J. Micromech. Microeng. 11, 126 (2001). 10.1088/0960-1317/11/2/307 [DOI] [Google Scholar]
- Kamholz A. E., Schilling E. A., and Yager P., Biophys. J. 80, 1967 (2001). 10.1016/S0006-3495(01)76166-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costin C. D. and Synovec R. E., Talanta 58, 551 (2002). 10.1016/S0039-9140(02)00321-1 [DOI] [PubMed] [Google Scholar]
- Costin C. D., Olund R. K., Staggemeier B. A., Torgerson A. K., and Synovec R. E., J. Chromatogr., A 1013, 77 (2003). 10.1016/S0021-9673(03)01101-4 [DOI] [PubMed] [Google Scholar]
- Wong S. H., Ward M. C. L., and Wharton C. W., Sens. Actuators B 100, 359 (2004). 10.1016/j.snb.2004.02.008 [DOI] [Google Scholar]
- Engler M., Kockmann N., Kiefer T., and Woias P., Chem. Eng. J. 101, 315 (2004). 10.1016/j.cej.2003.10.017 [DOI] [Google Scholar]
- Kockmann N., Kiefer T., Engler M., and Woias P., Sens. Actuators B 117, 495 (2006). 10.1016/j.snb.2006.01.004 [DOI] [Google Scholar]
- Abonnenc M., Josserand J., and Girault H. H., Lab Chip 9, 440 (2009). 10.1039/b815581j [DOI] [PubMed] [Google Scholar]
- Kockmann N., Dreher S., Engler M., and Woias P., Microfluid. Nanofluid. 3, 581 (2007). 10.1007/s10404-007-0149-4 [DOI] [Google Scholar]
- Glawdel T., Almutairi Z., Wang S., and Ren C., Lab Chip 9, 171 (2009). 10.1039/b805172k [DOI] [PubMed] [Google Scholar]
- Hoffmann M., Schluter M., and Rabiger N., Chem. Eng. Sci. 61, 2968 (2006). 10.1016/j.ces.2005.11.029 [DOI] [Google Scholar]
- Deen W. M., Analysis of Transport Phenomena (Oxford University Press, New York, 1998). [Google Scholar]
- Nising P., Zeilmann T., and Meyer T., Chem. Eng. Technol. 26, 599 (2003). 10.1002/ceat.200390092 [DOI] [Google Scholar]
- Sun Y., Kwok Y. C., and Nguyen N. T., J. Micromech. Microeng. 16, 1681 (2006). 10.1088/0960-1317/16/8/033 [DOI] [Google Scholar]
- Incropera F. P., Liquid Cooling of Electronic Devices by Single-Phase Convection (Wiley, New York, 1999). [Google Scholar]
- Patankar S. V., Numerical Heat Transfer and Fluid Flow (Hemisphere, New York, 1980). [Google Scholar]