Abstract
We consider using observational data to estimate the effect of a treatment on disease recurrence, when the decision to initiate treatment is based on longitudinal factors associated with the risk of recurrence. The effect of salvage androgen deprivation therapy (SADT) on the risk of recurrence of prostate cancer is inadequately described by existing literature. Furthermore, standard Cox regression yields biased estimates of the effect of SADT, since it is necessary to adjust for prostate-specific antigen (PSA), which is a time-dependent confounder and an intermediate variable. In this paper, we describe and compare two methods which appropriately adjust for PSA in estimating the effect of SADT. The first method is a two-stage method which jointly estimates the effect of SADT and the hazard of recurrence in the absence of treatment by SADT. In the first stage, PSA is predicted in the absence of SADT, and in the second stage, a time-dependent Cox model is used to estimate the benefit of SADT, adjusting for PSA. The second method, called sequential stratification, reorganizes the data to resemble a sequence of experiments in which treatment is conditionally randomized given the time-dependent covariates. Strata are formed, each consisting of a patient undergoing SADT and a set of appropriately matched controls, and analysis proceeds via stratified Cox regression. Both methods are applied to data from patients initially treated with radiation therapy for prostate cancer and give similar SADT effect estimates.
Keywords: treatment by indication, time-dependent confounder, proportional hazards model, causal effect, prostate cancer
1. Introduction
Prostate cancer is the most commonly diagnosed cancer among American men; however, the issue of determining the best course of treatment after initial diagnosis is relatively controversial [1]. Often, patients diagnosed with clinically localized prostate cancer undergo either external beam radiation therapy (EBRT) or radical prostatectomy, sometimes in combination with hormone therapies [2]. After initial treatment, patients are actively monitored for elevated and/or rising levels of prostate-specific antigen (PSA), which indicate an increased risk for the clinical recurrence of prostate cancer [3]. In these cases, patients sometimes receive additional new treatment (called salvage therapy) in order to prevent or delay recurrence.
One such additional salvage therapy treatment is androgen deprivation therapy (ADT). Salvage ADT (SADT) consists of either surgical or medical castration, although surgical castration (orchiectomy) is less prevalent due to the availability of safe medical alternatives, such as gonadotropin-releasing hormone agonists (GnRH-As). GnRH-As are administered as an injection or implant, and can last between one and six months according to dosage. GnRH-As produce testosterone levels comparable to those found after surgical castration within about three weeks [4]. Although SADT is generally thought to be beneficial in delaying the recurrence of prostate cancer, the magnitude of the benefit of SADT is not well quantified. A small number of randomized trials have been conducted to test the efficacy of early versus deferred androgen suppression, but these trials took place prior to the use of PSA and yielded inconclusive results [5]. Moreover, little attention has been given to evaluating the extent to which the effect of SADT depends on the current health status of the patient (e.g., on PSA or slope of PSA) or on other patient characteristics (e.g. age). Better understanding of this may help doctors decide when to initiate SADT.
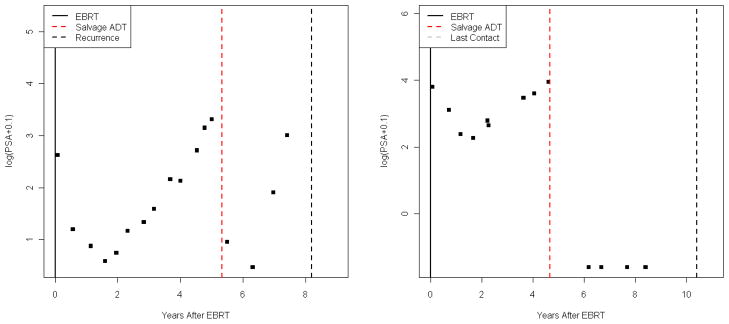
For at least the first few months after initiation of SADT, patients experience considerable decreases in PSA levels [6, 7]. Figure 1 shows typical log(PSA) patterns for two patients who received SADT. The first patient subsequently experienced a clinical recurrence of cancer, while the second patient was lost to follow-up.
Figure 1.
Typical log(PSA) patterns
Since elevated and/or rising PSA levels are a risk factor for recurrence of prostate cancer but are also a predictor of treatment by SADT, PSA and slope of PSA are (time-dependent) confounders in the relation between SADT and the prostate cancer recurrence hazard. In general, this type of relation between a time-dependent confounder and a time-varying treatment is typically present whenever there is “treatment by indication” [8]. Standard Cox regression [9] can be used to estimate the effect of a treatment on survival time in the presence of treatment by indication, as long as the covariates representing the ‘indication’ are not also intermediate variables (i.e., variables on the causal pathway between treatment and outcome), even if the covariates are time-dependent.
However, since PSA levels decrease after initiation of SADT, PSA and slope of PSA are also intermediate variables in the relation between SADT and recurrence of prostate cancer. Therefore, using standard time-dependent Cox regression to model the prostate cancer recurrence hazard as a function of SADT history would yield biased estimates of the causal effect of SADT on recurrence, whether or not adjustments were made for past confounder history [10, 11]. An analysis which adjusted for the observed time-dependent PSA values after SADT would estimate only the benefit of SADT beyond that due to the decrease in PSA at the time of initiation of SADT, rather than the recurrence-free survival benefit itself.
The methodological issues concerning adjustment in the case of treatment by indication are well-described in the causal inference literature. Since Rosenbaum (1984) examined the possible bias resulting from adjustment for ‘post-treatment’ variables in observational studies [10], a number of possible approaches have been proposed. Robins developed the g-computation algorithm estimator [12], structural nested models (SNMs) [11], and marginal structural models (MSMs) [13] to address the problem of adjustment for time-dependent confounders which are also intermediate variables. However, the g-computation algorithm does not include parameters which represent the treatment having no effect, thereby complicating the interpretation of corresponding confidence intervals for the estimated treatment effect [12]. SNMs and MSMs do include such parameters; however, SNMs do not estimate the effect of treatment on dichotomous outcomes (e.g., recurrence-free survival). Extensions of these methods (for example, dynamic treatment MSMs and history-adjusted MSMs) have also been developed [28, 27, 26]. More recently, propensity score and other related methods have been adapted for longitudinal observational studies [14, 15, 16, 17].
In this paper our goal is to investigate alternative approaches to estimating the treatment effect in a longitudinal study with treatment by indication. We will develop and compare two methods which appropriately adjust for time-dependent PSA and slope of PSA in estimating the causal effect of SADT on the risk of recurrence of prostate cancer. The first is a two-stage method which uses a linear mixed model to predict PSA and slope of PSA in the absence of SADT [18], and then uses a time-dependent Cox model to estimate the recurrence-free survival benefit of SADT, adjusting for predicted PSA and slope of PSA. This approach conditions on the latent SADT-free PSA process which, by construction, is unaffected by SADT. The observed PSA process, however, is of course affected by the receipt of SADT. Hence, this method eliminates the ‘intermediate variable’ status of the time-dependent PSA covariates, thereby allowing the use of a standard Cox regression analysis in the second stage. The second proposed method has been termed sequential stratification [16, 17] and is related to the approaches suggested in [14, 15]. This method reorganizes the observed data to resemble a sequence of randomized experiments occurring at the ordered SADT initiation times. Estimation is implemented via a stratified Cox model, with each stratum consisting of a SADT patient and a set of controls, matched on PSA-related covariates at the time of SADT.
Both methods can be extended to allow for the estimation of interaction effects between SADT and other fixed or time-dependent covariates. From a clinical perspective, the estimation of these interaction effects is very useful. Although SADT is thought to be beneficial, it also has potentially serious side effects [21]; thus, the decision about when to initiate the therapy is difficult. Any information about when SADT is likely to be most beneficial would aid in that decision.
The remainder of this article is organized as follows. In Sections 2 and 3, we describe the motivating data set and the basic model of interest, respectively. In Sections 4 and 5, we detail parameter estimation for the two-stage method, and then for the sequential stratification method. Section 6 is devoted to the estimation of interactions between SADT and fixed or time-dependent covariates. The prostate cancer data are analyzed in Section 7, and we compare and contrast the two methods and provide some concluding remarks in Section 8.
2. Prostate Cancer Data
The data consist of 2,781 patients with clinically localized prostate cancer, all of whom were initially treated with EBRT. Patients came from four cohorts: University of Michigan (Michigan, USA), Radiation Therapy Oncology Group, Peter MacCallum Cancer Centre (Melbourne, Australia), and William Beaumont Hospital (Michigan, USA). PSA (ng/ml), T-stage, and Gleason score were recorded prior to initial EBRT, with PSA monitored at periodic visits throughout follow-up. PSA, T-stage, and Gleason score are the three commonly measured variables in prostate cancer, with higher values of all three associated with worse prognosis. Table 1 describes the pooled data, a more complete description of which is given in Proust-Lima et al. (2008) [18].
Table 1.
Description of Data
| Patients (#) | 2,781 |
| PSA Measures (#) | 25,688 |
| Age (years) | 71.0 (57.5, 80.5) |
| Pretherapy PSA (ng/ml) | 8.0 (2.5, 33.8) |
| Clinical T-stage | |
| 1 | 1,016 (36.5%) |
| 2 | 1,571 (56.5%) |
| 3–4 | 194 (7.0%) |
| Gleason Score | |
| 2–6 | 1,846 (66.4%) |
| 7 | 735 (26.4%) |
| 8–10 | 184 (6.6%) |
| PSA Measures/Patient | 9 (3, 18) |
| SADT | 305 (11.0%) |
| Time to Salvage | |
| ADT (years) | 4.0 (1.5, 8.2) |
| Clinical Recurrence | |
| With prior ADT | 58 (2.1%) |
| Without prior ADT | 280 (10.1%) |
| Total | 338 (12.2%) |
| Time to Clinical | |
| Recurrence (years) | 4.0 (1.4, 9.2) |
| Time to Last | |
| Contact (years) | 5.2 (1.6, 10.6) |
For continuous data: median (5th, 95th percentiles)
For categorical data: number (percentage)
Note that only a small fraction of the patients received SADT (11.0%), and only a slightly larger fraction experienced a recurrence of prostate cancer (12.2%). In addition, there were 280 recurrences among the 2,476 patients who did not receive SADT (11.3%), and 58 recurrences among the 305 people who did receive SADT (19.0%). Therefore, the data is capable of providing information about the hazard of recurrence for both those who did and those who did not receive SADT.
3. Basic Model
For the ith subject (i = 1, …, n), let Ti be the possibly unobserved time to prostate cancer recurrence, and let Ci be the censoring time due to end of study observation period, loss to follow-up, or death from other cases. We then let Xi = Ti ∧ Ci be the observation time, and Δi = I(Ti < Ci) be the recurrence indicator. Let Si be the (possibly unobserved) time to treatment by SADT, so that the SADT status indicator at time t for subject i is I(Si ≤ t). Time t is measured from the date of end of EBRT. Further, let Zi be the ith subject’s value of a vector of various fixed baseline covariates (such as initial PSA level, T-stage, Gleason score, etc.), and P SAi(t) the PSA level at time t. P SAi(t) is observed at discrete times ti1, ti2, …, tini. Cohort membership is denoted by Li, and is a categorical variable taking 4 values.
Note that death is a competing risk for cancer recurrence, since death precludes observing cancer recurrence [9]. Since the hazard function of interest is the cause-specific hazard of recurrence (i.e., the hazard of recurrence among subjects while alive), pre-recurrence death can be aggregated with the other censoring mechanisms in order to compute a likelihood (in the context of the two-stage method) or to write down generalized estimating equations (in the context of sequential stratification). For these data, competing risks mostly serve as distractions from the main ideas presented in the article, and further discussion is postponed until Section 8.
Let be the unknown hazard of recurrence for subject i in the absence of treatment by SADT. Consider a fixed but unknown function of time that defines the natural disease progression (‘natural’ meaning free from intervention via SADT). We assume that SADT acts multiplicatively on this natural hazard function, with the model then given by:
| (1) |
where γ serves as the parameter of interest. In both the two-stage and the sequential stratification methods, γ can be generalized to depend on t, Zi, P SAi(Si), or other factors. Equation (1) defines the parameter γ of interest. Note that it is defined conditionally and at the individual level, i.e., it is the change in the person’s log-hazard effective immediately upon administration of SADT conditional on the function . Thus it has a mechanistic interpretation. This contrasts with the definitions of causal effects implied by MSM methodology, which are based on average population or marginal effects of interventions. Since the parameter γ of interest in this paper is a subject-specific quantity, we do not necessarily expect the MSM methods to be estimating γ.
In the two-stage approach we estimate γ by utilizing parametric models for and thus the appropriateness of the estimates for γ will be contingent on how well the models approximate the true . In the sequential stratification approach we use a matching and adjustment strategy so that, within each strata, are similar and thus differences in outcome between those who did and did not receive SADT can be used to estimate γ. The appropriateness of this approach for estimating γ will rely on the quality of the matching and adjustment strategies that we use. MSM approaches to estimating the effect of interventions use weighted estimating equations, with weights determined by models for the probability of the intervention. For our example, the use of such weights would require building models for the probability of SADT.
A naive approach to estimating γ would be to adjust for baseline covariates Zi only, with the model given by . However, the relationship between risk of recurrence and SADT is confounded by time-dependent PSA (since elevated/rising PSA levels are a risk factor for recurrence of prostate cancer but are also a predictor of treatment by SADT). This suggests that a better approach would be to use a time-dependent Cox model which adjusted for baseline covariates and time-dependent PSA, such as:
| (2) |
However, since PSA is both a time-dependent confounder and an intermediate variable (because PSA levels decrease after initiation of SADT), model (2) yields biased estimates of γ, the causal effect of SADT [11]. In model (2), γ only represents the benefit of SADT beyond that due to the decrease in PSA at the time of initiation of SADT, rather than the recurrence-free survival benefit itself. Using the data from all 2,781 prostate cancer patients, the estimated hazard ratio from model (2) is exp(γ) = 1.40, with a 95% confidence interval (CI) of (1.03, 1.89). This suggests that SADT is harmful with respect to prostate cancer recurrence, contrary to common belief. In contrast, both the two-stage method and sequential stratification overcome the problem of bias in the estimation of the causal effect γ.
4. Two-Stage Method
In this approach to estimation of γ it is necessary to specify a parametric form for the natural hazard in the model , and then jointly estimate γ and . A naive form for the natural hazard, in which , assumes that the shape of the natural hazard is the same for subjects with the same baseline covariates, and thus does not allow for much heterogeneity among patients. However, since time-dependent PSA and slope of PSA are strongly associated with recurrence, a better approach (and one that allows for heterogeneity in the shapes of the natural hazard curve among patients) is to let be linked to the time-course of PSA in the absence of SADT for each person, as if that time-course were subject-specific, i.e., determined at time zero by a finite number of subject-specific latent variables. Specifically, we could assume a model for of the form , using the observed PSA and slope of PSA data for subject i at time t in the absence of treatment by SADT. However, there are a number of complications in assuming this form for to fit model (1). First, PSA is not measured continuously in time. Second, PSA is measured with error, and thus it is not realistic to assume that it is determined by a finite number of subject-specific latent variables. And lastly, even if PSA was measured continuously and without error, it would be impossible to observe PSA in the absence of treatment by SADT for subjects who did in fact receive SADT. This suggests a two-stage approach in which we first obtain a smooth continuous path for PSA in the absence of treatment by SADT, and then use this continuous counterfactual PSA in fitting the hazard model.
Following Proust-Lima et al. (2008), log(PSA) in the absence of SADT for subject i was described by a model with three phases (0: post-therapy, 1: short-term evolution, 2: long-term evolution) using the following linear mixed model [18]:
| (3) |
| (4) |
where Pi(t) represents ‘true’ PSA, which when added to measurement error εi gives the observed data. In this model, (μ0, μ1, μ2), (u0, u1, u2), (Z0, Z1, Z2), and (α0, α1, α2) are phase-specific intercepts, random effects, baseline covariates, and parameter coefficients, respectively. The functions f1(t) = (1 + t)−1.5 −1 and f2(t) = t capture the short-term and long-term evolution, respectively, and were determined using a profile likelihood method. Note that the form f2(t) = t corresponds to exponential growth of PSA, which is well-justified in the context of tumor growth. Throughout the text we write log(PSA), although the actual transformation of PSA used is log(PSA+0.1).
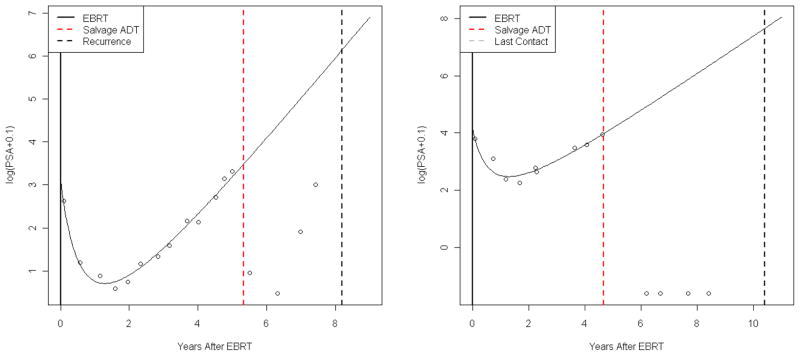
Figures 2(a) and (b) show the log(PSA) patterns from Figures 1(a) and (b), respectively (for two subjects who received SADT), along with the subject-specific estimated log Pi(t) patterns given by the linear mixed model (4). Note that, since only data prior to instances of SADT are used in fitting model (4), the corresponding estimated log Pi(t) patterns are not affected by initiation of SADT. For values of t which are greater than the time of initiation of SADT, Si, these estimated patterns represent log Pi(t) had SADT not been given.
Figure 2.
Typical log(PSA) patterns
Using the estimates of μ, u, and α, the BLUP estimates for log Pi(t) and slope of log Pi(t) (given by log P̂i(t) and , respectively) are obtained. We then obtain the estimates of β and γ in the model:
| (5) |
where γ is the parameter of interest, and l references the cohort. Note that model (5) is stratified by cohort; this allows for non-proportional baseline hazards across the four different cohorts.
Parameter and covariance estimates are given by the usual maximum partial likelihood estimates and the corresponding inverse information matrix, respectively. Note that the two-stage method described in this section can be fit using standard software (e.g., in SAS, PROC MIXED for model (4) and PROC PHREG for model (5), or in R/S-PLUS, lmer() from the ‘lme4’ package and coxph() from the ‘survival’ package).
5. Sequential Stratification Method
5.1. Estimation
The sequential stratification method reorganizes the observed data set in an attempt to mimic a sequence of conditionally randomized SADT assignments (i.e., assigned randomly, given the covariate information). At the time of each instance of SADT initiation, a stratum is created which includes the patient undergoing SADT (the “index case”) and matched patients at risk who are ‘similar’ to the index case, but who have not yet undergone SADT. Note that if the matching is set up such that “similar” subjects have similar natural hazards in equation (1), then this method will be estimating the parameter γ in equation (1). After strata are defined, a stratified Cox proportional hazards model (which allows for different baseline hazards across strata) can be used to estimate SADT benefit without adjusting for time-dependent variables.
Let S(j) be the jth ordered time of SADT initiation, with j = 1, …, nS and S(1) < S(2) < … < S(nS), where nS is the total number of patients undergoing SADT. With respect to the (j)th patient to initiate SADT (index patient (j)), the stratum-inclusion indicator for patient i is given by:
| (6) |
where Ai(j) equals 1 if patient i meets the criteria to warrant matching to patient (j) and 0 otherwise, and Li denotes cohort membership. For the sequential stratification method we chose to restrict matches to those from the same cohort, although this may not be necessary. Therefore, the (j)th stratum will include the index case undergoing SADT at time S(j), as well as all matched patients {i: eij = 1}. For all patients with eij = 1, we fit a model given by:
| (7) |
for (j) = 1, …, nS, where I{i = (j)} is an indicator for patient i being the index case. Using the survival analysis analog of generalized estimating equations [19], γ from model (7) can be estimated with the estimating equations from a stratified Cox model, where all nS index cases define a total of nS strata. A robust variance estimator is used in order to account for the inclusion of the same patients in multiple strata. Note that t in this model represents time from the end of radiation therapy, the same time axis used for the two-stage approach. However, if time t was measured from S(j) for each strata in model (7), the relative ordering of the failure times within strata (and hence the resulting estimator of γ) would be unchanged. As with the two-stage method, the sequential stratification method can be fit using standard software (e.g., by using the start/stop, or counting process, input file structure, with PROC PHREG in SAS or coxph() in R/S-PLUS).
In addition, the sequential stratification method is intended for observational data, with the absence of randomization requiring that unbiased contrasts between treatment groups be obtained through covariate adjustment. Accurate covariate adjustment is achieved through the combination of factors used to determine Ai(j) and factors incorporated into Zi. In practice, it would be desirable to adjust for all factors which affect the hazard function, whether or not these factors were associated with treatment assignment. Due to the non-linearity of the hazard model, substantial bias in the Cox model could result if an important hazard predictor were omitted, regardless of whether or not such a predictor was independent of treatment. The practitioner needs to make decisions regarding which adjustment factors should be included in the covariate vector, and which should be included as matching criteria. Factors which are very strong predictors of treatment and/or the hazard function are prime candidates for matching, as are factors which would be difficult to accurately model (e.g., a categorical covariate with 50 levels).
Finally, non-index-case patients who later undergo SADT are censored at the time of their SADT. As outlined in detail in Schaubel et al. [17], the sequential stratification method assumes that treatment (SADT, in this case) is assigned randomly given the matching variate and the time-dependent covariates. Depending on the application, inverse probability of censoring weighting (IPCW) may be required [20]; however, in this case, inverse weighting is not required since (as mentioned previously) only a small fraction of patients received SADT.
5.2. Analysis of prostate cancer data
We now describe the application of the sequential stratification method to the prostate cancer data set. The most important factors with respect to generating comparable sets of patients are time-dependent PSA and slope of PSA, factors for which we adjust using the matching indicator, Ai(j). Three different sets of PSA-related covariates were used with the indicator Ai(j) for this data set. For each, it was required that the location for patient i be equal to that of patient (j) (i.e., Li = L(j)). Method (1) uses only estimated log(PSA), method (2) uses estimated log(PSA) and slope of log(PSA), and method (3) uses estimated log(PSA), estimated slope of log(PSA), and the long-term phase (LTP) coefficient α̃2i, which is the BLUP estimate for the term in model (4). In addition, both thresholding and nearest-neighbor methods were used with the indicator Ai(j) to define which patients could be considered sufficiently similar with respect to the three different sets of PSA-related covariates.
Method (1), which does not match on slope of PSA, is probably not sufficient to ensure that the matched set is similar enough with respect to variables that are associated with the decision to initiate SADT. However, method (2), which matches on slope of PSA in addition to PSA, should provide a suitably similar set of matches to each index case. Method (3) adds the criterion of matching on expected future slope of PSA, which is a determinant of disease progression. This could provide improved efficiency for the sequential stratification method.
5.3. Matching criteria
Note that, as we have implemented them, all three matching methods require longitudinal modeling of PSA in order to obtain estimates of log(PSA), slope of PSA, and LTP. Similar methods based only on the observed PSA data could be devised, thus avoiding the need to specify a longitudinal model.
Let be the standardized estimated log(PSA):
| (8) |
where and . Similarly, let the standardized estimated slope of and LTP coefficient α̃2i be and , respectively, obtained from the longitudinal model.
The threshold-based Ai(j) indicator functions used were:
| (9) |
| (10) |
| (11) |
for threshold values c = 0.2, 0.5, and 1.0, and for time t = S(j).
The nearest-neighbor indicator functions , and equal one for the 10 patients nearest to the index case (with respect to Euclidean distance) in 1-dimensional log(PSA) space, 2-dimensional log(PSA) and slope of log(PSA) space, and 3-dimensional log(PSA), slope of log(PSA), and LTP coefficient space, respectively. For example, for patient i, if is among the 10 smallest values across all patients i such that Si ∧ Xi ≥ S(j) and Li = L(j).
Matched patients who subsequently received SADT were censored, and such censoring was treated as independent. This should not be a gross violation of the independent censoring assumption since, within strata (for matching methods 2 and 3), all subjects have similar PSA and slope of PSA. In a separate analysis of time to SADT, it was determined that the only factors which were strongly and consistently associated with initiation of SADT were PSA and slope of PSA. Thus, within each stratum, there is approximately independent censoring.
6. Estimation of Treatment-by-Covariate Interactions
Both the two-stage method and the sequential stratification method allow for easy generalization of γ to depend on covariates (such as time of SADT, age at time of SADT, estimated PSA or slope of PSA at time of SADT, T-stage, time, etc.). This allows for the estimation of interaction SADT effects. For example, it may be of interest to determine whether the effect of SADT is constant with respect to age. Since androgens in men tend to decrease after the age of approximately 40, SADT might be expected to have less benefit for older men, who have less androgens present to modify [22].
We consider a number of different extensions of equation (1) to represent different types of interactions. In the case of non-time-varying covariates, such as age, we extend equation (1) to be . In the case of time since SADT extend equation (1) to be . In the case where the interacting variable of interest is based on PSA, we extend equation (1) to be where Pi(Si) represents the true value of PSA for subject i at time Si. For estimation purposes we would replace Pi(Si) by P̂i(Si).
For the two-stage method, the approach for estimating the interaction effect of SADT with categorical age would be to assume the model (in place of model (5)):
| (12) |
where γ is the parameter of interest, l references the cohort, and ai(Si) is the age of subject i at the time of SADT.
For the sequential stratification method, the corresponding model (in place of model (7)) for estimating the interaction effect of SADT with categorical age would be:
| (13) |
where I(i = (j)) is an indicator for whether patient i is the index case, and ai(Si) is the age of subject i at the time of SADT. Similar generalizations of γ can be made for other, possibly time-dependent, covariate interactions, for both the two-stage and sequential stratification methods.
7. Results
Table 2 shows the estimates (and corresponding 95% CIs) of the hazard ratio of recurrence for the two-stage and sequential stratification methods. For the sequential stratification method, results are given for each of the three sets of matching variables, and for each of the three threshold values along with the 10 nearest-neighbor method; in addition, strata size statistics (median, and 5th and 95th percentiles) are given for each combination of matching variables and matching technique.
Table 2.
Estimated Effect of SADT
| Method and Matching Variables | Strata Size* | Hazard Ratio | 95% CI |
|---|---|---|---|
| Two-Stage: | |||
| NA | NA | 0.24 | (0.17, 0.33) |
| Sequential Stratification: | |||
| PSA, location | |||
| 0.2 Threshold | 11.0 (1.0, 112.2) | 0.29 | (0.19, 0.43) |
| 0.5 Threshold | 28.0 (3.0, 281.4) | 0.33 | (0.23, 0.47) |
| 1.0 Threshold | 73.0 (7.2, 508.4) | 0.44 | (0.32, 0.61) |
| 10-NN | 11.0 (11.0, 11.0) | 0.28 | (0.20, 0.40) |
| PSA, sPSA, location | |||
| 0.2 Threshold | 3.0 (1.0, 30.0) | 0.26 | (0.15, 0.45) |
| 0.5 Threshold | 13.0 (1.0, 159.2) | 0.25 | (0.17, 0.38) |
| 1.0 Threshold | 42.0 (4.0, 370.8) | 0.31 | (0.22, 0.45) |
| 10-NN | 11.0 (11.0, 11.0) | 0.29 | (0.21, 0.41) |
| PSA, sPSA, LTP, location | |||
| 0.2 Threshold | 1.0 (1.0, 6.0) | 0.37 | (0.16, 0.87) |
| 0.5 Threshold | 5.0 (1.0, 71.8) | 0.24 | (0.15, 0.38) |
| 1.0 Threshold | 28.0 (2.0, 297.8) | 0.31 | (0.21, 0.44) |
| 10-NN | 11.0 (11.0, 11.0) | 0.27 | (0.19, 0.39) |
Strata size is given by: median (5th, 95th percentiles)
Abbreviations: PSA indicates matching on standardized log(PSA + 0.1), sPSA indicates matching on standardized slope of log(PSA + 0.1), and LTP indicates matching on standardized long-term phase coefficient.
Using the two-stage method, SADT is associated with an estimated 76% decrease in the hazard of recurrence of prostate cancer (HR = 0.24, 95% CI: (0.17, 0.33)). Using the sequential stratification method, the estimated benefit ranges from a 56% decrease, matching on location and log(PSA), and using a threshold of c = 1.0 (HR = 0.44, 95% CI: (0.32, 0.61)), to a 76% decrease, matching on location, log(PSA), slope of log(PSA), and LTP coefficient, and using a threshold of c = 0.5 (HR = 0.24, 95% CI: (0.15, 0.38)). Each estimate from the sequential stratification method gives wider confidence intervals than that from the two-stage method.
Note that for the sequential stratification method using the thresholding technique, strata size decreases as the number of matching variables increases. This is expected since the matching criteria are more restrictive with additional matching variables (as long as the threshold value c is constant), so fewer patients are defined as matches to the index cases undergoing SADT. Although precision decreases, the estimated benefit itself increases as the number of matching variables increases (again keeping the threshold value constant), except for the analyses using the 0.2 threshold.
Conversely, the estimated benefit decreases as the threshold value increases (keeping the number of matching variables constant), except in the case of matching on all of PSA, sPSA, LTP, and location. This is reasonable since the matching criteria are less restrictive with increasing threshold values, therefore less similar patients are matched to index cases. In an unadjusted analysis (similar to a sequential stratification method which matched index cases to all patients at risk), SADT would be associated with an increase in the risk of recurrence of prostate cancer [18], since treatment assignment is not randomized, and patients who are at risk for recurrence are more likely to receive treatment by SADT than patients who are not at risk. For the nearest-neighbor technique, the estimated benefit and the corresponding precision are roughly constant across varying sets of matching variables.
Table 3 shows the SADT interaction effect estimates (hazard ratios), along with 95% CIs. Results are presented for the two-stage method and the sequential stratification method using 10 nearest-neighbors, with matching based on location, PSA, and slope of PSA. Cutpoints for interaction covariates were chosen so as to ensure roughly equal subgroup sizes, while also allowing for easy interpretation.
Table 3.
Estimation of Interaction SADT Effects
| Two-Stage Method | Seq. Strat. (10-NN) | |||||
|---|---|---|---|---|---|---|
| Interaction | Hazard Ratio | 95% CI | p* | Hazard Ratio | 95% CI | p* |
| Time of SADT (after radiation therapy) | ||||||
| 0–2.5 years | 0.26 | (0.16, 0.42) | 0.41 | 0.30 | (0.18, 0.50) | 0.76 |
| 2.5–4 years | 0.16 | (0.09, 0.26) | 0.24 | (0.13, 0.46) | ||
| 4–6 years | 0.27 | (0.15, 0.47) | 0.28 | (0.14, 0.54) | ||
| 6+ years | 0.33 | (0.15, 0.75) | 0.47 | (0.17, 1.30) | ||
| Age (at time of SADT) | ||||||
| ≤ 71 years | 0.22 | (0.13, 0.37) | 0.33 | 0.30 | (0.16, 0.55) | 0.31 |
| 71–76 years | 0.23 | (0.13, 0.43) | 0.19 | (0.09, 0.39) | ||
| 76–80 years | 0.18 | (0.10, 0.33) | 0.25 | (0.13, 0.48) | ||
| 80+ years | 0.36 | (0.21, 0.62) | 0.44 | (0.24, 0.79) | ||
| Predicted PSA† (at time of SADT) | ||||||
| ≤ 1.5 | 0.20 | (0.09, 0.46) | 0.36 | 0.37 | (0.16, 0.86) | 0.51 |
| 1.5–2 | 0.14 | (0.06, 0.31) | 0.22 | (0.09, 0.53) | ||
| 2–3 | 0.31 | (0.19, 0.48) | 0.36 | (0.22, 0.61) | ||
| 3+ | 0.24 | (0.15, 0.40) | 0.23 | (0.13, 0.39) | ||
| Predicted Slope of PSA† (at time of SADT) | ||||||
| ≤ 0.4 | 0.65 | (0.31, 1.35) | 0.04 | 0.94 | (0.41, 2.15) | 0.02 |
| 0.4–0.7 | 0.27 | (0.15, 0.49) | 0.35 | (0.17, 0.70) | ||
| 0.7–1 | 0.21 | (0.12, 0.37) | 0.17 | (0.08, 0.36) | ||
| 1+ | 0.19 | (0.12, 0.30) | 0.26 | (0.16, 0.41) | ||
| Predicted PSA, Slope of PSA† (at time of SADT) | ||||||
| PSA ≤ 2, Slope ≤ 0.7 | 0.30 | (0.15, 0.60) | 0.06 | 0.49 | (0.22, 1.07) | 0.10 |
| PSA > 2, Slope ≤ 0.7 | 0.41 | (0.22, 0.78) | 0.47 | (0.22, 0.98) | ||
| PSA ≤ 2, Slope > 0.7 | 0.07 | (0.02, 0.22) | 0.13 | (0.05, 0.34) | ||
| PSA > 2, Slope > 0.7 | 0.24 | (0.16, 0.37) | 0.25 | (0.16, 0.39) | ||
| Time (after SADT) | ||||||
| 0–1.5 years | 0.31 | (0.20, 0.47) | 0.14 | 0.37 | (0.24, 0.55) | 0.18 |
| 1.5–3 years | 0.20 | (0.11, 0.35) | 0.19 | (0.11, 0.33) | ||
| 3–5 years | 0.12 | (0.06, 0.27) | 0.24 | (0.07, 0.81) | ||
| 5+ years | 0.28 | (0.13, 0.59) | 0.66 | (0.11, 4.12) | ||
P-value for Wald test of equal interaction effects
Predicted PSA and slope of PSA are based on log(PSA + 0.1)
In general, the hazard ratio estimates from both the two-stage method and the sequential stratification method are similar. However, as was the case for the results displayed in Table 2, the sequential stratification method gives slightly wider confidence intervals than the two-stage method.
For both the two-stage method and the sequential stratification method, a Wald test of the null hypothesis of no interaction effect suggests that there is insufficient evidence for significant interaction effects between SADT and the time at which SADT is given, the age at which SADT given, predicted PSA at the time of SADT, and time (p-values range from 0.14 to 0.76).
However, both methods suggest significant interaction effects between SADT and slope of PSA at the time of SADT (p=0.04 and p=0.02 for the two-stage and sequential stratification methods, respectively), and marginally significant interaction effects between SADT and PSA and slope of PSA jointly (p=0.06 and p=0.10, respectively). SADT appears to be most beneficial for patients with higher slopes of PSA (at the time of SADT), and least beneficial for patients with lower slopes of PSA. When interaction effects for PSA and slope of PSA are explored jointly, patients with log(PSA) less than 2 and with slope of log(PSA) greater than 0.7 receive the most benefit from SADT, with an estimated 93% decrease in the hazard of recurrence using the two-stage method (HR = 0.07, 95% CI: (0.02, 0.22)), and an estimated 87% decrease using the sequential stratification method (HR = 0.13, 95% CI: (0.05, 0.34)).
8. Discussion
We have proposed two methods which appropriately adjust for time-dependent PSA and slope of PSA in estimating the causal effect of SADT on the risk of recurrence of prostate cancer. The first is a two-stage method which uses a linear mixed model to predict PSA and slope of PSA after EBRT, and then uses a time-dependent Cox model to estimate the recurrence-free survival benefit of SADT, adjusting for predicted PSA and slope of PSA. This method eliminates the ‘intermediate variable’ status of the time-dependent PSA and slope of PSA covariates, thereby allowing the use of a standard Cox regression analysis. The second method, sequential stratification, attempts to mimic a sequence of randomized experiments, occurring at the initiation times of SADT. After strata are defined by SADT patients who are matched with appropriate controls, a stratified Cox model can be used to estimate the benefit of SADT.
Although the methods developed in this paper were targeted to prostate cancer applications, they have broader applicability to other situations where the goal is to estimate a treatment effect which is given ‘by indication’ in an observational dataset. For the two-stage method, the key ingredient is a time-dependent marker of a disease which is associated with the outcome of interest, and which lends itself to longitudinal modeling. In most situations this marker will also be a strong determinant of when treatment is initiated. The sequential stratification method is applicable whenever there is a marker that determines the initiation of treatment. While longitudinal modeling of the marker is not strictly necessary for sequential stratification, it does facilitate matching.
The sequential stratification method does require choices to be made regarding the composition and size of strata. We recommend matching on variables that are strongly associated with the initiation of treatment and with the hazard of the event. In the prostate cancer application, the first matching criteria did not include the slope of PSA. Since the slope of PSA is probably the single most important determinant of recurrence and of the decision to start SADT, this is not ideal and may explain the larger variability in the estimated hazard ratio as the strata size changes. If multiple factors define the strata then there are many possible ways of combining the factors, some of which could be designed to give more weight to the factors that are considered more important. In the prostate cancer application, we used Euclidean distance on normalized covariates, but that could potentially be optimized.
The longitudinal model plays a crucial role, particularly for the two-stage method. Misspecification of that model could certainly cause bias in the estimate of the treatment effect. The model is explicitly used for extrapolation of marker values, which makes it even more important to have a model that can be trusted. In the prostate cancer application, the large longitudinal dataset did allow for a considerable amount of model building before arriving at a final form that fits the data well. In this application, extrapolation is somewhat justified since, once PSA starts to increase, the pattern is quite deterministically driven and linear (on a logarithmic scale) for typical patients. The sequential stratification approach also uses the fit of the longitudinal model, but in a far weaker way. Specifically, this model helps define ‘similar’ subjects for each stratum; thus, minor or even moderate misspecifications of the longitudinal model will not be crucial in the sequential stratification setting. In applying the two-stage and sequential stratification methods to the prostate cancer data, estimates were quite similar; this suggests that misspecification of the longitudinal model is not a major concern. In other applications with less longitudinal data and more heterogeneous patterns, the longitudinal model may be more critical.
In practice, assuming no unmeasured confounders, the decision to initiate the treatment can only be based on measured variables; however, there are some subtle deviations from this principle in the approaches described in this paper. First, the longitudinal model smoothes or interpolates the observed data, and it is implicitly assumed that it is this smoothed fit which determines the treatment initiation, rather than the observed data itself. In practice, the person making the decision to initiate treatment may be implementing their own form of smoothing, so the longitudinal model smoothing and interpolation could be similar to what happens in a clinical setting. A second subtle deviation is that the longitudinal model is fit to all the data (not just past data), and the prediction P̂i(t) is based on this fit. This can be viewed as an advanced form of smoothing [25], but it could also lead to bias.
For the sequential stratification method, a choice must be made regarding the size of each stratum. Smaller sizes give strata for which matched patients are more similar, but this could also result in a loss of efficiency. In this paper, we utilized two approaches in determining the strata, one based on a distance measure and the other using a fixed stratum size. While the results did vary, the differences between the two approaches were not substantial. Other methods of choosing strata could certainly be developed.
One limitation of the work presented in this paper is related to covariance estimation for the two-stage model. Covariance estimates for the parameters in model (5) are given by the usual inverse information matrix values; however, such an approach does not take into account the variance of the estimated log(PSA) and slope of log(PSA) quantities from model (4). Thus the standard errors from the two-stage method may be underestimates. One solution to this problem would be to use the bootstrap for inference (i.e., by iteratively fitting models (4) and (5) to bootstrap samples of the data). Another solution would be to use a joint longitudinal-survival modeling approach [23, 24], which is flexible but considerably more computationally complex. Joint modeling could also eliminate some of the possible bias in the parameter estimates when the longitudinal and survival analyses are performed separately.
In this paper we have focused on the relative hazard as the summary measure of the effectiveness of the SADT treatment. In practice, SADT is often thought of as delaying recurrence by a year or more, or by stretching the time to recurrence by a factor of two or more. Both methods presented in this paper could be adapted to provide these kinds of summary measures of the effect of SADT. For example, model (7) in the sequential stratification method could be replaced by an accelerated failure time model. The corresponding modification could potentially be more complex for the two-stage method, but a time-dependent accelerated failure time model could be used in place of equation (5).
Acknowledgments
Contract/grant sponsor: This research was partially supported by NIH grants CA083654 and CA110518.
References
- 1.Shipley WU, Thames HD, Sandler HM, Hanks GE, Zietman AL, Perez CA, Kuban DA, Hancock SL, Smith CD. Radiation therapy for clinically localized prostate cancer: A multi-institutional pooled analysis. Journal of the American Medical Association. 1999;281(17):1598–1604. doi: 10.1001/jama.281.17.1598. [DOI] [PubMed] [Google Scholar]
- 2.Agarwal PK, Sadetsky N, Konety BR, Resnick MI, Carroll PR. Treatment failure after primary and salvage therapy for prostate cancer. Cancer. 2007;112(2):307–314. doi: 10.1002/cncr.23161. [DOI] [PubMed] [Google Scholar]
- 3.Zagars GK, von Eschenbach AC. Prostate-specific antigen: An important marker for prostate cancer treated by external beam radiation therapy. Cancer. 1993;72(2):538–548. doi: 10.1002/1097-0142(19930715)72:2<538::aid-cncr2820720234>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 4.Sharifi N, Gulley JL, Dahut WL. Androgen deprivation therapy for prostate cancer. Journal of the American Medical Association. 2005;294(2):238–244. doi: 10.1001/jama.294.2.238. [DOI] [PubMed] [Google Scholar]
- 5.Wilt T, Nair B, MacDonald R, Rutks I. Early versus deferred androgen suppression in the treatment of advanced prostatic cancer. Cochrane Database of Systematic Reviews. 2001;(4) doi: 10.1002/14651858.CD003506. Art. No. CD003506. [DOI] [PubMed] [Google Scholar]
- 6.Stone NN, Clejan SJ. Response of prostate volume, prostate-specific antigen, and testosterone to flutamide in men with benign prostatic hyperplasia. Journal of Andrology. 1991;12:376–380. [PubMed] [Google Scholar]
- 7.Tyrrell CJ, Denis L, Newling D, Soloway M, Channer K, Cockshott ID. Casodex, 10–200 mg daily, used as monotherapy for the treatment of patients with advanced prostate cancer. European Urology. 1998;33:39–53. doi: 10.1159/000019526. [DOI] [PubMed] [Google Scholar]
- 8.Robins JM. The control of confounding by intermediate variables. Statistics in Medicine. 1989;8:679–701. doi: 10.1002/sim.4780080608. [DOI] [PubMed] [Google Scholar]
- 9.Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. New York: Wiley; 2002. [Google Scholar]
- 10.Rosenbaum PR. The consequences of adjustment for a concomitant variable that has been affected by the treatment. Journal of the Royal Statistical Society. 1984;147(5):656–666. [Google Scholar]
- 11.Robins JM. Structural nested failure time models. In: Armitage P, Colton T, editors. The Encyclopedia of Biostatistics. Chichester, UK: John Wiley and Sons LTD; 1998. pp. 4372–4389. [Google Scholar]
- 12.Robins JM. A new approach to causal inference in mortality studies with sustained exposure periods: Application to control of the healthy worker survivor effect. Mathematical Modelling. 1986;7:1393–1512. [Google Scholar]
- 13.Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran ME, Berry D, editors. Statistical Models in Epidemiology: The Environment and Clinical Trials. New York, NY: Springer-Verlag; 1999. pp. 95–134. [Google Scholar]
- 14.Li YP, Propert KJ, Rosenbaum PR. Balanced risk set matching. Journal of the American Statistical Association. 2001;96(455):870–882. [Google Scholar]
- 15.Lu B. Propensity score matching with time-dependent covariates. Biometrics. 2005;61:721–728. doi: 10.1111/j.1541-0420.2005.00356.x. [DOI] [PubMed] [Google Scholar]
- 16.Schaubel DE, Wolfe RA, Port FK. A sequential stratification method for estimating the effect of a time-dependent experimental treatment in observational studies. Biometrics. 2006;62:910–917. doi: 10.1111/j.1541-0420.2006.00527.x. [DOI] [PubMed] [Google Scholar]
- 17.Schaubel DE, Wolfe RA, Sima CS, Merion RM. Estimating the effect of a time-dependent treatment by levels of an internal time-dependent covariate: Application to the contrast between liver wait-list and posttransplant mortality. Journal of the American Statistical Association. 2009;104(485):49–59. [Google Scholar]
- 18.Proust-Lima C, Taylor JMG, Williams SG, Ankerst DP, Liu N, Kestin LL, Bae K, Sandler HM. Determinants of change in prostate-specific antigen over time and its association with recurrence after external beam radiation therapy for prostate cancer in five large cohorts. International Journal of Radiation Oncology Biology Physics. 2008;72(3):782–791. doi: 10.1016/j.ijrobp.2008.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 20.Robins JM, Rotnitzky A. Recovery of information and adjustment for dependent censoring using surrogate markers. In: Jewell N, Dietz K, Farewell V, editors. AIDS Epidemiology - Methodological Issues. Boston, MA: Birkhauser; 1992. pp. 297–331. [Google Scholar]
- 21.Keating NL, O’Malley AJ, Smith MR. Diabetes and cardiovascular disease during androgen deprivation therapy for prostate cancer. Journal of Clinical Oncology. 2006;24(27):4448–4456. doi: 10.1200/JCO.2006.06.2497. [DOI] [PubMed] [Google Scholar]
- 22.Gray A, Feldman HA, McKinlay JB, Longcope C. Age, disease, and changing sex hormone levels in middle-aged men: Results of the Massachusetts Male Aging Study. Journal of Clinical Endocrinology & Metabolism. 1991;73(5):1016–1025. doi: 10.1210/jcem-73-5-1016. [DOI] [PubMed] [Google Scholar]
- 23.Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. Journal of the American Statistical Association. 2001;96(455):895–905. doi: 10.1198/016214501753209031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wulfsohn MS, Tsiatis AA. A joint model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- 25.Bycott PW, Taylor JMG. A comparison of smoothing techniques for CD4 data measured with error in a time-dependent cox proportional hazards model. Statistics in Medicine. 1998;17:2061–2077. doi: 10.1002/(sici)1097-0258(19980930)17:18<2061::aid-sim896>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 26.Hernan MA, Lanoy E, Costagliola D, Robins JM. Comparison of dynamic treatment regimes via inverse probability weighting. Basic & Clinical Pharmacology & Toxicology. 2006;98:237–242. doi: 10.1111/j.1742-7843.2006.pto_329.x. [DOI] [PubMed] [Google Scholar]
- 27.Petersen ML, Deeks SG, Martin JN, van der Laan MJ. History-adjusted marginal structural models for estimating time-varying effect modification. American J Epidemiology. 2007;166:985–993. doi: 10.1093/aje/kwm232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.van der Laan MJ, Petersen ML. Causal effect models for realistic individualized treatment and intention to treat rules. Int J Biostat. 2007;3:1–51. doi: 10.2202/1557-4679.1022. [DOI] [PMC free article] [PubMed] [Google Scholar]