Fisher information and surrogate figures of merit for the task-based assessment of image quality

Abstract

Fisher information can be used as a surrogate for task-based measures of image quality based on ideal observer performance. A new and improved derivation of the Fisher information approximation for ideal-observer detectability is provided. This approximation depends only on the presence of a weak signal and does not depend on Gaussian statistical assumptions. This is also not an asymptotic result and therefore applies to imaging, where there is typically only one dataset, albeit a large one. Applications to statistical mixture models for image data are presented. For Gaussian and Poisson mixture models the results are used to connect reconstruction error with ideal-observer detection performance. When the task is the estimation of signal parameters of a weak signal, the ensemble mean squared error of the posterior mean estimator can also be expanded in powers of the signal amplitude. There is no linear term in this expansion, and it is shown that the quadratic term involves a Fisher information kernel that generalizes the standard Fisher information. Applications to imaging mixture models reveal a close connection between ideal performance on these estimation tasks and detection tasks for the same signals. Finally, for tasks that combine detection and estimation, we may also define a detectability that measures performance on this combined task and an ideal observer that maximizes this detectability. This detectability may also be expanded in powers of the signal amplitude, and the quadratic term again involves the Fisher information kernel. Applications of this approximation to imaging mixture models show a relation with the pure detection and pure estimation tasks for the same signals.

1. INTRODUCTION

The Fisher information matrix is usually primarily thought of as an important component of statistical estimation theory. This matrix is defined for a parameterized family of probability distribution functions (PDFs), where the parameter is a finite dimensional vector. The Cramer–Rao bound, for example, is derived from the Fisher information matrix and provides a lower bound on the variances of the components of an unbiased estimator of the vector parameter [1]. One problem with the Cramer–Rao lower bound, however, is that the minimum variance is achieved only for exponential families of PDFs, which is a very restricted class. In imaging, for example, if we want to include object variability as well as system noise, then, as we will see below, the PDFs are mixture distributions, which cannot be fit into the exponential family framework. Another problem with the Cramer–Rao bound is that it depends on the true parameter value, which is often a random quantity itself.

A second property of the Fisher information matrix is that the inverse of this matrix is asymptotically the same as the covariance matrix for the maximum likelihood estimator of the vector parameter [1]. Other asymptotic results relate Fisher information to ideal-observer detection performance [7]. The problem with these results in the imaging context is that we do not typically operate in an asymptotic regime, where you have many independent samples from a given member of the family of PDFs. In the imaging context we usually have only one image to work with and need to estimate a vector parameter and/or detect a signal without generating more images from the given object.

In a previous publication [2] we showed that there is a connection between the Fisher information matrix and the performance of the ideal Bayesian observer on a detection task, as measured by the area under the receiver operating characteristic (ROC) curve, a quantity known as the AUC (area under curve). The AUC is a figure of merit for detection tasks that can be directly related to observer performance on two-alternative forced choice (2AFC) tests. The Bayesian ideal observer maximizes the AUC by computing a likelihood ratio from the data and comparing it to a threshold [3]. The context in which the relation between Fisher information and ideal-observer AUC arises is when we are trying to detect a small change in the vector parameter of a parameterized family of PDFs. For instance, if a signal is weak then we may introduce an amplitude parameter and reduce the signal-detection problem to the detection of a small change in this parameter from zero. If we plot the AUC of the ideal observer versus signal amplitude, then the slope of this curve at the origin is determined by the Fisher information for the amplitude parameter. One useful aspect of this relationship is that there are no special requirements on the form of the family of PDFs. This is also not an asymptotic result, i.e., it does not depend on having a large number of independent data sets for each detection problem (see Chapter 6 in [7] for examples of asymptotic connections between detection performance and Fisher information). Asymptotic results are not very helpful in imaging, since we usually have only one large dimensional data set to work with. In Section 2 we present a new derivation of this relationship that puts it on a firmer mathematical footing and shows what happens when we try to compute higher-order terms, those beyond the lowest-order term that gives the slope result. In Section 3 we compute the Fisher information approximation to ideal-observer AUC for mixture models of the type that are needed in imaging to account for imaging noise and random background variations.

In Section 4 we present three examples of mixture models that are important in imaging. The first is a Gaussian mixture model with fixed covariance and random mean. The second example is a Poisson mixture model with random mean. The final example is again a Gaussian mixture model but now with random mean and covariance. In all of these cases we will see that the Fisher information approximation provides surrogate figures of merit for measuring the performance of imaging systems on detection tasks. A surrogate figure of merit is a quantity that correlates with ideal-observer task performance as measured by the AUC or some other task-based figure of merit but that is easier to compute.

In Section 5 we show that we can relate Fisher information to the ensemble mean squared error (EMSE) of the ideal Bayesian estimator, the posterior mean. This is the estimator that minimizes the EMSE [1]. The context for this relationship is that there are fixed parameters of the signal that we are not trying to estimate and random parameters that we are trying to estimate. We assume that the signal vanishes when the fixed parameters are all at some initial value, as would happen for an amplitude parameter, for example. Then the EMSE of the posterior mean estimator of the random parameters, for fixed parameters near their initial values (a weak signal), is determined by a Fisher information operator that involves derivatives with respect to the fixed parameters and expectations over the random parameters. In Section 6 we show how this approximation works out for mixture models of the type considered in Section 3. The end result is very similar to expressions for the Fisher information approximation for the detection task in Section 3.

In a previous paper we introduced the Estimation ROC (EROC) curve, which measures performance for tasks that involve detection and estimation [4]. The area under this curve (AEROC) can be used as a figure of merit and, as with AUC, is directly related to the performance of an observer on a 2AFC test involving detection and estimation. There is an ideal EROC observer, and the AEROC for this observer can also be related to a Fisher information operator under the same assumptions about signal parameters as in Section 5. In Section 7 we review these results in a more general setting than when they were originally derived, where the fixed parameter is a vector instead of a scalar. We also rewrite them in a notation compatible with the other sections of this paper. Then, in Section 8, we return to the mixture models of Section 3 and see what the Fisher information approximation to the ideal AEROC looks like for these models. Again, the result is similar to the Fisher information approximation for the detection task in Section 3.

We discuss these results and future research directions in Section 9, where we will also show how the results in this paper are related to some basic concepts in the field of information geometry. Appendices A–D contain some computations that are summarized in the main text.

2. FISHER INFORMATION AND DETECTABILITY

In detection tasks we are trying to determine whether the M-dimensional image data vector g is a sample from the signal-absent probability density function (PDF) pr(g|H₀) or the signal-present PDF pr(g|H₁). The optimal method, under several criteria, for deciding this question is to compute the likelihood ratio, given by

$$\mathrm{\Lambda }(\mathbf{g})=\frac{\text{pr}(\mathbf{g}\mid H_1)}{\text{pr}(\mathbf{g}\mid H_0)},$$ (1)

and compare the result to a threshold [3]. In particular, this procedure maximizes the AUC. An observer who follows this strategy is called an ideal observer. We will be considering the detection task when the signal-present hypothesis is distinguished from the signal-absent hypothesis by a change in an N-dimensional vector parameter a, and will write the corresponding likelihood ratio as

$${\mathrm{\Lambda }}_{\mathbf{a}}(\mathbf{g})=\frac{\text{pr}(\mathbf{g}\mid \mathbf{a})}{\text{pr}(\mathbf{g}\mid {\mathbf{a}}_0)}.$$ (2)

Thus, the signal-present hypothesis H₁ is that the parameter vector has the value a, while the signal-absent hypothesis H₀ is that the parameter vector has the value a₀. For example, the parameter a might be a scalar representing the amplitude of the signal, in which case a₀ = 0. More generally, we could think of this task as the detection of a change in the parameter from a₀ to a. We are interested in approximating the AUC for the ideal observer when the difference a−a₀ is small. In previous work [2] we found that the first four terms in the Taylor expansion about a₀ of the detectability, which is monotonically related to the AUC, are determined by the Fisher information matrix. The method used there did not provide any information about the following terms in the expansion. In this section we present a new derivation that puts the Taylor expansion on a firmer mathematical footing and shows that the fifth term, which would be fourth order in a−a₀, does not exist except under special circumstances.

A. Fisher Information

To define the Fisher information matrix we can start with the score, an N-dimensional vector valued function on data space given by sc(g|a) = ∇_aln[pr(g|a)]. All vectors in our discussions will be regarded as column vectors. The score is a zero-mean random vector, i.e., 〈sc(g|a)〉_g|a = 0, where angle brackets are used here, and throughout, for statistical expectations. The subscript on the angle brackets indicates what variable is being averaged over and whether the signal is present or absent for this averaging. The covariance of the score is the Fisher information matrix [1]:

$$\mathbf{F}(\mathbf{a})={\langle \mathbf{sc}(\mathbf{g}\mid \mathbf{a})\mathbf{s}{\mathbf{c}}^{†}(\mathbf{g}\mid \mathbf{a})\rangle }_{\mathbf{g}\mid \mathbf{a}}.$$ (3)

The Fisher information matrix is well known and has many important uses in statistical estimation theory. We will not be concerned with estimating a in the following, but in detecting a change in this parameter. The score at a=a₀ may also be written in terms of the likelihood ratio as sc(g|a₀) = ∇_aΛ_a(g)|_a0. This fact is what allows us to relate the Fisher information matrix to the AUC for the ideal observer trying to detect a small change in the value of a from a₀.

B. Augmented Likelihood Ratio

In order to derive the relation between ideal-observer AUC and Fisher information we will introduce an auxiliary random variable x with probability densities given by

$$pr(x\mid H_i)={(2\pi {\sigma }^2)}^{-1/2}exp\left[-\frac{{(x-i)}^2}{2{\sigma }^2}\right].$$ (4)

We may think of the random variable x as being an additional source of information about the signal that is statistically independent from our image data vector g. When σ is small the value of this variable very nearly determines the presence or absence of the signal. As σ increases, the information provided by x becomes increasingly unreliable. In the limit of infinite σ the value of x gives us no additional information beyond what is provided by the image data vector g. The general strategy is to derive expressions for derivatives of the detectability when σ is finite, and then take the limit as σ approaches infinity to get our results. To that end we define the augmented likelihood ratio as

$${\mathrm{\Lambda }}_{a,\sigma }(\mathbf{g},x)=\frac{\text{pr}(\mathbf{g}\mid \mathbf{a})\text{pr}(x\mid H_1)}{\text{pr}(\mathbf{g}\mid {\mathbf{a}}_0)\text{pr}(x\mid H_0)}={\mathrm{\Lambda }}_{\alpha }(\mathbf{g}){\mathrm{\Lambda }}_{\sigma }(x).$$ (5)

As σ approaches infinity, the augmented likelihood ratio approaches the ordinary likelihood ratio in Eq. (2).

A useful expression for the AUC of the likelihood ratio in the general case is provided by

$${\text{AUC}}_{\mathrm{\Lambda }}=1-\frac{1}{4\pi }{\int }_{-\infty }^{\infty }{\mid {\langle {\mathrm{\Lambda }}^{1/2+i\alpha }(\mathbf{g})\rangle }_{\mathbf{g}\mid H_0}\mid }^2\frac{d\alpha }{{\alpha }^2+\frac{1}{4}}.$$ (6)

This equation is by no means obvious, but can be derived from the standard definition of the AUC as the area under the ROC curve [3]. The reason for using this expression for the ideal-observer AUC in our calculations will become clear below. For the AUC of our augmented likelihood ratio we then have the expression

$$\text{AUC(}\mathbf{a},\sigma \text{)}=1-\frac{1}{4\pi }{\int }_{-\infty }^{\infty }{\mid {\langle {\mathrm{\Lambda }}_{\mathbf{a}}^{1/2+i\alpha }(\mathbf{g})\rangle }_{\mathbf{g}\mid {\mathbf{a}}_0}\mid }^2{\mid {\langle {\mathrm{\Lambda }}_{\sigma }^{1/2+i\alpha }(x)\rangle }_{x\mid H_0}\mid }^2\times \frac{d\alpha }{{\alpha }^2+\frac{1}{4}}.$$ (7)

After a short calculation this equation simplifies to

$$\text{AUC(}\mathbf{a},\sigma \text{)}=1-\frac{1}{4\pi }{\int }_{-\infty }^{\infty }{\mid {\langle {\mathrm{\Lambda }}_{\mathbf{a}}^{1/2+i\alpha }(\mathbf{g})\rangle }_{\mathbf{g}\mid {\mathbf{a}}_0}\mid }^2\times exp\left(-\frac{{\alpha }^2+\frac{1}{4}}{2{\sigma }^2}\right)\frac{d\alpha }{{\alpha }^2+\frac{1}{4}},$$ (8)

where we can see that the auxiliary random variable x provides a covergence factor in the integrand that is useful when we consider the limit as a approaches a₀. This is the reason for introducing the auxiliary random variable in the first place. Also note that, as σ approaches infinity, AUC(a, σ) converges to the AUC for the likelihood ratio in Eq. (2), given by

$$\text{AUC(}\mathbf{a}\text{)}=1-\frac{1}{4\pi }{\int }_{-\infty }^{\infty }{\mid {\langle {\mathrm{\Lambda }}_{\mathbf{a}}^{1/2+i\alpha }(\mathbf{g})\rangle }_{\mathbf{g}\mid {\mathbf{a}}_0}\mid }^2\frac{d\alpha }{{\alpha }^2+\frac{1}{4}}.$$ (9)

It is this function that we are interested in for values of a close to a₀. Unfortunately, as we will see below, this function is not differentiable at a=a₀, and so a Taylor expansion for AUC(a) about the point a₀ is out of the question. This motivates the introduction of the detectability, to which we now proceed.

C. Detectability

For the augmented likelihood ratio the detectability d(a, σ) is defined by the relation

$$\text{AUC}(\mathbf{a},\sigma )=\frac{1}{2}+\frac{1}{2}\text{erf}\left[\frac{1}{2}d(\mathbf{a},\sigma )\right].$$ (10)

This is usually motivated by considering the likelihood ratio for Gaussian statistics, where the detectablity can be identified with the signal-to-noise ratio. One end result of this section is that the detectability is fundamentally related to the Fisher information matrix regardless of the statistical assumptions. We can show that Eq. (10) is equivalent to the following integral expression [5]:

$$\text{AUC}(\mathbf{a},\sigma )=1-\frac{1}{4\pi }{\int }_{-\infty }^{\infty }exp\left[-\left({\alpha }^2+\frac{1}{4}\right)d^2(\mathbf{a},\sigma )\right]\frac{d\alpha }{{\alpha }^2+\frac{1}{4}}.$$ (11)

It is the similarity between this expression and Eq. (8) that leads to the relations between detectability and Fisher information. There are also equations corresponding to Eqs. (10) and (11) relating the detectability d(a) to AUC(a). To simplify the notation it is useful to define a function γ(a, σ) by the equation d²(a, σ) = γ(a, σ) +σ⁻². As σ approaches infinity we obtain a function γ(a) that is related to the detectability d(a)via

$$\gamma (\mathbf{a})=\underset{\sigma \to \infty }{lim}\gamma (\mathbf{a},\sigma )=\underset{\sigma \to \infty }{lim}{d}^2(\mathbf{a},\sigma )=d^2(\mathbf{a}).$$

We want to determine the Taylor series expansion for γ(a) about the point a=a₀. This will then give us an approximation to AUC(a) when a is close to a₀.

D. Taylor Series Expansion of Detectability

To find the terms of the desired Taylor series we begin with the equation that we now have relating γ(a, σ) to complex moments of the likelihood ratio Λ_a(g):

$${\int }_{C}exp\left[-{\mid z\mid }^2\gamma (\mathbf{a},\sigma )-\frac{{\mid z\mid }^2}{{\sigma }^2}\right]\frac{dz}{{\mid z\mid }^2}={\int }_C{\mid {\langle {\mathrm{\Lambda }}_{\mathbf{a}}^z(\mathbf{g})\rangle }_{\mathbf{g}\mid \mathbf{a}}\mid }^{2}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)\frac{dz}{{\mid z\mid }^2}.$$ (12)

In this equation the contour C is the vertical line $z=\frac{1}{2}+i\alpha$. (This line also appears in the Riemann Hypothesis but, to date, the authors have not found any connection between ideal-observer AUC and that famous conjecture.) By using implicit differentiation we can compute derivatives of γ(a, σ) at a=a₀. The details of this computation are somewhat tedious and are shown in Appendix A for the case of a scalar parameter. It is straightforward to generalize these calculations to a vector parameter. The end results for derivatives up to order three are as follows:

$$\gamma ({\mathbf{a}}_0,\sigma )=0,$$ (13)

$$\frac{\partial }{\partial a_k}\gamma ({\mathbf{a}}_0,\sigma )=0,$$ (14)

$$\frac{{\partial }^2}{\partial a_k\partial a_l}\gamma ({\mathbf{a}}_0,\sigma )=2F_{kl}({\mathbf{a}}_0),$$ (15)

$$\frac{{\partial }^3}{\partial a_k\partial a_l\partial a_m}\gamma ({\mathbf{a}}_0,\sigma )=\frac{\partial }{\partial a_{0k}}{F}_{lm}({\mathbf{a}}_0)+\frac{\partial }{\partial a_{0l}}{F}_{mk}({\mathbf{a}}_0)+\frac{\partial }{\partial a_{0m}}{F}_{kl}({\mathbf{a}}_0).$$ (16)

Since σ does not appear on the right-hand side in any of these expressions, they also give us the derivatives up to third order of γ(a) at a=a₀. For the fourth derivative and a scalar parameter we have

$$\frac{{\partial }^4}{\partial a^4}\gamma (a_0,\sigma )=L(a_0)-K(a_0){\sigma }^2,$$ (17)

where K(a₀) is the kurtosis of the score. Therefore, unless this kurtosis is zero, the fourth derivative of γ(a) at a =a₀ will be infinite. We are, however, most interested in the lowest-order non-vanishing term, and we can write, to lowest order in a−a₀, the following approximation for the square of the detectability:

$$d^2(\mathbf{a})\cong {(\mathbf{a}-{\mathbf{a}}_0)}^{†}\mathbf{F}({\mathbf{a}}_0)(\mathbf{a}-{\mathbf{a}}_0).$$ (18)

Since the third derivatives are known, the remainder theorem for the Taylor expansion could be used to estimate the error in this approximation.

We will examine some applications of this quadratic approximation to imaging in the next section. Note that, in contrast to other applications of the Fisher information matrix, such as the Cramer–Rao bound, the relation in Eq. (18) does not require inverting the matrix.

3. DETECTION IN IMAGING

The general equation g=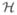f+n for a linear limaging system relates the finite-dimensional data vector g to an object function f(r), an imaging operator 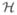, and a noise vector n. We are not necessarily assuming an additive noise model, so the statistical distribution of the noise vector may depend on f and 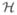. As an application of the results in Section 2 we will consider an imaging system where the data vector decomposes into three components: g=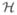f_b +a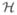f_s + n, where f_b is a randomly varying background function, f_s is a function representing a normalized version of the signal to be detected (which may also vary randomly), and a is an amplitude parameter for the signal. We may write this equation as g=b+as+n, where b is a vector in data space representing the data from the background and s is the signal as seen in data space. In all of our examples b will be a random vector with a PDF pr(b) defined on a subset B of data space. The signal vector s may be fixed, or it may be a random vector with PDF pr(s) defined on a subset S of data space. The vector n is the system noise, which, as noted above, may be statistically dependent on the background and signal. A statistical description of n provides the conditional PDF pr(g|b+as). We will set a₀ =0 so that the conditional PDF is pr(g|b) when the signal is absent.

A. SKE Detection

SKE refers to signal-known-exactly detection problems, so that the only sources of randomness are the background and system noise. The PDF for the data vector g in the signal-present case is given by

$$\text{pr}(\mathbf{g}\mid a)={\int }_B\text{pr}(\mathbf{g}\mid \mathbf{b}+a\mathbf{s})\text{pr}(\mathbf{b})d\mathbf{b}.$$ (19)

When the signal is absent this reduces to a PDF we will call pr(g) given by

$$\text{pr}(\mathbf{g})=\text{pr}(\mathbf{g}\mid 0)={\int }_B\text{pr}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b})d\mathbf{b}.$$ (20)

When the signal is absent the posterior PDF for the background conditioned on the data is given by Bayes’ rule:

$$\text{pr}(\mathbf{b}\mid \mathbf{g})=\frac{\text{pr}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b})}{\text{pr}(\mathbf{g})}.$$ (21)

This PDF plays an important role in all of our imaging examples. Expectations with this density can be computed using Markov chain Monte Carlo techniques. We may define the score vector for the background in the usual way by sc(g|b) = ∇_bln[pr(g|b)]. If we take the posterior mean of this vector the result is a vector function that depends on the data alone given by

$$\overline{\mathbf{sc}}(\mathbf{g})={\int }_B\mathbf{sc}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}.$$ (22)

To simplify the notation we will use angle brackets with a subscript 0 to indicate expectations of functions of data with respect to the signal-absent PDF pr(g). If we look at the mean value of this random vector $\overline{\mathbf{sc}}(\mathbf{g})$ when the signal is absent we obtain

$$\begin{array}{l}{\langle \overline{\mathbf{sc}}(\mathbf{g})\rangle }_0={\int }_G{\int }_B\mathbf{sc}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b}\mid \mathbf{g})\text{pr}(\mathbf{g})d\mathbf{b}d\mathbf{g}\\ ={\int }_B{\int }_G\mathbf{sc}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b})d\mathbf{g}d\mathbf{b}\\ ={\int }_B\left[{\int }_G{\nabla }_{\mathbf{b}}\text{pr}(\mathbf{g}\mid \mathbf{b})d\mathbf{g}\right]\text{pr}(\mathbf{b})d\mathbf{b}=0.\end{array}$$ (23)

The Fisher information with respect to the amplitude parameter a can now be expressed in terms of the covariance of this random vector as

$$F_{\mathit{SKE}}(0)=\text{tr}[\mathbf{s}{\mathbf{s}}^{†}{\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0]={\langle {\mid {\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})\mid }^2\rangle }_0.$$ (24)

Note that both expressions for the Fisher information involve an expectation of a product of a signal-dependent term and a background-dependent term. In this case Eq. (18) reduces to d²(a)≅a²F_SKE(0). One implication of these equations is that, for SKE detection, the covariance matrix ${\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0$ can be computed for a particular back-ground model, and then the detectability of various signals (in the weak signal limit) can be computed by changing the signal vector s. Of course, this covariance matrix may be very large, so an alternative is to simply compute the variance of the zero-mean random variable ${\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})$, which will then give the detectability for the given signal when the amplitude is small.

B. SKS Detection

SKS refers to signal-known-statistically detection problems, so the signal vector is now random and the PDF when the signal is present is given by

$$\text{pr}(\mathbf{g}\mid a)={\int }_S{\int }_B\text{pr}(\mathbf{g}\mid \mathbf{b}+a\mathbf{s})\text{pr}(\mathbf{b})\text{pr}(\mathbf{s})d\mathbf{b}d\mathbf{s}.$$ (25)

When a=0 the signal is absent and the integral over s is unity. The result is the same PDF pr(g) as in the SKE case. If we denote the mean signal vector as s̄, then the Fisher information with respect to the amplitude parameter is given by

$$F_{\mathit{SKS}}(0)=\text{tr}[\overline{\mathbf{s}}{\overline{\mathbf{s}}}^{†}{\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0]={\langle {\mid {\overline{\mathbf{s}}}^{†}\overline{\mathbf{sc}}(\mathbf{g})\mid }^2\rangle }_0.$$ (26)

The approximate detectability is now d²(a)≅a²F_SKS(0) and differs from the SKE detectability only in the replacement of the known signal with the mean of the signal ensemble. This reveals a close connection between SKE and SKS detectability when the signal is weak. The SKS model is more realistic, but, again for weak signals, it may be replaced with an equivalent SKE model for the purposes of computing detectability for the ideal observer.

C. RSKE Detection

RSKE refers to randomized-signal-known-exactly studies. In this case the square of the ideal-observer detectability is computed for each of an ensemble of signals as if the signal were known, and then the average over the signal ensemble is performed. The average Fisher information is given by

$$F_{\mathit{RSKE}}(0)=\text{tr}[\langle \mathbf{s}{\mathbf{s}}^{†}\rangle {\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0]={\langle {\langle {\mid {\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})\mid }^2\rangle }_0\rangle }_{\mathbf{s}},$$ (27)

which is just the expectation of the SKE Fisher information over the signal ensemble. The average of the square of the approximate detectability is now d²(a)≅a²F_RSKS(0). Note that F_RSKE(0)>F_SKS(0), since the covariance matrix of the signal vector is positive definite. This indicates, as expected, that RSKE performance will always be better than SKS performance on the detection task for a given signal ensemble.

4. EXAMPLES FROM IMAGING APPLICATIONS

In this section we consider some imaging examples where we specify the conditional probability pr(g|b)and compute the approximate figures of merit discussed above. All other PDFs, for the background and signal, will remain unspecified.

A. Gaussian Noise with Fixed Covariance

For this example we suppose that the conditional probability density pr(g|b) is given by a multivariate Gaussian with random mean b and a fixed covariance matrix K. The score vector for the background is easily computed to be sc(g|b) = K⁻¹(g−b). If we define the posterior mean estimate of the background in the usual way as

$$\widehat{\mathbf{b}}(\mathbf{g})={\int }_B\mathbf{b}\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b},$$ (28)

then the posterior mean of sc(g|b) is given by $\overline{\mathbf{sc}}(\mathbf{g})={\mathbf{K}}^{-1}[\mathbf{g}-\widehat{\mathbf{b}}(\mathbf{g})]$. We can define a posterior mean estimate of the noise as n̂(g) = g−b̂(g) and note that this is a zero-mean random vector when the signal is absent. The covariance of $\overline{\mathbf{sc}}(\mathbf{g})$ can now be written as a matrix product: ${\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0={\mathbf{K}}^{-1}{\mathbf{K}}_{\widehat{\mathbf{n}}}{\mathbf{K}}^{-1}$. We may now write out the coefficients of the second-order terms in the approximations for each of our detection figures of merit:

$$F_{\mathit{SKE}}(0)={\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0,$$ (29)

$$F_{\mathit{SKS}}(0)={\langle {\mid {\overline{\mathbf{s}}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0,$$ (30)

$$F_{\mathit{RSKE}}(0)={\langle {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\rangle }_{\mathbf{s}}.$$ (31)

Note that all of these expressions involve prewhitened inner products between signal related vectors and the posterior mean estimate of the noise when the signal is absent.

If the posterior mean estimate n̂(g) is replaced with the actual noise vector n, then, for example, F_SKE(0) becomes s^†K⁻¹s, which is usually called the Hotelling trace and gives the detectability for the ideal linear observer when the background is known. Each of the quantities in Eqs. (29)–(31) could be used as a surrogate figure of merit for the corresponding imaging task. For weak signals these surrogate figures of merit should correlate well with the performance of the corresponding ideal observers on the given tasks. The posterior mean estimate of the background will present difficulties for this approach, but we may be able to justify using some more easily computable estimate, such as a maximum a priori (MAP) estimate in its place. In cases where the mode of the posterior distribution pr(b|g) is close to the mean, this would be a good approximation. A maximum likelihood (ML) estimate of the background would probably not be a good estimate to use, since ML estimators do not take into account the prior pr(b), which describes background variability and is often an important determinant of task performance. In Appendix B we expand on these comments to produce upper and lower bounds for the surrogate figure of merit in Eq. (29) based on the Hotelling trace and alternate estimators of the background. The end results from these calculations are three interesting relations. The first of these relates the Fisher information figures of merit given above to our ability to estimate the background. For the SKE detection case we have

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0={\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}-{\langle {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_{\mathbf{g}\mid \mathbf{b}}\rangle }_{\mathbf{b}},$$ (32)

which tells us the Fisher information increases if the posterior mean produces a better estimate of the component of the prewhitened background that lies in the direction of the prewhitened signal. The second relation from Appendix B is

$${\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}-{\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\stackrel{\sim }{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_0\le {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\le {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s},$$ (33)

where b̃(g) is any estimate of the background. This estimate, for example, may result from a reconstruction algorithm that produces an estimate f̃_g of the background function f_b. We would then apply the system operator 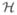to produce the estimate b̃(g). Therefore any reconstruction algorithm will provide a lower bound on detection task performance for weak signals, and may be useful as a way to generate a surrogate figure of merit.

We also show in Appendix B that, if we choose a linear estimator for b̃(g) and try to maximize the left hand side of (33), then the end result is the Wiener estimator [6], and this last inequality gives us

$${\mathbf{s}}^{†}{(\mathbf{K}+{\mathbf{K}}_b)}^{-1}\mathbf{s}\le {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\le {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s},$$ (34)

where K_b is the covariance matrix for the background vector b. If we wish to increase the lower bound for the Fisher information beyond the value given in this inequality, then we will have to use non-linear estimation of the background vector.

Another consequence of inequality (33) relates the Fisher information to an ensemble weighted mean square error for the background estimator b̃(g):

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\ge {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}\{1-{\langle {[\mathbf{b}-\stackrel{\sim }{\mathbf{b}}(\mathbf{g})]}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\stackrel{\sim }{\mathbf{b}}(\mathbf{g})]\rangle }_0\}.$$ (35)

For a white Gaussian mixture model this relation shows that the emsemble mean squared error of a background estimator can be related to task performance on a detection task. Now we suppose that the background estimator is the result of the system operator applied to an image reconstruction: b̃(g) = 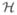f̃_g, where the function f̃_g(r) is the reconstructed object from the data vector g. Then we can conclude that

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\ge {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}\{1-{\left|\right|{\mathbf{K}}^{-1/2}\mathcal{H}\left|\right|}^2{\langle {\left|\right|f_b-f_g\left|\right|}^2\rangle }_0\}.$$ (36)

In this equation the quantity ||K^−1/2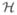|| represents the Hilbert space operator norm and ||f_b − f_g||² is the squared error between the reconstructed background object and the actual background object. Therefore the ensemble mean squared error between actual and reconstructed objects provides a lower bound on the Fisher information, which in turn provides an approximation to the detectability. This chain of reasoning indicates that, with these Gaussian mixture models the EMSE of reconstructed images may be useful as a surrogate figure of merit. The ensemble average over random backgrounds and system noise is important, however. The MSE of a single image reconstruction can tell us nothing about task performance unless we make restrictive (and, in the imaging context, unrealistic) assumptions about the background object statistics, such as stationarity and ergodicity.

B. Poisson Noise

For this example we suppose that the conditional probability distribution for the data is a multivariate Poisson distribution with mean b. This makes Pr(g) a Poisson mixture distribution. The notation Pr(g|b) and Pr(g) is used here since these are discrete distributions on nonnegative integer data vectors. The conditional score is also defined on non-negative integer vectors and is given by ${[\mathbf{sc}(\mathbf{g}\mid \mathbf{b})]}_m=g_m{b}_m^{-1}-1$. The posterior mean of the conditional score can be written as ${[\overline{\mathbf{sc}}(\mathbf{g})]}_m=g_m{\widehat{b}}_m^{-1}(\mathbf{g})-1$, where what we will call the Poisson posterior mean estimator b̂_m(g) of the background is given by

$${\widehat{b}}_m(\mathbf{g})={\left[{\int }_B\frac{1}{b_m}\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}\right]}^{-1}.$$ (37)

Now for F_SKE(0) we need the variance of ${\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})$ when the signal is absent. For the purposes of computing surrogate figures of merit, we may be able to replace the Poisson posterior mean estimator in Eq. (37) with a more easily computable estimate. We could, for example, use a MAP estimate for the background.

In Appendix C we derive an inequality for the Fisher information that relates task performance to our ability to estimate the true background:

$${\langle {[{\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})]}^2\rangle }_0\le {\left|\right|\mathbf{s}\left|\right|}^2\sum _{m=1}^M\left\{{\langle \frac{1}{b_m}\rangle }_0-{\langle g_m^2{\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]}^2\rangle }_0\right\}.$$ (38)

Unfortunately, this inequality holds only for the estimator in Eq. (37), but it does provide a quantitative relation between reconstruction accuracy and task performance.

C. Gaussian Noise with Background-Dependent Covariance

For the last example we consider mixture distributions where pr(g|b) is multivariate Gaussian with random mean b and a background-dependent covariance K_b. This type of distribution arises, for example, when we use channelized data for dimension reduction, and the original data follow a Poisson mixture distribution. To a good approximation the conditional distribution on the channelized data will be Gaussian due to the central limit theorem. Since the conditional covariance of the original data for a Poisson mixture depends on the background, the covariance for the channelized data will also.

It is notationally convenient to include the signal from the start for this example, so we will define the scalar differential operator D_s = s^†∇_b for the SKE detection case, with suitable changes for the other tasks. It is also useful to define a vector n(g, b) by $\mathbf{n}(\mathbf{g},\mathbf{b})={\mathbf{K}}_{\mathbf{b}}^{-1}(\mathbf{g}-\mathbf{b})$. The inner product of the signal with the conditional score can be written as a sum of three terms:

$${\mathbf{s}}^{†}\mathbf{sc}(\mathbf{g}\mid \mathbf{b})=-\frac{1}{2}\text{tr}[{\mathbf{K}}_{\mathbf{b}}^{-1}(D_{\mathbf{s}}{\mathbf{K}}_{\mathbf{b}})]+{\mathbf{s}}^{†}\mathbf{n}(\mathbf{g},\mathbf{b})+\frac{1}{2}{\mathbf{n}}^{†}(\mathbf{g},\mathbf{b})\times (D_{\mathbf{s}}{\mathbf{K}}_{\mathbf{b}})\mathbf{n}(\mathbf{g},\mathbf{b}),$$ (39)

where we have used standard results on the derivatives of determinants and inverses of matrices. The scalar product of the signal with the posterior mean of the conditional score is now given by the integral

$${\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})={\int }_B{\mathbf{s}}^{†}\mathbf{sc}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}.$$ (40)

As in the previous example, F_SKE(0) is the variance of this quantity when the signal is absent. For further progress here we will probably need numerical computations.

5. FISHER INFORMATION AND BAYESIAN ESTIMATION

For this section we will assume that there is a parameter vector v with a prior distribution pr(v) on a parameter space V that we are interested in estimating from the data vector g. We still have the parameter vector a, which we are not trying to estimate, and we are interested in the change in the performance of our estimator of v as a varies near a fixed value a₀. In general then our data have a conditional PDF pr(g|v,a) that depends on v and a. We will also assume that the value a₀ is singular in the sense that pr(g|v,a₀) = pr(g|a₀) does not depend on v. For example, the vector v could consist of parameters associated with a signal in a random background, and a could be a signal amplitude parameter, as in the examples above.

A. Utility Functions and Optimal Estimators

For each value of a, we will have an estimator function v̂(g|a). In general the utility of any estimate v̂ when the true value is v is given by a utility function u(v̂,v). The expected utility for our estimator v̂(g|a) is given by averaging the resulting estimates over all data vectors g and all parameter vectors v. This expected utility will still depend on a and is given by

$$U(\mathbf{a})={\int }_V\left\{{\int }_{G}u[\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a}),\mathbf{v}]\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})d\mathbf{g}\right\}\text{pr}(\mathbf{v})d\mathbf{v}.$$ (41)

The PDF for the data vector g is related to the conditional PDF and the prior via the usual relation

$$\text{pr}(\mathbf{g}\mid \mathbf{a})={\int }_V\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})\text{pr}(\mathbf{v})d\mathbf{v},$$ (42)

and the posterior PDF on the parameter vector v conditioned on the data is then given by Bayes’ rule as

$$\text{pr}(\mathbf{v}\mid \mathbf{g},\mathbf{a})=\frac{\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})\text{pr}(\mathbf{v})}{\text{pr}(\mathbf{g}\mid \mathbf{a})}.$$ (43)

In terms of the posterior PDF we may also write the expected utility for an estimator in the form

$$U(\mathbf{a})={\int }_G\left\{{\int }_{V}u[\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a}),\mathbf{v}]\text{pr}(\mathbf{v}\mid \mathbf{g},\mathbf{a})d\mathbf{v}\right\}\text{pr}(\mathbf{g}\mid \mathbf{a})d\mathbf{g}.$$ (44)

The ideal estimator is the one that maximizes the expected utility, and we are interested in expanding the function U(a) for the ideal estimator in the neighborhood of a=a₀. Therefore, in what follows, U(a) will be the expected utility for the ideal estimator corresponding to the given utility function. An advantage for us of the first form in Eq. (41) for the expected utility is that the vector a appears only twice. A disadvantage is that, for each value of the parameter vector v, the function v̂(g|a) must be chosen to maximize the inner integral over g. On the other hand, while the vector a appears three times in Eq. (44), we need only choose the vector v̂(g|a) for each data vector g to maximize the inner integral over v. We will, in fact, use both forms for the calculation of derivatives with respect to a.

B. Quadratic Utility Function

For simplicity we consider a quadratic utility function, although similar results can be derived for other utility functions. Suppose, then, that the utility function is given by $u(\widehat{\mathbf{v}},\mathbf{v})=1-\frac{1}{2}{\left|\right|\widehat{\mathbf{v}}-\mathbf{v}\left|\right|}^2$. In this case it is known that the ideal estimator is the posterior mean of the parameter vector [1], which is given by

$$\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a})={\int }_V\mathbf{v}\text{pr}(\mathbf{v}\mid \mathbf{g},\mathbf{a})d\mathbf{v}.$$ (45)

This estimator can also be written in terms of the conditional and prior PDFs in the form

$$\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a})=\frac{{\int }_V\mathbf{v}\text{pr(}\mathbf{v}\text{)pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})d\mathbf{v}}{pr(\mathbf{g}\mid \mathbf{a})}.$$ (46)

From this last equation we can see that, when we are at the singular point a=a₀, the ideal estimator is simply the mean parameter vector

$$\widehat{\mathbf{v}}(\mathbf{g}\mid {\mathbf{a}}_0)=\overline{\mathbf{v}}={\int }_V\mathbf{v}\text{pr}(\mathbf{v})d\mathbf{v},$$ (47)

and the expected utility for this estimator is related to the trace of K_v, the covariance matrix for v, by the equation $U({\mathbf{a}}_0)=1-\frac{1}{2}\text{tr}({\mathbf{K}}_{\mathbf{v}})$. In fact, this is the expected utility if we use the mean parameter vector as our estimator, independent of the value of the vector a. Since the mean of v could always be used as an estimator, we must have U(a₀) ≤ U(a) for any vector a. In Appendix D we show directly that ∇_aU(a₀) = 0, and this is consistent with the inequality U(a₀) ≤ U(a). We now have the first two terms in the Taylor series for U(a) about a₀, and we turn our attention to the third term, which will be second order in a.

For this third term we first define a conditional score vector via sc(g|v,a) = ∇_aln[pr(g|v,a)]. Note that this vector involves the gradient with respect to a, the vector parameter that we are not trying to estimate. For the traditional applications of the Fisher information we would use the gradient with respect to v, the vector parameter that we are trying to estimate. We show in Appendix D that the Hessian matrix ${\mathbf{H}}_U({\mathbf{a}}_0)={\nabla }_{\mathbf{a}}{\nabla }_{\mathbf{a}}^{†}U({\mathbf{a}}_0)$ is given by

$${\mathbf{H}}_U({\mathbf{a}}_0)={\langle {\langle (\mathbf{v}-\overline{\mathbf{v}})\mathbf{s}{\mathbf{c}}^{†}(\mathbf{g}\mid \mathbf{v},{\mathbf{a}}_0)\rangle }_{\mathbf{v}}^{†}{\langle (\mathbf{v}-\overline{\mathbf{v}})\mathbf{s}{\mathbf{c}}^{†}(\mathbf{g}\mid \mathbf{v},{\mathbf{a}}_0)\rangle }_{\mathbf{v}}\rangle }_{\mathbf{g}\mid {\mathbf{a}}_0}.$$ (48)

Note that this is a positive definite matrix, which is also consistent with the inequality U(a₀) ≤ U(a). If the expectation over the data vector g is performed first, then we must introduce a matrix valued Fisher information kernel with the equation

$$\mathbf{F}({\mathbf{a}}_0\mid \mathbf{v},{\mathbf{v}}^{\prime })={\langle \mathbf{sc}(\mathbf{g}\mid \mathbf{v},{\mathbf{a}}_0)\mathbf{s}{\mathbf{c}}^{†}(\mathbf{g}\mid {\mathbf{v}}^{\prime },{\mathbf{a}}_0)\rangle }_{\mathbf{g}\mid {\mathbf{a}}_0}.$$ (49)

This kernel can now be used to write the Hessian as a double expectation over independent and identically distributed parameter vectors v and v′:

$${\mathbf{H}}_U({\mathbf{a}}_0)={\langle \mathbf{F}({\mathbf{a}}_0\mid \mathbf{v},{\mathbf{v}}^{\prime }){(\mathbf{v}-\overline{\mathbf{v}})}^{†}({\mathbf{v}}^{\prime }-\overline{\mathbf{v}})\rangle }_{\mathbf{v},{\mathbf{v}}^{\prime }}.$$ (50)

The Taylor series expansion up to second order for U(a) at a₀ can now be written as

$$U(\mathbf{a})=1-\frac{1}{2}\text{tr}({\mathbf{K}}_{\mathbf{v}})+\frac{1}{2}{(\mathbf{a}-{\mathbf{a}}_0)}^{†}{\mathbf{H}}_U({\mathbf{a}}_0)(\mathbf{a}-{\mathbf{a}}_0)+\dots ,$$ (51)

with the Hessian matrix given by either Eq. (48) or Eq. (50). In the next section we will see how this plays out when the parameter vector v describes a random signal that is embedded in a random background, and a is a scalar amplitude parameter.

6. ESTIMATION IN IMAGING

For this example the data vector is composed of three components as before, random background, random signal, and noise. In this case the randomness of the signal is described explicitly by making the signal component a function of a random parameter vector v. The vector a will be a scalar amplitude factor on the signal component, with a₀ = 0 as before. Note that the parameter vector v may also contain a component that changes the amplitude of the signal. In this case the effect of decreasing the parameter a is to scale the PDF for this amplitude component of v and concentrate the probability near zero. A small value for the parameter a would therefore imply that the probability of a weak signal is high. In any case the data equation is now g=b+as(v)+n. With the same notation as in Section 2, the conditional probability for the data is given by an integral over the ensemble of random backgrounds,

$$\text{pr}(\mathbf{g}\mid \mathbf{v},a)={\int }_B\text{pr}(\mathbf{g}\mid \mathbf{b}+a\mathbf{s}(\mathbf{v}))\text{pr}(\mathbf{b})d\mathbf{b},$$ (52)

and the conditional score is a scalar given by

$$\text{sc}(\mathbf{g}\mid \mathbf{v},0)={\mathbf{s}}^{†}(\mathbf{v}){\int }_B\mathbf{sc}(\mathbf{g}\mid \mathbf{b})\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}={\mathbf{s}}^{†}(\mathbf{v})\overline{\mathbf{sc}}(\mathbf{g}).$$ (53)

If we define a cross covariance matrix between the signal parameters and the signal component of the data by the equation K_vs = 〈(v−v̄)s^†(v)〉_v, then the Hessian, which is a scalar in this example, is given by

$$\begin{array}{l}{H}_U(0)=\frac{d^2}{{da}^2}U(0)=\text{tr}[{\mathbf{K}}_{\mathbf{vs}}^{†}{\mathbf{K}}_{\mathbf{vs}}{\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0]\\ ={\langle {\left|\right|{\mathbf{K}}_{\mathbf{vs}}\overline{\mathbf{sc}}(\mathbf{g})\left|\right|}^2\rangle }_0.\end{array}$$ (54)

Note the similarity between this expression and the corresponding quantities for the detection tasks given in Eqs. (24) and (26). The approximate expected utility for the posterior mean estimator is then given by $U(a)\cong 1-\frac{1}{2}\text{tr}({\mathbf{K}}_{\mathbf{v}})+{(a-a_0)}^2{H}_U(0)$.

7. FISHER INFORMATION FOR COMBINED DETECTION AND ESTIMATION

For a combined detection and estimation task we are trying to determine whether the data were drawn from the signal-present ensemble with PDF pr(g|v,a) or the signal-absent ensemble with PDF pr(g|a₀). If we decide for the former hypothesis, then we must estimate the parameter vector v. In a previous publication [4] one of the authors (Clarkson) introduced the EROC curve as a tool for studying the performance of an observer on this task. The AEROC was also introduced as a figure of merit for observer performance. Since the task involves estimation, a utility function is needed in order to plot the EROC curve and measure a value for the AEROC. As with ordinary ROC analysis, there is an observer, the ideal EROC observer, that maximizes the AEROC for a given task and utility function, and expressions for the detection test statistic and estimator can also be found in [4]. For weak signals and positive utility functions the following approximation to the AEROC for the ideal observer was derived:

$$\text{AEROC}(\mathbf{a})\approx {\overline{u}}_0\left\{\frac{1}{2}+\frac{1}{2}\text{erf}\left[\frac{1}{2}d(\mathbf{a})\right]\right\}.$$ (55)

The original derivation of this equation used slightly different notation and a scalar parameter instead of the vector parameter a. The notation that we are using here emphasizes the similarity with the results relating Fisher information to detection and estimation performance in Sections 2 and 5, respectively. The extension from a scalar parameter to the vector parameter a is straightforward. Using the notation from Section 3, the constant ū₀ is given by

$${\overline{u}}_0={\int }_{V}u({\mathbf{v}}_0,\mathbf{v})\text{pr}(\mathbf{v})d\mathbf{v},$$ (56)

where the vector v₀ is defined as

$${\mathbf{v}}_0=arg\underset{{\mathbf{v}}^{\prime }}{max}\left[{\int }_{V}u({\mathbf{v}}^{\prime },\mathbf{v})\text{pr}(\mathbf{v})d\mathbf{v}\right].$$ (57)

When we use the quadratic utility function of Section 3, we have v₀ = v̄ and ${\overline{u}}_0=1-\frac{1}{2}\text{tr}({\mathbf{K}}_{\mathbf{v}})$. In order for the error function approximation for the AEROC to apply for this quadratic utility function, the parameter vector must be bounded to the range ||v||≤1. If the parameter vector is limited to a bounded set, then the parametrization can be shifted and scaled so that ||v||≤1. This is often the case in practice; however, if the parameter vector is unbounded, then a quadratic utility function cannot remain positive and the error function approximation for AEROC will not apply.

The function d²(a) is quadratic: d²(a) = (a−a₀)^†H(a₀)×(a−a₀), and the coefficient matrix for this quadratic form is expressed in terms of the Fisher information kernel function described earlier:

$$\mathbf{H}({\mathbf{a}}_0)=\frac{1}{{\overline{u}}_0^2}{\langle u({\mathbf{v}}_0,\mathbf{v})\mathbf{F}({\mathbf{a}}_0\mid \mathbf{v},{\mathbf{v}}^{\prime })u({\mathbf{v}}_0,{\mathbf{v}}^{\prime })\rangle }_{\mathbf{v},{\mathbf{v}}^{\prime }}.$$ (58)

In the next section we will apply these results to the imaging situation described in Section 6.

8. COMBINED DETECTION AND ESTIMATION IN IMAGING

With the same data equation as in Section 6, we find that the following utility-averaged signal is relevant for the AEROC approximation: s̃ = 1/ū₀〈u(v₀, v)s(v)〉_v. Making use of the calculations in Section 6, we can show that

$$H(a_0)=H(0)=\text{tr}[\stackrel{\sim }{\mathbf{s}}{\stackrel{\sim }{\mathbf{s}}}^{†}{\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0]={\langle {\mid {\stackrel{\sim }{\mathbf{s}}}^{†}\overline{\mathbf{sc}}(\mathbf{g})\mid }^2\rangle }_0.$$ (59)

Now we use d²(a) = (a−a₀)²H(0) to get the approximation to the ideal observer AEROC. Note the similarities to the detectability approximations for the SKE and SKS tasks. By comparing the results from this section with those in Sections 3 and 6 we can see that the matrix ${\langle \overline{\mathbf{sc}}(\mathbf{g}){\overline{\mathbf{sc}}}^{†}(\mathbf{g})\rangle }_0$ is important for approximating the ideal-observer figures of merit for all three types of tasks: detection, estimation, and combined detection/estimation. This matrix depends on the background ensemble and the imaging operator. It is independent of the task and the signal to be detected and/or estimated. We have seen in Section 4 how this matrix can lead to surrogate figures of merit for detection tasks. The same results can be modified slightly to apply to provide surrogate figures of merit for estimation and combined estimation/detection tasks also.

9. DISCUSSION

We have provided a new and more rigorous derivation of what we believe is an important relation between the Fisher information matrix and the AUC for the ideal observer trying to detect a change in a parameter of the PDF governing the statistics of the data vector. This new derivation shows why our previous derivation failed when we tried to find the fourth-order term in the expansion of the ideal-observer AUC in terms of the change in the parameter vector. In particular, for a scalar parameter, this fourth-order term does not exist unless the kurtosis of the score is zero. These results can be related to some concepts in information geometry through the idea of a divergence on the manifold of PDFs parameterized by the vector a. The square of the detectability, which we call γ(a) in Section 2, also depends on the base value a₀. If we modify the notation and call this quantity γ(a,a₀), then this function defines a divergence on . For any divergence the matrix of second derivatives evaluated at a = a₀ defines a Riemannian metric on . We have shown that, for the divergence defined by the detectability of the ideal observer, this metric is the canonical metric in information geometry, i.e., the Fisher information. Furthermore, any divergence on gives rise to a linear connection on this manifold via its third derivatives evaluated at a=a₀. Our computation of these third derivatives allows us to compute the connection coefficients that arise from the ideal-observer detectability. Thus, even though this divergence fails to have fourth derivatives along a=a₀, the existence of the second and third derivatives allows us to compute the Riemannian metric and linear connection induced by the ideal-observer detectability. We have yet to work out the implications of this interpretation of our calculations.

For signal detection in the imaging context we have shown that, when the parameter that is changing is the signal amplitude, the Fisher information approximation to the detectability is the trace of a product of two matrices, one of which depends on the statistics of the data generated by the signal and the other on the statistics of the data generated by the random background. This offers the possibility of optimizing an imaging system for the detection of arbitrary weak signals in a statistically specified ensemble of backgrounds. For this approach to be computationally feasible we would need an efficient method to calculate $\overline{\mathbf{sc}}(\mathbf{g})$, the posterior mean of the background score vector, or some approximation to this vector. As an example of the latter approach we could replace the posterior distribution pr(b|g) with a Gaussian approximation to it. Simulations or experiments would determine how the mean and covariance matrix of this Gaussian would depend on the data vector g.

We have calculated the details of the Fisher information approximation to detection figures of merit under three statistical models that are relevant to imaging. In the case of a Gaussian mixture model, where the mean of the Gaussian is background dependent, we have found a very simple and intuitive expression that makes use of the posterior mean estimate of the background. If this estimator is replaced with some more easily computable estimator that still makes use of prior information about the background statistics, then the result may be a surrogate figure of merit that will correlate well with ideal observer performance on a wide range of tasks. This possibility needs to be verified in simulation and that will be part of the next phase of this work. For the Poisson mixture model, and the Gaussian mixture when the background affects the mean and covariance of the Gaussian, we were not able to pursue the analytical calculations quite as far, but there is still the possibility of deriving surrogate figures of merit by replacing the posterior density with a Gaussian approximation as discussed above.

We have shown that, when the task is to estimate signal parameters for weak signals, the minimum possible EMSE can also be approximated with the use of a generalization of the Fisher information matrix, a matrix-valued Fisher information kernel. It is interesting that this kernel involves the gradient of the conditional distribution pr(g|v,a) with respect to the parameter vector a that we are not estimating. The standard application of Fisher information to estimation problems involves the gradient of the conditional distribution with respect to the parameter vector v that we are estimating. An essential aspect of this calculation is that there is a singularity in the statistical model pr(g|v,a). This singularity is described by the equation pr(g|v,a₀) = pr(g|a₀), which indicates that the signal is absent when a=a₀. It would be interesting to extend the techniques of information geometry to this situation, but that endeavor is beyond the scope of this work.

For signal parameter estimation in the imaging context, when the parameter that is not being estimated is the signal amplitude, we have shown that the Fisher information approximation to the minimum EMSE can again be expressed as the trace of a product of two matrices. The first of these matrices again depends only on the statistics of the signal in the data. The second matrix depends only on the background statistics in the data and is, in fact, the same matrix that appears in the Fisher information approximation to detectability in the imaging context. This raises the possibility that an imaging system that is optimized for detecting arbitrary weak signals in a given ensemble of random backgrounds will also optimize performance on the task of estimating signal parameters.

When the task is the detection of a signal and the estimation of signal parameters we have introduced the AEROC as a figure of merit in an earlier publication. In that publication we also showed that, when the utility function for the estimation part of the task is nonnegative, the AEROC for the ideal EROC observer can also be approximated for weak signals by using the Fisher information kernel introduced above for pure estimation tasks. We suspect that there are other classes of utility functions for which this approximation is valid, but we have not explored these possibilities at the present time. In this work we have applied this approximation to the imaging context and found that, once again, the Fisher information approximation to the ideal AEROC involves the trace of a product of matrices. The first matrix depends on the signal statistics in the data and the utility function. The second matrix depends on the background satistics in the data and is again the same matrix that appears in the Fisher information approximation to detectability. Thus, optimizing a system for detection of arbitrary weak signals in a random background may also optimize the system for combined detection and estimation tasks.

In summary we have found that, for the very general imaging model used in this work, our ability to estimate the random background, as quantified by the Fisher information matrix for this task, is a crucial determinant of task performance of ideal observers for detection, estimation and combined tasks. This is probably not very surprising, but the Fisher information approximations developed and examined in this work allow us to mathematically relate the background Fisher information matrix to ideal-observer figures of merit for all of these tasks. This relation, in turn, can be used to develop surrogate figures of merit that are correlated with ideal-observer task performance, but easier to compute. This work forms only the foundation for this latter pursuit and we will be exploring in this direction in the future.

APPENDIX A: COMPUTATIONS FOR SECTION 1

We use Eq. (12) to derive Eqs. (13)–(17). In this appendix we will show the calculations when the parameter vector a is a scalar a. Computing derivatives of the left-hand side of Eq. (12) with respect to a involves differentiating the quantity

$$D_0=exp[-{\mid z\mid }^2\gamma (a,\sigma )]=exp(-{\mid z\mid }^2\gamma ),$$ (A1)

where we have introduced a shorthand notation that will be useful. The symbol γ_n represents the nth derivative of γ with respect to a, and D_n represents the corresponding derivative of D₀.

$$D_1=-{\mid z\mid }^2{\gamma }_1{D}_0,$$ (A2)

$$D_2=(-{\mid z\mid }^2{\gamma }_2+{\mid z\mid }^4{\gamma }_1^2)D_0,$$ (A3)

$$D_3=(-{\mid z\mid }^2{\gamma }_3+3{\mid z\mid }^4{\gamma }_1{\gamma }_2-{\mid z\mid }^6{\gamma }_1^3)D_0,$$ (A4)

$$D_4=(-{\mid z\mid }^2{\gamma }_4+4{\mid z\mid }^4{\gamma }_1{\gamma }_3+3{\mid z\mid }^4{\gamma }_2^2-6{\mid z\mid }^6{\gamma }_1^2{\gamma }_2+{\mid z\mid }^8{\gamma }_1^4)D_0.$$ (A5)

It is the quantities γ_n at a = a₀ that we are interested in computing.

Computing derivatives on the right-hand side of Eq. (12) involves differentiating the quantity

$${\stackrel{\sim }{D}}_0={\mid {\langle {\mathrm{\Lambda }}_a^z(\mathbf{g})\rangle }_{\mathbf{g}\mid a}\mid }^2={\mid \langle {\mathrm{\Lambda }}^z\rangle \mid }^2$$ (A6)

with respect to a, where $z=\frac{1}{2}+i\alpha$, and the second equality introduces a shorthand notation for the computations. The notation Λ_n will, be used for the nth derivative of Λ_a(g) with respect to a, and D̃_n is the corresponding derivative of D̃₀. For the complex conjugate of z we write z̄ and note that z̄=1−z. The first four derivatives are given by

$${\stackrel{\sim }{D}}_1=z\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle +c.c.,$$ (A7)

$${\stackrel{\sim }{D}}_2=-{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1^2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle +z\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle +{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \times \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle +c.c.,$$ (A8)

$${\stackrel{\sim }{D}}_3=-{\mid z\mid }^2(z-2)\langle {\mathrm{\Lambda }}^{z-3}{\mathrm{\Lambda }}_1^3\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -3{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -2\overline{z}{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1^2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle +z\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_3\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle +2{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle -z{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-2}{\mathrm{\Lambda }}_1^2\rangle +{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_2\rangle +c.c.,$$ (A9)

$${\stackrel{\sim }{D}}_4=-{\mid z\mid }^2(z-2)(z-3)\langle {\mathrm{\Lambda }}^{z-4}{\mathrm{\Lambda }}_1^4\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -6{\mid z\mid }^2(z-2)\times \langle {\mathrm{\Lambda }}^{z-3}{\mathrm{\Lambda }}_1^2{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -3\overline{z}{\mid z\mid }^2(z-2)\langle {\mathrm{\Lambda }}^{z-3}{\mathrm{\Lambda }}_1^3\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle -3{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_2^2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -4{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_3\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle -9\overline{z}{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle +3{\mid z\mid }^4\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1^2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-2}{\mathrm{\Lambda }}_1^2\rangle -3\overline{z}{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-2}{\mathrm{\Lambda }}_1^2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_2\rangle +z\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_4\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}\rangle +3{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_3\rangle \langle {\mathrm{\Lambda }}^{\overline{z}}{\mathrm{\Lambda }}_1\rangle -3z{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-2}{\mathrm{\Lambda }}_1^2\rangle +3{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_2\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_2\rangle -z{\mid z\mid }^2(\overline{z}-2)\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \times \langle {\mathrm{\Lambda }}^{\overline{z}-3}{\mathrm{\Lambda }}_1^3\rangle -3z{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{z-1}{\mathrm{\Lambda }}_1\rangle \langle {\mathrm{\Lambda }}^{\overline{z}-2}{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\rangle +{\mid z\mid }^2\langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_1\rangle +\langle {\mathrm{\Lambda }}^{\overline{z}-1}{\mathrm{\Lambda }}_3\rangle +c.c.$$ (A10)

Now we will evaluate these derivative expressions at a=a₀. Many terms disappear in this limit because of two facts. The first fact is that Λ=1 at a=a₀. The second fact is that 〈Λ_n〉 =0 when a=a₀. This second fact depends on the interchange of differentiation with respect to a and the expectation operation. We will assume that our conditional PDF is such that this interchange can be performed. The surviving terms give us the following equations

$${\stackrel{\sim }{D}}_0=1,$$ (A11)

$${\stackrel{\sim }{D}}_1=0,$$ (A12)

$${\stackrel{\sim }{D}}_2=-2{\mid z\mid }^2\langle {\mathrm{\Lambda }}_1^2\rangle ,$$ (A13)

$${\stackrel{\sim }{D}}_3=-{\mid z\mid }^2(z-2)\langle {\mathrm{\Lambda }}_1^3\rangle -3{\mid z\mid }^2\langle {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\rangle +c.c.,$$ (A14)

$${\stackrel{\sim }{D}}_4=-{\mid z\mid }^2(z-2)(z-3)\langle {\mathrm{\Lambda }}_1^4\rangle -6{\mid z\mid }^2(z-2)\langle {\mathrm{\Lambda }}_1^2{\mathrm{\Lambda }}_2\rangle -3{\mid z\mid }^2\langle {\mathrm{\Lambda }}_2^2\rangle -4{\mid z\mid }^2\langle {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_3\rangle +3{\mid z\mid }^4\langle {\mathrm{\Lambda }}_1^2\rangle \langle {\mathrm{\Lambda }}_1^2\rangle +c.c.,$$ (A15)

Now we return to the left-hand side of Eq. (12) at a =a₀. Using D̃₀ =1 we find that D₀ =1 or, equivalently, γ= γ(a₀, σ)=0. Differentiating both sides of Eq. (12) once and using D̃₁ =0 together with the fact that integral

$${\int }_{C}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz=i\sqrt{\pi }\sigma exp\left(-\frac{1}{4{\sigma }^2}\right)=I(\sigma )$$ (A16)

is non-vanishing, we find that D₁ =0, which implies that

$${\gamma }_1=\frac{\partial }{\partial a}\gamma (a_0,\sigma )=0.$$ (A17)

This result is expected, since, as a function of a, γ(a,σ) reaches a minimum at a=a₀.

For the second derivative at a=a₀ we have D₂ =−|z|²γ², which implies that

$${\gamma }_2=\frac{{\partial }^2}{\partial a^2}\gamma (a_0,\sigma )=2\langle {\mathrm{\Lambda }}_1^2\rangle =2F(a_0).$$ (A18)

The last equality is a non-standard expression for the Fisher information, but it is easily checked to be equivalent to the standard one. For the third derivatives at a = a₀ we can use the fact that γ₁ =0 to obtain D₃ =−|z|²γ₃. For the right-hand side in this case we need the integral

$${\int }_{C}zexp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz={\int }_C\overline{z}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz=\frac{1}{2}I(\sigma ).$$ (A19)

Once again we have I(σ) as a multiplicative factor on both sides of the equation and, after canceling this factor, we arrive at

$${\gamma }_3=\frac{{\partial }^3}{\partial a^3}\gamma (a_0,\sigma )=-3\langle {\mathrm{\Lambda }}_1^3\rangle +6\langle {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2\rangle .$$ (A20)

This expression can be related to the derivative of the Fisher information, which is given explicitly by

$$\frac{d}{{da}_0}F(a_0)=\frac{d}{{da}_0}{\int }_{{\mathbb{R}}^M}\frac{{[{pr}^{\prime }(\mathbf{g}\mid a_0)]}^2}{pr(\mathbf{g}\mid a_0)}{d}^{M}g.$$ (A21)

A straightforward computation gives us

$${\gamma }_3=\frac{{\partial }^3}{\partial a^3}\gamma (a_0,\sigma )=3\frac{d}{{da}_0}F(a_0).$$ (A22)

Finally, for the fourth derivative at a=a₀ we use γ₁ =0 again to simplify and obtain $D_4=-{\mid z\mid }^2{\gamma }_4+3{\mid z\mid }^4{\gamma }_2^2$. To finish the computation we need the integrals

$${\int }_C{z}^{2}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz={\int }_C{\overline{z}}^{2}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz=I(\sigma )\left(\frac{1}{4}-\frac{{\sigma }^2}{2}\right)$$ (A23)

and

$${\int }_C{\mid z\mid }^{2}exp\left(-\frac{{\mid z\mid }^2}{{\sigma }^2}\right)dz=I(\sigma )\left(\frac{1}{4}+\frac{{\sigma }^2}{2}\right).$$ (A24)

Putting everything together we have on the left-hand side of the equation

$$I(\sigma )[-{\gamma }_4+3(1+2{\sigma }^2){\langle {\mathrm{\Lambda }}_1^2\rangle }^2],$$ (A25)

and on the right-hand side,

$$I(\sigma )\left[\left({\sigma }^2-\frac{15}{2}\right)\langle {\mathrm{\Lambda }}_1^4\rangle +18\langle {\mathrm{\Lambda }}_1^2{\mathrm{\Lambda }}_2\rangle -6\langle {\mathrm{\Lambda }}_2^2\rangle -8\langle {\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_3\rangle +(6+3{\sigma }^2){\langle {\mathrm{\Lambda }}_1^2\rangle }^2\right].$$ (A26)

Solving for γ₄ we find that the coefficient of σ² in the resulting expression is the negative of $\langle {\mathrm{\Lambda }}_1^4\rangle -3{\langle {\mathrm{\Lambda }}_1^2\rangle }^2$, which is the kurtosis of the score at a=a₀. This completes the computation for the results in Section 1.

APPENDIX B: COMPUTATIONS FOR SUBSECTION 4.A

In this Appendix we expand on some comments in Section 4 to produce upper and lower bounds, based on the Hotelling trace and alternate estimators of the background, for the surrogate figures of merit in Eqs. (29)–(31). First we start with a fact about posterior mean estimators. If c is a linear function of b via c=Lb, then the posterior mean estimate of c may be written as

$$\widehat{\mathbf{c}}(\mathbf{g})={\int }_C\mathbf{c}\left[{\int }_B\text{pr}(\mathbf{c}\mid \mathbf{b})\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}\right]d\mathbf{c}.$$ (B1)

Since c is a deterministic function of b, we have pr(c|b)=δ(c−Lb). Interchanging the integrals and using the delta function then gives us

$$\widehat{\mathbf{c}}(\mathbf{g})={\int }_B\mathbf{Lb}\text{pr}(\mathbf{b}\mid \mathbf{g})d\mathbf{b}=\mathbf{L}\widehat{\mathbf{b}}(\mathbf{g}).$$ (B2)

So the posterior mean estimate of c is the matrix L applied to the posterior mean of b.

The Fisher information expression from Eq. (29) can be written as

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0={\mathbf{s}}^{†}{\mathbf{K}}^{-1}{\langle [\mathbf{g}-\widehat{\mathbf{b}}(\mathbf{g})]{[\mathbf{g}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_0{\mathbf{K}}^{-1}\mathbf{s}.$$ (B3)

We expand the vector in square brackets as g−b̂(g) = [g−b]+[b−b̂(g)]. The cross terms in the resulting expansion are the term

$${\langle [\mathbf{g}-\mathbf{b}]{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_0={\langle \mathbf{g}{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_0-{\langle \mathbf{b}{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_0$$ (B4)

and its transpose. The first expectation on the right-hand side of this equation vanishes:

$${\langle \mathbf{g}{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_0={\langle {\langle \mathbf{g}{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle }_{\mathbf{b}\mid \mathbf{g}}\rangle }_{\mathbf{g}}=0.$$ (B5)

For the same reason we also have 〈b̂(g)[b−b̂(g)]^†〉 = 0. Therefore we may write

$$\langle \mathbf{b}{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle =\langle [\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]{[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]}^{†}\rangle .$$ (B6)

Similar remarks apply to the other cross term. Combining the two cross terms with the rest of the expansion gives us

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0={\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}-{\langle {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_{\mathbf{g}\mid \mathbf{b}}\rangle }_{\mathbf{b}}.$$ (B7)

Now we set c=s^†K⁻¹b and note that this quantity is linearly related to b. Using our remarks above about the posterior mean we have

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_0={\langle {\mid c-\widehat{c}(\mathbf{g})\mid }^2\rangle }_0.$$ (B8)

If b̃(g) is some other estimator of the background vector, then c̃(g) =s^†K⁻¹b̃(g) is an estimator of c. Since the posterior mean minimizes the EMSE, the EMSE for c̃(g) is greater than the EMSE for ĉ(g). This fact in turn implies that

$${\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\widehat{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_0\le {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\stackrel{\sim }{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_0.$$ (B9)

Therefore, we have proved the inequalities

$${\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}-{\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}[\mathbf{b}-\stackrel{\sim }{\mathbf{b}}(\mathbf{g})]\mid }^2\rangle }_0\le {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\le {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}.$$ (B10)

A linear estimator of the background vector has the form b̃(g) =Wg+w. We can choose the matrix W and the vector w to maximize the lower bound in the last inequality. This is a straightforward application of vector calculus and the end result is the estimator b̃(g) =K_b(K + K_b)⁻¹(g−b̄)+b̄, which is in fact the Wiener estimator for the background vector. Using this estimator and some algebra, the inequality for the Fisher information in the SKE detection case reduces to

$${\mathbf{s}}^{†}{(\mathbf{K}+{\mathbf{K}}_b)}^{-1}\mathbf{s}\le {\langle {\mid {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\widehat{\mathbf{n}}(\mathbf{g})\mid }^2\rangle }_0\le {\mathbf{s}}^{†}{\mathbf{K}}^{-1}\mathbf{s}.$$ (B11)

The other Fisher information figures of merit will be subject to similar inequalities.

APPENDIX C: COMPUTATIONS FOR SUBSECTION 4.B

To get an upper bound on the Fisher information for the Poisson case we start with the Schwarz inequality

$${\langle {[{\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})]}^2\rangle }_0={\langle {\left[\sum _{m=1}^M\frac{s_m{g}_m}{{\widehat{b}}_m(g_m)}-s_m\right]}^2\rangle }_0\le {\left|\right|\mathbf{s}\left|\right|}^2\sum _{m=1}^M{\langle {\left[\frac{g_m}{{\widehat{b}}_m(g_m)}-1\right]}^2\rangle }_0.$$ (C1)

In each square bracket on the leftmost sum we will subtract and add g_m/b_m and then square the result to get three terms. The first term is

$${\langle g_m^2{\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]}^2\rangle }_0.$$ (C2)

The last term can be simplified by averaging over g given b first and using the fact that the variance of a Poisson random variable is equal to its mean:

$${\langle {\left[\frac{g_m}{b_m}-1\right]}^2\rangle }_0={\langle \frac{1}{b_m}\rangle }_0.$$ (C3)

The middle term is

$$2{\langle g_m\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]\left[\frac{g_m}{b_m}-1\right]\rangle }_0.$$ (C4)

We will perform this expectation by averaging over b given g first and using the fact that

$${\langle \left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]\rangle }_{\mathbf{b}\mid \mathbf{g}}=0.$$ (C5)

In analogy with the Gaussian case this last equation gives us

$$\begin{array}{l}{\langle g_m\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]\rangle }_{\mathbf{b}\mid \mathbf{g}}={\langle \frac{g_m^2}{{\widehat{b}}_m(g_m)}\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]\rangle }_{\mathbf{b}\mid \mathbf{g}}\\ =0.\end{array}$$ (C6)

Therefore, for the middle term, we can write

$$2{\langle g_m\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]\left[\frac{g_m}{b_m}-1\right]\rangle }_0=-2{\langle g_m^2{\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]}^2\rangle }_0.$$ (C7)

Combining the three terms now gives the final result:

$${\langle {[{\mathbf{s}}^{†}\overline{\mathbf{sc}}(\mathbf{g})]}^2\rangle }_0\le {\left|\right|\mathbf{s}\left|\right|}^2\sum _{m=1}^M\left\{{\langle \frac{1}{b_m}\rangle }_0-{\langle g_m^2{\left[\frac{1}{{\widehat{b}}_m(g_m)}-\frac{1}{b_m}\right]}^2\rangle }_0\right\}.$$ (C8)

APPENDIX D: COMPUTATIONS FOR SECTION 5

The first step in the computation is the matrix equation

$${\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid \mathbf{a})=\frac{{\int }_V\mathbf{sc}(\mathbf{g}\mid \mathbf{v},\mathbf{a}){[\mathbf{v}-\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a})]}^{†}\text{pr}(\mathbf{v})\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})d\mathbf{v}}{{\int }_V\text{pr}(\mathbf{v})\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})d\mathbf{v}},$$ (D1)

which is derived by using the quotient rule and doing some rearranging. We can write this equation in the form of a posterior expectation as

$${\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid \mathbf{a})={\int }_V\mathbf{sc}(\mathbf{g}\mid \mathbf{v},\mathbf{a}){[\mathbf{v}-\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a})]}^{†}\text{pr}(\mathbf{v}\mid \mathbf{g},\mathbf{a})d\mathbf{v}.$$ (D2)

At a=a₀ this expression reduces to

$${\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid {\mathbf{a}}_0)={\int }_V\mathbf{sc}(\mathbf{g}\mid \mathbf{v},{\mathbf{a}}_0){(\mathbf{v}-\overline{\mathbf{v}})}^{†}\text{pr}(\mathbf{v})d\mathbf{v},$$ (D3)

which we will write in the form ∇_av̂^†(g|a₀) = 〈 sc(g|v, a₀)×(v−v̄)^†〉_v. Now we are ready to compute derivatives of U(a).

For the gradient of U(a) we have two terms ∇_aU(a) = U₁(a) +U₂(a), with the first term given by

$$U_1(\mathbf{a})={\int }_G{\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid \mathbf{a})\times \left[{{\nabla }_{{\mathbf{v}}^{\prime }}{\int }_{V}u({\mathbf{v}}^{\prime },\mathbf{v})\text{pr}(\mathbf{v}|\mathbf{g},\mathbf{a})d\mathbf{v}\mid }_{\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a})}\right]\text{pr}(\mathbf{g}\mid \mathbf{a})d\mathbf{g}$$ (D4)

and the second term by

$$U_2(\mathbf{a})={\int }_V\left\{{\int }_{G}u[\widehat{\mathbf{v}}(\mathbf{g}\mid \mathbf{a}),\mathbf{v}]{\nabla }_{\mathbf{a}}\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a})d\mathbf{g}\right\}\text{pr}(\mathbf{v})d\mathbf{v}.$$ (D5)

The first term vanishes for all values of a since v̂(g|a) maximizes the inner integral in the expression for U₁(a) by definition. When a=a₀ the second term reduces to

$$U_2({\mathbf{a}}_0)={\int }_{V}u(\widehat{\mathbf{v}},\mathbf{v})\left[{\int }_G{\nabla }_{\mathbf{a}}\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a}){\mid }_{{\mathbf{a}}_0}d\mathbf{g}\right]\text{pr}(\mathbf{v})d\mathbf{v},$$ (D6)

which also vanishes when the gradient operator is interchanged with the integral inside the square brackets. Therefore U₁(a₀) =0.

For the matrix of second derivatives we also have two terms arising from U₂(a) in the gradient ${\nabla }_{\mathbf{a}}{\nabla }_{\mathbf{a}}^{†}U({\mathbf{a}}_0)=U_3+U_4$ that are given by

$$U_4={\int }_{V}u(\overline{\mathbf{v}},\mathbf{v})\left[{\int }_G{\nabla }_{\mathbf{a}}{\nabla }_{\mathbf{a}}^{†}\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a}){\mid }_{{\mathbf{a}}_0}d\mathbf{g}\right]\text{pr}(\mathbf{v})d\mathbf{v}$$ (D7)

and

$$U_3={\int }_V\left[{\int }_G{\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid {\mathbf{a}}_0)\times \mid {\nabla }_{{\mathbf{v}}^{\prime }}u({\mathbf{v}}^{\prime },\mathbf{v}){\mid }_{\overline{\mathbf{v}}}{\nabla }_{\mathbf{a}}^{†}\text{pr}(\mathbf{g}\mid \mathbf{v},\mathbf{a}){\mid }_{{\mathbf{a}}_0}d\mathbf{g}\right]\text{pr}(\mathbf{v})d\mathbf{v}.$$ (D8)

Again, by interchanging differentiation and integration, we find that U₄ = 0. This leaves U₃, which, for the quadratic utility function, can be written as

$$U_3={\int }_G\left[{\int }_V{\nabla }_{\mathbf{a}}{\widehat{\mathbf{v}}}^{†}(\mathbf{g}\mid {\mathbf{a}}_0)(\mathbf{v}-\overline{\mathbf{v}})\mathbf{s}{\mathbf{c}}^{†}(\mathbf{g}\mid \mathbf{v},{\mathbf{a}}_0)\text{pr}(\mathbf{v})d\mathbf{v}\right]\times \text{pr}(\mathbf{g}\mid {\mathbf{a}}_0)d\mathbf{g}.$$ (D9)

Substituting Eq. (D3) into this expression now gives us Eq. (48). This completes the computation for the results in Section 3.