Characterizing the dynamics of functionally relevant complexes of formate dehydrogenase

Abstract

The potential for femtosecond to picosecond time-scale motions to influence the rate of the intrinsic chemical step in enzyme-catalyzed reactions is a source of significant controversy. Among the central challenges in resolving this controversy is the difficulty of experimentally characterizing thermally activated motions at this time scale in functionally relevant enzyme complexes. We report a series of measurements to address this problem using two-dimensional infrared spectroscopy to characterize the time scales of active-site motions in complexes of formate dehydrogenase with the transition-state-analog inhibitor azide (). We observe that the frequency–frequency time correlation functions (FFCF) for the ternary complexes with NAD⁺ and NADH decay completely with slow time constants of 3.2 ps and 4.6 ps, respectively. This result suggests that in the vicinity of the transition state, the active-site enzyme structure samples a narrow and relatively rigid conformational distribution indicating that the transition-state structure is well organized for the reaction. In contrast, for the binary complex, we observe a significant static contribution to the FFCF similar to what is seen in other enzymes, indicating the presence of the slow motions that occur on time scales longer than our measurement window.

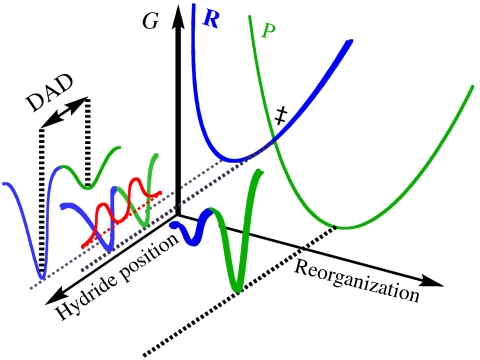
The functional role of protein motions at the femtosecond to picosecond time scale is a hotly debated topic in enzymology. Although such a role could be general in nature, many experimental (1–10) and theoretical (11–23) studies of enzyme-catalyzed hydrogen transfers have invoked protein motions at this time scale to explain anomalous kinetic isotope effects (KIE) and their temperature dependence. These studies result in the development of theoretical models, often referred to as Marcus-like models, in which the environmental reorganization that precedes the hydrogen-tunneling event has evolved to optimize the conformation of the transition state for tunneling (1, 7, 24). Fig. 1 illustrates the physical picture underlying such models. Heavy atom motions along the reorganization coordinate carry the system to a point where the donor and acceptor wells in the double-well hydrogen atom potential are degenerate and tunneling can proceed. At this position, the donor-acceptor distance and its fluctuations determine the tunneling probability. Mathematically, the rate constant for hydrogen transfer in these models is given by expressions of the form

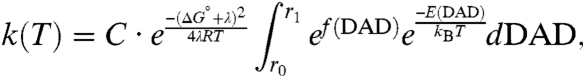where C is the fraction of reactive complexes, the first exponential, in analogy with the Marcus theory for electron transfer, reflects the reorganization of the heavy atoms that modulates the relative energies of the reactants and the products to minimize the energy defect between the zero-point levels of the donor and acceptor wells. ΔG° is the driving force for the reaction, and λ is the reorganization energy. The second exponential gives the overlap between the donor and acceptor wave functions as a function of the donor-acceptor distance that determines the tunneling probability, which is isotope dependent. The probability of having a particular donor-acceptor distance (DAD) is determined by the Boltzmann weight of the configurations having that DAD as given by the third exponential, which is temperature sensitive (4). These last two terms are integrated over the DAD coordinate to give the tunneling probability averaged over the distribution of DADs.

Fig. 1.

An illustration of the Marcus-like model. The reorganization axis indicates the motions of the heavy atoms that carry the system to the tunneling-ready configuration (TRC, ‡). The hydride transfer axis shows the two wells in the hydride coordinate that are separated by the donor-acceptor distance (DAD). R and P are the reactant and product diabatic surfaces, respectively. The red curves show the hydrogen nuclear wave functions in the reactant and product wells in the tunneling ready configuration. The overlap between them is proportional to the tunneling probability.

In the ideal case, near the tunneling ready configuration, the enzyme structure results in a DAD that strikes the optimum balance between wave-function overlap and repulsive interactions between the donor and acceptor resulting in efficient tunneling that is insensitive to thermally induced fluctuations about the average DAD. Any perturbation of the reaction conditions, such as site-specific mutations, detunes the enzyme structure from the optimal DAD, so that local, femtosecond to picosecond time scale fluctuations of the active site are required to bring the donor and acceptor close enough for efficient tunneling to take place, thereby resulting in a temperature-dependent isotope effect.

Owing to the small transient population of the transition state, it is difficult to study the motions of reactive enzyme complexes in the vicinity of the transition state experimentally. A close experimental approximation to this ideal is to study the dynamics of an enzyme in a complex with a transition-state-analog inhibitor. There have been several infrared spectroscopic studies of enzyme-ligand interaction dynamics with substrate-analog complexes that mimic the ground state (25–36). These studies use infrared echo and 2D IR spectroscopies to measure the frequency–frequency time correlation function (FFCF) that reveals the time scales for frequency fluctuations of the vibrational chromophore. These measurements use the stretching vibration of a small molecule bound at the active site of the protein to sample the conformational fluctuations and report them in the form of frequency fluctuations. Protein motions span time scales from femtoseconds to seconds. These IR studies are sensitive to motions from hundreds of femtoseconds up to 100 ps, the lower limit being dictated by the pulse-duration of the laser and the upper time scale being determined by the vibrational lifetime of the reporter vibration. As a result, protein motions that occur on longer time scales appear as a static, heterogeneous conformational distribution in the FFCF. These studies of protein dynamics typically reveal fluctuations on three time scales: the first ranges from motionally narrowed to a few hundreds of femtoseconds, the second ranges from a few to 20 ps, and the third involves motions at time scales longer than 20 ps that typically appear as a static contribution that typically represents 20–30% of the overall FFCF decay. These studies also show that solvent viscosity, point mutations of the protein, and substrate binding can modulate the time scales and relative amplitudes of protein dynamics (28).

We report a study of the enzyme formate dehydrogenase (FDH) that catalyzes the nicotinamide adenine dinucleotide (NAD⁺)-dependent oxidation of formate to carbon dioxide via hydride transfer to the C-4 carbon of the nicotinamide ring of NAD⁺ (37, 38). FDH is an industrially important enzyme in the regeneration of NADH and NADPH for biocatalysis (39, 40). Azide, which is an excellent vibrational chromophore, is a tight-binding inhibitor for FDH with an inhibition constant that we have measured as K_i = 40 nM. Because azide is isoelectronic with the carbon dioxide product and negatively charged like the formate anion reactant, it is a potent analog of the transition-state structure of the catalyzed reaction. Thus FDH serves as an ideal system to test the predictions of the Marcus-like model.

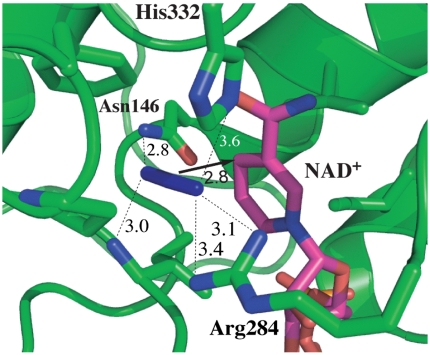
Fig. 2 illustrates the active-site structure of the ternary complex of FDH with azide and NAD⁺ based on a crystal structure of the ternary complex of FDH from Pseudomonas sp. 101, which has high sequence homology to the Candida boidinii enzyme used in our measurements (41, 42). The active-site structure is compact. It is located between two similar structural motifs each a sandwich of α-helix, parallel β-sheet, and α-helix. Several bulky, hydrophobic residues surround the azide and the nicotinamide ring bringing them close together. Azide forms H bonds to a pair of residues on each end, Arg-284 (using Pseudomonas numbering) and His-332 on one end and Ile-122 and Asn-146 on the other. These highly conserved residues bind the substrate in the active site and orient it for reaction. These four residues also connect to both rigid structural motifs providing a link between these two structural domains of the enzyme that close together to isolate the active site. Arg-284 and Asn-146 lie at the ends of α-helices on either side of the β-sheet forming the α-β-α sandwich on one side of the active site. Ile-122 is in a loop connecting a β-strand and an α-helix on the opposite side of the cavity. His-332 sits in a segment connecting a β-strand on one side of the active site to one of the α-helices of the α-β-α sandwich on the other side of the active site. Ligand binding leads to conformational changes in the enzyme that closes the active site, drawing these two secondary structural domains together (41).

Fig. 2.

Active-site structure of FDH-azide-NAD⁺ complex (PDB# 2NAD) (41). Azide is in blue and the NAD⁺ is in magenta. The arrow indicates the reaction path from the H^- donor to acceptor and the dashed lines represent the hydrogen bonds discussed in the text. All distances are in Å.

Our study of the temperature dependence of the KIE for FDH reveals a temperature-independent isotope effect over the temperature range from 5 °C to 45 °C (43). Under the framework of the Marcus-like model, this indicates that the active site of the enzyme provides an optimal DAD for tunneling; thus the fluctuations about this optimum DAD must be small amplitude motions suggesting that the active-site structure samples a narrow conformational distribution and that the fluctuations occur on short time scales. This result is corroborated by our recent infrared echo study of the ternary complex of FDH with azide anion, a transition-state-analog inhibitor, and NAD⁺ that reveals qualitatively distinct dynamics from those reported for other proteins (44). This ternary complex, whose conformation closely resembles the transition state for the catalyzed reaction, exhibits no static, heterogeneous contribution to the FFCF decay. This result indicates that the structure of the enzyme as it approaches the transition state is rigid and samples a narrow conformational distribution consistent with the emerging view of the catalyzed hydride transfer as described above.

The present work both extends and expands on earlier studies (43, 44) by measuring 2D IR spectra that allow us to extend the upper limit on the waiting time to 5 ps, to confirm the absence of a static component, and probing the dynamics of two other complexes, the ternary complex of azide-NADH-FDH and the azide-FDH binary complex. These complexes allow us to test the hypothesis that the narrow conformational distribution and rigid dynamics observed for the ternary complex with NAD⁺ reflect enzyme–ligand interactions that confer particular stability and rigidity consistent with the transition-state configuration.

Results

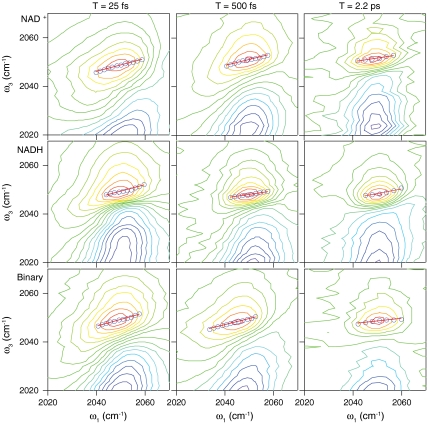
Fig. 3 shows 2D IR spectra for the ternary complexes with NAD⁺ (Top), NADH (Middle), and the binary complex (Bottom). We show 2D spectra for T = 25 fs (Left), 500 fs (Center), and 2.2 ps (Right). The red lobe represents increased transmission as a result of ground state bleaching and stimulated emission, whereas the blue lobes represent decreased transmission corresponding to the excited state absorption. At early waiting times, the lobes are elongated along the diagonal, indicating a strong correlation between the frequency ω₁, measured before the waiting time, and the frequency ω₃, measured after the waiting time. At later waiting times, however, the lobes rotate toward horizontal, indicating the loss of correlation between the frequency during ω₁ and that during ω₃. This loss of correlation and the corresponding change in peak shape reflect spectral diffusion resulting from the equilibrium environmental fluctuations. The FFCF, which is given by 〈δω(t)δω(0)〉, quantifies the time scales for the frequency fluctuations that report on the dynamics of the environment around the azide anion. To extract the FFCF from our 2D IR data, we use the center line slope (CLS) method introduced by the Fayer group (45, 46). In this method, we take slices through the 2D spectrum at each value of ω₁ and locate the position of the maximum in ω₃. The resulting sequence of points is the center line, shown as the blue circles in Fig. 3, and the slope of this line is proportional to the FFCF for this value of T. The red lines in each spectrum show the linear fits to the CLS at each waiting time. By measuring the CLS as a function of T, we quantify the time scales for the structural fluctuations in the environment of the chromophore. Following the method described by Kwak et al., we fit the decay of the CLS to a sum of exponentials plus a constant offset. Then using the relative amplitudes and time scales of the decay as input, we fit the infrared absorption line shape by varying the absolute amplitude of the FFCF (46).

Fig. 3.

2D IR spectra of the azide antisymmetric stretch for azide bound in the ternary complexes with NAD⁺ (top), NADH (middle) and the binary complex (bottom) for waiting times of T = 25 fs (left), 500 fs (middle), and 2.2 ps (right). The blue circles are the results of the CLS analysis described in the text and the red lines are the linear fits to the CLS.

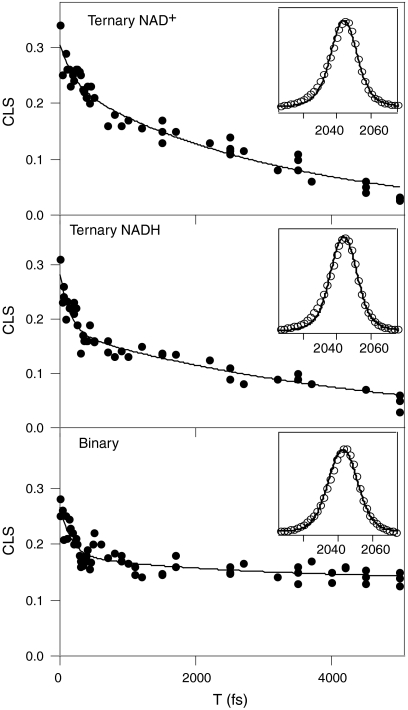
Fig. 4 shows the decay of the CLS vs. T for each of the three FDH complexes we have studied. In each case, we fit to as many as two exponentials and one static offset retaining the minimum number of terms necessary to accurately describe the decay. The CLS data are given by the points and the solid lines are the fits. The insets on each panel show the fits to the infrared absorption spectra using the fit decay parameters and adjusting the overall amplitude of the FFCF to fit the line shape in each case. It is important to note that the significant differences in the CLS decays, and thus the FFCF, are not apparent in the infrared absorptions spectra, underscoring the fact that the infrared absorption spectra cannot be analyzed to yield detailed information about structural fluctuations. Table 1 shows the values of the FFCF parameters resulting from the fits to the CLS decays and the infrared absorption spectra. These parameters correspond to the usual generalized Kubo line shape function of the form

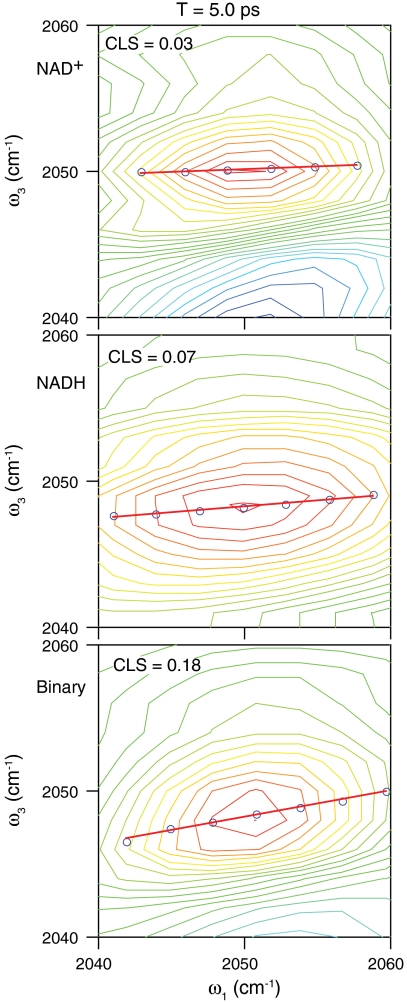
where the Δs reflect to the amplitude of the frequency fluctuations and the τs indicate the time scales of the motions responsible for those fluctuations (47). The ternary complex with NAD⁺ has a fast time constant of 210 fs, and the values for the ternary complex with NADH and the binary complex are about 150 fs and 160 fs, respectively. These values are all the same within experimental error and consistent with our previous measurement of 250 fs for the ternary complex with NAD⁺. The slow time constant for the ternary complexes with NAD⁺ and NADH are 3.2 ps and 4.6 ps, respectively. There is a small amplitude slow time component for the binary complex with a decay time of 2.6 ps. The more significant feature of the binary complex, however, is the significant static term in the correlation function. This static offset corresponds to 50% of the overall decay. In contrast, for the ternary complexes, a static offset of more than 5% results in a qualitatively poor fit of the CLS decay. Fig. 5 shows 2D IR spectra of each of the complexes at 5 ps. Comparing the CLS in each of these spectra at this relatively long delay time clearly illustrates the qualitative difference between the ternary complexes and the binary complex.

Fig. 4.

CLS decays for the ternary complexes with NAD⁺ (top) and NADH (middle) and the binary complex (bottom). The markers are the experimental values and the solid lines are biexponential fits to the decays. The insets show the linear absorption spectra along with the fits to the spectra using an FFCF with time constants and relative amplitudes determined from the CLS decays.

Table 1.

Frequency-frequency time correlation function (FFCF) parameters from the fits to the CLS decays and the linear absorption spectra

	Δ1, ps-1	τ1, ps	Δ2, ps-1	τ2, ps	Δ3, ps-1
NAD+	0.9 ± 0.2	0.21 ± 0.1	1.4 ± 0.2	3.2 ± 0.5	—
NADH	1.0 ± 0.2	0.15 ± 0.1	1.3 ± 0.2	4.6 ± 0.5	—
Binary	1.1 ± 0.2	0.16 ± 0.1	0.8 ± 0.2	2.6 ± 0.5	1.4 ± 0.2

Fig. 5.

2D IR spectra at T = 5 ps for the ternary complexes with NAD⁺ (top) and NADH (middle) and the binary complex (bottom). The blue circles are the results of the CLS analysis described in the text and the red lines are the linear fits to the CLS.

Discussion

Proteins exhibit thermally activated motions on times scales ranging from hundreds of femtoseconds for very localized motions to milliseconds or longer for domain motions involving larger segments of the protein (14, 16, 20, 22). Two-dimensional IR spectroscopy probes the FFCF, and thereby the protein motions that are sensed by the transition-state analogue (the IR chromophore), only for a few tens of picoseconds at most. Although these experiments cannot identify the time scales for spectral diffusion for motions that occur beyond this time range, they do characterize the distribution of frequencies determined by the distribution of structures resulting from these slower motions (25–35, 44). Motions at all time scales contribute to the initial value of the FFCF, but only those motions that occur on the femtosecond to picosecond time scale contribute to the FFCF decay probed in the 2D IR measurements. The remaining protein motions at longer time scales that still affect the chromophore give rise to an apparently static contribution to the FFCF. This static component does not mean that the protein does not move on longer time scales; rather there are slower motions that contribute to the frequency distribution that are not sampled within the experimental time window. The results of most previous studies of enzyme dynamics do exhibit a static contribution to the FFCF decay that is typically 20–40% of the initial value of the FFCF (26–30, 33–35, 48).

The ternary complexes of FDH with azide exhibit complete spectral diffusion within a few picoseconds. One possible explanation of the complete decay of the FFCF is that FDH actually does exhibit the expected slow structural dynamics, but that azide is insensitive to those motions. Careful inspection of the structure of the ternary complex, however, casts doubt on this idea. The azide antisymmetric stretch transition frequency is sensitive to hydrogen bonding interactions (26, 49–51). It is, therefore, reasonable to conclude that motions of the four hydrogen bonding partners, Asn-146, His-332, Ile-122, and Arg-284, make the dominant contributions to the observed FFCF. Each of these residues is located at the end of a major secondary structural component in the α-helix-β-sheet-α-helix motifs that flank either side of the active site. Given the locations of these residues at the ends of these secondary structural elements, it is unlikely that these motifs could undergo large amplitude motions without modulating the hydrogen-bond distances between these residues and the active-site-bound azide. Fluctuations of these hydrogen-bond lengths as a result of large amplitude motions of the secondary structural domains would appear as a static contribution to the FFCF. Thus, it seems unlikely that these groups are undergoing such long time scale, large amplitude motion. That does not mean that no part of the protein may be exhibiting more typical slow fluctuations, but such motions must involve parts of the protein that do not directly influence the active site or else we would see evidence of those motions in our measurements.

The more likely explanation for the absence of a static contribution to the FFCF is that the ternary complex is rigid and samples a narrow conformational distribution. Thus, the fluctuations at the active site are high-frequency, small-amplitude motions that are fully sampled within a few picoseconds. This explanation is consistent with the idea that the enzyme evolved to minimize the energy of the transition state. In the degrees of freedom orthogonal to the reaction coordinate, a transition state corresponds to a deep energy minimum. A transition-state-analog complex, like the ternary complex with azide and NAD⁺, takes advantage of those same interactions that stabilize the transition state, but does not have the unbound coordinate of a reactive complex. This structure is in a deep potential well with steep walls, the thermally accessible conformational space corresponds to a narrow structural distribution, and the fluctuations about the equilibrium structure are sampled on short time scales. That is not to suggest that the whole protein must be entirely rigid or that distal parts of the complex cannot undergo slow thermal motions. This rigidity perhaps exists only in the vicinity of the active site, the portion of the protein responsible for the enzyme-ligand-cofactor interactions and contributes to the lowering of the free energy barrier for the reaction. In accordance with the temperature independent KIEs measured for this enzyme, and their interpretation by the Marcus-like model, this rigidity may also correspond to the precise organization of the residues at the tunneling ready configuration necessary to achieve efficient tunneling (43).

If this interpretation of the data for the ternary complexes is correct, then we would predict that the binary complex should behave qualitatively differently because the binary complex lacks the NAD⁺ cofactor and, thus, is a poor mimic of the transition-state structure. Although both the ternary complexes show complete spectral diffusion on the picosecond time scale, the FFCF for the binary complex has a significant static component indicating persistent conformational heterogeneity beyond the first several picoseconds. The enzyme undergoes significant structural rearrangements upon binding the coenzyme. Because the coenzyme is not bound in the binary complex, these rearrangements have not taken place, and the binary complex does not represent the transition-state configuration. Thus the result for the binary complex indicates that the lack of a static component is not a property of this enzyme in general and supports our interpretation that complete spectral diffusion in the ternary complexes reflects the transition-state-analog nature of these complexes.

The fastest component of the FFCF in each complex, with decay times ranging from 150 to 210 fs, reflects the time scale of the local hydrogen-bond fluctuations of the four conserved hydrogen-bond partners that bind and orient the substrate in the active site. These motions are present in both the ternary and the binary complexes with similar amplitudes and time scales. The corresponding motions may well involve collective compression of the active-site residues corresponding to the “gating motions” referred to in the Marcus-like model that modulate the donor-acceptor distance (4, 24). Simulations of different enzymatic systems have suggested that the gating motions or promoting vibrations have frequencies between 50 and 170 cm^-1 corresponding to dynamics on a 200 to 700 fs time scale consistent with the dynamics we observe (15, 52). The picosecond time scale component of the FCCF is somewhat faster for the ternary complex with NAD⁺ than for NADH. This difference is reasonable because the ternary complex with the NAD⁺ has a higher charge density with the anionic azide and the cationic nicotinamide ring located within 3 Å of one another (41). The consequence of this high charge density is that structural fluctuations cost more energy for the ternary complex with NAD⁺ leading to faster dynamics.

Conclusion

We report the FFCF of azide, a transition-state analogue inhibitor of FDH, in ternary complexes that mimic the transition-state structure, and the binary FDH-N₃ complex that adopts a structure that is removed from the transition state. The FFCFs for the ternary complexes decay completely to zero with long time constants of a few picoseconds. In contrast, the FFCF for the binary complex exhibits a significant static contribution to the overall decay. These results are consistent with the interpretation that the active-site structure of the enzyme is rigid in the proximity of the transition state exhibiting dynamics only at the picosecond to subpicosecond time scale. Because the binary complex does exhibit a static component, it appears that the absence of the static component in the ternary complexes is a signature of the transition-state structure. This is consistent with the conclusion of our earlier KIE measurements that the active-site environment is well organized for the reaction (43). In addition, the subpicosecond contributions to the FFCF that we observe in each complex are of similar time scales and may reflect the kind of compressive active-site motions that have been invoked in reactions where gating is necessary to modulate the donor-acceptor distance and that are believed to be present in the enzyme even if such motions do not influence the temperature dependence of the KIE, as is the case for FDH (53). Further studies of this enzyme and several of its mutants are under way to test this hypothesis.

Materials and Methods

The experimental setup is similar to that described previously (54, 55). Briefly, the apparatus employs 100-fs laser pulses in the midinfrared in resonance with the azide antisymmetric stretch transition. A commercial Ti:sapphire laser with a repetition rate of 1 KHz produces pulses of 100-fs duration centered at 800 nm with a per pulse energy of approximately 1 mJ. A sequence of two nonlinear optical processes down-converts the 800-nm light into the mid-IR. First, an optical parametric amplifier based on β-barium borate (θ = 27°, type II) generates two tunable near-infrared pulses, signal and idler. The signal and idler combine to produce tunable midinfrared light through difference frequency generation in a 1-mm type-II AgGaS₂ crystal cut at θ = 50°. At 2,043 cm^-1, the azide antisymmetric stretch transition frequency, the typical pulse energy is 6.5 μJ and the pulse duration is approximately 100 fs.

For the 2D IR experiments, we separate the infrared beam into three pulses of approximately equal energy. A computer-controlled translation stage in each path determines the time delay between the pulses. A 90° off-axis parabolic mirror with effective focal length of 100 mm focuses the pulses into the sample in a box phase-matching geometry. The signal originating from the sample is overlapped spatially and temporally with a fourth, local oscillator, pulse, and signal and local oscillator disperse in a monochromator that measures the ω₃ frequency axis. For each value of T, we step the delay between the first two pulses, τ, and scan the ω₃ spectrum for each value of τ.

A liquid nitrogen cooled MCT detector measures the signal in the -k₁ + k₂ + k₃ direction. A gated integrator and lock-in amplifier referenced to an optical chopper with a chopping frequency of 500 Hz in the path of the third beam isolate the signal. We collect both rephasing and nonrephasing signal pathways by varying the order of the first two pulses. Fast Fourier transformation of the resulting spectra in τ gives the complex valued 2D rephasing and nonrephasing spectra. We phase these spectra and sum the absorptive components to get the 2D IR correlation spectra that we analyze to extract the FFCF.

We investigate three different samples: a binary complex of Candida Boidinii FDH (27 mM) and azide (27 mM), and ternary complexes of FDH (27 mM), azide (27 mM), and NAD⁺ or NADH (30 mM). We purchase the enzyme from Roche Applied Science and azides, NAD⁺ and NADH, from Sigma and use them without further purification. We prepare all the samples in 0.1 M phosphate buffer pH 7.5 in H₂O, which we choose because D₂O, the solvent we have used previously, exhibits a resonant response at high frequency from the tail of the OD stretching band that distorts the line shape of the azide transition and perturbs the CLS analysis. Our sample cell consists of 3-mm CaF₂ windows separated by a 25-μm Teflon spacer. We take the FTIR spectrum of each sample before and after the 2D IR experiments to confirm its viability.