Symmetry, Stability, and Reversibility Properties of Idealized Confined Microtubule Cytoskeletons

Abstract

Many cell cytoskeletons include an aster of microtubules, with the centrosome serving as the focal point. The position of the centrosome within the cell is important in such directional activities as wound closure and interactions of immune cells. Here we analyzed the centrosome positioning as it is dictated by microtubule elasticity alone in a mechanical model of an intrinsically fully symmetric microtubule aster. We demonstrate that the symmetry and the central position of the centrosome are unstable. The equilibrium deviation of the centrosome from the center is approximately proportional to the difference of the microtubule length and cell radius. The proportionality coefficient is 1 in flat cells and 2 in three-dimensional cells. The loss of symmetry is irreversible, and in general, the equilibrium form of the aster exhibits memory of past perturbations. The equilibrium position of the centrosome as a function of the microtubule length exhibits hysteresis, and the history of the length variation is reflected in the aster form. These properties of the simple aster of elastic microtubules must be taken into account in the analysis of more comprehensive theoretical models, and in the design and interpretation of experiments addressing the complex process of cytoskeleton morphogenesis.

Introduction

In many cell types that have been studied experimentally, the prominent structural feature is the aster of microtubules, which are anchored at the centrosome (1). Because the microtubules direct the transport of organelles and secretory vesicles, the position of the centrosome within the cell is important for various cellular activities, such as wound closure and migration (e.g., (2–4)), and cell interactions during immune response, e.g., between a T-killer cell and a tumor cell (5,6). In particular, induction of asymmetry of the microtubule aster in some situations, or maintenance of its symmetry within the cell outline in others, has been the subject of experimental investigation (e.g., (3,7–14)). In the compact immune cells, such as the lymphocytes, which have nearly spherical cell bodies, the eccentric position of the centrosome appears to be constitutive, and only its orientation to a specific side of the cell appears to be under the regulation induced by the antigen-mediated interaction with the other cell. An apparently similar case is presented by some Drosophila neuroblasts, in which asymmetric positioning of the centrosome is linked to the direction of asymmetric cell division (15). The thinly spread epithelioid cells of the wound-closure experiments, with the exception of the nucleus, are nearly flat. It is now generally accepted that although the centrosome in these cells may not be centered with respect to the nucleus, it is centered with respect to the cell outline (7,13). The apparent fundamental difference between the centrosome positioning in flat and spherical cells would require explanation and might serve as a test of our understanding of the centrosome positioning mechanisms.

The mechanism of positioning is not well understood. It is unclear how general the mechanisms are that have been implicated, or how exactly they interact or interfere in each cell type and individual cell. Among the mechanisms that have been experimentally implicated there are microtubule dynamics (11,12,16–18), action of cortically anchored molecular motors of the dynein type (10,12,19), movement of the entire cell body that entrains the centrosome (20,21), flow of cortical actomyosin that entrain microtubules (12,13), and even cell population-level kinetic selection linked to the direction of transport along the microtubules (22,23).

In view of the complexity of centrosome positioning and with the goal of progressing toward a generalized and integrated mechanistic understanding of it, it is imperative to study systematically the contributions and theoretical capacities of each contributing mechanism, starting from the first principles. Arguably the simplest of the contributions, and the one which is the most inseparable from the microtubule cytoskeleton itself, is the impact that the bending elasticity of microtubules must have on the positioning of the centrosome within the cell boundary. The fundamental role of the elastic compactization of the microtubule cytoskeleton within the constraints of the cell boundary for centrosome positioning was recognized early by Holy and co-authors. One version of the original theory considered the absolute energy minimum of an aster of a large finite number of evenly spaced microtubules of equal length, confined in a flat circular domain (24). It was shown that when the microtubule length exceeds the confining radius, the centrosome will be off-center, and the centrosome position was computed as a function of the length and radius.

An argument was made that the instability of the central position must be stronger in three dimensions than in two dimensions. The other variant of this pioneering theory (25) incorporated stochastic changes in lengths of individual microtubules, which might also affect centrosome positioning. The theory predicted approximate centering, when the microtubules were comparable in length with the radius of the confining boundary, and eccentric positioning of the centrosome, when the microtubules were longer. The asymmetric unstrained configuration of the model aster had an impact on the results of this pioneering study. In later theories that incorporated the microtubule bending elasticity (20,26–29), its effect was similarly compounded by other simultaneously acting mechanisms such as the stochastic microtubule assembly, cell surface dynamics, action of molecular motors, and random Brownian forces. Among the cited works, the theory by Howard (26) predicted centering of the centrosome in the cell, irrespective of the number of dimensions. In this respect it was similar to the one-dimensional theory without bending (30), whose principles proved applicable to fission yeast (31). The other models predicted an eccentric position for the centrosome in two as well as in three dimensions. (For the wider context of this specific problem, see also, for example, the recent analyses of the role of microtubule bending elasticity in mitotic spindles (32) and acentrosomal arrays (33), and of the interplay of confining boundaries and microtubule assembly kinetics (34,35).)

In this article, we will examine equilibria of an idealized microtubule cytoskeleton (an aster of microtubules converging on the centrosome) as it is dictated by the microtubule bending elasticity alone within the constraint of the cell boundary. We will pay special attention to the question whether symmetry or asymmetry of the cytoskeleton is favored, and in view of this goal will consider an idealized cytoskeleton whose unstrained configuration is symmetric. We will consider the cases of essentially two-dimensional (flat) and three-dimensional cytoplasmic domains, to which the cytoskeleton is constrained, and which mimic the experimentally studied cases of epithelioid and immune cells.

Methods

The task of finding the equilibrium conformation of the microtubule cytoskeleton is divided into finding the equilibrium forms of microtubules and finding the equilibrium position of the centrosome. Fig. 1 shows the geometry of the model insofar as finding the equilibrium of a single microtubule is concerned. Table 1 lists the model parameters.

Figure 1.

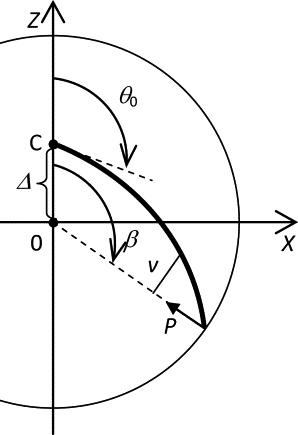
Diagram of the model for the equilibrium of a microtubule. See Table 1 for nomenclature. The bold line represents the microtubule. The circumference represents the cell boundary.

Table 1.

Nomenclature of the model

Symbol	Meaning
β	Angular coordinate of the microtubule contact with the boundary.
Δ	Distance between the centrosome and the cell center.
Δe	Equilibrium distance between the centrosome and the cell center.
θ	Angle of the tangent to the microtubule.
θ0	Angle at which the microtubule is clamped at the centrosome.
EI	Microtubule flexural rigidity.
F	Force exerted by all microtubules on the centrosome.
f	Vertical component of the force exerted by a microtubule on the centrosome.
L	Microtubule length.
M	Moment of the contact force.
N	Number of microtubules in the cell.
ni	Fraction of microtubules in the stable (i = 1) and metastable (i = 2) forms.
P	Contact force from the cell boundary on the distal microtubule end.
p = N/(2π)	Density of microtubules per unit of the angle θ0 in a flat cell.
p = N/(4π)	Density of microtubules per unit of the solid angle Ω in a three-dimensional cell.
R	Cell radius.
s	Axial coordinate in a microtubule.
v	Moment arm of the contact force.

The following equations specify the model for the single microtubule. They consist of the standard equilibrium beam equation, and of the boundary conditions of clamping on the centrosome and frictionless contact with the cell boundary. For the applicability of the beam equation to microtubules, see the book by Howard (36). That the microtubules are clamped rather than hinged on the centrosome may be deduced from images in the cited experimental articles, which invariably show that even strongly bent microtubules radiate from the centrosome in all directions before bending, instead of converging on the centrosome at sharp angles in a fanlike arrangement. (Note that, according to this criterion, microtubules do appear hinged on noncentrosomal microtubule-organizing centers assembled in some of the in vitro reconstitution experiments—see (29)—but our focus here is on centrosomal microtubules in cells.)

$$\frac{d}{ds}x\left(s\right)=\sin \theta \left(s\right),$$

$$\frac{d}{ds}z\left(s\right)=\cos \theta \left(s\right),$$

$$ds=\sqrt{d{x}^2+d{z}^2},$$

$$\frac{d}{ds}\theta \left(s\right)=\frac{M\left(s\right)}{EI},$$

$$M\left(s\right)=Pv\left(s\right),$$

$$v\left(s\right)=-x\left(s\right)\cos \beta +z\left(s\right)\sin \beta ,$$

$$x\left(0\right)=0,$$

$$z\left(0\right)=\Delta ,$$

$$\theta \left(0\right)={\theta }_0,$$

$$x\left(L\right)=R\sin \beta ,$$

$$z\left(L\right)=R\cos \beta$$

because

$$x\left(L\right)=x\left(L,\Delta ,{\theta }_0,P,\beta \right),$$

$$z\left(L\right)=z\left(L,\Delta ,{\theta }_0,P,\beta \right),$$

the contact conditions, which are the characteristic equations for the nonlinear boundary problem, specify the unknown parameters P and β as the functions

$$P=P\left(L,\Delta ,{\theta }_0\right),$$

$$\beta =\beta \left(L,\Delta ,{\theta }_0\right).$$

In the three-dimensional case, there is only one stable solution (see Results), and, correspondingly, one (P, β) pair. In the flat (two-dimensional) case, the nonlinearity leads to existence of two types of stable equilibrium forms of microtubules, and, accordingly, there are two branches of the functions for the unknown parameters:

$$P_i=P_i\left(L,\Delta ,{\theta }_0\right),$$

$${\beta }_i={\beta }_i\left(L,\Delta ,{\theta }_0\right),i=1,2.$$

With the known parameters (P, β), the differential equations of bending determine the deformed shape of each microtubule and the stresses in it. In particular, the action of each microtubule on the centrosome will be known. For each microtubule, we will have the component of the force

$$f\left({\theta }_0\right)=-P\left({\theta }_0\right)\cos \beta \left({\theta }_0\right)$$

that contributes to the total force on the centrosome. Let us introduce the number of microtubules in the cell, N; the angular density of microtubules, p; and the fraction of microtubules in the equilibrium form i, n_i. Then the total force on the centrosome is found in the two-dimensional case as

$$F=\sum _{i=1}^2{\int }_0^{\pi }2f\left({\theta }_0\right)n_i\left({\theta }_0\right)pd{\theta }_0,$$

and in the three-dimensional case as

$$F=\int f\left({\theta }_0\right)pd\Omega .$$

The equilibrium condition for the centrosome, and for the microtubule cytoskeleton as a whole, is F = 0.

The model is solved numerically. First, we observe that when Δ = 0, the problem of the equilibrium form of the microtubule is equivalent to the Euler problem dealing with an elastic rod hinged on both ends. (Although the centrosomal end of the microtubule is not hinged in our model, the moment of the force P at the centrosomal end is nonetheless zero in the special case of Δ = 0.) We start with the following approximation of the Euler-Lagrange solution:

$$P=\frac{{\pi }^{2}EI}{L^2}\frac{1+0.09{\varepsilon }^3}{1-\frac{1}{2}\varepsilon },$$

$$\beta -{\theta }_0=\pm \frac{2\sqrt{\varepsilon }}{1-\frac{5}{48}\varepsilon -\frac{1}{53}{\varepsilon }^2}.$$

Here, ɛ = (L – R)/L. These approximations have accuracy 0.25% and 0.05%, respectively. The ballistic method is used to refine the solution, and then to continue it with respect to Δ. The domain of existence of the metastable solution (i = 2) in the two-dimensional case is mapped numerically in the (L, θ₀, Δ) space. Variable step sizes are used to accurately account for the singularity at the boundary of this domain, when continuing the solution and integrating the force.

The above formulation in terms of angular densities p was validated by comparing its predictions with a variant of the model, in which there were a finite number of microtubules (see Fig. 2). In this discrete variant of the model, the integration to obtain the total force was replaced by summation over the finite number of microtubules.

Figure 2.

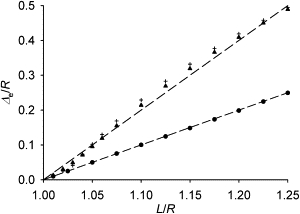
The equilibrium distance of the centrosome from the cell center. The triangles show the case of the continuous uniform spatial distribution of the unstrained directions of microtubule emanation from the centrosome in a spherical cell. The crosses show for comparison the discrete case in which 20 microtubules emanate in the directions of the vertices of a dodecahedron. The circles are the positions reached spontaneously after a small perturbation of a fully symmetric cytoskeleton in a flat round cell (in the continuous approximation as everywhere else in this article). The dashed lines have the slopes of 1 and 2 for reference. Please note that this plot starts from the (1, 0) point, and therefore the distance is approximately proportional to the excess length (length minus radius).

Results

Equilibria of a microtubule

Examples of equilibrium forms of microtubules confined between the centrosome and the cell boundary are shown in Fig. S1 in the Supporting Material. When the centrosome is in the center of the cell, the forms of a microtubule that differ in the direction of its buckling are symmetric about the axis which is the direction at which the microtubule is clamped at the centrosome, and they have the same energy. In three dimensions (in a spherical cell), an infinite number of such forms are connected by a continuous rotation about this axis. In two dimensions (in a flat round cell), there are only two such forms of a microtubule, and they correspond to diametrically opposed forms of the three-dimensional case.

With the displacement of the centrosome from the cell center, the described equivalency of the buckling forms of a microtubule is lost. Now the form which is convex in the direction of the centrosome displacement is bent less, and the opposite form is bent more. In three dimensions, these two diametrically opposed forms are the only remaining equilibrium forms. They lie in the plane defined by the displacement of the centrosome and by the unstrained direction of the microtubule. They are connected by a continuity of nonequilibrium forms, and there is no energy barrier between them. The microtubule therefore will adopt the lowest-energy form (the one which is convex in the direction of the centrosome displacement from the center). In two dimensions, the two equilibrium forms are connected only by higher-energy nonequilibrium forms in the plane of the cell. Therefore both of them are locally stable, and both can be occupied even after the displacement of the centrosome from the center.

The higher-energy form can be called metastable, and the lower-energy form, stable. Calculations show that with an increasing deviation of the centrosome from the center, a position will be reached beyond which the metastable equilibrium form does not exist anymore. When this happens, the microtubules will have to adopt the corresponding stable form. The dynamics of flipping into the only remaining equilibrium is not considered in our model, which deals only with equilibria, but it must be mentioned that the flipping is a unidirectional, energy-dissipating process. Therefore it cannot be reversed by simply returning the system to the domain of existence of the metastable solution.

Equilibria of the confined microtubule cytoskeleton

Each equilibrium form of a microtubule is characterized by the force and torque that it exerts on the centrosome. If the total force and torque exerted on the centrosome by all microtubules are zero, the entire microtubule cytoskeleton will be in equilibrium inside the cell. We will be interested in such equilibrium forms of the microtubule cytoskeleton as a whole. The simplest cytoskeleton is characterized by a uniform distribution of the unstressed directions at which the microtubules are clamped at the centrosome. In this case, a displacement of the centrosome from the center preserves the one axis of symmetry that coincides with the displacement. This residual symmetry makes the total torque zero and the total force collinear with the centrosome displacement.

In three dimensions, we mentioned that any deviation of the centrosome from the cell center specifies the direction of buckling for each microtubule, which is convex in the direction of the centrosome displacement. Thus, any such deviation generates a form of the cytoskeleton in which there is a nonzero total force on the centrosome, and the direction of this force is away from the center.

Calculations show (Fig. 2) that the equilibrium is reached, when the centrosome is removed from the cell center by a distance that is approximately twice as large as the difference of the microtubule length and cell radius. The triangles in Fig. 2 show the equilibrium centrosome displacement in the case of the continuous uniform spatial distribution of the unstrained directions of microtubule emanation from the centrosome. The crosses show for comparison the case in which 20 microtubules would emanate, when unstrained, in the directions of the vertices of a dodecahedron. The comparison shows that the simple continuous approximation, which we use in this article, is already accurate, when the number of microtubules is much lower than is typical in mammalian cells. Movie S1 in the Supporting Material shows the shape of the three-dimensional cytoskeleton at equilibrium. It is qualitatively consistent with the structure of the microtubule cytoskeleton in the nearly spherical cell bodies of lymphocytes (see, e.g., (37)). The simplicity of this case will contrast with the situation in two dimensions.

The two-dimensional case corresponds to microtubules confined in an essentially flat spatial domain, as in the thinly spread cells cultured on glass in most experiments today. The lowest-energy conformation of the microtubule cytoskeleton, in which each microtubule is in the lower-energy (stable) equilibrium form, can be computed as in the three-dimensional case. It will share the combed appearance with the three-dimensional case (see Movie S1), but this appearance is inconsistent with the images of flat cultured cells, in which neighboring microtubules are typically buckled in opposite directions (see, e.g., (7)).

In view of the observation that the centrosome in flat cells is maintained in the geometrical center of the cell outline (7,12,13), the conformation of special interest in the flat-cell case is the fully symmetric cytoskeleton (Fig. 3 A). The full symmetry in the usual cell-biological sense of the word is a reflection symmetry with respect to any axis that can be drawn through the center of the cell. (This implies an infinite-fold rotational, or circular, symmetry, but excludes the case of vortex polarization that the rotational symmetry alone would permit.) The full symmetry thus will require that the centrosome be in the cell center, that the unstrained directions of microtubules be uniformly distributed around the centrosome, and that the two directions of buckling for each unstrained direction be equally represented. It is clear that the fully symmetric conformation is an equilibrium.

Figure 3.

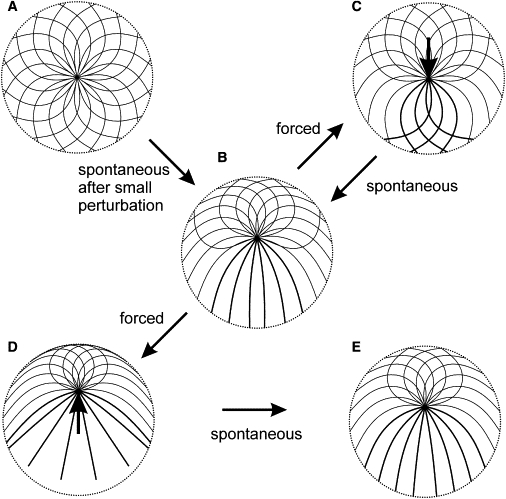
Conformations of idealized microtubule cytoskeletons in a flat cell. (A) The fully symmetric microtubule cytoskeleton. (B) The equilibrium which the fully symmetric cytoskeleton reaches spontaneously in response to a small perturbation. The perturbation in this example is an infinitesimal displacement of the centrosome upward in the plane of the image, which direction determines the final orientation of the centrosome. (C) The central centrosome position restored by application of an external force of 1.5 N EI/R² as shown (see arrow). (D) The equilibrium reached from the configuration shown in panel B, when external force 1.5 N EI/R² is applied to the centrosome in the direction away from the cell center. (E) The equilibrium reached from the configuration in panel D after removal of the external force. Curves show microtubule forms for 16 equally spaced directions of unstrained emanation from the centrosome. (There is an infinite number of such directions, and therefore microtubules, in the model, which are sampled here to show a finite number of microtubule forms in the figure.) Double-width lines show forms that are doubly represented, compared with the forms shown by the single-width lines (i.e., the double-width forms correspond to the angular density p, and the single-width forms, to p/2; see text). (Dotted circle) Cell boundary. L = 1.2 R.

Calculations show that small deviations of the centrosome from the center result in a third-power growth of the total force on the centrosome (F ∼ Δ³; see Fig. S2). This force is directed outward. Consequently, the symmetry is unstable. The new equilibrium is reached in which the centrosome is removed from the center by a distance approximately equal to the difference of the microtubule length and cell radius (Fig. 3 B and Fig. 4). Precise calculations show that it is slightly smaller than this difference, which means that unlike in the three-dimensional case, all microtubules in the flat equilibrium structure are in contact with the cell boundary and are bent. Metastable forms of microtubules gradually become lost beginning with the first inflection point on the forward branch of the force function (solid curve in Fig. 4 B). A reversal of the outward movement of the centrosome beyond this point places the system on a different branch of the force function. (In fact, there is a separate reverse branch for each reversal point in our continuous model, which makes the force function infinite-valued. A discrete model would have as many reverse branches of this function as there are microtubules, which number is in the hundreds in the typical flat cultured cell. In general, the force, according to our model, is a functional of the centrosome path.) As examples in Fig. 4 illustrate, the reverse branches are nonzero at the zero centrosome displacement. Thus, although the central position of the centrosome can be restored by forces external to the microtubule cytoskeleton, the new central position will not be an equilibrium (Fig. 3 C). The symmetry loss in response to a small perturbation proceeds spontaneously beyond the range of reversibility. One may also ask what happens if the centrosome is forced beyond the spontaneously achieved equilibrium (Fig. 3 D).

Figure 4.

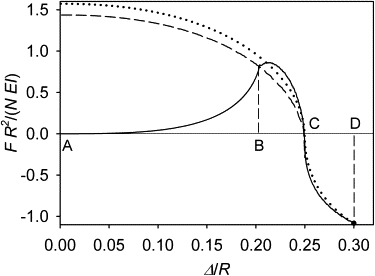
Total force exerted by the microtubules on the centrosome as a function of the centrosome position in a flat cell. (Solid curve) Branch traced in the course of a continuous displacement of the centrosome away from the cell center, starting in the fully symmetric state of the cytoskeleton (from A to D). It can also be traced in the reverse direction, but only between A and B. (Dashed curve) Branch traced during forced reversed displacement of the centrosome, starting at the eccentric equilibrium position (from C to A). (Dotted curve) Branch traced during reversed displacement of the centrosome, starting at the distance of 0.3 cell radii (from D to A). L = 1.25 R. This is a plot of F as a function of Δ, with the argument and the value of the function normalized to N, R, and EI in order to show the parameter-independent behavior of the nondimensionalized model.

Calculations show that the reverse branches from beyond the equilibrium point pass very close, within 1%, of the original equilibrium (see the example in Fig. 4). Therefore, the irreversible effect of the perturbation will not be detected by recording the centrosome position, and the eccentric equilibrium position of the centrosome in flat cells may be called stable for practical purposes. Even though the centrosome position is almost precisely restored after removal of the external force, forcing the centrosome farther away from the center leaves an irreversible trace in the cytoskeleton structure (Fig. 3 E). Taken together with the irreversible loss of symmetry in response to infinitesimal perturbations of it, this leads to a generalization that the equilibrium form of a microtubule cytoskeleton confined in a flat cell exhibits memory of past perturbations.

Centrosome position as a function of length in flat cells

To expand on the observation from the force plot that the equilibrium distance of the centrosome from the cell center in the flat case is approximately equal to the difference of the microtubule length and cell radius, the diamonds in Fig. 5 plot the positions to which the centrosome moves spontaneously in response to small perturbations of the fully symmetric cytoskeleton with the given ratio of the microtubule length to the cell size. The plot demonstrates that although the above relationship is not exact, it is a useful approximation. The sample points comprising this plot are not connected by a curve in Fig. 5, because each is a result of a separate process of relaxation from the fully symmetric state. Because of the already noted strong nonlinearity, the system will not move from one of these points to the other, when the microtubule length is varied continuously.

Figure 5.

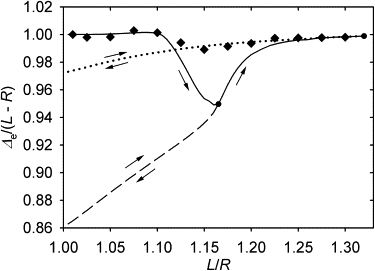
Equilibrium position of the centrosome as a function of microtubule length in a flat cell. (Diamonds) Position reached spontaneously after a small perturbation of a fully symmetric cytoskeleton. (Solid line) Evolution of the equilibrium position of the centrosome in the course of a continuous elongation of microtubules. The other two lines show the evolution of the equilibrium position in the course of shortening that starts from the two selected reversal points on the solid curve.

For comparison, the result of a continuous tuning of the equilibrium by varying the length is shown in Fig. 5 by continuous curves. The solid one corresponds to microtubule elongation. Two sample reverse branches of this function are also shown, which correspond to shortening from the two sample reversal points. Although all equilibrium distances from the center lie close to the difference of the microtubule length and cell radius, a hysteresis of the equilibrium centrosome position as a function of the microtubule length is observed (Fig. 5). Fig. S3 illustrates the underlying cause: elongation of microtubules expands the range of unstressed microtubule directions for which metastable forms no longer exist. The metastable forms lost during elongation are not restored during shortening, and this affects the equilibrium position of the centrosome: it does not return to the same position that it had when the length had the same value during elongation. Fig. 6 illustrates that the equilibrium cytoskeleton as a whole exhibits memory of the past variations of the microtubule length. Considering these results in toto, one may observe that the centrosome position can be controlled approximately linearly and reversibly by varying the microtubule length, despite the irreversibility of the evolution of the overall cytoskeleton form.

Figure 6.

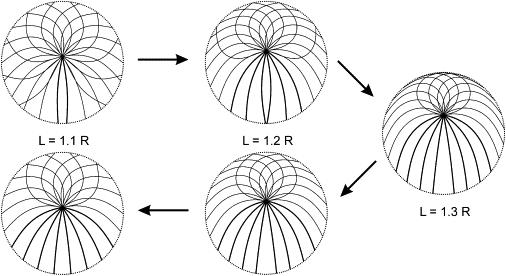
Equilibrium forms of a microtubule aster in a flat cell during elongation and subsequent shortening of the microtubules. Plotting conventions as in Fig. 3.

Discussion and Conclusions

New theoretical conclusions

Our analysis demonstrates that the asymmetry of a microtubule cytoskeleton will arise from the instability of the symmetric equilibrium due to the microtubule bending elasticity alone. The bending elasticity of microtubules is a property of any microtubule cytoskeleton. The asymmetries observed in the experiments (2–18) and in previous simulations that incorporated the bending elasticity (20,25,27,29), therefore, cannot be attributed to the other factors that also were at work: to asymmetry of the unstrained configuration of the cytoskeleton itself; to external asymmetries; to stochasticity; or to other forces. Instead, asymmetry in the light of our analysis should be viewed as inevitably arising in any confined microtubule cytoskeleton, insofar as its microtubules bend.

Our formal stability analysis of the symmetric state supports the cited previous theories that predicted emergence of asymmetry (20,24,25,27,29). Our simple model also allowed us to identify the one factor in the previous multifactorial models, which alone would be sufficient for such emergence, namely the microtubule bending elasticity. Our analysis at the same time shows that the equality of forces from buckled microtubules on different sides of the centrosome in the symmetric case (26) is not sufficient to predict the symmetry, because in two and three dimensions this equilibrium will be unstable.

Compared with the existing theory of confined microtubule asters shaped by microtubule bending elasticity alone (24), we believe the key new feature of our analysis was specification of the centered symmetric equilibrium conformation. It made possible the formal stability analysis of such a state. It also led to the recognition that the asymmetric equilibrium established in flat cells does not in general correspond to the absolute energy minimum that the original theory (24) considered. Instead, the asymmetric equilibrium displays special stability properties and history-dependence. This accounts for the different prediction that our model gives for the coefficient of approximate proportionality between the equilibrium distance of the centrosome from the center and the difference of the microtubule length and cell radius.

Our analysis predicts a coefficient of 1, whereas the initial slope in the energy-minimum theory (24) was close to 1.5 (before the function plateaued with the centrosome approaching the boundary). Extending this analysis to three-dimensional cells, we find that the asymmetric equilibrium in this case corresponds to the absolute energy minimum, and compute the coefficient of the approximate proportionality as equal to 2. The pioneering theory (24) put forward an argument that the instability of the centered position should be stronger in three dimensions than in two. We were able to demonstrate that in two dimensions, the instability is third-order, and in three dimensions it is of a special kind: infinitesimal displacements lead to a finite force.

Comparison with experiments

The case of the spherical cell in our model reproduces the salient features of the lymphocyte structure, namely the eccentric position of the centrosome and the combed arrangement of the microtubules (see, e.g., the three-dimensional reconstructions by Kuhn and Poenie (37)). This lends further support to the view that the microtubule cytoskeleton in these cells adopts the minimum-energy conformation, whereas the antigen-mediated conjugation with another cell provides the external reference frame with respect to which the other forces may orient the constitutively asymmetric microtubule aster (20,27).

As was mentioned above, whereas the experimental studies on lymphocytes concentrated on specific orientation (5,6,16,17,20–23,28) of the constitutively eccentric centrosome with respect to the other cell with which the lymphocyte is conjugated, the issue of central-versus-eccentric positioning of the centrosome was addressed as such in studies on flat cultured cells (2–4,7,12,13) and on biochemically reconstructed microtubule cytoskeletons in artificial chambers (18,25). Our model predicts that in a flat arrangement, the deviation of the centrosome from the center under the action of microtubule elasticity alone should be equal approximately to the difference of the microtubule length and the radius of the confining boundary, and that in three dimensions it should be, approximately, twice as large.

Direct comparison with experiments is not possible due to the lack of measurements that would provide the required information. Our theoretical results call for such measurements in the future experiments. Also, the number of microtubules in the biochemical reconstruction experiments (e.g., (18,25)) has been small, because of which the specific distribution of the few microtubules around the artificial centrosome, and their specific individual lengths, appear to affect the positioning greatly. From the published images, it appears that central positioning in the terminology of the in vitro reconstruction work at times referred to a degree of eccentricity that might be significant in the above quantitative frame of reference that our model has set.

Similarly, in the absence of measurements, it is not clear whether the terminology of central-versus-eccentric positioning is consistent between our new, to our knowledge, quantitative framework and the one that was used to qualitatively classify the positions of centrosomes in flat cultured cells in the cited work. The one experimental report (7) that specifies the deviation from the center that was still considered as insignificant sets this distance at 5 μm. Although the microtubule length and the cell size measurements are not at the same time reported, from the images one might judge the above magnitude of deviation as potentially comparable with the one that could be predicted by our model as the eccentric equilibrium. The notion that the centrosome is positioned in the geometric center of flat cells (7,12,13), contrary to the prediction of our model, should be reexamined by means of measurements done in the quantitative framework set by our model.

The nondimensional form in which the model results are presented here captures the parameter-independent behavior of the model. It permits derivation of specific quantitative predictions whenever specific parameter values are known, using only arithmetic. An example of such derivation, with concrete predictions for a potential experiment with an optical trap, is given in the Supporting Material.

Limitations and generalizability

The specific calculations in this article depended on the idealizations that were made in constructing the model. Some of the conclusions from the computational examples do not depend on these idealizations, and others do, yet without detriment to their applicability in research practice. The adequacy of the beam equation, which predicts the simple Euler forms of buckling, for intracellular microtubules is not universal in the light of observations of high-frequency buckling (38). It may be expected that the qualitative conclusions pertaining to the properties of symmetry, stability, and reversibility that our simple model has illuminated do not depend on how simple the buckled form is. At the same time, the simple buckling forms compatible with our model are also abundant in cells, as the images in the cited articles will attest (e.g., in (7,12)). Microtubules as semiflexible polymers undergo thermal fluctuations (see (36)), a fact that found its use in measurements of microtubule rigidity in vitro (e.g., (39)) and was incorporated in models of centrosome positioning (29).

Here we do not model fluctuations about the deterministic equilibrium, but expect the thermal fluctuations to be among those responsible for the deviations from it. Because according to our analysis infinitesimal perturbations of the fully symmetric conformation are amplified irreversibly, thermal forces are not necessary for the emergence of asymmetry, even though they may contribute to it. One of the strongest assumptions of our model is that all microtubules in the cell are of the same length.

Our conclusion that the symmetry is unstable due to microtubule elasticity alone is important for the interpretation of experiments on real cytoskeletons and of more complex, less idealized models, as discussed above. Although so broadly applicable, this theoretical principle could not be arrived at without the above idealization, which was required to conduct a formal stability analysis of the full symmetry of a confined microtubule aster. The conclusion that the evolution of the microtubule aster is in general irreversible should apply directly to more complex, realistic cytoskeletons. It does not depend on the simplicity of the aster structure in the computational examples shown, but only on the presence of metastable microtubule forms, which feature in our simulations is realistic, as discussed above. As an example of generalizability of the model, the Supporting Material contains a computation of the eccentric equilibrium in the case where microtubules in the model cell do not all have the same length, but a distribution of lengths.

Summary

The model establishes a qualitative difference between the flat and three-dimensional cases. Consistently with the experiment, the aster in three dimensions adopts the combed conformation, in which all microtubules are buckled in the same direction. Their distal (plus) ends are bent away from the direction of the centrosome displacement from the cell center. This kind of aster structure is memoryless: the directions of microtubule buckling remain the same if the centrosome is moved by external forces or if the microtubule length changes, and there is only one equilibrium centrosome position for the given microtubule length.

In contrast, and again consistently with the experiment, the microtubules in the two-dimensional (flat) equilibrium aster can be bent in both directions from the unstrained direction of their emanation from the centrosome. This gives the aster an uncombed appearance, and is at the source of the memory effects exhibited by such an aster: its structure depends on past perturbations, and the equilibrium position of the centrosome depends on the history of the microtubule length changes. The principles of the irreversible evolution and of the intrinsic instability of symmetry of the confined aster of elastic microtubules should be taken into consideration in the design and analysis of more general models and future experiments.