Modeling the Self-Organization Property of Keratin Intermediate Filaments

Abstract

Keratin intermediate filaments (IFs) fulfill an important function of structural support in epithelial cells. The necessary mechanical attributes require that IFs be organized into a crosslinked network and accordingly, keratin IFs are typically organized into large bundles in surface epithelia. For IFs comprised of keratins 5 and 14 (K5, K14), found in basal keratinocytes of epidermis, bundling can be self-driven through interactions between K14's carboxy-terminal tail domain and two regions in the central α-helical rod domain of K5. Here, we exploit theoretical principles and computational modeling to investigate how such cis-acting determinants best promote IF crosslinking. We develop a simple model where keratin IFs are treated as rigid rods to apply Brownian dynamics simulation. Our findings suggest that long-range interactions between IFs are required to initiate the formation of bundlelike configurations, while tail domain-mediated binding events act to stabilize them. Our model explains the differences observed in the mechanical properties of wild-type versus disease-causing, defective IF networks. This effort extends the notion that the structural support function of keratin IFs necessitates a combination of intrinsic and extrinsic determinants, and makes specific predictions about the mechanisms involved in the formation of crosslinked keratin networks in vivo.

Introduction

Intermediate filaments (IFs) provide structural and mechanical support vitally important to maintenance of cell and tissue integrity under stress. This function is provided by the protein products of a large number of IF genes (>70) regulated in a tissue-, differentiation-, and context-dependent fashion (1,2). In vitro studies established that IFs must be crosslinked into a network in order to generate the elasticity and mechanical properties (3,4) consistent with their mechanical support role in living cells (5,6). This principle also applies to actin microfilaments (7) and more generally to fibrous polymers (8).

Epithelial cells express type I and type II IF genes, whose protein products copolymerize to form 10-nm-wide IFs in their cytoplasm. Experimentally, various types of keratin IFs are able to self-organize into crosslinked networks at subphysiological concentrations (3,4,9), and it has been suggested that this unique property contributes to their structural support role in vivo (e.g., (10–12)). In vitro, self-organization of keratin IFs is promoted by addition of subphysiological amounts of salt or slight alkalinization of the assembly buffer conditions (3,4,11,13). For IFs composed of the type II keratin 5 (K5) and type I keratin 14 (K14), which are characteristic of progenitor basal cells in epidermis and related stratified epithelia (14,15), self-organization into crosslinked networks is mediated by the binding of the distal 25 amino acids in K14's C-terminal tail domain to two distinct regions in the central rod domain of K5, in vitro and in vivo (11,12). These crosslinking-promoting determinants operate independently from those driving 10 nm IF assembly (12).

A number of fundamental questions remain about the pathway through which cis-acting determinants exposed at the keratin IF surface can promote crosslinked network formation. Here we use theoretical principles and computational modeling to investigate the nature of the contribution of these determinants, and assess their role relative to extrinsic forces. The model attained as a result of our efforts makes clear predictions about the requirements for IF crosslinking and the specific contribution of intrinsic determinants. It also extends experimental evidence and provides a theoretical framework from which to assess how mutations in IF proteins can engender cell fragility and acute susceptibility to mechanical trauma.

Materials and Methods

Description of the model

For the time evolution of filament configurations, we employ Brownian dynamics simulation for rigid bodies. The dynamic equation, known as the Langevin equation, is written as

$$\Gamma \mathit{\xi }=\mathbf{F}+{\mathbf{F}}_R\left(t\right),$$ (1)

where

$$\mathit{\xi }={\left[{\mathit{\omega }}^T,{\mathbf{v}}^T\right]}^T$$

denotes the velocity of individual filaments. The values ω and v denote the angular and linear velocity of a rigid rod, respectively. Here,

$$\mathbf{F}={\left[{\mathit{\tau }}^T,{\mathbf{f}}^T\right]}^T$$

denotes the torque τ and the force f applied on the rigid filament. Random excitation term by thermal fluctuation is denoted as F_R(t). The property of F_R(t) is expressed as (16)

$$\langle {\mathbf{F}}_{R,i}\left(t\right),{\mathbf{F}}_{R,j}\left(t^{\prime }\right)\rangle =2k_{\text{B}}T{\delta }_{ij}\delta \left(t-t^{\prime }\right)\Gamma ,$$ (2)

where Γ denotes the damping coefficient matrix for the rigid rod. The values δ_ij and δ (t − t′) denote the Kronecker δ and the Dirac δ-function, respectively. The values k_B and T denote the Boltzmann constant and the absolute temperature, respectively. Additional details are provided in the Supporting Material.

Kinetics of tail domain binding

Because there is only scant information available on the binding of the K14 tail domain to its binding sites on K5-bound filaments (12), we opted to use a coarse-grained description. For association, we approximated the binding energy using the quadratic form

$$U=\frac{1}{2}k{\left(d-d_0\right)}^2,$$ (3)

where d denotes the distance between a tail domain on one filament and a binding site on the other filament (or the distance between two sticky points on the two filaments) and d₀ denotes intrinsic distance or distance between two sticky points in the energetically favorable configuration. We also define the cut-off distance, d_cutoff, for the tail domain binding. A tail domain and a binding site are considered bound through a spring of stiffness k when the distance between them is within the cut-off distance. This represents the simplest assumption for the binding event, which may include complicated processes such as conformational changes in the participating binding domains. This cut-off distance can also be used in the determination of stiffness. Details on how to obtain k are provided in the Supporting Material.

Dissociation events are described with the dissociation rate constant k_off, independently of the association events. We used the Gillespie's algorithm (16) for this matter. This algorithm is applied to the tail domains that are currently in a bound state. First, we generate one random number Y that follows the uniform distribution for one bound tail domain. Dwell time for the bound state τ_bound, or time for the tail domain to stay bound to its binding site, is computed as

$${\tau }_{\text{bound}}=-\frac{1}{k_{\text{off}}}\ln Y.$$ (4)

If τ_bound < Δt, then the tail domain detaches at the next step. If τ_bound > Δt, then the tail domain is treated as bound.

Hardware and software

All simulations performed in this study were done using MATLAB (Ver. 7.9, R2009b; The MathWorks, Natick, MA) software on a desktop PC computer (Core i7 CPU, 2.67 GHz).

Results

Modeling parameters and assumptions

We start with considering the experimental environment in the study by Lee and Coulombe (12). The concentration of the keratin proteins was 1 mg/mL (18.18 μM) with >98% being polymerized into filaments under assembly-promoting conditions. The space used in actual assembly assays was very large compared to the size of individual IFs, and is impractical for modeling and computation. Therefore we chose a small cubic space of dimensions 2 × 2 × 2 μm³ for initial modeling efforts. We further assumed that each 10-nm keratin IF is 1 μm in length, which corresponds to the persistence length of IFs in solution (17), and behaves as a rigid rod.

We note that the true length distribution of individual keratin IFs integrated in filament bundles is unknown. Selecting 1 μm for filament length greatly reduces the computational cost because we can treat individual IFs as rigid rods. Moreover, there is evidence that 1 μm corresponds to the persistence length of at least some types of IFs in vitro (17). The current understanding of IF substructure suggests 700 monomers per μm length (12,18). Combining these elements, our simulations were conducted using 125 rigid filaments of 1-μm length in a 2 × 2 × 2 μm³ space.

Given the density of K14 in polymerized K5-K14 IFs (350/μm length) and the accessibility of its tail domain to proteases when in that state (12), we assumed that K14 tail domains are axially spaced 22-nm apart along filaments. This spacing is reminiscent of the 21-nm axial repeat observed for several types of IFs visualized by electron microscopy (19). We also treated each filament as a continuous line when describing binding events (i.e., we considered the distance between the centerlines of participating filaments when computing binding forces). To reiterate, each filament is modeled as a 1-μm-long rigid and thin rod with sticky points evenly spaced 22-nm apart.

The dissociation equilibrium constant K_d defining binding between K14's tail domain and K5-K14 filaments is 2 μM (11,12). The association and dissociation rate constants for this binding event are unknown. For this reason, we initially assumed maximum binding conditions (i.e., dissociation rate constant k_off = 0). This assumption seems appropriate, initially, given the goal to verify whether the tail domain-mediated crosslinking of IFs occurs under maximally permissive conditions in silico. We do not distinguish between the position of a K14 tail domain on a filament or its binding sites on K5 molecules integrated in neighboring filaments (12). Because each filament is a continuous line and the 22-nm spacing between sticky points is markedly shorter than filament contour length, a sticky point can represent either a K14 tail domain or its binding site on K5. This assumption also reflects the absence of high-resolution information about the core architecture of IFs.

We approximate the binding free energy with a quadratic form, such that tail domains bound to their cognate binding sites are considered connected by a spring of stiffness k. Only linear springs are being considered as a first-order approximation; i.e., angular effects on tail domain binding are ignored. The value used in our study is k = 0.727 pN/nm (see the Supporting Material). We assume that the intrinsic distance for the tail domain binding is equal to the diameter of keratin IFs (d₀ = 10 nm). In the energetically favored configuration, two filaments are in contact via a Velcrolike attachment involving a (K14-bound) tail domain on one filament and its (K5-bound) binding site of the other. We also assume the theoretically maximal value for cut-off distance. This is consistent with the maximum binding assumption because a maximal cut-off distance also favors the possibility of tail domain binding. Because K14's tail domain is 52-residues' long (12) and under the assumption that it can be fully exposed at the IF surface, the cut-off distance between a tail domain and a binding site is estimated to be ∼5 nm, which is converted to d_cutoff = 15 nm given the 10-nm distance between the center lines of two filaments. Note that this cut-off distance should in theory be close to the hydrodynamic diameter of IFs and, indeed, the hydrodynamic diameter of desmin IF was reported to be 16∼18 nm (20).

In the initial configuration, keratin IFs are randomly positioned and oriented in the reference space. We do not include the excluded volume, or self-avoiding effect, in the simulations. Periodic boundary conditions are applied so that the cubic 2 × 2 × 2 μm³ space represents the continuum characteristics of the whole experimental space.

Assessing the impact of tail domain binding on filament interactions

Let us first consider the case where tail domain binding events are allowed, to test whether one can observe bundlelike network configurations given the conditions detailed above. The time step in this simulation is Δt = 43.24 ns. Fig. 1 A shows the initial configuration (t = 0) where filaments are randomly distributed. Fig. 1 B shows the resulting configuration after 10⁶ steps, or t = 43.24 ms (see Movie S1).

Figure 1.

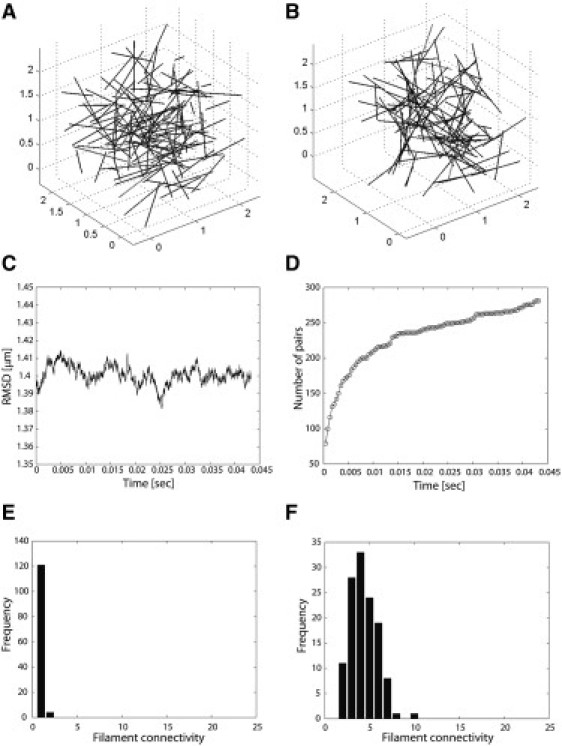
Simulation results where tail domain binding events are included. (A) Initial configuration in which 1-μm-long filaments are randomly distributed. (B) Configuration after 10⁶ steps, or 43.2 ms. (C) RMSD for translation after 10⁶ steps, or 43.2 ms. (D) Number of paired filaments after 10⁶ steps, or 43.2 ms. (E) Distribution of filament connectivity in the initial configuration. (F) Distribution of filament connectivity in the final configuration. The outcome of these simulations suggests that tail domain binding events are not sufficient to foster the formation of crosslinked networks as seen experimentally.

To assess whether the resulting configuration reaches equilibrium, we show the root-mean-square deviation (RMSD) between filament centers and number of filament pairs in Fig. 1, C and D, respectively. Here RMSD is calculated as

$$\text{RMSD}=\sqrt{\frac{1}{N}\sum _{i=1}^{N-1}\sum _{j=i+1}^N{\Vert {\mathbf{r}}_i-{\mathbf{r}}_j\Vert }^2},$$ (5)

where r_i denotes the position of the i^th filament center, and N denotes the number of filaments. These plots convey that the final configuration can be considered equilibrated. This can also be verified when tracking the temporal evolution of configurations (Movie S1).

Only partial crosslinking of filaments is achieved (Fig. 1 B and Movie S1). In the absence of an explicit tool to measure the diameter of the bundlelike crosslinked networks forming under these conditions, we calculated the connectivity among filaments, i.e., the number of filaments consecutively connected to a given starter filament. Fig. 1, in panels E and F, respectively, shows the distribution of filament connectivity in the initial and final configurations. A high connectivity number reflects a higher likelihood that the configuration achieved represents a bundlelike, crosslinked network. This metric supports the view that tail domain binding events are not sufficient to drive the formation of crosslinked networks of K5-K14 IFs, as reported in Lee and Coulombe (12).

Introducing long-range filament interactions

Available experimental evidence shows that the formation of crosslinked networks of K5-K14 IFs requires a slight alkalinization of the buffer (from pH = 7.5 to pH = 7.0), or that salt be added (3,4). Accordingly, crosslinking may require long-range interactions between filaments in addition to tail domain-mediated binding events. This notion is consistent with the short length of keratin tail domains. From this we surmise that the initial simulation conditions reflect a setting that does not promote such long-range interactions, explaining the low amount of filament crosslinking achieved.

Given the robust ionic strength dependency of interactions between keratin IFs in solution, electrostatic forces represent a possible source of long-range interactions. The van der Waals forces (21–23) and additional sources could also be involved. Because their source is unknown, we opted to approximate these long-range interactions with a quadratic energy function. Mathematically, this function is written as

$$U^{\text{f}}=\Delta G^{\text{f}}+\frac{1}{2}{k}^{\text{f}}{\left(d^{\text{f}}-d_0^{\text{f}}\right)}^2,$$ (6)

where ΔG^f, k^f, and d^f₀ denote the free energy, stiffness, and the intrinsic distance between two infinitesimal segments of filaments, respectively. When introducing a cut-off distance beyond which the force(s) driving long-range interactions have no effect, the relation between stiffness and the cut-off distance can be defined as

$$k^{\text{f}}=\frac{-2\Delta G^{\text{f}}}{{\left(d_{\text{cutoff}}^{\text{f}}-d_0^{\text{f}}\right)}^2}.$$ (7)

Thus, the hypothetical long-range interactions between filaments can be described using three parameters: ΔG^f, d^f_cutoff, and d^f₀ (see the Supporting Material for a graphical explanation). The unit of free energy is k_BT/μm², because these interactions involve two small segments in participating filaments. This approximation is sufficiently general so as to apply to any possible source of interactions with both attractive and repulsive effects.

The free energy for tail domain-mediated binding is ∼2.2 k_BT. Considering that the distance between tail domains is ∼22 nm (this study), one can extract the energy per μm² by treating this binding energy as the interaction between small segments of unit length 0.022 μm. The resulting interaction energy is ∼5 × 10³ k_BT/μm². Long-range interactions between filaments are expected to be much weaker than this.

We next repeated the simulation after adding long-range interactions and maintaining all other conditions equal (compare to Fig. 1). Fig. 2, A and B, shows some of resulting configurations after 21.6 ms with distinct sets of parameters ΔG^f, d^f_cutoff, and d^f₀. Varying these parameters amounts to varying ionic strength in the solution and assesses the associated impact on filament organization. Filament RMSD (Fig. 2, C and D) and number of paired filaments (Fig. 2, E and F) each convey the near-equilibrium state of the simulations. Fig. 2, G and H, relates filament connectivity for each set of parameters. Filament crosslinking (i.e., higher values of connectivity) is better promoted at larger magnitudes of interaction free energy |ΔG^f|. Interactions involving relatively longer intrinsic and cut-off distances result in lower filament connectivity within the networks formed. In all cases, one sees a robust trend toward the formation of a bundlelike organization of filaments (see Movie S2). Compared to the outcome reported in Fig. 1 F, the formation of crosslinked networks is markedly promoted by the introduction of long-range interactions between filaments, over a broad range of values for ΔG^f, d^f_cutoff, and d^f₀.

Figure 2.

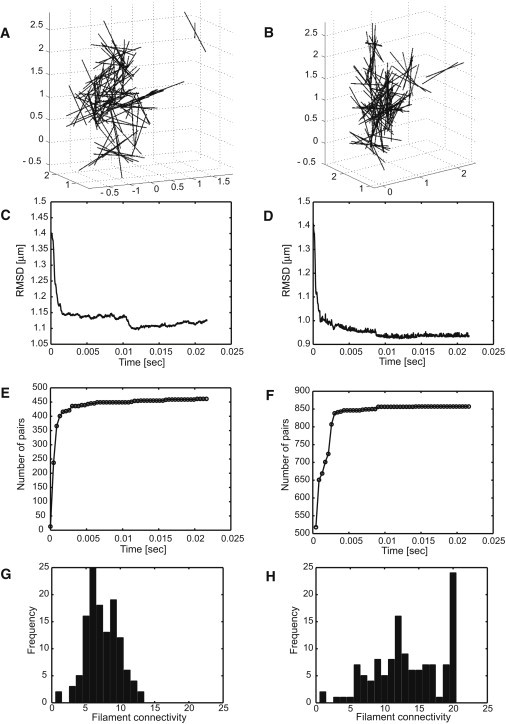
Filament configurations, RMSDs, number of paired filaments, and distribution of filament connectivity after 5 × 10⁵ steps or 21.6 ms, when including long-range interactions between filaments in addition to tail domain binding events. Simulations performed using two different sets of parameters for panels A, C, E, and G: ΔG^f = −50 k_BT/μm², $d_0^{\text{f}}=40$nm, and d^f_cutoff = 65 nm; and for panels B, D, F, and H: ΔG^f = −100 k_BT/μm², d^f₀ = 20 nm, and d^f_cutoff = 40 nm. Introducing long-range interactions brings about a robust trend toward formation of crosslinked networks over a broad range of parameters.

Impact of making tail domain-mediated interactions reversible

Until now, all the simulations reported assumed that tail domain-mediated binding events are permanent, i.e., k_off ∼0. We investigated the impact of introducing a discrete dissociation rate constant, k_off = 10 s⁻¹ (rationale presented in the Supporting Material). Given the known K_d (2 μM) for K14's tail domain binding, k_on was set at 5 μM⁻¹ × s⁻¹. The resulting filament configuration and connectivity after 2.2 ms (at near-equilibrium; data not shown) are shown in Fig. 3, panels A and C, respectively, and in Movie S3. Introducing dissociation events, even when rare, alters the topology of the resulting filament network (Fig. 3 A) but does not significantly impact the extent of crosslinking, as reflected by filament connectivity (Fig. 3 C; compare with Fig. 2). Next, the impact of lengthening filaments, from 1 μm to 2 μm, was assessed given that

• 1.In reality, the contour length of IFs seems longer than 1 μm, and
• 2.We wished to test the associated impact on network topology.

All other conditions (including rate constants for tail binding events) were maintained except that the simulation space was increased to 3 × 3 × 3 μm³ to maintain protein concentration at 18.18 μM. Under such conditions, all filaments are again integrated into a single large network (Fig. 3 B and Movie S4) in which individual filaments have formed thicker and wider bundlelike crosslinked networks, as reflected through a marked shift in connectivity (Fig. 3 D). Crosslinking of K5-K14 filaments thus can occur when the tail domain-mediated binding events are reversible; determinants such as filament length (as shown here) and filament shape (not addressed in this study) are expected to have a significant impact on the topology of the resulting filament networks.

Figure 3.

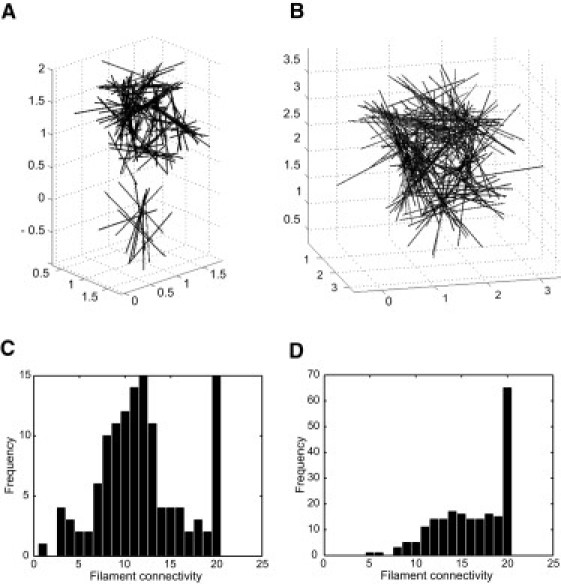
Simulation results when tail domain-mediated interactions are reversible (k_off = 10 s⁻¹). The parameters for filament interactions are ΔG^f = −100 k_BT/μm²; d^f₀ = 20 nm; and d^f_cutoff = 40 nm. (A and C) Configuration and distribution of filament connectivity after 5 × 10⁵ steps, or after 2.2 ms, respectively. (B and D) Configuration and distribution of filament connectivity when the filament length is longer up to L = 2 μm and the simulation space is increased to 3 × 3 × 3 μm³, with other parameters kept the same as in cases A and C. One can see that the introduction of dissociation events, even when rare, alters network topology (A and C) but does not much impact the extent of crosslinking. Increasing filament length leads to a single large network in which filaments form larger crosslinked networks.

The role of tail domain binding events toward network mechanical properties

To assess the role of tail domain-mediated linkages between filaments on the mechanical properties of the resulting cytoskeletal networks, we ran simulations in which forces ranging from 50 pN to 5 nN were applied to two types of assemblies: one in which filaments are dispersed (see Fig. 1 B), and another one in which most filaments are crosslinked (see Fig. 2 B). To simplify this effort, we assumed maximum tail domain binding conditions (k_off ∼0). Applying an external force affects the topology of filament networks. Plotting the stretch strain as a function of external force applied shows that the crosslinked filament network is stiffer across the range of deformation forces simulated (Fig. 4 A). This finding is consistent with rheological measurements obtained on disperse and crosslinked arrays of K5-K14 IFs in vitro (3,4). This modeling effort also highlights the nonlinear elastic behavior of IF networks, i.e., strain-hardening, which again has been seen for K5-K14 (3) and vimentin IFs (24).

Figure 4.

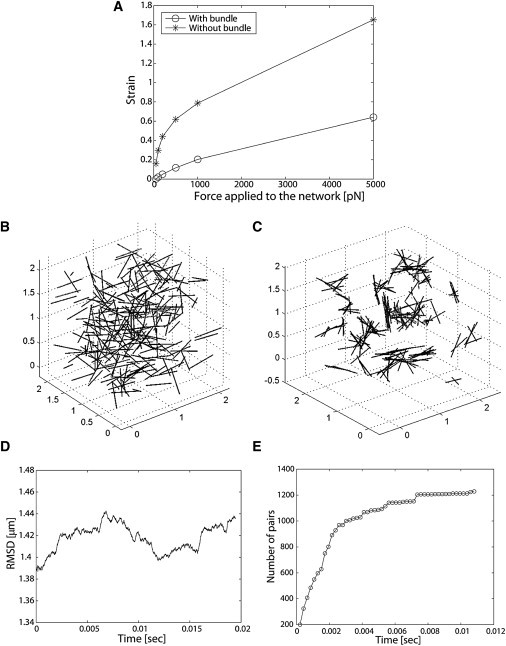
(A) Plot of strain versus force applied to the network. For simplicity, we consider additional tail domain binding events resulting from application of the external force. We also employ maximum binding conditions. The outcome shows that the crosslinked network (as shown in Fig. 2B) is stiffer than the dispersed one (as shown in Fig. 1 B). (B and C) Initial and final configurations when filament length is reduced to 0.5 μm, after 5 × 10⁵ steps (or 10.8 ms) and including tail domain binding events and long-range filament interactions (ΔG^f = −100 k_BT/μm²; d^f₀ = 20 nm; and d^f_cutoff = 40 nm). (D and E) RMSD and number of paired filaments for the cases shown in B and C, respectively. The configuration shown in panel C cannot sustain mechanical deformation due to external stress. This result conveys the fragility of epithelial cells expressing disease-causing mutations in K5 and K14.

Impact of shortening filaments on network topology and mechanical properties

A subset of Epidermolysis bullosa simplex (EBS)-causing mutations in K5 or K14 causes a dramatic shortening in keratin IF structure (25,26), engendering cellular fragility and susceptibility to trauma-induced cell lysis. We conducted simulations with 0.5-μm-long filaments to verify the impact of shortening filament length on network topology and filament connectivity. All other parameters—2 × 2 × 2 μm³ simulation space; tail binding events; long-range interactions among filaments (ΔG^f = −100 k_BT/μm²; d^f_cutoff = 40 nm; and d^f₀ = 20 nm, see Fig. 2 B)—were preserved. The initial and final configurations of the filament network are shown in Fig. 4, B and C, respectively (see Movie S5); RMSD and number of filament pairs are reported in Fig. 4, D and E.

The near-equilibrium configuration (see Fig. 4, D and E) that results from a modest shortening of filaments is akin to forming several separate copies of miniature crosslinked filament networks (Fig. 4 C), and is reminiscent of the topology of keratin networks seen in keratinocytes isolated and cultured from EBS patients (e.g., (25)). Clearly, shorter filaments cannot form a large network in which most filaments are crosslinked (compare Fig. 4 C and Fig. 3 B), even though filament pairs are achieved in greater number (by ∼75%; compare Fig. 4 E with Fig. 2 F). Subjecting this type of network to deformation, as simulated in Fig. 4 A, would generate very little elasticity and readily rupture under strain. These findings provide an additional layer of support for the modeling parameters and conclusions reached in our study.

Discussion and Conclusion

The main objectives of this study were to simulate the self-driven organization of keratin IFs into crosslinked networks, and assess the role of tail domain-mediated interactions in this process. Using factual evidence, conservative assumptions, and readily available computer hardware and software, we devised in silico conditions in which suspensions of randomly oriented K5-K14 IFs self-organize, over short periods of time, to give rise to crosslinked networks rich in bundlelike elements. Our efforts show that long-range interactions between filaments are required to initiate the formation of crosslinked networks. They suggest that the experimentally observed interactions involving K14's nonhelical domain, which given its primary structure must be small relative to 10-nm filaments (12), cannot single-handedly drive the formation of crosslinked networks. These tail domain-mediated, short-range interactions come into play, once participating filaments become sufficiently close to one another, and act to stabilize interfilament associations.

Simulations in which the K14 tail domain is deleted from filaments further support the idea that it plays a key role in self-organization of K5-K14 IFs (see Fig. S1, A and B). The model resulting from our efforts accounts for the experimentally observed impact of filament shortening on the topology and mechanical properties of K4-K15 filament networks (e.g., (3,27)), and makes specific predictions for the mechanisms involved in the formation of crosslinked networks in vivo. Because other types of keratin IFs, such as K8-K18 (4) and K1-K10 (9), manifest the property of self-organization, we believe that the significance of our finding extend beyond the K5-K14 pair.

Because it addresses a different set of issues via a distinct strategy, our study complements previous computer-based simulation efforts. Beil et al. (28,29) investigated the formation of keratin IF networks through computer simulations built upon the tessellation or Markov process. Their efforts were primarily aimed at studying the generation of branched network by 10-nm keratin filaments in a two-dimensional space, whereas our efforts were focused on the formation of crosslinked filament networks in the three-dimensional space.

Our findings show that long-range interactions between participating keratin filaments are likely essential to the formation of crosslinked networks. The source of such interactions remains to be defined. They should originate from the bulk effect. Coulombic forces represent an attractive possibility for mediating such long-range interactions. Both K5 and K14 have highly basic, or positively charged, head and tail domains. Estimated isoelectric points (PI) for the K5 head and tail domains are 11.35 and 9.37, respectively. Estimated PI values for K14's head and tail domains are 9.02 and 10.26, respectively. In contrast, the central rod domains of K5 and K14 show an overtly acidic character (estimated PIs of 5.06 and 4.74, respectively) and should be negatively charged at physiological pH. Given such features, a repetitive pattern of positive and negative charges should occur at the surface of K5-K14 IFs, thereby promoting electrostatic interactions between them. Another possible source is van der Waals interactions which, when of a repulsive nature, play an important role in the equilibrium structure of simple liquids (30). These two types of forces, Coulombic and van der Waals, can also act in combination to give rise to the stable lattice structure seen in crystalline gels of rodlike tobacco mosaic virus (22). There are additional possibilities for long-range forces, as suggested from theoretical considerations of the structure of striated muscle (31).

Well-documented cellular processes are poised to contribute to bring keratin IFs in suitably close proximity to allow for tail domain-mediated interactions to promote the formation of bundles. One such process is the attachment of keratin IFs at high density at sites of cell adhesions, whether of the cell-cell (e.g., desmosomes) or the cell-matrix (e.g., hemidesmosomes) variety (32). Another one is the continuous centripetal movement of keratin IFs from the periphery of epithelial cells, where 10-nm filaments are believed to be born, toward the proximity of the centrally-located nucleus, where they are believed to turn over via disassembly (e.g., (33,34)). Live imaging studies documenting this phenomenon show that keratin IFs interact along their lateral surfaces to form large bundles as they are moving inwardly in an actin-dependent fashion (35). Another process of interest is cellular stretching, which brings keratin IFs in close proximity and promote the formation of bundles that persist well-beyond cessation of the stretch force applied (36). These are examples of bona fide cellular processes that could play a role in bringing neighboring filaments within the close physical range necessary for short-range forces, such as those mediated by K14's tail domain, to be put to use toward the formation of stable crosslinked networks. Further experimentation and modeling can help assess whether these phenomena assist the long-range component of filament-filament interactions during the formation of crosslinked networks.

Additional observations point to an important contribution from the nonhelical C-terminus of IF proteins to the properties of assembled IFs in vivo (37). For instance, partial or complete deletion of K5's tail domain causes filament shortening (13,27). EBS-causing, frameshift mutations altering the sequence of K5's tail domain exhibit similar defects, suggesting that the tail participates in determining IF length (see (38) for related findings on NF-L). When such mutants are expressed in epithelial cells, they typically give rise to aggregates in the cytoplasm. In addition, the severe EBS-causing R125C hot-spot mutation located within the 1A domain of K14 exhibits a similar phenotype, consisting of shortened 10-nm IFs in vitro and numerous aggregates in the cytoplasm of transfected cells. Whereas such mutations in the K5 tail domain and K14 rod domain likely affect 10-nm filament formation in a distinct fashion, dramatically shortened filaments represent a common end point. Our modeling efforts involving shorter filaments thus provide a conceptual basis for how such mutations result in the formation of small aggregates, and give rise to fragile cytoskeletal networks, in vivo.

The observed property of self-organization occurs at semidilute concentration of filaments in solution (3,10), and distinguishes keratin IFs from F-actin and microtubule polymers. F-actin also functions as crosslinked networks but utilizes a broad variety of cellular proteins to achieve various network configurations (24). For both the K5-K14 and K8-K18 keratin pairs, filament crosslinking can be achieved through cis-acting determinants (4). Simulations in which K14's tail domain is treated as a free (soluble) entity, under otherwise identical conditions, fail to yield crosslinked network configurations (Fig. S2, A–G). This latter finding highlights the importance and the significance of having the crosslinking determinants covalently attached to the protein, and underscores how the unique modular domain makeup of keratin proteins likely serves their support function in vivo.