Absolute Protein-Protein Association Rate Constants from Flexible, Coarse-Grained Brownian Dynamics Simulations: The Role of Intermolecular Hydrodynamic Interactions in Barnase-Barstar Association

Abstract

Theory and computation have long been used to rationalize the experimental association rate constants of protein-protein complexes, and Brownian dynamics (BD) simulations, in particular, have been successful in reproducing the relative rate constants of wild-type and mutant protein pairs. Missing from previous BD studies of association kinetics, however, has been the description of hydrodynamic interactions (HIs) between, and within, the diffusing proteins. Here we address this issue by rigorously including HIs in BD simulations of the barnase-barstar association reaction. We first show that even very simplified representations of the proteins—involving approximately one pseudoatom for every three residues in the protein—can provide excellent reproduction of the absolute association rate constants of wild-type and mutant protein pairs. We then show that simulations that include intermolecular HIs also produce excellent estimates of association rate constants, but, for a given reaction criterion, yield values that are decreased by ∼35–80% relative to those obtained in the absence of intermolecular HIs. The neglect of intermolecular HIs in previous BD simulation studies, therefore, is likely to have contributed to the somewhat overestimated absolute rate constants previously obtained. Consequently, intermolecular HIs could be an important component to include in accurate modeling of the kinetics of macromolecular association events.

A variety of theoretical and computational approaches have been used to rationalize and predict experimentally observed rates of protein-protein association (see (1) for a comprehensive review). One common approach is to use Brownian dynamics (BD) simulations (2) to determine the rate constant for association by explicitly simulating thousands of encounter trajectories for the two binding partners (3); this approach has been successfully used to model the association kinetics of a number of protein-protein complexes (see, e.g., (4–6)). Although faster approaches, such as those based on calculating electrostatic interactions in the native complex (1), have proven equally adept at predicting the effects of charge-mutations on binary association rate constants, the BD method has the advantage of being readily extended to the modeling of multimolecular processes (7). Recent BD studies of protein-protein associations in crowded conditions (8), and of protein diffusion in a model of the bacterial cytoplasm (9), provide indications of the applicability of the method to complex systems.

A common element in previous BD studies of protein-protein association kinetics has been to neglect hydrodynamic interactions (HIs) between the two approaching partners (4–6). This omission can be justified in part by the fact that the effects of HIs predicted by theory (10–12) are comparatively modest: Wolynes and Deutch (12), for example, predict that the inclusion of HIs should decrease the rate constants for the association of uncharged spheres by ∼30%, but cause less of an effect (∼20%) on the association of oppositely-charged spheres. Shusin's (13) more recent analysis predicts that short-range HIs can reduce rate constants for the association of nonspherical models by ∼3–5-fold. The applicability of these predictions to real protein-protein association reactions has not yet been established; the only BD-based studies of association kinetics that we are aware of have modeled a prototypical enzyme-substrate reaction using rigid dumbbells to model the binding partners (e.g., (14)). This work attempts to provide a more complete examination of the effects of intermolecular HIs by considering their role in determining the association rate constant of the barnase-barstar complex, a paradigm for electrostatically accelerated protein-protein association (15). Specifically, we compute rate constants for the association of barstar with wild-type barnase and three charge-mutants, both in the presence and absence of intermolecular HIs.

One major reason that previous atomically detailed BD studies of this system (e.g., (4,6)) have omitted HIs is that they are extremely expensive to compute. In the simplest implementation, the cost of calculating the correlated random displacements required of HIs scales as N³, where N is the number of moving particles in the system; because obtaining rate constants from BD simulations requires computing many thousands of independent binding trajectories (3,4), the total computational costs can be formidable. This is especially so if—as is the case here—flexible protein models are used. A number of innovative attempts have been made to accelerate the calculation of HIs in BD simulations (e.g., (16)), but here we opt for the simpler approach of reducing the number of particles in the simulation by simplifying the structures of the participating molecules, i.e., by coarse-graining them. We model barnase (110 residues) with 33 pseudoatoms, and its partner, barstar (89 residues) with 27 pseudoatoms; these pseudoatoms are evenly distributed within each protein's volume using the q_pdb utility in the SITUS suite of programs (17). The resulting arrangements nicely capture the characteristics of each protein's shape (Fig. 1); covalent bonds between pseudoatom pairs ensure that this shape is retained during simulations.

Figure 1.

Atomic barnase (blue)–barstar (red) complex superimposed on pseudoatomic model.

Use of so few pseudoatoms is a significant simplification; therefore, prior to exploring the effects of including intermolecular HIs on the rates of barnase-barstar association, we must first ask the following question: Can simplified models, that retain only the basic shape and electrostatic properties of their parent proteins, produce accurate estimates of rate constants for protein-protein association reactions?

This question has been answered by performing BD simulations conceptually similar to those reported previously (4–6). Full details of our methods are provided in the Supporting Material, but there are essentially three key differences from previous approaches. First, we replace the rigid atomic models used in prior studies with flexible, pseudoatomic models. Second, because each pseudoatom has its own diffusive characteristics, we include intramolecular HIs in the BD simulations even when we neglect the proteins' intermolecular HIs. We do this because we have shown previously that flexible protein models simulated in the absence of explicit solvent diffuse far more slowly than is realistic, unless intramolecular HIs are included (18). In preliminary simulations we have verified that the translational and rotational diffusion coefficients of our pseudoatomic models agree well with those predicted for barnase and barstar by the hydrodynamics program HYDROPRO (19; see Table S1 in the Supporting Material). Third, we have chosen to define reaction criteria using terminology borrowed from the protein-folding simulation community (20): a successful complex is assumed to occur when the fraction of native intermolecular contacts formed by the complex, Q, reaches some threshold value, Q_rxn (see the Supporting Material for a definition of the native contacts). One key feature that is retained from previous BD studies (e.g., (4,6,7,9)) is the requirement that the pseudoatomic models be capable of adequately reproducing the electrostatic potentials generated by their all-atom parent structures; this is done using the effective charge method (21). Importantly, the effective charges are the only simulation parameter that differs between the wild-type barnase model and its mutants.

From simulations of the wild-type barnase-barstar association—in the absence of intermolecular HIs—we find that the experimental rate constant (2.86 × 10⁸ M⁻¹ s⁻¹; (15)) is reproduced when a threshold, Q_rxn = 0.47, is used. When this same threshold is applied to simulations of the R59A, R87A, and E60A barnase mutants, the computed absolute rate constants are in good agreement with experiment (Fig. 2; open symbols): r² = 0.99 for the three mutant data points. Even highly simplified structural models, therefore, can reproduce—with high accuracy—the effects of single residue charge mutations on association rate constants.

Figure 2.

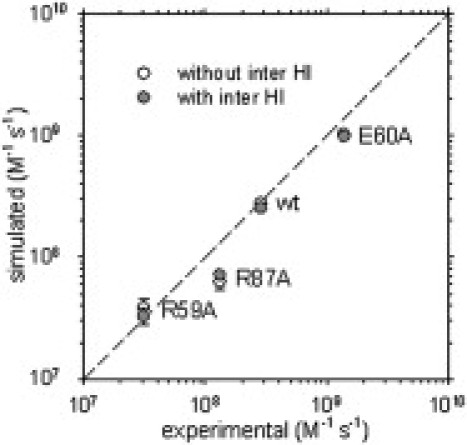
Comparison of BD-simulated and predicted rate constants for barnase–barstar association.

Having shown that the simplified pseudoatomic protein models work well for the barnase-barstar system, we can now ask: what is the effect of including intermolecular HIs between the associating protein models?

From simulations of the wild-type barnase-barstar association—in the presence of intermolecular HIs—we find that the experimental rate constant is reproduced when a threshold, Q_rxn = 0.32, is used. When this threshold is applied in simulations of the three mutants, the computed rate constants are again in very good agreement with experimental measurements (Fig. 2; solid symbols). The inclusion of intermolecular HIs, therefore, has no discernable effect on the simulation model's ability to reproduce the relative effects of charge-mutations on association rate constants.

For a fixed value of Q_rxn, however, the inclusion of intermolecular HIs has a significant impact on the computed rate constants. This can be seen in Fig. 3, which plots the ratio of the rate constants calculated with and without intermolecular HIs as a function of Q_rxn. Clearly, the inclusion of intermolecular HIs causes a decrease in the computed rate constants for all values of Q_rxn: for the values of Q_rxn that produce good estimates of the absolute association rate constants (0.32 < Q_rxn < 0.47), the inclusion of intermolecular HIs slows the association rate constant for the wild-type complex by 70–80%, and even for the smallest measureable threshold (Q_rxn = 0.029), the decrease in rate constant is ∼35%. These decreases in rate constants are similar to those predicted theoretically (12,13). Importantly, they may explain in part why previous BD simulation studies—that neglected intermolecular HIs—consistently overestimated the absolute values of association rate constants (see, e.g., (4–6)).

Figure 3.

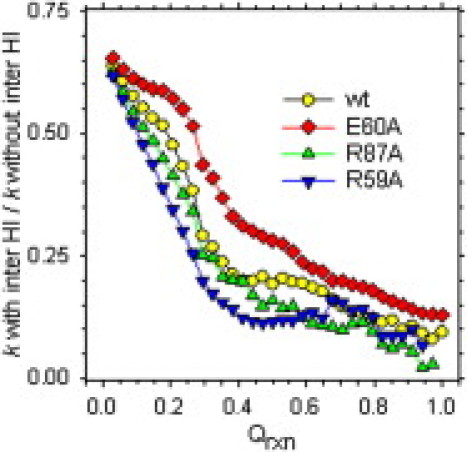
Ratio of rate constants calculated from simulation with and without intermolecular HIs.

Interestingly, a comparison of the behavior of the various charge-mutants shows that the impact of intermolecular HIs is more pronounced on the slower associating mutants: for Q_rxn = 0.32, the rate constant of the fastest associating mutant (E60A) is decreased by a factor of only ∼2.5, whereas that of the slowest associating mutant (R59A) is decreased by a factor of ∼5. Again, this effect is qualitatively consistent with theoretical predictions for charged sphere-sphere association (11,12). It is to be anticipated that the effects of intermolecular HIs might be even more pronounced in complexes whose association is not driven by any complementary electrostatic interactions (e.g., (5)). Unfortunately, computational costs currently prevent us from obtaining statistically robust estimates for the (hypothetical) association of barnase and barstar in the complete absence of electrostatic interactions. We have, however, performed simulations of the wild-type barnase-barstar association in 500 mM salt and obtained, as reported in previous studies (see, e.g., (4–6)), good qualitative agreement, but poor quantitative agreement with experiment (see the Supporting Material).

In summary, we have shown here that a), simple molecular models can accurately reproduce the association rate constants for the model barnase-barstar system; b), the inclusion of intermolecular HIs decreases the computed association rate constants, an effect that becomes more pronounced as the threshold for defining association becomes more stringent; and c), these effects of intermolecular HIs appear greater in those mutants that have weaker attractive electrostatic interactions driving association.

When absolute association rate constants are required, therefore, intermolecular HIs may be important to include; this may be especially true in attempts to study nonelectrostatically driven macromolecular associations.