Single Molecule Diffusion of Membrane-Bound Proteins: Window into Lipid Contacts and Bilayer Dynamics

Abstract

Membrane targeting proteins are recruited to specific membranes during cell signaling events, including signals at the leading edge of chemotaxing cells. Recognition and binding to specific lipids play a central role in targeting reactions, but it remains difficult to analyze the molecular features of such protein-lipid interactions. We propose that the surface diffusion constant of peripheral membrane-bound proteins contains useful information about protein-lipid contacts and membrane dynamics. To test this hypothesis, we use single-molecule fluorescence microscopy to probe the effects of lipid binding stoichiometry on the diffusion constants of engineered proteins containing one to three pleckstrin homology domains coupled by flexible linkers. Within error, the lateral diffusion constants of these engineered constructs are inversely proportional to the number of tightly bound phosphatidylinositol-(3,4,5)-trisphosphate lipids. The same trend is observed in coarse-grained molecular dynamics simulations and hydrodynamic bead calculations of lipid multimers connected by model tethers. Overall, single molecule diffusion measurements are found to provide molecular information about protein-lipid interactions. Moreover, the experimental and computational results independently indicate that the frictional contributions of multiple, coupled but well-separated lipids are additive, analogous to the free-draining limit for isotropic fluids—an insight with significant implications for theoretical description of bilayer lipid dynamics.

Introduction

Membrane targeting protein domains are key components of many cell signaling pathways. These domains typically mediate the selective recruitment of proteins to specific membrane surfaces upon accumulation of a second messenger, such as Ca²⁺ or a signaling lipid (1–6). Because these domains can have a variety of target lipids and modes of recruitment, it is perhaps not surprising that many full-length proteins contain multiple membrane targeting domains, for example multiple pleckstrin homology (PH) or C2 domains (2,7–11). Binding of these multiple membrane targeting domains to more than one target lipid is essential for proper targeting and regulation, as illustrated by conventional protein kinase C isoforms that require three lipids (phosphatidylserine, phosphatidylinositol-4,5-bisphosphate, and diacylglycerol) for specific plasma membrane targeting and full kinase activation (12–15). The recognition of multiple lipid targets has been hypothesized to be essential for rapid, specific membrane targeting, and for cooperative enhancement of target membrane affinity (2,14,16–19).

Central to understanding the recruitment of membrane targeting proteins, as well as the protein-lipid interactions of peripheral membrane proteins in general, is the ability to measure the number of high affinity protein-lipid contacts under a given set of conditions. If this stoichiometry can be measured for bilayers of different lipid composition, it should be possible to directly determine the number and types of target lipids bound by a given peripheral protein. Current methods for determining lipid binding stoichiometry typically involve measurements of:

• 1.Domain binding to membrane-associated lipids that are difficult to extend to multidomain proteins;
• 2.Domain or full protein binding to soluble lipids or lipid headgroups for which the loss of bilayer constraints may alter the binding geometry and stoichiometry; or
• 3.Protein activity in the presence of varying membrane-bound or soluble lipids that provides only indirect information on lipid stoichiometry.

Recently we used single molecule total internal reflection fluorescence microscopy (TIRFM) to examine the lipid dependence of protein lateral diffusion on bilayers (20). Our findings led us to hypothesize that lateral diffusion is highly sensitive to protein-lipid contacts, and that quantitation of diffusion constants could represent a powerful new tool for the analysis of lipid binding stoichiometry.

To test this hypothesis, here we systematically analyze the dependence of the lateral diffusion constant on the number of tightly bound lipids for a representative peripheral membrane protein. The model system is the PH domain of the general receptor for phosphoinositides, isoform 1 (GRP1, also known as cytohesin 3). When bound to a target membrane, GRP1 PH domain binds tightly to its target lipid, phosphatidylinositol-3,4,5-trisphosphate (PIP₃), but has minimal interaction with the background lipid phosphatidylcholine (PC) (20).

In this study, lateral diffusion constants are measured for GRP1 PH domain monomers, dimers, and trimers bound to PIP₃ embedded in a supported PC/PIP₃ bilayer. Diffusion is monitored by TIRFM with single particle tracking, allowing the resolution of multiple PH domain populations. Focusing on the major mobile population, the findings reveal a simple, additive dependence of the frictional coefficient on the number of tightly bound lipid molecules, indicating that the diffusion coefficient is a useful reporter of lipid binding stoichiometry in this system. Furthermore, the ratios of measured diffusion constants for dimeric and trimeric PH domains are found to be in close agreement with molecular dynamics simulations of a coarse-grained (CG) dipalmitoylphosphatidylcholine (DPPC) bilayer with two or three of the lipids tethered together on each leaflet, respectively, and with hydrodynamic estimates for tethered beads in an isotropic medium. Together, the experimental and computational findings have important implications for the theoretical description of lipid diffusion in bilayers.

Materials and Methods

Reagents

Synthetic phospholipids 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, PC); 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (LRB-DOPE, LRB-PE); and 1,2-dioleoyl-sn-glycero-3-phosphoinositol-3,4,5-trisphosphate (DOPI(3,4,5)P3, PI(3,4,5)P3) were from Avanti Polar Lipids (Alabaster, AL). Alexa Fluor 555 (AF555) C2-maleimide was from Invitrogen (Carlsbad, CA). 2-Mercaptoethanol was from Fluka (Buchs, Germany). CoA trilithium salt was from Sigma (St. Louis, MO).

Construction of vectors for expression of multimeric GRP1 PH domains

Multimers of the GRP1 PH domain and an enzymatic labeling sequence were cloned into a vector previously generated in the Falke laboratory for expression of glutathione S-transferase fusions (16). For 1PH, oligonucleotides were synthesized (Integrated DNA Technologies, Coralville, IA) encoding the 11-amino-acid recognition sequence for Sfp phosphopantethienyltransferase (Fig. 1) (21). This sequence was inserted just upstream of the GRP1 PH sequence in the original expression plasmid (16). Similarly, the 2PH plasmid contained the Sfp recognition sequence followed by a PH domain coding sequence, 5-amino acid linker (Fig. 1), and second PH domain coding sequence.

Figure 1.

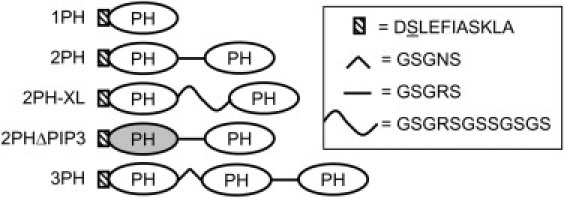
Engineered multi-PH domain constructs used in this study. Schematic diagram in which ovals represent the individual human GRP1 PH domain (residues 255–392) and other symbols represent engineered N-terminal and linker peptides (sequences as indicated). Each construct is enzymatically labeled with Alexa Fluor 555-CoA at the underlined serine residue on the N-terminal, 11-residue tagging sequence (21,23). The 2PHΔPIP3 protein contains the K273A/R284A double mutation in the first PH domain (gray) known to inactivate the PIP₃ binding site (45).

For 3PH, DNA encoding a third PH domain was inserted before the first coding sequence in the 2PH plasmid. To minimize recombination due to identical PH domain coding sequences, DNA from mouse GRP1 PH domain was used for this third domain, from a construct provided by B. Tycko (Saxena et al. (22)). The mouse and human DNA sequences encode the same amino acid sequence.

For 2PH-XL, DNA encoding GSSGSGS was inserted into the linker region of the 2PH plasmid. For 2PHΔPIP3, a GRP1 PH domain coding sequence containing the K273A/R284A double mutation was generated using site-directed mutagenesis (Stratagene, Cedar Creek, TX). The first PH domain sequence was removed from the 2PH plasmid by endonuclease digestion, and the mutated PH domain sequence was ligated into this position. The correct full sequence of all constructs was confirmed by DNA sequencing. All PH domains are comprised of amino acids 255–392 of the human GRP1 protein (16,20).

Protein expression, purification, and labeling

Proteins were expressed in Escherichia coli as N-terminal glutathione S-transferase fusions, and purified using glutathione affinity beads with thrombin cleavage as described previously (16). Proteins were labeled with Alexa Fluor 555 (AF555) using Sfp based on a published protocol (23). Briefly, ∼2 μM protein was incubated with 2.5 μM AF555-CoA conjugate and 0.5 μM Sfp at room temperature for 2 h. Excess fluorophore was removed by buffer exchange using Vivaspin concentrators (Sartorius Stedim, Göttingen, Germany) until the flowthrough was not visibly colored. Concentration of labeled protein was determined based on absorbance of AF555.

Sample preparation for single-molecule experiments

Supported lipid bilayers were prepared on glass coverslips as described previously (20). Briefly, glass coverslips (Pella, Redding, CA) were soaked for 1 h in piranha solution, rinsed extensively with Milli-Q water (Millipore, Billerica, MA), dried under a stream of N₂, and irradiated 0.8 h in a PSD-UV ozone cleaner (Novascan, Ames, IA). Bilayers were formed via the vesicle fusion method using sonicated PC/PIP₃ vesicles prepared as described previously (16,20). Bilayers were rinsed extensively with Milli-Q water (Millipore) and then exchanged into assay buffer (140 mM KCl, 0.5 mM MgCl₂, 15 mM NaCl, 20 mM 2-mercaptoethanol, 25 mM HEPES, pH 7.5).

TIRFM measurement

TIRFM measurements were taken essentially as described previously (20). Supported lipid bilayers (above) were imaged before and after addition of fluorescent protein, to ensure that background fluorescent contamination was negligible. After addition of protein, samples were allowed to equilibrate 5 min to approach room temperature, which in these experiments was 20 ± 1°C. To minimize contributions from immobile fluorescent particles during diffusion measurements, a high-power bleach pulse (∼30-fold higher than used for imaging) was applied for 2–5 s, then fluorescence was allowed to recover for 60 s before data acquisition. It should be noted that any immobile particles that bind to the bilayer during this recovery step, or mobile particles that become immobilized, would be visible in Movie S1, Movie S2, and Movie S3 in the Supporting Material, but would not contribute to the measured diffusion constants due to exclusions used in data analysis. Movies at frame rates of 20 frames/s and 50 frames/s were acquired for each sample using MetaMorph software (AG Heinze, Lake Forest, CA), subsequent analysis was carried out using ImageJ (24), and data processing and fitting were carried out using Mathematica (Wolfram Research, Champaign, IL).

For determination of mobile fraction, the bleach pulse was omitted. Movies (200 frames, 20 frames/s) were recorded on previously unexposed areas. The mobile fraction was determined as the number of spots that were observed to move within 1 s, divided by the total number of spots visible in the first frame of the recording. This analysis was performed on multiple movies from ≥2 experiments.

Single particle tracking and analysis

As in our previous study (20), diffusion trajectories of single molecules were determined using the Particle Tracker plugin for ImageJ (24), then imported into Mathematica for further analysis. The chosen tracking parameters resulted in some spurious detection of noise, which may become linked together into short trajectories. These spurious detections, along with rapidly dissociating particles and unusually bright or dim contaminants, were eliminated from analysis using a series of exclusion criteria in Mathematica that we have described and validated previously (20). The resulting excluded trajectories were shorter than five frames, or had an average intensity outside of an empirically determined range.

Single molecule diffusion analysis

To resolve large groups of diffusion trajectories into the observed immobile, slow, and mobile populations, data from all movies at 50-ms frame rates were pooled and analyzed together. Displacements from all trajectories at Δt = 8 frames (0.4 s) were calculated and converted to probability distribution histograms with 100 equally spaced bins. These were fit to a single Rayleigh distribution (Eq. 1), the sum of two Rayleigh distributions (Eq. 2), or the sum of three Rayleigh distributions (Eq. 3),

$$N_S\left(r\right)=\frac{P_{1}r}{{\sigma }_1^2}{e}^{\frac{-r^2}{2{\sigma }_1^2}},$$ (1)

$$N_S\left(r\right)=\frac{P_{1}r}{{\sigma }_1^2}{e}^{\frac{-r^2}{2{\sigma }_1^2}}+\frac{P_{2}r}{{\sigma }_2^2}{e}^{\frac{-r^2}{2{\sigma }_2^2}},$$ (2)

$$N_S\left(r\right)=\frac{P_{1}r}{{\sigma }_1^2}{e}^{\frac{-r^2}{2{\sigma }_1^2}}+\frac{P_{2}r}{{\sigma }_2^2}{e}^{\frac{-r^2}{2{\sigma }_2^2}}+\frac{P_{3}r}{{\sigma }_3^2}{e}^{\frac{-r^2}{2{\sigma }_3^2}},$$ (3)

where N_S(r) represents the distribution of the number of steps as a function of distance r, the σ_i are related to the diffusion constants D_i by σ_i² = 2D_iΔt, and the P_i are relative populations of the different components. In all cases, the three-component fit was statistically superior using a Fisher F-test, and thus was used for the diffusion analysis summarized in Table 1 and detailed in Fig. S2.

Table 1.

Best-fit multicomponent diffusion parameters

Molecule	D1 (μm2/s)	P1	D2 (μm2/s)	P2	D3 (μm2/s)	P3	n (samples)	n (movies)	n (trajectories)
Lipid (LRB-DOPE)	0.003 ± 0.001	1 ± 1%	0.03 ± 0.01	4 ± 1%	2.8 ± 0.1	94 ± 1%	8	14	3489
1PH	0.0020 ± 0.0004	4 ± 1%	0.04 ± 0.01	5 ± 1%	2.7 ± 0.1	92 ± 3%	4	8	1038
2PH	0.0023 ± 0.0001	10 ± 1%	0.05 ± 0.01	7 ± 1%	1.4 ± 0.1	83 ± 2%	4	8	1204
3PH	0.0013 ± 0.0001	61 ± 1%	0.05 ± 0.01	10 ± 1%	0.9 ± 0.1	29 ± 2%	8	11	782
2PH-XL	0.0016 ± 0.0001	13 ± 1%	0.08 ± 0.02	5 ± 1%	1.4 ± 0.1	83 ± 2%	3	6	1359
2PHΔPIP3	0.0020 ± 0.0003	4 ± 1%	0.08 ± 0.02	5 ± 1%	2.6 ± 0.1	91 ± 2%	4	8	1405

Data for a step-time of Δt = 0.4 s were pooled from multiple movies at 50-ms frame rates and fit as described in Materials and Methods. For each parameter, the best-fit value and 95% confidence interval is shown. The pooled step-size distributions and best-fit curves are displayed in Fig. S2. The fitting assumed a three-component population and revealed immobile (within limits of spatiotemporal resolution, D₁, P₁), slow (D₂, P₂), and mobile (D₃, P₃) particles. Measurements were performed on PC/PIP3 (98:2) membranes at room temperature (20 ± 1°C) in a near-physiological buffer (see Materials and Methods).

For comparison, the one-component analysis we described previously (20), based on the method of Schütz et al. (25), was also carried out to determine the diffusion coefficient of the mobile population. For each movie, the cumulative probability distribution 1-P(r², Δt) of square displacement r² or greater over a given time interval Δt was calculated for Δt values from one to eight frames. It was observed that some trajectories that passed the exclusion criteria represented molecules that switched back and forth between mobile and immobile or extremely slow moving states. To focus analysis on the mobile population, trajectories whose overall diffusion constant was <0.1 μm²/s (i.e., were immobile for the duration of the trajectory) were excluded. From the remaining trajectories, only steps of r² > 0.4 μm² for each value of Δt were fit to the single-component diffusion model given by Eq. 4 (25),

$$P\left(r^2,\Delta t\right)=1-e^{-r^2/\langle r^2\rangle },$$ (4)

where 〈r²〉 is the mean-square displacement. This quantity is linearly related to Δt as described by Eq. 5,

$$\langle {\mathit{r}}^{\mathit{2}}\rangle =4\mathit{D}\Delta \mathit{t,}$$ (5)

where D is the two-dimensional diffusion constant. It was found that 〈r²〉 values based on Δt = 1 frame or two frames consistently underrepresented the diffusion constant, possibly due to the averaging of the molecular position over the exposure time in each frame. Therefore, D values for each movie were determined from linear fits to 〈r²〉 versus Δt for Δt values from three to eight frames, as illustrated in Fig. S3 and summarized in Table S2.

Computational simulations of diffusion

Molecular dynamics (MD) simulations were performed using GROMACS 4.0.5 (26) with the MARTINI coarse-grained (CG) force field (27). A simplified model was adopted: two lipids in each leaflet of a DPPC bilayer were tethered at 10, 40, or 60 Å to model the experimental homodimer; three lipids were tethered in a linear array with neighbors separated by 60 Å to model the homotrimer. These simplifications were adopted because PIP₃ is not yet available in the MARTINI force field. Consequently, only the ratios of the multimer to monomer diffusion constants are appropriate to compare with experiment. The absolute values are much larger than experiment because of simplifications of the CG model (27), and differences in the lipids. An all-atom model would be expected to yield diffusion constants closer to experiment (28); however, such a simulation is not currently feasible.

Two system sizes were simulated: 1), 512 lipids with 6000 waters, and 2), 2048 lipids with 50,784 waters. Each was equilibrated for 100 ns and then simulated for an additional 500 ns of constant pressure (NPT) production at 50°C by using periodic boundary conditions and a 20-fs timestep. Snapshots were saved every 50 ps.

Dimer and trimer systems were prepared by choosing random snapshots from the production run and tethering one multimer per leaflet at the desired distance. The lipids were tethered at the distances noted above by a harmonic restraint with a force constant of 1250 kJ mol⁻¹ nm⁻² between all pairs of phosphate particles; this is the same force constant used between two bonded particles of a MARTINI lipid. First, 100 replicates of the 512 lipid 10 Å and 40 Å dimer systems were equilibrated for 50 ns and then run for 460 ns of NPT production. After statistical convergence was verified, 50 replicates of each remaining system were simulated for 50 ns of equilibration followed by 460 ns of NPT production, yielding similar statistical convergence. A total of 138 μs of production data were analyzed.

By construction, the molecular dynamics simulations contained only one population of mobile tethered particles. Mean-squared displacements of individual molecules were calculated over their entire trajectories with averaging over equal displacements, and the curves were averaged over all molecules and replicates. Diffusion constants were then calculated using Eq. 5 over the range 1–200 ns (this ignores fast motions on the subnanosecond timescale). Standard errors were calculated by comparing the diffusion constants of molecules from the upper and lower leaflets.

Bead model hydrodynamics

Although there are differences between two-dimensional and three-dimensional diffusion (29,30), it is informative to include results for diffusion of beads interacting by an Oseen tensor in an isotropic medium, and assuming that diffusion for a single bead is governed by the Stokes-Einstein relation. To model the experiment, only the two components on the diffusion tensor, D_xx and D_zz are averaged; i.e., diffusion along the bilayer normal is neglected. The diffusion tensor for a dimer can be evaluated analytically (31). For identical beads of radius a separated by distance r, and with frictions given by Stokes Law with stick boundary conditions, the ratio of the diffusion constants of a dimer and a monomer is

$${\mathit{D}}_{\text{dimer}}/{\mathit{D}}_{\text{monomer}}=\text{1}/\text{2}+9\mathit{a}/\left(16\mathit{r}\right).$$ (6)

(The preceding ratio is 1/2 + a/(2r) when D_yy is added.) The diffusion tensor for the trimer and larger multimers is most simply obtained by numerical matrix inversion; a detailed description is presented in Pastor and Karplus (32). For calculations here, a = 4.5 Å, corresponding to 64 Å²/lipid.

Results

Strategy: construction of labeled multi-PH domain proteins

The goal of this study is to probe the effects of multiple independent lipid binding sites on the lateral diffusion of membrane-bound proteins. Lateral diffusion constants of membrane-bound proteins are readily measured using TIRFM single-molecule tracking. This technique yields reliable diffusion measurements over micrometer-distance scales, and can discriminate multiple states that interconvert on the seconds-timescale or slower (33–35).

Covalent oligomers of the GRP1 PH domain were chosen as a model system for multiple independent lipid binding sites. We previously found that when presented with a PC/PIP₃ (98:2) bilayer, this PH domain associates with high affinity and specificity to the headgroup of PIP₃, but exhibits minimal bilayer penetration and interacts only weakly with background PC lipids (16,20). Under these conditions, the probability of the PH domain undergoing a through-solution microdissociation event (defined as dissociation from one target PIP₃ and rapid rebinding to another nearby PIP₃) during a given 50-ms frame is ≤0.25% and can be neglected (20). Strikingly, the membrane-bound PH domain exhibits a lateral diffusion constant identical, within error, to that of a lipid molecule in the same bilayer (20). It follows that the diffusion of the protein-lipid complex is dominated by the friction experienced by the bilayer-embedded lipid, rather than the water-exposed protein, which is not surprising because the effective viscosity of the bilayer is two orders of magnitude higher than that of water (20).

Plasmids were constructed for expression of one, two, or three GRP1 PH domains linked together by either five-amino-acid (GSGRS or GSGNS) or 12-amino-acid linkers (GSGRSGSSGSGS). Linker length and flexibility were augmented by the natural flexibility of the N- and C termini of the PH domain, which each include 11 residues that are not involved in secondary structure elements as defined by the known crystal structure of the domain (36). These designs are illustrated schematically in Fig. 1.

For single-molecule measurements, proteins were labeled with Alexa Fluor 555. Our previous study with the single GRP1 PH domain used proteins labeled via maleimide coupling to a single engineered cysteine residue. This method required mutation of three intrinsic Cys residues to Ala or Ser, and resulted in a protein that was somewhat more difficult to purify than the wild-type domain. This study employed the wild-type domain in all constructs, with the addition of an 11-residue tagging sequence (21,23) N-terminal to the first PH domain, allowing enzymatic labeling with AF555. As demonstrated by fluorescence imaging of SDS-PAGE gels, the labeled single, double, and triple PH domains were >90% pure and correspond to the expected masses (Fig. S1).

The lateral membrane diffusion constants of these PH domain constructs and control fluorescent lipids were measured by using single-molecule TIRFM acquisition, as described in Materials and Methods. Briefly, lipid bilayers composed of 98% DOPC and 2% DOPI(3,4,5)P₃ were prepared on ultra-clean glass coverslips. Proteins were added to the solution above the bilayer, providing accessibility to PIP₃ on the exposed bilayer leaflet. For lipid diffusion measurements, bilayers were prepared containing 98% DOPC, 2% DOPI(3,4,5)P₃, and 150 ppb lissamine rhodamine B-DOPE (LRB-DOPE). Bilayer-associated fluorescent molecules were imaged using TIRFM. In each case, a subpopulation of immobilized fluorescent particles was detected and its fractional population was estimated as summarized in Table S1. The low levels of immobilized particles observed for fluorescent lipid or the single PH domain are typical of supported bilayer studies, and are believed to arise from highly localized bilayer or glass defects as previously discussed (20). The contribution of these immobilized particles to diffusion analysis was minimized by a premovie bleach and recovery step that destroyed immobile fluors and allowed mobile fluors to repopulate the window. After bleaching and recovery, a larger fraction of the observed fluorescent particles was mobile (Table 1), and these were observed to diffuse randomly (Fig. 2, Movie S1, Movie S2, and Movie S3). Individual particle trajectories were defined by tracking software, and trajectories were included in analysis if they met a set of selection criteria designed to exclude mobile fluorescent contaminants.

Figure 2.

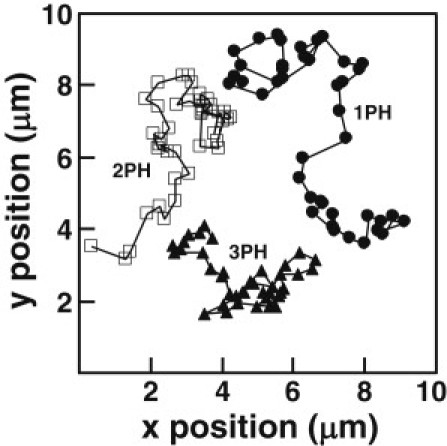
Single particle tracks of single, double, and triple PH domains. Representative lateral diffusion trajectories of each mobile species are shown, where each trajectory is 42 frames of a single protein diffusing on PC/PIP₃ (98:2) bilayers acquired at 20 frames/s. Molecules were tracked using the Particle Tracker plugin for ImageJ (24). Coordinates of trajectories have been offset for clarity. Note that the net lateral displacement decreases as the number of PIP₃-bound domains increases.

The resulting postbleach trajectories were pooled and analyzed to 1), resolve the mobile components from distinct slow and immobile components; and 2), determine the diffusion coefficient of each component. As summarized in Table 1 and detailed in Fig. S2, the pooled data were best fit to a three-component model yielding the fractional populations and average diffusion coefficients of mobile (P₃, D₃), slow (P₂, D₂), and immobile (P₁, D₁) components. The faster P₃ population always dominated over the slow P₂ component and exhibited a diffusion constant D₃ at least 17-fold and 7000-fold larger than D₂ and D₁, respectively (Table 1). For the fluorescent lipid and monomeric PH domain, the mobile component exceeded 90% of the population (Table 1). For the engineered dimeric and trimeric PH domain constructs, the fractional mobile component dropped to 83 ± 2% and 29 ± 2%, respectively, while the immobile component grew to 10 ± 1% and 61 ± 1%, respectively. Thus, immobility increased nonlinearly with the number of domains, presumably due to misfolded or microaggregate particles with nonnative membrane interactions. Coupling together identical β-sandwich domains is likely to stimulate interdomain β-strand swapping (37) and may yield linker tangling; such processes could account for the increased immobility of multidomain constructs. The slow component was always minor, yielding a 4–10% contribution, and presumably arises from slow-moving contaminants that escaped our exclusion criteria, as well as transiently immobile proteins that were mobile for some, but not all, of a given Δt window (Fig. S2).

All subsequent analysis, unless noted otherwise, focuses on the mobile component of each data set, which was observed to diffuse randomly and freely (Fig. 2, Movie S1, Movie S2, and Movie S3). The diffusion coefficients determined for these mobile particles by the three-component fit are robust, because an alternative method quantitating just the mobile component (Fig. 3 and Fig. S3) yielded the same diffusion coefficients within error (compare Table 1 and Table S2).

Figure 3.

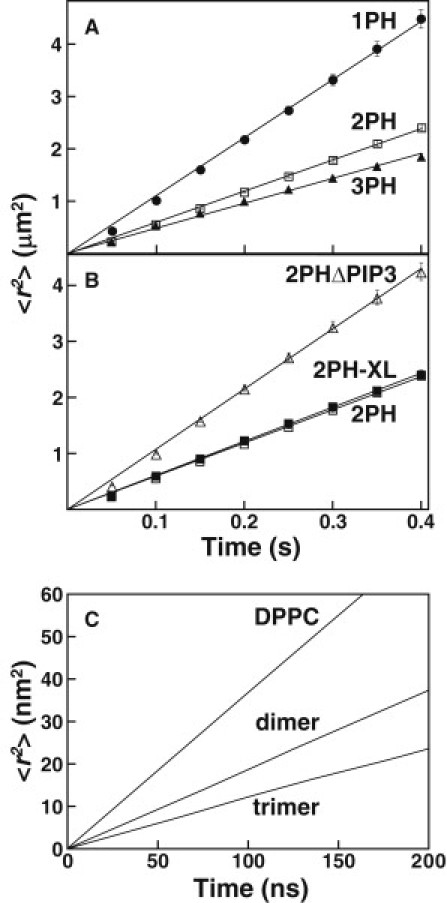
Mean-square displacement versus time plots for PH domain constructs and simulated tethered lipids. Plots of mean-square displacement versus Δt are shown for (A) mobile populations of 1PH, 2PH, and 3PH; (B) mobile populations of 2PH, 2PHXL, and 2PHΔPIP3; and (C) monomeric DPPC, and dimeric and trimeric tethered DPPC from coarse-grained (CG) simulations of the 2048 lipid systems. For single molecule protein diffusion (A and B), the representative plots shown are data sets of 4400–8500 steps from a single representative movie for each species. Linear fits (solid lines) yielded diffusion constants averaged in Table S2. Error bars are calculated as described (46) and, when not visible, are smaller than the symbols. For both the experimental and simulated systems, linearities demonstrate the lack of large-scale barriers to diffusion of mobile particles, indicating a homogeneous bilayer.

Diffusion of lipids and GRP1PH monomer

Consistent with our previous report, single GRP1 PH domains diffuse as fast as lipid molecules on PC/PIP₃ (98:2) bilayers (20). The diffusion constants of lipid and mobile 1PH are within error of each other, 2.8 ± 0.1 and 2.7 ± 0.1 μm²/s, respectively (D₃ in Table 1) and are also within error of our previous measurements for the same lipid and the maleimide-labeled single-cysteine PH domain (3.0 ± 0.2 and 3.0 ± 0.3 μm²/s, respectively) at a slightly higher temperature (∼21.5°C) (20).

Diffusion of tandem homodimers

A tandem homodimer of GRP1 PH domains (2PH) binds simultaneously to two PIP₃ molecules on the supported bilayer. Mobile molecules of this construct demonstrate free diffusion in the bilayer (Fig. 2, Movie S2) and exhibit a diffusion coefficient approximately half that of the individual domain, 1.4 ± 0.1 μm²/s (Table 1).

To verify that the two domains in the tandem dimer are binding two PIP₃ molecules independently, we engineered a second version of 2PH with an extended linker between the two domains (2PH-XL, Fig. 1). This protein also diffused freely with an identical diffusion constant of 1.4 ± 0.1 μm²/s, demonstrating that in both constructs the linker is sufficiently long to prevent interference with binding or diffusion (Table 1).

As a further control, a version of the tandem dimer was generated with one of the two PH domains inactivated by mutagenesis of its PIP₃ binding site (2PHΔPIP3, Fig. 1). This mutant dimer was stable and soluble but exhibited a membrane affinity significantly lower than the standard dimer, similar to the lower affinity observed for the monomeric domain as judged by the protein concentration needed to generate a given density of membrane-bound fluorescent particles. Moreover, the diffusion constant of the mutant dimer, 2.6 ± 0.1 μm²/s, is significantly larger than that of the standard dimer, and is within error of that measured for the single domain (Table 1), confirming that diffusion is independent of the total surface area exposed to aqueous solvent. Together the controls demonstrate that the diffusion constants of the dimeric constructs depend only on the number of tightly bound PIP₃ molecules.

Diffusion of triple PH homotrimer

A triple PH domain homotrimer (3PH) bound to PIP₃ diffuses with a lateral diffusion constant of 0.9 ± 0.1 μm²/s (Table 1), approximately one-third that of an individual lipid or the single PH domain. This 3PH construct appeared to have a stability and solubility similar to 2PH during purification and labeling (Fig. S1), but exhibited a relatively high population of immobile states when bound to the membrane (Table 1, Table S1, and Movie S3). One advantage of multicomponent, single-molecule analysis is the ability to exclude immobile particles and focus only on the diffusion coefficient of the freely mobile population, which was essential for analysis of this construct.

Theoretical analysis and simulated diffusion of linked phospholipids

Mean-square displacements versus time for the MD simulations for all of the 2048-lipid systems are plotted in Fig. 3 C. The trend is strikingly similar to that found experimentally, although the absolute MD diffusion coefficients are significantly faster than the corresponding experimental values. This faster diffusion is expected because the simulations were of CG saturated lipids at 50°C (the experimental study employed unsaturated lipids at 20 ± 1°C). Table 2 lists the diffusion constants from the simulations, and compares the multimer/monomer ratios with those from the bead model and experiment. The agreement between theoretical and experimental ratios is superb. The measured ratios lie between those calculated at 40 and 60 Å, but closer to 60 Å; thus, the simulations predict that the effective experimental linker length may approach 60 Å. The trimers were restrained to be linear in the MD simulations. Relaxing that restriction should lead to a more compact structure, and thus to greater hydrodynamic screening and faster diffusion. As demonstrated by bead models (Table 2), this effect is relatively small. The effect of hydrodynamic screening is evident when the tether length is reduced to 10 Å. In this case, the dimer/monomer ratio is 0.7 ± 0.2 from the simulation and 0.75 from Eq. 6.

Table 2.

Summary diffusion constants from MD simulations of tethered lipids in a DPPC bilayer, and ratios of multimer and monomer diffusion constants from MD, bead model, and experiment

System	D (μm2/s)	MD ratio	Bead model ratio∗	Measured ratio∗,†
512 lipids, DPPC	81.7 ± 0.5
10 Å dimer	60 ± 10	0.7 ± 0.2	0.75
40 Å dimer	48 ± 3	0.58 ± 0.03	0.56
60 Å dimer	39 ± 6	0.48 ± 0.07	0.54
2048 lipids, DPPC	93 ± 4
60 Å dimer	46 ± 9	0.5 ± 0.1	0.54	0.52 ± 0.06
60 Å trimer	30 ± 9	0.32 ± 0.08	0.38–0.41‡	0.33 ± 0.05

^∗The bead model and measured results do not depend on system size.

^†Measured ratios are calculated using the mobile component (D₃) from Table 1.

^‡The ratio for the bead model trimer increases continuously from 0.38 to 0.41 as the angle between the subunits is decreased from 180° to 30°.

As a technical point, both the absolute values of the MD diffusion constants and their ratios differ for the 512-lipid and 2048-lipid systems. Yeh and Hummer (38) have shown that translational diffusion constants calculated from MD of cubic boxes with periodic boundary conditions exhibit a system-size dependence. Although the analytic formula is still under development for bilayers in noncubic boxes (M. G. Lerner and R. W. Pastor, unpublished), a similar effect is responsible for the results shown here.

Discussion

Lateral diffusion constants reflect fundamental features of membrane-bound proteins. This study leads to three broad conclusions:

• 1.Single-molecule TIRFM is a superior method for measuring lateral diffusion of membrane targeting proteins, particularly ones that may exhibit complex diffusion behavior;
• 2.The diffusion of multi-PH domain oligomers on PC/PIP₃ membranes is roughly inversely proportional to the number of tightly bound PIP₃ molecules, suggesting the approach will be broadly useful in analyzing the lipid stoichiometry of simple peripheral proteins; and
• 3.Experimental, theoretical, and computational analysis reveals that the hydrodynamic free-draining limit, which is well defined in three-dimensional diffusion in isotropic fluids, is an important limit in the two-dimensional diffusion of lipids in bilayers as well.

Isotropic molecular diffusion in fluids is generally described by the Stokes-Einstein relationship,

$$\mathit{D}={\mathit{k}}_{\text{B}}\mathit{T/f,}$$ (7)

in which D is the diffusion constant, k_B is Boltzmann's constant, T is temperature, and f is the frictional drag coefficient. Polymers are commonly modeled as strings of beads (monomers) with friction constants f_i. When the separation between monomers becomes large, the total friction is simply the sum of monomer frictions, and the diffusion constant for a polymer of N monomers is given by the so-called free draining limit (31,32,39),

$$\mathit{D}={\mathit{k}}_{\text{B}}\mathit{T/}\left(f_{\mathit{1}}+f_{\mathit{2}}+\mathrm{\dots }{\mathit{f}}_N\right).$$ (8)

The free-draining limit is well established for three-dimensional polymer diffusion in isotropic media (32), but has not been proposed to describe two-dimensional diffusion in lipid bilayers. If the free-draining limit does apply to a protein that tightly binds N lipids at binding sites that are sufficiently well separated, and if the protein has little contact with other lipids, Eq. 8 predicts that the protein diffusion constant D_P(N) will be

$${\mathit{D}}_{\text{P}\left(\text{N}\right)}={\mathit{D}}_{\text{L}}\mathit{/N,}$$ (9)

where D_L represents the lateral diffusion constant of a single lipid in the bilayer. This equation indicates that the overall diffusion rate will be inversely proportional to the number of tightly bound lipids, and if only one lipid is bound, the protein will have the same diffusion coefficient as a single lipid.

Here we find that the frictional coefficients of multiple lipid molecules bound tightly by a peripheral membrane protein are indeed additive within error, as implied by Eq. 8. The lateral diffusion constant of PIP₃-bound GRP1 PH domain multimers decreases from 2.7 ± 0.1 μm²/s for a single domain to 1.4 ± 0.1 μm²/s for the dimer, to 0.9 ± 0.1 μm²/s for the trimer (Table 1). As shown in Fig. 4, this dependence of diffusion constant on the number of PIP₃-bound PH domains is well represented by the inversely proportional relationship of Eq. 9, assuming that the diffusion coefficient of a single PIP₃ molecule is 2.7 μm²/s, a value within error of the measured lipid diffusion constant 2.8 ± 0.1 μm²/s (Table 1). Thus, the data support the hypothesis that the frictional coefficients of PIP₃ molecules bound to different PH domains are additive, indicating that the hydrodynamic free draining limit pertains to well-separated lipids in bilayers. Due to the inverse relationship between D_P(N) and N, changes in diffusion constant will become more difficult to quantitate for large numbers of tightly bound lipids (Eq. 9). While these results indicate that resolution of 2PH and 3PH diffusion constants is possible (Table 1), resolution of N = 3 from N ≥ 4 may become impractical. More generally, weakly bound lipids may also slow diffusion and complicate the stoichiometry analysis, as observed for the weak association of the GRP1 PH domain with phosphatidylserine (PS) on PC/PS/PIP₃ (73.5:24.5:2) bilayers (20). However, an advantage of the single molecule diffusion approach is the ability to eliminate weakly bound lipids from the supported bilayer, thereby enabling a focus on just the tightly bound lipids.

Figure 4.

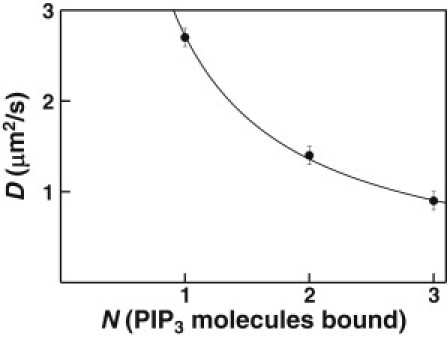
Lipid stoichiometry dependence of diffusion constant. Measured diffusion constants for 1PH, 2PH, and 3PH (solid circles) lie within error on the curve predicted by Eq. 9 (solid line) with a best-fit single lipid diffusion coefficient of D_L = 2.7 ± 0.2 μm²/s.

For multiple bound lipids to exhibit additive frictional coefficients, the tethered lipids must be well separated, or else they may hydrodynamically screen each other (as observed in Table 2 when separation is decreased to 10 Å). It has been shown by computational and theoretical approaches that the diffusion of nearby lipid molecules is coupled: as one lipid moves in a particular direction, its neighbors also exhibit a preference for moving in that direction (40,41), though the distance scale over which this coupling is felt is controversial. All-atom MD simulations have indicated that translational jumps of next-nearest neighbors (i.e., separations of up to 1.6 nm) are correlated (28); longer length scale correlations were not observed but could not be completely ruled out because of the relatively small system size (288 lipids) simulated. Here, we show via the first systematic experimental and computational studies of linked lipids that the mobilities of two lipids tethered roughly 4–6 nm apart are in the free draining limit on the millisecond timescale of our experimental measurements. Previous studies provide additional evidence to support this picture. In 1988, Tamm (42) observed in fluorescence-recovery-after-photobleaching experiments that a bivalent antibody bound to two lipids at least 3-nm apart (the diameter of one FAB domain) on a supported bilayer had a lateral diffusion constant that was one-half that of the lipid molecules. He proposed that the antibody would have a diffusion constant one-half that of individual lipids if the two bound lipids possess additive frictional coefficients and the friction felt in the aqueous solution was negligible, as we and others have observed (43). Similarly, Gambin et al. (44) found that two transmembrane helices tethered 2-nm apart exhibited a diffusion constant one-half that of a single transmembrane helix. While this result was interpreted as supportive of a 1/R dependence of diffusion for transmembrane proteins, it is also consistent with additive frictional coefficients of tethered particles that diffuse without hydrodynamically screening each other.

Together, the available data suggest that the widely employed Saffman-Delbrück description of diffusion in bilayers needs revision. Although Saffman-Delbrück theory can be extended to tethered dimers and trimers, the parameters from the original study predict that the free-draining limit will not apply to the systems studied here (M. G. Lerner and R. W. Pastor, unpublished), in contradiction to our experimental and computational results.

In conclusion, the findings presented in this article indicate that the frictional coefficients of coupled, well-separated lipids in a bilayer are additive, and that such lipids are in a hydrodynamic free-draining limit. Multi-GRP1 PH domain constructs bound to multiple PIP₃ molecules on PC/PIP₃ membranes exhibit such additivity, indicating that their bound PIP₃ ligands are sufficiently well separated to effectively eliminate hydrodynamic interactions. More generally, single-molecule lateral diffusion measurements can shed light on lipid-binding stoichiometries of full-length proteins containing multiple lipid-binding domains. Because the method measures ratios of diffusion constants, it is independent of any friction between the bilayer and glass support, and should work equally well in freestanding bilayers or vesicles. This potential use illustrates yet another powerful capability of single-molecule fluorescence microscopy in determining molecular mechanisms of protein membrane interactions, one molecule at a time.