The estimation of statistical parameters for local alignment score distributions

Abstract

The distribution of optimal local alignment scores of random sequences plays a vital role in evaluating the statistical significance of sequence alignments. These scores can be well described by an extreme-value distribution. The distribution’s parameters depend upon the scoring system employed and the random letter frequencies; in general they cannot be derived analytically, but must be estimated by curve fitting. For obtaining accurate parameter estimates, a form of the recently described ‘island’ method has several advantages. We describe this method in detail, and use it to investigate the functional dependence of these parameters on finite-length edge effects.

INTRODUCTION

Local sequence alignment is perhaps the most widely used tool in computational molecular biology, with most protein and DNA database search programs (1–4) implementing heuristic versions of local alignment algorithms (5,6). These algorithms seek the highest-scoring alignment of segments from the two sequences being compared. An alignment’s score is calculated by adding substitution scores, defined for each aligned pair of letters, and gap scores for each run of letters in one segment aligned with null characters inserted into the other.

A key question is what alignment scores may be expected to occur purely by chance. This question is generally addressed by analyzing the distribution of optimal alignment scores from random or real but unrelated sequences. We confine attention to random sequences, defined as strings of independent letters chosen with fixed background probabilities, because they are easier to control and study. Depending upon the details of the alignment scoring system and the background letter probabilities, the optimal score for the alignment of two random sequences of length n tends to grow proportionally either to n or to log(n) (7–10). The linear scoring regime corresponds to optimal alignments that tend to involve virtually the entire sequences; the logarithmic regime, with substitution and gap scores that are on average more negative, corresponds to optimal alignments that are relatively short. Many alignments representing true biological relationships involve only segments of the sequences compared, but these will tend to be outscored by long ‘random alignments’ when a scoring system in the linear regime is employed. Therefore, attention has focused primarily on scoring systems in the logarithmic regime, and we deal here exclusively with such scores.

In the asymptotic limit of long sequences, optimal local alignment scores follow an extreme-value distribution (11), described by two parameters λ and K. For the type of scoring system in most general use, these parameters cannot be calculated but must instead be estimated by random simulation. Most directly, one may generate optimal alignment scores for a large number of random sequence pairs, and fit an extreme-value distribution to these scores. Recently, an alternative approach has been described; it uses scores for local alignment ‘islands’ generated by a slight modification of the Smith–Waterman algorithm (12). We will discuss in detail the implementation and application of the island parameter estimation method, and compare it to the direct method in several ways. The island method has a number of useful features. (i) It renders explicit a tradeoff between parameter estimate bias and stochastic error, and allows this tradeoff to be easily controlled. (ii) It estimates accurately the tail behavior of score distributions for small-length comparisons. (iii) It allows parameter estimates to be obtained for arbitrary length sequence comparisons, including the infinite-length limit. In some circumstances, the first two of these features can be transferred advantageously to the direct method, appropriately modified. For asymptotic parameter estimation, however, the island method has a clear speed advantage.

THE DIRECT ESTIMATION OF STATISTICAL PARAMETERS

An asymptotic theory for local alignment scores has been developed for the case in which no gaps are permitted. In brief, for the comparison of random sequences of sufficient lengths m and n, the number of distinct local alignments with score at least x is approximately Poisson distributed, with mean

E(x) ≈ Kmne^–λx, 1

where λ and K are easily calculated parameters (13,14). This implies that the optimal alignment score S′ approximately follows an extreme-value distribution (11), with

Prob (S′ ≥ x) ≈ 1 – exp(–Kmne^–λx). 2

For local alignments that allow gaps, no asymptotic score distribution has been established analytically. However, computational experiments strongly suggest that equations 1 and 2 apply to this type of alignment as well (12,15–22). The key to using equations 1 and 2 is the accurate estimation of the statistical parameters λ and K. Perhaps the most direct approach to estimating these parameters for a fixed scoring system and set of background letter frequencies is to generate a large number of pairs of random sequences of equal length n, and find the optimal local alignment score for each pair. From these scores one may calculate maximum-likelihood estimates and for the statistical parameters in equation 2 (23). If R scores are generated, the ratio /λ is approximately normally distributed, with mean 1 and standard error 0.78/√R (23). Note that the estimates developed by Lawless (23) assume continuous data, whereas alignment scores are almost always discrete. If the scale parameter λ times the lattice spacing of possible scores is small, the error introduced by assuming continuous scores is minor. One may, however, derive maximum-likelihood estimates and that explicitly assume discrete scores (Appendix).

Because λ enters equations 1 and 2 exponentially, accurate estimates of λ are particularly important. Marginally significant alignments from current database searches typically have a scaled score λx > 25, for which even a 4% error in λ leads to an estimated E-value in error by greater than a factor of 2.7. Thus, standard errors of <2%, or even 1%, in may be desirable.

THE ISLAND METHOD

Recently, Olsen et al. (12) proposed the island method for estimating λ and K; it is a variant of ideas introduced by Waterman and Vingron (18,19) that translates into a very efficient algorithm. Rather than finding optimal alignment scores for pairs of random sequences, they propose generating scores for each island (as defined below) in a path graph. To generate sufficiently many scores for accurate parameter estimation, a single large or multiple smaller pairwise comparisons may be used.

Briefly, the Smith–Waterman algorithm generates a score for each cell C in a path graph, corresponding to the highest-scoring local alignment ending at C (5). This local alignment starts at a specific anchoring cell, and an island consists of all cells with identical anchors (Fig. 1). The score assigned to an island is the maximum score of the cells it contains. A simple modification of the Smith–Waterman algorithm, involving only a fixed amount of extra computation per cell, allows one to record which island each cell belongs to, and to keep track of each island’s score. Note also that as one moves row by row through a path graph with n columns, there can be at most O(n) islands represented on any given row. This allows one to tabulate all island scores generated by an m × n path graph in O(mn) time, and using only O(n) space.

Figure 1.

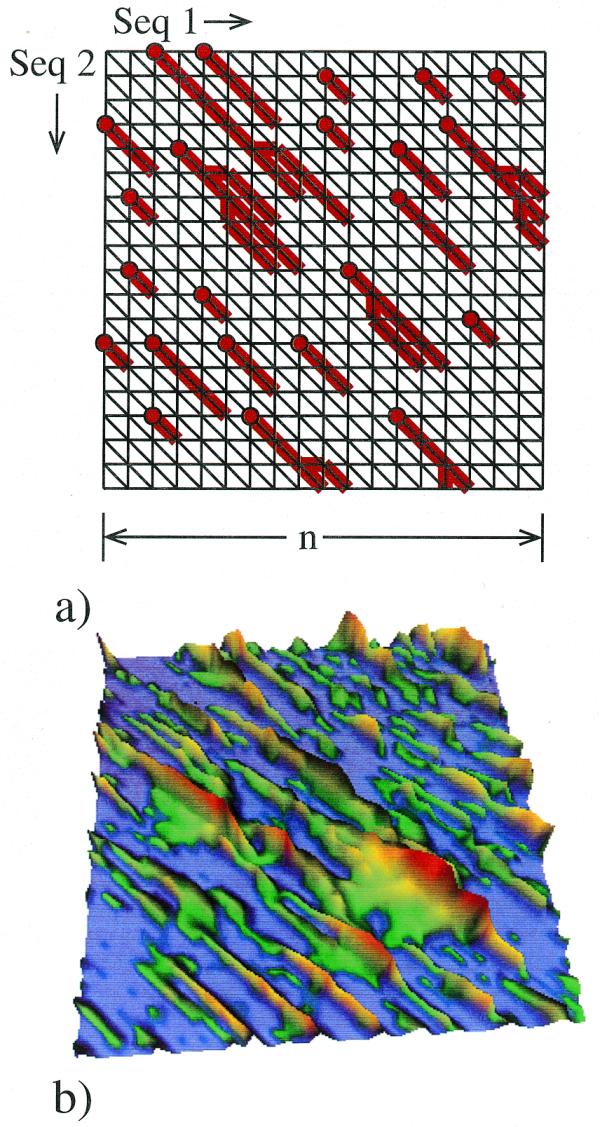
Islands in a local alignment path graph. (a) Schematic representation of the path graph. In every cell C the red line recalls the choice made by the optimization procedure of the Smith–Waterman algorithm. By these lines, all the cells with non-zero scores are partitioned into islands according to which anchoring points (circles) they are connected to. (b) Score landscape on a 50 × 50 path graph. The score at every cell of the path graph is represented by its height above the surface and color-coded with zero scores corresponding to blue areas and increasingly red colors for higher scores. The example shown is generated with a BLOSUM-62 scoring matrix, and a score –(11 + k) for each gap of length k. The islands are easily seen.

Island scores correspond to distinct locally optimal alignments, and thus the number of islands with score at least x should be well described by equation 1 when x is sufficiently large. The island method generates maximum-likelihood estimates of λ and K from equation 1, while the direct method generates these estimates from equation 2.

The concept of two or more local alignments being distinct is a subtle one, and a variety of definitions have been proposed (6,12,24,25). The differences among these definitions are relevant more for the comparison of real than random sequences. Because using any reasonable definition of distinct alignments should yield equivalent statistical results, the advantage of the ‘island’ (12) over the ‘declumping’ definition (18,19,24,25) for parameter estimation is its algorithmic efficiency.

In general, equation 1 becomes increasingly accurate for larger values of x, so to obtain a good estimate for λ one should confine attention to islands whose score attains at least some threshold value c. Assume the set I_c of such islands has cardinality R_c, and let be the mean score in excess of c of these islands:

, 3

where S(i) is the score of island i. Then, assuming island scores are integral, with unit lattice spacing, the maximum-likelihood estimate (Appendix) for λ is

. 4

The standard error of /λ is

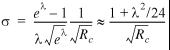, 5

where the approximation holds to better than 0.05% for λ < 1. If the island scores were continuous, the maximum-likelihood estimate would instead be simply 1/, and the standard error of /λ would be 1/√R_c.

In conjunction with , the maximum-likelihood estimate for K is

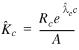, 6

where A is the aggregate ‘area’ of the search space from which the collection of islands were drawn. If a single pair of sequences, of lengths m and n, were compared to generate the islands, then A = mn; if B such comparisons were performed, then A = Bmn.

The parameters λ and K of equations 1 and 2 properly apply only in the limit of infinite-length sequences. If one uses either the island or direct method to estimate λ for sequences of finite length, one obtains estimates with an observable finite-length bias. As will be discussed below, this bias can be explained in terms of ‘edge effects’, for which a simple correction can be applied to the lengths m and n in equations 1 and 2. The resulting formulas retain the asymptotic values of λ and K, so it is desirable to avoid any finite-length bias in the estimation of these parameters. We note here that, by eliminating edge effects, the island method can estimate asymptotic values of λ and K directly. This is done by embedding a length n × n sequence comparison within a larger (n + 2b) × (n + 2b) comparison, with a border of length b on each side (Fig. 2). Only islands anchored within the central n × n region are recorded. When b is sufficiently large, edge effects are essentially abolished.

Figure 2.

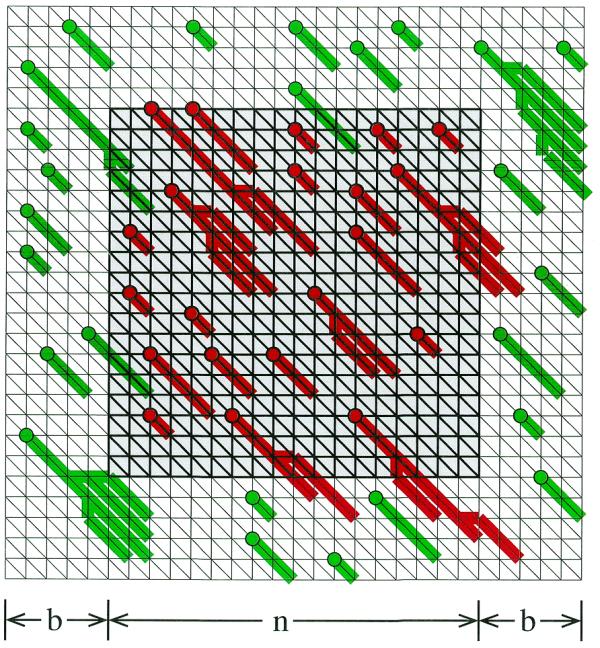
Schematic representation of a path graph used to avoid edge effects in the estimation of λ and K via the island method. The n × n scoring lattice (gray square in the middle) is surrounded by a border of width b. Only islands that are anchored within the central n × n area (shown in dark red) are counted. Islands anchored outside this area (green) are ignored. Note that some of the ignored islands reach into the inner area and some of the accepted islands reach into the border region since the classification of an island depends only on the position of its anchor (circles); borders thus are required on all sides to suppress edge effects properly.

THE TRADEOFF OF SPEED, BIAS AND PRECISION

Because of λ’s exponential role in equations 1 and 2, accurate estimates for λ are far more important than those for K, and we shall therefore focus on the estimation of λ. A key question for applying the island method effectively is how to choose an appropriate threshold parameter c for use in equation 4.

While we believe that the qualitative features presented here are truly independent of the scoring system used, we will illustrate below the issues involved in choosing c using a specific example. To obtain extremely accurate parameter estimates for this case study, we performed a massive random simulation for a particular local alignment scoring system. Specifically, we used a set of standard amino acid frequencies for proteins (26) to generate over 92 000 pairs of length-7000 ‘random amino acid sequences’. We compared each pair using the BLOSUM-62 amino acid substitution matrix (27), in conjunction with affine gap scores (28–31) of –(11 + k) for gaps of length k. To suppress edge effects, scores were tabulated only for islands anchored within the central 5000 × 5000 square of each pairwise comparison; approximately 10¹² total island scores were recorded. Using equations 3–6, estimates of λ and K were obtained from these data for a range of cutoff scores c; the results are summarized in Table 1 and the values of are plotted in Figure 3.

Table 1. Island method estimates for λ and K.

c	Rc	λc	Kc
20	508 087 143	0.2790 0.0000 (0.00%)	0.058
21	382 046 389	0.2771 0.0000 (0.01%)	0.056
22	288 047 946	0.2754 0.0000 (0.01%)	0.053
23	217 666 586	0.2739 0.0000 (0.01%)	0.051
24	164 854 001	0.2726 0.0000 (0.01%)	0.050
25	125 090 432	0.2716 0.0000 (0.01%)	0.048
26	95 080 777	0.2707 0.0000 (0.01%)	0.047
27	72 367 615	0.2700 0.0000 (0.01%)	0.046
28	55 135 823	0.2694 0.0000 (0.01%)	0.045
29	42 040 928	0.2689 0.0000 (0.02%)	0.044
30	32 087 753	0.2685 0.0000 (0.02%)	0.044
31	24 502 349	0.2681 0.0001 (0.02%)	0.043
32	18 721 366	0.2678 0.0001 (0.02%)	0.043
33	14 312 497	0.2676 0.0001 (0.03%)	0.042
34	10 945 852	0.2674 0.0001 (0.03%)	0.042
35	8 372 081	0.2672 0.0001 (0.03%)	0.042
36	6 407 611	0.2671 0.0001 (0.04%)	0.042
37	4 904 102	0.2670 0.0001 (0.05%)	0.041
38	3 755 281	0.2671 0.0001 (0.05%)	0.042
39	2 874 422	0.2670 0.0002 (0.06%)	0.041
40	2 201 167	0.2671 0.0002 (0.07%)	0.042
41	1 684 893	0.2670 0.0002 (0.08%)	0.041
42	1 289 490	0.2669 0.0002 (0.09%)	0.041
43	986 932	0.2667 0.0003 (0.10%)	0.041
44	756 060	0.2668 0.0003 (0.12%)	0.041
45	579 087	0.2668 0.0004 (0.13%)	0.041
46	443 934	0.2671 0.0004 (0.15%)	0.042
47	339 913	0.2671 0.0005 (0.17%)	0.042
48	260 519	0.2675 0.0005 (0.20%)	0.042
49	199 117	0.2671 0.0006 (0.22%)	0.042
50	152 595	0.2674 0.0007 (0.26%)	0.042
51	116 705	0.2671 0.0008 (0.29%)	0.042
52	89 323	0.2671 0.0009 (0.34%)	0.042
53	68 605	0.2680 0.0010 (0.38%)	0.044
54	52 570	0.2686 0.0012 (0.44%)	0.045
55	40 242	0.2690 0.0013 (0.50%)	0.046
56	30 746	0.2690 0.0015 (0.57%)	0.046
57	23 481	0.2688 0.0018 (0.65%)	0.046
58	17 888	0.2678 0.0020 (0.75%)	0.043
59	13 662	0.2673 0.0023 (0.86%)	0.042
60	10 427	0.2664 0.0026 (0.98%)	0.039

A total of 92 441 pairs of length 7000 random sequences were generated using a set of standard amino acid frequencies (26). Island scores were generated for each pair using an extension of the Smith–Waterman algorithm (5), modified for affine gap scores (28). Substitutions were scored using the BLOSUM-62 matrix (27), and gaps of length k were assessed the score –(11 + k). Scores were recorded only for islands anchored within the central 5000 × 5000 square of each pairwise comparison. Maximum-likelihood estimates for λ and K were obtained using equations 4–6.

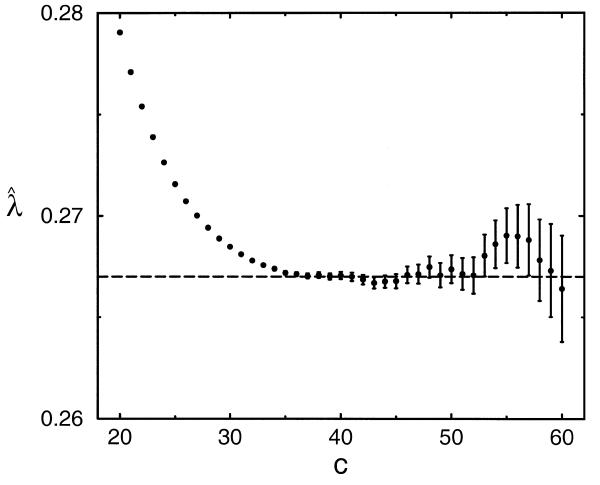
Figure 3.

Estimates obtained via the island method with different cutoffs c. Standard errors for the estimates are shown with error bars. The plotted horizontal line indicates the best estimate of the asymptotic λ. Details of the simulation are given in the legend to Table 1.

While the estimates of Table 1 should be essentially free of edge-effect bias, there is another systematic and easily understood bias (12) evident for small values of c. Optimal local alignments with low score are unlikely to contain a gap, as will be discussed further below, and for low thresholds is therefore biased towards the higher λ applicable to local alignments that exclude gaps. In this example, falls monotonically for c ≥ 20, until it reaches the value 0.2670 at c = 37; thereafter, appears to fluctuate randomly about this value. Of course a yet larger simulation, yielding smaller stochastic errors, might detect systematic bias even beyond c = 37.

There is a tension between the bias of and its precision, for the larger the value of c chosen, the fewer the islands that attain score c, and the larger the standard error of . To illustrate the point, consider a realistically sized random simulation, 10 000 times smaller than that shown in Table 1, which would require ~2 min on a modern workstation. The systematic bias in the from such a simulation should be the same as seen in Table 1, but the standard errors will be 100 times larger. Table 2 shows the resulting tradeoff between bias and precision. The best tradeoff probably occurs near c = 28, where the sum (~2.2%) of the bias and the standard error are minimized. As the size of the random simulation grows, the bias at a given cutoff remains fixed, whereas the standard error decreases. Thus in general the optimal tradeoff for larger simulations will tend to occur at higher values of c.

Table 2. Tradeoff between bias and precision in the estimation of λ.

c	Bias (%)	Standard error (%)
22	3.1	0.6
23	2.6	0.7
24	2.1	0.8
25	1.7	0.9
26	1.4	1.0
27	1.1	1.2
28	0.9	1.3
29	0.7	1.5
30	0.6	1.8
31	0.4	2.0
32	0.3	2.3
33	0.2	2.6
34	0.1	3.0
35	0.1	3.5
36	0.0	4.0
37	0.0	4.5

The bias in the estimation of λ is calculated from Table 1, assuming λ’s true value is 0.2670. The standard error assumes an experiment generating 1/10 000 the number of island scores shown in Table 1.

For a given simulation one may estimate well the standard error at any given c, but not the bias; if one could estimate bias, one could correct for it. The analysis of a relatively small simulation given in Table 2 is possible only because a much larger simulation has in fact been performed. In practice, one must choose the c at which to estimate λ without knowing to any certainty how much bias it entails. We have investigated automatic procedures for choosing c, and found several reasonable methods, but none for which an argument of optimality can be advanced. In outline, decreases systematically for increasing c, until its increasing standard error obscures any further change. It is at this point that the cutoff c should be chosen.

EDGE EFFECTS AND THEIR CORRECTION

Independently of the type of bias in estimating λ described above, varies substantially as a function of m and n when λ is estimated from traditional borderless (i.e. b = 0) m × n sequence comparisons (20). One may therefore argue that one’s estimate of λ and K should depend upon the lengths of the real sequences to which they will be applied (22). We here take the alternative view that the length-dependence of is merely an artifact of finite-length sequence comparison edge effects, and that a correction for these effects is best applied to m and n in equations 1 and 2 rather than to λ and K.

The central idea of the ‘edge effect’ correction is that high-scoring local alignments from the comparison of two random sequences have an expected length l(x), dependent upon their score x, and therefore cannot begin arbitrarily close to the end of either sequence. Accordingly, in place of m and n in equations 1 and 2, the ‘effective’ lengths of the sequences should be taken to be m′ = m – l(x) and n′ = n – l(x) (20).

Empirically, the mean length l(x) of high-scoring random alignments with sufficiently large score x depends linearly on x

l(x) = αx + β. 7

We will discuss in a later section the interpretation of α and β, but note here that these parameters may be estimated by recording the lengths as well as the scores of optimal island alignments. The length of a gapped alignment is interpreted as the average length of the two segments it involves.

For the island method, the way that edge effects bias is easy to understand. The decay in the observed number of alignments with score at least x is steeper than would be estimated from equation 1 because the effective lengths m′ and n′ shrink with increasing x. Some simple calculus suggests the apparent λ from the comparison of sequences of sufficient lengths m and n should be given approximately by

. 8

For the specific scoring system studied in the massive random simulation above, we estimate α = 1.90 ± 0.02 (see discussion below). Therefore, we expect the apparent λ for n × n comparisons to follow the equation

. 9

To test this theory, we used the island method to estimate λ for the same scoring system studied in the simulation above. We generated islands from many n × n random sequence comparisons, but with no border for suppressing edge effects. Sufficient comparisons were performed to yield over 10⁶ islands with a score of at least 37 for each of the 12 lengths n studied; as described above, using this threshold eliminates almost all cutoff-based bias. 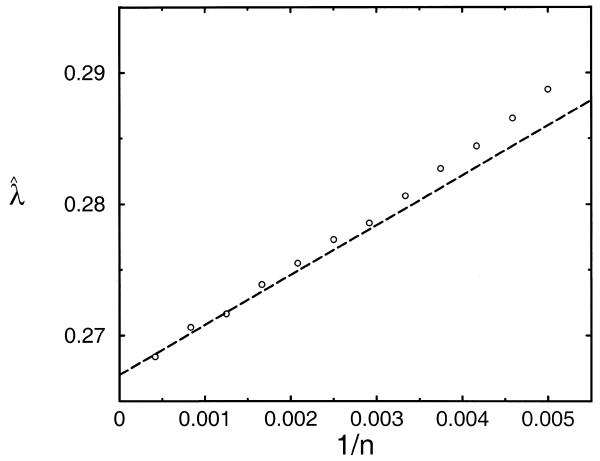The resulting maximum-likelihood estimates (n,n) have a standard error of 0.1%, and are shown as open circles in Figure 4. Given our small uncertainty in λ and α, for n > 400 (1/n < 0.0025 in Fig. 4) the data fit the theory of equation 9 to within stochastic error (i.e. two standard deviations). Furthermore, (n,n) deviates from equation 9 by <0.5% for n > 218 (1/n < 0.0045), and by <1% throughout the range studied. For each n, we calculated a χ² goodness-of-fit test to the geometric distribution; in all 12 cases, the data fit the model with a P-value > 0.09.

Figure 4.

Estimates 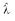derived from borderless n × n sequence comparisons by the island method as a function of 1/n. Approximately 1 000 000 islands with a score of at least 37 were generated to produce the estimates, which thus have a standard error of 0.1%; the size of the symbols represents one standard error. The plotted line represents the theory of equation 9 for the apparent 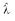(n,n). The scoring system and random sequence model are the same as those described in the legend to Table 1.

We emphasize that we do not argue that the line plotted in Figure 4 is more accurate in describing score distribution tail behavior than the experimental (n,n) produced by the island method. Rather, the good agreement implies the correction we recommend for finite lengths m and n should be sufficiently accurate for comparing proteins of typical size. In evaluating the statistical significance of actual sequence comparisons, one may apply edge-effect corrections either to the sequence lengths, as we suggest, or to λ, but one should not combine the two corrections. We emphasize further that equation 8 does not permit one to estimate λ accurately from a ‘finite-size’ simulation that estimates (m,n) because such a simulation will not yield an estimate of the asymptotic value of α.

The island method with borders allows one to estimate the ‘infinite-length’ or asymptotic parameters λ and K directly, and simultaneously to estimate, as described below, the edge-effect correction parameters α and β. A single simulation that estimates these four parameters thus permits the statistical evaluation of comparisons of sequences of arbitrary length.

COMPARISON OF THE DIRECT AND ISLAND METHODS

For estimating the asymptotic parameters λ, K, α and β, the island method has a distinct speed advantage over the direct method, as we will discuss below. However, it is easiest first to compare the two methods on the problem of estimating (n,n) studied in the previous section. In this ‘finite size’ case, the methods have contrasting advantages. To achieve a standard error σ in (n,n)/(n,n), the island method must generate approximately 1/σ² data points (see equation 5), while the direct method need generate only about 0.61/σ² points (23). Furthermore, the algorithm for generating island scores requires more computation than that for generating maximal local alignment scores because it must keep track to which island the score of each path graph cell belongs. Our implementation and timing experiments show the direct method uses only ~70% of the time per cell that the island method does. These two factors combined yield a speed advantage of ~240% for the direct method. On the other hand, the island method may generate multiple data points from each n × n sequence comparison. The expected number of such points depends both upon the length of the sequences being compared and upon the threshold score c as given by equation 1. The total speed advantage of the island over the direct method is then Kn²e^–λc/2.4. In our case study we have been employing c = 37 and very many data points to obtain extremely accurate parameter estimates, but as stated above c = 28 would be appropriate for a comparison of more typical accuracy. At this threshold, the comparison of two sequences of length 340 yields about 2.4 islands on average, counterbalancing the direct method’s speed advantages. For comparisons larger than this, the island method will be faster than the direct method, and slower for smaller comparisons.

This analysis, however, tells only part of the story, because the biases of the direct and island methods in estimating (n,n) vary with n. To study the extent of this bias, for each length n considered in the previous section we generated sufficient data points for both the direct method and the island method with c = 28 to produce estimates (n,n) with a standard error of 0.1%. We then compared these estimates to the independent and effectively unbiased estimates (also with standard error 0.1%) shown by the points plotted in Figure 4; the resulting estimates of bias are given in Table 3. For sequence lengths n ≤ 343 the direct method tends to overestimate (n,n) by >1%. Some reflection reveals why this should be the case. For the scoring system under study, ~81% of all optimal alignments from 343 × 343 comparisons have a score less than 37, and >7% have a score less than 28. As we learned from our analysis of the island method, including low scoring, largely ungapped, alignments introduces noticeable bias into estimates of λ. The problem is amplified for the direct method because, due to the extremely fast decay of the left-hand tail of the extreme-value distribution, the data points upon which the maximum-likelihood estimate most strongly depends are those with lowest score.

Table 3. Bias in the estimation of λ(n,n) of the island, direct and censored direct methods, and their relative speeds.

n	Bias (%)			Speed ratio
	Island	Direct	Censored	Island:direct	Island:censored
2400	+0.9	–0.2	–0.2	60	60
1200	+0.7	0.0	0.0	14	14
800	+0.8	+0.4	+0.4	6	6
600	+0.6	+0.5	+0.5	3	3
480	+0.5	+0.8	+0.6	2	2
400	+0.4	+0.8	+0.3	1.4	1.5
343	+0.4	+1.2	+0.4	1.0	1.2
300	+0.3	+1.4	+0.5	0.8	1.1
267	+0.1	+1.4	+0.3	0.6	1.0
240	0.0	+1.6	+0.1	0.5	0.9
218	–0.1	+1.4	–0.1	0.4	0.8
200	0.0	+1.6	–0.1	0.3	0.8

Maximum-likelihood estimates λ were derived using the island, direct and censored methods from n × n sequence comparisons. For the island method with cutoff score c = 28, approximately 10⁶ scores were generated, yielding a standard error of 0.1%. For the direct method, approximately 6.1 × 10⁵ scores were generated, yielding a standard error of 0.1%. For the censored method, sufficient scores above the threshold c = 28 were generated to yield a standard error of 0.1% (23); this number ranged from 6.1 × 10⁵ for n = 2400 to 8.4 × 10⁵ for n = 200. Biases are calculated assuming the correct values for λ(n,n) are those of the points plotted in Figure 4. Speed ratios are the computation times required, respectively, by the direct and censored methods divided by the time required by the island method; high speed ratios favor the island method.

Borrowing from our analysis of the island method, it is possible to greatly reduce the bias of the direct method by basing its maximum-likelihood estimate only on those scores that reach a minimum threshold c (23) (see Appendix). This refinement is achieved at a cost in speed, however, because not every n × n comparison will yield a data point, and because such ‘censoring’ increases the number of data points required to achieve a given standard error (23). For example, only 56% of 200 × 200 comparisons have a maximal alignment score of at least 28, and with this degree of censoring the number of data points required for a given error increases by 40% (23). For this size comparison, the censored direct method is thus 2.5 times slower than the unmodified method, while still 20% faster than the island method. A fuller analysis gives the speed advantage to the island over the censored method only for comparisons larger than about 280 × 280. Of course as the size of the comparisons grows, so does the island method’s relative speed advantage (Table 3), reaching a factor greater than 3 for comparisons of size 600 × 600.

The island method has a major speed advantage for comparisons of size ≥ 800 × 800, but it appears to have a corresponding disadvantage with respect to bias (Table 3). This arises because over 99.8% of the optimal alignment scores from 800 × 800 comparisons are at least 31, and at least 34 from 1200 × 1200 comparisons. Effectively, the score ‘threshold’ for the direct method increases with comparison size, while we have used a fixed score threshold of 28 for all the island comparisons in Table 3. Were this threshold raised for large comparisons, it would be possible to achieve equivalent bias to the direct method, while retaining a >3-fold speed advantage. However, for large comparisons, one has the option with the island method to choose greater speed over smaller bias.

If all the island method had to offer were a 2–3-fold speed advantage for comparisons in the size range 500 × 500 to 800 × 800, it would hardly constitute a significant advance. However, our main point is that in lieu of estimating statistical parameters for various finite-size comparisons, a single estimate of the asymptotic λ and K along with the edge-effect correction parameters α and β will suffice. In this context, the island method has major advantages to the direct method. Most simply, the island method can accurately estimate the asymptotic λ by increasing the dimensions of its comparisons to such an extent that finite-size effects become negligible. Because the number of data points the island method generates grows in proportion to the area of its comparisons, there is no loss in speed. In contrast, as we have seen, the direct method pays a heavy penalty in speed as the size of its comparisons grow.

To avoid unduly increasing the comparison size, one might consider adding borders to direct method comparisons, as described above for the island method (Fig. 2). This, however, imposes substantial computational overheads. First, one must record where local alignments are ‘rooted’, to avoid counting local alignments rooted outside the central square. The extra computation per cell is similar to keeping track of which island a cell belongs to and increases run time by a factor greater than 1.4. Second, borders can greatly increase the computational area of medium-sized comparisons. For example, a border of moderate length 200 (see the next section) increases the area of a 600 × 600 comparison by a factor of 2.8. The two effects combined would slow such a comparison down by a factor close to 4. In contrast, for asymptotic parameter estimation, borders may be added to the island method comparisons at essentially no computational cost: first because the island method must record the roots of local alignments in any case; second because the comparisons’ underlying dimensions may be enlarged arbitrarily, rendering inconsequential the additional area entailed by the inclusion of borders.

In conclusion, for finite-size parameter estimation, the island method begins to have a speed advantage only for the comparison of sequences of moderate length. However, for the asymptotic parameter estimation we recommend, the island method has a speed advantage to the direct method approaching an order of magnitude.

THE ESTIMATION OF α AND β

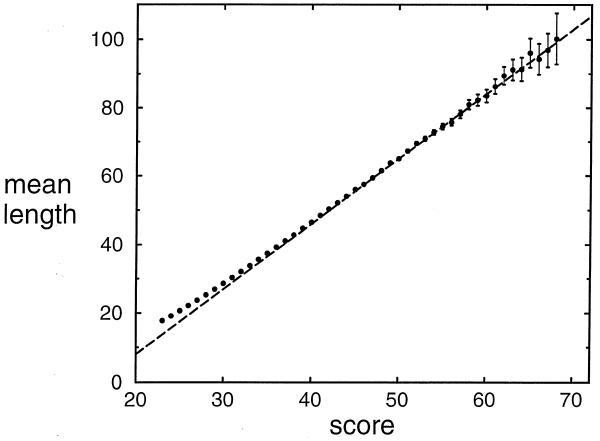
For optimal local alignments of a given score x, the standard deviation in the distribution of alignment lengths is large: about the same as the mean length. Nevertheless, the mean length can be seen to grow approximately linearly with x, as illustrated by data from the massive simulation above, plotted in Figure 5. The slope of this dependence does not approach its asymptotic value until x is sufficiently large. Therefore, as with estimates of λ, estimates of the parameters α and β in equation 7 are best calculated by confining attention to alignments with a score greater than or equal to a threshold value c. In Table 4 we give, for various thresholds, estimates of α and β obtained by linear regression on the lengths of the optimal island alignments. Once again, choosing a threshold that balances bias and stochastic error is to some degree arbitrary. We show in Figure 5 the line implied by the estimates = 1.90 and = –30, yielded by the threshold c = 47. These estimates agree within stochastic error to those for all c ≥ 44.

Figure 5.

The mean length l(x) of optimal island alignments, as a function of the alignment score x. Error bars, representing one standard error, grow with score primarily because the number of alignments on which the mean length estimates are based decreases. The plotted line represents a linear regression on the data for scores ≥47. Details of the simulation are given in the legend to Table 1.

Table 4. The estimation of α and β.

c	αc	βc
33	1.840 0.002	–26.9 0.1
34	1.847 0.002	–27.2 0.1
35	1.852 0.002	–27.4 0.1
36	1.858 0.003	–27.7 0.1
37	1.864 0.003	–27.9 0.1
38	1.869 0.004	–28.2 0.2
39	1.873 0.005	–28.4 0.2
40	1.877 0.005	–28.5 0.2
41	1.874 0.006	–28.4 0.3
42	1.877 0.007	–28.5 0.3
43	1.88 0.01	–28.8 0.4
44	1.89 0.01	–29.0 0.5
45	1.89 0.01	–29.3 0.6
46	1.91 0.01	–30.2 0.7
47	1.90 0.02	–30 1
48	1.89 0.02	–29 1
49	1.88 0.02	–29 1
50	1.91 0.03	–30 1
51	1.89 0.03	–29 2
52	1.90 0.03	–30 2
53	1.94 0.04	–32 2
54	1.96 0.05	–33 3

Estimates for α and β were obtained by linear regression of alignment length versus score for islands with score at least c. Details of the simulation are given in the legend to Table 1.

While the standard error for is 1% at c = 47, one is forced to settle for much larger errors in simulations of more realistic size. However, α and β are used only to correct the lengths of the sequences being compared, and the significance of alignment scores depends only linearly upon these lengths. Therefore it is generally quite acceptable to estimate α to within 10 or even 20%. The data generated to provide reasonably accurate estimates of the far more important parameter λ easily suffice for this purpose.

At a score of 95, the highest score achieved in this simulation, the predicted mean length is less than 150. Therefore, even though the standard deviation of the alignment length is approximately equal to the mean length, the border of length 1000 used in our simulation should be much more than sufficient for estimating the asymptotic values of the parameters λ, K, α and β, corresponding to ‘infinite length’ comparisons. For comparisons performed without borders, or with borders of insufficient length, estimates of α and β deviate from the asymptotic values, just as estimates of λ were shown to deviate above.

The expected length of gapped alignments with a high score clearly places limits on the applicability of equations 1 and 2 to the comparison of short sequences, even after edge effects have been corrected for. Specifically, if the expected length of an optimal alignment is longer than the shorter of the two sequences being compared, then one has effectively entered the realm of global sequence comparison, to which our theory no longer applies. This is perhaps best seen as an indication that the combination of substitution and gap costs being employed are tailored for too ‘distant’ similarities, and that a scoring system with a greater relative entropy should be used instead (32).

RELATIVE ENTROPY AND THE RELATION OF α TO β

It has recently been established under certain simplifying assumptions that in the no-gap case, the edge-effect correction outlined above is the proper first-order correction to equations 1 and 2 for finite-length sequences (J.L.Spouge, personal communication). For high-scoring local alignments without gaps, it can be shown (33) that the average length of alignments with score x is well approximated by

, 10

where H_u is the relative entropy of the scoring system in nats (32), and the subscript u indicates we are speaking of ungapped alignments. It is therefore reasonable to define, and estimate, the relative entropy per amino acid pair for gapped alignments by the formula

H_g = λ_g/α_g, 11

where the subscript g indicates the gapped case.

Given this definition, we estimate H_g for the scoring system studied above to be 0.141 ± 2% nats. Note that for the identical scoring system, Altschul and Gish (20) obtained the much greater estimate of 0.25 nats for H_g, due primarily to their assumption that β is 0 in equation 7. This assumption yields a good estimate of H_g only in the limit of very large scores x, a limit not nearly approached in simulations of practical size.

Given that for ungapped alignments β_u is near zero, as seen experimentally (see Table 5 for some examples), one may ask why β_g should be distinctly negative. An understanding is to realize that for a scoring system in which a gap of length 1 has score –G, at each end of an optimal alignment there must be a section with score +G that does not include gaps. The average lengths of these sections will be described better by the ungapped than by the gapped α. This is a much stronger effect than the fact that an optimal alignment may not begin or end with a negatively scoring aligned pair of letters, which causes β_u to be slightly negative. Together, these two effects lead to the prediction that the parameter β_g can be approximated by the formula

Table 5. The estimation of β using α.

Matrix	BLOSUM-45	BLOSUM-62	BLOSUM-80	PAM-70	PAM-30
αu	0.9113	0.7916	0.5222	0.3250	0.1938
βu	–5.7	–3.2	–1.6	–0.7	–0.3
Gap existence	14	11	10	10	9
Gap extension	2	1	1	1	1
αg	1.92 0.03	1.90 0.02	1.07 0.02	0.70 0.01	0.48 0.01
βg	–37.2 1.6	–29.7 1.0	–12.5 0.8	–8.1 0.5	–5.9 0.3
2G(αu – αg) + βu	–38.0 1.0	–29.8 0.5	–13.7 0.4	–9.0 0.3	–6.0 0.2

Estimates for α and β were obtained by linear regression of alignment length versus score, for scores attaining at least a cutoff value. Sequences were generated using a set of standard amino acid frequencies (26). Substitution scores were from either the BLOSUM (27) or PAM (37,38) series. Affine gap scores charged an existence penalty for each gap, and an extension penalty for each residue within a gap. Cutoff scores were chosen sufficiently high to avoid detectable bias in estimating α. Sufficient data points were generated to estimate α with a standard error of <2%. For each scoring system studied, this required over 500 pairs of random sequences, recording islands anchored within the central 5000 × 5000 square of each pairwise comparison. Borders of length 1000 were used for the BLOSUM-45 and BLOSUM-62 scoring systems, and of length 500 for all others.

β_g ≈ 2G(α_u – α_g) + β_u. 12

For the particular scoring system and random letter frequencies we have been studying, G = 12, α_u = 0.79 and β_u = –3.2. In conjunction with our estimate of 1.90 ± 0.02 for α_g, this yields an estimate of –29.8 ± 0.5 for β_g, which coincides with the experimental value of –30 ± 1 within the precision of measurement. Similar agreement is found for other gap costs and scoring systems that are not too close to the log-linear transition (see Table 5).

Equation 12 suggests that, with a knowledge of the easily accessible α_u and β_u, the estimation of α_g alone is sufficient for the edge-effect correction. In practice, however, estimating β_g requires no more work than estimating α_g, so one might as well use the experimental value.

DISCUSSION AND CONCLUSION

It was originally claimed that the primary advantage of the island over the direct method for estimating statistical parameters lay in speed (12). We have shown here that this is substantially true only for asymptotic parameter estimation. However, we also have argued that edge-effect parameters allow a single estimation of asymptotic parameters to replace all finite-size parameter estimates. Furthermore, the island method permits simple maximum-likelihood estimation of λ that accounts for discrete score data, and it allows for simultaneous parameter estimation using various score thresholds c, and thus the controlled tradeoff of systematic bias and stochastic error.

The parameter λ depends not only upon the scoring system employed, but also upon the letter frequencies of the sequences being compared. In practice, λ may sometimes vary by >10% from one pair of sequences to another, due merely to variations in sequence composition. Yet, in the context of a database search, it is simply too time consuming to re-estimate λ for each pairwise comparison of potential interest: one moderately accurate estimate of λ requires as much time as searching a typical current database using standard heuristic methods (4). Thus, while one may precompute highly accurate estimates of λ for a fixed ‘standard’ composition, isn’t this accuracy vitiated by varying compositions?

Two solutions to the problem of varying background frequencies have been proposed, both of which can make use of accurate parameter estimation procedures. Altschul et al. (4) have suggested that for non-standard letter frequencies, the substitution scores be rescaled so as to set the calculable (13) parameter λ_u equal to that for the original substitution scores used with standard frequencies. The conjecture is that the precalculated λ_g will then apply to gapped alignments using the rescaled substitution scores in the context of the non-standard frequencies. This procedure has been implemented with good results (34). Alternatively, Mott (22) has used random simulations for a very large number of different scoring systems, gap costs, sequence compositions and sequence lengths to derive an empirical formula for λ, dependent upon variables calculable from the scoring system, letter frequencies and sequence lengths. Because the values of used in deriving this formula were calculated by the direct method, frequently with short sequences, some improvement in Mott’s formula may be obtainable using the methods described here. To be more conservative, statistical parameters may be based upon residue compositions within sequence regions containing the aligned segments of interest. In general, by improving the precision with which statistical parameters are estimated for local sequence alignment, more accurate judgments can be rendered concerning the biological relevance of protein and DNA sequence similarities.

APPENDIX

Maximum-likelihood fitting

In this appendix we explain the maximum-likelihood fitting technique in the presence of discrete scores. In the case of the extreme-value distribution this extends the more commonly used maximum-likelihood fitting for continuous scores as it is, e.g. presented by Lawless (23). By analogy to some analytical results on discrete extreme-value distributions (35), for small lattice spacing we expect only small deviations in the estimated parameters due to the discreteness of the scores as long as we perform uncensored fits. However, for alignment scores it is often necessary to estimate the parameters only for a subset of the observed scores. For such a censored fit, the discreteness of the scores must be taken into account, as discussed here, to obtain correct maximum-likelihood estimates of the parameters of the underlying distribution.

Throughout the appendix we will assume that sufficiently large island scores S follow a geometric distribution

Prob(S = x) = Dp^x, 13

where we write p = exp(–λ) in order to emphasize the discrete character of the scores S. In the simplest case, the distribution is of this geometric form for all x ≥ 0 which fixes the prefactor D through normalization to D = 1 – p. Let us assume that we observed n islands with the scores x₁, …, x_N and we wish to find the value of p (i.e. λ) which best describes these observed scores. Since the probability of observing these scores is just the product of their individual probabilities the logarithm of the total probability (i.e. the log-likelihood) is

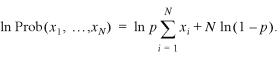14

The best value of p is the one which maximizes this expression. We can obtain it by equating the first derivative of this expression to zero. This yields after some simple algebra

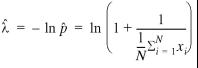. 15

In our application, the distribution of island scores is not of the geometric form (equation 13) for all scores x. It follows this form only asymptotically for large scores x. In this case, the prefactor D is no longer fixed by normalization. Rather, it depends on the shape of the distribution for small x. In order to get a good estimate for p we have to perform a censored fit, i.e. we keep only those island scores x with value at least c. The integer cutoff c is chosen so that the geometric form (equation 13) is a reasonable description of the data. This is commonly called Type I censoring (23). We expect the censored scores to be distributed according to the restricted probabilities

16

which is independent of the unknown normalization factor D. If, out of n total scores, the scores x₁, …, x_M attain a value of c or larger, the logarithm of the probability is

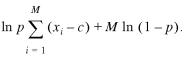17

This log-likelihood function is identical to the one without censoring presented in equation 14 except for the shift of all scores by the cutoff c. Thus, the optimal value is given by

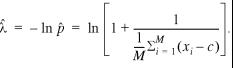18

From this expression it becomes obvious why it is important to take the discreteness of the scores into account for censored fits. The maximum-likelihood estimate depends explicitly on the cutoff, as c appears in equation 18, but the set of scores x₁, …, x_M remains unchanged as the cutoff c is varied between two adjacent integers. Therefore, it is important to demand that c be integral, taking the discreteness of the scores into account. In order to get an estimate for the other distribution parameter K, we have to employ the expected number E(x) of islands with score at least x given by equation 1. If we observe R_c islands with score at least c in B pairwise comparisons we get R_c ≈ BE(c) ≈ B^mnc which can be rearranged into equation 6 for the maximum-likelihood estimate . If we choose the direct rather than the island method to estimate λ, we are interested in the distribution

Prob(S′ = x′) = Prob(S′ ≤ x′) – Prob(S′ ≤ x′ – 1) 19

of the optimal local alignment scores. The optimal local alignment score S′ is the maximum of all the approximately ρmn island scores of the two sequences compared, where ρ describes the typical island density. Thus, the two probabilities on the right-hand side of equation 19 can be expressed by the distribution of island scores S, and S′ is distributed according to

Prob(S′ = x′) = Prob(S ≤ x′)^ρmn – Prob(S ≤ x′ – 1)^ρmn. 20

Since each island score follows the geometric distribution (equation 13) we get

21

with K = ρD/(1 – p). The last approximation is justified since Dp^x′/(1 – p) is a small number for all the scores x′ that we are interested in. Equation 21 suggests that the optimal alignment scores are indeed extreme-value distributed. The only influence of the discreteness of the scores is that the probability Prob(S′ = x′) is given by finite differences of the extreme-value distribution instead of being a proper probability density, i.e. the derivative of the extreme-value distribution. Let us now assume that we performed B comparisons. We again choose a cutoff c, and keep only the m optimal local alignment scores x′₁, …, x′_M that are greater than or equal to c. (If we are interested in an uncensored fit, we can always choose c = 0 since all local alignment scores are non-negative.) These scores are expected to follow the distribution

22

The logarithm L(p,K) = ln Prob(x′₁, …, x′_M | x′₁ ≥ c, …, x′_M ≥ c) of the probability of observing the censored scores x′₁, …, x′_M then becomes

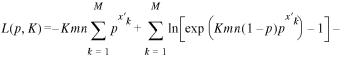
23

As before, the best estimates = exp(–) and of the two parameters p and K, given the observed data x′₁, …, x′_M, are the ones which maximize the function L(p,K). We could try to find this maximum by taking the derivatives of L(p,K) with respect to p and K and equating them to zero. However, this leads to a pair of equations that can only be solved numerically. Therefore, it is better to directly use a numerical minimization algorithm applied to the function –L(p,K). We used the downhill simplex method in two dimensions (36). In order to improve convergence, it can be conveniently started at the values of and which are obtained by the relatively simple uncensored, continuous extreme value fit to the data. Then, it converges rapidly towards the global minimum (,) of the function –L(p,K).