Unifying mechanical and thermodynamic descriptions across the thioredoxin protein family

Abstract

We compare various predicted mechanical and thermodynamic properties of nine oxidized thioredoxins (TRX) using a Distance Constraint Model (DCM). The DCM is based on a nonadditive free energy decomposition scheme, where entropic contributions are determined from rigidity and flexibility of structure based on distance constraints. We perform averages over an ensemble of constraint topologies to calculate several thermodynamic and mechanical response functions that together yield quantitative stability/flexibility relationships (QSFR). Applied to the TRX protein family, QSFR metrics display a rich variety of similarities and differences. In particular, backbone flexibility is well conserved across the family, whereas cooperativity correlation describing mechanical and thermodynamic couplings between residue pairs exhibit distinctive features that readily standout. The diversity in predicted QSFR metrics that describe cooperativity correlation between pairs of residues is largely explained by a global flexibility order parameter describing the amount of intrinsic flexibility within the protein. A free energy landscape is calculated as a function of the flexibility order parameter, and key values are determined where the native-state, transition-state and unfolded-state are located. Another key value identifies a mechanical transition where the global nature of the protein changes from flexible to rigid. The key values of the flexibility order parameter help characterize how mechanical and thermodynamic response is linked. Variation in QSFR metrics, and key characteristics of global flexibility are related to the native state x-ray crystal structure primarily through the hydrogen bond network. Furthermore, comparison of three TRX redox pairs reveals differences in thermodynamic response (i.e., relative melting point) and mechanical properties (i.e., backbone flexibility and cooperativity correlation) that are consistent with experimental data on thermal stabilities and NMR dynamical profiles. The results taken together demonstrate that small-scale structural variations are amplified into discernible global differences by propagating mechanical couplings through the H-bond network.

INTRODUCTION

Thioredoxin (TRX) is a small, ~110 residue α/β protein found in all organisms [1]. Its intracellular function is to regulate the oxidative state of target proteins by maintaining them in reduced form, while itself becoming oxidized through formation of a disulfide bond. The cysteine residues of the disulfide occur in a conserved C-X-X-C motif found in thioredoxins and other thioredoxin fold members. The greater stability of oxidized TRX emphasizes its intracellular role in maintaining substrate proteins in their reduced form [2]. Extensively studied for decades (see [3, 4] for two recent reviews), many TRX sequences and structures are available. TRX influences a wide variety of physiological functions due to its pivotal role in regulating cellular redox balance [5]. As a consequence, TRX is associated with a number of human diseases, including: cancer, cardiac disease, viral disease, etc. In recent years, TRX is receiving increasing attention for its therapeutic potential as a regulator of processes such as cell growth, apoptosis, and inflammation [6].

Here, we compare relationships between stability and flexibility metrics across the TRX family using a Distance Constraint Model (DCM). Various interactions, such as covalent bonds, hydrogen bonds (H-bonds) and local residue conformational states are modeled as a network of distance constraints, where each distance constraint is assigned an energy and entropy contribution. Statistical mechanics is employed to calculate thermodynamic properties over an ensemble of distance constraint networks (constraint topologies). The ensemble of constraint topologies represents all possible structural conformations ranging from native state fluctuations, partial unfolded states, all the way through to the unfolded state. For each constraint topology: Total enthalpy is given as the sum over enthalpy contributions from each distance constraint present, and, a good estimate for total entropy is given as a sum over entropy contributions from independent distance constraints that are identified using graph-rigidity algorithms [7–15]. In addition to thermodynamic properties, mechanical properties (i.e., local flexibility/rigidity profiles, correlated motions, etc.) are readily calculated. Due to the extraordinarily large number of accessible constraint topologies, a hybrid method combining Monte Carlo sampling with a mean field approximation is employed [7, 13].

The results presented here are based on a minimal distance constraint model (mDCM) that we describe briefly (see [13, 14] for a complete description). Accessible constraint topologies are limited to perturbations away from the native protein structure. In other words, non-native contacts are not considered, as is commonly done in Go-like models [17–19], COREX [20, 21], and other Ising-like models [22, 23]. Covalent bonds are modeled as distance constraints, but since they do not break and form, their enthalpy and entropy contributions factor out and play no role in thermodynamic response. In contrast, H-bonds and salt-bridges can break and form, and local conformational states of residues defined by internal dihedral angles fluctuate. These fluctuating noncovalent interactions govern the interesting thermodynamic and mechanical response. The backbone and side-chain dihedral angles that define the conformational state of a residue are modeled to be either native-like or disordered. The distance constraints that are used to enforce native-like or disordered dihedral angle basins are called torsion constraints. The characteristics of all native torsion constraints are considered to be the same, independent of residue type. Likewise, all disordered torsion constraints share the same characteristics. The mDCM has three adjustable parameters determined by fitting to experimental data (heretofore, heat capacity, C_p, curves). The mDCM was previously employed to identify conserved stability/flexibility relationships across a mesophilic/thermophilic RNase H ortholog pair [16], and its predictions were markedly consistent with earlier experimental conclusions [24]. The mDCM was also used to understand fragment stability in E. coli TRX, and it reconciled contradictory experimental descriptions of TRX folding [15]. More recently, the mDCM has been used to highlight the importance of the hydrogen bond network in four homologous periplasmic binding proteins [25]. Despite its simplicity, the mDCM has provided key insight into the interplay between stability and flexibility for a diverse set of proteins.

In this report, we expand upon our earlier work on E. coli TRX by comparing various QSFR metrics across a family of nine different oxidized TRX homologs spanning from prokaryota to human. In addition, three reduced TRX structures are also considered. Concentrating on the group of nine well-conserved structures of the same function, we determine, for the first time, how conserved (or diverse) the various QSFR properties are across the TRX family. To circumvent finding three adjustable parameters per protein, we transfer the same three parameters obtained from the E. coli TRX to all other members. With this fixed parameterization, we verified the mDCM correctly predicts all TRX homologs to have a two-state folding/unfolding transition, and the single peak in C_p is used to define the melting temperature, T_m. We find the native state backbone flexibility at respective T_m for each protein is well conserved. Surprisingly, QSFR metrics involving residue-residue correlations within the native state at respective T_m show significant distinguishing features across the family. Several model predictions are supported by experimental conclusions; however, the scarcity of biophysical characterizations across the family limits our ability to corroborate the full set of predictions. Intriguingly, most of the QSFR diversity revealed here is explained by the relative locations of key points in the flexibility order parameter that characterize the free energy landscape, and the mechanical transition between globally rigid and flexible. Remarkably, the observed QSFR variations, including these key points, do not correlate to global structural similarity measures, such as the root mean squared deviation (RMSD) in atomic positions. Moreover, the mDCM predictions of mechanical and thermodynamic response cannot be explained from small differences in global properties of the H-bond network. In fact, even the most similar TRX pair in regards to the H-bond network reveals substantial QSFR variance due to just a few critical H-bonds. This result highlights the sensitivity of QSFR analysis to the detailed properties of the underlying H-bond network.

RESULTS AND DISCUSSION

Thermodynamic properties

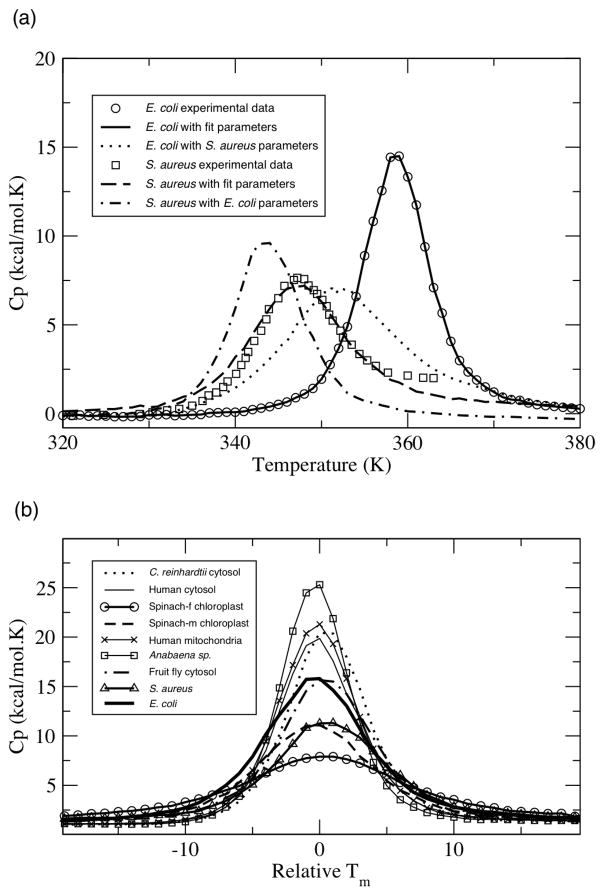
Published C_p curves for two (E. coli and S. aureus) oxidized TRX homologs are currently available [26, 27]. Using our previously described simulated annealing procedure [15], best-fit parameters, {u, v, δ_nat}, have been determined for each. The two best-fit parameter sets, which are qualitatively similar, are provided in Table 2. Crossing the best-fit parameters, meaning applying the E. coli parameters to S. aureus and vice versa, causes the melting temperature, T_m, to be downshifted a small amount; however, a two-state transition and single C_p peak is maintained (see Figure 1a). Conservation of a cooperative transition indicates that the mDCM provides reasonable thermodynamic descriptions; even when less than perfect parameters are applied. Consequently, to eliminate arbitrariness, we subsequently apply the E. coli best-fit parameters to the other TRXs considered here.

Table 2.

Best-fit parameter values.¹

	E. coli	S. aureus
u	−2.24	−2.44
v	−0.89	−0.95
δnat	0.97	1.48

¹The units of u and v are kcal/mol, whereas δ_nat is a dimensionless pure entropy.

Figure 1.

Oxidized thioredoxin heat capacity, C_p, curves. (a) C_p curves of the E. coli and S. aureus homologs are shown. Open circles are experimental data [26, 27], whereas lines are predicted best-fit C_p curves obtained from simulated annealing. In addition, the predicted C_p curves after crossing the “crossing” the best-fit parameters are also shown. (b) C_p curves, shifted to a relative melting point, of all nine thioredoxins using the E. coli best-fit parameters.

Application of the E. coli best-fit parameters to all TRXs results in two-state transitions and a single peak in C_p (Figure 1b). The assumption of parameter transferability is reasonable given that DCM parameters are constructed to have physical meaning, and thus such values should be more or less constant across the relatively homogeneous family. Sequence and structure conservation across the TRX family has been appreciated for some time [28]. Previously, we have used the same strategy on four bacterial periplasmic binding proteins (bPBPs). In the bPBP work, we demonstrated that the height of predicted C_p curves, called C_p^max, are linearly related to the number of H-bonds within the structure (R = 0.90). Interestingly, this is not the case here (R = 0.12). This result is naively counterintuitive. One might expect greater correlation between a global H-bond characteristic and thermodynamic descriptions in more conserved families. However, just the opposite is found. When H-bond networks are similar, there is not enough diversity present to correlate to differences in C_p^max. In contrast, the large variance found in the H-bond network within the bPBP family did manifest as the dominant factor governing C_p^max. For example, the number of H-bonds varies between 293 and 504 within the bPBP dataset, whereas the variance in H-bond number within the TRX family is only 18. A similar decrease in correlation between number of H-bonds and T_m is found. The number of H-bonds was more correlated to T_m in our previous investigation across the bPBP family (R = 0.69) than that across the TRX family (R = 0.41). In fact, no single structural parameter identified here is strongly correlated to TRX C_pmax. These results highlight how subtle variations within the H-bond network and the strength of individual H-bonds can result in pronounced and unexpected changes in thermodynamic and/or mechanical response. This high level of sensitivity is rooted in the nonadditive properties of the free energy decomposition [13–16].

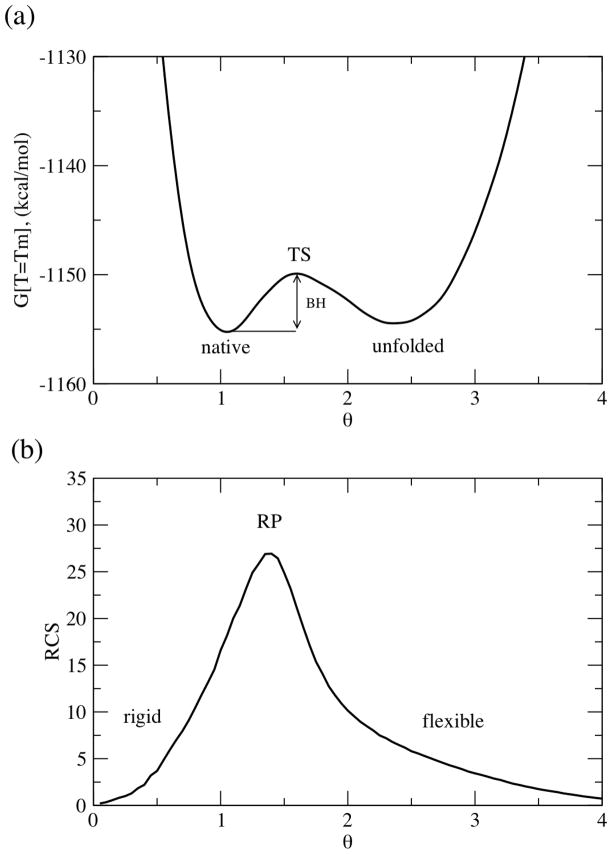
The two-state nature of the transition is identified using the free energy landscape. While the free energy landscape is initially computed as a function of the number of native torsion constraints and number of H-bonds, as seen in Eq. (1), it is convenient to express the free energy as a function of the global flexibility order parameter, θ. The global flexibility order parameter is defined by: θ(N_nt, N _hb) ≡ I_dis(N_nt, N_hb)/n, where I_dis(N_nt, N_hb) is the average number of independent disordered constraints and n is the number of residues within the protein. Figure 2a plots a typical free energy landscape, G(T,θ). At T=T_m, all free energy landscapes include two minima, which highlight the native and unfolded metastable states, and a straddling free energy barrier, G_bar. Table 3 underscores that there is much variability within G_bar,, whereas the location of key points along the one-dimensional free energy landscape are much more conserved. The height of the free energy barrier is not correlated with any structural input; however, it is strongly correlated (R = 0.89) with C_p^max. A similar result was observed in the bPBP family.

Figure 2.

An exemplar (a) free energy and (b) rigid cluster susceptibility landscape. The native state, unfolded state, and crossover point are labeled in each panel.

Table 3.

Characterization of the TRX homologs used in this report.

Source	Tm1	Cpmax2	Hyst.3	Gbar4	θnat5	θTS	θ unf	θRP
E. coli	359	13.9	10.0	0.6	0.9	1.8	2.2	1.2
S. aureus	343	11.3	9.9	1.2	1.2	1.6	2.1	1.2
Spinach-m cholorplast	349	11.1	18.8	1.0	1.3	1.7	2.2	1.3
Anabaena sp.	366	25.3	62.8	5.4	1.0	1.6	2.4	1.4
Human mitochondria	376	21.3	61.0	2.5	1.1	1.7	2.2	1.3
C. reinhardtii cytosol	385	20.4	67.9	5.1	1.1	1.7	2.3	1.3
Spinach-f cholorplast	366	7.9	9.0	0.4	1.5	1.8	2.3	1.4
Fruit fly cytosol	379	15.6	30.0	1.9	1.3	1.9	2.5	1.4
Human cytosol	369	19.9	52.9	3.6	1.2	1.7	2.4	1.3
Average	365.8	16.3	35.8	2.4	1.2	1.7	2.3	1.3
Standard deviation	13.7	5.8	25.2	1.9	0.2	0.1	0.1	0.1

¹Melting temperature (K).

²Peak height of the heat capacity curve in units of kcal/mol·K.

³Hysteresis temperature range (K).

⁴The height of the straddling free energy barrier (units are kcal/mol) separating the native and unfolded basins within the one-dimensional free energy landscapes.

⁵Key points along the one-dimensional free energy landscape at the respective T_m are provided: θ_nat ≡ minimum of the native free energy basin, θ_TS ≡ location of the transition state barrier, θ_unf ≡ the minimum of the unfolded free energy basin, and θ_RP ≡ rigid cluster percolation threshold.

Hysteresis is identified when both the native and unfolded states are present within the ensemble. Previously [16], we have used the hysteresis temperature range to help explain the varying mechanisms of thermal denaturation between E. coli and T. thermophilus RNase H orthologs. The sizes of the TRX hysteresis temperature ranges are provided in Table 3, which are strongly correlated to G_bar and C_p^max (R = 0.93 and 0.81, respectively). These relationships are not surprising because they are related to ensemble populations in similar way. Specifically, C_p is a direct measure of energetic fluctuations across the ensemble, G_bar characterizes the kinetics of the native → unfolded transition, and hysteresis highlights the temperature regime in which the transitions occur. Our previous comparison of the orthologous RNase H pair revealed that native state energy, at T_m, is quantitatively conserved, whereas native state entropy was much more variable. We find the same trend here. The standard deviation within H(T_m, θ_nat) is 24.2 kcal/mol, whereas the standard deviation within -T_mS(T_m, θ_nat) is nearly twice that (48.1 kcal/mol). This result is due to the nonadditive nature of component entropies within the DCM and highlights how global properties nontrivially emerge from local variations with the network topology. For example, while H(T_m, θ_nat) is strongly correlated to total H-bond energy (R = 0.89), -TS(T_m, θ_nat) is not (R = 0.28). (Note that H(T_m, θ_nat) is not perfectly correlated to total H-bond energy due to the presence of native torsion energies and the fact that competing H-bonds to solvent vary as a percentage of the parent intramolecular H-bond.)

Characterizing the mechanical transition

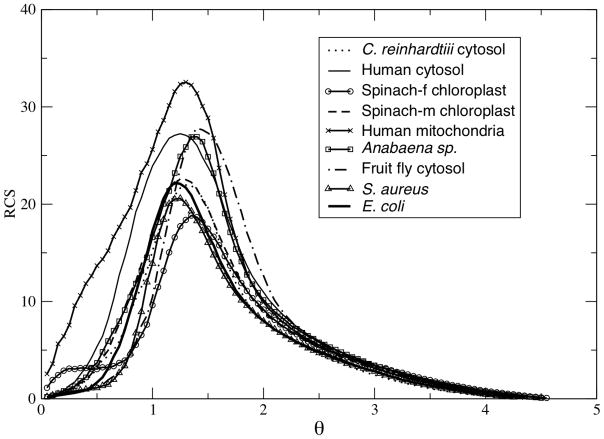
As the flexibility order parameter increases, the protein transitions from a native to unfolded state. The one-dimensional free energy landscapes characterize the thermodynamic aspects of the transition (Figure 2a). Similar to how heat capacity is be used to locate the thermodynamic melting temperature, the rigid cluster susceptibility, RCS, characterizes a mechanical transition that describes the protein changing between being globally rigid to flexible (Figure 2b). Specifically, RCS quantifies the amount of rigid cluster size fluctuations occurring across the ensemble (see [14] for details). At low θ, the protein is principally exploring the native state. The native state is predominately composed of a single large rigid cluster, plus many attached small rigid clusters forming non-cooperative flexible sidechains. At large θ, the protein is primarily exploring the unfolded state, which is composed of many disjoint small clusters. The largest rigid clusters at large θ generally come from α-helices that remain intact due to their intrinsic stability. At both extremes, RCS is low due to lack of fluctuations. However, at intermediate values of θ, the RCS peak signifies the point, called the rigidity percolation threshold (θ_RP), where there is maximum rigid cluster size fluctuation (see Figure 2b). The rigidity threshold corresponds to a point where the protein transitions mechanically from a globally rigid to flexible structure, or vice versa. Figure 3 compares RCS for all nine oxidized TRXs. While the location of θ_RP is somewhat conserved, there are significant differences within the amount of fluctuations (characterized by RCS peak height and width) occurring across the ensemble. No correlation to structural input is found for either RCS peak height or width. However, RCS peak height is correlated to C_p^max (R = 0.71). Again, this result is not surprising as both metrics quantify fluctuations, albeit from fundamentally different points of view, across the ensemble. This result is extremely important because it highlights how the underlying ensemble of constraint topologies fundamentally couples the mechanical and thermodynamic descriptions.

Figure 3.

Rigid cluster susceptibility curves for all nine thioredoxins. The peak marks the mechanical transition of the protein from being predominantly composed of a small number of larger rigid clusters to it being composed of a large number of small clusters.

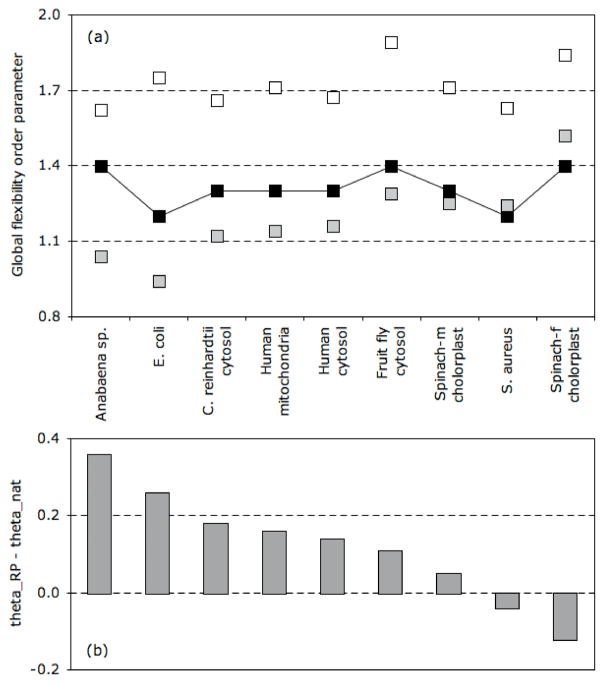
The θ_RP values are provided in Table 3. As with key points along the free energy landscape, no global correlation to structure input is observed. However, interesting properties emerge when comparing θ_RP to key points along the one-dimensional free energy landscape. Previously [14], we have compared θ_RP to θ_TS in order to assess the compactness of the transition state. Across the nine oxidized TRXs, θ_RP < θ_TS, meaning the TRX transition states are voluminous since the mechanical transition precedes the thermodynamic transition. In fact, the mechanical transition actually precedes the location of the native state basin in two cases. Consequently, the native states, in addition to the transition states, of these two TRX homologs are also rather voluminous. Figure 4 highlights the relationship between the mechanical and thermodynamic transitions in each of the nine oxidized homologs. The native state of TRX-2 from Anabaena sp. is predicted to be extremely compact (θ_RP ≫ θ_nat), which results in noteworthy mechanical linkage properties. At the other extreme, the native state of TRX-f from spinach chloroplast is predicted to be voluminous (θ_RP < θ_nat), which, in turn, results in clearly distinct mechanical linkage properties. The key points that characterize certain types of mechanical and thermodynamic response, when taken together lend themselves for defining a global flexibility signature for a protein, discussed further below.

Figure 4.

(a) Relative locations of key points along the free energy landscape and mechanical response functions are indicated. The grey and white squares indicate θ_nat and θ_TS, respectively, whereas the black squares indicate θ_RP (the solid line is provided to guide the eye). (b) Across the TRX family, most of the differences within QSFR can be explained by the relative locations of the native state and mechanical transition, θ_RP − θ_nat. Specifically, TRX homologs in which the native state basin significantly precedes the mechanical transition (i.e., Anabaena sp. and E. coli) are predicted to be more compact, whereas TRX-f from spinach chloroplast is expected to be voluminous since θ_RP < θ_nat.

Backbone flexibility

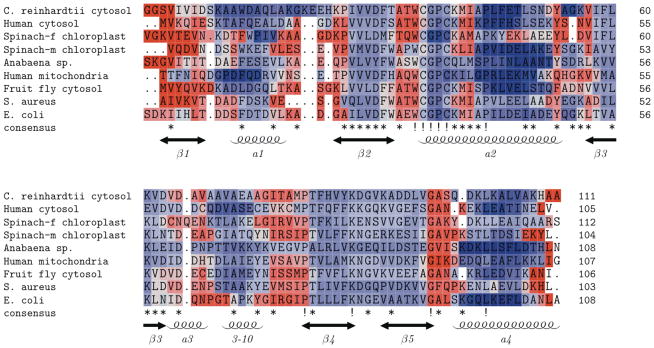
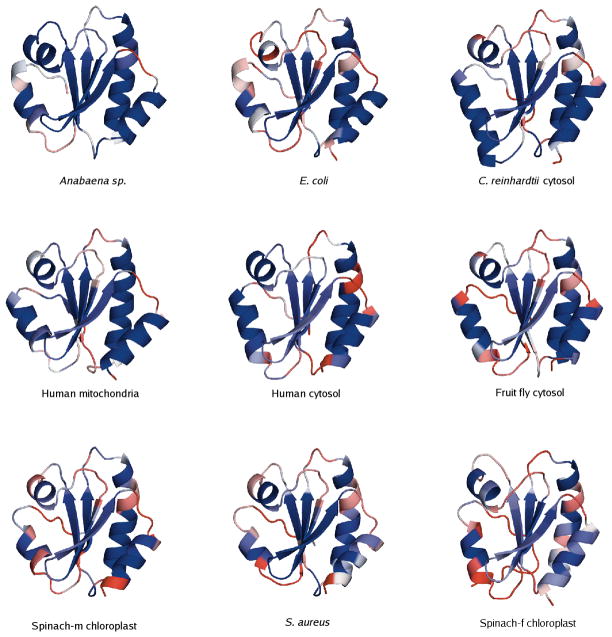
A QSFR flexibility metric, F_index, characterizes backbone flexibility. Positive F_index values reflect the amount of excess degrees of freedom in flexible regions, and negative values reflect the amount of excess constraints in rigid regions (see [25] for an exact definition). In our earlier investigation of bPBPs, we found that F_index is largely conserved across that family. Plotting F_index against the aligned backbone position for the nine oxidized TRXs reveals F_index conservation is even greater across the TRX family. The general conservation of backbone flexibility is highlighted in Figure 5, where the multiple alignment has been color-coded by F_index (red = flexible; blue = rigid) using TEXshade [31]. Across the alignment, secondary structure elements appear more rigid, whereas intervening loop regions are more flexible. In all cases, the N- and C-terminus have high flexibility, and the flexibility of the N-terminus extends through strand β1. All other B-strands are marginally rigid, while there is considerable variation in the α-helices. Helices α1 and α4 are among the most rigid portions of the protein, whereas the short helix α3 is somewhat flexible. The long helix α2, containing the conserved active site sequence WCGPC, displays the most intriguing behavior. Tracing from the N-terminus, the tryptophan is flexible, yet the redox-active cysteines are rigid. Immediately after the active site, there is a curious stretch of flexibility within α2 from all but two of the TRX homologs. For the most part, the remainder of the helix is very rigid. Ribbon diagrams (Figure 6) highlight the active site differences across all nine homologs, while also displaying an overall conservation of flexibility/rigidity profiles.

Figure 5.

Multiple sequence alignment of the nine oxidized thioredoxins color-coded by F_index values. Isostatic residues, F_index = 0, are colored white, flexible residues are colored red, and rigid residues are colored blue. While local variations are present, a global conservation of backbone flexibility that is consistent with secondary structure is observed.

Figure 6.

Ribbon diagrams of the nine oxidized thioredoxins color-coded by F_index. Obvious differences within the active site are present; nevertheless, an overall conservation of flexibility/rigidity is observed. Each structure is oriented in the same way and centered on the active site region. Ordering is based on the relative values of θ_RP and θ_nat.

Exceptions to the above canonical rigidity/flexibility profiles are: (i.) the lack of the small flexible region within TRX-2 from Anabaena sp. and human mitochondria, (ii.) the lack of flexibility within the coil region connecting the 3–10 helix and strand β4 in the Anabaena sp. homolog, and (iii.) decreased rigidity of the c-terminal end of helix α2 within TRX-f from spinach chloroplast, TRX from E. coli, and TRX from S. aureus. The increased rigidity of TRX-2 from Anabaena sp. and the diminished rigidity within the spinach chloroplast and S. aureus homologs follow along with naïve expectations based on the above θ_RP versus θ_nat comparisons. On the other hand, the diminished rigidity of TRX from E. coli is puzzling as this trend is actually counter the θ_RP versus θ_nat comparisons. Finally, the θ_RP versus θ_nat comparisons do not suggest anything unique about human mitochondria TRX-2. Nevertheless, like TRX-2 from Anabaena sp., it too lacks the flexible region within α2 at the active site. It is worth noting that these are the only two TRX-2 orthologs within the dataset, which may explain their similarity in this regard. Another interesting variation occurs within the active site flexibility of the two TRX homologs from spinach chloroplast. The active site tryptophan of TRX-f is predicted to be more flexible than that of TRX-m, with F_index values of 0.39 vs. −0.12. Encouragingly, the same result had been seen in previous crystallographic analysis, where the flexibility of the active site tryptophan in TRX-f was seen as a possible factor in explaining the different substrate specificities of the two spinach TRXs [32].

Cooperativity correlation

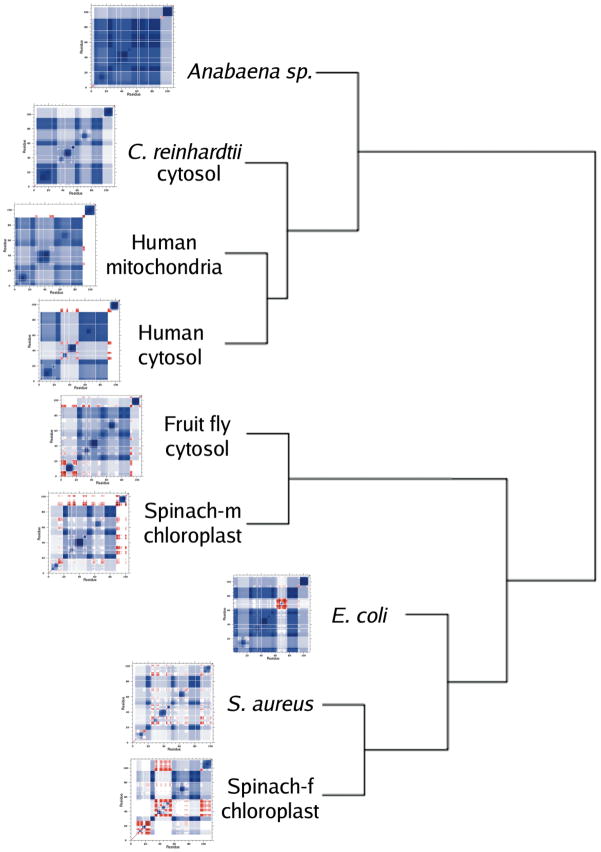
Cooperativity correlation plots describe correlations between a pair of residues in the native state at the respective T_m that are either rigidity correlated, flexibly correlated, or not correlated. Blue regions correspond to rigidity correlation, giving the extent that two residues simultaneously fall within the same rigid cluster. Red regions correspond to flexibility correlation, giving the extent that a pair of residues is simultaneously flexible within a path that flexibility can propagate. White regions indicate no discernable mechanical coupling between the two residues. In our investigation of bPBPs, we observed a large amount of variation within cooperativity correlation. While bPBP backbone flexibility was generally conserved, bPBP cooperativity correlation was not. The variability within cooperativity correlation was ultimately explained by key differences within the H-bond network, even after normalizing for the different sizes of the proteins. Because the TRX H-bond network is much more conserved, we initially expected QSFR metrics to exhibit conserved properties. Surprisingly, we observe considerable diversity and richness in cooperativity correlation, as shown in Figure 7, for all nine oxidized TRX proteins. To quantify the degree of similarity and differences, all 36 pairwise correlations coefficients were calculated. The average Pearson pairwise correlation coefficient over all 36 pairs is 0.68 (standard deviation = 0.10). The all-to-all pairwise statistical analysis reveals that while some local patterns are well conserved, as was also the case in the bPBP family, certain features of each protein are quite distinct. Some interesting specific details on the similarities and differences are now discussed.

Figure 7.

Cooperativity correlation plots describing intramolecular couplings for the nine oxidized thioredoxins. Blue regions indicate the extent that two residues are simultaneously within the same rigid cluster. Red regions indicate the extent that two residues exist within the same flexible region where the flexibility contiguously propagates. White indicates no correlation between two residues in regards to their rigidity and flexibility. While some similarity in patterns can be seen, the details of each protein are quite distinct. The presented dendrogram describes the hierarchical clustering of a correlation matrix constructed from all 36 pairwise comparisons using the Pearson correlation coefficient. In all cases but one, clustering preserves the relative values of θ_RP and θ_nat.

The large amount of blue color indicates that the native states of all TRX homologs are primarily composed of one large rigid cluster. However, the size and details of the rigid cluster are quite variable. For example, the largest rigid cluster in TRX-2 from Anabaena sp. covers, on average, residues 5–91. Across the other seven homologs, the largest rigid cluster is not contiguous in sequence. The large swaths of lighter color (and, at the extreme, red color) demarcate regions not included within the rigid cluster. Most often, it is the region spanning from helix α2 to strand β3 (~25–55) that is not included within the rigid core. Additionally, in all of the TRXs, the c-terminal helix α4 is disjoint from the rest of the network. While α4 is, in and of itself, mostly rigid (see Figure 5), it is generally not part of the core of the protein. However, we stress that the cooperativity correlation plots represent averages of mechanical couplings between two residues based on the ensemble of constraint topologies. As such, the extent of α4 separation from the core rigid cluster varies across the family. There is virtually no interaction of α4 and the core (as highlighted by the predominantly white band at the c-terminal end of Figure 7) within the human cytosol, human mitochondria, and spinach chloroplast (TRX-m) homologs. Conversely, there is noticeable interaction within Anabaena sp. TRX-2. Note that we have previously reported this separation of α4 from the core in our description of the E. coli homolog [15]. In fact, we demonstrated that cleaving the backbone just prior to the start of α4 was actually stabilizing due to conformational entropy effects.

The mostly rigidly correlated behavior of Anabaena sp. TRX-2 is consistent with the above θ_RP versus θ_nat analysis, indicating the native state is mainly a single large rigid cluster. Expanding this analysis to all nine homologs reveals a clear relationship between the relative positions of θ_RP and θ_nat, and the extent of cooperativity correlation. The Anabaena sp., E. coli, C. reinhardtii, human mitochondria, and human cytosol homologs are predicted to have the most compact native states, which is consistent with their structures being mostly rigidly correlated, θ_RP ≫ θ_nat. The native states of TRX from fruit fly cytosol and TRX-m from spinach chloroplast are also expected to be compact, θ_RP > θ_nat, but not as much as the previous five. A concomitant reduction of rigidity correlation is observed in these two. Finally, TRX from S. aureus and TRX-f from spinach chloroplast, which are identified as having voluminous native states (θ_RP < θ_nat), are the most flexibly correlated (an thus, the least rigidly correlated).

Similarity and differences within the cooperativity correlations are quantified by constructing a dendragram (see Figure 7) from a distance matrix based on the 36 pairwise comparisons introduced above (see Supplementary Table 1). Amazingly, with only a single exception, the clustering in Figure 7 is exactly consistent with the differences between θ_RP and θ_nat plotted in Figure 4. Specifically, the largest cluster of four TRX homologs, which includes Anabaena sp., C. reinhardtii, human cytosol, and human mitochondria, represent four (of the five) homologs with the largest difference between the thermodynamic and rigidity transitions, defined as θ_RP ≫ θ_nat. The two TRXs with the smallest positive difference, θ_RP > θ_nat, (namely, TRX-m from spinach chloroplast and TRX from fruit fly cytosol) cluster together, whereas the two TRXs with θ_RP < θ_nat (namely, TRX-f from spinach chloroplast and TRX from S. aureus) form a cluster distinct from the rest of the family. The sole outlier is the E. coli TRX, which clusters near the fruit fly TRX/spinach TRX-m cluster. By eye, it is clear that the large swath of reduced rigidity approximately centered on residue 40 that is present in three of the four TRXs in the largest cluster is absent within the E. coli homolog. Moreover, traces of the decreased rigidity about α4 within the E. coli homolog can be observed within the homologs it clusters with.

Identifying allostery using cooperativity correlation

It is evident that identifying relationships between the mechanical and thermodynamic transitions may have far-reaching consequences, including, connecting cooperativity correlation to allostery. Successful identification of allostery from cooperativity correlation data rest on the assumption that the intrinsic equilibrium fluctuations of the native state appropriately reflects the response of a protein to perturbation. This critical assumption is in the spirit of linear response theory, for which there is mounting evidence from computational [33] and experimental [34] studies that this assumption works well. Along this same line, we have demonstrated that the distribution of rigidity throughout a protein is a statistically significant determinant for long-range intramolecular couplings that exhibit nonadditivity in free energy changes within double mutant cycles [35]. Meaning, the intrinsic properties of mechanical response of a protein correlates to free energy couplings between two point mutations. Because a cooperativity correlation plot is based on an ensemble average of mechanical couplings, the “old” view of allostery [36] is captured as a series of concerted mechanical events propagating through the protein structure. Specifically, regions within the cooperativity correlation plots colored blue are mechanically coupled through rigidity, whereas mechanical pathways in which flexibility can propagate are colored red. The high density of constraints that defines a rigid cluster provides a network of interactions that physically couple all residue pairs within the cluster. However, the rigid regions are not necessarily static, as they themselves are allowed to fluctuate as constraints break and form.

The “new” [36] view of allostery (commonly called the population shift model [37–41]) is also captured because the appropriate Boltzmann factors are accounted for during ensemble averaging. In other words, the free energy basin (a local minimum) controls the most probable constraint topologies, and the fluctuations of constraints around the most probable topology unify mechanical and thermal response. For example, as the temperature is lowered or raised, constraints are more easily formed or broken, and the mechanical properties change. More interestingly, the temperature dependence for a constraint to break (or form) strongly depends on all other constraints (i.e. their strength and where they are distributed) because network rigidity is a long-range interaction. Consequently, cooperativity correlations depend on solvent and thermodynamic conditions, and are sensitive to mutations that induce changes in constraint topology, so that the “old” mechanical view and the “new” thermodynamic view are united. Despite overall similarity between the TRX proteins within the family, the diversity found in cooperativity correlation suggests that allosteric response will also vary significantly within the TRX family, which is consistent with observations across other protein families [42–47]. To understand allostery further with a direct connection to experimental data, the next step is to calculate redistributions in backbone flexibility and cooperativity correlation due to an external perturbation. Recording the response of a protein to an applied external perturbation that increases or decreases a local energy term has proved to be a successful approach using Ising-like models [48–51] that stress thermodynamic aspects, and with elastic network models [52, 53] that stress mechanical aspects. This perturbation approach is in progress using the mDCM, where both the thermodynamic and mechanical nature of the response is tracked.

Pairwise comparisons

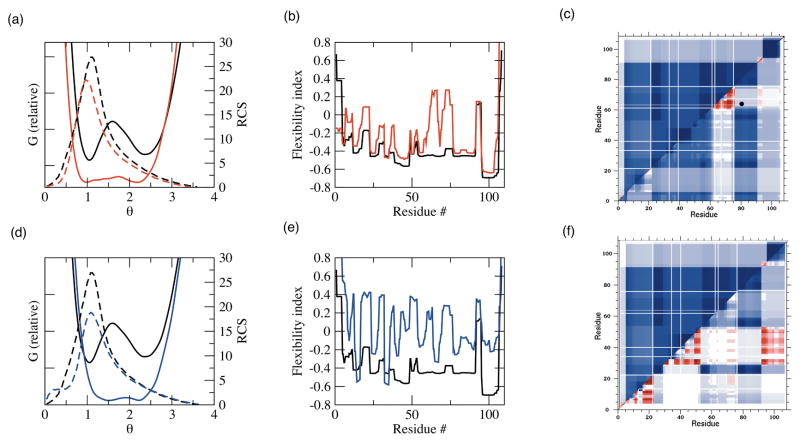
The chief problem of analyzing such large amounts of QSFR data is being able to concisely explain all mechanistic variations. As such, we chose to primarily focus on two exemplar pairwise comparisons, specifically: Anabaena sp. TRX-2 to E. coli TRX and Anabaena sp. TRX-2 to TRX-f from spinach chloroplast. The Anabaena sp. and E. coli homologs represent the case with the largest gap between θ_RP and θ_nat, whereas the TRX-f from spinach chloroplast homolog represents the opposite trend. As such, these two pairs bookend the full range of observed variations in QSFR metrics across the nine TRX proteins. Figure 8 highlights that the pairs are near the two extremes of pairwise H-bond conservation across the dataset. As expected, H-bond network conservation is closely related to pairwise structural (Figure 8a) and sequence similarity. After adding additional protein families to the analysis (unpublished results), a quadratic relationship between pairwise H-bond conservation and pairwise structure or sequence similarity is revealed that resembles the famous Chotia and Lesk plot [54] showing a similar relationship between pairwise sequence and structure similarity. The H-bond networks within the Anabaena sp./E. coli pair are 70% conserved (averaging over Figure 8b), whereas they are only 39% conserved across the Anabaena sp./spinach chloroplast pair. Across the former pair, it is remarkable that such drastic QSFR variations can occur in spite of such global similarity within their underlying H-bond networks (see Figure 9a–c). This result highlights the long-range nature of rigidity and how a small number of well-placed constraint differences will drastically affect the mechanical linkage properties. As expected, the latter pair exhibits even greater diversity within the QSFR metrics (Figure 9d–f). Curiously, despite only 23% pairwise sequence identity, TRX-2 from Anabaena sp. displays some known functional relationships to TRX-f from spinach chloroplast. Differing with respect to all other TRXs, it has been shown that TRX-2 and TRX-f easily reduce spinach chloroplast fructose bisphosphatase [55]. This functional similarity is not suggested by the QSFR analysis herein. While functional relationships might be inferred by consideration of QSFR measures, this type of approach would require application of more sophisticated pattern recognition methods, and doing so is beyond the scope of the current work. However, it is known that TRX-f has other distinguishing properties that differentiate it from all other TRXs such as the ability to be reduced by glutathione and the lack of many otherwise conserved TRX residues. Therefore, the large QSFR differences predicted between TRX-f and other TRXs is intriguing.

Figure 8.

Pairwise H-bond comparisons across the dataset. (a) Pairwise H-bond conservation vs. pairwise RMSD. Closed circles represent the 36 pairwise comparison of the nine oxidized thioredoxins. Grey indicates the two pairs described in (c) and (d), whereas open circles identify the three redox pairs. (b) Pairwise H-bond conservation vs. pairwise sequence identity (%). Color-coding is the same as in (a). (c) Pairwise H-bond conservation vs. H-bond cut-off energy for the Anabaena sp. TRX-2 to E. coli TRX pair (grey) and the Anabaena sp. TRX-2 to spinach chloroplast TRX-f pair (black). As can be clearly seen, the extent of H-bond conservation diminishes at more stringent cut-offs. (d) The rank ordering (1=most conserved; 36=least conserved) of the H-bond conservation over each of cut-off energy.

Figure 9.

Pairwise comparisons of QSFR descriptions. The TRX-2 from Anabaena sp. and TRX from E. coli pair are shown on top, whereas the TRX-2 from Anabaena sp. and TRX-f from spinach chloroplast pair on shown on bottom. The thermodynamic (G(T=T_m,θ)) and mechanical (RCS) landscapes are shown in (a) and (d). G(T=T_m,θ) is shown in solid line, whereas RCS is shown in dashed line. Backbone flexibility, F_index, is shown in (b) and (e). In panels (a), (b), (d), and (e), TRX-2 from Anabaena sp. is colored black, TRX from E. coli is colored red, and TRX-f from spinach chloroplast is colored blue. In panels (c) and (f), cooperativity correlation is compared for each TRX pair (TRX-2 is always in the top-left). Color-coding in the cooperativity correlation plots is the same as in Figure 7.

The QSFR analysis described above shows TRX-2 from Anabaena sp. is one of the most atypical across our dataset. The Anabaena sp. homolog shows much more extensive regions of correlated rigidity compared to the others. The striking difference between it and the E. coli homolog (Figure 9c) is especially surprising considering the large amount of H-bond network similarity. Moreover, global descriptions of the H-bond network (i.e., number of H-bonds, average H-bond energy, and total H-bond energy) are virtually identical. Despite great global similarities in the H-bond network, it is known that TRX-2 from Anabaena sp., like TRX-f from spinach chloroplast, actually possesses quite different functional properties (i.e., unusual enzymatic activities and substrate specificities) from other common TRXs [56]. It is encouraging that the mDCM is sensitive to such subtle differences in H-bond topology and strength.

The effect of redox state

Crystal structures for three reduced/oxidized TRX pairs are currently available. As such, we attempt to elucidate the differences within QSFR that arise from the loss of the active site disulfide. Human cytosolic TRX was the first redox pair solved, with the oxidized form obtained from reduced form crystals by air exposure [57]. The pair showed only minute overall differences (pairwise RMSD = 0.2Å), with the greatest changes, as expected, localized at the active site. Structural changes were also observed near the dimer interface. The first redox pair of crystals grown independently was from fruit fly cytosol TRX [58]. Once again, few global differences were observed (pairwise RMSD = 0.5Å), and the largest localized differences occurred near the active site. Finally, a third redox pair has been crystallized from human mitochondria [59]. Like the previous two pairs, the redox pair is nearly equivalent (pairwise RMSD = 0.2Å). After averaging over the six molecules in the asymmetric unit, there is less deviation between redox pair than there is after averaging only over the oxidized (or, similarly, reduced) structures. Meaning, TRX exhibits minimal global conformational changes during its functional cycling between oxidized and reduced forms.

While the static structures of oxidized and reduced TRXs appear mostly similar, putative dynamic differences are impossible to fully quantify from the static comparisons. The DCM is well suited to detect differences in these structures based on their underlying H-bond networks. Using the same parameter set as above, the reduced structures exhibit a two-state folding transition, albeit the heat capacity curves have slightly smaller C_p^max values (Figure 10a) with lower melting temperatures. The lowered T_m values of the reduced structures are consistent with the diminished stability of the reduced form, as demonstrated by the thermal stability analysis of Hiraoki et al. [60]. This consistency between our predicted relative stabilities and those determined experimentally gives confidence that the mDCM is qualitatively identifying proper two-state transitions. As can be seen in Figure 10b, the subtle structure rearrangements have a marked effect on backbone flexibility. Overall, the two human structure pairs, where the reduced form was obtained from oxidized crystals, display more similar flexibility differences. Some of the differences seen for the fruit fly TRX may be due to the differing crystal forms used. In all three examples, there is considerable flexibility increase at the active site. This is expected because the loss of the constraint specified by the disulfide bond should lead to increased mechanical flexibility in the immediate surrounding region. While most differences, few that they are, between TRX redox pairs are localized to the active site [57–59], a general “loosening” of the entire protein structure is revealed by NMR order parameters [61, 62]. In line with these NMR results, we also observe that several structurally remote regions exhibit increased flexibility.

Figure 10.

(a) Heat capacity curves for oxidized (solid lines) and reduced (dashed lines) TRX pairs. In each case the reduced form curve shifts to a lower T_m. (b) Change in backbone flexibility, $F_{\mathit{index}}^{\mathit{red}}-F_{\mathit{index}}^{ox}$, upon variation within redox state. (c) Cooperativity correlation plots comparing each reduced (top triangle) and oxidized (bottom triangle) TRX pairs. Color-coding is the same as in Figure 7.

Intriguingly, our results also indicate that some regions actually become more rigid upon reduction. This effect occurs due to the release of strain energy contained within the oxidized active site region [15]. Removal of the disulfide allows other regions to become better packed, resulting in a more optimized H-bond network. The NMR work described above is for E. coli TRX (to the best of our knowledge, NMR order parameters comparing oxidized and reduced human or fruit fly TRX pairs do not exist). It is interesting to note that the protection factors reported in [61] indicate that there is a small region of increased rigidity just prior to the active site that is consistent with the rigidity increase we observe in the fruit fly TRX (see Figure 10b). However, an increase in rigidity in this specific region is not predicted by the mDCM for the two human TRX pairs. For the same reason of better packing, the two reduced human TRXs are predicted to have an increase in rigidity at the c-terminal ends. While the predictions form the mDCM are subject to being an artifact of an oversimplified model or the uncertainties within the X-ray crystal structure, these results point to a plausible mechanism of structural rearrangement. There is also the general problem that the time scale probed by NMR is very fast (ps-ns), whereas the DCM flexibility predictions describe quasi-stationary motions. It will be interesting to know if future experiments will be able to confirm the nuanced details of where increased rigidity is predicted in the different TRX pairs, such as the c-terminal ends that we predict for the two reduced human TRXs.

Figure 10c compares cooperativity correlation between the reduced and oxidized pairs. In two of the three cases (TRX-2 from human mitochondria and TRC from human cytosol), there is a general decrease in rigidity correlation, whereas the human cytosol pair is virtually unchanged. Consistent with the above results, the relative changes within rigidity correlation are consistent with the relative locations of θ_RP and θ_nat. To highlight this point, we define χ as the change in the relative positions of θ_RP and θ_nat of the oxidized and reduced structures (see Table 4). In the fruit fly cytosol pair, χ = 0.0, which is consistent with the pair’s strongly conserved cooperativity correlation plots. Conversely, the other two pairs show diminished rigidity correlation, which is predicted by χ = 0.3 and 0.4. Likewise, the increased flexibility within the reduced human homologs parallels the reduced rigidity correlation, even though the exact details and extent of the change are not conserved. Taken as a whole, the general trends in QSFR upon TRX reduction is consistent with the observations across the nine TRX homologs. It is important to note that attempts to understand how QSFR is manifest in terms of simple global metrics all failed, and rather, the differences are attributed to subtle differences in the H-bond network.

Table 4.

Comparisons of oxidized and reduced thioredoxin pairs.¹

Source	Tm	Cpmax	Hyst.	Gbar	θnat	θTS	θunf	θRP	χ2
Human mitoch. (ox)	376	21.3	61.0	2.5	1.1	1.7	2.2	1.3	--
Human mitoch. (red)	360	11.4	36.9	2.3	1.4	1.9	2.4	1.3	--
Difference	16	9.9	24.1	0.2	−0.3	−0.2	−0.2	0.0	0.3
Fruit fly cytosol (ox)	379	15.6	30.0	1.9	1.3	1.9	2.5	1.4	--
Fruit fly cytosol (red)	354	6.4	7.5	0.4	1.5	1.8	2.2	1.2	--
Difference	25	9.2	22.5	1.5	−0.2	0.1	0.3	0.2	0.0
Human cytosol (ox)	369	19.9	52.9	3.6	1.2	1.7	2.4	1.3	--
Human cytosol (red)	357	16.1	43.0	3.1	1.2	1.8	2.4	1.3	--
Difference	12	3.8	9.9	0.5	0.0	−0.1	0.0	0.0	0.4

¹Thermodynamic descriptions of oxidized and reduced pairs. The first nine columns are the same as in Table 3.

²The change in the relative positions of the mechanical and thermodynamic transitions is described by: $\chi \equiv ({\theta }_{RP}^{ox}-{\theta }_{RP}^{\mathit{red}})-({\theta }_{\mathit{nat}}^{ox}-{\theta }_{\mathit{nat}}^{\mathit{red}})$.

CONCLUSIONS

Using the mDCM, we analyze QSFR descriptions of nine oxidized and three reduced members of the TRX family. While backbone flexibility is well conserved in the family, other QSFR metrics reveal rich amounts of diversity in mechanical and thermodynamic response. Intriguingly, QSFR diversity can be mostly explained by comparing the relative locations of the mechanical and thermodynamic transitions, described by θ_RP and θ_nat. However, none of the predicted QSFR properties, including θ_RP and θ_nat, are correlated to global structural properties (i.e., number of H-bonds, average H-bond strength, total H-bond energy, etc.). This result demonstrates how small-scale structural variations are amplified into discernible global differences by propagating mechanical couplings through the H-bond network. Despite the simplicity of the mDCM, its predicted QSFR differences are largely consistent with known functional differences and variations within allosteric response. Further detailed comparisons will be possible upon completion of a more sophisticated DCM that is currently underway, to predict thermodynamic and mechanical response upon perturbation of the protein by mutation or ligand binding.

METHODS

The minimal distance constraint model

All results were obtained by employing the mDCM, which has been extensively defined and explained in previously published work [7, 9, 13–15, 25]. The critical elements are highlighted here. Interactions are modeled as distance constraints that are assigned enthalpy and entropy values. The three-dimensional structure is mapped onto a graph where nodes and edges represent atoms and distance constraints respectively. This graph defines a constraint topology. A fixed constraint topology consists of all accessible molecular conformations consistent with a given set of distance constraints between pairs of atoms. Starting with the input graph, an ensemble of diverse constraint topologies is generated by perturbing away from the input constraint topology. Since each internal dihedral angle can be locked with either a native or disordered distance constraint, and each H-bond or salt-bridge can be present or not, there are ~2⁶³⁵ accessible constraint topologies for thioredoxin. Due to the immense number of possible constraint topologies (graphs), a mean field approximation is invoked by binning states together that have the same total numbers of native torsion constraints and H-bonds, which defines the macrostate of a protein. The number of native torsion constraints and number of H-bonds are used as order parameters. The non-trivial feature of the DCM is that nonadditivity of component entropies is explicitly modeled. Rigidity and flexibility properties of the structure are used to determine if a distance constraint as independent or redundant [10]. The total enthalpy is simply a sum of all enthalpic components; however, the total entropy, which is a nonadditive property [29, 30], is only evaluated over the set of independent constraints.

Using the nonadditivity principles described above, the free energy of each macrostate is calculated by Monte Carlo sampling over topological frameworks that are constrained to satisfy the two order parameters. From this involved, yet computationally efficient procedure, the free energy landscape, partition function, and all resultant thermodynamic quantities, are calculated for TRX in less than a minute on a single CPU. Once the free energy landscape is constructed, it is used to appropriately weight mechanical properties to obtain proper thermodynamic averages. Meaning, the essence of the DCM is to use the mechanical properties to make more accurate thermodynamic calculations based on macromolecular structure, and then, in turn, to use the thermodynamic properties to predict emergent mechanical response.

The free energy function of each macrostate is given by:

$$G(N_{nt},N_{hb})=U_{hb}(N_{hb})-{uN}_{hb}+{vN}_{nt}-T[S_c(N_{nt},N_{hb}\mid {\delta }_{\mathit{nat}})+S_m(N_{nt},N_{hb})]$$ Eq. (1)

where U_hb is the intramolecular H-bond energy, uN_hb describes H-bonding to solvent, vN_nt describes native torsion force energy, S_c(N_nt,N_hb|δ_nat) is the conformational entropy, and S_m(N_nt,N_hb) is the mixing entropy associated with sampling the specified macrostate. The values of the three phenomenological parameters u, v, and δ_nat are determined by fitting to experimental C_p curves from differential scanning calorimetry (DSC). While not specified here, S_c(N_nt,N_hb|δ_nat) is calculated over the set of independent constraints, and this set is sampled using Monte Carlo. Previous work has demonstrated that the predicted thermodynamic and, even more so, mechanical properties are robust to slight parameterization differences. Therefore, a priori assuming parameter transferability is reasonable [14].

Structure preparation

Nine different oxidized and three reduced TRX homologs are investigated here in order to provide a large evolutionary cross-section for analysis, while still being a tractable number for data handling and visual comparison. The dataset (see Table 1) includes homologs from prokaryotic bacteria (E. coli, S. aureus, and Anabaena sp.), eukaryotic microbes (C. reinhardtii), plants (two distinct spinach chloroplast paralogs), and animals (fruit flies and humans) [27, 32, 56–59, 63, 64]. All TRXs investigated here have x-ray crystal structures solved at high resolution (greater than 2.3 Å resolution). Moreover, the structures are remarkably similar; the pairwise α-carbon root mean square deviation (RMSD), computed by combinatorial extension [65], ranges from 0.7 to 1.6 Å. NMR structures of TRXs were also attempted, but gave poorly defined heat capacity transitions. Thus, they were excluded from further analysis.

Table 1.

Summary statistics describing the structures used in this report.

Protein	Source	PDBID	Resol.1	# Res.	# HB	Avg HB E2	RMSD3	Seq Id4
Oxidized structures
TRX	E. coli	2TRX	1.7 Å	108	141	−2.6	0.0 Å	100 %
TRX	S. aureus	2O7K	2.2 Å	103	142	−2.3	1.3 Å	51 %
TRX-m	Spinach cholorplast	1FB6	2.1 Å	104	130	−2.4	1.0 Å	48 %
TRX-2	Anabaena sp.	1THX	1.6 Å	108	142	−2.6	1.0 Å	43 %
TRX-2	Human mitochondria	1W4V	1.8 Å	107	142	−2.5	1.2 Å	38 %
TRX-h	C. reinhardtii cytosol	1EP7	2.1 Å	112	142	−2.5	1.4 Å	36 %
TRX-f	Spinach cholorplast	1F9M	1.9 Å	112	148	−2.5	1.4 Å	32 %
TRX	Fruit fly cytosol	1XWA	2.2 Å	106	145	−2.4	1.2 Å	31 %
TRX	Human cytosol	1ERU	2.1 Å	105	146	−2.4	1.3 Å	27 %
Reduced structures
TRX-2	Human mitochondria	1UVZ	2.0 Å	107	140	−2.3	0.2 Å	100 %
TRX	Fruit fly cytosol	1XWC	2.3 Å	106	141	−2.3	0.5 Å	100 %
TRX	Human cytosol	1ERT	1.7 Å	105	155	−2.2	0.2 Å	100 %

¹The x-ray crystallographic resolution.

²The average hydrogen bond energy (kcal/mol).

³The α-carbon root mean square deviation comparing each structure to the E. coli homolog. In the case of the reduced TRXs, the comparison is to the oxidized state of the same homolog.

⁴The pairwise percent residue identity comparing each sequence to the E. coli homolog. In the case of the reduced TRXs, the comparison is to its oxidized state.

Hydrogen atoms are added to initial structures using H++ web server [66]. In addition to adding missing hydrogen atoms, H++ uses Poisson-Boltzmann continuum electrostatic theory to calculate the appropriate ionization state of the protein and performs an optimization of hydrogen positions. H++ is a convenient method to generate input structures to the mDCM, involving minimal perturbation away from the experimental structure. Employed electrostatic parameters include a salinity of 0.15 M and external/internal dielectrics of 80 and 6, respectively. Output structures were protonated assuming a pH of 7.0, which is consistent with the conditions used in the original DSC experiments.

Hydrogen bond network comparisons

H-bond network similarity is computed on a pairwise basis. Starting with the pairwise sequence alignment of two TRX homologs, equivalent residue positions are identified. Equivalent H-bonds are simply defined by identical donor and acceptor residue pairs. While this residue-level approach does not identify variations that can occur at the atomic-level, a cursory overview of the results suggests that the variation between the two approaches is insignificant. As such, overall H-bond network similarity is simply computed as the ratio of equivalent H-bonds to the average number within each being considered. However, it does not necessarily make sense to consider equivalence within a feeble (E_hb ~ −0.1 kcal/mol) and a strong (E_hb < −6.0 kcal/mol) H-bond. As such, we invoke a series of H-bond energy cut-offs, such that only H-bonds stronger than the cut-off are considered present.

Hierarchical comparison of cooperativity correlation

Using R (http://www.r-project.org/), each cooperativity correlation plot pair is compared using the Pearson correlation coefficients, which are hierarchically clustered using Ward’s method with Euclidean distances. Note that the results are generally conserved when using the Spearman rank correlation instead of Pearson.