Abstract
Camperi and Wang (Comput Neurosci 5:383–405, 1998) presented a network model for working memory that combines intrinsic cellular bistability with the recurrent network architecture of the neocortex. While Fall and Rinzel (Comput Neurosci 20:97–107, 2006) replaced this intrinsic bistability with a biological mechanism-Ca2+ release subsystem. In this study, we aim to further expand the above work. We integrate the traditional firing-rate network with Ca2+ subsystem-induced bistability, amend the synaptic weights and suggest that Ca2+ concentration only increase the efficacy of synaptic input but has nothing to do with the external input for the transient cue. We found that our network model maintained the persistent activity in response to a brief transient stimulus like that of the previous two models and the working memory performance was resistant to noise and distraction stimulus if Ca2+ subsystem was tuned to be bistable.
Keywords: Working memory, Bistability, Computational model, Calcium signaling
Introduction
Since the German psychologist Hermann Ebbinghaus initiated experimental study of human memory, memory has always been the important aspect of research in cognitive psychology. From the research of animals and human beings, according to how long the information can be stored, memory can be divided into long term memory and short term memory which is also known as working memory. Working memory, regarded as a hub of cognitive function by psychologists, provides temporary storage and manipulation of the information necessary for complex cognitive tasks such as language comprehension, learning and reasoning. It is a hot topic of cognitive psychology and cognitive neuroscience research (Baddeley 2003; TaiZhen and FuMei 1998; Guo 2007).
Working memory is the ability to retain and manipulate goal-related information during short periods of time (Fuster 1997). The prefrontal cortex (PFC) is the most closely linked brain structure to working memory (Olesen et al. 2003). During delayed-response tasks, some specific PFC neurons exhibit elevated persistent activity during the whole delay period, whose persistent activity carries information about previous stimulus to guide forthcoming responses to working memory tasks. Thus this type of working memory mainly depends on the maintenance of enhanced firing activity in specific subpopulations of PFC neurons. Furthermore the response accuracy is closely related to delayed time and the longer the delayed time, the lower the response accuracy (Tarnow 2008, 2009).
Different network models have been explored to simulate and explain electrophysiological observations of working memory tasks, including connectionist models (Moody et al. 1998) which neglect the temporospatial dynamics of neurons and synapses, firing-rate models containing some biophysically meaningful time constants, and biophysically realistic spiking-neuron models. Firing-rate and spiking-neuron models have been used to model normal behavior and clinical conditions, learning, neuromodulation and activity profiles in working memory tasks (Braver et al. 1999; Zipser et al. 1993; Colliaux et al. 2009), since they are more closely related to the biophysical mechanisms than connectionist models.
As mentioned earlier, working memory mainly depends on the elevated persistent activity. There are diverse mechanisms that can generate persistent activity. One mechanism is based on the idea that strong recurrent excitatory connections in a ‘cell assembly’ can sustain activity (Hebb 1949). Another hypothesis is that activity circulates in loops, called ‘synfire chains’ (Corticonics 1991), consisting of feedback-connected subgroups of neurons without direct feedback links between successive groups. It is also possible that single neurons can maintain activity via membrane currents that allow cellular bistability (Marder et al. 1996), which is the focus of our research for simplicity.
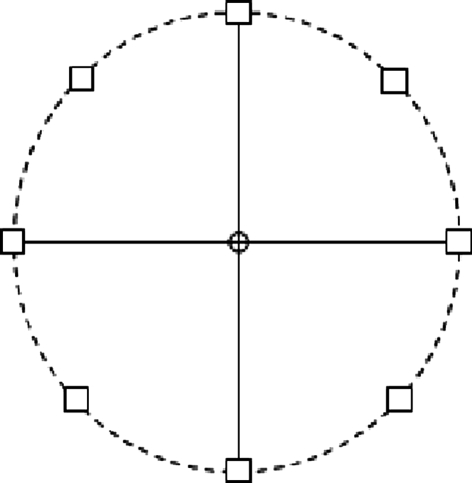
The network model (C-W model) by Camperi and Wang (1998) aims to model and simulate the working memory activity during memory-guided oculomotor delayed-response experiment by Funahashi et al. (1989). In this experiment, monkeys are trained to fixate a central light spot (known as fixation spot) in a monitor (Fig. 1). First, a cue light spot is presented to the monkey transiently for 0.5 s at one of eight different positions (in a random sequence) separated by 45° along a circle centered at the fixation spot. Then the fixation signal is presented during the whole delay period (3–5 s) that follows the extinction of the cue input. After this delay, the fixation spot is turned off, which constitutes the “go” signal for monkeys, who then make a saccadic eye movement toward the original position of the cue.
Fig. 1.
Eye positions in the visually guided saccade task
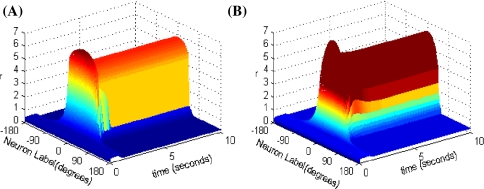
C-W model combines recurrent network synaptic mechanisms with intrinsic cellular bistability which can enhance the robustness against noise and distraction stimulus. By cellular bistability we mean the ability of a single neuron to possess two stable membrane states. For instance, a neuron can be either in a spontaneous low-rate firing state or in an elevated firing state when a transient input is present. The time course of the network activity in response to a transient stimulus for the C-W model is shown in Fig. 2A. Fall and Rinzel (2006) subsequently presented a network model of working memory replacing the intrinsic conditional bistability in C-W model with an intracellular Ca2+ subsystem, which seems more biologically meaningful. The Ca2+ subsystem is tunable through different dynamic regimes. And its bistability is affected by the second messenger inositol 1, 4, 5 trisphosphate (IP3). As the level of IP3 increases, it shows transitions from a steady low Ca2+ state to bistability to a steady high Ca2+ state. The network and Ca2+ subsystem interact on each other, such that Ca2+ increases the efficacy of synaptic input and synaptic input increases cytosolic Ca2+ in reverse. The network is able to sustain IP3-dependent persistent activity in response to a stimulus (see in Fig. 2B), and it is resistant to noise. We found that both network models can maintain elevated activity during delayed-period time.
Fig. 2.
Space-time plots of the firing activity. A C-W model, B Fall and Rinzel’s model
In this work, we dedicate to further extending the above work. Our model adopts traditional firing-rate network which replaces the cubic firing rate function with an unit-slope and zero-crossing linear function. That simplifies the recurrent network; as the weights of synaptic connections changes over time, which is a dynamically changing process, therefore the model proposed in this paper amends the synaptic weights. We also suggest that Ca2+ concentration only increase the efficacy of synaptic input but has nothing to do with the external input for the transient cue. Some specific PFC neurons are able to be “switched on” into a persistent firing pattern by transient cue stimulus and be “switched off” back to its resting state of spontaneous activity by a suitable “go” signal. However, it is unknown yet how the persistent activity in PFC neurons is turned off after the delay period. In C-W model, an artificially uniform inhibitory input was used to simulate the go signal, which is not regarded in our present model. And the Ca2+ subsystem is not the only biological mechanism that possesses intrinsic bistability. Na+ ion channel can also produce such bistability. But here we focus on the Ca2+ subsystem. Through simulation, we find that our network model also maintains the persistent activity in response to a brief transient stimulus like that of the previous two models and the working memory performance is resistant to noise and distraction stimulus.
Network model
In the C-W model, the nonlinear cubic function of the firing rate f(r) is the key factor to get stable persistent activity, which can induce bistability over a range of input values when it is tuned to be N-shaped. Fall and Rinzel replaced this conditional bistability with Ca2+ subsystem, but still cubic in firing rate function just tuned to be monotonic, while our model adopts the traditional firing-rate network model (Vogels and Abbott 2005). The network consists of N neurons, each labeled by its preferred cue location or memory field θi with range from −π to π along a circle. We assume that the neurons cover uniformly all the angles. In this limit, the firing rate r(θi, t) obeys the following equation:
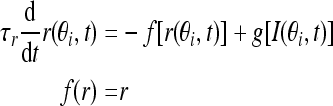 |
1 |
where τr is time constant. The function f(r) and g(I) represent the intrinsic properties of the neuron. By setting dr/dt = 0 we can obtain the steady state of this system, thereby obtaining the neuronal input-output relation r = g(I). The function g(I) has the following piece-wise linear function form:
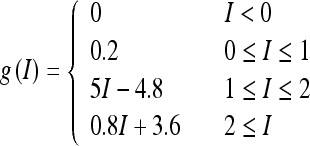 |
2 |
The total input to each neuron I consists of an external input Iext for the transient cue and a recurrent synaptic input Isyn. Considering that Ca2+ release might increase the efficacy of synaptic input, thus the input I is represented as:
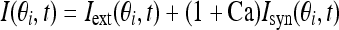 |
3 |
The external input Iext contains a constant bias input I0 and a cue stimulus:
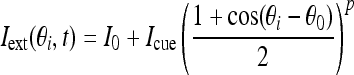 |
4 |
where constant Icue is nonzero only when the transient cue stimulus is present. In our paper, we assume the cue stimulus starts at 1 s and lasts for 500 ms. The variable θ0 represents the cue position and p controls the width of cue stimulus.
The synaptic input Isyn is given by convolution over the weights and firing rates:
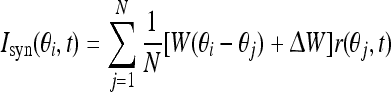 |
5 |
The static connectivity weight W between two neurons has an inhibition form which is given by:
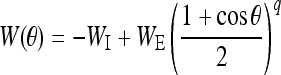 |
6 |
where constants WI and WE represent the strengths of the inhibitory and excitatory interactions, respectively. ΔW is the amendment of the synaptic weights. It is given by (Adam Ponzi 2008; Shriki et al. 2003):
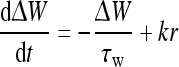 |
7 |
Here, τw is the time constant and k is the proportional coefficient.
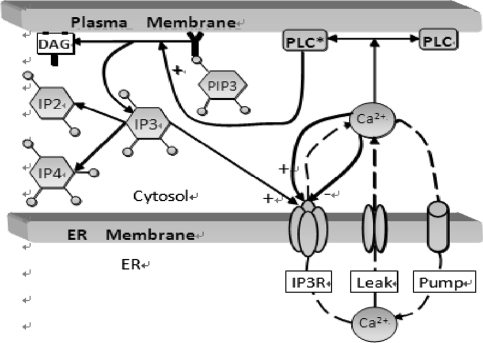
The dynamics of Ca2+ subsystem (Fig. 3) depends on the level of the second messenger inositol 1, 4, 5 trisphosphate (IP3). Water-soluble IP3 diffuses in the cytosol and combines with the specific receptors from the internal endoplasmic reticulum (ER). These receptors are IP3 sensitive Ca2+ channels, which can lead to Ca2+ release from Ca2+ library. That is, Ca2+ is released from the ER via the IP3 sensitive Ca2+ channel (known as the IP3 receptor or IP3R), and reuptake occurs via SERCA ATPase pumps (Fall et al. 2004). Thus a balance equation describing the evolution of Ca includes release of Ca2+ through the IP3R into the cytosol (JIP3R), removal of Ca2+ (JSERPM) induced by the reuptake of SERCA pumps from the cytosol, a leak flux from the ER to the cytosol (JLeak) used maintain basal Ca concentration and an important contribution to Ca2+ influx from network activity Jsyn (Fall and Rinzel 2006).
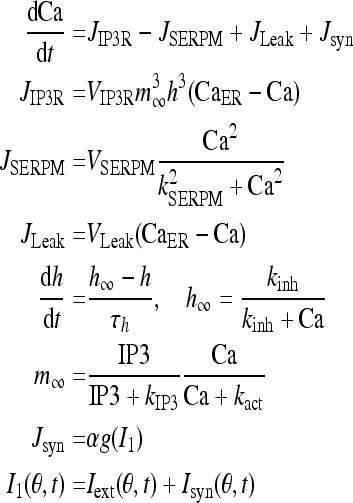 |
8 |
Fig. 3.
Cartoon diagram illustrating the IP3-modulated Ca2+ subsystem. Source Fall et al. (2004)
Note that I1 and I that couples Eqs. 1 and 8 are not equal. That is because if they were identical, then there would be an additional positive feedback to the Ca dynamics, which would lead to oversensitivity to parameter variations in the model due to such symmetrical coupling. The variable h represents the proportion of IP3R’s not inactivated by Ca. The gating relation m∞ represents the fast activation and α is the proportional coefficient.
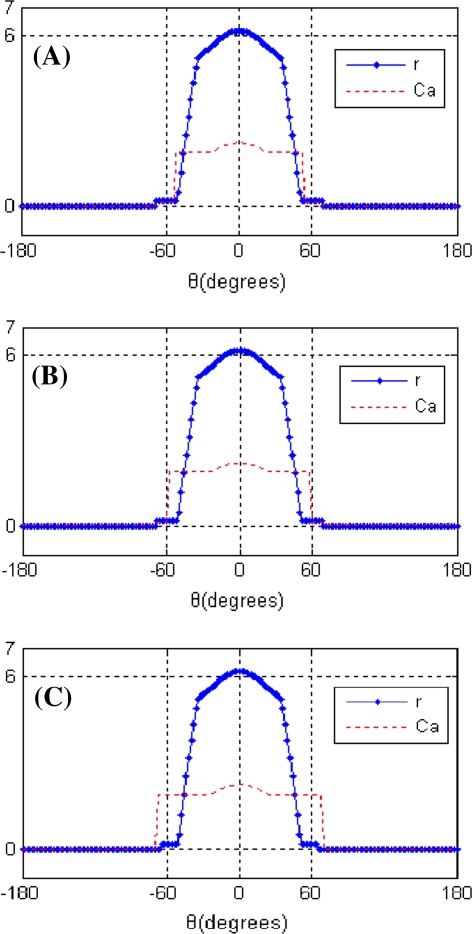
The working memory of the cue stimulus is encoded by the peak of the network activity profile. That is, the activity profile peaks at the location of the original cue (Fig. 6A). However with the perturbations of noise and a distraction stimulus presented during the delay period, the peak location may drift over time. And too large drift can produce incorrect memory. Therefore we should know the memorized cue position during delay-period activity, that is, the peak location. The peak function is given by Camperi and Wang (1998):
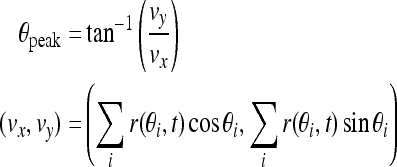 |
9 |
Fig. 6.
Profiles of stable elevated states
We retain nondimensionality in the firing rate model like that of C-W, but the Ca2+ subsystem has physical units: IP3 and Ca are both expressed in μM. In this paper, we simulate using Matlab (R2007b) with a time step of 0.005 s. The number of neurons is 128. Signal-to-noise ratio is 20 dB, which is added to the input I. The parameter values used are WI = 2, WE = 2.8, τr = 0.1, I0 = 0.2, θ0 = 0o, τh = 0.1, α = 0.7, τw = 0.02, k = 0.1, IP3 = 0.6 unless otherwise indicated and other parameter values are identical to those used in the model by Fall and Rinzel (2006).
Results
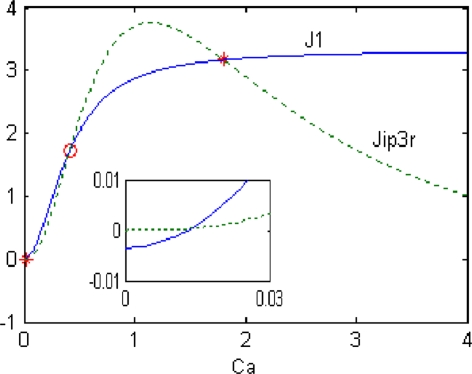
Figure 4 illustrates one possible scenario leading to bistability with Ca2+ subsystem standing alone (Jsyn = 0). By setting dCa/dt = 0, Ca2+ is seen to be steady only when J1 = JSERPM − JLeak = JIP3R. The values of Ca2+ at which this occurs can be found by looking for the intersections of the sigmoidal J1 curve (solid line) and bell-shaped JIP3R curve (dashed line). Note that there are three intersections. It is easy to show that the state in the center (indicated by the red open circle) is unstable, whereas the high and low Ca2+ states (indicated by red asterisk) are stable. The existence of these two very different stable physiological states means that the Ca2+ subsystem is bistable. When IP3 changes, the JIP3R curve may not intersects J1 curve exactly cubic owing to JIP3R’s sensitivity to IP3. That is the Ca2+ subsystem loses bistability. By numerical simulation, three intersections occur over a range of IP3 values between 0.48 and 1.14 μM, which is also the region of bistability. The inset is an amplification of the curves around the origin.
Fig. 4.
Bistability resulting from the balance between the Ca2+ release and uptake by the ER
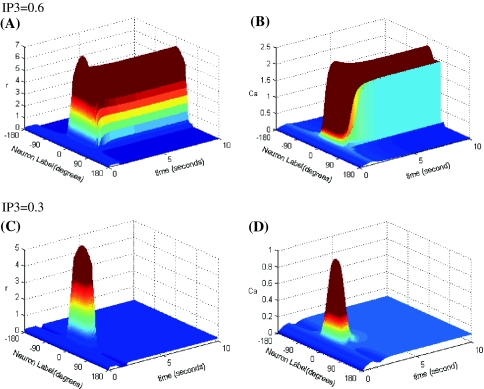
The bistability of Ca2+ subsystem depends on the level of the second messenger IP3. Three-dimensional maps of the network activity and Ca concentration with memory field θ and at time t are showed in Fig. 5. As shown in Fig. 5A, B, when IP3 is elevated to the point where the Ca2+ subsystem is bistable (here IP3 = 0.6 μM), we found that the model is able to sustain the elevated firing rate over a range of time in response to the transient stimulus, that is performance of working memory, and peaks at the location of the original cue. When IP3 is reduced to the point that is beyond the region of bistability (here IP3 = 0.3 μM), there is no sustained firing pattern as seen in Fig. 5C, D.
Fig. 5.
Space-time plots of the firing activity and Ca concentration for low and elevated IP3
Steady-state profiles of the persistent network activity during delay period are show in Fig. 6A, C. The circles in these figures represent the individual firing rate of each neuron. Figure 6A shows the network tuned to bistability (IP3 = 0.6 μM). Note that the firing rate reaches the maximum at the location of original cue, and the more away from original cue, the smaller the firing rate of neurons. Furthermore the Ca2+ profile is slightly wider than the activity profile. The reason for this is that cells in the neighborhood of the neuron labeled by the original cue location, due to their bistable Ca2+ subsystem, can be activated to the high-Ca2+ state by the stimulus and then induce the elevated firing rates. While the firing rates of those edge cells are constrained by the lateral inhibition from the weight function. Thus they do not demonstrate elevated firing although they still retain an elevated Ca2+ level. Figure 6C, D are the profiles when a wider (p = 0.1) and a higher amplitude (Icue = 2) stimulus are presented to the network, respectively. We found that in both cases, Ca2+ profiles were wider.
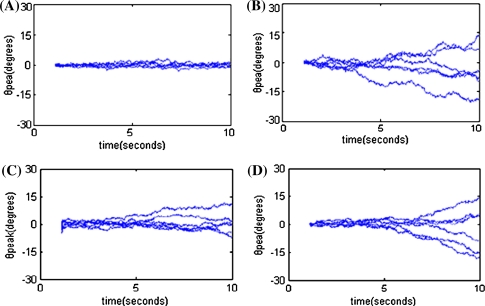
Whether the model can retain an accurate memory of cue information depends on its ability to keep its peak activity localized near the neurons whose memory field represents the cue location. In other words, we should determine whether the actual cue position θpeak stays close to the location of the original cue in presence of random noise perturbations. Figure 7A–D show the time courses of θpeak during delay period with white noise added to input I. Figure 7A shows that the model is tuned to be bistable. Figure 7B represents the results without bistability, that is without Ca2+ subsystem, with WI = 2, WE = 4.5. Note that the network with bistability is able to stabilize θpeak near θ0 for a long time (Fig. 7A). By contrast, the network with only sigmoid cellular input-output relation displays a significant random drift in θpeak. Figure 7C, D show that the model is presented respectively with a wider (p = 0.1) and a higher amplitude (Icue = 2) stimulus. We found that the network can no longer stabilize θpeak near θ0 and demonstrate a significant drift over time instead. The robustness against noise is reduced. This may be because that with wider and higher amplitude stimulus, more neurons are activated to high-Ca2+ state (as in Fig. 6B, C), which makes more neurons prone to high firing rates. Thus the network activity is easier to drift in the presence of noise.
Fig. 7.
Noise-induced drift during delay period
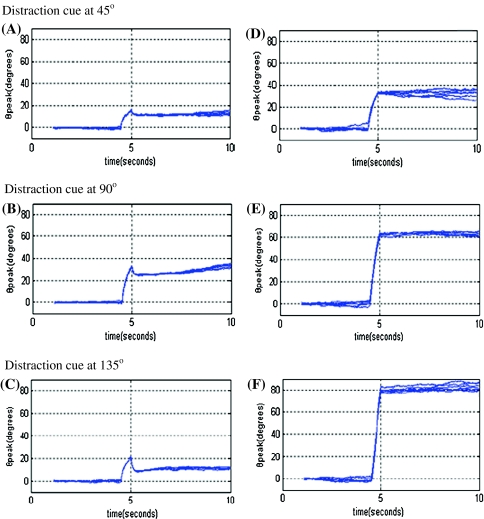
Another way to determine the stability of model performance is to observe its response to a distraction stimulus. The distraction stimulus is a second input presented during delay period, with the same amplitude and duration with original stimulus but placed in different positions. Figure 8 shows the time courses of θpeak during delay period. Distraction stimulus is added at about 4.5 s and the positions localize at 45°, 90° and 135°. Noise is added to network but with smaller amplitude compared to Fig. 7 in order to reduce the interference caused by noise-induced drift. Figure 8A–C shows the results of network that is tuned to bistability and Fig. 8D–F shows the results without bistability. As seen in the figures, the actual cue position θpeak somewhat displays drift affected by distraction in the model with bistability, but remains much closer to original cue position θ0 than to distraction position θdistraction, which means the network can still store correct information for stimulus. While in the model without Ca2+ subsystem-induced bistability, the actual cue position is much closer to distraction position.
Fig. 8.
Distraction-induced drift during delay period
Conclusion
Here we have shown that our present model can also demonstrate the elevated persistent activity and has strong robustness against noise and distraction stimulus. Camperi and Wang (1998) presented a model for working memory which combines recurrent network synaptic mechanisms with intrinsic cellular bistability, while Fall and Rinzel (2006) replaced the intrinsic bistability in C-W model with a Ca2+ subsystem which seems more biologically realistic. We simplifies the recurrent network model by using an unit-slope and zero-crossing linear function to replace the cubic firing rate function; We amend the synaptic weights considering that the weights of synaptic connections is a dynamically changing process over time; We also suggest that Ca2+ concentration only increases the synaptic input not including the external input for the transient cue. Our model seems more biologically plausible and the simulation results agree well with experiment data by Funahashi et al. (1989).
The present computational work is based on the premise that the persistent activity is generated locally within the dorsolateral PFC. But anatomical studies show that the three structures most implicated in working memory are the PFC, the basal ganglia (BG) and the midbrain dopamine nuclei (Fuster 1995; Goldman-Rakic 1995). The PFC plays a central role in the maintenance of information in working memory, while the BG and dopamine nuclei are believed to be involved in helping protect memories against noise and some distracters. We may investigate the feasibility by considering the BG and dopamine nuclei in our model instead of Ca2+ subsystem.
We study the simple firing-rate model in this paper. In future research we can propose a biologically more realistic model, using spiking neurons, two (excitatory and inhibitory) populations of cells, and synaptic currents with realistic gating kinetics. It is still not clear how the go signal is generated, how the persistent activity return back to its rest state at the end of delay period in PFC and how the persistent activity is turned on and turned off by the second messenger subsystem. All these work is the focus of our future study.
Acknowledgments
Project (10872068, 10672057) supported by National Natural Science Foundation of China (NSFC). Supported by “the Fundamental Research Funds for the Central Universities”.
References
- Abeles M. Corticonics: neural circuits of the cerebral cortex. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Baddeley AD. Working memory: looking back and looking forward. Nat Rev Neurosci. 2003;4(10):829–839. doi: 10.1038/nrn1201. [DOI] [PubMed] [Google Scholar]
- Braver TS, Barch DM, Cohen JD. Cognition and control in schizophrenia: a computational model of dopamine and prefrontal function. Biol Psychiatry. 1999;46:312–328. doi: 10.1016/S0006-3223(99)00116-X. [DOI] [PubMed] [Google Scholar]
- Camperi M, Wang XJ. A model of visuo-spatial working memory in prefrontal cortex: recurrent network and cellular bi-stability. Comput Neurosci. 1998;5(4):383–405. doi: 10.1023/A:1008837311948. [DOI] [PubMed] [Google Scholar]
- Colliaux D, Molter C, Yamaguchi Y. Working memory dynamics and spontaneous activity in a flip-flop oscillations network model with a Milnor attractor. Cogn Neurodyn. 2009;3(2):141–151. doi: 10.1007/s11571-009-9078-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fall CP, Rinzel J. An intracellular Ca2+ subsystem as a biologically plausible source of intrinsic conditional bi-stability in a network model of working memory. J Comput Neurosci. 2006;20:97–107. doi: 10.1007/s10827-006-4791-8. [DOI] [PubMed] [Google Scholar]
- Fall CP, Wagner JM, Loew LM, Nuccitelli R. Cortically restricted production of IP3 leads to propagation of the fertilization Ca2+ wave along the cell surface in a model of the Xenopus egg. J Theor Biol. 2004;231(4):487–496. doi: 10.1016/j.jtbi.2004.06.019. [DOI] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, Goldman-Rakic P. Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. J Neurophysiol. 1989;61:331–349. doi: 10.1152/jn.1989.61.2.331. [DOI] [PubMed] [Google Scholar]
- Fuster J. Memory in the cerebral cortex. Cambridge: MTT Press; 1995. [Google Scholar]
- Fuster JM. The prefrontal cortex: anatomy, physiology, and neuropsychology of the frontal lobe. 3. New York: Lippincott-Raven; 1997. [Google Scholar]
- Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14(3):477–485. doi: 10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- Guo C. Working memory: a concerned research area. Adv Psychol Sci. 2007;15(1):1–7. [Google Scholar]
- Hebb DO. The organization of behavior. New York: Wiley; 1949. [Google Scholar]
- Marder E, Abbott LF, Turrigiano GG, Liu Z, Golowasch J. Memory from the dynamics of intrinsic membrane currents. Proc Natl Acad Sci USA. 1996;93:13481–13486. doi: 10.1073/pnas.93.24.13481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moody SL, Wise SP, Di Pellegrino G, Zipser D. A model that accounts for activity in primate frontal cortex during a delayed matching to sample task. Neuroscience. 1998;18:399–410. doi: 10.1523/JNEUROSCI.18-01-00399.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olesen PJ, Westerberg H, Klingberg T (2003) Increased prefrontal and parietal activity after training of working memory. Neuroscience [DOI] [PubMed]
- Ponzi A (2008) Dynamical model of action reinforcement by gated working memory. Adv Cogn Neurodyn [DOI] [PubMed]
- Shriki O, Hansel D, Sompolinsky H. Rate models for conductance-based cortical neural networks. Neural Comput. 2003;15:1809–1841. doi: 10.1162/08997660360675053. [DOI] [PubMed] [Google Scholar]
- TaiZhen H, FuMei W (1998) Neurobiology of learning and memory. The joint press of Beijing Medical University and China Concord Medical Science University, pp 14–27
- Tarnow E. Response probability and response time: a straight line, the tagging/retagging interpretation of short term memory, an operational definition of meaningfulness and short term memory time decay and search time. Cogn Neurodyn. 2008;2(4):347–353. doi: 10.1007/s11571-008-9056-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarnow E. Short term memory may be the depletion of the readily releasable pool of pre-synaptic neurotransmitter vesicles of a meta-stable long term memory trace pattern. Cogn Neurodyn. 2009;3(3):263–269. doi: 10.1007/s11571-009-9085-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels TP, Rajan K, Abbott LF. Neural network dynamics. Rev Neurosci. 2005;28(3):57–76. doi: 10.1146/annurev.neuro.28.061604.135637. [DOI] [PubMed] [Google Scholar]
- Zipser D, Kehoe B, Littlewort G, Fuster J. A spiking network model of short-term active memory. Neuroscience. 1993;13:3406–3420. doi: 10.1523/JNEUROSCI.13-08-03406.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]