How sequence directs bending in tropomyosin and other two-stranded alpha-helical coiled coils

Abstract

A quantitative analysis of the direction of bending of two-stranded alpha-helical coiled coils in crystal structures has been carried out to help determine how the amino acid sequence of the coiled coil influences its shape and function. Change in the axial staggering of the coiled coil, occurring at the boundaries of either clusters of core alanines in tropomyosin or of clusters of core bulky residues in the myosin rod, causes bending within the plane of the local dimer. The results also reveal that large gaps in the core of the coiled coil, which are seen for small core residues near large core residues or for unbranched core residues near canonical branched core residues, are correlated with bending out of the local dimeric plane. Comparison of tropomyosin structures determined in independent crystal environments provides further evidence for the concept that sequence directs the bending of the coiled coil, but that crystal environment is at least as important as sequence for determining the magnitude of bending. Tropomyosin thus appears to consist of more directionally restrained hinge-like joints rather than directionally variable universal joints, which helps account for and predicts the geometric and dynamic nature of its binding to F-actin.

Introduction

Alpha-helical coiled coils represent the most well understood three-dimensional structural motif in proteins, and perform a number of functions, from dimerization (transcription factors) to actin stabilization and regulation of muscle contraction (tropomyosin).^1–3 A fundamental structural feature of the alpha-helical coiled coil is its simple linearly periodic nature. These structures are generally characterized by a sequence with a seven-residue (so-called “heptad”) repeat, where the first and fourth amino acid residues in this repeat are usually apolar. The winding of two (or more) alpha helices around one another permits a systematic interlocking of these residues, located at the interhelical interface (or “core”), in a knobs-into-holes fashion to stabilize the molecule.^4,5 The specific geometry of the knobs-into-holes interaction was first visualized at high resolution for the relatively short stable “leucine zipper,”¹ and has since formed a basis for identifying alpha-helical coiled coil structures in the rapidly expanding data bank of protein structures.^6–8 The ability to predict the presence of an alpha-helical coiled coil structure from sequence alone^9–11 distinguishes this motif from many other types of protein structures. Moreover, it has also been possible to identify specific types of residues or patterns of residues, most often in the core, that lead to specified variations in the coiled-coil structure. In this regard, general features related to the association of the alpha-helical chains, such as relative polarity of the component chains and the number of chains that associate, as well as detailed features of its structure including the local radius and pitch, have been well investigated.^12–14 A widely used computer program TWISTER¹⁵ has also been developed to provide a residue-by-residue quantitative description of certain of these and other structural features of alpha-helical coiled coils.

The function of some coiled coils, especially that of tropomyosin, depends on another geometrical feature that affects the overall shape of the molecule: the bending of the coiled-coil axis.^3,16 Tropomyosin, for example, must wind around F-actin for its regulatory control of muscle contraction. High resolution crystal structure determinations of fragments of tropomyosin have revealed the existence of different types of bends in the axis that appear to be related to patterns in the residues in the core. The most well-understood bend is that created at the boundary of axially staggered chains containing clusters of core alanines with axially in-register chains rich in canonical leucine-type residues in the core.^17,18 These bends are directed roughly within the local plane of the dimer (also called “bending into the major axis”). This type of bend has so far been visualized in about four of tropomyosin's alanine clusters.^17,19–21 In addition, in other segments of tropomyosin, where isolated core alanines are surrounded by large core residues, variable bending roughly either in the local plane or out of the local plane (i.e., into the minor axis) has been described.^19–21 These descriptions have been limited, however, to quantitative measurements of the magnitude of the bend, but only qualitative descriptions of the direction of bending based on simple visual inspections.

A major question relevant to the function of alpha-helical coiled coils such as tropomyosin is whether the shape of the molecule is, as suggested above, controlled primarily by its amino acid sequence²² or whether the molecule is generally flexible and readily conforms to its environment.^20,23 I have written a computer program, CCBENDS, that helps address this question, as well as advancing our understanding of coiled-coil geometry, by quantitatively measuring the direction as well as magnitude of coiled-coil bends. The program has been applied to crystal structures of tropomyosin and other parallel homodimeric coiled coils, and has revealed new relationships between the sequence in the core and the conformation of the molecule, as well as a new physical basis for semi-flexibility of tropomyosin.

Methods

A schematic of the geometrical transformations used to calculate the direction of bending, as well as an example of the output of the CCBENDS program, are shown in Figure 1. A few points are reinforced to facilitate an understanding of the results and discussion in this manuscript.

Figure 1.

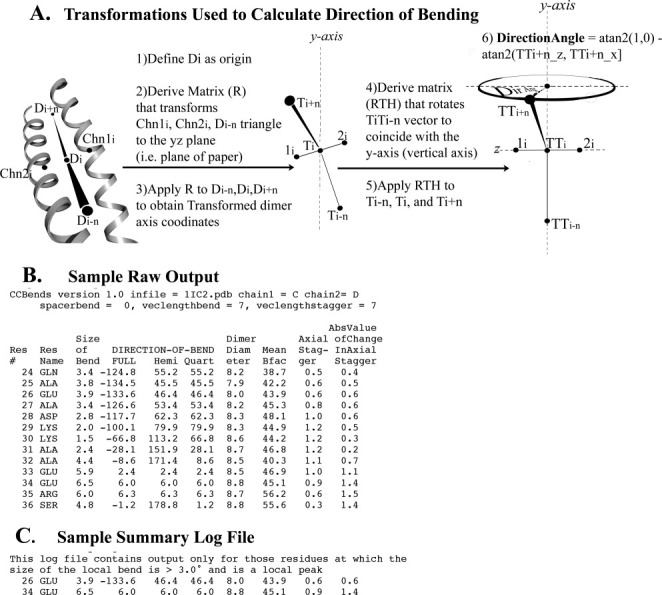
Direction of bending calculation and output files of CCBENDS. A: The indicated transformations facilitate calculation of the fully signed bending direction angle of a parallel dimeric alpha-helical coiled coil axis using the atan2 function. Value of 0° indicates bending of the axis within the local plane towards chain 1, ±180° indicate in-plane bending towards chain 2, ±90° indicate out-of-plane bending, and ±45° or ±135° indicate diagonal bending (see also Table SI in Supporting Information). The example schematic shown in this figure displays a direction of bending of c. +70°, nearly out of the plane of the local dimer. (Note that the chain axis at each residue is calculated using the coordinates of the nearest five alpha-carbons, and the dimer axis is the simple average of the chain axes.) B: Sample raw output file includes fully signed and symmetry-reduced (“hemi” or “quart”) local bend direction angles, as well as other coiled-coil parameters for each residue (See Methods for explanations). C: Corresponding summary file extracts from the raw output file those residues at which the size of the bend is both >3.0° and is a local peak, that is, greater than that of the prior and subsequent residue. [In this example, the fully signed measurement shows that the two local bends, which bracket an axially staggered stretch, are oppositely signed (i.e., closer to 180° apart than 0° apart), which is a signature of this (near) in-plane bending design. Such pairs of nearly oppositely signed near-in-plane local bending angles also surround three other axially staggered alanine clusters in tropomyosin as well as axially staggered clusters of bulky core residues in myosin. See also Fig. 3.]

Bends described here are for the central axis of the parallel homodimeric alpha-helical coiled coil. The magnitude of the bend of this axis at any given residue, i, typically involves calculating the angle between the vector from i to i+n and the vector from i−n to i. After transforming the local coiled coil segment to a convenient coordinate frame, the direction of bending is determined by calculating the angle between a projection of the vector from i to i+n and a vector in a plane defined by the coordinates of the two helical axes at i and those of the central dimer axis at i−n (see Fig. 1). (Note that in a typical coiled-coil, with a non-infinite pitch, the orientation of the local dimeric plane relative to a globally defined plane varies from residue to residue; the bends that we describe here are relative to the local dimeric plane.) The user of the program can choose the value of n. The results described here are for relatively short-range bends with n = 7. Vectors with lengths much less than 7 residues tend to magnify coordinate errors and produce a noisy series of bend angles, whereas lengths much greater than 7 residues risk the merging of closely spaced individual bends.

The direction of bending involves the use of the atan2 function to calculate a fully signed angle that can span 360° (by convention from −180° to 180°). This calculation is necessary for unambiguously describing the direction of bending of a heterodimer's central axis (e.g., distinguishing in-plane bending towards chain 1 from in-plane bending towards chain 2) or for comparing two or more bends to one another in any dimer. The results and analyses presented here, however, are primarily for individual local bends of parallel homodimeric coiled coils, and are thus based on symmetry-reduced values [see Fig. 1(B)]. Reduction to a hemicircle (by adding 180° to all negative values) provides an unambiguous description, with bending into the 0–90° quadrant conformationally distinguishable from (albeit related to) bending into the 90–180° quadrant. Further reduction to a quartercircle (by subtracting any value in the second quadrant from 180°) is necessary for certain calculations (such as standard deviations described below) and is informative for certain coiled-coil design concepts (such as knobs-into-holes or gaps in the core) that by themselves display additional, that is, mirror, symmetries. According to the program's convention, values of 0 or ±180° indicate bending of the axis within the local plane of the dimer (similar to scoliosis of a spine), ±90° indicate bending out of the local plane (similar to kyphosis or lordosis), and ±45° or ±135° indicate diagonal bending.

An example of the raw, residue-by-residue, output of the program, which contains the bend angles as well as other geometric features, is shown in Figure 1(B). Most of the results and discussion, however, are based on analyses of summary log files where only those residues at the center (vertex) of significant bends (>3° in magnitude) are listed [Fig. 1(C)]. Summary log files were computed for all relatively high resolution crystal structures of parallel homodimeric coiled coils according to SCOP⁸ as of January 15, 2009. These files were combined in a master spreadsheet, from which scatter plots relating the direction of bending to other geometric features were derived (Figs. 2–4 and Figures in the Supporting Information).

Figure 4.

Large gaps at the interhelical interface promote out-of-plane bending. A: Same database of structures is used as in Figure 3. For each bend at residue i listed in the summary log file, the coordinates of residues i−7 to i+7 from each chain were extracted using PDBCUR from the CCP4 suite,⁴³ and the gap volume was obtained using the Protein–Protein Interface Comparison server.²⁸ Over all 117 bends, the median gap volume is 567 ų. B: The 16 bends with the largest gap volumes. Tropomyosin residues 128, 131, and 117 are from pdb i.d. 2b9c, 185, and 215 are from 2d3e, and 217 is from 2efr. C: Two types of gap-containing structures in which the main chains are propped apart at the locations of small or medially unbranched side chains. See also text.

The CCBENDS program, documentation, and example script and output files can be obtained from http://www.bio.brandeis.edu/ccbends/. Please also see Supporting Information.

Results

The scatter plot in Figure 2 summarizes the direction of all bends found in the various (homodimeric striated muscle) tropomyosin crystal structures, and those of Figures 3 and 4 include other parallel homodimeric alpha-helical coiled coils as well. In addition to the previous simplified visual descriptions of in-plane and out-of-plane bends,^{16,17,19–21} the current calculations show that nearly all possible bending geometries are observed in one location or another of the tropomyosin sequence as well as in other classes of coiled coils. These geometries include a sampling of nearly all degrees of diagonally directed bending between pure in-plane and pure out-of-plane bending, as well as of both quadrants of hemicircle-reduced bending space.

Figure 2.

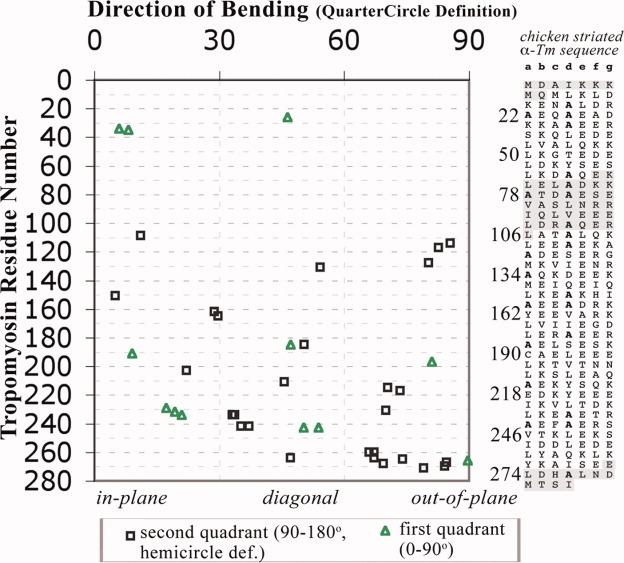
Direction of bending is relatively conserved at most locations of tropomyosin. Scatter plot of all 39 local bends [from summary log files as in Fig. 1(C)] found in crystal structures of fragments of vertebrate striated alpha-tropomyosin (pdb i.d. 1ic2, 2b9c, 1kql, 2d3e, 2efr, 2efs, 2z5h, 2z5i: see also Table SII in Supporting Information), with the x-axis showing the quartercircle-reduced direction of bending. [Only those residues more than seven residues from a non-tropomyosin or non-coiled-coil region are included. The program was run separately on each of the crystallographically independent copies of the coiled coil, except for chains CD of 2d3e and chains EF and GH of 2z5I, which have nearly identical (<0.1 RMS different) conformations to those included.] Twenty-three of the bends are from eight locations in which bending occurs in more than one crystal environment (see text). Sequence (see right panel) appears to be the more important factor controlling the direction of bends of the tropomyosin coiled coil, whereas crystal environment play at least as important a role for determining the magnitude of the bend (see text and Fig. S1 in Supporting Information). Shaded sequences have not been examined by CCBENDS because either there is no crystal structure available or because the position is within 10 residues of a terminus of the structure. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 3.

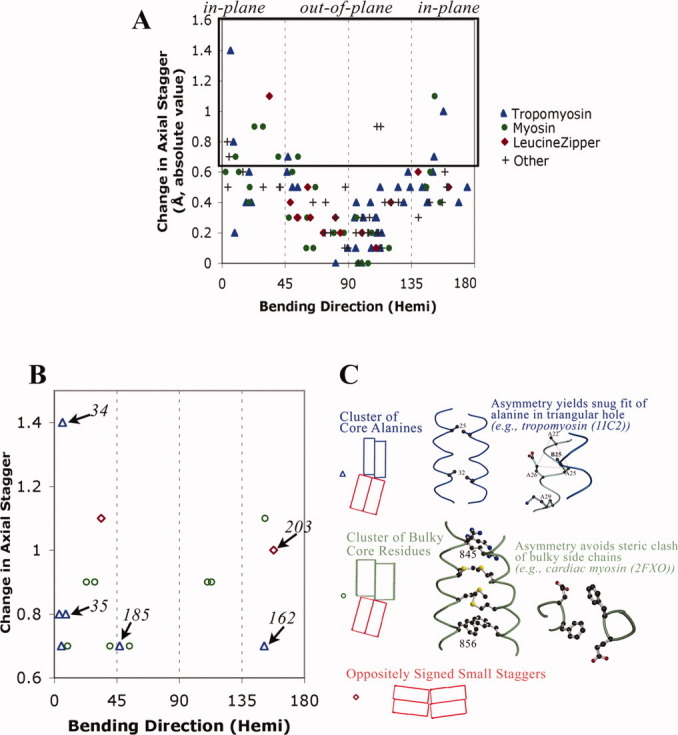
Large changes in axial staggering of the α-helices promote in-plane bending. A: Scatter plot of results from summary log files of all relatively high resolution crystal structures of parallel homodimeric coiled coil according to SCOP⁸ as of January 15, 2009. In addition to tropomyosin (see Fig. 2), coiled coils are from myosin (pdb i.d. 1nkn; 3bas; 3bat; 2fxm; 2fxo), leucine zipper domain (2zta, 1zik, 2ahp, 1zil, 1pyI, 1zme, 1hwt, 2hap, 1qp9, 1gd2, 1gu4, 1gtw, 1h8A, 1h88, 1hjb, 1io4, 1nwq, 2c9l, 2c9n), and other proteins (1dkg, 1d7m, 1deb, 1joc, 1no4, 1noh, 1uix, 1s1c, 1x79, 1tu3, 1T6F, 1uii, 2gzd, 2gzh, 2d7c, 2hv8, and 2ocy) (see also Table SIII). The hemicircle-reduced direction of bending is shown on the x-axis. At each position along the sequence, i, the change in axial stagger per heptad = [axial stagger at position (i+3) + stagger at position (i+4) − stagger at (i−3) − stagger at (i−4)]/2.0, and the absolute value is printed out on the y-axis. B: The 16 bends with greatest change in axial staggering. Italicized numbers are tropomyosin residues. C: Two major designs that promote axial staggering. See also text.

Tropomyosin in different crystal environments: Direction of bending (in contrast to magnitude of bending) is relatively conserved

Of the 39 individual local bends found in the tropomyosin crystal structures, the vertices of 23 bends are from eight specific locations in the sequence (residue 34/35, 185, 231/232, 234, 242/243, 260, 264-268, and 270/271) for which local bending is found in two or more independent crystal environments. (This grouping is based on having the peak of the bend within one residue of the peak of another bend in the group.) For either the (quartercircle-reduced) direction of bending, magnitude of bending, or random numbers, a “composite sample standard deviation” for the 23 bends from these eight locations was calculated, based on differences for each value from the particular mean of the values at the relevant specific location. In addition, an “overall sample standard deviation” was calculated for all 39 bends, based on differences from the overall mean. Dividing the composite value by the overall value yields a “variability index” for the measured feature. A calculation for random numbers yielded a variability index of 0.99.

This statistical treatment suggests that the direction of bending of the tropomyosin coiled coil is relatively conserved at any given location, with a composite sample standard deviation of only 11.2° compared to an overall sample standard deviation of 26.4° yielding a direction of bending variability index of only 0.42. In this regard only bending centered at residue 231/232 was found to be directed in widely divergent directions (nearly in the local plane in one crystal, nearly out of the local plane in another); each of the other seven locations showed a narrow range of bending directions among the different crystal environments, and excluding the two outliers yields a composite sample standard deviation of only 8.7° and a variability index of only 0.33. This conservation occurs for bends whether they are directed near in-plane (such as at residues 34/35 and 234), near out-of-plane (such as for the C-terminal region), or diagonally (as for 185 and 242/243), although variability does occur with respect to the sign (quadrant) of these diagonally directed bends (See Methods).

In contrast, the magnitude of bending of the tropomyosin coiled coil is relatively variable at any given location. Its variability index for the above eight locations is 0.58 (or 0.49 if the two highest outliers are omitted) (see also Fig. S1 in Supporting Information). Moreover, in the case of magnitude of bending, these values probably underestimate the variability since, as described previously, there are also numerous locations, such as at residue 26 (see Ref. 17), residue 215 (see Ref. 20), and residue 243 (see Ref. 21), where the dimer axis is bent in some crystal environments but is straight in others (and hence not included in the summary log files or the variability index).

Taken together, these sets of observations and statistical analyses indicate that the crystal environment appears to play a significant role in determining whether and to what degree the tropomyosin coiled coil bends at any particular location—but when the coiled coil does bend, the direction of the bend relative to the local dimeric plane is usually insensitive to the environment. As we show later (see Discussion), tropomyosin has the type of sequence that lends itself to this semi-flexibility. These results also suggest how tropomyosin may readily shift between specific binding states on F-actin (see Discussion).

Deciphering specific bending designs for coiled coils

The concept that sequence directs bending in tropomyosin crystal structures is further supported by Figures 3 and 4, in which relationships between specific sequence features and specific bending geometries are determined. A strategy is used that facilitates the connection of sequence to specific conformation based on the identification of an intermediate feature of the coiled coil and based on physical or chemical models. The database now used is that of all relatively high-resolution crystal structures of the parallel homodimeric coiled coils available as of January, 2009. The finding of positive correlations, in the combined summary log files of this database, between the magnitude of a proposed coiled-coil feature and the magnitude and direction of bending indicates that this feature may promote (or be a consequence of) bending in a specific direction. Simple physical or other models are then sought to provide evidence for a causal, rather than merely correlative, relationship between the feature and the bend. The structures of those bends with the most extreme values of this feature are then inspected to identify underlying sequence patterns, and to develop physical or chemical models that may causally relate the proposed sequence pattern to the coiled-coil feature. Two coiled-coil features that appear to connect sequence and direction of bending are now described.

Changes in axial staggering cause bends in the local plane of the dimer

Figure 3(A) quantitatively confirms on a large scale what we have previously shown by visual inspection of a few structures—that change in the axial staggering is correlated with in-plane (rather than out-of-plane) bending of the alpha-helical coiled coil. In fact, this correlation is very strong; change in axial staggering nearly always leads to relatively in-plane bending, and in-plane bending is almost always accompanied by a change in axial staggering. The magnitude of the change in axial stagger also correlates with the magnitude of this bend (see Fig. S2 in Supporting Information). The mechanical model of the causal relationship between change in axial stagger and in-plane bending is based on the simple wedge as has been described previously.^17,24

Having established a correlation between change in axial stagger and in-plane bends, the 16 bends with the highest values of change of axial stagger [Fig. 3(B)] are inspected to decipher sequence patterns [Fig. 3(C)]. As described previously, clusters of core alanines (or other small residues) in axially staggered regions adjacent to clusters of canonical leucine type core side chains is one pattern found in regions with high change of axial staggering, and is the major such pattern in tropomyosin. A physical model, based on the tendency of small side chains to bind to one end of the diamond-shaped hole of the partner alpha-helix [Fig. 3(C), blue and see Ref. 25], has been developed to account for their role in promoting axial shifts between alpha helices.^17,26

Other sequence patterns that coincide with large changes in axial staggering and, hence, in-plane bending are also observed. In human cardiac myosin, for example, there are two cases of stretches of core bulky residues such as phenylalanine, tyrosine, and methionine that also appear to promote axial staggering, and when situated adjacent to leucine type regions also cause near in-plane bending. The physical basis for this axial staggering appears to be steric hindrance. In contrast to small side chains or canonical residues such as leucine and valine, two large residues from the two chains cannot both fit into the core at the same time, so an asymmetry results where one side chain forms the knob-into-hole interaction and the other side chain is oriented out of the core. In these cases, the asymmetries in side-chain conformations of consecutive core bulky residues appear to reinforce each other and may thus promote the axial staggering asymmetry between the main chains [Fig. 3(C), green]. (Steric hindrance by bulky residues also breaks symmetry in certain antiparallel beta sheets.^18,27)

In summary, although tropomyosin uses clusters of core alanines adjacent to core leucines to achieve near in-plane bends, other coiled coils are also seen to use other types of core residues next to core leucines to achieve the same underlying design. Note also that while the general direction of bending surrounding these clusters of core residues is relatively in-plane, the precise values do vary, including strictly in-plane, near in-plane, and diagonal directions. Future studies will aim to provide the physical and chemical basis for this fine variation.

Large gaps in core promote bends out of the local plane of the dimer

Whereas the first inspection of tropomyosin¹⁷ revealed the importance of change in axial staggering, the more recent literature has also revealed poorly packed or “broken” cores as a second important feature implicated in certain bends, with initial visual inspections suggestive of variably directed bends.^19,21 To study this matter further, a quantitative study of the size of the holes in the core has been carried out. Using the Protein–Protein Interface Comparison Server,²⁸ a “gap volume” has been calculated at the location of each bend [Fig. 4(A) and see legend]. The gap volume correlates with the magnitude of the bend (see Fig. S3 in Supporting Information), indicative of generally poor core packing of side chains at the locations of bends (see use of SOCKET⁶ described in Fig. S3 legend). Most strikingly, the gap volume also correlates with the direction of bending: nearly all (15 out of the 16) bends with large holes in the core (gap volume >812 ų) are in fact directed closer to out-of-plane than in-plane [Fig. 4(A,B)].

An entropic model may explain this observation, where out-of-plane bending imposes the fewest constraints on the structure. Out-of-plane bending requires deformations of the alpha helices (e.g., its main-chain hydrogen bonds) only at the location of the bend. In contrast, in addition to local deformations of the alpha-helices, in-plane bending appears to impose the additional constraint of different extents of axial staggering on the two sides of the bend, as seen in Figure 3 (see also Ref. 16). In this regard, we should also note that the majority (∼64%) of the bends in coiled coils, whether tropomyosin (Figs. 2–4) or others (Figs. 3 and 4), are nearer to out-of-plane than to in-plane. In addition, there is a significant correlation between the size and direction of bends: 17 of the 18 largest bends (those >6.5° in magnitude) are directed nearer to out-of-plane than to in-plane (see Fig. S4 in Supporting Information). Taken together, these observations and models suggest that, unless there are specialized sequences elsewhere in the structure, the direction of bending about local nodes of instability is most easily generated out-of-plane.

Inspection of the structures of the 16 bends with the highest values of gap volume show two major, mechanically related, sequence patterns [Fig. 4(C)]. As described previously,¹⁹ certain large gaps in tropomyosin (and in some non-tropomyosin coiled coils) are created at the locations of small core residues when the alpha-helical main chains are propped apart by nearby bulky core residues [Fig. 4(C), top]. (See also Ref. 21 for the role of core acidic/polar residues.) A similar design, although with a different sequence pattern, is also seen in a few non-tropomyosin coiled coils. Here, at the locations of certain core lysines or arginines whose medially unbranched side chains extend straight out of the core, the main chains are propped apart by the branched nature of neighboring canonical core side chains such as leucine or isoleucine. The lack of a beta- or gamma-branched methyl group in the lysine or arginine side chain results in a gap [Fig. 4(C), second from top]. [Note that such gaps at the locations of core lysines are avoided either when the side chain puckers into the core (such as lysine 881 in the scallop myosin rod²⁹) or when the neighboring core residues are also unbranched and the coiled-coil diameter is hence relatively small, such as in the first alanine cluster of tropomyosin.¹⁷]

Discussion

Analysis of the first high-resolution structure of a fragment of tropomyosin indicated a source of semi-flexibility for the molecule—one where bistability is a necessary consequence of an asymmetric interaction between two chemically identical chains.^17,18 The current study reveals a second type of semi-flexibility. Clusters of core alanines or small residues, such as at 18–32/36 (see also Ref. 17), 151–158 (see also Ref. 19), 179–183/186/190 (see also Ref. 21), and 235–242 (see also Ref. 21), each display increased local axial staggering between the helices; each axially staggered segment, in turn, generates two oppositely signed, relatively in-plane bends of the dimer axis, at its junctions with relatively canonical in-register segments [Figs. 1(C), 2, and 3]. Poorly packed cores, such as at residues 113–141, 212–219, and the C-terminus, associated with a proximity of small and bulky core residues¹⁹ or the presence of acidic/polar residues in the core,²¹ promote bends nearly out of the local plane of the dimer (Figs. 2 and 4). But for these particular sequence patterns and coiled-coil features, varying magnitudes of bending (see Results and Fig. S1 in Supporting Information), as well as straight conformations (see references 20, 21), are also accessible. It would appear that a straight conformation should be at least as likely as any specific degree of (out-of-plane) bent conformation about a poorly packed core. With regard to in-plane bends, although alanine side chains appear to make best interactions when binding close to the ends of diamond-shaped holes of alpha-helices,^17,25,26 there is no hard (steric) hindrance that precludes them from binding at incremental positions closer to the middle of the diamond shaped hole and thus yielding small or no staggering between the chains (as occurs for tropomyosin residues 235–242 in one of the crystal structures, pdb i.d. 2D3E²⁰). In addition, some level of axial staggering can occur in canonical regions (e.g., for tropomyosin residues 3–18 in one of the molecules of the asymmetric unit¹⁷). It is thus possible for the coiled coil to also be straight, minimally bent, or gradually bent at the junctions of clusters of core alanines and canonical regions, when the difference between their axial staggers is lessened. (In contrast, it remains to be determined whether clusters of bulky core residues as found in the cardiac myosin rod will also show variability in the magnitude of bending; here, it is unclear how there can be any incremental or intermediate level of axial staggering accessible.) In these ways, the tropomyosin sequence not only specifies the direction of bending but also encodes for a measured variability in the magnitude of its bends.

The current analyses suggest that tropomyosin, at least in crystal structures, is a semi-flexible rod consisting of directionally restrained hinge-like joints rather than directionally variable universal joints. This “middle-of-the-road” view of the structural and dynamic nature of tropomyosin helps account for recent highly divergent descriptions of the molecule. Some researchers in the field have described tropomyosin as a “seamless rubber rod” with generalized flexibility, based on comparison of the magnitude of geometrical features in certain structures²¹ and on mutational studies of certain alanine clusters in actin binding assays and excimer fluorescence experiments.²³ Others have viewed the molecule as having a “pre-shaped semi-rigid architecture” designed on average to match the shape of F-actin, based on the modeling of certain crystal structures onto F-actin²² and on a combined study using electron microscopy and molecular dynamics simulations.³⁰ This latter viewpoint is consistent with the relatively conserved direction of bending of tropomyosin among different crystal environments (Fig. 2)—but only when the structure adopts the bent rather than straight conformations (Fig. S1 and see Results). The observation that clusters of core bulky residues in cardiac myosin lead to axial staggering and the same near-in-plane bending design as do alanine clusters [Fig. 3(C)] suggests that the same specific bends may also occur around other types of clusters of core residues; the mutations of alanine clusters to amide side chain clusters³¹ may thus not lead to the suggested generalized bending but rather to the same fundamental in-plane bending design (see also reference 3).

The semi-flexible nature of tropomyosin derived from the quantitative analysis of coiled-coil bending has implications for the dynamic and geometric nature of tropomyosin's binding to F-actin. When the end-to-end bonded tropomyosin filament is bound to F-actin, one tropomyosin molecule spans seven consecutive (identical) actin monomers along the F-actin long pitch helix, so that each half-turn of the tropomyosin alpha-helical coiled coil makes quasi-equivalent interactions with each actin monomer.^32–34 Tropomyosin binds fairly loosely to F-actin and readily shifts between different yet specific azimuthal positions, the equilibrium between them being influenced by troponin and myosin according to binding assays and electron microscopic observations (see references 35–37 and references therein). Two potential mechanisms by which tropomyosin undergoes these azimuthal shifts, “rolling” and “sliding,” have been described.^3,33,38,39 The observed variability in the magnitude of bending at any given location in different tropomyosin crystal environments offers hinge-type flexing between bent and straight conformations as another possible mechanism for accommodating tropomyosin's azimuthal motions on F-actin.

In contrast to the azimuthal location, other geometrical aspects of tropomyosin's binding to F-actin have not been directly observed, but have been inferred from various experiments and modeling studies. The polarity of the tropomyosin-actin complex, with the N-terminus of tropomyosin oriented towards the “pointed” end of actin, has been indicated by immunoelectron microscopy of antibody-labeled TnT fragments on the thin filament⁴⁰ and is consistent with the binding of tropomodulin to the pointed end of actin and to the N-terminal region of tropomyosin.^41,42 A model of the axial position of tropomyosin on actin (in the Ca²⁺ activated state) has been derived from the matching of surface electrostatic and apolar side chains,¹⁹ which suggests a relatively fixed axial position. This modeling study also implies some broad specificity in the rotational orientation of tropomyosin relative to actin: at any given axial location, there may be a preference for the edge, broad face, or an intermediate aspect of the tropomyosin dimer to face actin in order to optimize the chemical interactions. The current quantitative analyses provide additional evidence for such specificity. If physiological tropomyosin resembles that in the crystals, then a restricted hinge-like, rather than universally flexible, bending of the coiled coil at any given location would require a preferential rotational orientation of tropomyosin relative to actin—so that subsequent portions of tropomyosin could follow, rather than deviate from, the contour of the long-pitch helix of F-actin.