The Confounding Effects of Population Structure, Genetic Diversity and the Sampling Scheme on the Detection and Quantification of Population Size Changes

Abstract

The idea that molecular data should contain information on the recent evolutionary history of populations is rather old. However, much of the work carried out today owes to the work of the statisticians and theoreticians who demonstrated that it was possible to detect departures from equilibrium conditions (e.g., panmictic population/mutation–drift equilibrium) and interpret them in terms of deviations from neutrality or stationarity. During the last 20 years the detection of population size changes has usually been carried out under the assumption that samples were obtained from populations that can be approximated by a Wright–Fisher model (i.e., assuming panmixia, demographic stationarity, etc.). However, natural populations are usually part of spatial networks and are interconnected through gene flow. Here we simulated genetic data at mutation and migration–drift equilibrium under an n-island and a stepping-stone model. The simulated populations were thus stationary and not subject to any population size change. We varied the level of gene flow between populations and the scaled mutation rate. We also used several sampling schemes. We then analyzed the simulated samples using the Bayesian method implemented in MSVAR, the Markov Chain Monte Carlo simulation program, to detect and quantify putative population size changes using microsatellite data. Our results show that all three factors (genetic differentiation/gene flow, genetic diversity, and the sampling scheme) play a role in generating false bottleneck signals. We also suggest an ad hoc method to counter this effect. The confounding effect of population structure and of the sampling scheme has practical implications for many conservation studies. Indeed, if population structure is creating “spurious” bottleneck signals, the interpretation of bottleneck signals from genetic data might be less straightforward than it would seem, and several studies may have overestimated or incorrectly detected bottlenecks in endangered species.

THE idea that molecular data should contain information on the recent evolutionary history of populations is not new and traces back to the beginning of the 20th century (e.g., Hirschfeld and Hirschfeld 1919). However, much of the work carried out today owes to the seminal work of the statisticians and theoreticians who demonstrated that it was possible to detect departures from equilibrium conditions (e.g., panmictic population/mutation–drift equilibrium) and interpret them in terms of deviations from neutrality (Watterson 1975; Tajima 1989b) or stationarity (Nei et al. 1975; Tajima 1989a). Following this period most studies have primarily been concerned with the statistical properties of relatively simple models such as the Wright–Fisher (WF) or Moran models (Ewens 2004). During the last 20 years the detection of population size changes (e.g., Tajima 1989b; Slatkin and Hudson 1991; Rogers and Harpending 1992; Cornuet and Luikart 1996; Beaumont 1999; Garza and Williamson 2001; Storz and Beaumont 2002) has usually been carried out under the assumption that samples were obtained from populations that can be approximated by a WF model. However, natural populations are usually part of spatial networks and are interconnected through gene flow. They are hence rarely isolated as in the WF model. To be clear, structured models with several populations or demes such as the n-island (Wright 1931) or the stepping-stone models (Kimura and Weiss 1964) have been proposed decades ago in population genetics. Also, a number of authors have proposed methods to infer parameters under structured models (Wakeley 1999; Beerli and Felsenstein 2001; Chikhi et al. 2001; Hey and Nielsen 2004; Excoffier et al. 2005; Beerli 2006; Becquet and Przeworski 2007; Bray et al. 2009). However, the number of populations involved is generally limited compared to the n-island and stepping-stone models (but see Beerli and Felsenstein 2001; De Iorio et al. 2005). Models accounting for both population structure and population size changes would probably be more realistic for most species but the only inferential method currently available (Hey 2005) remains little tested under cases of structured populations (but see Strasburg and Rieseberg 2010 for a very recent study). While it would be important to develop and test flexible approaches allowing the detection and quantification of population size changes in structured populations (Hey 2005) it is also important to quantify the robustness of existing methods to population structure. In particular it would be important to determine the extent to which methods that are widely used but ignore structure can correctly detect or quantify bottlenecks or expansions. This has both practical and theoretical reasons.

In a seminal work, Wakeley (1999) showed that when populations are structured according to an n-island model, a false signal of population bottleneck can be observed within single demes. The reason behind this confounding effect can be understood in terms of coalescent trees. The genealogy of a sample taken from one deme in an n-island model will have short branches for the lineages that coalesce within the sampled deme. However, for lineages that arrived in the sampled deme through gene flow, we expect to observe much longer branches, since coalescent events will then be dependent on the effective size of the whole set of demes (Wakeley 1999). Thus, a typical gene tree is expected to have a combination of sets of short branches connected to each other by long branches. This kind of genealogy is exactly what is expected in a bottlenecked population (Hudson 1990; Beaumont 2003a; Hein et al. 2005). How strong this effect will be should depend on the relative rate of gene flow (m) and within population coalescence events (1/N, where N is the effective size of a deme). When gene flow is high over wide geographical areas, the whole set of populations sampled may behave as a single large population and it may be reasonable to keep assuming a WF model. Similarly, when gene flow is very limited, as might be the case for some isolated populations, most alleles will likely coalesce within the sampled population and the WF model may apply again. Thus, in these extreme cases, it seems reasonable to apply the methods developed to detect and quantify population size changes (Cornuet and Luikart 1996; Beaumont 1999; Garza and Williamson 2001; Storz and Beaumont 2002). Intermediate situations are likely to be present in real-life cases but this confounding effect has been little studied.

Another issue that has little been explored is that of the sampling scheme. In most studies, whether they are based on simulated or real data, it is usually assumed that samples are taken from single demes. However, with real species the delimitation between populations is rarely clear. Samples obtained in nature may thus come from more than one population. This is particularly crucial in endangered species, where small samples taken from different demes (for instance forest fragments) may need to be pooled for some analyses. This may also be problematic in species where social groups may create another level of substructure that would also violate the random mating assumptions. To understand the potential effect of the sampling strategy on the detection of bottlenecks, we can take the extreme and hypothetical case where each sampled individual or gene comes from a different deme. It is expected that coalescence times will follow a standard coalescent with an effective population size equal to that of the metapopulation (Wakeley 1999). While this extreme case is unlikely to happen by chance, it suggests that the sampling scheme might counter, to some extent, the bottleneck effect due to population structure. This may seem counterintuitive but has recently been confirmed by Städler et al. (2009) who found that when one population is sampled in a stepping-stone or n-island model, positive Tajima D values (corresponding to bottlenecks in a WF model) are typically observed and that the Tajima D values tend toward zero (stationary population in a WF model) when samples from different demes are pooled together and gene flow is high.

The confounding effects of population structure and of the sampling scheme have practical implications for many conservation studies. Indeed, in recent years there has been an increasing use of genetic data to reconstruct the demographic history of endangered species, often to detect, quantify, and/or date bottlenecks (Garza and Williamson 2001; Goossens et al. 2006; Leblois et al. 2006; Okello et al. 2008; Olivieri et al. 2008; Craul et al. 2009). Endangered species are often thought or known to have undergone bottlenecks due to hunting, the introduction of alien species, or habitat loss (Goossens et al. 2006; Olivieri et al. 2008; Craul et al. 2009; Quéméré et al. 2009; Sousa et al. 2009b). However, if population structure is creating spurious bottleneck signals, the interpretation of bottleneck signals from genetic data might be less straightforward than it would seem, and several studies may have overestimated or incorrectly detected bottlenecks.

In this study we analyze the effect of the sampling scheme, the amount of gene flow, and genetic diversity on the generation of signals of population size change using the method of Beaumont (1999). We used this method because it is a full-likelihood Bayesian method that is expected to use the genetic data efficiently, hence detecting bottlenecks when summary statistics-based methods are potentially unable to detect significant departures (e.g., Olivieri et al. 2008; Sousa et al. 2008). To do this, we simulated genetic data at mutation and migration–drift equilibrium under an n-island and a stepping-stone model. The simulated populations were thus stationary and not subject to any population size change. We varied the level of gene flow between populations and the scaled mutation rate. We also used several sampling schemes. We then analyzed the simulated samples using the Bayesian method implemented in the MSVAR program (Beaumont 1999) to detect and quantify putative population size changes. Our results show that all three factors (gene flow/genetic differentiation, genetic diversity, and the sampling scheme) play a role in generating false bottleneck signals. We also suggest an ad hoc method to counter this effect.

MATERIALS AND METHODS

Simulated data sets:

n-island model:

Data were simulated using the coalescent algorithm of Beaumont and Nichols (1996) for an n-island equilibrium model with n = 100 islands. All islands were assumed to be of size N individuals and to exchange migrants at a constant rate m. The model is fully characterized by the scaled mutation rate (θ = 4dNμ), where μ is the per locus mutation rate, d is the number of demes or islands, and by the scaled migration rate (M = 4Nm). Since we were interested in microsatellite rather than sequence data, mutations were assumed to occur under the stepwise mutation model (SMM), at the same rate for all loci. The SMM was also used as it is the mutation model assumed by the method of Beaumont (1999). We investigated the effect of varying θ and M on the detection of false bottlenecks by simulating data sets with θ = (1, 10) and M = (99, 19, 9, 3). The values of M were chosen so as to correspond to the F_ST values expected at equilibrium for an infinite island model, namely F_ST = (0.01, 0.05, 0.1, 0.25), respectively, according to the expression F_ST = 1/(1 + M). These values typically encompass the values observed in most real data sets published in conservation genetics, e.g., F_ST = 0.00–0.14 in the Mediterranean toad (Gonçalves et al. 2009), F_ST = 0.00–0.20 in mouse lemurs (Olivieri et al. 2008), and F_ST = 0.01–0.12 in the Bornean orangutan (Goossens et al. 2005). Note that these expected F_ST values are theoretically valid only under the infinite allele model (IAM) and infinite-island model (or n-island when n is large). Due to homoplasy, lower F_ST values are expected under the SMM. As a simple test we thus performed 1000 simulations under the SMM to determine the extent to which the F_ST distributions and averages obtained in the simulated data would be different from the theoretical values above. Our results (supporting information, Figure S1) suggest that the observed means and expected values are very close to each other under the n-island model whether we assume the SMM or the IAM (Figure S1, a and b). For the stepping-stone model the F_ST distribution between neighboring demes exhibited averages slightly smaller than expected under the IAM and n-island model (Figure S1, c and d). For simplicity, we will keep referring to the equilibrium F_ST values given above throughout the manuscript but the reader should be aware of this. We also note that the F_ST values given should not be taken at face value as measures of genetic differentiation (e.g., Chikhi et al. 1997; Jost 2008). Throughout the manuscript we provide both M and the corresponding equilibrium F_ST values for comparison with real-case studies for which the level of gene flow is unknown but F_ST values are provided.

We also investigated the effect of the sampling scheme by considering three different sampling strategies. In all cases we considered that 50 diploid individuals were sampled in total (100 gene copies). In the first scheme, the genetic data were sampled from 1 deme (this is the usual assumption). In the second case we pooled the samples obtained in 2 different demes (25 individuals in each). In the third case we obtained samples from 50 demes, i.e., one individual per deme. Altogether there were 24 different combinations of sampling scheme and parameter values for θ and M (θ = (1, 10) and M = (3, 9, 19, 99)). For each of them 10 independent data sets (replicates) were simulated with 5 loci. This number of loci was chosen due to the fact that MSVAR is highly computational (several days were typically necessary for one replicate/run). To determine whether the number of loci had a major effect on our results, we also repeated some of these analyses with 10 loci as many published microsatellite data typically have between 8 and 12 loci. The samples were taken from 1 deme and the parameter values used for these simulations were θ = (1, 10) and M = (99, 19, 9) (i.e., F_ST = (0.01, 0.05, 0.10)).

Stepping-stone model:

To determine whether our results were robust to the population structure model we repeated some of the simulations assuming a stepping-stone model. Here the simulations were performed assuming 5 loci, θ = (1, 10) and two values of M = (19, 3) (i.e., F_ST = (0.05, 0.25)). All parameter combinations were repeated 10 times, hence corresponding to 40 additional data sets. Thus, altogether 340 independent data sets (corresponding to 34 combinations of parameter values, model, or sampling scheme) were analyzed using MSVAR under the n-island (300) and stepping-stone (40) model with 5 or 10 loci. This is to our knowledge one of the largest tests performed on a full-likelihood method and the first to test the robustness with a reasonably large number of simulations (see Table S1).

Analysis with MSVAR:

MSVAR implements a full-likelihood Bayesian inferential method developed by Beaumont (1999). The model assumes that a single stable population of size N₁ started to decrease (or increase) t_a generations ago to the current population size, N₀. The change in population size can be either linear or exponential, and mutations are assumed to occur under a SMM model, with rate θ₀ = 4N₀μ, where μ is the locus mutation rate. Using a coalescent-based MCMC approach, the method estimates the posterior probability distributions of (i) the magnitude of population size change r = N₀/N₁, (ii) the time since the population started changing size scaled by N₀, t_f = t_a/N₀, and (iii) the scaled mutation rate θ₀ = 4N₀μ. The method uses the full allelic distribution taking into account the relative size of microsatellite alleles. It is thus expected to be more efficient at detecting population size changes than methods based on summary statistics. The simulated data sets were given as input to MSVAR, assuming an exponential model for the population size change. Wide uniform prior distributions were chosen, between −5 and 5 on a log₁₀ scale for log₁₀(r), log₁₀(θ), and log₁₀(t_f), as in Olivieri et al. (2008). For each data set one long run of 5 × 10⁹ steps was performed, with a thinning of 50,000 steps. Preliminary tests showed that these runs were long enough to reach equilibrium. This was also confirmed by our experience with real data sets (e.g., Goossens et al. 2006; Olivieri et al. 2008; Sousa et al. 2008). The first 10% of the chain was discarded (as burn-in) and the remaining was assumed to be a sample from the joint posterior distribution. We used the R language (R Development Core Team 2008) to analyze the outputs of MSVAR, using the locfit (Loader 2007), coda (Plummer et al. 2009), mcmc (Geyer 2009), and MCMCpack (Martin et al. 2009) packages. The convergence of the chains was tested with the Geweke (1992) statistic. Note, however, that we were not interested in inferring precisely the change in population size. Indeed, we were interested in determining whether there was a clear bias toward either bottlenecks or expansions, not whether the quantiles were precisely estimated or whether the mean was known with high precision. This is why convergence was not as serious an issue for us as it would be with real data sets for which several independent runs would need to be performed for each data set (e.g., Okello et al. 2008; Olivieri et al. 2008; Sousa et al. 2009a). Even in the very few cases where convergence had not been reached (based on Geweke's statistic) visual inspection of the chains suggested that the chain was close to equilibrium and the signal for either population increase or decrease was clear.

Since we were interested in the detection of population size changes we focused on the marginal posterior distribution of log₁₀(r) = log₁₀(N₀/N₁). Negative values correspond to a population decrease (N₀ < N₁), whereas positive values point to a population expansion (N₀ > N₁). Values close to zero suggest a stable population (N₀ = N₁). Flat posterior distributions suggest either a lack of information or no strong signal for a change in population size. For each data set we also recorded the mean and variance of the posterior distribution and plotted the latter against the former.

Data from two Iberian minnow species and Bornean orangutan populations:

To determine whether we could identify true from spurious bottleneck signatures in real data sets, we compared the results obtained from two Iberian minnows and orangutan populations using MSVAR (Goossens et al. 2006; Sousa et al. 2008, 2009b) with the simulation results. The Iberian minnow data sets consisted of six microsatellite loci typed at 212 and 192 individuals from Iberochondrostoma lusitanicum and I. almacai, respectively. For each species, six populations were sampled with sample sizes ranging from 21 to 43 in I. lusitanicum and from 12 to 50 in I. almacai, although most of the populations had ∼40 individuals. Note that one locus was monomorphic in I. lusitanicum. Thus, these real data set samples were similar to the simulations, with 50 diploid individuals typed at five loci. The magnitude of the population size changes (mean log₁₀(N₀/N₁) estimated with MSVAR under the same prior as the simulations), ranged from −3.14 to 0.18 in I. lusitanicum and from −3.34 to −1.92 in I. almacai. These species were characterized by F estimates, which are analogous to average F_ST, obtained with the method of Vitalis and Couvet (2001b) implemented in the program ESTIM (Vitalis and Couvet 2001a). The F estimates ranged from −0.03 to 0.42 in I. lusitanicum and from −0.14 to 0.44 in I. almacai. This range is the same as the average pairwise F_ST for each population against all the others and is thus a reasonable measure of drift within each population. The results of the two fish species were compared with the simulations by dividing the data sets into two groups to test for the effect of the population differentiation: (i) F_ST < 0.1 and (ii) F_ST ≥ 0.1. The low expected heterozygosity H_e found in these species (H_e < 0.45) and the MSVAR estimates for θ₀ = 4N₀μ suggested that the markers are characterized by low θ. Thus, the results were compared with the simulations with θ = 1. We computed the expected heterozygosity for the simulated data sets and found indeed H_e values mostly between 0.08 and 0.68 with an average of 0.47.

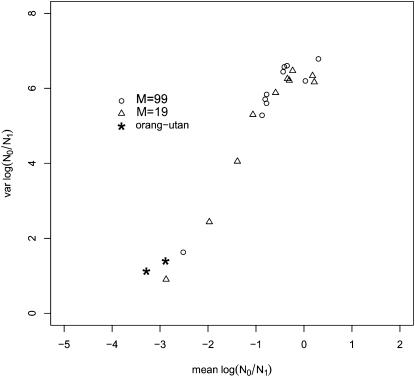
The orangutan data were obtained from Goossens et al. (2006) and consisted of 200 individuals sampled in nine forest fragments (S1–S9) located on the two sides of the Kinabatangan River and genotyped at 14 microsatellites. The F_ST values varied between 0.01 and 0.12 but the highest values were observed between samples obtained from different sides of the Kinabatangan, shown to be a barrier to gene flow (Goossens et al. 2005). When samples were taken from the same river side the F_ST values varied between 0.01 and 0.03 and between 0.01 and 0.06, with averages slightly above 0.02. In a study aiming at determining whether orangutans had been subject to population size changes (Goossens et al. 2006), two samples were analyzed, namely S1 and S2, each from a different side of the river, due to the computational cost of the method. For a comparison between the orangutan data with the simulated data sets we randomly sampled two subdata sets with 10 loci from the original orangutan 14 loci data from S1 and S2 and analyzed them with MSVAR. The results were compared with the simulation results obtained under the n-island and stepping-stone models, with M = (99, 19) corresponding to the following expected F_ST = (0.01, 0.05) and assuming θ = 1. Indeed, the estimated value for θ for single demes was ∼0.007, suggesting a global value of θ = 0.7, assuming d = 100 demes.

RESULTS

MCMC convergence:

The Geweke (1992) test suggested that most of the MCMC chains reached equilibrium (337 out of 340, Figure S2). Exceptions corresponded to data sets with 10 loci and θ = 10, where the Geweke statistic values suggest that convergence was not reached even though the chains were visually not different from other chains. We note that in the vast majority of the runs the posteriors were either similar to the prior or suggested a population decrease. It is thus unlikely that convergence affected our main conclusion that population structure mimics population bottlenecks (see below).

Genetic differentiation and diversity:

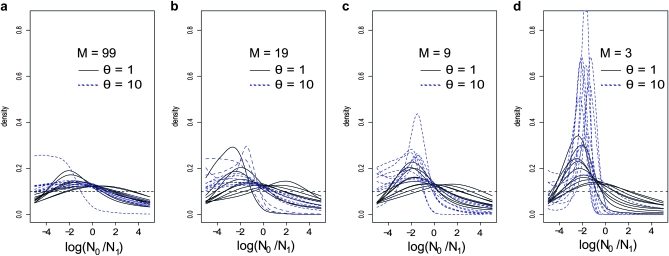
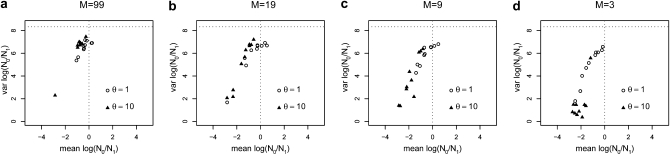
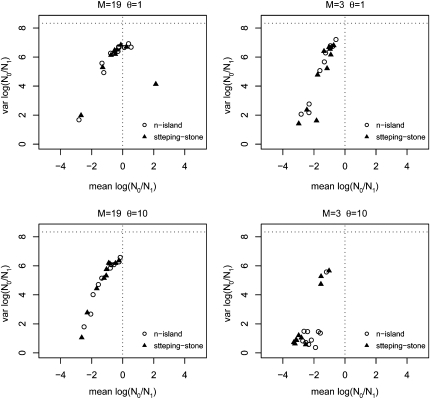
Figure 1 shows the posterior distributions obtained for log₁₀(r) with five loci. The main results are that (i) the posterior distributions are shifted toward the left (negative values corresponding to a bottleneck), (ii) the intensity of this confounding effect is dependent on the amount of gene flow between populations, (iii) the effect of population structure on the posteriors is itself significantly increased when θ = 10 compared to θ = 1 (dashed vs. solid lines). When gene flow is high with M = 99 (i.e., genetic differentiation is limited, F_ST = 0.01) and to a lesser extent for M = 19 (F_ST = 0.05) most posterior distributions do not lead to a significant signal, as they are relatively flat and exhibit large variances that are very similar to those of the prior (Figure 2). This is particularly true when θ = 1. The bottleneck effect is however extremely clear for small M values when θ = 10. Indeed, real data exhibiting similar posteriors would be interpreted as strong evidence for a population decrease around two orders of magnitude (Figures 1, c and d and 2, c and d). However, we note that even for low levels of gene flow (M values as low as 3 or F_ST values as high as 0.25), there are cases where the posteriors had a mean close to zero and a large variance (Figure 2d). This is more frequent for θ = 1 but even with θ = 10 we found 1 case out of 10, with a very wide and flat posterior distribution. Thus, it appears that population structure creates a spurious bottleneck effect that increases with genetic differentiation and with genetic diversity. The F_ST values at which this bottleneck effect is detected are typically found in the literature of both endangered and nonendangered species (e.g., Goossens et al. 2006; Olivieri et al. 2008; Craul et al. 2009; Holsinger and Weir 2009; Rosel et al. 2009). Another result apparent in Figure 2 (and in Figures 3 through 7) is the linear relationship (on a log–log scale) between the mean and variance of the posteriors obtained for the simulated data sets. The meaning of this relationship is unclear but it suggests that it may be possible to identify points that are clearly outside this “trend” and correspond to populations that are unlikely to exhibit bottleneck signals due to population structure.

Figure 1.—

Influence of gene flow and genetic diversity in the detection of bottlenecks—posteriors. Posterior distributions were obtained for log₁₀(r), where r is the ratio of present (N₀) over ancient (N₁) population size change. Negative and positive values of log₁₀(r) correspond to population bottlenecks and expansions, respectively. For all analyses the prior for log₁₀(r) was a uniform between −5 and 5 and is represented by the horizontal dashed line. The results were obtained with five loci and 50 diploid individuals sampled from a single deme assuming a 100-island model (see text for details). (a) Posteriors obtained for all the simulations performed for M = 99 (i.e., F_ST = 0.01) and for θ = 1 (solid lines) and θ = 10 (dashed lines). (b) Same as in a, but for M = 19 (i.e., F_ST = 0.05). (c) Same as in a, but for M = 9 (i.e., F_ST = 0.10). (d) Same as in a, but for M = 3 (i.e., F_ST = 0.25). Most posterior distributions are shifted to the left but are in general relatively flat for high levels of gene flow and not very different from the prior. Posteriors indicating a potential bottleneck were obtained for the lowest levels of gene flow and the highest genetic.

Figure 2.—

Influence of gene flow and genetic diversity in the detection of bottlenecks—means and variances. This figure represents on the x- and y-axes, respectively, the means and variances computed for the posterior distributions represented in Figure 1 for log₁₀(r) where r = N₀/N₁. For comparison, the mean and variance of the prior are represented by the vertical and horizontal dotted lines, respectively. Negative means correspond to population bottlenecks, whereas positive means correspond to population expansions. The open circles correspond to posteriors obtained for θ = 1, whereas the triangles were obtained with θ = 10. (a) Results correspond to simulations with 5 loci and 50 diploid individuals sampled from a single deme, assuming M = 99 (average equilibrium F_ST = 0.01) in a 100-island model (see text for details). (b) Same as in a, for M = 19 (F_ST = 0.05). (c) Same as in a, for M = 9 (F_ST = 0.10). (d) Same as in a, for M = 3 (F_ST = 0.25).

The sampling scheme:

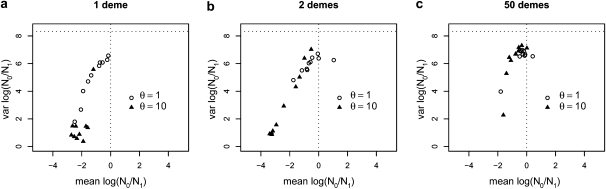
The effect of the sampling scheme appears in Figure 3 where, for M = 3 or F_ST = 0.25, we plotted the variance against the mean in cases where 2 and 50 demes were sampled (corresponding to 40 posteriors). They show that the means and variances of the posterior distributions tend toward the values of the prior when the number of sampled demes increases (Figure 3c). Interestingly, when two demes are sampled for the most extreme case of gene flow (M = 3, F_ST = 0.25), we can see a pattern similar to that observed for M = 9 (F_ST = 0.1) when only 1 deme is sampled (Figure 2c). When 50 demes are sampled (one diploid individual from each deme) the situation is even more extreme with most posteriors exhibiting little bottleneck signal as for the data obtained for M = 99 (F_ST = 0.01) when only 1 deme is sampled. These results suggest that the chances of obtaining estimates suggesting a spurious population decrease are higher when analyzing samples taken from a single deme than samples mixing more than 1 deme. It also suggests that one way of countering this spurious effect is to analyze samples taken from as many demes as possible.

Figure 3.—

Effect of the sampling scheme. The x- and y-axes are the same as in Figure 2, representing the mean and variance of the posterior distributions for log₁₀(r) obtained for three sampling schemes and with 2 scaled mutation rates (θ = (1, 10)) and for M = 3 (F_ST = 0.25). The open circles correspond to posteriors obtained for θ = 1, whereas the triangles were obtained with θ = 10. In all cases, 50 diploid individuals were sampled, using 5 loci and assuming a 100-island model. (a) All individuals were sampled from the same deme. This is identical to d in Figure 2 and is represented here for comparison. (b) Same as in a, but all individuals were sampled from 2 demes (i.e., 25 individuals from each). (c) Same as in a, but individuals were sampled from 50 demes (i.e., one individual from each).

The number of loci and the model of population structure:

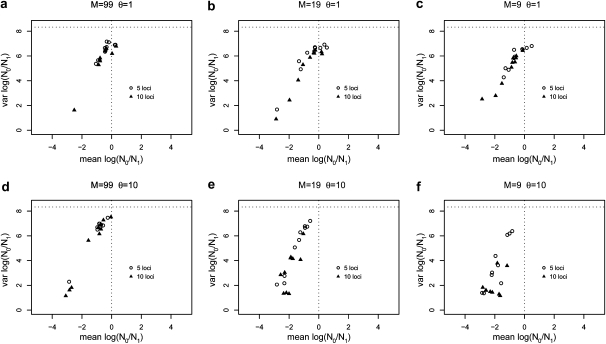
As Figure 4 shows, there were differences when 10 loci were used instead of 5. In general the means of the posteriors were shifted more toward negative values, but this effect was stronger for θ = 10 than for θ = 1. In general, the analyses with 10 loci tended to return more precise posterior distributions (smaller variance), thus increasing the support for spurious population declines. However, for θ = 1 and high gene flow (M = (99, 19), i.e., F_ST = (0.01, 0.05)) we note that the use of 10 loci did not have a very strong effect. As can be seen in Figure 5 there are no major differences between the results obtained under the stepping-stone model and the island model. For higher scaled mutation rates and lower levels of gene flow (lower right panel) the means under the stepping-stone model tend to be slightly lower than under the island model, suggesting a slightly stronger spurious bottleneck effect.

Figure 4.—

Effect of the number of loci on population size change estimates. Means and variances of the posterior distributions for log₁₀(r) are shown for samples using 5 and 10 loci for different levels of gene flow and for the two scaled mutation rates (θ = 1 for a, b, and c; θ = 10 for d, e, and f). The results were obtained by sampling 50 diploid individuals from a single deme in a 100-island model.

Figure 5.—

Comparison of the stepping-stone and n-island models. Means and variances of the posterior distributions for log₁₀(r) are shown for samples obtained for different levels of gene flow M = (19, 3) (F_ST = (0.05, 0.25) at equilibrium), and scaled mutation rates θ = (1, 10), under the n-island (open circles) and a two-dimensional stepping-stone model (solid triangles). In both cases, 50 diploid individuals sampled from a single deme and typed at 5 loci were analyzed.

Comparison of the simulations with real data:

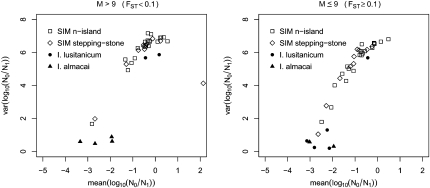
In Figure 6 the results of the fish data are compared with the distribution of the mean and variance of the magnitude of the population size change (log₁₀(r) where r = N₀/N₁) obtained in the simulations. The results of the two species fall outside the points generated with the simulations, which represent the expected distribution for the means and variances of log₁₀(r) values if population structure was the only factor. Compared with the simulations, the real data had a lower variance and in four samples the mean was more negative than the lowest value obtained with the simulations. Also, contrary to the distribution found with the simulations, the results of the fish species appear to be independent of the F_ST estimates, with most of the points in the region of means between −3 and −2 and variances between 0 and 2 in both the right and left panels (i.e., with both high and low F_ST values). For the orangutan data, the comparison with the simulated data (Figure 7) shows that the real data are more extreme, exhibiting a stronger and clearer bottleneck than expected in the simulations. This suggests that population structure alone may not fully explain the bottleneck signal detected by Goossens et al. (2006).

Figure 6.—

Comparison of the Iberian minnow data with the simulations. Means and variances of the posterior distributions for log₁₀(r) are shown for samples generated under different levels of gene flow M = (99, 19) (i.e., F_ST = (0.01, 0.05), left) and M = (9, 3) (F_ST = (0.10, 0.25), right) with scaled mutation rate θ = 1, under the n-island model and a two-dimensional stepping-stone model. In both cases, 50 diploid individuals sampled from a single deme and typed at five loci were analyzed. The results obtained for Iberochondrostoma lusitanicum and I. almacai in Sousa et al. (2008, 2009b) are represented by the solid circles and triangles, respectively. The F_ST values for the fish data were computed using the Vitalis and Couvet (2001b) method as in the original studies.

Figure 7.—

Comparison of the orangutan data with the simulations. Means and variances of the posterior distributions for log₁₀(r) are shown for samples generated under different levels of gene flow M = (99, 19) (F_ST = (0.01, 0.05)) with scaled mutation rate θ = 1. In both cases, 50 diploid individuals sampled from a single deme and typed at 10 loci were analyzed.

DISCUSSION

The importance of population structure:

The simulations presented here show that when samples are obtained from populations that are actually stationary and at mutation–drift equilibrium but are interconnected by gene flow, MSVAR detects bottlenecks that are apparently not distinguishable from real bottlenecks in WF populations. While this effect has been known from a theoretical point of view (Wakeley 1999; Beaumont 2003b, 2004; Nielsen and Beaumont 2009), it had not been quantified for data sets simulated with different levels of gene flow and diversity. We found that the effect was limited when genetic differentiation was low but that it could be observed for values of F_ST that are typically reported in the literature (e.g., Gonçalves et al. 2009; Holsinger and Weir 2009; Quéméré et al. 2009; Rosel et al. 2009). We found that the effect was particularly strong with high values of θ, which either correspond to highly variable markers or to species with large effective population sizes. This is particularly interesting as it means that structured populations with large effective sizes are the ones that are most likely to exhibit this spurious bottleneck effect.

This may seem counterintuitive but is in agreement with several recent studies as we discuss later in this section, and in particular with Wakeley (1999). It is also worrying because a large population that has recently been affected by environmental change may exhibit a bottleneck signal not necessarily because of the recent habitat contraction but also because it used to be large and structured. This is likely to be the kind of species that attracts interest of conservation biologists. That is, our results suggest that we might have found a bottleneck signal, even if we had sampled an abundant and structured species before it started decreasing. Given that several vertebrate species currently endangered used to be widely distributed and were probably structured, this result may apply to some of them. Also, the fact that for most of these species we do not have access to nondisturbed populations, due to major habitat losses that have taken place in the last centuries, we may not be able to obtain samples from undisturbed populations for which the spurious bottleneck effect could be quantified.

This result does not mean that a bottleneck detected today is necessarily unrelated to recent demographic changes due to habitat loss and fragmentation in endangered species, but it does suggest that it is currently difficult to separate the two effects (population structure and collapse). For instance, one could imagine a hypothetical situation where MSVAR identifies population size decreases by three orders of magnitude, but that population structure contributed to a 100-fold decrease, as some of our simulations suggest, whereas the actual demographic decrease was “only” 10-fold. One could probably imagine any combination of these two effects. At this stage it is difficult to say how population structure and population size change may interact, whether it is additive or not.

It is also important to stress that most inference methods available to users that explicitly model population size change ignore population structure, except for simple models with few populations (Hey and Nielsen 2004; Hey 2005). Also, it seems reasonable to state that this confounding effect is general, as it is related to the statistical properties of the gene trees generated under different scenarios (population structure/collapse). It is expected to affect all methods or statistics currently used to detect, quantify, or date population size changes. Here we used the method of Beaumont (1999) because it is expected to be very efficient at retrieving information from the full allelic distribution and because full-likelihood methods tend to be less tested than those based on summary statistics (Table S1). The effect on other methods that use only part of this information through the computation of one or several statistics may vary but there is no particular reason to assume that the problem discussed here should be specific to MSVAR. Indeed, the null distributions of the statistics used by other methods are derived or computed assuming a simple WF model without population structure. This has been confirmed by Städler et al. (2009) for the widely used Tajima (1989b) and Fu and Li (1993) statistics. Another recent study by Broquet et al. (2010) also found deviations from stationarity using the method of Cornuet and Luikart (1996) under scenarios of habitat loss and fragmentation. They found that reduction in the amount of gene flow between isolated fragments could lead to signals of bottleneck using the ΔH statistic.

Our results are in agreement with the results of Wakeley (1999) who showed that structured populations can exhibit a signal of population bottlenecks even if they are actually growing and increasingly exchanging migrants. His study was partly motivated by the observation that many genetic studies on humans were finding signals of population bottlenecks when present-day population sizes are most likely greater than that of prehistoric humans. Our results are also similar to those of Städler et al. (2009) who studied the effect of population structure on two summary statistics used to detect selection or population size changes in sequence data. They too simulated data under n-island and stepping-stone models of population structure and found that genetic differentiation was biasing Tajima's D (Tajima 1989b) and Fu and Li's D (Fu and Li 1993) toward positive values that are typically observed in declining and isolated WF populations. Städler et al. (2009) were mostly interested in detecting potential spatial expansions and in quantifying the extent to which population structure and the sampling scheme could hinder this detection. Here, by contrast, we are interested in bottlenecks and determining the conditions under which bottlenecks are spuriously detected. Städler et al. (2009) studied scenarios where an ancestral population suddenly became structured, while either staying demographically stationary or increasing significantly in size. Their results showed that the above two summary statistics were strongly influenced by population structure and the sampling scheme. Moreover, they were interested in sequence data, whereas we were interested in microsatellite data and in methods using the full allele frequency information. The latter point is particularly important as full-likelihood methods are supposed to use genetic information more efficiently. We show here that instead of providing better and more precise results, full-likelihood methods can provide stronger support for incorrect answers, at least under some conditions.

In another study Leblois et al. (2006) tried to address a different but related issue. These authors used an isolation-by-distance model, where each node corresponds to an individual rather than a deme. They then analyzed genetic samples after a fragmentation event, by sampling individuals from the only remaining habitat fragment. They applied the summary statistics-based methods of Cornuet and Luikart (1996) and Garza and Williamson (2001) to determine whether the fragmentation event led to signals of bottleneck. Their analyses suggested that a rather complex set of results could be observed. They found, as expected, that bottlenecks could be detected, but, very surprisingly, they also found a significant proportion of expansion signals. This is particularly interesting since expansion signals have also been observed in real data sets from endangered species known to have rapidly decreased in the last decades due to habitat fragmentation when the method of Cornuet and Luikart (1996) was used (e.g., Cook et al. 2007; Johnson et al. 2008; Olivieri et al. 2008). We have also found this in another set of simulations to which the Bottleneck program was applied (L. Chikhi and V. Sousa, unpublished data). Altogether, the studies mentioned above (Wakeley 1999; Leblois et al. 2006; Städler et al. 2009; Broquet et al. 2010) and ours, suggest that structured populations can generate genetic signatures and patterns that cannot be properly studied by using simple WF models. It is important to note that this is true for nonspatial (n-island) or spatially structured (stepping-stone) models. The interest for spatially explicit models has increased in the last few years, notably for nonequilibrium situations. For instance, a recent set of studies has shown that spatial expansions can generate genetic signatures that can be very different from those expected under a simple WF model (Ray et al. 2003; Edmonds et al. 2004; Klopfstein et al. 2006; Currat et al. 2006, 2008). For instance Currat et al. (2006) showed that a spatial expansion can favor the surfing behavior of neutral alleles that are rare in the source populations. This can lead to near-fixation in some of the expanding populations. Such large allele frequency differences can then be mistaken for the signature of selection. Clearly, all these and other recent studies and reviews (e.g., Goldstein and Chikhi 2002; Edmonds et al. 2004; Nielsen and Beaumont 2009; Ray and Excoffier 2009) strongly suggest that there is still much to be learned about the properties of genetic samples taken from structured populations, with or without expansion.

While this was not the focus of our article, it is worth mentioning that, to our knowledge, this is one of the first studies to perform a robustness test on a full-likelihood coalescent-based method (see, however, Strasburg and Rieseberg 2010). Indeed, the data sets typically used to test full-likelihood methods in simulation studies are usually generated under the model of interest. Our study differs from previous tests in that we simulated data under a model that is likely to be more realistic than a WF model for most species. We thus tested the robustness of the method to a specific model misspecification. Our results suggest that robustness should be better investigated in the future and that conclusions drawn from model-based methods might need to be reevaluated.

Our results would appear to suggest that the MSVAR program has a bias toward detecting bottlenecks. As noted in the Introduction, Wakeley (1999) has shown that if samples are taken from a structured population, one gene per deme, the expected genealogy should be the same as that of a rescaled WF model. In such a case we would expect that MSVAR and other methods should not detect any signal of population size change. Figure 3c showed that indeed, when we were sampling individuals from different demes the bottleneck signal was nearly absent. There is still a tendency to detect bottlenecks, however, which may lead to incorrect inference when the number of loci used increases. However, in this case we were sampling two rather than one gene per deme. Of course, one can simply sample only one gene per individual, but for endangered species, this may lead to a reduction in sample size. Another explanation for the “bias” is that Wakeley's result is based on the infinite-island model. As a simple test, we simulated data from an n-island model, where one gene is sampled from each of the 100 islands, and from a random mating population for θ = 1 and analyzed the data with MSVAR. Our results show that most posteriors are very flat, indicating no population size change. However, even for the panmictic model, we do observe a slight bias in the point estimate toward negative values (Figure S3). From a Bayesian perspective the notion of bias of point estimates is not very relevant: providing the true parameter values are distributed according to the prior (and providing the MCMC implementation has converged), then the coverage of the credible intervals is guaranteed to be exact—e.g., the true parameter value is guaranteed to be within, say, the 90% limits, 90% of the time. However, given that point values are often reported in the literature, and there is often a naive expectation that these should be unbiased, our observation has some cautionary relevance.

We also note that there is a literature bias since MSVAR has been mostly used to analyze genetic data from endangered species, i.e., species that are more likely to have experienced bottlenecks than expansions. We note that despite this bias, there are several cases where expansions or no population size changes were detected (Storz and Beaumont 2002) even when bottlenecks were known to have taken place (Bonhomme et al. 2008).

Genetic data for conservation genetics:

Genetic data are increasingly used in conservation biology and it is expected that management decisions may increasingly depend on the results of genetic studies. However, genetic data may be interpreted in different ways. For instance an endangered species may lack genetic diversity for several reasons. It could be because it has been subjected to a significant population decrease or because it has had a small population size for long periods of time (Johnson et al. 2008; Okello et al. 2008). The statistical methods used to detect population size changes usually ignore population subdivision and our results show that this may generate incorrect results under conditions that are likely to be common in nature. It may thus be necessary to reevaluate a number of older studies that detected past population size changes. At the same time, we found that when the samples are taken from several demes, MSVAR did not detect bottlenecks in most cases. This suggests an ad hoc approach to counter this effect and determine whether the single sampled populations have indeed been subject to a population size change. If a bottleneck is still detected when samples come from several demes, it may be that the whole metapopulation was subject to a population size change. This ad hoc approach would require analysis of samples obtained by maximizing the number of subpopulations. Indeed, for many endangered species currently living in a fragmented environment, one could take one individual per fragment, and if the number of fragments sampled is limited, one could take individuals from different social groups or locations within each fragment. Another solution was also proposed by Beaumont (2003a) for another model of population size change without mutations (pure drift). In this model he found that the results were improved by using temporal samples.

At another time scale, serially sampled data (i.e., present and ancient DNA) may prove extremely useful in disentangling structure and population size change. The reason for this was pointed out to us by J. Thorne (personal communication). If we assume that we have both modern and ancient samples from the same deme, we can consider two possibilities. Either this deme is isolated (i.e., no population structure) or it is connected to other demes by gene flow (population structure). If we now consider the sampled genes that have not yet coalesced at the time of the ancient samples we can see that the situation is very different with or without structure. If there were no structure, then all noncoalesced lineages will be exchangeable, whether they were from modern or ancient DNA samples. On the other hand, if there were some form of population structure, only the modern-day lineages that have not coalesced yet will have a probability to be in another deme. Thus the coalescence rates with the genes sampled in the past will be different. Thus, this differential rate of coalescence times suggests that with sufficient data there should be a way to statistically separate the two models.

Another ad hoc way to assess whether population structure is the main factor responsible for the genetic patterns is to compare the real data with the simulations results. The comparison of the MSVAR estimates of the two Iberian minnow species I. lusitanicum and I. almacai (Sousa et al. 2008, 2009b) with the simulations shows that the real data fall outside the expected distribution, suggesting that population structure alone may not explain the results of these two species. Despite the fact that the real data sets consisted of individuals genotyped at six loci (against five in the simulations) and the fact that populations had different sample sizes, these results indicate that the populations in the two species are probably undergoing a population decrease. This is in agreement with field data indicating a recent population decline in both species (Alves and Coelho 1994; Cabral et al. 2005). We also note that the two species had very low levels of genetic diversity (with H_e < 0.5). The comparison with the simulations and with θ = 1 was thus probably conservative. For the orangutans the data also appeared to be outside the distribution of the simulated data. However, the results are not completely clear and we believe that more work is necessary to confirm or contradict the conclusions of the Goossens et al. (2006) study. Of course, these ad hoc methods are tentative only as many complexities of real-life systems could still cause false bottleneck signals.

It is finally worth noting that most population genetic studies typically try to identify “populations” to which population genetics methods can be applied to estimate parameters such as admixture rates, divergence times, population size changes, etc. What our work and several other studies implicitly or explicitly suggest (Leblois et al. 2006; Städler et al. 2009; Broquet et al. 2010) is that this approach can be misleading because the identified populations are rarely isolated. Thus, it will be important to determine when the identified populations can be approximated by an isolated WF model and when they cannot, as we tried here for the quantification of population size changes.

CONCLUSION AND PERSPECTIVES

Altogether our results and those of several previous studies (Leblois et al. 2006; Städler et al. 2009) suggest that population and conservation geneticists should be very careful while interpreting genetic data. This is true for endangered populations subject to habitat loss and fragmentation but it is just as true for other areas of population genetics. As inferential methods have become increasingly powerful, they may also have become more sensitive to departures from model assumptions. Methods that account for both population subdivision and population size change may be difficult to implement as the number of parameters to estimate may grow very quickly. An alternative solution may come from the use of model-choice approaches. The recent development of methods based on the approximate Bayesian computation framework suggests that it is becoming possible to choose among several models (e.g., Fagundes et al. 2007; Cornuet et al. 2008; Bray et al. 2009; Lopes et al. 2009; V. C. Sousa, unpublished results). In that case it should be possible to determine whether data are more likely to come from a structured model than from a model with population size change (Peter et al. 2010).

It is important to add that all the simulations performed here were done assuming only one kind of departure from the model underlying MSVAR analyses. In real data, other departures could also contribute in creating false bottleneck signals. This is particularly the case with the mutation model. If the microsatellite data were generated by a mutation process where insertion or deletion of more than one repeat unit are possible, then this too could create gaps in the microsatellite distribution, which would also be interpreted as signals of bottlenecks. It is not clear how important this effect would be. Thus, there is a place for further research on the detection of past population size changes using genetic data.