Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Nov 12.
Published in final edited form as: J Biomech. 2009 May 9;42(9):1275–1281. doi: 10.1016/j.jbiomech.2009.03.034

Two-Dimensional Strain Fields on the Cross-Section of the Human Patellofemoral Joint under Physiological Loading

Clare Canal Guterl *, Thomas R Gardner +, Vikram Rajan †, Christopher S Ahmad +, Clark T Hung *, Gerard A Ateshian *,†
PMCID: PMC2980285  NIHMSID: NIHMS108737  PMID: 19433326

Abstract

The objective of this study was to provide a detailed experimental assessment of the two-dimensional cartilage strain distribution on the cross-section of the human patellofemoral joint (PFJ) subjected to physiological load magnitudes and rates. The medial side of six human PFJs sectioned along their mid-sagittal plane was loaded up to the equivalent of two body weights on a whole joint, and strain measurements obtained from digital image correlation are reported at 0.5s. Normal strains tangential to the articular surface and shear strains in the plane of the cross-section showed consistent patterns among all specimens, whereas normal strains perpendicular to the articular surface exhibited some variability that may be attributed to subject-specific variations in material properties through the depth of the articular layers. Elevated tensile and compressive principal normal strains were observed near the articular surface, around the center of the contact region, with additional locations of elevated compressive strains occurring at the bone-cartilage interface. Under an average contact stress of ∼3.3 MPa, the peak compressive principal normal strains for the patella and femur averaged -0.158 ± 0.072 and -0.118 ± 0.051 respectively, magnitudes that are significantly greater than the relative changes in cartilage thickness, -0.090 ± 0.030 and -0.072 ± 0.038 (p < 0.005). These experimental results provide a detailed description of the manner by which human PFJ articular layers deform in situ under physiological load conditions.

INTRODUCTION

Articular cartilage is described as a soft tissue whose primary function is to transmit load across diarthrodial joints, while maintaining low friction and wear. In the human patellofemoral joint (PFJ), for low to moderate activities of daily living (such as walking or rising from a chair), the load on the patella is estimated to range up to 4 body weights (BW) (Ahmed and Burke, 1983; Ahmed et al., 1987; Cohen et al., 2001; Haut, 1989; Paul, 1976). The strain distribution across the articular layers under such physiological load magnitudes has not been well described; thus it is unclear whether cartilage strains are on the order of ∼10% or ∼50%, or some other representative value, for normal activities of daily living. Furthermore, it is uncertain whether the greatest strain magnitudes occur near the articular surface or near the cartilage-bone interface; under impact loading, failure of cartilage has been reported at both locations (Atkinson and Haut, 1995; Atkinson and Haut, 2001b; Haut et al., 1995; Thompson et al., 1993).

Though the strain distribution in the PFJ articular layers is poorly understood, the relative change in articular layer thickness has been reported from magnetic resonance imaging studies (Herberhold et al., 1999); under static loading of cadaver joints, the thickness was observed to decrease by 44% on average, after 32 h of loading under a mean contact pressure of 3.6 MPa. Under in vivo conditions, the residual change in thickness, subsequent to knee bend or squatting exercises, was less than 5%. These results place a bound on the range of strains to be expected in the human PFJ articular layers under normal function. Other studies have also reported on the magnitude and patterns of deformation across the articular layers of diarthrodial joints, using a variety of invasive or non-invasive measurement techniques (Armstrong et al., 1979; Kaab et al., 1998; Macirowski et al., 1994; Suh et al., 2001; Thambyah and Broom, 2007).

The objective of this study is to provide a more detailed assessment of the strain distribution across the articular layers of the human PFJ, under load magnitudes and rates that are representative of physiological loading conditions under activities of daily living. The specific aim is to determine the peak strain magnitudes and their location across the articular layers; to provide a measure of the strain inhomogeneity; and to assess inter-subject variability. This characterization is intended to shed greater insight into the structure-function relationship of articular cartilage, aid in the understanding of potential degenerative or failure mechanisms under repetitive or injurious loading, and provide further insight into the local mechanical environment of chondrocytes (Chahine et al., 2007; Choi et al., 2007).

The experimental objective is achieved by sectioning the joint in half along the sagittal plane, ramping the load to an equivalent of 2 BW (for a whole joint) over 0.5 s or applying a dynamic load of the same peak-to-peak amplitude at a frequency of 1 Hz, and measuring the two-dimensional strain distribution on the articular layer cross-sections. The methodology employed here closely follows that of our recent study on the bovine humeral head (Canal et al., 2008). This technique relies on the method of digital image correlation to measure strains on textured surfaces, similar to other techniques described in the cartilage biomechanics literature (Erne et al., 2005; Guilak et al., 1995; Narmoneva et al., 1999; Neu et al., 2005; Schinagl et al., 1996; Wang et al., 2002).

MATERIALS AND METHODS

Specimen Preparation

Six fresh frozen human knee joints were used, sectioned 20 cm proximally at the femur and 20 cm distally at the tibia. Specimens used in this study were male ranging in age from 42 to 58 years old, (avg. 49.3 ± 7.2 s.d.); two pairs were left and right knee joints from the same donor. Joints were thawed overnight at 4°C and dissected free of skin and musculature, leaving the ligaments, capsular tissues and quadriceps tendon intact. Knees were mounted on a lightweight custom rig at a flexion angle of 45°, with a small (∼20 N) load applied on the quadriceps tendon to remove any slack and maintain the PFJ in an anatomically correct configuration. The joint was then frozen in this configuration at -25°C overnight and removed from the custom rig. Radiographs were obtained to determine the exact sagittal midline of the PFJ (and to exclude grossly arthritic joints), and the frozen joint was then sectioned along its mid-sagittal plane using a band saw.

With the joint still frozen, a rectangular acrylic template with four uniformly spaced holes was placed on the sagittal cross-section of the medial half; using these holes as guides, four small holes were drilled into the trabecular bone underlying the articular layers, two each in the patella and the femur, to serve as markers for subsequent alignment and to mark the line of action for the applied load dictated by the bisection of the angle made by the quadriceps and patella tendon. Upon thawing of the medial half, all capsular tissues, ligaments and tendons were dissected away and the tibia removed. Further visual assessment of the PFJ cartilage was performed, and only joints with visually normal or mildly fibrillated cartilage were included in this study.

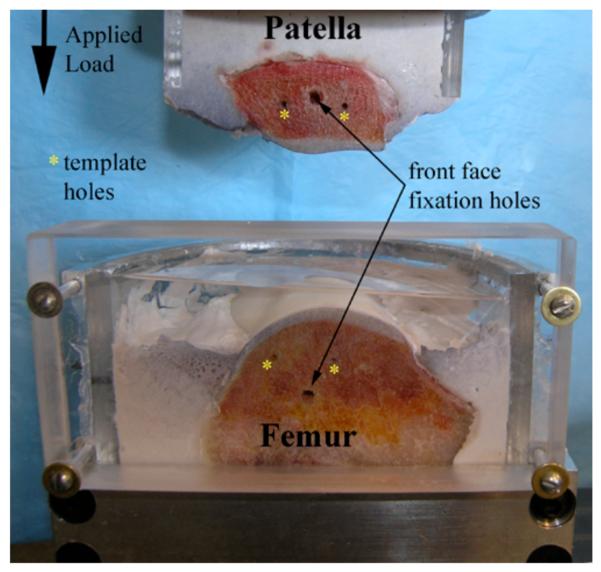
The bony ends of the patellar and femoral medial halves were each potted in custom acrylic semi-circular containers using expansion cement (Dental Stone by Super-Dent; Carlisle Laboratories, Rockville, NY), reinforced with 2.5 mm threaded rods with sharpened tips. The sagittal cross-section was placed flush against a flat acrylic plate held temporarily in place until the expansion cement had set, to ensure that the cross-sectional area was flush with the front of the container. The side wall of the femoral container rose well above the articular surface to provide for a reservoir for the testing bath solution (Fig. 1). The articular surfaces were kept covered with saline-moistened gauze at all times during sample preparation.

Figure 1.

Figure 1

Open in a new tab

Potted patella and femur. Temporary front faces were affixed to joints during cement curing to assure perfectly smooth cement and joint cross-sectional areas. Template holes were used to align the joint after the temporary faces were removed, and before the transparent face (shown here) was attached and the joint loaded.

The joint was then mounted on a material testing system (MTS 858 Bionix, Eden Prairie, MN) (Fig. 2). The patella and femur were returned to their relative orientation in the anatomically correct flexed configuration as follows: (a) The patella was potted in such a way that when threaded into the actuator of the MTS, the line of action of the load coincided with that of the frozen configuration as dictated by the template holes; and (b) after lowering the patella to articulate with the femur, the acrylic template was placed on the PFJ cross-section to realign the patella and femur to their anatomical configuration by suitably rotating the femur, mounted on an adjustable angle vise. The vise was subsequently clamped down, leaving only a degree of freedom along the antero-posterior loading direction. A 25 mm thick transparent acrylic face was then secured flush against the cross-section of the PFJ, to minimize out of plane cartilage deformation, and provide a sealed reservoir space for the bathing solution (Fig. 2). Testing was performed in a bath of phosphate buffered saline containing protease inhibitors (Protease Inhibitor Tablets, Roche Applied Sciences, Indianapolis, IN).

Figure 2.

Figure 2

Open in a new tab

Testing setup: The patellar and femoral sagittal sections are flush with the thick transparent wall for the specimen chamber.

Loading Protocol

Step and dynamic loading protocols were used in this study, both with a peak load amplitudes of F0 , set to one body weight (BW), with a representative value of 1 BW=800 N. Since 1 BW was applied to the medial half of the joint, this protocol is equivalent to applying approximately 2 BW on a complete PFJ.

For step loading, the loading history F(t) had a step-and-hold profile, with the peak load F0 reached in 0.5 s and held constant for 20 minutes. Dynamic loading was applied using a sinusoidal waveform, F(t)= F0(1—cos2π ft)/2 , with a peak-to-peak amplitude of F0 and a loading frequency f = 1 Hz. To ensure stable actuation under load control, dynamic testing was initiated after the application of a 5N tare load; the testing duration for dynamic loading was 10 minutes. Specimens were allowed a recovery period of 90 minutes after removal of step loading, prior to the application of the dynamic loading sequence. In a subset of two joints, the average contact stress was calculated by estimating the contact area at the completion of dynamic loading: India ink was injected into the bath while the articular layers were still contacting, and the patellar footprint on the femur, where the dye was excluded by the contacting surfaces, was subsequently acquired with a spatial linkage digitizer (MicroScribe G2X 3D Digitizer, Immersion Corporation, San Jose, CA) and calculated in a geometric modeling software environment (Rhinoceros 3.0, Robert McNeel & Associates, Seattle, WA).

Imaging of Cartilage Deformation

Prior to mounting the specimen on the testing apparatus, black Verhoeff elastin stain was sprayed on the cartilage cross-sections using an airbrush as reported in previous experiments (Canal et al., 2008; Canal et al., 2003; Narmoneva et al., 1999), producing markers ∼40-100 μm in diameter. This type of stain, which has been commonly used for optical measurements of strain in ligaments (Woo et al., 1983), has negligible stiffness and does not influence the tissue’s mechanical response. During loading, movies were acquired of the contacting articular cross-sections using a high definition digital video camera (Digital HDV Camcorder GR-HD1, JVC Americas Corp, www.jvc.com) with a resolution of 1280×720 pixels, at 30 frames per second (fps) in macro mode. The average image resolution for this setup was approximately 30 μm/pixel. Digital video images were saved to digital tape during filming and downloaded to a personal computer after completion of loading, for subsequent post-processing. The output from the load cell was synchronized with the video images using a light-emitting diode that was turned off at the start of load acquisition (Fig. S 1b).

2D Strain Fields

Two-dimensional strain analysis was performed using a commercial digital image correlation (DIC) software (Vic 2D, West Columbia, SC) as described in our recent study (Canal et al., 2008). For each specimen, at a rate of 30 fps, there were respectively 36000 and 18000 time points available for analysis, from the step and dynamic loading tests. The following key time points were chosen: 0 s, 0.5 s, 1.0 s, 5.0 s, 30 s, 1 min, 5 min, 10 min, 15 min, and 20 min (the last two time points are only applicable to step loading). For dynamic loading, the images corresponding to the peak compressive load in a cycle were employed. Along with local deformation and strain fields, the relative change in articular layer thickness (“engineering strain”) at the center of contact of both articular layers was also determined, at each of these time points.

Two-dimensional strain fields Exx, Eyy and Exy were evaluated in a local x — y — z coordinate system, where x and y represent approximately the directions tangential and normal to the articular surfaces, respectively, in the plane of the cross-section, while z is the direction normal to the cross-section. In addition, principal normal strains, E1 and E2, and the maximum shear strain Gmax = |E1 — E2|/2 in the plane of the cross-section, were evaluated under the assumption that the out-of-plane shear strain components are negligible (Canal et al., 2008),

[E]=ExxExy0ExyEyy000Ezz (1.1)

Detailed reports of the accuracy of the DIC methodology for measuring 2D strains in articular cartilage are reported in an earlier study (Wang et al., 2002). Repeatability of strain measurements for the technique presented in this study, as assessed from two consecutive identical loading protocols on six bovine humeral heads, has also been reported in a previous study (Canal et al., 2008). The root mean square difference between principal normal strains measured in the first and second test was better than 0.1% strain.

RESULTS

Movies acquired from a representative joint are available as Supplementary Data online (Fig. S 1). For all joints, under step loading, the contact width on the sagittal cross-section ranged from 12.2 ± 2.1 mm at t = 0.5s to 18.1 ± 2.5 mm at t=10 min, reaching 19.5 ± 2.1 mm at t = 20min. For dynamic loading, the contact width was 12.0 ± 3.0 mm in the first cycle, increasing to 16.8 ± 2.6 mm in the last cycle at t=10min. From measurements of the contact area in two of the joints, the average contact stress at the completion of dynamic loading was estimated at 3.3 MPa.

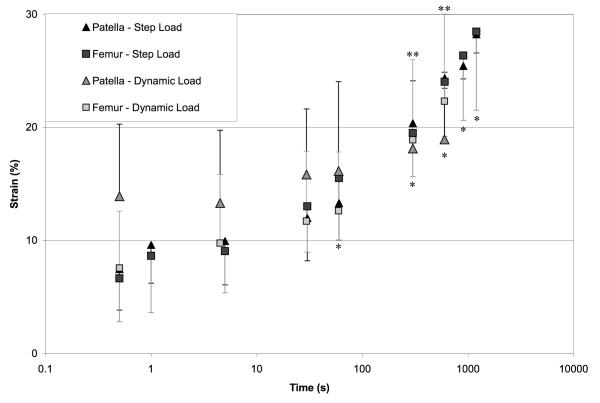
The relative change in articular layer thickness at the center of contact is reported in Fig. 3, for step and dynamic loading, in the patella and femur. This engineering strain increased significantly over time (p<0.05) over the duration of both dynamic and step loading tests. The amplitude of the strain from tare to peak load during dynamic loading was 0.0345 ± 0.025 and 0.0308 ± 0.025 for the first cycle, and 0.0290 ± 0.024 and 0.0156 ± 0.009 for the final cycle, in the patella and femur respectively.

Figure 3.

Figure 3

Open in a new tab

Averages and standard deviations of relative change in articular layer thickness, for dynamic and step loading. When compared to the t=0.5s time point, engineering strain magnitudes increased significantly with time starting at t=60s for step loading (* p <0.05) and t=300s for dynamic load (**p<0.05).

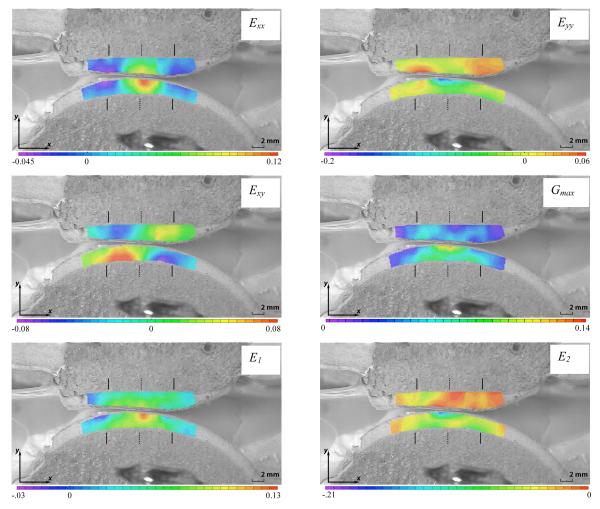
Detailed strain fields are only reported for the step loading configuration at t=0.5 s, as these represent the most physiologically relevant results. The short-time response to dynamic loading was nearly identical to that of step loading (results not shown). Two-dimensional strain maps for one of the specimens (male, right knee, age 52) are presented in Fig. 4, and corresponding strain maps for the remaining five specimens are provided as Supplementary Data online (Fig. S 2 a-e). Since DIC calculates localized deformation based on a window of pixels surrounding any given analysis point, the regions of interest selected in each of the patellar and femoral articular layers were slightly recessed from the articular surface, to avoid including pixels from the patella in the strain analysis of the femur, and vice-versa, particularly near the contact interface.

Figure 4.

Figure 4

Open in a new tab

Representative 2D strain plots of the PFJ at the end of the loading ramp (800N load, t = 0.5s) superimposed on the undeformed image. Solid lines above and below articulating layers signify contact edge locations for each layer; dashed lines signify centers of contact. Note that the range of strains for the color legend on each panel differs.

Some features of the strain distribution, such as patterns of higher or lower strain magnitudes, and positive or negative values, recurred consistently in all specimens, whereas other features exhibited inter-specimen variability, as outlined here. Consistency of these patterns, or lack thereof, was assessed qualitatively from the color contour plots, since meaningful quantitative measures of consistency are not readily available. In all specimens, the normal strain tangential to the articular surface ( Exx ) was tensile and greatest in magnitude at the center of contact, for patellar and femoral articular layers (Fig. 4). In all femoral layers and 4 of 6 patellar layers, the peak value of Exx occurred at the articular surface; in the remaining patella specimens the peak value occurred in the deep zone (Fig. S 2a) or middle zone (Fig. S 2b). Conversely, at the edges of the contact region (whose location is indicated by vertical solid bars in Fig. 4 and Fig. S 2), Exx was compressive near the articular surfaces, in both femoral and patellar articular layers. A visual assessment (Fig. 4 and Fig. S 2) indicates that Exx achieved higher magnitudes in the patellar layer in three joints, and in the femoral layer in the remaining three joints.

The normal strain in the direction normal to the articular surfaces ( Eyy ) showed less consistent patterns than Exx. In the femoral layer, Eyy was compressive at the center of contact, throughout the articular layer thickness; however, the peak compressive magnitude occurred in the superficial zone in the case of four specimens (including Fig. 4), and in the deep zone for the remaining specimens. At the edges of the contact region, Eyy was moderately tensile in most femoral layers, indicative of a slight bulging of the tissue in the direction normal to the articular surface. In the patella, Eyy was compressive at the center of the contact region, in the superficial zone, in only three specimens (including Fig. 4); the remaining specimens showed negligible strain magnitudes in that region. However, all six specimens showed elevated tensile values of Eyy at the edges of the contact area, in the superficial zone (Fig. 4 and Fig. S 2), indicative of significant bulging in the direction normal to the articular surface. Three specimens exhibited a pronounced increase in the magnitude of compressive Eyy in the deep zone of the patellar layer (Fig. S 2a, b & d) and only one specimen showed elevated compressive Eyy in the superficial zone (Fig. S 2c). In all specimens, the patellar layer exhibited much more significant bulging normal to the articular surface, at the edge of the contact region, than the femoral layer, as determined from the tensile values of Eyy. However, the peak compressive magnitude of Eyy showed less consistency, occurring in the patella in four specimens, and in the femur in the remaining specimens.

The shear strain distribution over the plane of the cross-section ( Exy ) was very consistent among all specimens, as well as between the patellar and femoral layers. Exy, a measure of distortion, was elevated in the regions between the center and edge of the contact area, in a nearly symmetric pattern across the center of contact (indicated by a dashed vertical line in Fig. 4 and Fig. S 2), with its peak magnitude generally occurring at the cartilage-bone interface. Peak magnitudes of Exy were highest in the patellar layer in three specimens, and comparable between patellar and femoral layers in the remaining specimens.

Maximum shear strain plots ( Gmax ) exhibited higher intensities at the cartilage bone interface at the edges of contact, and at the articular surface about the center of contact. The location of the peak in these intensities varied between specimens. In the representative sample shown in Fig. 4, this peak value is located at the center of contact at the articular surface of the femoral layer.

Contour plots of maximum principal normal strain ( E1 ) were similar to plots of Exx, with peak tensile strains located at the center of the contact area. The minimum principal normal strain ( E2 ) showed less inter-specimen variability than Eyy, with intensities of compressive strain located at the cartilage-bone interface at the edges of contact, and at the articular surface near the center of contact, similar to Gmax.

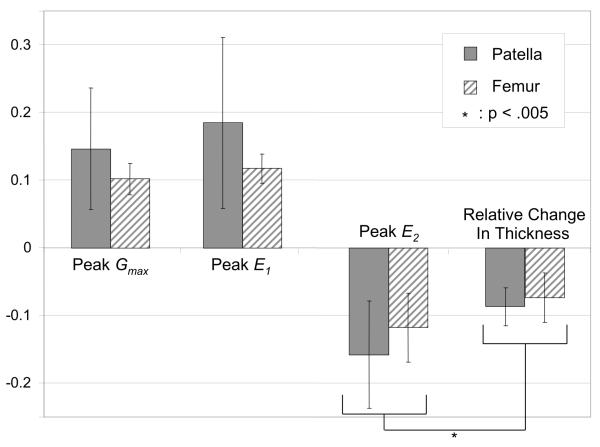
Means and standard deviations of the peak values of E1, E2 and Gmax over each of the patellar and femoral articular layers, and the relative change of thickness at the center of contact at t=0.5 s, are reported in Fig. 6. Peak values of the minimum principal strains ( E2 ) were significantly higher than corresponding engineering strains in the patellar and femoral layers (p < 0.005). Peak tensile strains ( E1 ) were not significantly different from the magnitude of peak compressive strains ( E2 ) (p = 0.794), nor was there any significant difference in peak strain values between femoral and patellar articular layers (p = 0.259).

Figure 6.

Figure 6

Open in a new tab

Averages and standard deviations of peak principal normal and maximum shear strain values, and relative change in thickness, over all patellae and femurs, at t=0.5 s.

DISCUSSION

The 2D strain distributions on the cross-section of the human patellofemoral joint observed in this study provide the most direct evidence to date of the manner by which contacting articular layers redistribute the applied load. Plots of Exx and E1 (Fig. 4) indicate that, in the central region of contact, the articular cartilage in the superficial zone expands laterally, in the plane tangential to the articular surface; at the edges of the contact, the tissue is compressed in this tangential plane, as the central expansion is resisted by the undeformed tissue farther outside of the contact region. In the deep zone, since the cartilage is anchored to the bone, this lateral expansion reduces to zero, as suggested by the values of Exx in that region.

Plots of Eyy indicate that the tissue in the center of the contact region is compressed along the direction normal to the articular surface; this axial compression at the center is accompanied by bulging of the tissue at the edges of the contact, normal to the articular surface. This phenomenon has been reported from theory previously (for example, see Fig. 3 in (Ateshian and Wang, 1995)) and is expected to occur when the deformation is nearly isochoric. An interesting observation is that the variation of Eyy through the depth of the articular layer does not show a consistent pattern for all joints. In our recent companion study of immature and mature bovine humeral head contacting a flat glass slide (Canal et al., 2008), it was observed that Eyy is always greatest at the articular surface and decreases toward the deep zone. In contrast, the current study of human PFJ suggests that some specimens exhibit peak values of Eyy and E2 in the deep zone.

Theoretical studies of the contact of biphasic cartilage layers have suggested that peak values of Eyy and E2 would occur in the deep zone if the solid matrix of the articular layers were modeled with homogeneous properties through the depth, behaving as a linear isotropic elastic material (Ateshian et al., 1994; Ateshian and Wang, 1995). Interestingly, this outcome was also predicted when accounting for the disparity between tensile and compressive properties of cartilage, and using inhomogeneous properties obtained from experimental measurements of human PFJ cartilage (Krishnan et al., 2003). The fact that Eyy and E2 are found to be consistently higher in the superficial zone of bovine humeral head cartilage, and occasionally higher in the superficial zone of human PFJ articular layers, implies that the precise variation in the depth-dependent tensile and compressive properties of the solid matrix has a very significant influence on these strain measures. Thus, accurate predictions of this observed behavior from theoretical models requires a more detailed specimen-specific characterization of the tissue’s inhomogeneous material properties, under tension, compression and shear.

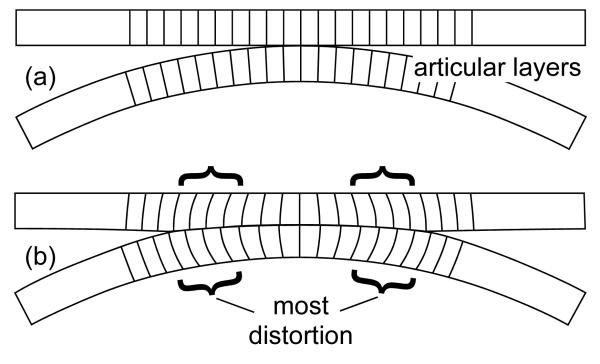
Plots of Exy showed consistent patterns (Fig. 4) that may be interpreted as follows: Since the cartilage layer is anchored to the bone in the deep zone but expands laterally in the superficial zone, the greatest amount of distortion (hence, the greatest magnitude of Exy ) occurs at the cartilage-bone interface, away from the center of contact. This can be visualized by imagining a series of nearly parallel straight lines drawn on the cross-section of the articular layer, perpendicular to the cartilage-bone interface; as the tissue is loaded, the line at the center of contact remains perpendicular to the bone, whereas lines on either side of the center of contact will bow laterally, increasing or decreasing their angle relative to the subchondral bone surface (Fig. 5).

Figure 5.

Figure 5

Open in a new tab

Schematic representation of the shear strain in contacting articular layers, visualized as distortional changes: (a) Before deformation, lines may be drawn across the articular layer thickness, at right angle to the cartilage-bone interface. (b) Upon deformation, the lines situated on either side of the centerline of contact (indicated with braces) bow laterally, while remaining anchored to the bony substrate; the change in angle from perpendicularity is an indication of distortion (change in shape).

If the shear modulus does not increase substantially with depth from the articular surface, the greatest shear strain occurs at the cartilage-bone interface, as also predicted from theory (Ateshian et al., 1994; Ateshian and Wang, 1995; Krishnan et al., 2003). This observed behavior is consistent with the shear strain measurements in the mature bovine humeral head (Canal et al., 2008); in contrast, the immature bovine humeral head exhibits peak shear strains nearer the articular surface, suggesting that its shear modulus exhibits a much more significant increase with increasing depth from the surface, which limits the amount of distortion in the deep zone. Indeed, measurements of the properties of adult human PFJ cartilage suggest that solid matrix equilibrium moduli vary by a factor ranging from ∼2 to ∼3 from the superficial to the deep zone (Krishnan et al., 2003); in contrast, the equilibrium shear and compressive moduli of immature bovine cartilage increase by a factor as high as ∼10 (Buckley et al., 2008; Wang et al., 2002). These comparisons further emphasize that variations in depth-dependent properties have a very significant influence on the strain patterns.

The locations of peak strains reported in plots of the principal normal strains and maximum shear strain are consistent with experimental studies showing that the primary locations for cartilage injury under impact or blunt injury loading are either at the articular surface or the cartilage-bone interface (Arokoski et al., 2000; Atkinson and Haut, 2001a; Atkinson et al., 1998; Ewers et al., 2002; Vener et al., 1992). The variability in injury sites reported in the prior literature seems to be reflected in the variability observed in the current study on the site of peak tensile ( E1 ) and shear ( Gmax ) strains. Peak tensile strains found in the superficial zone are also consistent with sites of surface fibrillation and degeneration usually reported in the PFJ, though the specimens used in this study did not exhibit any significant fibrillation. It has been suggested previously that the softer patellar cartilage would be more susceptible to fibrillation than femoral cartilage (Froimson et al., 1997), however the current study shows that peak strains magnitudes may occur variably in the patellar or femoral layer, on a subject-specific basis (Fig. 4 and Fig. S 2). On average, no significant differences were found in peak strain magnitudes between patellar and trochlear cartilage, though greater variability was observed in the patella as indicated by the larger standard deviations in Fig. 6. These variable outcomes may be attributed to different stages of early tissue degradation that were not evident from visual and radiographic assessment of the articular layers.

As expected, the peak magnitudes of localized strain were generally higher than the relative change in thickness (Fig. 6), since the strain represents a local measure. The finding that the peak magnitudes of principal normal and maximum shear strains in the human PFJ range from ∼10% to ∼20% in the early time response to a physiological joint contact force equivalent to 2 BW answers a key question in the cartilage literature, in regard to the magnitudes and patterns of strain distribution experienced by cartilage under normal function. Insights gained from these results improve our understanding of the in situ mechanical environment of articular cartilage and its ability to withstand the loading environment of diarthrodial joints.

The experimental protocol of this study has certain limitations, which derive primarily from the need to section the joint in half in order to visualize two-dimensional deformations and strain on a cross-section of the articular layers. Our recent companion study on bovine humeral head strains discusses these limitations in greater detail (Canal et al., 2008). These limitations cannot be entirely overcome experimentally; thus, computational analyses of the three-dimensional contact of articular layers may still provide valuable information to complement experimental findings. Our future studies will investigate methods for validating cartilage constitutive relations and computational models of articular contact, using the experimental findings of this study. The mechanical properties, biochemical composition, and histology of the preserved second half of the joints used in this study may be assessed to provide greater insight into these strain measurements and provide the necessary properties for finite element analyses.

Supplementary Material

Fig S1a and S1b

Fig. S 1 High definition movie for the response of a human PFJ (same specimen as in Fig. 4) to (a) step loading and (b) dynamic loading. The joint has been sectioned along its mid-sagittal plane and optical texturing has been applied to the cross-section by spraying a fine mist of Verhoeff stain. Only the first ∼60 s of loading are displayed. The file format for these movies is MPEG-4 and it can be viewed, for example, using the free QuickTime Player (www.apple.com/quicktime/).

Download video file (31.9MB, mov)
Download video file (36MB, mov)
Figure S2

Two-dimensional strain maps for five human PFJ specimens (all male): (a) age 45, left knee; (b) age 52, left knee; (c) age 42, left knee; (d) age 42, right knee; (e) age 54, left knee.

ACKNOWLEDGMENTS

This study was supported with funds from the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the U.S. National Institutes of Health (AR46532).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

REFERENCES

  1. Ahmed AM, Burke DL. In-vitro measurement of static pressure distribution in synovial joints--Part I: Tibial surface of the knee. J Biomech Eng. 1983;105:216–225. doi: 10.1115/1.3138409. [DOI] [PubMed] [Google Scholar]
  2. Ahmed AM, Burke DL, Hyder A. Force analysis of the patellar mechanism. J Orthop Res. 1987;5:69–85. doi: 10.1002/jor.1100050110. [DOI] [PubMed] [Google Scholar]
  3. Armstrong CG, Bahrani AS, Gardner DL. In vitro measurement of articular cartilage deformations in the intact human hip joint under load. J Bone Joint Surg Am. 1979;61:744–755. [PubMed] [Google Scholar]
  4. Arokoski JP, Jurvelin JS, Vaatainen U, Helminen HJ. Normal and pathological adaptations of articular cartilage to joint loading. Scand J Med Sci Sports. 2000;10:186–198. doi: 10.1034/j.1600-0838.2000.010004186.x. [DOI] [PubMed] [Google Scholar]
  5. Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech. 1994;27:1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
  6. Ateshian GA, Wang H. A theoretical solution for the frictionless rolling contact of cylindrical biphasic articular cartilage layers. J Biomech. 1995;28:1341–1355. doi: 10.1016/0021-9290(95)00008-6. [DOI] [PubMed] [Google Scholar]
  7. Atkinson PJ, Haut RC. Subfracture insult to the human cadaver patellofemoral joint produces occult injury. J Orthop Res. 1995;13:936–944. doi: 10.1002/jor.1100130619. [DOI] [PubMed] [Google Scholar]
  8. Atkinson PJ, Haut RC. Impact responses of the flexed human knee using a deformable impact interface. J Biomech Eng. 2001a;123:205–211. doi: 10.1115/1.1372320. [DOI] [PubMed] [Google Scholar]
  9. Atkinson PJ, Haut RC. Injuries produced by blunt trauma to the human patellofemoral joint vary with flexion angle of the knee. J Orthop Res. 2001b;19:827–833. doi: 10.1016/S0736-0266(00)00073-5. [DOI] [PubMed] [Google Scholar]
  10. Atkinson TS, Haut RC, Altiero NJ. Impact-induced fissuring of articular cartilage: an investigation of failure criteria. J Biomech Eng. 1998;120:181–187. doi: 10.1115/1.2798300. [DOI] [PubMed] [Google Scholar]
  11. Buckley MR, Gleghorn JP, Bonassar LJ, Cohen I. Mapping the depth dependence of shear properties in articular cartilage. J Biomech. 2008;41:2430–2437. doi: 10.1016/j.jbiomech.2008.05.021. [DOI] [PubMed] [Google Scholar]
  12. Canal CE, Hung CT, Ateshian GA. Two-dimensional strain fields on the cross-section of the bovine humeral head under contact loading. Journal of Biomechanics. 2008 doi: 10.1016/j.jbiomech.2008.08.031. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Canal CE, Meade NK, Wang CC, Hung CT, Ateshian GA. Optical measurement of in situ strain fields within osteochondral tissue under indentation. Summer Bioengineering Conference; 2003. Paper #363. [Google Scholar]
  14. Chahine NO, Hung CT, Ateshian GA. In-situ measurements of chondrocyte deformation under transient loading. Eur Cell Mater. 2007;13:100–111. doi: 10.22203/ecm.v013a11. discussion 111. [DOI] [PubMed] [Google Scholar]
  15. Choi JB, Youn I, Cao L, Leddy HA, Gilchrist CL, Setton LA, Guilak F. Zonal changes in the three-dimensional morphology of the chondron under compression: the relationship among cellular, pericellular, and extracellular deformation in articular cartilage. J Biomech. 2007;40:2596–2603. doi: 10.1016/j.jbiomech.2007.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Cohen ZA, Roglic H, Grelsamer RP, Henry JH, Levine WN, Mow VC, Ateshian GA. Patellofemoral stresses during open and closed kinetic chain exercises. An analysis using computer simulation. Am J Sports Med. 2001;29:480–487. doi: 10.1177/03635465010290041701. [DOI] [PubMed] [Google Scholar]
  17. Erne OK, Reid JB, Ehmke LW, Sommers MB, Madey SM, Bottlang M. Depth-dependent strain of patellofemoral articular cartilage in unconfined compression. J Biomech. 2005;38:667–672. doi: 10.1016/j.jbiomech.2004.04.005. [DOI] [PubMed] [Google Scholar]
  18. Ewers BJ, Weaver BT, Sevensma ET, Haut RC. Chronic changes in rabbit retro-patellar cartilage and subchondral bone after blunt impact loading of the patellofemoral joint. J Orthop Res. 2002;20:545–550. doi: 10.1016/S0736-0266(01)00135-8. [DOI] [PubMed] [Google Scholar]
  19. Froimson MI, Ratcliffe A, Gardner TR, Mow VC. Differences in patellofemoral joint cartilage material properties and their significance to the etiology of cartilage surface fibrillation. Osteoarthritis Cartilage. 1997;5:377–386. doi: 10.1016/s1063-4584(97)80042-8. [DOI] [PubMed] [Google Scholar]
  20. Guilak F, Ratcliffe A, Mow VC. Chondrocyte deformation and local tissue strain in articular cartilage: a confocal microscopy study. J Orthop Res. 1995;13:410–421. doi: 10.1002/jor.1100130315. [DOI] [PubMed] [Google Scholar]
  21. Haut RC. Contact pressures in the patellofemoral joint during impact loading on the human flexed knee. J Orthop Res. 1989;7:272–280. doi: 10.1002/jor.1100070216. [DOI] [PubMed] [Google Scholar]
  22. Haut RC, Ide TM, De Camp CE. Mechanical responses of the rabbit patello-femoral joint to blunt impact. J Biomech Eng. 1995;117:402–408. doi: 10.1115/1.2794199. [DOI] [PubMed] [Google Scholar]
  23. Herberhold C, Faber S, Stammberger T, Steinlechner M, Putz R, Englmeier KH, Reiser M, Eckstein F. In situ measurement of articular cartilage deformation in intact femoropatellar joints under static loading. J Biomech. 1999;32:1287–1295. doi: 10.1016/s0021-9290(99)00130-x. [DOI] [PubMed] [Google Scholar]
  24. Kaab MJ, Ito K, Clark JM, Notzli HP. Deformation of articular cartilage collagen structure under static and cyclic loading. J Orthop Res. 1998;16:743–751. doi: 10.1002/jor.1100160617. [DOI] [PubMed] [Google Scholar]
  25. Krishnan R, Park S, Eckstein F, Ateshian GA. Inhomogeneous cartilage properties enhance superficial interstitial fluid support and frictional properties, but do not provide a homogeneous state of stress. J Biomech Eng. 2003;125:569–577. doi: 10.1115/1.1610018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Macirowski T, Tepic S, Mann RW. Cartilage stresses in the human hip joint. J Biomech Eng. 1994;116:10–18. doi: 10.1115/1.2895693. [DOI] [PubMed] [Google Scholar]
  27. Narmoneva DA, Wang JY, Setton LA. Nonuniform swelling-induced residual strains in articular cartilage. J Biomech. 1999;32:401–408. doi: 10.1016/s0021-9290(98)00184-5. [DOI] [PubMed] [Google Scholar]
  28. Neu CP, Hull ML, Walton JH. Heterogeneous three-dimensional strain fields during unconfined cyclic compression in bovine articular cartilage explants. J Orthop Res. 2005;23:1390–1398. doi: 10.1016/j.orthres.2005.03.022.1100230622. [DOI] [PubMed] [Google Scholar]
  29. Paul JP. Force actions transmitted by joints in the human body. Proc R Soc Lond B Biol Sci. 1976;192:163–172. doi: 10.1098/rspb.1976.0004. [DOI] [PubMed] [Google Scholar]
  30. Schinagl RM, Ting MK, Price JH, Sah RL. Video microscopy to quantitate the inhomogeneous equilibrium strain within articular cartilage during confined compression. Ann Biomed Eng. 1996;24:500–512. doi: 10.1007/BF02648112. [DOI] [PubMed] [Google Scholar]
  31. Suh JK, Youn I, Fu FH. An in situ calibration of an ultrasound transducer: a potential application for an ultrasonic indentation test of articular cartilage. J Biomech. 2001;34:1347–1353. doi: 10.1016/s0021-9290(01)00088-4. [DOI] [PubMed] [Google Scholar]
  32. Thambyah A, Broom N. On how degeneration influences load-bearing in the cartilage-bone system: a microstructural and micromechanical study. Osteoarthritis Cartilage. 2007;15:1410–1423. doi: 10.1016/j.joca.2007.05.006. [DOI] [PubMed] [Google Scholar]
  33. Thompson RC, Jr., Vener MJ, Griffiths HJ, Lewis JL, Oegema TR, Jr., Wallace L. Scanning electron-microscopic and magnetic resonance-imaging studies of injuries to the patellofemoral joint after acute transarticular loading. J Bone Joint Surg Am. 1993;75:704–713. doi: 10.2106/00004623-199305000-00010. [DOI] [PubMed] [Google Scholar]
  34. Vener MJ, Thompson RC, Jr., Lewis JL, Oegema TR., Jr. Subchondral damage after acute transarticular loading: an in vitro model of joint injury. J Orthop Res. 1992;10:759–765. doi: 10.1002/jor.1100100603. [DOI] [PubMed] [Google Scholar]
  35. Wang CC, Deng JM, Ateshian GA, Hung CT. An automated approach for direct measurement of two-dimensional strain distributions within articular cartilage under unconfined compression. J Biomech Eng. 2002;124:557–567. doi: 10.1115/1.1503795. [DOI] [PubMed] [Google Scholar]
  36. Woo SL, Gomez MA, Seguchi Y, Endo CM, Akeson WH. Measurement of mechanical properties of ligament substance from a bone-ligament-bone preparation. J Orthop Res. 1983;1:22–29. doi: 10.1002/jor.1100010104. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Fig S1a and S1b

Fig. S 1 High definition movie for the response of a human PFJ (same specimen as in Fig. 4) to (a) step loading and (b) dynamic loading. The joint has been sectioned along its mid-sagittal plane and optical texturing has been applied to the cross-section by spraying a fine mist of Verhoeff stain. Only the first ∼60 s of loading are displayed. The file format for these movies is MPEG-4 and it can be viewed, for example, using the free QuickTime Player (www.apple.com/quicktime/).

Download video file (31.9MB, mov)
Download video file (36MB, mov)
Figure S2

Two-dimensional strain maps for five human PFJ specimens (all male): (a) age 45, left knee; (b) age 52, left knee; (c) age 42, left knee; (d) age 42, right knee; (e) age 54, left knee.

NIHMS108737-supplement-Fig__S2.pdf (22.7MB, pdf)

RESOURCES