Measurements of Transmembrane Potential and Magnetic Field at the Apex of the Heart

Abstract

We studied the transmembrane potential and magnetic fields from electrical activity at the apex of the isolated rabbit heart experimentally using optical mapping and superconducting quantum interference device microscopy, and theoretically using monodomain and bidomain models. The cardiac apex has a complex spiral fiber architecture that plays an important role in the development and propagation of action currents during stimulation at the apex. This spiral fiber orientation contains both radial electric currents that contribute to the electrocardiogram and electrically silent circular currents that cannot be detected by the electrocardiogram but are detectable by their magnetic field, B_z. In our experiments, the transmembrane potential, V_m, was first measured optically and then B_z was measured with a superconducting quantum interference device microscope. Based on a simple model of the spiral structure of the apex, V_m was expected to exhibit circular wave front patterns and B_z to reflect the circular component of the action currents. Although the circular V_m wave fronts were detected, the B_z maps were not as simple as expected. However, we observed a pattern consistent with a tilted axis for the apex spiral fiber geometry. We were able to simulate similar patterns in both a monodomain model of a tilted stack of rings of dipole current and a bidomain model of a tilted stack of spiraled cardiac tissue that was stimulated at the apex. The fact that the spatial pattern of the magnetic data was more complex than the simple circles observed for V_m suggests that the magnetic data contain information that cannot be found electrically.

Introduction

Electrocardiography is the most common way to obtain information about electrical behavior in the heart. However, researchers have suggested that magnetocardiograms may contain information that is not present in electrocardiograms (1–4). One place to search for such new information is at the apex of the heart (5), where mathematical modeling has shown that identical electric signals can give rise to different magnetic signals depending on the electrical anisotropy and fiber geometry. As shown in Fig. 1, the apex has a characteristic spiral fiber geometry (6,7) that is different from the fiber orientation at other locations in the heart.

Figure 1.

Wrapped multilayer spiral structure of the apex (6,7).

Fig. 2 shows schematically the expected distributions of transmembrane potential, V_m, and magnetic field, B_z, at two areas in the heart: 1), a region with a uniform straight fiber geometry; and 2), the apex. When the fibers are uniform, the V_m distribution arising from an outwardly propagating wave front forms an ellipse, with the long axis along the fiber direction (Fig. 2 a). Sepulveda and Wikswo (8) predicted that such a wave front will produce a quadrupolar B_z pattern (Fig. 2 c), and Baudenbacher et al. (9) confirmed this prediction experimentally. At the apex of the heart, the expected V_m and B_z distributions are quite different. When initiated at the apex, the outwardly propagating wave front should be circular (Fig. 2 b) since all directions radially outward from the apex are equivalent. The B_z distribution depends on the direction of rotation of the fibers. If the fibers spiral outward in a counterclockwise direction (as shown in Fig. 2, b and d), B_z will be like the magnetic field from a counterclockwise circular loop of current, i.e., out of the paper in the center of the wave front, and into the paper outside the wave front. If the fibers rotate clockwise, the V_m distribution will be the same, but the B_z pattern will change sign because of the opposite direction of the current. Thus, the magnetic field contains information about the fiber geometry that is not present in the transmembrane potential.

Figure 2.

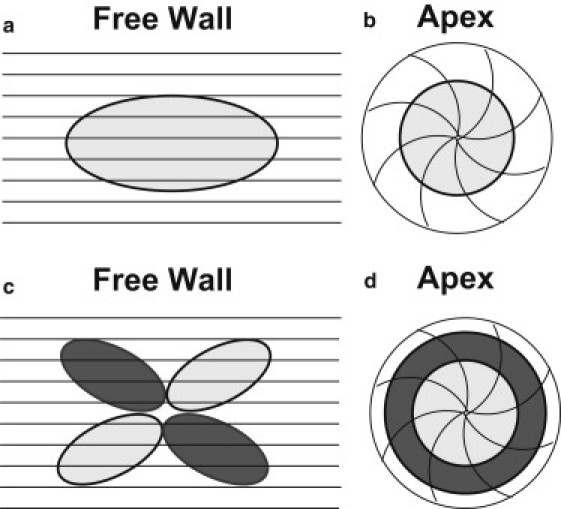
Representations of cardiac fiber structures of the left ventricle free wall and apex. The black lines represent the fiber direction. (a and b) The light gray oval and circle represent wave-front propagation. (c and d) The light and dark gray ovals and circles represent the magnetic field patterns with respect to the action current propagation (light and dark gray correspond to the magnetic field coming out of and into the paper, respectively).

In this study, our goals were to 1), measure both the transmembrane potential and magnetic field at the apex of the heart; 2), compare these measurements with mathematical predictions; and 3), test the hypothesis about their distribution shown in Fig. 2, b and d. We measured V_m using optical mapping (10) and B_z using a high-spatial-resolution superconducting quantum interference device (SQUID) magnetometer (9,11). Both monodomain and bidomain models were used for the mathematical calculations.

Materials and Methods

Cardiac preparation

All experiments were conducted in accordance with National Institutes of Health regulations for the ethical use of animals in research, and approved in advance by the Vanderbilt Institutional Animal Care and Use Committee.

The hearts used in this experiment were extracted from New Zealand white rabbits that weighed on average 3–4 kg. Each rabbit was first preanesthetized via an injection of intramuscular ketamine (50 mg/kg) into one of the hind leg muscles. Once the rabbit was sedated, it was placed in a restraint device and then injected with 2000 units of heparin and anesthetized with sodium pentobarbital (50 mg/kg) by way of the main ear vein. Once the rabbit was anesthetized, the heart was rapidly excised by a midsternal incision. The heart was immediately mounted on a Langendorff perfusion system for retrograde aortic perfusion with oxygenated Tyrode's solution containing 130 mM NaCl, 4 mM KCl, 1.5 mM NaH₂PO₄, 10 mM glucose, 23 mM NaHCO₃, 1 mM MgCl₂, and 2 mM CaCl_2, adjusted to a pH of 7.40 ± 0.05 with 1 M NaOH. The perfusate solution was constantly saturated with a 95% O₂/5% CO₂ gas mixture and kept at a temperature of 37°C for the duration of the experiment (12).

To prepare for the apex experiments, the left atrium was first cut to expose the mitral valve. The isolated Langendorff-perfused heart was then mounted upside-down on a Teflon post in an open acrylic chamber that contained the temperature-controlled perfusate bath. The Teflon post, which had a hole through its center for electrode placement, was inserted first into the left atrium and then through the mitral valve into the left ventricle to hold the heart in place. The acrylic chamber was supported by a pedestal that allowed easy transfer of the heart between the optical and magnetic measuring setups. An electromechanical uncoupling agent, 2,3-butanedione monoxime (also known as BDM or diacetyl monoxime; Sigma, St. Louis, MO), was added to the perfusate solution at a concentration of 15 mM to block muscle contraction (13). A bipolar stimulus electrode was threaded through the hole of the Teflon post until it was ∼50 μm from the surface of the apex of the heart. A 10 μm thick Mylar film was attached to the acrylic dish to stabilize and protect the heart during scans. The electrode was constructed using a 100 μm diameter platinum-iridium alloy wire inside a 1 mm diameter brass tube. The setup is shown in Fig. 3. The electrical stimulation was provided by a computer-controlled current source (Bloom Associates, Narberth, PA). The heart was paced at a 350 ms cycle length with 4 ms electrical stimuli. The amplitude of the stimuli was ∼0.6 mA, just above the diastolic stimulation threshold. The fiber geometry on the epicardium at the apex is counterclockwise and conserved across multiple species (14).

Figure 3.

Experimental setup for measuring the apex under the SQUID microscope. Inset: Apex stimulation setup: (a) SQUID sensor pickup coil, (b) SQUID microscope Dewar tail, (c) heart, (d) apex, (e) cathodal electrode, (f) Teflon post, (g) anodal electrode, and (h) perfusate bath. The cathodal stimulation occurred ∼50 μm below the surface of the apex.

When comparing images from both optical and magnetic experimental measurements, it is important to achieve spatial registration. We determined the spatial arrangement using two thin wires placed perpendicular to each other across a corner of the imaging area, as shown in Fig. 4. The wires were then imaged optically along with a ruler marked in millimeters. We achieved magnetic registration by applying a small current through each individual wire, which was imaged magnetically with the SQUID microscope. Each magnetic recording was a measurement of the magnetic field as a function of position. When both individual wire images were combined, a zero-crossing of the magnetic field provided the location of the wire relative to the magnetic image. This zero-crossing was also located in the optical images. With this technique, the two sets of images were aligned with an accuracy of ∼0.5 mm (13).

Figure 4.

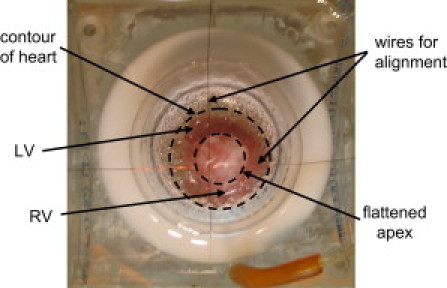
Experimental setup of a heart in a pedestal bath with the apex facing up. LV, left ventricle; RV, right ventricle. The crossed wires are for alignment. The dotted circles show the flattened apex relative to the contour of the heart.

Optical imaging and data analysis

We obtained experimental measurements of transmembrane potential using the optical imaging system previously described by Sidorov et al. (12). The hearts were stained with 200 μL of a solution containing 5 mg voltage-sensitive styryl dye di-4-ANEPPS (Molecular Probes, Eugene, OR) and 10 mL dimethyl sulfoxide. The heart preparation took ∼30 min and included a 15 min stabilization period after dye staining. A 2 W diode-pumped, solid-state laser (Verdi; Coherent, Santa Clara, CA) with a wavelength of 532 nm was delivered to the apex through a set of fiber-optic bundles. The laser light was used to excite the voltage-sensitive dye, causing fluorescence that was imaged using a high-speed CCD camera (model CA D1-0128T; Dalsa, Waterloo, Canada) filtered by a 607 nm high-pass filter (#25 Red; Tiffen, Hauppauge, NY). The image data were acquired at a frame rate of 500 frames/s for a couple of paced beats with a 12-bit resolution over a 128 × 128 grid of pixels corresponding to a 12 mm × 12 mm area in the time period between 30 and 35 min after the excision.

The voltage-sensitive dye allowed us to measure the ratio of the change in fluorescence intensity from the excited tissue, ΔF, to the fluorescence intensity from the diastolic (resting) tissue, F_D (also known as −ΔF/F_D). The negative sign corrects for the decrease in the intensity of fluorescence with a more positive potential (13). The optical data were preprocessed by employing a 5 × 5 Gaussian spatial filter and a five-point mean temporal filter (12).

Magnetic imaging and data analysis

After the optical measurements were taken, the pedestal containing the heart and bath was moved from the optical recording setup and quickly placed on the scanning stage under the SQUID microscope (Fig. 3) to measure B_z. The SQUID microscope used a pickup coil to directly couple B_z to the flux transformer of the SQUID sensor. The pickup coil consisted of 20 turns of 25 μm diameter niobium wire wound in two layers around a 500 μm diameter sapphire bobbin at the tip of a 4 cm long sapphire rod. The bobbin was mounted in the tail of the SQUID microscope, and when under vacuum was maintained close to 4.2 K by a thermally coupled liquid helium reservoir. The pickup coil was positioned ∼250 μm from a 25 μm thick sapphire window that separated the vacuum from the outside atmosphere. For further discussion of the SQUID microscope, see Baudenbacher et al. (9,11,15).

The SQUID microscope window touched the mylar foil slightly during the scans, resulting in a distance of ∼300 μm between the tip of the pickup coil and the surface of the heart. The SQUID was operated in a flux-locked loop at a bandwidth of 1 kHz (DC-5000 controller; Quantum Design, San Diego, CA). The output was collected using a PCI-MIO card (National Instruments) with 16-bit resolution at a sampling rate of 5 kHz. The data acquisition was triggered by the stimulation pulse pacing the heart at a constant cycle length of 350 ms, and magnetic action potential fields for three successive beads were recorded at 0.5 mm steps in an x-y raster scan. The 30 × 30 magnetic action potential fields were then combined using the stimulus pulse for synchronization to produce a time series of two-dimensional virtual magnetic field maps. The time interval between successive field maps was limited by the bandwidth of the flux-locked loop electronics to ∼1 ms. Recording a complete series of magnetic field maps took 15 min. Magnetic field maps were also constructed from successive beats or successive raster scans as a control, but they generally did not differ significantly. Because the data acquisition was triggered at the rising edge of the 4 ms stimulation pulse, the termination of stimulus was determined with an accuracy of 1 ms. This allowed synchronization of the magnetic and optical data to an accuracy of 2 ms. The magnetic data were then spatially filtered with a rotationally symmetric Gaussian low-pass filter of 2.5 mm size with a standard deviation of 0.5 mm. We reduced the 5 kHz bandwidth of the measured magnetic data to 1 kHz bandwidth by computing the mean of five sequential data points (13).

Monodomain model

The apical magnetic field pattern was calculated with the use of a numerical monodomain model composed of a stack of spiral discrete current dipoles that represented the cardiac apex structure. The law of Biot-Savart was used to calculate B_z for a stack of 10 rings containing 100 discrete angled current dipoles. The ring had a diameter of 600 μm and the stack height was 1 mm. The grid step size was 3 μm with a discretization of 200 points. Fig. 5 shows a single ring of 100 current dipoles with an angled orientation of 33° (shown more clearly in the enlarged inset).

Figure 5.

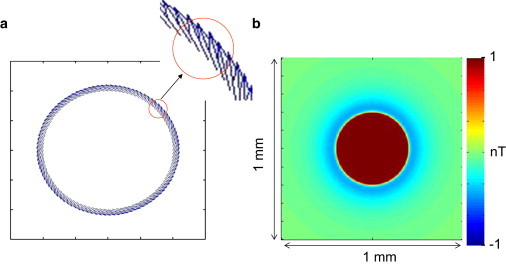
(a) Monodomain model of a ring of 100 current dipoles angled at 33° at a radius of 600 μm. (b) Calculated magnetic field from a stack of 10 concentric rings spanning a depth of 1 mm.

Bidomain model

A more precise nonlinear, time-dependent bidomain model with spiral symmetry provided a finite-difference solution to the doubly anisotropic bidomain equations (16). The equation for the transmembrane potential was solved using a forward Euler explicit method, with the membrane kinetics represented by the Beeler-Reuter model (17). The equation for the extracellular potential was solved using successive overrelaxation. Several of the parameters used in the calculation are given in Table 1. The intra- and extracellular conductivity tensors depended on location via the angle θ between the x axis and the fiber direction (18). The fibers were oriented as a logarithmic spiral (5) with an angle of 45° to the radial direction. The center of the spiral represents the apex of the heart. In some cases, the location of the center of the spiral depended on depth (a skewed stack). The stimulus was applied through a small unipolar cathode (0.25 mm diameter) on the epicardial surface, with the return electrode being a 1.5 mm diameter anode on the endocardial surface. Except under the electrodes, all surfaces were sealed. The stimulus strength was 0.6 mA and the stimulus pulse had a duration of 4 ms. The tissue slab was 10 mm × 10 mm in area (x, y) and 2 mm thick (z). The space step was 0.1 mm in the x and y directions and 0.05 mm in the z direction. The time step was 10 μs. The magnetic field was calculated by numerically integrating the Biot-Savart law over the tissue volume. The z-component of the magnetic field was calculated over a plane 0.5 mm above the epicardial surface.

Table 1.

Bidomain parameters

Intracellular longitudinal conductivity	0.1863 S/m
Intracellular transverse conductivity	0.0179 S/m
Extracellular longitudinal conductivity	0.1863 S/m
Extracellular transverse conductivity	0.0894 S/m
Surface/volume ratio	0.3 × 106 m−1
Membrane capacitance	0.01 F/m2

Results

We performed experimental measurements to map, using optical techniques, the expanding, circular V_m wave front as it propagated outward from the electrode, and, using SQUID imaging, the corresponding B_z pattern. A 12 mm × 12 mm section of the cardiac apex was examined, and the results are shown in Fig. 6. The first row shows V_m images that demonstrated the wave-front propagation that results from electrical stimulation at the apex, and the second row shows the B_z images of the magnetic field associated with action currents. The measured amplitude of the B_z field is in nT. The time is referenced to the termination of the cathodal stimulus. The saturated dipolar pattern of B_z in the 1 ms frame is caused by stimulus artifacts in combination with the temporal filtering, which propagates stimulus artifacts in the 3 ms time frame.

Figure 6.

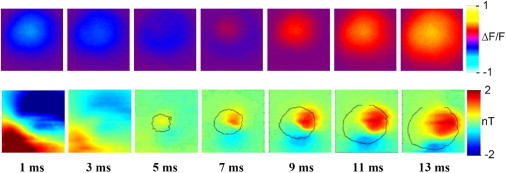
Experimental data recorded at the rabbit cardiac apex, with spiral fiber structure. The first frame is 1 ms after termination of stimulus. Top: Circular wave-front propagation measured optically. Bottom: Dipolar stimulus and propagation patterns measured magnetically. The circular wave-front contour is overlaid on the respective magnetic data.

The V_m images in Fig. 6 demonstrate a circular wave-front propagation that is similar to the results expected based on our models (Fig. 2 c). The B_z field, however, shows a broad dipolar pattern associated with the stimulus current (1 ms), followed by a more localized dipolar pattern of opposite polarity that expands with time (5–13 ms) with the component out of the paper growing in extent as time goes by. The contour of the V_m wave front is overlaid onto the B_z color map.

The monodomain and bidomain models were then used to gain insight into the origin of the observed data. By changing the stimulus and spiral orientation parameters in these models, we were able to explain the experimental data. Fig. 5 shows the B_z field produced by a stack of 10 vertically aligned rings of current dipoles in the monodomain model. This shows the expected circular B_z pattern (Fig. 2 d). In addition, the bidomain model for a vertically aligned stack of a logarithmic spiral bidomain tissue demonstrated this pattern. The top row of Fig. 7 shows the V_m wave-front propagation, and the bottom row shows the B_z field from the action current propagation during the respective time step. Both rows demonstrate the circular propagation pattern associated with the spiral tissue symmetry.

Figure 7.

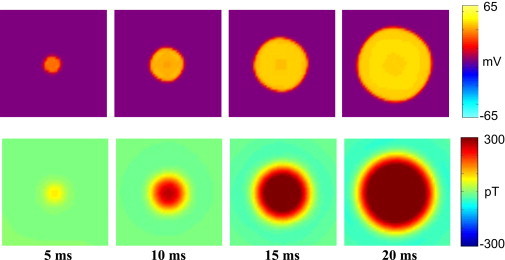
Bidomain model of concentric apex tissue (10 mm ×10 mm, 1 mm deep). Top: Circular wave-front propagation. Bottom: Circular magnetic pattern associated with electrical signal.

Results more similar to the experimental data were obtained from a skewed stack of apical tissue in which each layer was shifted laterally by 0.1 mm from the one above. Fig. 8 shows a monodomain model B_z calculation of a skewed stack of current dipole rings. Careful examination of the image from this monodomain model reveals a dipole-like B_z image. The bidomain model provides an even more obvious dipole-like magnetic field. Fig. 9 shows a comparison of the experimental versus bidomain model data of a skewed stack of slabs of logarithmic-spiral apex tissue, with Fig. 9 c indicating the direction of the skew to this stack. On the epicardium closest to the plane where B_z is imaged, the apex center is above the center of the image, and it has shifted to below the center of the image by the endocardial layer. The total shift from epicardium to endocardium is 1 mm. In Fig. 9 b the V_m wave-front propagation is shown in the first row and B_z images are shown in the second row. The time steps start at the beginning of the 4 ms cathodal stimulus and are shown every 2 ms thereafter. The wave front is circular, in similarity to the experimental data in Fig. 9 a and as expected (Fig. 2 c). The B_z patterns also look remarkably similar to the experimental data. There is a large dipolar response to the stimulation current at the first two time points that is followed by a response associated with the action currents of reversed polarity, which becomes more monopolar with time.

Figure 8.

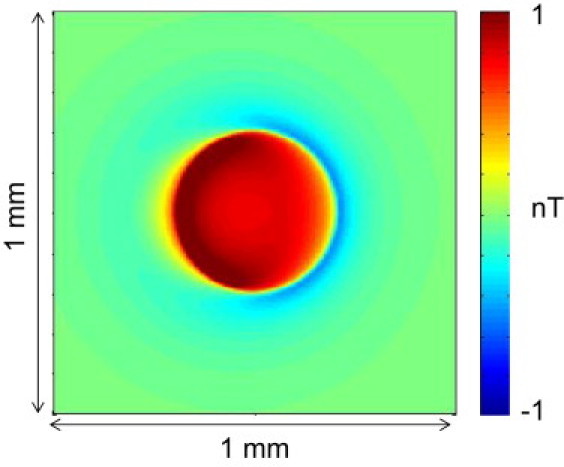
Monodomain model of the magnetic field of a shifted stack of current dipole rings. The total shift is 0.36 mm.

Figure 9.

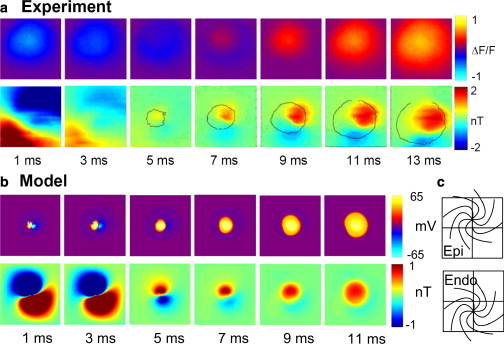
(a) Experimental data from the cardiac apex. Top row: Circular wave-front propagation. Bottom row: Dipolar magnetic pattern of stimulation and propagation. (b) Bidomain model of a skewed stack of spirals at the apex. Top row: Circular wave-front propagation. Bottom row: Dipolar magnetic pattern of stimulation and propagation. (c) Skewed stack shift from epicardium to endocardium with the apex at center. The total shift is 1 mm.

Discussion

For stimulation at the cardiac apex, we expected that the spiral fiber architecture would produce circular patterns for both V_m and B_z. Although our optical measurements of V_m wave-front propagation were consistent with this, our SQUID microscope measurements of the B_z field from the action currents revealed a more complex B_z pattern than expected. The pattern was consistent with a tilted axis for the apex spiral. We used a monodomain model of the cardiac apex to calculate B_z and a bidomain model to calculate both V_m wave-front propagation and the corresponding B_z field from the stimulation and propagating action currents. When we modeled the apex with a simple, vertically aligned spiral structure, we observed circular wave-front patterns for V_m and a similar circular pattern in the B_z field from circular action currents. The skewed stack of rings of current dipoles in the monodomain model demonstrated patterns similar to those obtained from the bidomain model of a skewed stack of spiraled cardiac tissue that stimulated the apex. The fact that the electrical signal from the apex resembled circular wave-front propagation, whereas the magnetic data showed dipolar images, suggests that electrical measurements alone may not determine the extent of diagnostic information that can be found in the magnetocardiogram. Furthermore, our results suggest that the spiral complexity of the apex contains more information that cannot be detected with electrocardiogram recordings, due to electrically silent circular currents. This experiment provides further evidence that the ability of the magnetocardiogram to measure electrically silent currents may provide a useful complement to electrical measurements.