Thermodynamic Calculations for Biochemical Transport and Reaction Processes in Metabolic Networks

Abstract

Thermodynamic analysis of metabolic networks has recently generated increasing interest for its ability to add constraints on metabolic network operation, and to combine metabolic fluxes and metabolite measurements in a mechanistic manner. Concepts for the calculation of the change in Gibbs energy of biochemical reactions have long been established. However, a concept for incorporation of cross-membrane transport in these calculations is still missing, although the theory for calculating thermodynamic properties of transport processes is long known. Here, we have developed two equivalent equations to calculate the change in Gibbs energy of combined transport and reaction processes based on two different ways of treating biochemical thermodynamics. We illustrate the need for these equations by showing that in some cases there is a significant difference between the proposed correct calculation and using an approximative method. With the developed equations, thermodynamic analysis of metabolic networks spanning over multiple physical compartments can now be correctly described.

Introduction

Theoretical and computational studies of metabolic network function are increasingly applying thermodynamic principles. Recent applications include analysis of the thermodynamic feasibility of reaction fluxes in pathways (1–6), cellular-scale networks (7–18), and the thermodynamic feasibility of metabolite concentrations in large-scale networks (19,20). Theoretical analyses of the relationships between metabolic flux and Gibbs energy have been developed (21–23); and thermodynamics has also been used as constraints in kinetic models (24–29).

Thermodynamic analyses of biochemical systems are complicated by a number of factors. One major complicating factor is that biochemical reactions occur in aqueous solutions, and thus biochemical reactants (e.g., ATP) are typically made up of a number of rapidly interconverting proton-bound or metal cation-bound species (e.g., ATP⁴⁻, HATP³⁻, and H₂ATP²⁻). A concentration of a biochemical reactant is therefore typically a lumped sum of the concentrations of individual species. Concentrations of the individual species are usually neither measured nor reported (i.e., even with state-of-the art metabolomics platforms as described in Büscher et al. (30)), requiring a concept that can predict the distribution of a biochemical reactant into multiple species, given a certain pH, metal ion concentrations, temperature, and ionic strength. Alberty's (31) Legendre transform formalism provides such a concept and allows us to make thermodynamics calculations based on reactant concentrations. Another approach uses binding polynomials to calculate species concentrations from reactant concentrations (32,33).

Another factor that complicates thermodynamic analysis of metabolic networks is that these systems are often distributed over multiple compartments with different physiochemical properties, such as pH or ionic strength. To calculate the change in Gibbs energy of cross-membrane transport processes, the electrochemical potential of that process needs to be considered (34). To make such a calculation, one has to consider the specific species that are transported. Thus, the equations of biochemical thermodynamics that use reactant concentrations must be extended to allow description of thermodynamics of transport processes. Unfortunately, to our knowledge, this does not yet exist, but it is required for correct thermodynamic analysis of genome-scale metabolic networks.

In this article, we develop a framework for the thermodynamic description of biochemical transport and reaction processes based on reactant concentrations. We illustrate how this framework may be practically applied for the calculation of thermodynamics of reactions, transport processes, and of coupled reaction and transport processes. Furthermore, we show the effect that the correct consideration of species has on the calculated change in Gibbs energy for transport/reaction processes. We envision that the proposed framework provides the necessary tool for thermodynamic analysis of metabolic networks with compartments.

Results

To derive a formulation for the calculation of the change in Gibbs energy (ΔG) of any transport/reaction process based on the concentrations of the involved reactants, we start from the basic equation to calculate the ΔG of a chemical reaction,

$$\Delta G=\sum _i{s}_i{\Delta }_f{G}_i^0+RT\sum _i{s}_i\ln c_i,$$ (1)

where Δ_fG⁰_i values are the Gibbs energies of formation for each involved species i, s_i values are the stoichiometric coefficients for the reacting species, and c_i values are the concentrations of each species. To calculate the ΔG of a biochemical process using Eq. 1, we would need to know the species concentration c_i. Because the concentrations of the species are usually not measured, we require a formulation to calculate the ΔG of a reaction in terms of reactant concentrations.

Alberty (31) developed such a concept, in which the ΔG of a reaction is calculated with the equation,

$$\Delta G=\sum _j{S}_j{\Delta }_f{G}_j^{\prime 0}+RT\sum _j{S}_j\ln C_j,$$ (2)

where the ${\Delta }_f{G}_j^{\prime 0}$ values are the so-called transformed Gibbs energies of formation for a reactant j and C_j values are the reactant concentrations. S_j values are the stoichiometric coefficients of reactants and are the sum of the stoichiometric coefficients of the constituting species that participate in the reaction,

$$S_j={\sum }_{i\epsilon I\left(j\right)}{s}_i.$$

For example, when 1 mol of a reactant participates in a reaction as 0.5 mol of species 1 and 0.5 mol of species 2, the stoichiometric coefficients s₁ and s₂ are 0.5 and 0.5, respectively. The transformed Gibbs energy of formation is a formation energy that incorporates the pH of the environment, in which the reaction takes place. In the derivation of Eq. 2, the pH is introduced by a Legendre transformation (see Eq. A2i in the Supporting Material). In biochemical reactions, a proton is not considered as a reactant. In Eq. 2, the protons are considered in the transformed Gibbs energies of formation. See Section 1 of the Supporting Material for a complete derivation of Eq. 2 and the equation to calculate the transformed Gibbs energies of formation for reactants.

An equivalent way to calculate the ΔG of a reaction in terms of reactant concentrations is by using the concept of binding polynomials (32,33). By using binding polynomials, we can calculate a species concentration from the reactant concentration and can then use this concentration with Eq. 1. The binding polynomials can be incorporated in Eq. 1 as

$$\Delta G=\sum _j{S}_j{\Delta }_f{G}_{i_{\text{ref}}}^0+RT\sum _j{S}_j\ln C_j-RT\sum _j{S}_j\ln P_j\left(\left[{\text{H}}^{+}\right]\right)+\sum _{i\epsilon \text{protons}}{s}_i{\Delta }_f{G}_{{\text{H}}^{+}}^0+RT\sum _{i\epsilon \text{protons}}{s}_i\ln \left[{\text{H}}^{+}\right],$$ (3)

where ${\Delta }_f{G}_{i_{\text{ref}}}^0$values are the Gibbs energies of formation for the reference species, C_j values are the reactant concentrations, P_j([H⁺]) values are the binding polynomials, and Δ_fG⁰_H+ values the Gibbs energy of formation for a hydrogen ion. Because in biochemical reactions protons are not considered as a reactant, the last two terms of Eq. 3 are added to incorporate the effect of the proton concentration, or pH. See Section 1 in the Supporting Material for a complete derivation of Eq. 3. With Eqs. 2 and 3, the ΔG of any biochemical reaction can be calculated based on reactant concentrations.

We would now like to incorporate the effect of transport of a specific species across membranes into the calculation of the ΔG, because metabolites are often transported by proteins with a structure that allows only a specific species to be transported (35). We can start again from the species level with Eq. 1. To calculate the contribution of transport on the ΔG, Eq. 1 can be extended to incorporate the effect of the electrochemical potential (34),

$$\Delta G=\sum _i{s}_i{\Delta }_f{G}_i^0+RT\sum _i{s}_i\ln c_i+F\Delta {\varphi }_m\sum _{i\epsilon \text{inside}}{s}_i{z}_i,$$ (4)

where F is the Faraday constant, z_i is the charge of species i, and Δϕ_m is the membrane potential difference defined as the difference of the inside minus the outside electric potential for transport to the inside. The sum over the stoichiometric coefficients of the transported species, with charge z_i, in the inside compartment (${\sum }_{i\epsilon \text{inside}}{s}_i{z}_i$) is introduced to calculate the charge that is transferred over the membrane.

To translate Eq. 4 into an equation that only uses reactant concentrations, we must make a distinction between the reacting biochemical reactants, as in Eqs. 2 and 3, and the transported chemical species. To make this distinction, we define the species in Eq. 4 as a group of three types of species,

$$i=\left\{i\epsilon I\left(j\right),i\epsilon \text{protons},i\epsilon \text{transported}\right\},$$ (5)

where i ε I (j) are the constituting species of reactants j, i ε protons are the free protons participating in a reaction, and i ε transported are the species that are transported. With Eq. 5, we separate the different species that can participate in a transport/reaction process and classify them into the three different groups. In Fig. 1A, the process of ATP synthesis is illustrated on a species level. In Fig. 1 B, it is then shown which species belong to the different groups of stoichiometric coefficients from Eq. 5.

Figure 1.

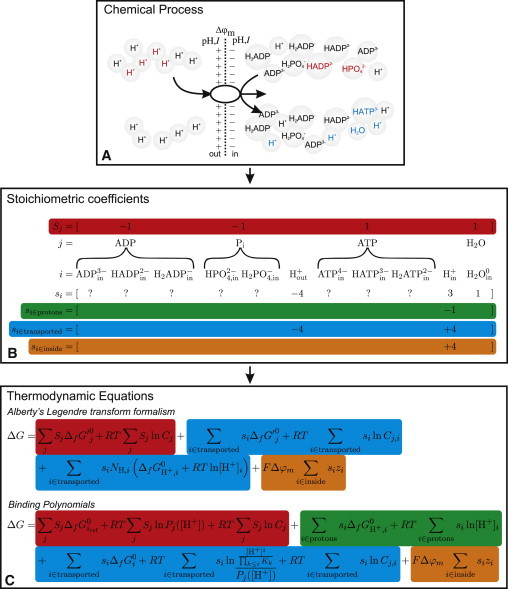
(A) The biochemical transport/reaction process ATP synthase, where ATP is generated from the transport of four protons from the cytosol (out) to the mitochondrium (in), is represented on a species level, with species that have a negative stoichiometric coefficient in red and species that have a positive stoichiometric coefficient in blue. Several species, with each having their own concentration (c_i), are shown for each reactant. (B) Because we do not know for each reactant which species reacts, we define a vector of stoichiometries for reactants (S_j). For the protons that participate in the reaction, a separate vector (s_iεprotons) is defined. For the transported species, the vector (s_{iεtransported}) is defined, and the vector (s_iεinside) is the equivalent of the transported species vector but only contains the stoichiometric coefficients of the inside species. (C) Then we can apply the two equations that can be used to calculated the ΔG of the process. Where in the reaction equation the information for the ΔG equations is obtained is indicated by similar colors. See Section 2 in the Supporting Material for a detailed derivation of the equations.

Now, we can define equations to calculate the ΔG of transport/reaction processes by using the two different ways of dealing with biochemical thermodynamics. The derivation of Eqs. 6 and 7 is shown in detail in Section 2 in the Supporting Material. Using Alberty's Legendre transform formalism, we obtain the following equation for a transport/reaction process,

$$\Delta G=\sum _j{S}_j{\Delta }_f{G}_j^{\prime 0}+RT\sum _j{S}_j\ln C_j+\sum _{i\epsilon \text{transported}}{s}_i{\Delta }_f{G}_j^{\prime 0}+\sum _{i\epsilon \text{transported}}{s}_i{N}_{\text{H},i}\left({\Delta }_f{G}_{{\text{H}}^{+},i}^0+RT\ln {\left[{\text{H}}^{+}\right]}_i\right)+RT\sum _{i\epsilon \text{transported}}{s}_i\ln C_{j,i}+F\Delta {\varphi }_m\sum _{i\epsilon \text{inside}}{s}_i{z}_i,$$ (6)

and by using the concept of binding polynomials we obtain the following equation,

$$\Delta G=\sum _j{S}_j{\Delta }_f{G}_{i_{\text{ref}}}^0-RT\sum _j{S}_j\ln P_j\left(\left[{\text{H}}^{+}\right]\right)+RT\sum _j{S}_j\ln C_j+\sum _{i\epsilon \text{protons}}{s}_i{\Delta }_f{G}_{H^{+},i}^0+RT\sum _{i\epsilon \text{protons}}{s}_i\ln {\left[{\text{H}}^{+}\right]}_i+\sum _{i\epsilon \text{transported}}{s}_i{\Delta }_f{G}_i^0+RT\sum _{i\epsilon \text{transported}}{s}_i\ln \frac{\frac{{\left[H^{+}\right]}^i}{{\Pi }_{k\le i}{K}_k}}{P_j\left(\left[{\text{H}}^{+}\right]\right)}+RT\sum _{i\epsilon \text{transported}}{s}_i\ln C_{j,i}+F\Delta {\varphi }_m\sum _{i\epsilon \text{inside}}{s}_i{z}_i,$$ (7)

where [H⁺]_i and ${\Delta }_f{G}_{{\text{H}}^{+},i}^{\prime 0}$ values are the concentration and the transformed Gibbs energy of formation of a hydrogen ion in the compartment of species i. The value C_j,i is the concentration of the reactant of which the transported species i is part. Equations 6 and 7 are now written only in terms of concentrations of reactants but do account for the specific species that are being transported.

Examples

To show how these equations can be applied, we consider the process of succinate transport over a membrane into a cell. Here we assume that all biochemical conditions (ionic strength, temperature, and pressure) other than pH are equal on both sides of the membrane. Furthermore, we assume that succinate may associate with hydrogen ions but not with other dissolved cations such as potassium or magnesium. The biochemical process can be described as

$${\text{Succ}}_{\text{out}}^0\rightleftharpoons {\text{Succ}}_{\text{in}}^0,$$ (8)

where Succ⁰ indicates the uncharged form of succinate (i.e., the acid with two protons bound), which is transported from the outside to the inside compartment. From Eq. 8, we can define the stoichiometric coefficients as defined in Eq. 5,

$$\begin{array}{c}{S}_j=\left[\begin{array}{cc}0& 0\end{array}\right],\\ s_{i\epsilon \text{protons}}=\left[\begin{array}{cc}0& 0\end{array}\right],\\ s_{i\epsilon \text{transported}}=\left[\begin{array}{cc}-1& 1\end{array}\right],\end{array}$$ (9)

where the indices represent ${\text{Succ}}_{\text{out}}^0$ and ${\text{Succ}}_{\text{in}}^0$, respectively. Now using the information from Table 1, we have all the information to calculate the ΔG of the transport process. In Fig. 2 a (solid line), the value of the ΔG is shown as a function of inside pH with outside pH held constant. When the pH of the inside compartment changes, the relative abundances of the different species of succinate (e.g., Succ⁻², Succ⁻¹, and Succ⁰) will change. The difference in relative abundances of the species in each compartment has an effect on the ΔG of the transport process because the gradients of the species over the membrane are different than the gradient of the reactants.

Table 1.

Data used in the example calculations for the processes shown in Eqs. 8 and 10

		ATP	ADP	Pi	H2O	${\text{Succ}}_{\text{out}}^0$	${\text{Succ}}_{\text{in}}^0$
ΔfG0 (kJ mol−1)
Species charge	−4	−2768.1
	−3	−2811.48	−1906.13
	−2	−2838.18	−1947.1	−1069.1		−690.44	−690.44
	−1		−1971.98	−1137.3		−722.62	−722.62
	0				−237.19	−746.64	−746.64
P		1.28	1.42	1.54	1.00	2.54	1.14
Cj (mM)		1	0.5	10	1000	0.05	0.5
pK1		6.44	6.62	6.73	1	5.15	5.15
pK2		3.87	3.94			3.96	3.96

Data on Δ_fG⁰ and pK values are at a temperature T = 298.15 K and obtained from Alberty (31). The Faraday constant is F = 96.49 kC mol⁻¹ and the gas constant is R = 8.314 × 10⁻³ kJ K⁻¹ mol⁻¹. Concentrations are chosen to be in a physiological range (36,37).

Figure 2.

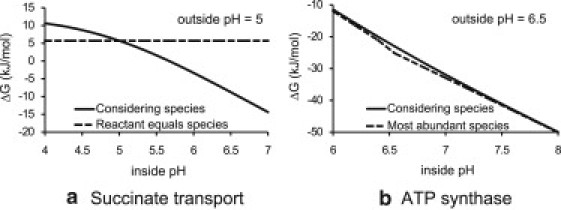
(a) The ΔG of succinate transport (see Eq. 8) is shown at varying pH of the inside compartment. Comparison of correctly considering the presence of species (solid line) versus assuming that the reactant concentration is equal to the transported species concentration (dashed line). Reactant concentrations (see Table 1) are kept constant, outside pH is 5, the membrane potential difference (ϕ_m) is 40 mV, and ionic strengths are kept 0.15 M in both compartments. (b) The ΔG of ATP hydrolysis is shown at varying pH of the inside compartment. Comparison of correctly considering the presence of species (solid line) versus assuming that the reactant concentration approximates the most abundant species concentration (dashed line). Reactant concentrations (see Table 1) are kept constant, the outside pH is 6.5, the membrane potential difference (ϕ_m) is −180 mV, and ionic strengths are kept 0.15 M in both compartments. See Section 3 in the Supporting Material for detailed examples of such calculations.

When the different species of the reactant succinate are not considered and Eq. 4 would be used with the reactant concentration, the value of the ΔG does not depend on the pH (Fig. 2 a, dashed line), because the reactant concentrations are independent of pH. This way of calculating the ΔG is sometimes applied for the analysis of genome-scale metabolic networks. The resulting ΔG is equal to the calculated ΔG that considers species, at an inside pH of 5. This is because, at pH 5, both compartments have an equal pH, which makes the relative abundance of the species equal in both compartments, and therefore the gradient of each species over the membrane equal to the total reactant concentration gradient over the membrane. From Fig. 2 a we can see that the effect of considering species on the calculated ΔG at an inside pH of 6.5 is ∼15 kJ/mol, which is a significant difference.

Another example is the synthesis of ATP. This is a process in which ADP is phosphorylated to ATP by the transport of protons over the mitochondrial membrane driven by their electrochemical potential. The biochemical process can be described as

$$\text{ADP}+{\text{P}}_{\text{i}}+4{\text{H}}_{\text{out}}^{+}\rightleftharpoons \text{ATP}+{\text{H}}_2\text{O}+4{\text{H}}_{\text{in}}^{+}.$$ (10)

Under concentrations found in the mitochondrial matrix, in vivo synthesis of ATP from ADP and P_i is thermodynamically unfavorable. The source of energy to drive this process is the transport of positively charged hydrogen ions down the electrochemical gradient across the mitochondrial inner membrane.

In Fig. 1 a, the ATP synthase reaction is shown schematically on the species level. From Eq. 10, we can define the stoichiometric coefficients that we can use in Eqs. 6 and 7,

$$\begin{array}{c}{S}_j=\left[\begin{array}{cccccc}-1& -1& 0& 1& 1& 0\end{array}\right],\\ s_{i\epsilon \text{transported}}=\left[\begin{array}{cccccc}0& 0& -4& 0& 0& 4\end{array}\right],\\ s_{i\epsilon \text{inside}}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 4\end{array}\right],\end{array}$$ (11)

where the indices represent ADP, P_i, ${\text{H}}_{\text{out}}^{+}$, ATP, H₂O, and ${\text{H}}_{\text{in}}^{+}$, respectively. With the stoichiometric coefficients as defined above, and the data on ${\Delta }_f{G}_i^0$ values in Table 1, Eq. 6 can be used to calculate the ΔG of the transport/reaction process (note that when we define [H⁺] = 10^−pH, then ${\Delta }_f{G}_{{\text{H}}^{+}}^0=0,$ because a pH is defined as the hydrogen ion chemical activity, which includes the effects of ionic strength and temperature).

To calculate the ΔG using binding polynomials (Eq. 7), we must first define the chemical reaction in terms of reference species for each reactant. Here, we use as the reference species of each reactant the most unbound species (i.e., the species with the least bound ions). In terms of reference species, Eq. 10 becomes

$${\text{ADP}}^{3-}+{\text{P}}_{\text{i}}^{2-}+4{\text{H}}_{\text{out}}^{+}\rightleftharpoons {\text{ATP}}^{4-}+{\text{H}}_2\text{O}+3{\text{H}}_{\text{in}}^{+}.$$ (12)

Now we can define the stoichiometry of reacting protons,

$$s_{i\epsilon \text{protons}}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& -1\end{array}\right],$$ (13)

with the order of indices equal to Eq. 11. With the additional information on the stoichiometry of the reacting protons, we can also calculate the ΔG according to Eq. 7. For simplicity, we consider only binding of protons, and ignore binding of other ions such as magnesium. In Section 3 in the Supporting Material, we provide a table with all the data that is used in the examples, and we show in detail how to calculate the ΔG for such transport/reaction processes and how to correct for ionic strength.

We obtain the same ΔG as the value calculated with Alberty's Legendre transform formalism (Eq. 6). In Fig. 2 b we show the ΔG as a function of inside pH. The ΔG that is calculated when considering the species (i.e., using Eqs. 6 or 7) is compared to assuming that the reactant concentration represents the most abundant species. In this case we can see that considering species does not have a significant effect on the calculated ΔG.

With Eqs. 6 and 7 we have a framework to calculate changes in Gibbs energies for reaction, transport, and transport/reaction processes. The example calculations show that in certain cases it is important to consider the various species that exist for each reactant. The difference in ΔG shown in Fig. 2 a is large at physiological conditions, and can even mean the difference between a positive or negative value of the ΔG. For the ATP synthase example, we see that there is only a minimal difference between correctly considering species and assuming that the reactant concentration represents the most abundant species concentration.

Conclusions

In this work, we have developed equations to correctly describe the thermodynamics of biochemical transport/reaction processes. Specifically, we have formulated two equivalent equations to calculate the change in Gibbs energy of a transport/reaction process based on two different ways of treating biochemical thermodynamics. We illustrate the need of these equations by showing that in some cases there is a significant difference between considering species and by assuming the reactant concentration represents a species concentration. Therefore, for the analysis of metabolic networks where many different reactions are analyzed, it is relevant to be able to consider species for the calculation of ΔG values by using metabolite concentrations. With the developed equations, thermodynamic analysis of metabolic networks spanning over multiple physical compartments can now be correctly described.