Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2010 May 5;277(1695):2857–2865. doi: 10.1098/rspb.2010.0575

Spread of Q fever within dairy cattle herds: key parameters inferred using a Bayesian approach

Aurélie Courcoul 1,2,*, Elisabeta Vergu 3, Jean-Baptiste Denis 3, François Beaudeau 1,2
PMCID: PMC2981993  PMID: 20444719

Abstract

Q fever is a worldwide zoonosis caused by Coxiella burnetii. Although ruminants are recognized as the most important source of human infection, no previous studies have focused on assessing the characteristics of the bacterial spread within a cattle herd and no epidemic model has been proposed in this context. We assess the key epidemiological parameters from field data in a Bayesian framework that takes into account the available knowledge, missing data and the uncertainty of the observation process owing to the imperfection of diagnostic tests. We propose an original individual-based Markovian model in discrete time describing the evolution of the infection for each animal. Markov chain Monte Carlo methodology is used to estimate parameters of interest from data consisting of individual health states of 217 cows of five chronically infected dairy herds sampled every week for a four-week period. Outputs are the posterior distributions of the probabilities of transition between health states and of the environmental bacterial load. Our findings show that some herds are characterized by a very low infection risk while others have a mild infection risk and a non-negligible intermittent shedding probability. Moreover, the antibody status seems to be a key point in the bacterial spread (shedders with antibodies shed for a longer period of time than shedders without antibodies). In addition to the biological insights, these estimates also provide information for calibrating simulation models to assess control strategies for C. burnetii infection.

Keywords: Bayesian inference, epidemiology, modelling, zoonosis, Q fever, cattle

1. Introduction

Q fever is a zoonotic disease caused by Coxiella burnetii, a bacterium found worldwide in a wide range of animals. Since 2007, Q fever has become an important public health problem in several parts of Europe (McCaughey et al. 2008; Karagiannis et al. 2009; Panaiotov et al. 2009; Schimmer et al. 2009). Although Q fever in humans is asymptomatic in more than 60 per cent of cases, it may lead to either an acute or a chronic disease (Raoult et al. 2000). The acute disease is mainly flu-like but severe complications, such as pneumonia or hepatitis can occur. In its chronic form, endocarditis is the most frequent manifestation, especially in patients with pre-existing heart valve lesions. Abortion in pregnant women can also occur. Recently, a large epidemic of Q fever emerged in the southern part of the Netherlands causing more than 3000 human cases since 2007 (Anonymous 2009). A link has been established between some human cases and farms of small ruminants where abortions owing to Q fever were detected (Schimmer et al. 2009). Ruminants are recognized as the main source of human infection (Norlander 2000; McQuiston & Childs 2002). Infected animals shed the bacterium through various routes such as parturition products, faeces, urine, vaginal mucus or milk (Berri et al. 2001; Arricau-Bouvery et al. 2003; Guatteo et al. 2006). The transmission of infection both between ruminants and between ruminants and humans is mainly owing to inhalation of aerosolized bacteria or contaminated dust (Marrie 1990). The bacterium survives very well in the environment (Welsh et al. 1958) and can infect humans and animals for a long period after it has been excreted by the host. Therefore, the control of infection within ruminant herds is the most important factor influencing the occurrence of human outbreaks. Besides these obvious implications in terms of public health, controlling the spread of Q fever is also motivated by economic and animal health concerns. Indeed, in ruminants, the infection may also cause abortions, infertility, metritis or chronic mastitis (Plommet et al. 1973; Aitken 1989; Bildfell et al. 2000; Berri et al. 2001).

Previous studies of Q fever in ruminants have shown that some infected animals shed the bacteria in a discontinuous way: this intermittent shedding has been described in the milk and faeces of goats (Arricau-Bouvery et al. 2003) as well as in the milk, faeces and vaginal mucus of cows (Durand 1993; Guatteo et al. 2007; Rodolakis et al. 2007). However, little information is available on the characteristics of the spread of C. burnetii within a cattle herd, a key point in the understanding and the control of the disease. Specifically, the probability that a susceptible cow will become infected when introduced into a chronically infected herd, the duration of shedding for an infectious cow, the differences between the shedding patterns of seronegative and seropositive cows, the probability of intermittent shedding and the duration of non-shedding periods are all key parameters, which have not been assessed. In order to address these issues, we propose an original modelling-based Bayesian approach to quantify the epidemiological parameters related to the transmission of C. burnetii within a dairy cattle herd.

We have built a dynamic discrete time individual-based stochastic model describing the evolution of health states with time for each animal. Because of the imperfection of diagnostic tests (assessed by sensitivity (Se) and specificity (Sp) parameters), the observed health state of a cow in our data can differ from its real health state. Thus, this uncertainty in observations has to be explicitly incorporated in the model to provide more accurate estimates of the parameters, particularly of the transition rates. We use the Bayesian paradigm to deal with this uncertainty, the missing data (since for some animals the health state was not identified at every moment in the follow-up) and to account for the hierarchical structure of the process (e.g. some parameters are herd-dependent). Inference is performed from field data (described in Guatteo et al. 2007) using Markov chain Monte Carlo (MCMC) methodology (Gilks et al. 1996), which is being increasingly used in epidemic modelling (O'Neill & Roberts 1999; Cauchemez et al. 2004; Streftaris & Gibson 2004; Höhle et al. 2005; Lekone & Finkenstädt 2006). Posterior distributions of model parameters are analysed and biological interpretations are proposed.

2. Data

A one-month longitudinal study was carried out in five French dairy cattle herds infected with C. burnetii, but without any clinical sign attributable to Q fever. The selected herds were chosen to satisfy two major criteria: (i) the presence of the bacterium C. burnetii within the herd; this was certified by a positive polymerase chain reaction (PCR) result on bulk tank milk and more than 20 per cent of cows seropositive for C. burnetii, and (ii) the absence of any control measure (i.e. antibiotics or vaccination directed against C. burnetii) before the end of the study. The protocol of the study is described in detail in Guatteo et al. (2007). To assess the dynamics of C. burnetii infection, the lactating cows of these herds were sampled from one to five times on a weekly basis. The observed individual state of each cow was determined at each sampling time using an enzyme linked immunosorbent assay (ELISA) test (LSI ELISA Cox Ruminants, Lissieu, France) on serum and a real-time PCR (LSI Taqvet C. burnetii, Lissieu, France) on three different samples (milk, faeces and vaginal mucus). The results of the ELISA test were expressed by the ratio (S/P) between optical densities of the sample and the positive control, and a cow was considered seropositive when the S/P ratio in serum was greater than or equal to 0.4. For the PCR test, only the samples presenting a typical amplification curve (demonstrating C. burnetii DNA detection) with a Ct (cycle threshold) below 40 were considered positive. A cow was identified as PCR-positive when at least one of its three samples was PCR-positive. At the initial point of the follow-up (t0), the sizes of the five herds ranged from 24 to 79 lactating cows and a total of 217 cows were tested (electronic supplementary material, tables S1 and S2). Thereafter, 100 per cent of the initially (at t0) PCR-positive cows, 100 per cent (or 50% in herds with more than 40 lactating cows) of the initially seropositive/PCR-negative cows and 65 per cent of the initially seronegative/PCR-negative cows were retained for the follow-up. Thus, during the following month, between 55 and 79 per cent of the cows of each herd were tested every week (at t7, t14, t21 and t28) in the same way in order to determine their individual health state. The cows entering one of the herds during the study (as a consequence of a purchase or a first calving) were also included. According to the PCR results and the ELISA test, at t0 between 35 and 74 per cent of cows per herd were identified as PCR-negative/seronegative, between 1 and 23 per cent were PCR-positive/seronegative, between 2 and 35 per cent were PCR-positive/seropositive and between 17 and 37 per cent were PCR-negative/seropositive. At the endpoint of the follow-up (day 28 to t28), the herds comprised between 24 and 81 lactating cows. Altogether, 821 individual health states were determined and 235 (complete or incomplete) temporal trajectories of individual health status were available.

3. Model and methods

Based on the available knowledge concerning the clinical and epidemiological aspects of Q fever, an epidemic model describing its spread within a dairy cattle herd was built. First, the allowed transitions between the health states of the epidemiological model are described. Then, the dynamic model representing the temporal evolution of observed individual health states is presented. Finally, we detail the assumed priors and calculated posterior distributions of the model parameters in the Bayesian framework (using MCMC methods).

(a). Epidemic model

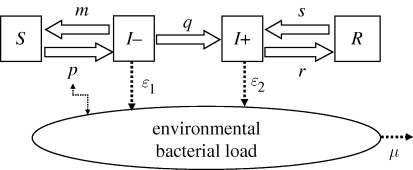
Each individual of the population of lactating cows is in one of the four mutually exclusive health states at a given time, as shown in figure 1. By inhaling bacteria contained in the environment, a susceptible cow, S (non-shedder without antibodies), can become infectious, I− (shedder without antibodies) and start shedding. Either it manages to eliminate the bacterium and becomes S again (non-shedder without antibodies and then apparently susceptible) or it produces antibodies and continues being infectious and shedding, I+ (shedder with antibodies). When it stops shedding, it becomes R (non-shedder with antibodies). Since the shedding is intermittent (Guatteo et al. 2007; Rodolakis et al. 2007), a transition from R to I+ is assumed. Antibodies can last for several years in humans (Fournier et al. 1998) and at least several months in cattle (Plommet et al. 1973). Here, we assume that the probability of observing a cow lose its antibodies over the period of study (one month) is very low and negligible, especially in chronically infected herds where immunity is probably steadily stimulated. Therefore, no transition from health states with antibodies (I+ or R) to health states without antibodies (I−or S) is allowed in our model. Shedders (I − and I + ) contribute to filling the environment compartment (E) with the bacteria: ɛ1 and ɛ2 are the quantities of bacteria shed during a time step (one week in our case) by an individual I − and I + respectively. The probability of infection or re-infection, p (transition from S to I − ) is expressed at each time step as pt = 1 − exp( − Et), where Et is the quantity of bacteria in the environment of the herd at time t (one unit of Et corresponding to a probability of transition from S to I − of (1 − 1/e)). The mortality rate of C. burnetii in the environment, μ, includes the natural mortality of the bacterium and its removal in relation to the periodic cleaning of the cattle housing carried out by the farmer.

Figure 1.

Figure 1.

Open in a new tab

Flow diagram describing the modelled spread of C. burnetii within a cattle herd. The health states are: S, non-shedder cow without antibodies; I − , shedder cow without any antibodies; I + , shedder cow with antibodies and R, non-shedder cow with antibodies. The model parameters are: p, the probability of infection or re-infection (equal to 1 − exp(−E) with E the environmental bacterial load); m, the probability of transition from I − to S; q, the probability of transition from I − to I + ; r, the probability of transition from I + to R; s, the probability of transition from R to I + ; ɛ1 and ɛ2, the quantities of bacteria shed during a time step by an individual I − and I + respectively, and μ, the mortality rate of C. burnetii in the environment.

(b). Bayesian framework

We develop a dynamic discrete time individual-based stochastic model to represent the temporal evolution of the observed health state of each cow. This is done in two main steps: first, the temporal evolution of the real individual health state is modelled using Markovian transitions and second, the uncertainty of the observations is incorporated using the Se and Sp of the two diagnostic tests.

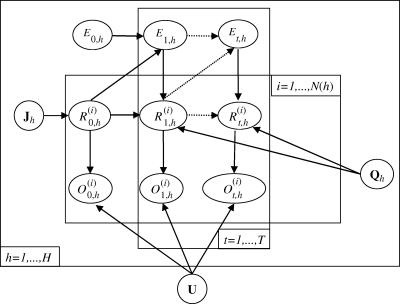
Let 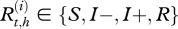Inline graphic be the real health state of individual i belonging to herd h (i Є {1, … , N(h)} with N(h) the total number of cows in the herd h, h Є {1, … , H} and H the number of herds) at time t (t Є {0, … , T} with t28 = T and t0 = 0). As illustrated by the graph in figure 2, for t > t0, 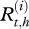Inline graphic, depends on 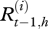Inline graphic and on Et,h, the quantity of bacteria in the environment of herd h at time t. The transition probabilities can be gathered in the matrix Qt,h:

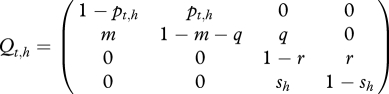(b). 3.1

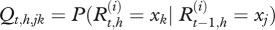where Inline graphic for t = 1, … ,T, i = 1, … , 4 and xj, xk Є {x1= S, x2 = I − , x3 = I + , x4 = R}.

Figure 2.

Figure 2.

Open in a new tab

Network describing the temporal evolution of individual health states of animals within an infected dairy cattle herd. 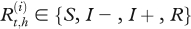Inline graphic represents the real and non-observed health state of individual i belonging to herd h (i ∈ {1, … N(h)} with N(h) the total number of cows in the herd h, h ∈ {1, … H} and H the number of herds) at time t (t ∈ {0, … T)} with t28 = T and t0 = 0). Et,h describes the quantity of bacteria in the environment of the herd h at time t. 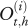Inline graphic represents the observed health state associated with 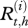Inline graphic. Jh is the probability distribution of the initial real health states in the herd h and U is the matrix of the uncertainty parameters (Se and Sp of tests) linking real and observed health states. 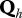Inline graphic contains the parameters of transitions between real health states in herd h except those characterizing the S↔I− transitions. 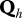Inline graphic is a 3 × 4 matrix corresponding to the last three rows of matrix 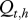Inline graphic described in equation (3.1).

The transition probability from S to I− varies with time and herd since pt = 1−exp(−Et). This is not the case for the other transition probabilities: m, q and r are assumed constant. As s is related to the intermittency of shedding, possibly owing to a stress specifically occurring in a given herd (like an anti-parasitic treatment or a modification in herd management), this parameter is considered herd-dependent.

The initial real health states, 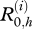Inline graphic, are independent random variables with a probability distribution specified by J, where 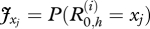Inline graphic for xj Є {x1= S, x2 = I − , x3 = I + , x4 = R}. The environment dynamics is expressed by the equation: 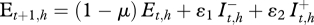Inline graphic, as it is dependent on the quantity of bacteria in the environment and the prevalence of shedders (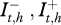Inline graphic) at the previous time (figure 2). Since the beginning of the follow-up does not correspond to the infection onset, the initial content of C. burnetii in the environment of each herd, E0,h, is not zero and has to be introduced and then estimated.

The observation level accounts for the uncertainty of the observations 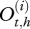Inline graphic and describes their relationship with the real health states 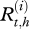Inline graphic using the 4 × 4 matrix U:

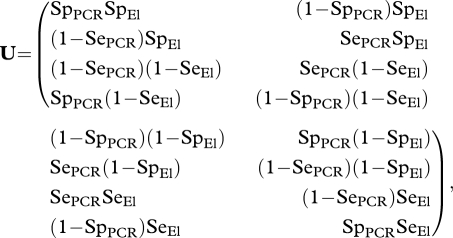(b). 3.2

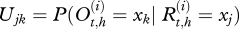where Inline graphic for t = 0 … T, i = 1 … 4 and xi, xk Є {x1 = S, x2 = I − , x3 = I + , x4 = R}.

We consider that the assumption of conditional independence between ELISA and PCR is reasonable because the two tests have different bases: ELISA relies on the detection of antibodies, while PCR is a DNA-based technique to detect bacteria. Enoe et al. (2000) made the same assumption to assess the sensitivities and specificities of a nested PCR and a microscopic examination of kidney imprints for the detection of Nucleospora salmonis in rainbow trout. Elements of U are then defined as combinations of the specificities of the PCR and ELISA tests (SpPCR and SpEl, respectively) and their respective sensitivities (SePCR and SeEl).

(c). Bayesian inference: calculation of the posterior distribution of the model parameters from likelihood and prior distribution

In the Bayesian paradigm, the joint posterior distributions of model parameters can be written as 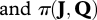Inline graphic Inline graphic are the likelihood function and the joint prior distribution of model parameters, respectively, and 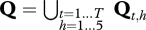Inline graphic (see the electronic supplementary material for more details).

Since the uncertainty parameters of the matrix U are fixed, they are not considered in the joint prior density 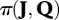Inline graphic. The Se of the ELISA test is set equal to 0.85 (according to a recent estimation; R. Guatteo 2009, personal communication) and the Sp is taken to be equal to 0.95, while for the real-time PCR, both Se and Sp are fixed at 0.95. As no published data on the test characteristics are available, these values were chosen in accordance with expert opinion.

Available knowledge is incorporated into the model through prior distributions. Given that C. burnetii withstands hard environmental conditions (Marrie 1990), the median of its life expectancy (1/μ) on the farm in an infectious form is considered to be 4.5 weeks with a 95 per cent credible interval (CI) of 0.7–14 weeks. To determine the prior distribution of the initial real health state J, we use independent data from six other French infected dairy cattle herds. On an average per herd 38 per cent (min = 20.9%, max = 50%) of cows were observed to be in state S, 12 per cent (3.2%, 17.9%) in state I − , 27 per cent (10.3%, 51.2%) in state I+ and 23 per cent (14%, 29.4%) in state R (R. Guatteo 2009, personal communication). As the initial proportions of S, I − , I+ and R should sum to 1 (as they represent a partition of the individual health states), an appropriate prior distribution of the initial health state J is a Dirichlet distribution, D (3.5, 1, 2.5, 2). Its coefficients are chosen to account for the observed proportions in the extra data (e.g. proportion of S is 3.5/9 = 38%, etc). Concerning the transition parameters (p, m, q, r and s), minimally informative prior densities reflecting the lack of information are chosen. As these parameters are assumed to lie between 0 and 1, beta distributions are used for the probabilities of transition from S to I− (p), I+ to R (r) and R to I+ (s) health states. A Dirichlet distribution is assumed for the probabilities of transition from I− to S(m) and I+ (q), respectively, since the sum of m, q and ‘the probability of staying in I − ’ is equal to 1. The marginal distributions of m, q, and beta distributions for r and s are rather flat. As C. burnetii spreads moderately quickly in cows (Huebner & Bell 1951; Angelakis & Raoult 2010), we use a beta distribution with a median of 0.33 and a 95% CI = (0.05–0.77) in order to penalize high values of p. As the environmental bacterial load E can be expressed with respect to the probability of infection p, the prior on E is deduced from the prior on p (median = 0.4, 95% CI = (0.05–1.44)). Concerning the excretion parameters ɛ, we faced a complete lack of information. However, as ɛ is the quantity of bacteria shed per week by a shedder cow, a plausible assumption is that ɛ = ɛ1 + ɛ2 is lower than the environmental bacterial load E. Hence, we use a truncated normal distribution with a median of 0.23 and 95% CI = (0–0.72) for both ɛ1 and ɛ2. All these prior distributions are detailed in table 1.

Table 1.

Priors and posteriors for the model parameters. (For the posterior distributions, medians and 95% credible intervals (CI) are shown (see also the electronic supplementary material, table S4).)

model parameter prior distribution or mathematical expression prior median and 95% CI posterior median and 95% CI
herd 1 herd 2 herd 3 herd 4 herd 5
transition rate I −→ S, m (week−1) Dirichlet (α1, α2, α3), αi ∼ Uniform(0.5,10) 0.32 (0.01–0.76) 0.695 (0.542–0.844)
transition rate I− →I + , q (week−1) 0.017 (0.001–0.082)
time spent in state I− by an individual (weeks) 1/(m + q) 1.4 (1.0–4) 1.4 (1.1–1.8)
transition rate I +→ R, r (week−1) beta(1,1) 0.50 (0.03–0.98) 0.204 (0.121–0.294)
time spent in state I+ by an individual (weeks) 1/r 2.0 (1.0–33.3) 4.9 (3.4–8.3)
transition rate R → I + , s (week−1) beta(1,1) 0.50 (0.02–0.98) 0.037 (0.006–0.159) 0.170 (0.042–0.345) 0.036 (0.006–0.162) 0.380 (0.070–0.737) 0.277 (0.109–0.466)
time spent in state R by an individual (weeks) 1/s 2.0 (1.0–34.1) 26.6 ( 6.3–159.9) 5.9 (2.8–23.9) 28.1 (6.1–163.7) 2.6 (1.3–14.3) 3.6 (2.1–9.2)
quantity of bacteria shed by an I− per week, ɛ1 normal(0.25,0.25) 0.30 (0.02–0.76) 0.003 (0.000–0.018)
quantity of bacteria shed by an I+ per week, ɛ2 normal(0.25,0.25) 0.30 (0.02–0.76) 0.004 (0.000–0.016)
mortality rate of the bacterium, μ (week−1) 1/μ ∼ beta(2.16,38.51) 0.21 (0.07–0.80) 0.289 (0.079–0.926) 0.274 (0.079–0.869) 0.289 (0.082–0.874) 0.171 (0.068–0.407) 0.203 (0.071–0.760)
transition rate S → I − , p1 (infection risk at t0) beta(1.77,3.3) 0.33 (0.05–0.77) 0.135 (0.021–0.436) 0.124 (0.024–0.325) 0.073 (0.014–0.213) 0.466 (0.272–0.660) 0.230 (0.044–0.455)
bacterial load in the environment at t0, E0 −log(1 − p1) 0.40 (0.05–1.46) 0.146 (0.021–0.572) 0.133 (0.024–0.392) 0.076 (0.014–0.240) 0.627 (0.318–1.078) 0.261 (0.045–0.606)
transition rate S → I−, p5 (infection risk at t28) 1−exp(−E4) variable function of herds 0.095 (0.010–0.282) 0.136 (0.024–0.334) 0.044 (0.005–0.134) 0.403 (0.204–0.622) 0.428 (0.182–0.722)
bacterial load in the environment at t28, E4 E4= (1 − μ)E3 + ɛ1*I −+ ɛ2*I+ variable function of herds 0.100 (0.010–0.331) 0.146 (0.024–0.406) 0.044 (0.005–0.143) 0.517 (0.228–0.973) 0.558 (0.201–1.278)
Open in a new tab

Since posterior distributions are not analytically tractable, inference is based on computationally intensive methodology: MCMC methods based on the Gibbs sampling algorithm implemented in JAGS 1.0.3 are used. Bayesian MCMC allows datasets with missing data to be fully modelled by sampling missing data points from the posterior distributions (in equation S1 of the electronic supplementary material, the matrix O is not entirely observed). Results are analysed with R 2.8.1 (R Development Core Team 2008) and R package code (Plummer et al. 2009).

(d). Model adequacy

In order to check the model adequacy for the data, a subsequent assessment is performed. We simulate infection spread in five cattle herds with the same size, same initial environmental content and same number of missing data as in the original dataset, using parameters drawn from inferred posterior distributions. The missing pattern (i.e. missing data during the follow-up are more frequent for PCR-negative cows at t0 than for PCR-positive ones) is not taken into account. The quantiles of the numbers of transitions between observed health states in each herd for a time interval of one week are calculated and compared with the data.

4. Results

Visual inspection of the chain pattern does not indicate non-convergence of the MCMC algorithm (results not shown). Most of the parameters have a potential scale reduction factor of the Gelman–Rubin diagnostic (Gelman & Rubin 1992) close to 1 (less than or equal to 1.05). However, 5 of the 35 independent parameters monitored have values of potential scale reduction factors between 1.05 and 1.27. For these parameters, the results have to be interpreted with care (for details see the electronic supplementary material, table S3).

Median values and 95% CI of posterior densities (represented in the electronic supplementary material, figures S1 and S2) of inferred parameters are given in table 1 and in the electronic supplementary material, tables S3 and S4.

(a). Parameters of transition between health states

The spread of C. burnetii within a dairy cattle herd is mainly characterized by shedding parameters and probabilities of transition between health states, which are also interpretable as sojourn times in these states (equal to the inverse of transition parameters). For all these parameters, the posterior distributions cover shorter intervals than those defined by the prior distributions, which reveals that the data provide information. The probability of transition from the non-infectious state S to the shedder state I− (corresponding to the infection risk) seems moderate in some herds (for example in herd 3 with a median p at time 1 of 0.073 and a 95% CI = (0.014–0.213)) but quite high in others (e.g. in herd 4 with a median p at t0 of 0.466 and 95% CI = (0.272–0.660)). Whereas the transition from the shedder state without antibodies, I − , to the non-infected state S is relatively more rapid (median of m equal to 0.695 week−1, 95% CI = (0.542–0.844)), the acquisition of antibodies in the infectious state (transition I − → I + ) is rather rare (median of q equal to 0.017 week−1, 95% CI = (0.001–0.082)). Moreover, the duration in health state I − is shorter than in I + : posterior distributions do not overlap and if we compare the medians, the median duration in I− is more than three times shorter than that in I+ (1.4 versus 4.9 weeks, respectively). The median time spent in state R before new shedding (representing the intermittency of shedding) is less than 3.6 months in two of the five herds (herds 4 and 5) but can potentially be longer in the other three (e.g. 26.6, 95% CI = (6.3–159.9) in herd 1).

(b). Environment-related parameters

Concerning the shedding parameters, as the posterior distributions of the quantities of bacteria excreted by infectious cows without antibodies (ɛ1) and with antibodies (ɛ2) are almost superimposed, we cannot determine if I− animals shed more than, at a similar level to, or less than I+ animals. For all but herd 5, the posterior distributions of the environmental bacterial load do not vary much with respect to time (electronic supplementary material, figure S2). Therefore, it is not possible to know how the environmental bacterial load evolves with time. For herd 5, as the posterior distribution shifts to the right from t0 to t28 it is possible that the environmental bacterial load increases with time (at t0: median of 0.261, 95% CI = (0.045–0.606), at t28: median of 0.558, 95% CI = (0.201–1.278)). Since at a given time posterior distributions of E widely overlap, we cannot determine if environmental bacterial loads differ between herds. For the parameter μ, the posterior distributions are close to the prior distribution regardless of the herd. It seems that the dataset does not contain sufficient information to assess this parameter.

(c). Checking of model adequacy for the data

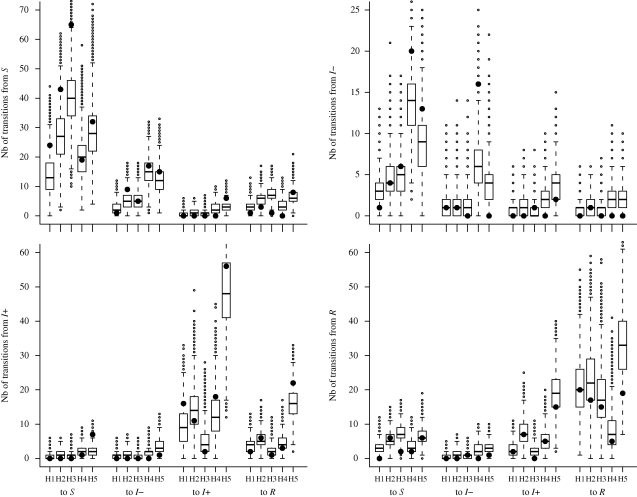
The goodness-of-fit is assessed in figure 3. We verify the ability of the model to reproduce observed summary statistics, defined as the total number of transitions per week between observed individual health states for each herd, during a month, when parameters are sampled from posterior densities. Sixty-three per cent (expected 50%) of observed summary statistics lie within the predicted 50% CI and 94 per cent (expected 95%) of them belong to the 95% CI of the simulated numbers of transitions.

Figure 3.

Figure 3.

Open in a new tab

Goodness-of-fit assessment. Boxplots summarize the posterior predictive distributions of simulated numbers of weekly transitions between observed health states (S, I − , I+ and R) in each herd (H1–H5) during the one-month follow-up. The quartiles are represented by horizontal lines. The whiskers indicate maximum and minimum values of the simulated distributions that lie less than 1.5 interquartile range lower or higher than the first or the third quartiles, respectively. Simulated values beyond the ends of the whiskers are indicated by a point. Black circles represent numbers of transitions between observed health states in our dataset.

5. Discussion

This study, based on a Bayesian modelling approach, provides the first quantitative assessment of parameters describing the spread of C. burnetii within chronically infected dairy herds. Previous studies that focused on Bayesian statistical inference of disease parameters have already proposed discrete time stochastic epidemic models (Morton & Finkenstädt 2005; Lekone & Finkenstädt 2006). However, our approach differs from these as it is individual-based.

The Bayesian framework enables the combination in the same model of previous knowledge about C. burnetii (mainly concerning the life-expectancy of the bacteria in the environment and the proportions of different health states within an infected herd) with information coming from the present dataset. Moreover, it allows differences between herds to be accounted for in a flexible manner through a hierarchical representation of the processes involved. The convergence of the MCMC is not perfect, particularly for the initial real health states. Although estimations of these parameters seem biologically consistent, our dataset is probably not informative enough to provide good assessments of all inferred parameters. However, for most of the parameters, convergence is achieved, the results are biologically plausible and the goodness-of-fit is satisfactory overall. Nevertheless, the choice of simulated missing data (that is, of cows with unknown health states for the t7–t28 period) was made random whereas in the field protocol, the selection of the weekly sampled cows was not made at random. Moreover, a possible way to further improve the adequacy of the model for the data is to consider that the uncertainty on the observed health states would differ for each observation as a function of the quantitative results provided by the diagnostic tests (S/P ratios for the ELISA and Ct values for the PCR). In fact, dichotomizing the test result of an ELISA can be unnecessary and, to some extent, counter-productive (Nielsen et al. 2007). The relevancy of this option could be explored in further studies.

As shown by the present results, some chronically infected herds (like herd 3) are characterized by a low probability of infection and then a slow spread of the disease while others (like herd 4) are characterized by a quite high probability of infection and then faster infection dynamics. Also, intermittency of shedding is less likely to occur in some herds (like herds 1 and 3) but seems usual in others (like herd 5).

When a cow becomes infected, clearance of the bacterium without seroconversion (transitions from I− to S) is very common, while the transition from the seronegative to the seropositive state (I −→ I + ) is very rare, which means that very few cows of the analysed dataset seroconverted over the month studied (which did not correspond to the beginning of the infection). Moreover, in herds where the infection dynamics are faster, some cows are restrained to transitions between the non-infected state and shedding without antibodies state (S ↔ I − ), while others are restrained to transitions between the infectious seropositive state and the non-shedding seropositive state (I + ↔R). Thus, two categories of animals seem to exist with two different types of infection response: a response with or without any antibody production. Finally, the antibody status seems to play a major role in the involvement of a given cow in the bacterial spread: shedders with antibodies (I + ) release bacteria for a longer time than animals in the shedding state without antibodies.

Estimations of the environmental bacterial load are also provided. Although these values do not have any obvious biological meaning, they are related to the infection/re-infection probability of an animal within an infected herd. Our results do not show if the infection risk varies with time but it is likely that some herds (like herd 5 and maybe herd 4 at the end of the study) have quite high infection risks. As the present dataset does not contain enough information to significantly update the prior distribution of the mortality rate of C. burnetii (parameter μ), we cannot claim that this potential by high probability of infection is owing to an ineffective cleaning process of the cattle housing or is directly related to differences in the prevalence of shedding cows. Further work is needed to provide relevant indicators of the environmental contamination. The time scale of our study is probably insufficient to investigate environmental content variations; a period longer than one month is probably required.

The present data do not distinguish real susceptible individuals from non-shedding seronegative ones: all are gathered in the unique category S. Thus, the estimated transition rate from the non-shedding to the shedding without antibodies state is a mix between an infection rate and a re-infection rate. These two rates are different as, in the latter, the cell immunity should already have been activated. However, it is not possible with the current diagnostic tests to differentiate primary infected from re-infected animals. The relevance of cell immunity tests (i.e. skin tests) to study the immunity responses in chronically infected herds would be a profitable area of research.

To conclude, this work provides, to our knowledge, the first quantitative estimation of key parameters from field data based on an original modelling approach, enabling a better understanding of C. burnetii infection dynamics within chronically infected dairy herds. Besides the biological insights provided by the estimated values of parameters, the outputs can be further used to calibrate a simulation model representing the infection dynamics within a cattle herd over a longer time scale and assessing the effectiveness of different control strategies for C. burnetii infection.

Acknowledgements

The authors thank Annie Rodolakis and Raphaël Guatteo for useful discussions on data and biological aspects related to Q fever and the referees for their comments and suggestions.

References

  1. Aitken I. D.1989Clinical aspects and prevention of Q fever in animals. Eur. J. Epidemiol. 5, 420–424 (doi:10.1007/BF00140132) [DOI] [PubMed] [Google Scholar]
  2. Angelakis E., Raoult D.2010Q fever. Vet. Microbiol. 140, 297–309 (doi:10.1016/j.vetmic.2009.07.016) [DOI] [PubMed] [Google Scholar]
  3. Anonymous. Centers for disease control and prevention. 2009. See http://www.n.cdc.gov/travel/content/id/1769.aspx . (Accessed on 21/12/2009)
  4. Arricau-Bouvery N., Souriau A., Lechopier P., Rodolakis A.2003Experimental Coxiella burnetii infection in pregnant goats: excretion routes. Vet. Res. 34, 423–433 (doi:10.1051/vetres:2003017) [DOI] [PubMed] [Google Scholar]
  5. Berri M., Souriau A., Crosby M., Crochet D., Lechopier P., Rodolakis A.2001Relationships between the shedding of Coxiella burnetii, clinical signs and serological responses of 34 sheep. Vet. Rec. 148, 502–505 [DOI] [PubMed] [Google Scholar]
  6. Bildfell R. J., Thomson G. W., Haines D. M., McEwen B. J., Smart N.2000Coxiella burnetii infection is associated with placentitis in cases of bovine abortion. J. Vet. Diagn. Invest. 12, 419–425 [DOI] [PubMed] [Google Scholar]
  7. Cauchemez S., Carrat F., Viboud C., Valleron A. J., Boëlle P. Y.2004A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data. Stat. Med. 23, 3469–3487 (doi:10.1002/sim.1912) [DOI] [PubMed] [Google Scholar]
  8. Durand M. P.1993Lacteal and placental excretion of Coxiella burnetti, agent of Q fever, in the cow. Importance and prevention. Bull. Acad. Natl Med. 177, 935–945 (discussion 945–946) [PubMed] [Google Scholar]
  9. Enoe C., Georgiadis M. P., Johnson W. O.2000Estimation of sensitivity and specificity of diagnostic tests and disease prevalence when the true disease state is unknown. Prev. Vet. Med. 45, 61–81 (doi:10.1016/S0167-5877(00)00117-3) [DOI] [PubMed] [Google Scholar]
  10. Fournier P. E., Marrie T. J., Raoult D.1998Diagnosis of Q fever. J. Clin. Microbiol. 36, 1823–1834 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gelman A., Rubin D. B.1992Inference for iterative simulation using multiple sequences. Stat. Sci. 7, 457–511 (doi:10.1214/ss/1177011136) [Google Scholar]
  12. Gilks W. R., Richardson S., Spiegelhalter D. J.1996Markov chain Monte Carlo in practice. London, UK: Chapman & Hall [Google Scholar]
  13. Guatteo R., Beaudeau F., Berri M., Rodolakis A., Joly A., Seegers H.2006Shedding routes of Coxiella burnetii in dairy cows: implications for detection and control. Vet. Res. 37, 827–833 (doi:10.1051/vetres:2006038) [DOI] [PubMed] [Google Scholar]
  14. Guatteo R., Beaudeau F., Joly A., Seegers H.2007Performances of an ELISA applied to serum and milk for the detection of antibodies to Coxiella burnetii in dairy cattle. Revue Méd. Vét. 158, 250–252 [Google Scholar]
  15. Höhle M., Jorgensen E., O'Neill P. D.2005Inference in disease transmission experiments by using stochastic epidemic models. Appl. Stat. 54, 349–366 (doi:10.1017/S0950268808001908) [Google Scholar]
  16. Huebner R. J., Bell J. A.1951Q fever studies in Southern California. Summary of current results and a discussion of possible control measures. J. Am. Med. Assoc. 145, 301–305 [DOI] [PubMed] [Google Scholar]
  17. Karagiannis I., et al. 2009Investigation of a Q fever outbreak in a rural area of The Netherlands. Epidemiol. Infect. 137, 1283–1294 [DOI] [PubMed] [Google Scholar]
  18. Lekone P. E., Finkenstädt B. F.2006Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics 62, 1170–1177 (doi:10.1111/j.1541-0420.2006.00609) [DOI] [PubMed] [Google Scholar]
  19. McCaughey C., McKenna J., McKenna C., Coyle P. V., O'Neill H. J., Wyatt D. E., Smyth B., Murray L. J.2008Human seroprevalence to Coxiella burnetii (Q fever) in Northern Ireland. Zoonoses Public Health 55, 189–194 (doi:10.1111/j.1863-2378.2008.01109) [DOI] [PubMed] [Google Scholar]
  20. McQuiston J. H., Childs J. E.2002Q fever in humans and animals in the United States. Vector Borne Zoonotic Dis. 2, 179–191 (doi:10.1089/15303660260613747) [DOI] [PubMed] [Google Scholar]
  21. Marrie T. J.1990Q fever: a review. Can. Vet. J. 31, 555–563 [PMC free article] [PubMed] [Google Scholar]
  22. Morton A., Finkenstädt B. F.2005Discrete time modelling of disease incidence time series by using Markov chain Monte Carlo methods. Appl. Stat. 54, 575–594 (doi:0.1111/j.1467-9876.2005.05366) [Google Scholar]
  23. Nielsen S. S., Toft N., Jorgensen E., Bibby B. M.2007Bayesian mixture models for within-herd prevalence estimates of bovine paratuberculosis based on a continuous ELISA response. Prev. Vet. Med. 81, 290–305 (doi:10.1016/j.prevetmed.2007.05.001) [DOI] [PubMed] [Google Scholar]
  24. Norlander L.2000Q fever epidemiology and pathogenesis. Microbes Infect. 2, 417–424 (doi:10.1016/S1286-4579(00)00325-7) [DOI] [PubMed] [Google Scholar]
  25. O'Neill P. D., Roberts G. O.1999Bayesian inference for partially observed stochastic epidemics. J. R. Stat. Soc. A 162, 121–129 (doi:10.1111/1467-985X.00125) [Google Scholar]
  26. Panaiotov S., Ciccozzi M., Brankova N., Levterova V., Mitova-Tiholova M., Amicosante M., Rezza G., Kantardjiev T.2009An outbreak of Q fever in Bulgaria. Ann. Ist Super Sanita 45, 83–86 [PubMed] [Google Scholar]
  27. Plommet M., Capponi M., Gestin J., Renoux G.1973Fièvre Q expérimentale des bovins. Ann. Rech. vétér. 4, 325–346 [Google Scholar]
  28. Plummer M., Best N., Cowles K., Vines K.2009Coda: output analysis and diagnostics for MCMC. R package version 0.13-4. [Google Scholar]
  29. Raoult D., et al. 2000Q fever 1985–1998. Clinical and epidemiologic features of 1,383 infections. Medicine (Baltimore) 79, 109–123 [DOI] [PubMed] [Google Scholar]
  30. R Development Core Team 2008R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; See http://www.R-project.org (ISBN 3-900051-07-0, URL) [Google Scholar]
  31. Rodolakis A., et al. 2007Comparison of Coxiella burnetii shedding in milk of dairy bovine, caprine, and ovine herds. J. Dairy Sci. 90, 5352–5360 (doi:10.3168/jds.2006-815) [DOI] [PubMed] [Google Scholar]
  32. Schimmer B., Dijkstra F., Vellema P., Schneeberger P. M., Hackert V., ter Schegget R., Wijkmans C., Van Duynhoven Y., Van der Hoek W.2009Sustained intensive transmission of Q fever in the south of the Netherlands, 2009. Euro Surveill. 14, pii = 19210. See http://www.eurosurveillance.org/ViewArticle.aspx?ArticleId=19210 [DOI] [PubMed] [Google Scholar]
  33. Streftaris G., Gibson G. J.2004Bayesian analysis of experimental epidemics of foot-and-mouth disease. Proc. R. Soc. Lond. B 271, 1111–1117 (doi:10.1098/rspb.2004.2715) [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Welsh H. H., Lennette E. H., Abinanti F. R., Winn J. F.1958Air-borne transmission of Q fever: the role of parturition in the generation of infective aerosols. Ann. NY Acad. Sci. 70, 528–540 (doi:10.1111/j.1749-6632.1958.tb35409.x) [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES