Sequence-dependent Kink-and-Slide Deformations of Nucleosomal DNA Facilitated by Histone Arginines Bound in the Minor Groove

Abstract

In addition to bending and twisting deformabilities, the lateral displacements of the DNA axis (Kink-and-Slide) play an important role in DNA wrapping around the histone core (M. Y. Tolstorukov, A. V. Colasanti, D. M. McCandlish, W. K. Olson, V. B. Zhurkin, J. Mol. Biol. 371, 725-738 (2007)). Here, we show that these Kink-and-Slide deformations are likely to be stabilized by the arginine residues of histones interacting with the minor groove of DNA. The arginines are positioned asymmetrically in the minor groove, being closer to one strand. The asymmetric arginine-DNA interactions facilitate lateral displacement of base pairs across the DNA grooves, thus leading to a stepwise accumulation of the superhelical pitch of nucleosomal DNA.

To understand the sequence dependence of such Kink-and-Slide deformations, we performed all-atom calculations of DNA hexamers with the YR and RY steps in the center. We found that when the unrestrained DNA deformations are allowed, the YR steps tend to bend into the major groove, and RY steps bend into the minor groove. However, when the nucleosomal Kink-and-Slide deformation is considered, the YR steps prove to be more favorable for bending into the minor groove. Overall, the Kink-and-Slide deformation energy of DNA increases in the order TA < CA < CG < GC < AC < AT. We propose a simple stereochemical model accounting for this sequence dependence. Our results agree with experimental data indicating that the TA step most frequently occurs in the minor-groove kink positions in the most stable nucleosomes.

Our computations demonstrate that the Kink-and-Slide distortion is accompanied by the BI to BII transition. This fact, together with irregularities in the two-dimensional (Roll, Slide) energy contour maps, suggest that the Kink-and-Slide deformations represent a nonharmonic behavior of the duplex. This explains the difference between the two estimates of the DNA deformation energy in nucleosome – the earlier one made using knowledge-based elastic energy functions, and the current one based on all-atom calculations.

Our findings are useful for refining the score functions for the prediction of nucleosome positioning. In addition, the reverse bending behavior of the YR and RY steps revealed under the Kink-and-Slide constraint is important for understanding the molecular mechanisms of binding transcription factors (such as p53) to DNA exposed on the surface of nucleosome.

Introduction

What are the ‘rules’ guiding sequence-dependent packing of DNA in nucleosomes? Structural biologists still seek to answer this long-standing question. Nucleosomes provide a general mechanism for compaction of eukaryotic DNA and regulation of gene expression. More and more observations suggest that certain DNA sequences have stronger binding affinities to the histone octamer core than others, which is revealed in specific sequence-dependent positioning of nucleosomes on DNA (1-4). A detailed analysis of the X-ray structures of nucleosome core particles at high resolution (5) demonstrates that the path of the nucleosomal DNA superhelix is not regular. Instead of being wrapped smoothly, DNA is distorted through bends and lateral displacements (6), especially at the sites of minor-groove bending. The Kink-and-Slide distortions in nucleosomes are highly sequence-specific, which is critical for the nucleosome positioning (6).

In previous studies, fourteen arginines were found to interact with the minor groove of DNA at locations where the minor groove faces the histone core (5,7). These minor-groove arginines are frequently associated with the Kink-and-Slide DNA distortions in currently available nucleosomal structures. Furthermore, they are all strongly conserved in major forms of histones in all eukaryotic species. However, previous studies (5,7) lacked detailed explanations of how the positively charged arginines facilitate nucleosomal DNA wrapping around the histone core. Here, we re-analyze the X-ray nucleosomal structures to elucidate the structural role of these minor-groove arginines.

The early study of anisotropic bending of DNA suggested a ‘mini-kink’ model for nucleosomal DNA (8). This model postulated DNA bends of about 20 degrees directed into the minor and major grooves alternatively, separated by 5 bp segments. It is generally consistent with the bending behavior of DNA in the X-ray nucleosomal structures (5). However, there are problems with predictions of the sequence dependence of DNA wrapping in the nucleosome based on this model. Numerous observations of naked DNA in solution as well as DNA crystals indicate that the pyrimidine-purine dimeric steps, YR, tend to bend into the major groove, while the purine-pyrimidine steps RY prefer bending into the minor groove (9,10). This simple rule apparently contradicts the fact that in the strongly positioned nucleosomes, the TA dimers are frequently found at the positions with minor groove DNA bending (11,12). To resolve this contradiction, more sophisticated computations are necessary – first, analyzing the lateral displacements in nucleosomal DNA (i.e., considering the Kink-and-Slide distortions) and second, going beyond the level of dimeric steps (that is, accounting for the context-dependence of DNA deformability).

Recently, molecular dynamics (MD) simulations of naked DNA oligomers were undertaken to elucidate the sequence dependence of DNA conformation and flexibility (13,14). Naturally, these studies focused on the conformational fluctuations around the optimal (averaged) structures at physiological conditions. However, the DNA conformations at the highly distorted Kink-and-Slide positions in crystallized nucleosomes are substantially different from the equilibrium structures of naked DNA (6). For example, according to the MD calculations (13), the average Roll and Slide parameters of the central step in DNA octamers in those studies are around 5° and −1.0 Å, respectively, but these two parameters are about −20° and 2.5 Å, respectively, at the distorted position SHL −3.5 in the best-resolved nucleosomal structure, 1KX5 (5). Thus, the equilibrium conformations are about 4-5 RMSD away from the Kink-and-Slide structures observed in nucleosomes. It is clear that such large DNA deformations are not captured in the published MD simulations performed without constraints (13,14), and it is hardly appropriate to draw conclusions about the mechanisms of nucleosomal DNA wrapping around the histone core, based on those results.

To better understand the mechanism of DNA wrapping in the nucleosome and its sequence-dependent preferences, we used two different approaches. First, we analyzed nine nucleosomal structures and focused on the structural arrangement of arginines at the positions which are associated with the Kink-and-Slide deformations. Second, we took the Kink-and-Slide deformations into account to address the sequence-dependent preferences of DNA by using all-atom energy calculation in the internal helical coordinate space (three rotational and three translational parameters). We paid special attention to the following questions:

1. How do histone arginines facilitate nucleosomal DNA wrapping?

2. How are the Kink-and-Slide distortions related to histone-DNA interactions?

3. How do YR and RY energy profiles behave with and without Kink-and-Slide constraints?

4. What is the general trend for the YR and RY dimeric steps in terms of the energy cost of the Kink-and-Slide deformation?

Part I. Histone arginines facilitate Kink-and-Slide deformations in DNA: Analysis of nucleosomal structures

Flexibility of arginines penetrating into the minor groove

As soon as the crystal structures of nucleosome core particle at atomic resolution were solved (15,16), researchers began to emphasize the participation of arginines in DNA-histone contacts. Since then, these interactions have been the subject of a number of investigations (5,7,17). Here, we analyze the relationships between the arginine-DNA interactions and the Kink-and-Slide structural motifs employed by DNA wrapped around the histone octamer (6). Specifically, we will consider twelve arginines inserted into the narrow minor groove of DNA at half-integer Superhelix Locations (SHLs) where the minor groove faces the histone octamer (marked by blue and magenta circles in Figure 1A). Two additional arginines interact with the phosphate backbone, at the terminal positions SHLs ±6.5 (7) but do not penetrate inside the minor groove (5). We compared positions and orientations of the side chains of these twelve ‘built-in’ arginines in crystallized nucleosomes, and found that they can be divided in two groups based on their flexibility (Figures 1B and C). Eight arginines (marked by blue circles: SHLs ±0.5, ±2.5, ±3.5 and ±5.5) are more conformationally ‘rigid’ than the other four (marked by magenta circles in Figure 1A). For example, in the case of ‘rigid’ R77 (H2A) at SHL −5.5 the largest distance between the positions of the Cζ atom in superimposed histone octamers from different nucleosomal structures is 1.1 Å (Figure 1B), but it is 7.7 Å for the ‘flexible’ R63 (H3) at SHL −1.5 (Figure 1C). This difference in conformational variability is apparently related to the fact that all ‘rigid’ arginines reside in the helix-loop-helix motifs, while the ‘flexible’ arginines belong to the histone tails.

Figure 1.

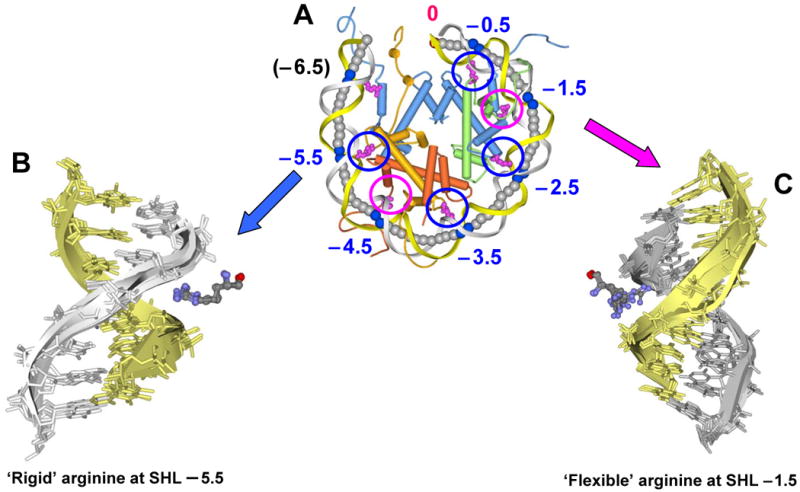
Variability of arginines penetrating into the DNA minor groove in a nucleosome. The 5′-end ‘sequence’ strand is shown in yellow and the 3′-end ‘non-sequence’ strand is in gray.

A. Superhelix Locations (SHLs) in the ‘anterior’ half of nucleosomal crystal structure, PDB 1KX5 (5). The dyad axis is marked by 0 (in red). To distinguish between the two halves of the nucleosome related by twofold pseudo-symmetry, we call the first half ‘anterior’ and the second half ‘posterior.’ Seven arginines interacting with the DNA minor groove are shown in magenta. Blue circles show conformationally ‘rigid’ arginines, and magenta circles show ‘flexible’ arginines. H3, H4, H2A and H2B histones are shown in blue, green, yellow and orange, respectively.

B. Conformationally ‘rigid’ R77 (H2A) penetrating into the minor groove at SHL −5.5. Images shown here are based on nine nucleosomal structures aligned through 300 Cα atoms of histone α-helices conserved in all nucleosomes. (The PDB entries are 1KX5, 1KX3, 1KX4, 1ID3, 1EQZ, 2CV5, 2PYO, 2NQB and 2NZD. These nine structures were selected to represent variability in the DNA sequence and length, as well as in the origin of histones – yeast, fly, frog, chicken and human.) For clarity, only four structures are shown (1KX5, 1KX3, 1ID3 and 1EQZ). Note that all nine arginines have nearly identical conformation – the distance between two positions of Cζ atom varies from 0.1 to 1.1 Å.

C. Conformationally ‘flexible’ R63 (H3) interacting with the minor groove of DNA at SHL −1.5. Note that the side chain of R63 (H3) is more variable than that of R77 (H2A) shown in B – the distance between two positions of the Cζ atom varies from 0.3 to 7.7 Å.

Differences in the flexibility (i.e., positional variability) of the minor groove-bound arginines imply that they may play different roles in stabilizing DNA wrapping around the histone octamer. In particular, one would expect that the ‘rigid’ arginines would be especially important for ‘freezing’ the DNA conformation and nucleosome positioning, and their mutations would facilitate histone translocation along the DNA. Indeed, data on SIN and lrs mutants (reviewed in (18)) indicate that substitutions of the ‘rigid’ arginines significantly increased the accessibility of nucleosomal DNA and sliding of nucleosomes, or affected chromatin silencing in yeast. These substitutions are the R45H and R45C mutants of H4 and the R83A mutant of H3, affecting the histone-DNA interactions at SHLs ±0.5 and ±2.5, respectively. It is reasonable to expect that mutations of the other ‘rigid’ arginines 77 and 42 of H2A, interacting with DNA at SHLs ±5.5 and ±3.5, would have a similar effect. As to the conformationally ‘flexible’ arginines, it is probably too early to speculate what would be the effect of their mutations.

Notably, our selection of the conformationally ‘rigid’ and ‘flexible’ arginines is consistent with the previous classification suggested by Harp et al. (16), who divided the minor-groove binding arginines into two groups, denoted the α and β motifs. Our SHLs ±1.5 and ±4.5 correspond to their sites mGI 2 and mGI 5 (α binding motif), while SHLs ±0.5, ±2.5, ±3.5 and ±5.5 are the same as their sites mGI 1, 3, 4 and 6 (β binding motif).

Asymmetric positions of arginines in the minor groove

Recently, Honig and coworkers (17,19) analyzed the binding of arginine residues to the minor groove in various protein-DNA complexes including the Hox family of transcription factors. They found that arginines are enriched in narrow regions of the DNA minor groove, thereby providing the structural basis for a readout mechanism exploiting a connection between the DNA sequence and shape. They specifically emphasized the negative electrostatic potential of DNA calculated at geometric midpoints between the opposite O4′ oxygens from the two strands. Some of their work was presented at Albany 2009: The 16^th Conversation (20).

Below we demonstrate that in nucleosomes, a typical arrangement of arginines in the DNA minor groove at the half-integer SHLs differs from that in the complex with Hox and other proteins. As an example, consider the well-known 434 repressor-DNA complex (21). Here, the arginine is ‘docked’ in the center of the groove, so that its NH₂ groups are equidistant from the DNA strands (Figure 2A). In contrast, the nucleosomal arginines are positioned asymmetrically in the minor groove, in most cases being closer to the gray ‘non-sequence’ strand in the first (anterior) half of the nucleosome and to the yellow ‘sequence’ strand in the second (posterior) half (Figures 1A, 1C and 2B, Table I).

Figure 2.

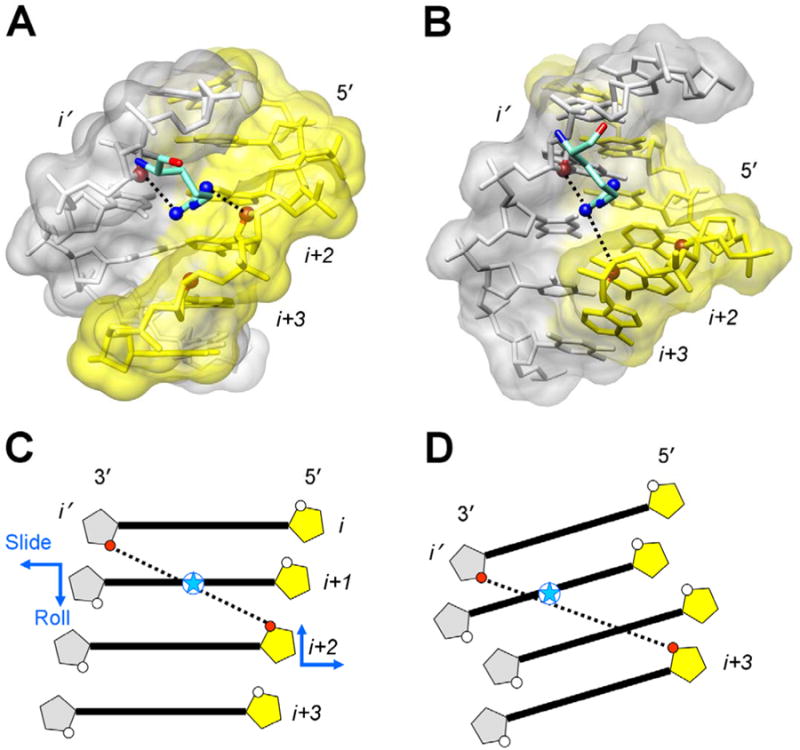
Arginines in the minor groove of the 434 repressor-DNA complex and in the nucleosome.

A. Symmetrically positioned arginine 43 in the minor groove of DNA in complex with the 434 repressor (21). The distances between the guanidinium NH₂ groups and the closest O4′ atoms from nucleotides (i′) and (i+2) are 3.59 and 3.61 Å. The O4′ atoms are shown as red balls. (The distance between the left NH₂ group and O4′(i+3) is 4.3 Å.)

B. Asymmetrically positioned arginine 77 (H2A) in the minor groove of nucleosomal DNA (5) at the site SHL −5.5 with a strong Kink-and-Slide distortion. Arginine is closer to the gray strand than to the yellow ‘sequence’ strand – the distances between the guanidinium NH₂ groups and the O4′ atoms from nucleotides (i′) and (i+3) are 3.38 Å and 4.36 Å, respectively. (The distance between the right NH₂ group and O4′(i+2) is 6.7 Å.)

C, D. Schematic representation of the DNA minor groove in the 434 repressor-DNA complex (canonical B-DNA), C, and in the nucleosome (at the site with the Kink-and-Slide distortion), D. In C, the closest opposite O4′ atoms belong to nucleotides (i′) and (i+2), with the O4′-O4′ distance 6.8 Å. Position of the guanidinium group of arginine (blue star) is close to the center of O4′-O4′ vector (see panel A). In D, geometry of the minor groove differs from that in canonical B-form because of the strong positive Slide and negative Roll (shown by blue arrows in panel C). As a result, the two closest O4′ atoms belong to nucleotides (i′) and (i+3), the O4′-O4′ distance being 7.1 Å. The guanidinium group of arginine (blue star) is closer to the non-sequence strand shown in gray (see panel B).

Table I.

Distances between arginines and the O4′ atoms of nucleosomal DNA

SHL	ID1 Chain I		Dist1 (Å)	ID2 Chain J		Dist2 (Å)	Groove width (Å)	Histone (Chain ID)	Arg
−6.5	7	(−67)	4.96	4′	(70)	6.58	6.93	H3 (E)	R49
−5.5	19	(−55)	4.36	16′	(58)	3.38	7.05	H2A (C)	R77
−4.5	28	(−46)	5.82	25′	(49)	3.05	8.65	H2B (D)	R30
−3.5	39	(−35)	3.78	36′	(38)	2.84	6.32	H2A (C)	R42
−2.5	51	(−23)	3.98	48′	(26)	3.37	7.00	H3 (A)	R83
−1.5	61	(−13)	4.53	58′	(16)	5.51	6.89	H3 (A)	R63
−0.5	70	(−4)	4.00	67′	(7)	3.50	7.44	H4 (B)	R45
0.5	81	(7)	3.57	78′	(−4)	4.02	7.50	H4 (F)	R45
1.5	92	(18)	6.28	89′	(−15)	8.11	7.06	H3 (E)	R63
2.5	100	(26)	3.98	97′	(−23)	3.91	7.00	H3 (E)	R83
3.5	112	(38)	2.80	109′	(−35)	4.27	6.46	H2A (G)	R42
4.5	123	(49)	3.03	120′	(−46)	5.85	8.71	H2B (H)	R30
5.5	132	(58)	3.35	129′	(−55)	3.98	6.95	H2A (G)	R77
6.5	144	(70)	7.00	141′	(−67)	5.23	6.85	H3 (A)	R49

The data are presented for the arginines interacting with the DNA minor groove in the half–integer SHL sites, in the high–resolution nucleosomal structure, PDB 1KX5 (5). For each arginine, the shortest distance between the guanidinium NH₂ groups and the O4′ atoms from both DNA strands is selected (shown in boldface in the column Dist1 or Dist2). The corresponding nucleotide number is given in the column ID1 or ID2. (Two numbering schemes are presented – from 1 to 147, as in Figures 2 and 3, and from −73 to 73, as in PDB 1KX5, in parentheses.) In the opposite strand, the O4′ atom is selected following the ‘i+3’ rule (see Figure 2D). The distance between the two O4′ atoms defines the minor groove width.

In the first half of the nucleosome, most of the arginines are closer to the non–sequence strand (see the Dist2 values underlined), whereas in the second half, the arginines are closer to the sequence strand (Dist1). The SHL sites where this rule holds are shown in boldface and underlined (together with the shorter of two distances, Dist1 or Dist2.)

Another difference is the relative positions of the nucleotides from the two strands that directly interact with arginine. In the 434 repressor-DNA complex, the guanidinium groups of arginine ‘bridge’ the deoxyribose O4′ atoms from nucleotides (i′) and (i+2), whereas in the nucleosome the two bridged O4′ atoms are most frequently from nucleotides (i′) and (i+3) (see Figures 2C and D). The data on arginine positioning are shown in Table I for the highest-resolution nucleosomal structure, 1KX5 (5). (Preliminary data for other nucleosomal structures – 1KX3, 1ID3 and 1EQZ – show similar trends.) In most of the cases, the atom O4′(i+3) from the opposite strand is the closest one in that strand to the guanidinium group of arginine (e.g., at SHLs ±5.5, ±3.5, ±2.5 and ±0.5; data not shown). The exceptions from the ‘i+3’ rule occur at SHLs ±4.5 and −1.5. In particular, at SHL −4.5, the O4′ atom from nucleotide #27 (−45) in Chain I is separated from the arginine NH₂ group by 4.74 Å, which is less than 5.82 Å for the atom O4′ from nucleotide #28 (−46). This does not affect the general tendency, however – the arginine 30 (H2B) remains closer to the non-sequence strand (Chain J in Table I).

Interestingly, the arginines whose ‘behavior’ is not consistent with the rules described above, belong to the group of ‘flexible’ arginines interacting with DNA at the SHLs ±4.5 and ±1.5, with the distances (NH₂–O4′) exceeding 5-6 Å, especially at SHLs ±1.5. Note in this regard that Davey et al. (5) did not include the SHLs ±1.5 in the list of sites where the arginines interact with the minor groove. On the other hand, Harp et al. (16) included these sites in the list of “minor groove–in” positions, together with the other SHLs, from SHL −5.5 to SHL 5.5. Apparently, this classification depends on the authors' criteria.

In summary, the arginine in the minor groove is inserted between two deoxyriboses from the opposite strands separated either by one base pair (in the 434 repressor) or by two base pairs (in the nucleosome). This difference between the two modes of interaction is clearly due to the Kink-and-Slide distortions in nucleosomal DNA. At the qualitative level, the structural rearrangements in nucleosomal DNA can be understood from a comparison of Figures 2C and D. The strong positive Slide, or displacement of the pair (i+2) to the right, leads to a significant increase in the distance between O4′(i′) and O4′(i+2) from 6.8 Å (Figure 2C) to 9.0 Å (Figure 2D). This is a general trend – practically all Kink-and-Slide positions are characterized by an increased separation between the DNA strands.

At the same time, negative Roll is similar to the local B-to-C transition (22), so the base pairs are inclined as shown in Figure 2D – this shortens the distance between O4′(i′) and O4′(i+3). As a consequence, the oxygen O4′ from nucleotide (i+3) becomes the closest one to O4′(i′) and to the guanidinium group of arginine.

Arginine-DNA interactions facilitate DNA axial dislocations

To illustrate how arginine-DNA interactions facilitate DNA axial dislocations, we aligned two DNA fragments (Figure 3). The first one is the nucleosomal DNA fragment at SHL −5.5 with a strong positive Slide (2.56 Å), and the second one was modeled with the same base-pair step parameters as in the first fragment, except for Slide which was set to zero. As follows from Figure 3, if DNA is bent without a concomitant lateral displacement (Slide) then there is a prohibitive steric hindrance between the arginine side chain and the DNA backbone. This clash is relieved if Slide is positive and base pair #16 is moved to the left (Figure 3). Thus, we see that the histone arginines (asymmetrically positioned in the minor groove) facilitate the Kink-and-Slide deformations in nucleosomal DNA.

Figure 3.

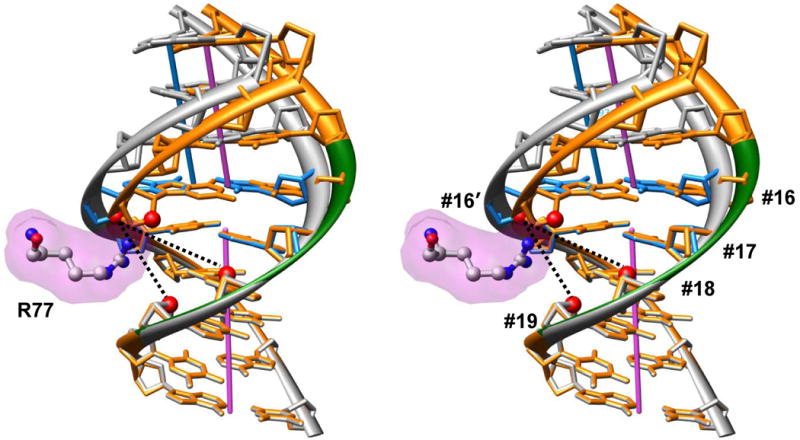
Arginines facilitate the lateral displacement (Slide) in the nucleosomal DNA (stereo image). The DNA fragment shown in gray is the same as in Figure 2B – arginine 77 of H2A (magenta surface) asymmetrically penetrates into the minor groove at SHL −5.5. The base pairs shown as blue sticks represent the Kink-and-Slide step (positions #16 and #17 in 147-bp long DNA fragment (4)). For comparison, the DNA conformation modeled with Slide = 0 at this step is shown in orange; in this case, there is unacceptable steric hindrance between arginine and sugar ring of the DNA backbone. Note that the arginine NH₂ group is close to the line connecting O4′(#16′) and O4′(#19) atoms (red balls). That is, arginine 77 ‘bridges’ deoxyribose oxygens located at the 3′-ends of tetramer 16-19 (marked by green ribbon in the sequence strand). The line between O4′(#16′) and O4′(#18), which is distant from the arginine NH₂ groups, corresponds to the line (i′, i+2) in the complex with the 434 repressor (Figures 2A, C).

Note that a strong positive Slide is energetically costly for naked DNA, either alone or in combination with negative Roll (i.e., bending into the minor groove). The arginine protruding into the minor groove helps compensate this energy cost. Is this lateral displacement of DNA (Slide) a direct consequence of interactions with the arginine side chain or is it merely due to DNA folding in a tight superhelical loop? This question is directly addressed in Part II, where we show that Roll and Slide are strongly correlated for the YR sequences (especially for TA), so that the arginine may be considered as stabilizing the Kink-and-Slide conformation caused by DNA bending into the minor groove. For the RY sequences, however, correlation between Roll and Slide is less pronounced, and the arginine apparently plays a more active role, bringing about an additional lateral displacement in bent DNA.

Furthermore, arginines can act cooperatively to facilitate the axial displacement of DNA. The conformationally ‘rigid’ arginines described above are naturally grouped in pairs based on the structural architecture of the histone core. For example, arginines 42 and 77 in histone H2A are located in the L1 and L2 loops at the opposite ends of the H2A α2 helix (5,15,16); they interact with DNA at SHLs −3.5 and −5.5 (Figure 4). Arginine 77 is ‘pushing’ the gray strand of DNA at SHL −5.5 in the ‘North-West’ direction; at the same time, arginine 42 is ‘pulling’ the same DNA strand at SHL −3.5 in the same direction (see the white arrows in Figure 4B). We hypothesize that these two actions are coupled together in the ‘pushing-and-pulling’ effort applied to the same non-sequence DNA strand, leading to the strong axial dislocations of DNA visible in Figure 4A. Due to the dyad symmetry of a nucleosome, the minor-groove arginines in the second (posterior) half of the core particle have the same effect on the sequence strand of DNA (yellow arrows in Figure 4A).

Figure 4.

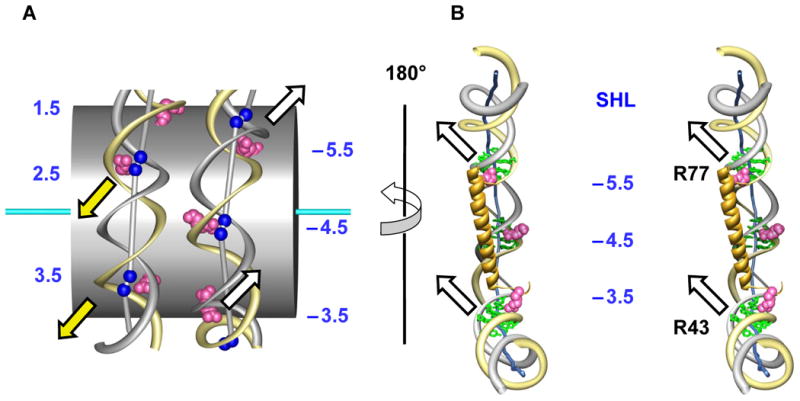
Histone arginines facilitate the axial dislocation of DNA in the nucleosome.

A. ‘Outside’ view. The zig-zag trajectory of DNA (yellow and gray ribbons) around the histone core (gray cylinder). For clarity, only arginines at SHLs −5.5, −4.5, −3.5 and 1.5, 2.5 and 3.5 are shown (magenta balls). The centers of base pairs corresponding to dimeric steps with Kink-and-Slide deformations are shown as blue balls. These balls are linked by sticks to emphasize the zig-zag trajectory of the DNA axis. The arrows indicate directions of the base pair movements facilitated by arginines: white arrows for the ‘anterior’ half and yellow arrows for the ‘posterior’ half of the nucleosome.

B. Stereo ‘inside’ view of the nucleosomal DNA fragment. Arginines 77 and 42 at the ends of H2A α2 helix, interacting with the non-sequence DNA strand (gray ribbon), produce a cooperative effect leading to the lateral Slide displacements and the Roll angles (white arrows at SHLs −5.5 and −3.5).

A similar cooperative effect is likely to occur at SHLs −2.5 and −0.5 (Figure 1A). Here, the two ‘rigid’ arginines 83 and 45 reside in the L1 loops at the termini of α2 helices in H3 and H4, respectively, which are tightly held together by a ‘hand-shake’ interaction (9,16).

Relationship between the minor groove width, kinks and arginine positions

Traditionally, the minor groove width has been measured either by calculating splines through the DNA backbone (23) or by using the cross-strand inter-phosphate distances (24). However, since our aim was to describe the positions of histone arginines ‘intercalating’ between the deoxyriboses, for the purposes of this analysis we defined the minor groove width as a minimal cross-strand O4′-O4′ distance. As follows from Figure 2, this measurement is different for the canonical B-DNA and nucleosomal DNA. In B-DNA, the closest opposite oxygens are O4′(i′) and O4′(i+2), but in nucleosomal DNA the two closest oxygens are O4′(i′) and O4′(i+3) (see Figures 2C and D). We found that the minimal O4′(i′)-O4′(i+3) distances (at the half-integer SHLs) are generally shorter than the O4′(i′)-O4′(i+2) distances, especially in the central 40 bp fragment of nucleosomal DNA in the 1KX5 structure (data not shown).

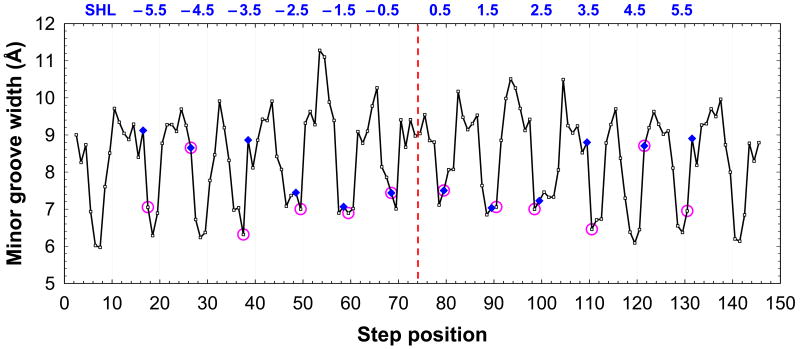
Next, we analyzed the relationship between the minor groove width, kinks and the arginine positions (Figure 5). As mentioned above, twelve arginines penetrate into the narrow minor groove of nucleosomal DNA (Figure 1), close to the Kink-and-Slide distortions in DNA (Figure 3). The positions of these arginines (assigned according to our definition, see legend to Figure 5) coincide with the positions of kinks in four cases out of twelve (SHLs ±0.5 and ±4.5); in the other eight cases, the two positions are shifted from each other by 1 bp (Figure 5).

Figure 5.

Minor groove width, kinks and arginine positions in nucleosome 1KX5 (5). The minor groove width is measured as the distance between the O4′ atoms in nucleotides (i′) and (i+3), see Figure 2D; this value is assigned to the midpoint position (i+1.5). The arginine positions (pink circles) are defined as follows. For each arginine, the O4′ atom is selected, which is the closest to its guanidinium NH₂ groups. The opposite O4′ atom is selected from the complementary DNA strand, according to the ‘i+3’ rule described above. Then, the arginine is assigned to the center of the tetramer (i, i+3), that is, to the position (i+1.5). For example, for arginine 77 of H2A in Figure 3, the closest oxygen is O4′(#16′) and the opposite one is O4′(#19); therefore, the arginine position is defined as 17.5. The dimeric steps with Kink-and-Slide distortions are shown as blue diamonds; their positions are also half-integer, in particular, the kink between base pairs #16 and #17 is assigned to position 16.5 (Figure 3). The SHL sites are shown at the top; see Table I for the description of arginines interacting with the minor groove at each SHL site.

In ten cases, the positions of arginines closely correspond to the narrowest minor groove (with the O4′-O4′ distance of 6.5 - 7.5 Å), and only two arginines located at SHLs ±4.5 are placed in the positions with relatively wide grooves ∼9 Å (Figure 5). Overall, our data provide a strong support to the observation made by Honig and coauthors (17,19) that arginines bind mostly in narrow regions of the DNA minor groove. The main difference between our approach and that used earlier (17,19) is that we assign the histone arginine position and the groove width to a base-pair step, i.e., to the center of the (i, i+3) tetramer (Figures 2B, D and 3), while Honig and coauthors (17,19) assigned the arginine position to a base pair (as in Figures 2A and C). In our opinion, the assignment of arginines to base-pair steps (used here) is more advantageous, because it describes more accurately the positions of arginines relative to the nucleosomal DNA. Note also that with such assignments, a larger fraction of the twelve ‘built-in’ arginines corresponds to the local minima of the minor groove width, compared to the assignments used by Rohs et al. (17).

We wish to emphasize that the asymmetric positioning of the histone arginines in the minor groove is favorable electrostatically, especially at sites with strong Kink-and-Slide distortions (SHLs ±5.5, ±4.5 and ±3.5). We compared the electrostatic interaction energies between the probe Na⁺ ion and nucleosomal DNA, using various locations of the probe and assuming that the dielectric constant is distance-dependent (ε = r). This treatment mimics computations of the electrostatic interactions between arginine and DNA (17,19). The probe ion was placed inside the minor groove in two different ways. First, it was placed at the geometric midpoints between the two opposite O4′ atoms. Alternatively, the probe positions coincided with the ‘real’ positions of the guanidinium NH₂ groups. In the latter case, the electrostatic interaction between the probe and DNA was more favorable than for the idealized midpoint positions, the difference being as high as 2-3 kcal/mol. (This result is qualitatively obvious because positioning a cation at the geometric midpoint between two negatively charged oxygens creates an unstable equilibrium. A shift toward one of the oxygens is more favorable than staying at the midpoint.)

Thus, we conclude that the asymmetric arrangement of arginines in the minor groove at the half-integer SHLs of nucleosomal DNA is favorable both locally and globally. Locally, it is advantageous in terms of electrostatic interactions between the positively charged arginines and the negatively charged DNA backbone. Globally, this asymmetry is critical for stabilization of the zig-zag DNA trajectory shown in Figures 3 and 4.

Finally, we suggest a simple mechanistic interpretation of the arginine-DNA interactions, details of which were described above. The nucleosomal DNA wrapped around the histone octamer (Figure 1A) is analogous to a bicycle chain coiled around a sprocket. The bicycle chain is held in place by the teeth of the sprocket meshing with the holes in the links of the chain. In a nucleosome, the role of the teeth is played by the arginine side chains penetrating into the DNA minor grooves. According to this ‘sprocket’ model, in order to have a strong induced fit, the nucleosomal DNA is forced to follow the zig-zag trajectory predetermined by the positions of arginines on the surface of the histone octamer core, Figure 4A.

Part II. Sequence dependence of Kink-and Slide deformations: All-atom energy calculations of DNA hexamers

Computational Methods

The DNA structures and their conformational energies were calculated with DNAminiCarlo (25). This program uses the base-pair and dimeric step parameters (26) as independent degrees of freedom, which significantly increases the efficiency of energy minimization (and Monte Carlo simulations). The rotational and translational parameters used in DNAminiCarlo were first introduced by us (8,27) and later described in more detail by Calladine (28), Hunter (29) and Olson (30) and colleagues. The force field developed earlier (31) was used for calculation of the internal energy of DNA. The solvent damping of electrostatic interactions $E_{\text{ele}}=332\frac{q_i\cdot q_j}{\varepsilon \cdot r_{\mathit{\text{ij}}}}$ (in kcal/mol) was modeled with a simple distance-dependent dielectric function (ε = r_ij, where r_ij is the distance (in Å) between two interacting point changes q_i and q_j.). It is computationally effective way to qualitatively treat screening effects in biological macromolecules and is widely used in molecular modeling when the solvent molecules are not explicitly considered (32). The total phosphate charges were reduced to −0.25 e, which corresponds to 75% neutralization of phosphates according to the condensation theory (33).

Calculations have been carried out for six base-pair DNA fragments, with the Roll and Slide in the central step S3 (Figure 6) serving as ‘principal’ variables when computing bending profiles of energy (Figure 7) and two-dimensional energy contour plots (Figure 8). For each sequence, the first and last step (S1 and S5) parameters were fixed at the average values of the step parameters among all 146 steps in the nucleosomal DNA in PDB 1KX5 (5); see Figure 6. Propeller twists of the terminal base pairs (#1 and #6) were fixed at −5° and the corresponding Buckle angles were fixed at 3.0° and −3.0° for the RY and YR base pairs, respectively (34). Also, in the terminal base pairs, the pseudo-rotation angle of a sugar ring and the glycosidic angle χ[C2′-C1′-N-C4/C2] were fixed at 155 and 140°, respectively, for purines, and at 145 and 135°, respectively, for pyrimidines. All Opening, Sx, Sy and Sz base-pair parameters were fixed at zero values, as well as Tilt and Dx parameters of the steps S1, S3 and S5.

Figure 6.

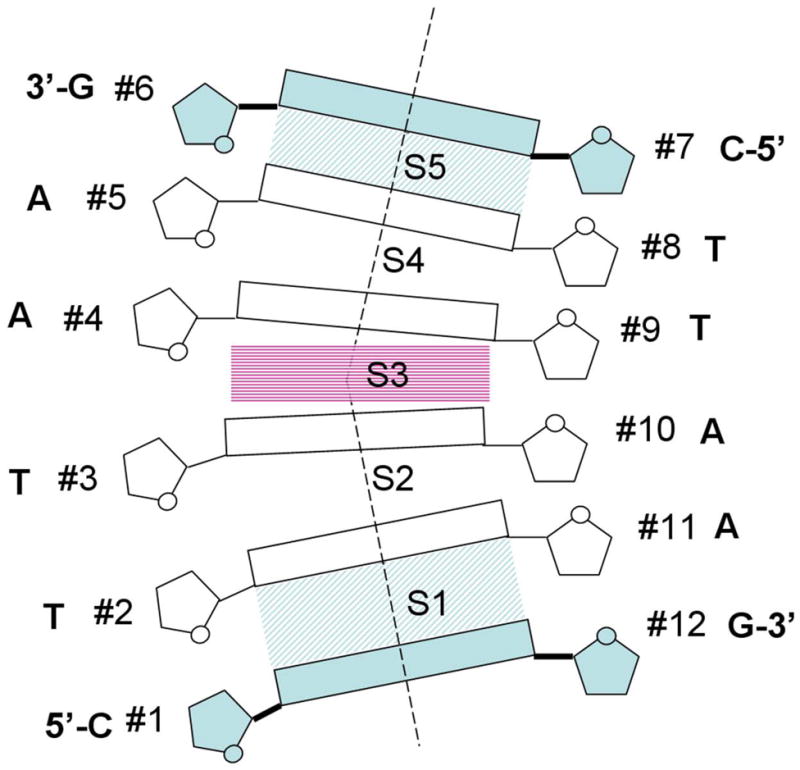
Schematic representation of hexamers calculated in this study. Roll and Slide in the central step S3 served as ‘principal’ variables during minimization. The dimeric step parameters in the terminal steps S1 and S5, as well as Propeller twist and Buckle in the terminal base pairs (#1):(#12) and (#6):(#7) were fixed – see Methods for details.

Figure 7.

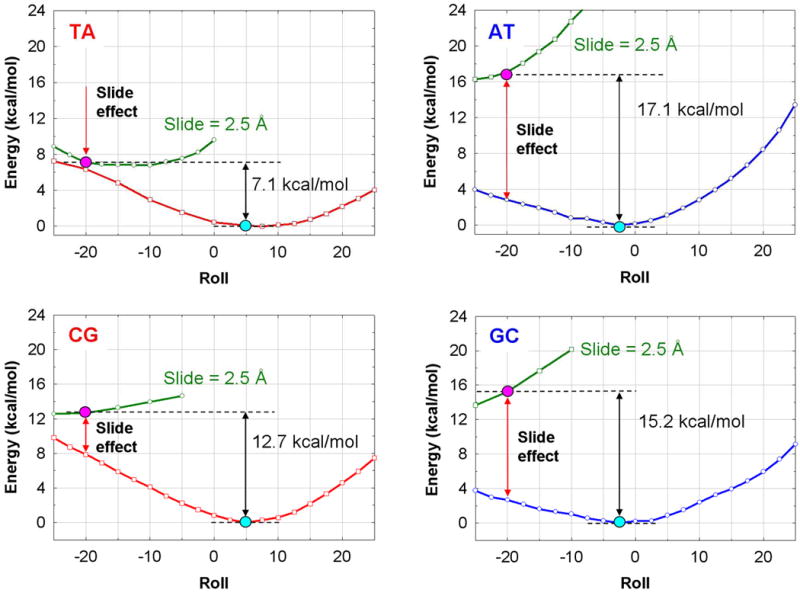
Bending profiles of energy versus Roll angle for hexamers with the YR (TA and CG) and RY (AT and GC) central steps (see Methods for the hexamer sequences). Red and blue lines: the YR and RY deformation energies versus Roll without the Slide constraint. The energetically optimal structures are shown by blue dots. Green lines: the energy profiles for Roll scan with the Slide constraint of 2.5 Å. The Kink-and-Slide deformed structures with Roll = −20° and Slide = 2.5 Å are shown by red dots.

Figure 8.

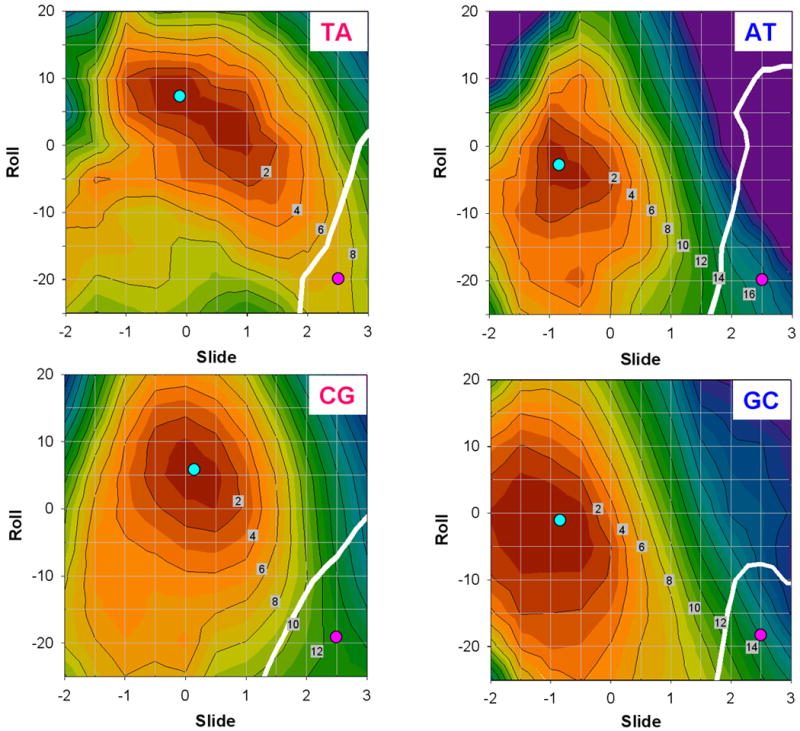
Two-dimensional (Roll versus Slide) energy contour plots for hexamers with the YR and RY central steps. The hexamer sequences are the same as in Figure 7. The contour line separation is 2 kcal/mol. Cyan circles: the optimal structures. Pink circles: the Kink-and-Slide deformed structures. White thick lines: the boundary between BI and BII forms, i.e. structures with equal backbone dihedral angles ε and ζ.

These constraints make the boundary geometries of the calculated hexamers close to the experimentally observed hexamers with the Kink-and-Slide distortion at the central step (5). In addition, this approach reduces the number of internal variables for energy minimization and significantly reduces the computational effort required.

We are mostly interested in comparing the bending preferences of the YR and RY dimers. Therefore, we used for computations various YYYRRR and RRRYYY hexamers, with the YR and RY dimeric steps in the center. The following six hexamers were analyzed in detail: CTTAAG, GAATTC, CTCGAG, GAGCTC, CTCAAG, GAACTC. Note that all possible YR and RY steps are embedded in the center of the hexamers (underlined). Results for the first four of these hexamers are presented in Figures 7 and 8. To investigate the effect of flanking sequences, we analyzed six additional hexamers: CCTAGG, GGATCC, CCCGGG, GGGCCC, CCCAGG, GGACCC. The results are presented in Table II.

Table II.

Comparison of all-atom and elastic energies (in kcal/mol)

All-atom energy*				Elastic energy**
CTTAAG	7.1	CCTAGG	7.0	TA	5.5	(5.9)
GAATTC	17.1	GGATCC	16.7	AT	34.7	(36.9)
CTCGAG	12.7	CCCGGG	12.5	CG	9.4	(12.5)
GAGCTC	15.2	GGGCCC	15.0	GC	8.7	(9.5)
CTCAAG	10.3	CCCAAA	10.5	CA	4.7	(7.8)
GAACTC	15.9	AAACCC	15.2	AC	21.9	(24.5)

^*Increase in energy of the shown hexamers required to form the Kink-and-Slide conformation in the central step: Roll = − 20°, Slide = 2.5 Å.

^**Dimeric deformation energies calculated by Tolstorukov et al. (5) were averaged over the six Kink-and-Slide steps at positions ±58 (SHLs ±5.5), ±48 (SHLs ±4.5) and ±36 (SHLs ±3.5) in the nucleosomal structure 1KX5 (4). In parentheses: Deformation elastic energies for Roll = − 20°, Slide = 2.5 Å and Twist = 42.8° calculated using knowledge-based scoring functions described by Olson et al. (34). (Twist = 42.8° is the average value for the six calculated Kink-and-Slide conformations – see the hexamers shown in the left column.) The elastic energy values were obtained by multiplying a unitless statistical score (6, 34) by a factor 0.6 (RT = 0.6 kcal/mol for the room temperature).

Sequence dependence of Kink-and-Slide deformations

Since the lateral displacement Slide plays such an important role in adjusting the nucleosomal DNA trajectory to the histone arginines, we investigated the impact of Slide on the sequence dependence of DNA bending. To this aim, we first calculated the energy profiles versus Roll angle without any constraints, and then compared the results with those obtained when the Slide constraint was imposed on the DNA conformation.

In Figure 7, the energy profiles versus Roll angle are presented for the dimeric steps YR and RY (TA, AT, CG and GC) embedded in the center of hexamers CTYRAG and GARYTC. The YR dimers (TA and CG) are energetically more favorable for bending into the major groove while the RY steps (AT and GC) favor the minor groove bend (see red and blue lines in Figure 7). These results are consistent with our earlier computations (27) and numerous crystallographic observations (9,34). Conformational preferences for the YR and RY steps can be explained by the ‘Calladine rules’ (35), that is, the major groove bending relieves the purine-purine clashes in the minor groove of YR, whereas the minor groove bending diminishes unfavorable clashes in the major groove of RY.

These sequence-dependent preferences change to the opposite, however, when Slide is fixed at 2.5 Å as in the nucleosomal Kink-and-Slide dimeric steps. Namely, the YR steps become more favorable than the RY steps for the minor groove-directed bending (see green curves in Figure 7). The deformation energy is the lowest for the TA dimer, and the highest for the AT dimer, the energy difference between them being about 10 kcal/mol (Table II). A similar but less pronounced effect is observed for the CG and GC steps – in this case, the energy difference is 2.5 kcal/mol.

It is evident that the observed ‘Slide effect’ is strongly unfavorable for the purine-pyrimidine dimeric steps, RY. How can one understand this sequence dependence at the atomic level? Since this effect involves both Roll and Slide parameters, it cannot be easily explained by the ‘Calladine rules’ (35) which imply that the Twist, Roll and other parameters are changing independently. Therefore, we investigated the conformational preferences of the YR and RY steps in the two-dimensional (Roll and Slide) conformational space.

Deformation energy maps for the YR and RY dimeric steps are shown in Figure 8. Note that for the TA step, the long principal axis of the equipotential contours is inclined more than for the other steps. In other words, Roll has a strong negative correlation with Slide, which is consistent with our earlier result obtained for the TTAA tetramer (27). This means that the two structural parameters are linked together in such a way that an increase in Slide leads to a decrease in Roll (and the other way around). When Roll changes from its optimal value to −20°, Slide simultaneously increases to 2.0 Å. Therefore, the transition path between the optimal structure (cyan circle) and the Kink-and-Slide deformation with Roll = −20° and Slide = 2.5 Å (pink circle), closely follows the direction of the long principal axis (see TA plot in Figure 8). Accordingly, the energy cost of this conformational transition is relatively low. A similar trend was observed for the CA:TG dimeric step (data not shown.)

On the other hand, there is practically no correlation between Roll and Slide for the AT step, and Slide does not change much when Roll changes from −20° to 20°. The transition path between the optimal state and the Kink-and-Slide structure is far from the direction of the long principal axis; see the AT plot in Figure 8. In addition, Slide is −1.0 Å in the optimal structure of AT. As a consequence, the deformation energy is ∼10 kcal/mol for the AT step when Slide changes from −1.0 to 1.0 Å, and this energy cost significantly increases further when Slide becomes larger than 2.0 Å.

The CG and GC dimeric steps are intermediate between the TA and AT steps in terms of the Roll-Slide relationship (Figure 8). In the Roll interval between −10° and 10°, both CG and GC are characterized by a modest negative correlation between Roll and Slide, but for CG this correlation becomes positive when Roll is less than −10°. As for the GC step, its optimal structure has Slide about −1.0 Å (which is far from the target value of 2.5 Å). Therefore, these two dimers require more deformation energy to form the Kink-and-Slide structure than does the TA dimer (Table II).

Stereochemical interpretation

A simple stereochemical interpretation of the obtained results is presented in Figure 9. In the absence of any constraints, the sequence-dependent DNA bending preferences follow the ‘Calladine rules’ (35). Namely, the pyrimidine-purine dimeric steps, YR, prefer bending into the major groove (Roll > 0), because this bend relieves the purine-purine clashes in the minor groove of YR. If, however, the positive Slide ≥ 2.0 Å is imposed on the conformation of the YR step, the purine-purine clash becomes less severe, but instead, the two pyrimidines strongly overlap in the major groove (Figure 9B). As a consequence, the YR bending into the minor groove (Roll < 0) becomes relatively ‘inexpensive’ energetically (Figure 7 and Table II). Furthermore, our scheme explains why the CG step is the least favorable for the minor groove bending among the YR dimers (Table II). As follows from Figures 9A and B, the NH₂ groups of two guanines in the CG dimer are in direct contact in the minor groove. This contact, although weakened by a positive Slide, still remains unfavorable. A similar contact between two adenines, or between adenine and guanine, is less unfavorable; therefore, the minor-groove bending is less ‘expensive’ for the TA and CA:TG steps than for the CG step.

Figure 9.

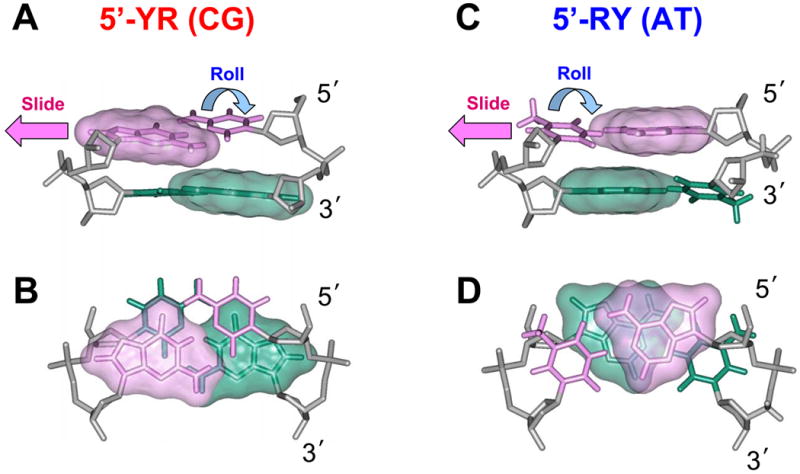
The Kink-and-Slide deformation is more favorable for the YR dimeric steps than for the RY steps. The Kink-and-Slide structures of the CG (A, B) and AT dimers (C, D) are shown. Note that in the CG dimers, the purine-purine repulsion (overlap between the pink and green surfaces) is relatively weak compared to that in AT.

In contrast, the unrestrained purine-pyrimidine dimers, RY, prefer bending into the minor groove, thereby relieving the purine-purine repulsion in the major groove (35). Again, the situation changes drastically if the positive Slide is imposed by interactions with the histone arginines (Figure 3). In this case, the two purines move so close to each other that they overlap not only in the major groove, but also in the minor groove (Figure 9D). Hence, the minor groove bending becomes extremely ‘expensive’ energetically (nearly prohibitive) for the RY dimers (Figure 8).

Nonharmonic behavior of nucleosomal DNA. BI to BII transition

In general, our Roll-Slide equipotential contours are consistent with those derived from the knowledge-based elastic energy functions (34), especially in the vicinity of the energy minima. However, when Slide is larger than 2 Å, the equipotential curves in our maps show nonharmonic behavior (Figure 8). This may be related to the BI to BII transition in the DNA backbone occurring in the highly deformed steps – note the white lines marking the boundaries between the BI and BII ‘areas’. The phosphate backbone of the Kink-and-Slide deformed step in each calculated hexamer is in BII form. It is consistent with the fact that all six strongly deformed dimeric steps (SHLs ±5.5, ±4.5 and ±3.5) in nucleosome 1KX5 adopt BII conformation in both strands (5). Note that overall, our calculated Kink-and-Slide structures are close to those observed in the nucleosome, see Figure 10.

Figure 10.

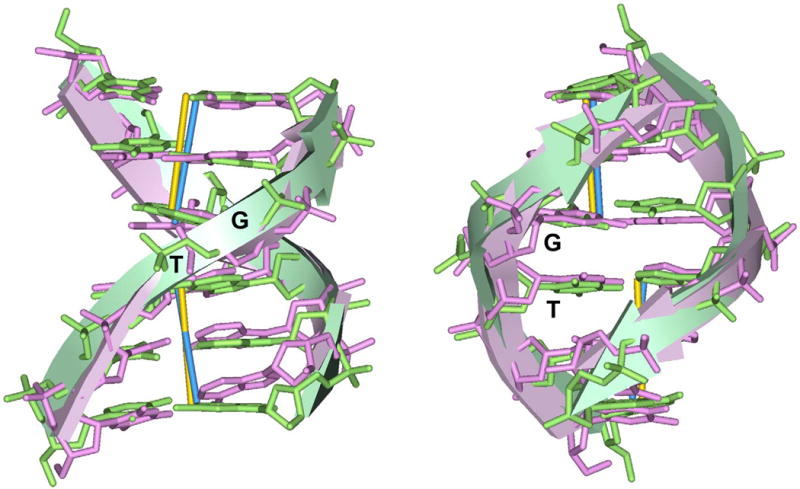
Comparison of the hexamer at SHL −3.5 in 1KX5 (Roll = −18° and Slide = 2.7 Å) and the calculated structure with the Kink-and-Slide deformation (Roll = −20° and Slide = 2.5 Å), aligned together through the base-pair centers. In both hexamers, the central dimer is TG:CA. The hexamer at SHL −3.5 in the X-ray structure (5) is shown in pink stick rendering, and the calculated structure is shown in green sticks. The RMSD of six base pair centers is 0.71 Å.

These results entirely agree with the earlier observations that the BII conformation of the sugar-phosphate backbone occurs more frequently in the dimeric steps with strong negative Roll and positive Slide (36-39). It is also known that the YR steps are more prone to stabilization of the BII conformation. This may be an additional stereochemical factor facilitating the Kink-and-Slide deformation in the YR steps.

All-atom computations and elastic deformation energies

It is interesting to compare the all-atom deformation energies for six dimeric steps obtained here, with the elastic energies calculated by Tolstorukov et al. (6); see Table II. Both methods predict that the Kink-and-Slide distortion is the most favorable for the TA and CA:TG dimeric steps, and the least favorable for the AT and AC:GT steps. The CG and GC steps are intermediate in this regard. There are two notable differences between these sets of data. First, our results indicate that the most easily deformed dimeric step is TA, followed by CA:TG, whereas the data presented by Tolstorukov et al. (6) suggested the reverse order, CA < TA. Note, however, that in the latter case, the deformation energies were averaged over the six Kink-and-Slide steps in the nucleosomal structure 1KX5 (5). Our results correspond to the idealized conformation with Roll = −20° and Slide = 2.5 Å. If we use these Roll and Slide values and calculate the elastic energies as described by Olson et al. (34), we will obtain the same result, TA < CA (Table II). Recently, Balasubramanian et al. (40) used an updated version of the elastic energy functions (based on an extended set of x-ray structures) and also found that the TA step is the most flexible.

Second, the elastic functions predict a sharp increase in the deformation energy for the AT and AC:GT steps (compared to the other dimers), while the all-atom computations suggest that the deformation energy values for all dimeric steps form a tight cluster. In our opinion, this difference is related to the nonharmonic behavior of the all-atom deformation energy. See, for example, Figure 8, where the Kink-and-Slide energy of the AT step is ∼17 kcal/mol, which is much less than ∼35 kcal/mol estimated by harmonic elastic energy functions (Table II).

The role of flanking sequences

To investigate how the Kink-and-Slide deformation energy depends on the flanking sequences, we used two extreme ways of changing these sequences. First, we changed the sequences for the hexamers but kept the YYYRRR and RRRYYY patterns unchanged. Second, we changed the YYYRRR sequence patterns to RRYRYY.

We expected that the energy difference would be small if we followed the same pyrimidine-purine patterns and only made minimal sequence changes. (For example, CTTAAG is changed to CCTAGG for the central step TA and GAATTC is changed to GGATCC for AT.) Indeed, when the YYYRRR and RRRYYY patterns are kept intact, the deformation energy of a hexamer is essentially defined by the central dimer and does not depend on the flanking sequences (Table II). The largest energy difference between the two sets of sequences is less than 0.4 kcal/mol. The order of the deformation energies remains the same: TA < CA < CG < GC < AC < AT. Remarkably, all the YR steps are more favorable than the RY steps for the Kink-and-Slide deformation.

However, when the YYYRRR pattern was changed to RRYRYY, substantial changes in the deformation energy were observed for the TA and CG steps. For example, when the hexamer CTTAAG was substituted by GATATC, the deformation energy cost increased by ∼5 kcal/mol (data not shown). In the case of CG, when the sequence was changed from CTCGAG to GGCGCC, the deformation energy increased by 1.4 kcal/mol. Our preliminary analysis indicates that the Buckle parameter (whose behavior differs for the YYRR and RYRY sequences) may play a role in such an effect. We are currently investigating the influence of flanking sequences for other central dimers.

Our results on deformability of the TA step are generally consistent with the results of MD simulations (13) suggesting that TA is more flexible in the context of TTAA compared to ATAT. But for the CG step, the MD simulations indicate that it is more flexible in GCGC than in TCGA and CCGG. This is in contrast to our results. One should be cautious, however, when comparing these two results because we analyzed conformational behavior of the DNA hexamers far from their energy minima. On the other hand, ensembles of DNA conformations obtained in the course of MD simulations (13,14) reflect fluctuations around the equilibrium structures. Accordingly, the harmonic energy functions deduced from the MD ensemble are hardly suitable for analysis of the DNA deformability in the nonharmonic areas of the Kink-and-Slide distortions.

Dependence of the TA and CG deformability on the flanking sequences may be directly related to the mechanism of nucleosome positioning. If the results presented above (on the difference between the YYRR and RYRY motifs) are confirmed for the other sequences containing the YR steps, it will be a strong argument in favor of the idea that the strongest minor-groove bending motifs are the TA and CA:TG dimers in the context YYRR. The early experimental evidence supporting this idea was obtained by Dickerson and coworkers (41) who showed that the YCAR motif is bent into the minor groove. Recently, this notion was supported by bioinformatics data. Namely, as shown in the accompanying paper by Cui and Zhurkin (42), the accuracy of prediction of the nucleosome positioning in vitro increases significantly, if the YR steps in the context YYRR (positioned in the minor-groove bending sites) are assigned a higher weight compared to RYRY. We anticipate that future investigations will show more exciting examples of how the local DNA deformability (including the Kink-and-Slide distortions) is defined by long-range interactions in the duplex.

Conclusion

Several conclusions can be drawn from the first part of our study. (i) We have demonstrated that the spatial arrangement of the histone arginines in the minor-groove of nucleosomal DNA is similar to the teeth of a sprocket meshing with the holes in the links of a chain. The zig-zag superhelical trajectory of nucleosomal DNA is determined by the positions of arginines residing on the histone core surface. (ii) We observed that the conformationally ‘rigid’ arginines in the minor groove at SHLs ±0.5, ±2.5, ±3.5 and ±5.5 are located in the helix-loop-helix motifs of histones. They are likely to hinder the histone core repositioning along DNA. Experimentally, this notion is partially confirmed by the effects of SIN and lrs mutations at SHLs ±0.5 and ±2.5. (iii) Arginines are asymmetrically positioned in the minor groove of the nucleosomal DNA, i.e., they are closer to one strand. This asymmetric arrangement of arginines (stabilized by electrostatic interactions with DNA) facilitates local Kink-and-Slide deformations in nucleosomal DNA. (iv) Arginines (R77 and R42) at SHLs ±5.5 and ±3.5 are ‘attached’ to the opposite ends of the α2 helix in histone H2A; they are coupled together by ‘pushing-and-pulling’ the nucleosomal DNA, stabilizing a large axial dislocation in DNA.

From the second part of our work, we conclude that: (i) In free DNA, the YR dimers tend to bend into the major groove, while the RY dimers favor the minor groove bending. This confirms the results of our earlier calculations (27) and numerous crystallographic data (34). (ii) With the Kink-and-Slide constraint mimicking the DNA deformation in the nucleosome, the trend is reversed: the energy cost for YR bending into the minor groove is less than that for the RY bending. (iii) 2D energy maps indicate that TA is the most easily deformed dimeric step, readily adopting the Kink-and-Slide distortion. This agrees with the fact that the TA steps frequently occur in the minor groove kink positions in the most stable nucleosomes (11,12). In addition, the YR steps are more likely than the RY steps to have such distorted conformations. These results can be explained by the purine-purine clashes in the minor groove of the RY dimers in the Kink-and-Slide conformation. (iv) Comparison of the all-atom calculations and the elastic energy estimates indicates that the deformation energy of the RY steps is probably overestimated by the elastic functions, because the Kink-and-Slide conformations are in the nonharmonic regions of the 2D energy surfaces.

Our findings should be useful for refining the knowledge-based score functions for the prediction of nucleosome positioning (6,40,42). In addition, the reverse bending behavior of the YR and RY steps revealed under the Kink-and-Slide constraint may help understanding the molecular mechanisms of binding transcription factors to DNA exposed on the surface of the histone octamer (43-47). Consider, for example, the tumor suppressor protein p53 that strongly binds to nucleosomal DNA as a tetramer (48,49). The consensus p53 binding site contains YYYRRR in the center (50). Our earlier computations (51) suggested that when p53 tetramer binds to the 20-bp long cognate site, the DNA is severely distorted in the center of the site – it undergoes bending into the minor groove and the lateral displacement (Slide ∼2 Å). It was unclear, however, how to reconcile this kind of distortion with the known tendency of the YR dimeric steps to bend into the major groove (see Introduction).

Our new results apparently solve this problem. As shown above, the YYYRRR motif is optimal for bending into the minor-groove with concomitant positive Slide, as it happens in nucleosome. This means that the DNA distortions which are energetically costly for free DNA are stabilized by interactions with the histone arginines. In other words, the nucleosomal DNA is pre-deformed in a conformation optimal for the p53 binding, and this accounts for a high affinity of p53 to DNA wrapped in nucleosome (49) or in chromatin fibril (48). In general, our findings suggest an intriguing possibility that the Kink-and-Slide distortions of DNA in nucleosome provide additional conformational possibilities compared to free DNA, thus expanding the repertoire of the DNA binding sites selectively recognized by proteins.