Multilevel Latent Class Models with Dirichlet Mixing Distribution

Summary

Latent class analysis (LCA) and latent class regression (LCR) are widely used for modeling multivariate categorical outcomes in social science and biomedical studies. Standard analyses assume data of different respondents to be mutually independent, excluding application of the methods to familial and other designs in which participants are clustered. In this paper, we consider multilevel latent class models, in which subpopulation mixing probabilities are treated as random effects that vary among clusters according to a common Dirichlet distribution. We apply the Expectation-Maximization (EM) algorithm for model fitting by maximum likelihood (ML). This approach works well, but is computationally intensive when either the number of classes or the cluster size is large. We propose a maximum pairwise likelihood (MPL) approach via a modified EM algorithm for this case. We also show that a simple latent class analysis, combined with robust standard errors, provides another consistent, robust, but less efficient inferential procedure. Simulation studies suggest that the three methods work well in finite samples, and that the MPL estimates often enjoy comparable precision as the ML estimates. We apply our methods to the analysis of comorbid symptoms in the Obsessive Compulsive Disorder study. Our models' random effects structure has more straightforward interpretation than those of competing methods, thus should usefully augment tools available for latent class analysis of multilevel data.

1. Introduction

Latent class analysis (LCA; Clogg, 1995) and regression (LCR; Bandeen-Roche et al., 1997) are widely used in psychosocial, educational, and health research. These models treat a population of interest as being composed of several subpopulations, 1,…, M, to which subjects belong with probabilities π₁, …, π_M. They also assume that responses of different subjects are independent of each other. However, this independence assumption may not be valid for commonly employed designs: for instance, in family studies, relatives may be more likely to fall into the same subpopulation, or ‘class,’ than members of different families. Application of the models to studies involving clustered participants has been limited as a result.

In standard latent class models, the mixing probabilities π = (π₁, π₂, …, π_M) are considered as fixed parameters. Allowing these to vary among clusters provides one mechanism for introducing intra-cluster dependence, if clustering may reasonably be thought to induce exchangeable association. Vermunt (2003, 2008) proposed multilevel latent class (MLC) models with cluster specific class mixing probabilities ṵ_i = (u_i1, …, u_iM) as random effects for cluster i. A first model proposed (henceforth denoted as “MLC-V1”) assumes that ṵ_i vary according to a normal random effect v_i,

$$\{\begin{array}{l}log\frac{u_{im}}{u_{i1}}={\gamma }_m+{\lambda }_m{v}_i,m=2,\cdots ,M,\\ v_i\sim N(0,{\sigma }^2),\end{array}$$ (1)

where γ_m, λ_m and σ² are unknown parameters and one typically assumes λ₂ = 1 for identifiability. Maximum likelihood estimation for this model involves numerical integration over v_i, and the unidimensionality of v_i makes the approach computationally convenient. However, the random effects have a latent factor interpretation that is contingent on ‘loadings’ λ and may therefore be somewhat obscure. Moreover, the model (1) forces restrictions on the joint distribution of the random effects that may not be realistic (Web Appendix A). Vermunt (2003) also introduced a more flexible model with vector v̰_i that assumes that the (M − 1) generalized logits follow a multivariate normal distribution (denoted as “MLC-V2”), i.e.,

$$\{\begin{array}{l}log\frac{u_{im}}{u_{iM}}={\gamma }_m+v_{im},m=2,\cdots ,M-1,\\ {\underset{\sim }{v}}_i=(v_{i2},\cdots ,v_{i(M-1)})\sim \mathit{\text{MVN}}(\mathbf{0},\mathbf{\sum }),\end{array}$$ (2)

where the γ_m's and Σ ∈ R^{(M−1)×(M−1)} are unknown parameters; however, the computational burden of this model grows exponentially with M. Alternatively, a “nonparametric” MLC model (henceforth denoted as “MLC-VN”) assumes the existence of higher level latent classes such that there are S hidden types of clusters with prevalences (τ₁, ⋯, τ_S) and

$${\underset{\sim }{u}}_i=({\psi }_{s1},\cdots ,{\psi }_{sM}),\text{if cluster i belongs to type}s\in \{1,\cdots ,S\}.$$ (3)

Parameters τ_s and ψ_sm need to be estimated from the data. Vermunt (2003) noted that the MLC-VN model is nonparametric and flexible. However, model interpretation, identifiability, and selection are complicated by the additional level of latent classes, and these issues were not well understood.

This paper alternatively considers MLC models assuming Dirichlet distributed mixing probabilities ṵ_i (henceforth denoted as “MLC-D”). The Dirichlet distribution has implications for analytic interpretation; however, we believe its direct linking to the probability scale and freedom from loadings make it natural and interpretable relative to alternatives. The proposed model allows simple formulas for marginal class prevalences (MCPs) and intra-cluster correlations (ICCs), and is convenient to interpret. Moreover, as we shall demonstrate, conjugacy between the Dirichlet and multinomial distributions eases computation burden.

We were motivated to the present research by our collaboration in the Obsessive-Compulsive Disorder (OCD) study, a family-based study aiming to understand the comorbidity of OCD with other disorders. Obsessive-Compulsive Disorder is an anxiety disorder characterized by recurrent thoughts (obsessions) or repetitive behaviors (compulsions) which attempt to neutralize the obsessions (see, e.g, Jenike et al. 1990). A total of 999 subjects in 238 families were enrolled into this study, among which 706 subjects from 238 families were OCD cases. Diagnosis was made of 8 other disorders including major depression, generalized anxiety disorder, and panic disorder. It was hypothesized that there exist subtypes of OCD based on comorbidity with the other disorders (Nestadt et al., 2003). Latent class analysis is a natural tool for evaluating this hypothesis; however, the clustering within families must be taken into account if correct and efficient inference is to be made. It is also of interest to estimate the subtype heritability: in statistical terms, the intra-cluster correlation among class memberships.

This paper develops MLC models with Dirichlet mixing distribution in Section 2, proposes model fitting using both maximum likelihood in Section 3 and maximum pairwise likelihood methods in Section 4. We also investigate the use of simple latent class model by ignoring clustering in Section 5. We evaluate these methods' performance using simulation studies in Section 6 and an application to the OCD study in Section 7.

2. Multilevel Latent Class Models

2.1 MLC model with Dirichlet distribution (MLC-D)

Latent class models typically involve vector data per individual, comprising multiple categorical ‘item’ responses. Though these handle categorical responses in general, for simplicity of notation we primarily consider binary data. Let Y_ijk denote the response of the j^th subject of the i^th cluster on the k^th item; i = 1, 2, …, n; j = 1, 2, …, n_i; k = 1, 2, …, K. We denote the K-vector of a subject's responses by Y̰_ij. Let η_ij denote the class membership for subject j in cluster i, taking values in {1, 2, …, M}, and η̰_i = {η_i1, η_i2, …, η_ini}. Standard latent class models decompose the mass function of a subject's item responses as

$$\begin{array}{l}Pr({\underset{\sim }{Y}}_{ij}=\underset{\sim }{y})=\sum _{m=1}^{M}Pr({\eta }_{ij}=m)Pr({\underset{\sim }{Y}}_{ij}=\underset{\sim }{y}\mid {\eta }_{ij}=m)\\ =\sum _{m=1}^{M}Pr({\eta }_{ij}=m)\prod _{k=1}^{K}Pr(Y_{\mathit{\text{ijk}}}=y_k\mid {\eta }_{ij}=m)\\ =\sum _{m=1}^M{u}_{im}\prod _{k=1}^K{p}_{km}^{y_k}{(1-p_{km})}^{1-y_k},\end{array}$$ (4)

where u_im is the prevalence of class m in cluster i and p_km = Pr(Y_ijk = 1 ∣ η_ij = m) is the conditional probability of positive response for item k given the subject belongs to class m. These models often impose the “conditional independence” assumption (as revealed in the equations above) that a subject's responses on the items are independent given his class membership (Clogg, 1995). The conditional probabilities define the “measurement” part of the model. They are often parameterized in the logit scale via β_km = logit(p_km) = log{p_km/(1 − p_km)}. The distribution of M classes in the population defines the “mixing” part of the model, which involves (u_i1, ⋯, u_iM) ∈ {(u₁, ⋯, u_M) ∈ [0, 1]^M : u₁ + ⋯ + u_M = 1}.

A simple latent class model that ignores clustering (denoted as “LC-S”) assumes that the mixing distribution is the same for all clusters, namely,

$${\underset{\sim }{u}}_i=({\pi }_1,{\pi }_2,\cdots ,{\pi }_M),$$ (5)

where π_m's are fixed parameters that sum up to 1 and each π_m is interpreted as the prevalence of class m in the population.

To account for potential correlation among response vectors of subjects within the same cluster, MLC models view class mixing probabilities (u_i1, ⋯, u_iM) as random effects that vary from cluster to cluster, arising from a common distribution. Vermunt (2003, 2008) considered different versions of MLC models with random effects structure (1), (2) or (3). In this paper, we consider multilevel latent class models with Dirichlet mixing distribution (henceforth denoted “MLC-D”), formulated as (4) in addition to

$$\{\begin{array}{l}Pr({\eta }_{ij}=m\mid {\underset{\sim }{u}}_i)=u_{im}\\ {\underset{\sim }{u}}_i=(u_{i1},\dots ,u_{iM})\sim \text{Dirichlet}({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_M),\end{array}$$ (6)

where α̰ = (α₁, ⋯, α_M) are non-negative parameters for the Dirichlet distribution. For convenience, we model the conditional probabilities in the logit scale using β_km = logit(p_km) = log{p_km/(1 − p_km)}, and then the natural parameters in the model are θ = (β̰, α̰).

We consider there to be between-cluster heterogeneity in the probabilities of underlying class membership, and not additionally in the item response distribution given class membership. Clustering is accounted for in the sense that subjects from the same cluster are more likely to fall into same classes since they share the same cluster specific random effects. Modeling class membership probabilities as random effects straightforwardly expresses clusterwise heterogeneity: in the OCD example, probabilities of having each type of comorbidity may vary from family to family. The Dirichlet distribution is natural for random effects ṵ_i = (u_i1, ⋯, u_iM), since they are non-negative probabilities constrained to sum to 1. It also explicitly acknowledges classes as competing, such that membership in one class precludes membership in another. As the following Lemma shows, a few meaningful quantities have simple forms under the MLC-D model.

Lemma 1. Let ${\alpha }_0={\sum }_{m=1}^M{\alpha }_m$. Under the MLC-D model (4) and (6), the following results hold for any m, q ∈ {1, 2, ⋯, M} and m ≠ q,

1. $\text{E}(u_{im})=\frac{{\alpha }_m}{{\alpha }_0},var({\text{u}}_{\text{im}})=\frac{{\alpha }_{\text{m}}({\alpha }_0-{\alpha }_{\text{m}})}{{\alpha }_0^2({\alpha }_0+1)},cov({\text{u}}_{\text{im}},{\text{u}}_{\text{iq}})=-\frac{{\alpha }_{\text{m}}{\alpha }_{\text{q}}}{{\alpha }_0^2({\alpha }_0+1)};$

2. ${\pi }_m≔Pr({\eta }_{ij}=m)=\frac{{\alpha }_m}{{\alpha }_0},var\{\text{I}({\eta }_{\text{ij}}=\text{m})\}=\frac{{\alpha }_{\text{m}}\left({\alpha }_0-{\alpha }_{\text{m}}\right)}{{\alpha }_0^2};$

3. ${\rho }_{mm}≔\text{cor}\{\text{I}({\eta }_{\text{ij}}=\text{m}),\text{I}({\eta }_{\text{ik}}=\text{m})\}=\frac{1}{{\alpha }_0+1},{\rho }_{mq}≔\text{cor}\{\text{I}({\eta }_{\text{ij}}=\text{m}),\text{I}({\eta }_{\text{ik}}=\text{q})\}=-\frac{1}{{\alpha }_0+1}\cdot \sqrt{\frac{{\alpha }_{\text{m}}{\alpha }_{\text{q}}}{({\alpha }_0-{\alpha }_{\text{m}})({\alpha }_0-{\alpha }_{\text{q}})}}.$

Based on Lemma 1, in the population, the marginal class prevalences (MCPs) for M classes are (α₁/α₀, α₂/α₀, ⋯, α_M/α₀), respectively. The variance of the cluster-specific prevalences ṵ_i varies inversely with the scale parameter, α₀, such that the correlation in same-class membership between same-cluster members is

$${\rho }_{mm}=\text{Corr}\{\text{I}({\eta }_{ij}=m),I({\eta }_{ik}=m)\}=\frac{1}{{\alpha }_0+1},\text{for all}m\in \{1,\cdots ,M\}.$$

Here ρ_mm is the intra-cluster correlation (ICC) coefficient for class m, i.e, heritability in the family studies setting. The MLC-D model implicitly assumes that the ICCs for same-class membership are class-invariant, thus we denote it as ρ in the following. The Dirichlet random effects assumptions induce simple analytic formulas for calculating the MCPs and ICCs. Web Appendix A provides additional implications of the MLC-D model. In contrast, other multilevel latent class models such as MLC-V1 do not yield closed form formulas for MCPs and ICCs.

The measurement part of the MLC-D model is the same as that for the simple latent class model and other MLC models. The conditional independence assumption is retained, i.e, responses on different items are assumed to be independent given class membership. The possible clustering effect is reflected in the mixing part, that is, potential associations among the class membership indicators {η_ij : i = 1, 2, …, n; j = 1, …, n_i}. The Dirichlet random effects structure specifies the joint distribution of the class membership vector η̰_i = {η_i1, η_i2, …, η_ini} for cluster i as

$$Pr({\underset{\sim }{\eta }}_i=\underset{\sim }{z})=\int \prod _{j=1}^{n_i}Pr({\eta }_{ij}=z_j\mid {\underset{\sim }{u}}_i)f({\underset{\sim }{u}}_i)d{\underset{\sim }{u}}_i=\frac{\mathrm{\Gamma }({\alpha }_0)}{\mathrm{\Gamma }({\alpha }_0+n_i)}\prod _m\frac{\mathrm{\Gamma }({\alpha }_m+q_m^{(i)})}{\mathrm{\Gamma }({\alpha }_m)},$$

where $q_m^{(i)}={\sum }_{j}I(z_j=m)$, the number of subjects from cluster i that belong to class m. This nice analytic formula is due to the conjugacy between multinomial and Dirichlet distributions, and eases implementation and interpretation. In models (1)-(3), in contrast, Pr(η̰_i = z̰) does not have a closed form. Exchangeable within-cluster association is implied, meaning the sets of associations among class memberships for any two subjects from the same cluster are the same.

2.2 Random effects distributions: MLC-D versus MLC-V1

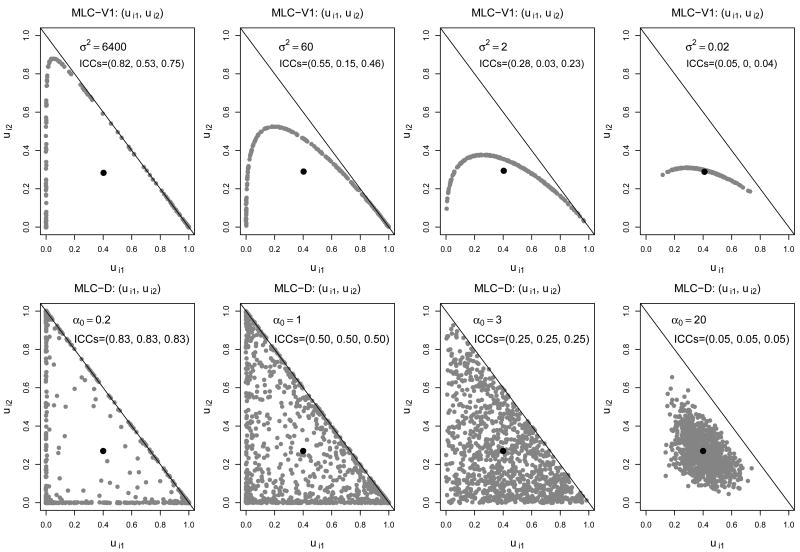
In this subsection, we briefly compare distributional assumptions of random effects ṵ_i based on the MLC-D and MLC-V1 models. For illustrative purposes, we consider three-class models. When M = 3, it suffices to consider the distribution of the pair (u_i1, u_i2), since u_i3 = 1 − u_i1 − u_i2 is fully determined by u_i1 and u_i2. Figure 1 displays joint distributions of (u_i1, u_i2) under both models, four scenarios per model. In each scenario, the parameters are chosen so that the marginal class prevalences are fixed as 0.40, 0.27 and 0.33 for three classes, respectively.

Figure 1.

Distributional assumptions of random effects (u_i1, u_i2) based on 3-class MLC-V1 and MLC-D models. The first and second rows correspond to MLC-V1 and MLC-D models, respectively. In each row, the four figures display four scenarios corresponding to high, medium, low and little ICCs. Each subfigure displays 200 randomly generated samples of (u_i1, u_i2) pairs.

Under the MLC-V1 model (1), the variance parameter σ² controls the degree of heterogeneity among clusters. When σ² = 0, ṵ_i is constant for all clusters and the model reduces to a simple latent class model without clustering. When σ² is large, the ṵ_i's differ considerably across clusters, indicating large heterogeneity and high ICCs. The first row of Figure 1 illustrates distributions of (u_i1, u_i2) under various σ² values, with four panels corresponding to high, medium, low and little ICCs, respectively. The parameter values of (σ², λ₃, γ₁, γ₂) are (6400, 1.704, 2.5, −0.3), (60, 1.704, 0.6, −0.3), (2, 1.704, 0, −0.3) and (0.02, 1.704, −0.3, −0.3) for four scenarios, respectively. They are chosen so that the four scenarios have the same marginal class prevalences (0.40, 0.27, 0.33), but different σ²'s and ICCs.

Under the MLC-D model (6), the scale parameter α₀ controls the degree of heterogeneity, similar to the role of 1/σ² for the MLC-V1 model. When α₀ is large, cluster specific random effects ṵ_i are close to each other and thus ICCs are close to 0, indicating little heterogeneity. In the limiting case with α₀ → ∞ and α_m/α₀ → π_m for m ∈ {1, ⋯, M}, the MLC-D model reduces to a simple latent class model without clustering. When α₀ is small, ṵ_i's vary substantially among clusters and the same-class ICCs are high, reflecting large between cluster heterogeneity. The second row of Figure 1 illustrates implications of various α₀ on the distribution of (u_i1, u_i2). In these four scenarios, (α₁/α₀, α₂/α₀, α₃/α₀) are fixed as (0.4, 0.27, 0.33) while α₀ varies among values 0.2, 1, 3 and 20.

We note that the natural domain of (u_i1, u_i2) is Ω_u = {(u₁, u₂) ∈ [0, 1]² : u₁ + u₂ ≤ 1}, which is intrinsically a two-dimensional subspace of [0, 1]². However, the MLC-V1 model only allows (u_i1, u_i2) to take values in a one-dimensional subspace for fixed parameters γ_m's and λ_m's (see Figure 1). In contrast, the MLC-D model allows (u_i1, u_i2) to take values freely in its domain Ω_u for any fixed parameters α_m's. From this perspective, the Dirichlet distributional assumption specified by the MLC-D model is more natural.

3. Estimation and Inference: Maximum Likelihood

3.1 Estimation: EM algorithm

The EM (Expectation-Maximization) algorithm (Dempster et al., 1977) well suits the incompletely observed nature of mixture models. Provided a set of regularity conditions (e.g, in Dempster et al 1977) which are met in our model, it is stable and ensures that the likelihood monotonely increases over iterations. For these reasons, we propose to use the EM algorithm for estimation.

For the multilevel latent class model (6), the complete likelihood contributed by cluster i is

$${\mathit{\text{L}}}_i^c(\beta ,\alpha )=Pr({\underset{\sim }{Y}}_i\mid {\underset{\sim }{\eta }}_i)Pr({\underset{\sim }{\eta }}_i\mid {\underset{\sim }{u}}_i)f({\underset{\sim }{u}}_i)=\prod _{j=1}^{n_i}\left[\prod _{k=1}^{K}Pr(Y_{\mathit{\text{ijk}}}\mid {\eta }_{ij})Pr({\eta }_{ij}\mid {\underset{\sim }{u}}_i)\right]f({\underset{\sim }{u}}_i).$$

For the E step, take the parameter estimates as β^(h), α^(h) at the h^th iteration. Then, we need to calculate the expected value of the log complete likelihood:

$$\begin{array}{l}Q(\beta ,\alpha ;{\beta }^{(h)},{\alpha }^{(h)})=E_{({\beta }^{(h)},{\alpha }^{(h)})}\left[\sum _{i=1}log{\mathit{\text{L}}}_i^c(\beta ,\alpha )\mid Y_i;{\beta }^{(h)},{\alpha }^{(h)}\right]\\ =\sum _{i=1}^n\sum _{j=1}^{n_i}\sum _{m=1}^M{w}_{\mathit{\text{ijm}}}{U}_{\mathit{\text{ijm}}}(\beta )+\sum _{i=1}^n{\mathit{\text{c}}}_i^T\alpha +n\left\{log\mathrm{\Gamma }({\alpha }_0)-\sum _{m=1}^{M}log\mathrm{\Gamma }({\alpha }_m)\right\}+\mathit{\text{Constant}}\end{array}$$ (7)

where U_ijm(β) = log Pr(Y̰_ij∣η_ij = m; β) = Σ_k log Pr(Y_ijk∣η_ij = m; β), w_ijm = Pr(η_ij = m∣Y̰_i; β^(h), α^(h)), ${\mathit{\text{c}}}_i^T=(c_{i1},c_{i2},\dots ,c_{iM})$ and c_im = E[log(u_im)∣Y̰_i; β^(h), α^(h)]. The current parameter estimates β^(h), α^(h) enter the Q function only through w_ijm's and c_im's. To obtain weights w_ij, we need the posterior distribution of η̰_i given Y_i, which can be calculated by Bayes' rule,

$$Pr({\underset{\sim }{\eta }}_i\mid {\underset{\sim }{Y}}_i)=\frac{Pr({\underset{\sim }{\eta }}_i){\prod }_{j=1}^{n_i}{\prod }_{k=1}^{K}Pr(Y_{\mathit{\text{ijk}}}\mid {\eta }_{ij})}{{\sum }_{{\underset{\sim }{\eta }}_i}\left[Pr({\underset{\sim }{\eta }}_i){\prod }_{j=1}^{n_i}{\prod }_{k=1}^{K}Pr(Y_{\mathit{\text{ijk}}}\mid {\eta }_{ij})\right]}$$

Here the sum above is taken over all possible class membership combinations for cluster i, totaling M^n_i possibilities. To obtain weights c̰_i, we use the double expectation technique c_im = E{E[log(u_im)∣Y̰_i, η̰_i; β^(h), α^(h)] ∣Y̰_i; β^(h), α^(h)}. Here,

$$E[log(u_{im})\mid {\underset{\sim }{Y}}_i,{\underset{\sim }{\eta }}_i;{\beta }^{(h)},{\alpha }^{(h)}]=D\mathrm{\Gamma }({\alpha }_m^{(h)}+q_m^{(i)})-D\mathrm{\Gamma }({\sum }_m{\alpha }_m^{(h)}+n_i)$$

where $D\mathrm{\Gamma }(x)=\frac{d}{dx}log\mathrm{\Gamma }(x)$, and $q_m^{(i)}={\sum }_{j}I({\eta }_{ij}=m)$, the number of subjects from cluster i belonging to class m; see Web Appendix B. We then take expectation conditional on Y_i to obtain the v_i's, which again involves summing over M^n_i possible patterns of class memberships in cluster i.

Once we obtain the Q function as in equation (7), the M step is relatively straightforward. The β parameters appear only in the first term of (7), and the α parameters appear only in the second and third terms. Maximization over β is equivalent to fitting a logistic regression model with weights w_ij. Thus in practice, we can conveniently call any routine that fits weighted logistic regression for this part of the M step. The first and second derivatives with respect to α are:

$$\begin{array}{l}\frac{\partial Q}{\partial \alpha }=\sum _{i=1}^n{c}_i+n[D\mathrm{\Gamma }({\alpha }_0)1_{\text{M}\times 1}-D\mathrm{\Gamma }(\alpha )],\\ \frac{{\partial }^{2}Q}{\partial \alpha \partial {\alpha }^{\prime }}=n[T\mathrm{\Gamma }({\alpha }_0)1_{\text{M}\times \text{M}}-\mathit{\text{Diag}}\{T\mathrm{\Gamma }({\alpha }_1),\dots ,T\mathrm{\Gamma }({\alpha }_M)\}],\end{array}$$

where $T\mathrm{\Gamma }(x)≔\frac{{\partial }^2}{\partial x^2}log\mathrm{\Gamma }(x)$. Thus, we can carry out a one or multi-step Newton-Raphson algorithm for this part of the M step. The cross-derivative $\frac{{\partial }^{2}Q}{\partial \beta \partial {\alpha }^{\prime }}$ is 0, so the two parts can be carried out separately.

Finally, we iterate between the E step and M step until a suitable convergence criterion is met.

3.2 Inference and Prediction

We use the observed Fisher information matrix to estimate the standard errors of the estimated parameters. The EM algorithm does not directly provide the Hessian matrix of log likelihood; rather, methods are available to estimate it from EM outputs, e.g. Louis (1982). For our problem the application of such methods is computationally complex. Instead, we numerically calculate the observed Fisher information matrix following Oakes (1999). The technical details can be found in Web Appendix B.

As a by-product of the EM algorithm, we can easily obtain best predictions of the random effects given the data, which includes both latent class memberships η_ij's and cluster-specific class prevalence ṵ_i's. The posterior probabilities of class membership for each subject, Pr(η_ij = m∣Y̰_i; β, α), m = 1, …, M, are calculated as weights in the E-step. As for the cluster-specific random effect ṵ_i = (u_i1, …, u_iM), the best prediction is its posterior mean, whose m^th component is provided by

$$\text{E}[u_{im}\mid {\underset{\sim }{Y}}_i;\beta ,\alpha ]=\text{E}\{\text{E}[u_{im}\mid {\underset{\sim }{Y}}_i,{\underset{\sim }{\eta }}_i;\beta ,\alpha ]\mid {\underset{\sim }{Y}}_i;\beta ,\alpha \}.$$

It can be shown that the inner expectation is $({\alpha }_m+q_m^{(i)})/({\sum }_m{\alpha }_m+n_i)$, since [ṵ_i ∣ η̰_i, Ỹ_i] is Dirichlet-distributed with parameter $({\alpha }_1+q_1^{(i)},\dots ,{\alpha }_M+q_M^{(i)})$. We then marginalize over all possible patterns of η̰_i to obtain the outer expectation.

There are other important practical issues on MLC models, e.g., dealing with missing data and selecting the number of classes. Some developments and discussion on these topics are included in Web Appendex B.

4. Estimation and Inference: Maximum Pairwise Likelihood

In computing weights for the EM Q function (7), the computational burden increases exponentially, O(n · M^J), with the number of classes M and cluster size J ≔ max{n_i, i = 1, …, n}. Thus, we recommend using EM fitting when both M and n_i are relatively small, and otherwise using the maximum pairwise likelihood approach we now propose.

In clustered data with complex (e.g. spatial) correlation structure, the joint likelihood may be difficult to specify or computationally complicated, and maximum likelihood inferences may be sensitive to model assumptions. The pairwise likelihood approach nicely overcomes these difficulties. Pairwise likelihood falls within the general concept of “composite likelihood” (Lindsay, 1988), which has been used for a variety of problems (Nott and Ryden, 1999; Kuk and Nott, 2000; Cox and Reid, 2004; Renard et al., 2004; Varin et al., 2005).

Applying this concept to the MLC setting, rather than specifying the joint distribution for each cluster, we specify only pairwise distributions and then take the product over all possible pairs:

$$L^p(\beta ,\alpha )=\prod _{i=1}^n{\mathit{\text{L}}}_i^p(\beta ,\alpha )=\prod _{i:n_i>1}\left[\prod _{j_1<j_2}Pr(Y_{i{j}_1},Y_{i{j}_2};\beta ,\alpha )\right]\cdot \prod _{i:n_i=1}Pr(Y_i;\beta ,\alpha )$$

where

$$Pr(Y_{i{j}_1},Y_{i{j}_2};\beta ,\alpha )=\sum _{m_1=1}^M\sum _{m_2=1}^{M}Pr(Y_{i{j}_1}\mid {\eta }_{i{j}_1}=m_1;\beta )Pr(Y_{i{j}_2}\mid {\eta }_{i{j}_2}=m_2;\beta )\cdot Pr({\eta }_{i{j}_1}=m_1,{\eta }_{i{j}_2}=m_2;\alpha ),\text{for i in}\{i:n_i>1\}$$

and

$$Pr(Y_i;\beta )=\sum _{m=1}^{M}Pr(Y_i\mid {\eta }_i=m;\beta )Pr({\eta }_i=m;\alpha ),\text{for i in}\{i:n_i=1\}.$$

The maximum pairwise likelihood estimates are defined as parameter values that maximizes L^p(β, α). From composite likelihood theory Lindsay (1988), one can obtain the following asymptotic properties of pairwise likelihood estimation.

Proposition 1. Assume that {Y̰_ij : i = 1, …, n; j = 1, …, n_i} are generated from the MLC-D model (6). Let (β*, α*) denote true parameter values and (β̂^P, α̂^P) denote the maximum pairwise likelihood estimators that maximize l^P(θ) = l^P(β, α) = log L^P(β, α). Under suitable regularity conditions,

1. $\text{E}\{\frac{\partial log{L}^P}{\partial \beta };{\beta }^{\ast },{\alpha }^{\ast }\}=0,\text{E}\{\frac{\partial log{L}^P}{\partial \alpha };{\beta }^{\ast },{\alpha }^{\ast }\}=0$;

2. As $n\to \infty ,{\widehat{\beta }}^P\stackrel{P}{\to }{\beta }^{\ast },{\widehat{\alpha }}^P\stackrel{P}{\to }{\alpha }^{\ast }$;

3. $\sqrt{n}\left(\begin{array}{c}{\widehat{\beta }}^P-{\beta }^{\ast }\\ {\widehat{\alpha }}^P-{\alpha }^{\ast }\end{array}\right)\stackrel{D}{\to }N(0,{\sum }^P)$, where ${\sum }^P=\underset{n\to \infty }{lim}n{\left\{\text{E}\frac{{\partial }^2{l}^P}{\partial \theta \partial {\theta }^{\prime }}\right\}}^{-1}\cdot \text{E}\left\{\frac{\partial l^{P^T}}{\partial \theta }\frac{\partial l^P}{\partial \theta }\right\}\cdot {\left\{\text{E}\frac{{\partial }^2{l}^P}{\partial \theta \partial {\theta }^{\prime }}\right\}}^{-1}$.

The asymptotic variance of MPL estimates can be consistently estimated by the “sandwich” variance estimator (Royall, 1986) that replaces the expectations in the above formula with empirical estimates.

The pairwise likelihood (MPL) approach has both advantages and disadvantages compared to the ML approach. MPL relies only on bivariate distributional assumptions rather than those for the full distribution, thus is more robust than ML. On the other hand, the asymptotic efficiency of MPL can be no better than for ML, and may be worse if the true joint distribution is correctly specified.

In terms of computational burden, MPL has an advantage over ML, since each pair contains at most two subjects. The computational complexity is O(n M²J(J − 1)/2) for MPL, as opposed to O(n M^J) for ML. When the number of classes is less than 4 or the cluster size is less than 6, the difference in computational burden may still be acceptable. However, the improvement of MPL is substantial if the cluster size is greater than 5 and the number of classes is greater than 3. For instance, ML requires 146 times the computations as MPL does to fit a 4-class model with cluster size 8. For the OCD example, the cluster sizes range from 1 to 10. It took approximately 3 hours to fit a 3-class model using ML, compared to less than 30 minutes using MPL, on a workstation with Intel Pentium M 725 (1.6 GHz) processor and 512MB memory.

5. Comparison with simple latent class analysis

It is of interest how simple latent class analysis performs when it is incorrectly applied to multilevel data. To investigate this, we consider a general class of MLC models, i.e. the semiparametric model

$$\{\begin{array}{l}Pr({\underset{\sim }{Y}}_{ij}=\underset{\sim }{y})=\sum _{m=1}^{M}Pr({\eta }_{ij}=m)\cdot \prod _{k=1}^K{p}_{km}^{y_k}{(1-p_{km})}^{1-y_k}\\ {\underset{\sim }{\eta }}_i=({\eta }_{i1},\cdots ,{\eta }_{i{n}_i})\sim f({\underset{\sim }{\eta }}_i;\pi ,\delta )\\ Pr({\eta }_{ij}=m)={\pi }_m\end{array}$$ (8)

where the joint distribution f(η̰_i; π, δ) is unspecified but subject to the constraint that each subject belongs to class m with probability π_m marginally. Both MLC-D and MLC-V1 are parametric submodels of the general model (8). The following result implies that the maximum likelihood estimators of the simple latent class model consistently estimate the π and β parameters.

Proposition 2. Assume that {Y̰_ij : i = 1, …, n; j = 1, …, n_i} are generated from the semiparametric model (8) with true parameter values (β*, π*, δ*). Let l^S(θ₁) ≔ l^S(β, π) ≔ Σ_i Σ_j log f(Y̰_ij) denote the log likelihood function from the simple LC model (4), and let (β̂^S, π̂^S) maximize l^S(θ₁). Under suitable regularity conditions,

1. $\text{E}\{\frac{\partial l^S}{\partial \beta };{\beta }^{\ast },{\pi }^{\ast },{\delta }^{\ast }\}=0,\text{E}\{\frac{\partial l^S}{\partial \pi };{\beta }^{\ast },{\pi }^{\ast },{\delta }^{\ast }\}=0$;

2. As $n\to \infty ,{\widehat{\beta }}^S\stackrel{P}{\to }{\beta }^{\ast },{\widehat{\pi }}^S\stackrel{P}{\to }{\pi }^{\ast }$;

3. $\sqrt{n}\left(\begin{array}{l}{\widehat{\beta }}^S-{\beta }^{\ast }\\ {\widehat{\pi }}^S-{\pi }^{\ast }\end{array}\right)\stackrel{D}{\to }N(0,{\sum }^S)$, where ${\sum }^S=\underset{n\to \infty }{lim}n{\left\{\text{E}\frac{{\partial }^2{l}^S}{\partial {\theta }_1\partial {\theta }_1^{\prime }}\right\}}^{-1}\cdot \text{E}\left\{\frac{\partial l^{S^T}}{\partial {\theta }_1}\frac{\partial l^S}{\partial {\theta }_1}\right\}\cdot {\left\{\text{E}\frac{{\partial }^2{l}^S}{\partial {\theta }_1\partial {\theta }_1^{\prime }}\right\}}^{-1}$.

The proof is given in Web Appendix C. Since the MLC-D model (6) is a parametric submodel of the general semiparametric model (8), the results of Proposition 2 apply to it as a corollary.

Proposition 2 suggests an alternative inference procedure if the goal is to understand the measurement model and marginal class prevalences: one can simply ignore clustering and fit the simple latent class model. The next step is to fix the standard errors by the sandwich estimator. This method is simple and fast to implement, compared to the two methods developed above. However, it may suffer some loss of efficiency when the data follow a multilevel model with appreciable between-cluster heterogeneity. Moreover it does not provide a measure of within cluster association.

We also note that there is an important connection between this result and that for marginal modeling for longitudinal or clustered data. If we ignore the measurement part of the model, the latent class indicators η_ij's are clustered data, correlated within clusters. The simple latent class model corresponds to a marginal model for η_ij's with working independence correlation, while various MLC models correspond to marginal models with working exchangeable correlation. Similarly as with generalized estimating equations (GEE, Liang and Zeger 1986), even if the working correlation is misspecified as independence, the estimators of marginal parameters π_m's are consistent, and their standard errors can be consistently estimated using the robust variance estimator. Moreover, Proposition 2 indicates that the measurement model parameters (β's) can also be consistently estimated under such model misspecification.

If the within cluster association is of interest, or higher efficiency is needed, the simple latent class model would not be appropriate. Parametric submodels, such as the MLC-V1 and MLC-D, provide alternatives when the parametric assumptions are reasonable, but robustness no longer holds generally.

6. Simulations

6.1 Setting I

We evaluated the finite sample performance of our procedure in simulation studies. In Simulation Setting I described below, we aim to assess the performance of our methods when the MLC-D model is true. Data were generated from the following true settings: n = 200 or 500 clusters, J = 4 subjects per cluster, K = 5 items, M = 2 classes. The true model was the MLC-D model (4) and (6). The true α parameters were chosen as (α₁, α₂) = (1.5, 2.3). The log odds of reporting “1” for class 1 members were (β₁₁, β₂₁, β₃₁, β₄₁, β₅₁) = (−1.21, 0.28, 1.08, −2.35, 0.43) for five items, and the log odds for class 2 members were (β₁₂, β₂₂, β₃₂, β₄₂, β₅₂) = (0.51, −0.57, −0.55, −0.56, −0.89). We conducted 1000 simulation runs, and in each run three methods were used to fit the multilevel latent class model, maximum likelihood for Dirichlet model (ML), maximum pairwise likelihood for Dirichlet model (MPL), and maximum likelihood for simple latent class model with robust standard errors (ML-S).

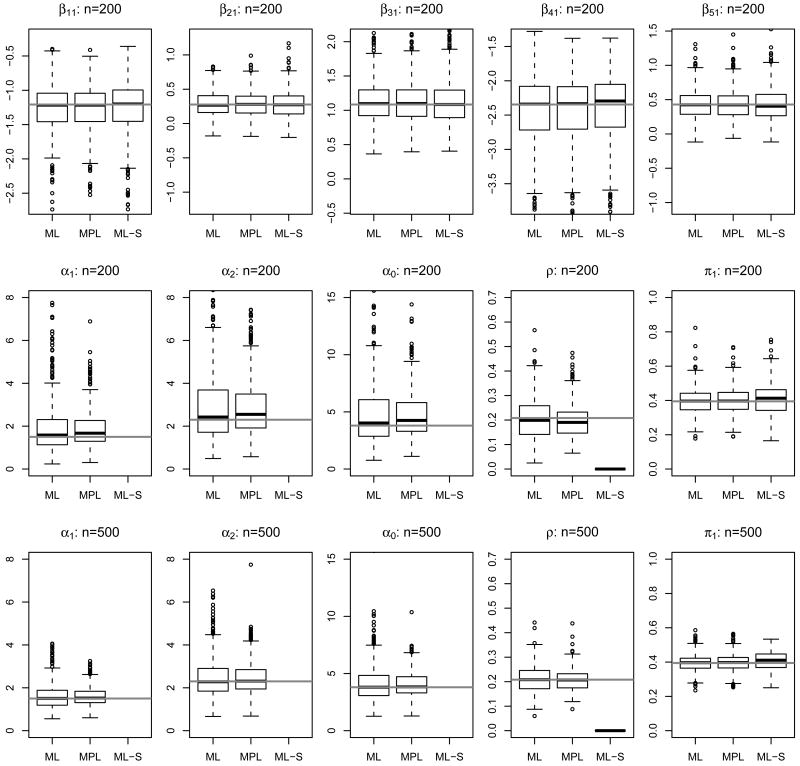
First we consider findings for estimation of the measurement models. The first row of Figure 2 displays boxplots of selected β estimates using n = 200 clusters. The gray solid lines in each figure represent true parameter values. For each method and parameter, estimator distributions centered closely around true values, exhibited relatively small dispersion, and included few outliers. The dispersion of MPL was similar to that of ML, suggesting high relative efficiency of the MPL estimates. The dispersion of ML-S, however, was larger than that for ML or MPL, implying loss of efficiency by ignoring the within cluster correlation. Table 1 confirms the larger standard errors, i.e., the loss in efficiency of ML-S. Simulation results using n = 500 clusters displayed similar patterns but with narrower confidence intervals, and these results are omitted. In summary, the β parameters were well estimated by both ML and MPL methods based on the Dirichlet model, and the simple latent class model estimators were consistent, but generally less efficient.

Figure 2.

Boxplots of β and α estimates under Simulation Setting I. “ML” and “MPL” are maximum likelihood and maximum pairwise likelihood estimates from the Dirichlet model (4) and (6), while “ML-S” stands for maximum likelihood estimates from the simple latent class model (4) and (5). In all subfigures, solid gray lines represent true parameter values. The first row displays β estimates from simulations with n = 200. Here we show results for (β₁₁, β₂₁, β₃₁, β₄₁, β₅₁), i.e., the log odds of reporting “1” for five items conditional on class 1, and omit those for class 2 parameters β_k2's. The second and third rows show estimates of α parameters from simulations with n = 200 and n = 500, respectively. The five columns correspond to α₁, α₂, α₀ = α₁ + α₂ (scale parameter), ρ = 1/(1 + α₀) (ICC) and π₁ = α₁/α₀ (marginal prevalence of class 1), respectively.

Table 1.

Standard errors and coverage probabilities under Simulation Setting I. “ML” and “MPL” are maximum likelihood and maximum pairwise likelihood estimates from the Dirichlet model (4) and (6), while “ML-S” stands for maximum likelihood estimates from the simple latent class model (4) and (5). “simu. SE” means empirical standard errors across simulations, “est. SE” means model-based standard errors, and “cov. prob” means coverage probabilities (%) for model based 95% confidence intervals.

Class	Method	Quantity	αm	${\pi }_m=\frac{{\alpha }_m}{{\alpha }_0}$	β1m	β2m	β3m	β4m	β5m
Class 1 (m=1)	ML	simu. SE	1.90	0.081	0.37	0.19	0.34	0.77	0.22
		est. SE	1.96	0.083	0.36	0.19	0.32	0.69	0.22
		cov. prob.	92.0	92.2	95.2	96.6	95.6	93.4	95.0
	MPL	simu. SE	0.87	0.079	0.37	0.19	0.33	0.86	0.23
		est. SE	1.08	0.095	0.40	0.20	0.36	0.83	0.24
		cov. prob.	95.4	95.8	95.4	95.8	95.6	94.0	96.2
	ML-S	simu. SE	-	0.089	0.52	0.20	0.37	1.03	0.24
		est. SE	-	0.093	0.43	0.20	0.38	0.90	0.26
		cov. prob.	-	93.8	95.6	95.0	96.2	93.0	95.8
Class 2 (m=2)	ML	simu. SE	2.85	0.081	0.19	0.14	0.26	0.15	0.18
		est. SE	3.17	0.083	0.19	0.14	0.23	0.16	0.18
		cov. prob.	90.8	92.2	95.6	95.6	93.6	96.0	94.0
	MPL	simu. SE	1.40	0.079	0.18	0.14	0.19	0.15	0.18
		est. SE	1.69	0.095	0.20	0.15	0.20	0.17	0.19
		cov. prob.	95.6	95.8	96.4	96.6	95.4	97.0	95.0
	ML-S	simu. SE	-	0.089	0.20	0.15	0.20	0.16	0.19
		est. SE	-	0.093	0.22	0.16	0.21	0.17	0.20
		cov. prob.	-	93.8	95.0	96.0	94.8	96.4	95.4

Turning to findings relating to the mixing distribution, the distributions of the α parameter estimates were widely dispersed and exhibited heavy tails (Row 2 and 3 of Figure 2). Researchers typically will be most interested in conveniently interpreted transformations of the α parameters, including the marginal class prevalence π_m = α_m/α₀, the scale parameter α₀ = α₁ + … + α_M, and the intra-cluster correlation parameter ρ. Figure 2 shows that the population-average class prevalences and the intra-cluster correlation were well estimated, with distributions centering around the true values and having narrow spreads. Estimates of the scale parameter α₀ exhibited substantial variability, as is often the case for variance components. Finally, MPL estimates for α parameters enjoyed high finite-sample efficiency compared to ML estimates. For α parameters, MPL estimates even seemed to have slightly smaller variances than the ML estimates in finite samples. There appeared to be a bias of roughly 5% when n = 200, but the bias vanishes when n increases to 500. The simple latent class model (ML-S) did not provide information on the scale parameter α₀ or intra-cluster correlation ρ. It did estimate the marginal class prevalences π_m's well.

Table 1 displays standard errors and coverage probabilities of model-based 95% confidence intervals for the three methods. The simulated standard errors are the sample standard deviations of estimates across runs, and thus reflect the underlying uncertainty. The estimated standard errors are the average of model-based standard errors across simulations, thus indicate the uncertainty estimated by the model. The two sets of standard errors were generally close to each other for all methods. Coverage probabilities primarily were close to the 95% nominal value. Standard error agreement and coverage probabilities were worse for the α parameters than for the β parameters. Finally, Table 1 confirmed high efficiency of the MPL estimators. When the MLC-D model is true, our simulation study suggests that both ML and MPL well accomplish estimation and inference for multilevel latent class models in finite samples.

6.2 Settings II and III

We also conducted simulation studies to evaluate performance of various MLC models under more complex settings. To mimic the OCD application, we generated n = 200 clusters, J subjects per cluster, M = 3 classes and K = 8 items in Settings II and III. In Setting II, the true model was the MLC-D with true parameter values being the maximum likelihood estimates from the OCD application (see Table 3). In Setting III, the true model was the MLC-V1. The true parameter values were chosen as the maximum likelihood estimates based on MLC-V1 for the OCD example, with p_km's close to those reported in Table 3 and the remaining parameters as λ₂ = 1, λ₃ = 1.704, γ₂ = 1.542, γ = 0.011 and σ² = 24.154. These simulations allow us to evaluate performance of various MLC models under more complex settings and under model mis-specifications. Here we focus on the comparison between MLC-D and MLC-V1.

Table 3.

Model fitting for OCD data using maximum likelihood based on the MLC-D model. “Est.” means point estimates for corresponding parameters, and “95% CI” gives their 95% confidence intervals.

	Class 1		Class 2		Class 3
	Est.	95% CI	Est.	95% CI	Est.	95% CI
Measurement part: conditional probabilities
GAD	0.12	(0.05, 0.25)	0.56	(0.42, 0.69)	0.67	(0.57, 0.76)
SAD	0.11	(0.05, 0.20)	0.26	(0.17, 0.37)	0.41	(0.33, 0.50)
Panic	0.10	(0.06, 0.17)	0.03	(0.00, 0.21)	0.48	(0.38, 0.59)
Tics	0.13	(0.07, 0.23)	0.41	(0.30, 0.52)	0.27	(0.20, 0.35)
MDD	0.27	(0.20, 0.36)	0.23	(0.15, 0.35)	0.68	(0.56, 0.77)
Man	0.03	(0.01, 0.09)	0.00	(0.00, 0.04)	0.19	(0.13, 0.27)
GrD	0.16	(0.08, 0.28)	0.48	(0.37, 0.59)	0.59	(0.50, 0.68)
BDD	0.06	(0.02, 0.13)	0.16	(0.09, 0.26)	0.53	(0.43, 0.63)
Mixing part: α parameters
αm	0.49	(0.25, 0.96)	0.40	(0.19, 0.86)	0.38	(0.20, 0.71)
πm	0.38	(0.27, 0.52)	0.32	(0.20, 0.46)	0.30	(0.22, 0.39)
ρmm	0.44	(0.30, 0.59)	0.44	(0.30, 0.59)	0.44	(0.30, 0.59)

Under each setting, two methods were used to fit simulated data regardless of the underlying true model: maximum likelihood estimation based on the MLC-D model (denoted as “ML”) and maximum likelihood estimation based on the MLC-V1 model (denoted as “ML-V1”). Table 2 shows the bias, standard deviation (SD; square root of variance) and root mean square error (RMSE) for nine selected parameters under Settings II and III: measurement parameters (β₁₁, β₁₂, β₁₃), marginal class prevalences (π₁, π₂, π₃) and ICC parameters (ρ₁₁, ρ₂₂, ρ₃₃).

Table 2.

Comparison of MLC-D versus MLC-V1 under Simulation Settings II and III. Under either setting, “ML” and “ML-V1” correspond to maximum likelihood estimates under models MLC-D and MLC-V1, respectively. “Bias”, “SD” and “RMSE” represent bias, standard deviation and root mean square error of parameter estimates. Results for 9 selected parameters were displayed, measurement parameters (β₁₁, β₁₂, β₁₃), marginal class prevalences (π₁, π₂, π₃) and ICC parameters (ρ₁₁, ρ₂₂, ρ₃₃). The scale for all numbers is 10⁻².

Method	Quantity	β11	β12	β13	π1	π2	π3	ρ11	ρ22	ρ33
Setting II: true model is MLC-D
ML	Bias	-0.40	0.65	-0.05	-0.16	0.33	-0.17	-0.28	-0.28	-0.28
	SD	4.43	7.20	3.92	6.70	7.04	4.03	5.94	5.94	5.94
	RMSE	4.45	7.23	3.92	6.70	7.05	4.03	5.94	5.94	5.94
ML-V1	Bias	0.68	-0.84	0.15	0.12	-0.42	0.24	-1.11	5.32	0.75
	SD	5.91	9.07	4.19	9.07	9.45	4.30	19.21	29.75	10.72
	RMSE	5.95	9.11	4.19	9.07	9.46	4.31	19.24	30.22	10.74
Setting III: true model is MLC-V1
ML	Bias	0.57	-1.06	0.97	-1.22	-3.02	4.23	-0.56	38.61	9.11
	SD	3.77	7.53	3.52	6.51	6.35	5.00	7.48	7.48	7.48
	RMSE	3.81	7.60	3.65	6.63	7.03	6.55	7.50	39.32	11.79
ML-V1	bias	-0.70	0.94	0.01	-1.44	-0.83	2.27	-2.42	0.70	-3.63
	SD	4.17	7.31	4.03	5.92	5.73	6.09	11.49	12.28	10.45
	RMSE	4.23	7.37	4.03	6.09	5.79	6.50	11.74	12.30	11.07

First, we look at results when the true model is MLC-D, i.e., Setting II. The ML method, which correctly specifies the underlying model, yield estimates with little bias and relatively small variance and RMSEs for all parameters. The ML-V1 method, which mis-specifies the model as MLC-V1, yield estimates with larger RMSEs. More specifically, for β_km and π_m parameters, ML-V1 estimates have small biases but larger variances, and roughly 20% larger RMSEs than those of ML. For ICC parameters ρ_mm's, ML-V1 estimates show large biases and very large SDs, and thus on average more than 200% larger RMSEs than those of ML. To conclude, when the true model is MLC-D, maximum likelihood estimates based on MLC-V1 generally have larger biases, variances and RMSEs than those based on MLC-D.

Next, we consider situations when the true model is MLC-V1, i.e., Setting III. The ML-V1 method correctly specifies the underlying model in this case and yields estimates with small biases and variances. The ML method now mis-specifies the model as MLC-D, and not surprisingly, ML estimates demonstrate larger biases for many parameters. Variances for ML estimates are often smaller than or similar to those of ML-V1 estimates. As a result, the RMSEs of ML are similar to those of ML-V1 for β_km and π_m parameters. Regarding ICC parameters, ML estimates have a much larger RMSE compared to ML-V1 for ρ₂₂, and similar or smaller RMSEs for ρ₁₁ and ρ₃₃. To summarize, when the true model is MLC-V1, maximum likelihood estimates for many parameters based on MLC-D may have lower variances and RMSEs than those based on the MLC-V1, although the former is subject to large biases especially for certain ICC parameters. More details of simulation results under Settings II and III can be found in Web Appendix D.

7. Application: Analysis of Obsessive Compulsive Disorder data

We apply the multilevel latent class model to the OCD data described in the Introduction Section. Our colleagues identified 8 disorders that often co-occur with OCD: generalized anxiety disorder (GAD), separation anxiety disorder (SAD), panic disorder (PD), tics disorder, major depressive disorder (MDD), mania disorder, grooming disorders (GrD; trichotillomania, pathological skin picking), and body dysmorphic disorder (BDD). The analytic aim is to identify subtypes of OCD based on comorbidity with the 8 disorders. Data for 706 OCD cases from 238 families were used for the analysis. The family sizes range from 1 to 10, and most families contain two to five members.

We began by selecting among models with two, three and four classes. We used an adaptation of BIC, which repeatedly subsampled single individuals per cluster to aid in model selection (See Web Appendix B.4). The BICs for two, three and four class models were 1031, 1062 and 1091, respectively, and thus the two-class model was modestly preferred. However, it is known that BIC may underestimate the number of classes in sample sizes like ours (Yang, 2006). Given that the choice was equivocal, we present the more illustrative three class model. For the three class model, both ML and MPL methods converged successfully, and they gave similar results, hence we only report the model fitted by ML (Table 3). Subjects in the first class were characterized by low prevalence of each comorbid disorder except depression, which was estimated to occur in rougly a quarter of class members. In the second class there were moderate prevalences of GAD, SAD, tics, MDD and GrD, in conjunction with low prevalences of panic disorder and mania. Subjects in the third class were at moderate to high risk for nearly all disorders. The marginal prevalence of the three classes were estimated as 38%, 32% and 30%, respectively.

The same-class ICC, ρ, was estimated as 0.44 (95% CI: 0.30, 0.59), while estimated different-class ICCs for same-cluster members were -0.20 on average. This indicates a moderate level of heritability for OCD subtypes, such that members of the same family are considerably more likely to have similar types of OCD comorbidity than subjects from different families.

We compared results from the MLC-D model with those from the MLC-V1 model. The models gave similar latent class structure for the measurement parameters β's. As to the mixing parts, these models estimated similar marginal class prevalences but had different implications on ICCs. For example, MLC-V1 estimated same-class ICCs to be 0.71, 0.31 and 0.61, respectively for three classes. The log-likelihood values from LC-S, MLC-D and MLC-V1 were −2819.751, −2796.591 and −2791.388, respectively. One could see that the two MLC models improve substantially over the simple standard latent class model, with 1 and 2 additional parameters for MLC-D and MLC-V1, respectively. As to the distribution of random effects ṵ_i's, fitted MLC-D and MLC-V1 models demonstrate similar features as panels (1, 2) and (2, 2) of Figure 1 (see Web Appendix E for more details), respectively. It is clear that MLC-V1 restricts (u_i1, u_i2, u_i3) to take values only in a one-dimensional subspace of its domain Ω_u = {(u₁, u₂, u₃) ∈ [0, 1]³ : u₁ + u₂ + u₃ ≤ 1}. In contrast, the Dirichlet model allows ṵ_i's to take values freely in Ω_u. From this perspective, it seems that the random effects structure induced by MLC-D is more natural. It is hard to argue which MLC model is superior, but both imply qualitatively compatible results: similar latent class structures and a moderate level of heritability on average.

8. Discussion

Latent class models have proven useful for modeling multiple categorical outcomes in the social sciences and biomedical studies. In such studies multilevel or hierarchical designs are increasingly common. This paper considered an alternate model to the ones proposed by Vermunt (2003, 2008), employing a Dirichlet mixing distribution. Three methods for model fitting and inference, ML, MPL and ML-S, were developed and compared. We also investigated the consequences of ignoring clustering with a simple latent class model. Our models' random effects structure has more straightforward interpretation than those of competing methods, thus should usefully augment tools available for latent class analysis of clustered data.

The proposed MLC-D model has limitations due to the Dirichlet distributional assumption. For example, our model assumes ICCs to be class invariant. Such assumption may sometimes be questionable, say, in genetic studies where different classes may have different heritability. If we are concerned about such assumptions, generalized Dirichlet distributions (Wong, 1998) might serve as an alternative. In contrast, MLC-V1, MLC-V2 and MLC-VN allow the ICCs to differ, but they also impose restrictions from their parametric assumptions (Web Appendix A.2). We thank a reviewer for pointing out other options, e.g., multiple factor normal random effect models and models with multivariate normal mixture distributions.

We point out that MLC models, including MLC-V1 and MLC-D, are appropriate for studies with many clusters and relatively small cluster size. Asymptotic properties for estimators generally hold when the number of clusters approaches infinity while the cluster size is fixed or bounded. Thus, in settings with few large clusters, validity of inferences based on MLC models is questionable.

There remain other issues that would benefit from further research. First, model selection is complicated by the multilevel structure. Though marginalization provides a workable solution, simpler criteria would be useful. Proposing new criteria as well as assessing their performances need more work. Second, diagnostics and model checking techniques are needed. Third, the MLC model makes the conditional independence assumption. The clustering is assumed to affect only the mixing model, not the measurement model. Models allowing dependence in family members' tendencies to report specific items, and not only their class memberships, are needed to address this. Finally, it would be of interest to develop multilevel latent class regression models that incorporate covariates in subpopulation mixing distribution. Vermunt (2005) considered some models with covariates, and it would be interesting to extend the MLC-D model to allow covariates as well.