Abstract
A simple analytic theory is developed to describe FRET efficiency histograms constructed from a photon trajectory generated by a molecule with multiple conformational states. The histograms are approximated by a sum of Gaussians with the parameters explicitly determined by the FRET efficiencies of the states and the rates of the transitions between the states. The theory, which has been tested against exact histograms for two conformational states and simulated data for three and four conformational states, accurately describes how the peaks in the histograms collapse as the transition rates or the bin time increase.
I. INTRODUCTION
In the past decade, single-molecule fluorescence experiments emerged as a powerful tool to study conformational dynamics of biological molecules [1–15]. Förster resonance energy transfer (FRET) between donor and acceptor fluorophores can be exploited to probe fluctuations in the interdye distances between about 1 nm and 10 nm. The output of single-molecule FRET experiments is a sequence of photons of different colors emitted by the donor and acceptor fluorophores. Changes in intramolecular distances modulate the observed pattern of photon colors.
The principal tool for analyzing such photon trajectories is a FRET efficiency histogram. This is constructed by binning the photons and calculating a FRET efficiency in each bin as the fraction of acceptor photon counts. The shape of a histogram potentially provides information about both the structure and the dynamics of the molecule. However, with few notable exceptions [15–19], FRET efficiency histograms have been primarily used as a tool to resolve separate species. More extensive application of these histograms has been impeded by the lack of a simple analytic theory. An exact expression for the FRET efficiency histograms does exist for a two-state molecule [20–22]. However, even in this case, it is extremely complicated (involving integrals over Bessel functions) and it is unlikely that it can be generalized to the molecules with more than two states.
In this paper we derive an accurate approximate analytic expression for the FRET efficiency histogram of a molecule that has multiple conformational states. It is assumed that the distribution of the donor and acceptor photons emitted by each state is Poissonian and the mean total number of photons is the same for all states. The approximation is a sum of Gaussians each with a weight, mean, and variance that are not adjustable but rather explicit functions of the model parameters (the rate constants and the apparent FRET efficiencies) and the bin time. The basic idea of our approximation is to describe the contribution of time bins that contain no transitions and those that involve transitions between just two states by Gaussians with the appropriate mean and variance. The contribution of all other bins is described by a single Gaussian with parameters chosen to ensure that the entire FRET efficiency histogram is normalized and has the exact mean and variance for all bin times.
The above strategy is implemented in Sec. II to derive our multi-Gaussian approximation to FRET efficiency histograms. In Sec. III, this approximation is tested for two-, three-, and four-state systems. In the last Section, we discuss how the Gaussian approximation can be used to analyze free diffusion experiments where the distribution of the total number of photons is non-Poissonian.
II. THEORY
Consider a sequence of photons divided into bins of duration T. Each bin contains a different number of NA acceptor and ND donor photons. FRET efficiency in a bin is defined as E = NA/(NA + ND). This is a random quantity that fluctuates due to shot noise and conformational dynamics on a time scale slower or comparable to the interphoton time. We are interested in how the shape of the FRET efficiency histograms depends on the rate of conformational changes and on the bin time. When the bin time is short so that the interdye distance does not change during the bin time, the histogram is a superposition of several peaks, each broadened by shot noise. At long bin times, the interdye distance is averaged out and the peaks collapse into a single peak. This collapse is a signature of conformational dynamics.
In the absence of conformational dynamics, the interdye distance is fixed and the donor and acceptor photons are uncorrelated and obey Poisson statistics. Poisson statistics is characterized by the acceptor and donor count rates, nA and nD, which are the mean numbers of acceptor and donor photons detected per unit time. The ratio of the acceptor count rate to the total count rate is the apparent mean FRET efficiency, denoted by 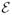 = nA/(nA + nD). The count rates and, therefore, the apparent FRET efficiency are related to the interdye distance. The precise relationship depends on the dye’s photophysics, detection efficiencies, dynamics on the submicrosecond time scale, etc.
= nA/(nA + nD). The count rates and, therefore, the apparent FRET efficiency are related to the interdye distance. The precise relationship depends on the dye’s photophysics, detection efficiencies, dynamics on the submicrosecond time scale, etc.
When the interdye distance fluctuates, so do the photon count rates. We describe these fluctuations by a kinetic scheme. The molecule emitting photons has M conformational states. Each state i is characterized by the apparent FRET efficiency 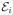 = nAi/(nAi + nDi). We assume that the total count rate n = nAi + nDi does not depend on conformation. The transitions between the states are described by the rate matrix K. Its element Kij is the rate of the j → i transition. The diagonal elements are negative, Kii = −Σm≠i Kmi. The equilibrium populations of states are found by solving Kp = 0, where p is the vector of equilibrium populations with the elements pi. These populations are normalized,
. The detailed balance condition, Kijpj = Kjipi, imposes a constraint on the transition rates.
= nAi/(nAi + nDi). We assume that the total count rate n = nAi + nDi does not depend on conformation. The transitions between the states are described by the rate matrix K. Its element Kij is the rate of the j → i transition. The diagonal elements are negative, Kii = −Σm≠i Kmi. The equilibrium populations of states are found by solving Kp = 0, where p is the vector of equilibrium populations with the elements pi. These populations are normalized,
. The detailed balance condition, Kijpj = Kjipi, imposes a constraint on the transition rates.
The FRET efficiency distribution is simply related to the joint probability, P(NA, ND), of detecting NA acceptor and ND donor photons in bin time T. When the interdye distance does not change, this distribution is a product of Poisson distributions of acceptor and donor photons. When the interdye distance fluctuates, the photon count rates are random functions of time. In this case the Poisson distribution is generalized to
| (1) |
where , which are still random since they depend on the conformational states visited during time T. 〈…〉c denotes an average over all conformational trajectories starting from the equilibrium distribution.
Our approximation is based on the first two moments of the FRET efficiency, and we start by finding them. The mean of the FRET efficiency is found by multiplying the above joint distribution (with a proper normalization factor) by NA/(NA + ND) and evaluating the sums over NA and ND subject to NA + ND ≥ NT, where NT is the threshold imposed on the total number of acceptor and donor photons. [27] When the total count rate does not fluctuate, nA(t) + nD(t) = n, one can show that the mean FRET efficiency is
| (2) |
where
with 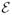 (t) ≡ nA(t)/n and
is the equilibrium average of the FRET efficiency. The first equality follows directly from the definition after evaluating the sums over the numbers of photons. The second equality is obtained by evaluating the average over the conformational trajectories.
(t) ≡ nA(t)/n and
is the equilibrium average of the FRET efficiency. The first equality follows directly from the definition after evaluating the sums over the numbers of photons. The second equality is obtained by evaluating the average over the conformational trajectories.
Analogously, the second moment can be expressed as
| (3) |
where 〈N−1〉 is the reciprocal of the total number of photons in a bin averaged over the distribution of the total number of photons, . Note that 〈N−1〉 depends on both laser intensity (through the total count rate n) and the bin time T.
The average 〈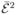 〉c can be related to the autocorrelation function of the apparent efficiency by [20]
〉c can be related to the autocorrelation function of the apparent efficiency by [20]
| (4) |
where [exp(Kt)]ij is the ij element of the matrix exponential of K. Simple analytic expressions for 〈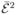 〉c can be found for two- and three-state systems (see below). In general, it can be directly obtained numerically using a program such as Mathematica [23].
〉c can be found for two- and three-state systems (see below). In general, it can be directly obtained numerically using a program such as Mathematica [23].
With the two moments in hand, we can now derive the approximation for FRET efficiency histograms. Let us divide the bins that contribute to the FRET efficiency histogram into those that 1) have no transitions during the bin time; 2) have transitions only between two states; 3) have transitions between three or more states. The contributions to the FRET efficiency histogram made by bins of the first two types are approximated by Gaussians labeled by index ij, i, j = 1, … M i ≤ j. The diagonal terms ii correspond to the bins with no transitions during the bin time. The off-diagonal terms ij (i < j) correspond to the bins with transitions only between states i and j. Finally, the Gaussian labeled by the index 0 corresponds to the remaining bins. Thus the FRET efficiency histogram (FEH) is approximated as
| (5) |
Let us first consider the parameters of the diagonal terms in the sum. The iith Gaussian describes the contribution of those bins where the molecule is in state i during the entire bin time. Its weight cii is the fraction of such bins, which is the probability to be in state i during the entire bin time, pi exp(KiiT), where the matrix element Kii = −Σm≠i Kmi is the negative of the sum of all rates out of state i. The mean FRET efficiency calculated from the subset of such bins is equal to the apparent efficiency of the state, 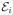 , and the second moment is
(see eq 3). Equating these with the moments of the iith Gaussian (
, and the second moment is
(see eq 3). Equating these with the moments of the iith Gaussian (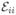 and
), we have
and
), we have
| (6a) |
| (6b) |
| (6c) |
for i = 1, …, M. Note that is the variance due solely to shot noise [22].
Now consider the off-diagonal terms. The ijth Gaussian corresponds to the bins that have transitions only between states i and j. Its weight cij is the fraction of such bins, which is equal to the probability to be in states i and j during the bin time (at least one transitions between i and j must occur but none to any other state). To find these weights, let us first obtain the probability aij to be in state i at time T starting from equilibrium when only states i or j were visited during the bin time. The subscript ij specifies the two states visited during the bin time with the first index being the state at time T. These probabilities satisfy the rate equations:
| (7) |
subject to equilibrium initial conditions aij(0) = pi, aji(0) = pj. The diagonal elements Kii(Kjj) are the negative of the sum of all rates out of state i(j). They describe both the reversible relaxation of states i and j due to mutual interconversion as well as the irreversible decay due to transitions to other states. Solving eq 7 and using the detailed balance condition Kijpj = Kjipi, we find that
| (8) |
where . The sum of aij and aji equals to the fraction of bins where the molecule visits only states i or j, and thus cii + cjj + cij = aij + aji. This condition determines the weights cij.
The other two parameters of the off-diagonal Gaussians, 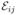 and
, are found from the requirement that the first two moments of the FRET efficiency of the sum of the iith, jjth, and ijth Gaussians are equal to those obtained from the bins during which the molecule visits only states i or j. Using the same procedure that we used previously when all bins were considered (e.g., the way we obtained eqs 2 and 3), we now find:
and
, are found from the requirement that the first two moments of the FRET efficiency of the sum of the iith, jjth, and ijth Gaussians are equal to those obtained from the bins during which the molecule visits only states i or j. Using the same procedure that we used previously when all bins were considered (e.g., the way we obtained eqs 2 and 3), we now find:
| (9a) |
| (9b) |
where 〈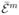 〉i∨j, m = 1, 2, is the conditional average of the mth power of
over the subset of bins during which the molecule visits only states i or j. Although these averages can be found exactly, they can be well approximated by simpler expressions. The first moment 〈
〉i∨j, m = 1, 2, is the conditional average of the mth power of
over the subset of bins during which the molecule visits only states i or j. Although these averages can be found exactly, they can be well approximated by simpler expressions. The first moment 〈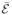 〉i∨j is obtained from the mean 〈
〉i∨j is obtained from the mean 〈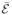 〉c for an isolated two-state system consisting of states i and j,
〉c for an isolated two-state system consisting of states i and j, 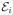 pi +
pi + 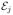 pj, by replacing pi and pj by qij and qji, where qij = aij/(aij + aji) and qji = 1 − qij. Thus,
pj, by replacing pi and pj by qij and qji, where qij = aij/(aij + aji) and qji = 1 − qij. Thus,
| (10) |
It can be shown from eq 4 that the second moment 〈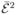 〉c for the isolated two-state system is (
〉c for the isolated two-state system is (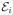 pi +
pi + 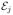 pj)2 + pipj(
pj)2 + pipj(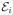 −
− 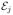 )2 (1 − φ((Kij + Kji)T)), where
)2 (1 − φ((Kij + Kji)T)), where
| (11) |
Replacing pi and pj by qij and qji we have
| (12) |
These approximations are especially good when the interconversion rates between i and j are much larger than other rates involving these states, which is when the contribution of the ijth Gaussian is the most significant.
Substituting the above expressions for the conditional averages into eqs 9 and solving these sequentially, we find that the parameters of the off-diagonal Gaussians (i < j) are given by
| (13a) |
| (13b) |
| (13c) |
| (13d) |
where φ (τ) is given in eq 11 and fij = (aij − cii)/cij = 1 − fji. In deriving eqs 13, we used the identity .
Finally, the parameters for the zeroth Gaussian, c0, 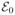 , and
, are found from the requirements that the entire distribution is normalized and the first two moments are exact (i.e., equal to those in eqs 2 and 3). In this way we find that
, and
, are found from the requirements that the entire distribution is normalized and the first two moments are exact (i.e., equal to those in eqs 2 and 3). In this way we find that
| (14a) |
| (14b) |
| (14c) |
where
and 〈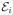 〉c is given in eq 4. These equations are solved sequentially to find c0,
〉c is given in eq 4. These equations are solved sequentially to find c0, 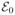 , and
.
, and
.
The sum of Gaussians in eq 5 with the parameters in eqs 6, 13 and 14 describes the FRET efficiency histogram of a molecule with M conformational states for arbitrary bin times. At bin times short compared to the time between transitions, only the diagonal terms contribute. At long bin times, all Gaussians vanish except the zeroth Gaussian. The mean and variance of FRET efficiency are exact at all times.
For two conformational states, there are only three Gaussians, 11, 22, and 12 (c0 = 0 for all T in this case). The diagonal terms (i = 1, 2) are (see eq 6)
| (15a) |
| (15b) |
| (15c) |
where K21 (K12) is the rate of 1 → 2 (2 → 1) transition, p1 = K12/(K12 + K12) = 1 − p2. The coefficients that determine the 12 Gaussian are (see eq 13)
| (16a) |
| (16b) |
| (16c) |
| (16d) |
where φ(τ) is given in eq 11 and f12 = (p1 − c11)/c12 = 1 − f21. This special case [24] has been recently applied to extract transition rates from experimental data on a two-state protein [19].
FRET efficiency histograms for three conformational states with transitions between all states are described by seven Gaussians. The parameters of the Gaussians can be found from eqs 6, 13 and 14 using the formulas given in the Appendix A. Our theory has the important property that the Gaussian approximation of the FRET efficiency histogram for a three-state system reduces analytically to the appropriate two-state approximation in all limiting cases when the three-state kinetic scheme reduces to a two-state one (e.g., transitions between any two states become sufficiently fast).
III. ILLUSTRATIVE CALCULATIONS
To test the approximation, we compare the distributions calculated using the Gaussian approximation with those obtained from the exact histograms for a two-state model [21, 22] and from simulated photon trajectories for a three- and four-state model. Details of the simulations are described in Ref. [25].
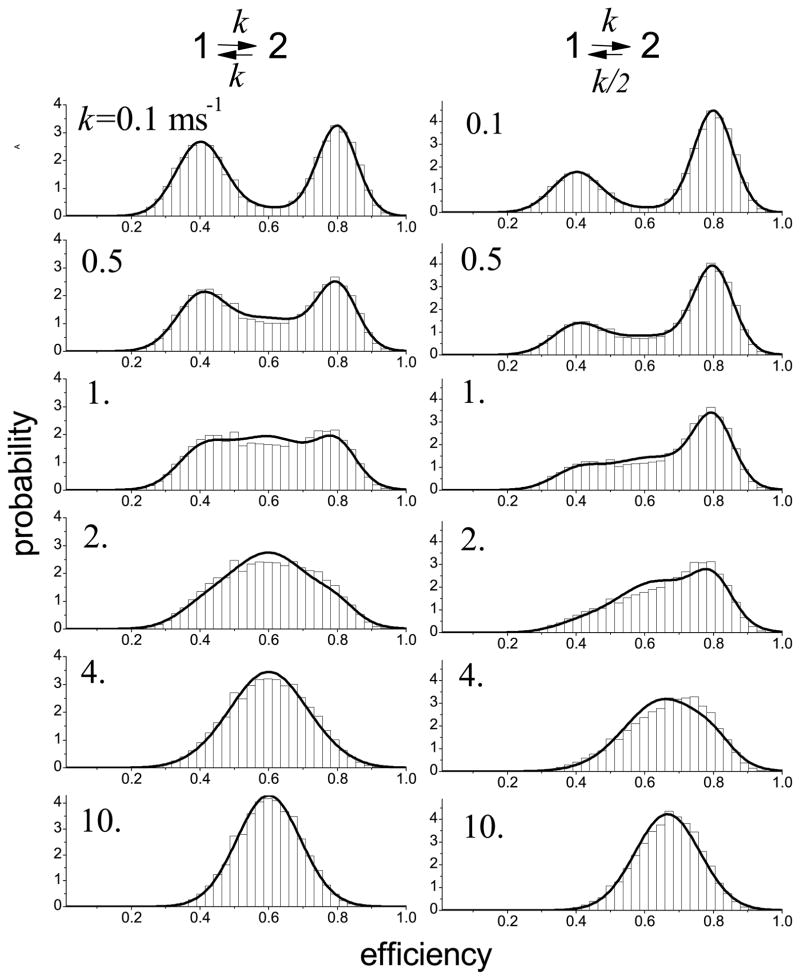
Figure 1 shows results for two interconverting conformational states, 1 ⇌ 2. The approximation is the sum of three Gaussians with weights, means, and variances defined in eqs 15 and 16. The left and right columns show performance at equal (the rates are K12 = K21 = k) and unequal (2K12 = K21 = k) populations of the states. For the purposes of illustration, we vary the rate of the transitions between the states, k, keeping the total count rate and the bin size a constant.
FIG. 1.
The Gaussian approximation (full curves) tested against exact FRET efficiency histograms (bars) for two conformational states with FRET efficiencies 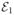 = 0.4 and
= 0.4 and 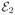 = 0.8 and different values of the transition rate given in the upper left corner of each histogram. Left column: the equilibrium probabilities of the two states are the same. Right column: the probabilities differ by a factor of 2. The total count rate n = 50 ms−1, the bin time is T = 1 ms, threshold value is NT = 30, histogram step h = 1/41. The Gaussian approximation, eq 5, consists of three Gaussians with parameters in eqs 15 and 16.
= 0.8 and different values of the transition rate given in the upper left corner of each histogram. Left column: the equilibrium probabilities of the two states are the same. Right column: the probabilities differ by a factor of 2. The total count rate n = 50 ms−1, the bin time is T = 1 ms, threshold value is NT = 30, histogram step h = 1/41. The Gaussian approximation, eq 5, consists of three Gaussians with parameters in eqs 15 and 16.
The shape of the histograms is sensitive to the product of the bin time and conformational relaxation rate (which is 2k and 3k/2 for the left and right columns, respectively). When the bin time is short compared to the conformational relaxation time (kT ≪ 1), the histogram is a sum of two peaks centered on the efficiencies of the states (the first row). The peaks are broadened only by shot noise. The shot noise width depends on the total number of photons during the bin time through 〈N−1〉. As the relaxation rate increases, these peaks do not move, but their amplitude drops and a new peak (approximately located at the mean FRET efficiency) appears. At large kT (the bottom row) only this peak survives, which is broadened by shot noise and conformational dynamics. The approximation is very accurate at small and large kT. The deviation from the exact histograms is most noticeable when the amplitudes of the three Gaussians are comparable.
If k is fixed at k = 1 ms−1 and the bin size T is varied, the resulting histograms look similar (of course, identical for T = 1 ms) to those shown in Fig. 1 with k being replaced by T. However, the peaks are slightly wider for T < 1 ms and narrower for T > 1 ms because of different average number of photons in a bin.
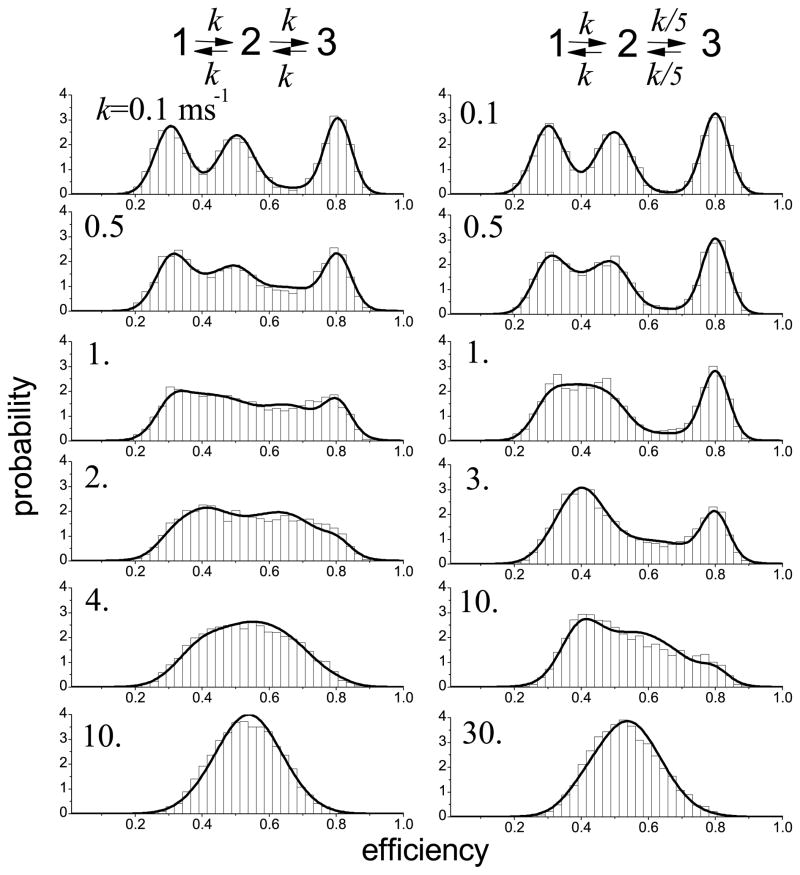
Figure 2 compares the Gaussian approximation and simulated histograms for a linear three-state model 1 ⇌ 2 ⇌ 3 with equal equilibrium populations. The approximation consists of six Gaussians (no transitions between states 1 and 3, so that c13 = 0). The parameters of the Gaussians are explicit functions of the efficiencies of the three states, 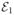 ,
, 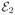 , and
, and 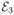 , and the rate k (see eqs 6, 13, 14, and Appendix A). In the first column, the transitions rates are the same. It can be seen that the collapse of the three peaks into one as the transition rate increases is well described. In the second column, the transitions between states occur on different time scales, i.e., the transitions between states 1 and 2 are much faster than those between 2 and 3. The histogram has three well resolved peaks when the bin time is much shorter than the relaxation time of fast transition between states 1 and 2 (the first row). As the transition rate increases, the first and the second peaks collapse (the diagonal 11th and 22th Gaussians disappear and the 12th Gaussian appears). The remaining two peaks eventually collapse to a single peak when the bin time becomes longer than the relaxation time of states 2 and 3.
, and the rate k (see eqs 6, 13, 14, and Appendix A). In the first column, the transitions rates are the same. It can be seen that the collapse of the three peaks into one as the transition rate increases is well described. In the second column, the transitions between states occur on different time scales, i.e., the transitions between states 1 and 2 are much faster than those between 2 and 3. The histogram has three well resolved peaks when the bin time is much shorter than the relaxation time of fast transition between states 1 and 2 (the first row). As the transition rate increases, the first and the second peaks collapse (the diagonal 11th and 22th Gaussians disappear and the 12th Gaussian appears). The remaining two peaks eventually collapse to a single peak when the bin time becomes longer than the relaxation time of states 2 and 3.
FIG. 2.
The Gaussian approximation (full curves) tested against simulated FRET efficiency histograms (bars) for a three-state model with FRET efficiencies 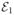 = 0.3,
= 0.3, 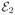 = 0.5,
= 0.5, 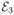 = 0.8 and different values of the transition rate given in the upper left corner of each histogram. Left column: equal transition rates. Right column: the transitions between states 1 and 2 are faster than those between 2 and 3. The simulated histograms were obtained from 5000 bins of duration T = 1 ms, the total count rate is n = 100 ms−1, other parameters are the same as in Fig. 1.
= 0.8 and different values of the transition rate given in the upper left corner of each histogram. Left column: equal transition rates. Right column: the transitions between states 1 and 2 are faster than those between 2 and 3. The simulated histograms were obtained from 5000 bins of duration T = 1 ms, the total count rate is n = 100 ms−1, other parameters are the same as in Fig. 1.
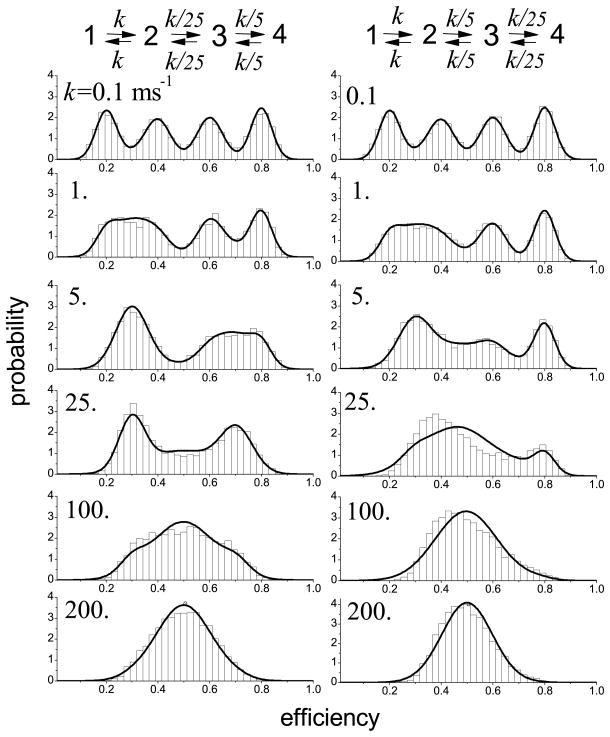
Figure 3 shows results for a linear four-state model 1 ⇌ 2 ⇌ 3 ⇌ 4 when the transitions occur on three different time scales. The approximation, which consists of eight Gaussians, describes the shape of the histograms remarkably well, except in the right column when k = 25 ms−1. In this case, which was specifically chosen because it is the most demanding for our approximation, most bins involve transitions among states 1, 2, and 3, or no transitions at all (i.e., the system stays in the state 4 during the entire bin time). There are very few bins in which all the states are visited. Our theory does not properly describe contributions from bins when more that two, but not all, states are visited during the bin time. Note that this problem does not arise for the kinetic scheme in the left column. Here, when k = 25 ms−1, most bins have transitions between a pair of states (i.e., 1 and 2 or 3 and 4) and this is correctly handled by the theory. Thus for a large number of states, even though it is always correct at short and long times, our approximation can deteriorate when transitions occur on many different time scales.
FIG. 3.
Same as Fig. 2, for four conformational states with FRET efficiencies 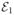 = 0.2,
= 0.2, 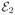 = 0.4,
= 0.4, 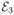 = 0.6,
= 0.6, 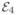 = 0.8 and transitions between the states on three different time scales. Left column: the fastest transitions are those between states 1 and 2 and the slowest ones are between states 2 and 3. Right column: the slowest transitions are between states 3 and 4.
= 0.8 and transitions between the states on three different time scales. Left column: the fastest transitions are those between states 1 and 2 and the slowest ones are between states 2 and 3. Right column: the slowest transitions are between states 3 and 4.
IV. CONCLUDING REMARKS
We have derived a simple expression for FRET efficiency histograms obtained in single-molecule measurements. For M interconverting conformational states, the FRET efficiency histogram is approximated by a sum of Gaussians (three for a two-state, seven for a general three-state system, etc.). The weights, means and variances of the Gaussians are not adjustable parameters, but are given by eqs 6, 13, and 14, in terms of the FRET efficiencies of the states and the transition rates. The variances of the Gaussians also involve the average of the reciprocal of the sum of donor and acceptor photons, 〈N−1〉. This depends on the laser intensity (through the total count rate), bin size and threshold value and can be obtained directly from the experimental data.
The Gaussian approximation can be readily used to analyze experimental histograms and extract the rates of conformational changes and the FRET efficiencies of the conformers. The efficiencies can be then related to the interdye distances after correcting for crosstalk, background noise, and fast polymer dynamics [24, 26]. Such complications do not influence the rates. The shape of FRET efficiency histograms is sensitive to the product of the bin time T and the conformational relaxation rates (i.e., the eigenvalues of the rate matrix), especially when one of these products is close to unity. In order to show the effect of conformational dynamics on the shape of the histogram, one can change the bin size (by simply rebinning the photon trajectory). Alternatively, one can change the conformational relaxation rate (e.g., by adding denaturant when studying protein folding). Chung et al. [19] have recently applied the three-Gaussian approximation with the parameters in eqs 15 and 16 to two-state protein folding and compared the extracted rates and apparent FRET efficiencies with those obtained by a likelihood method that does not require binning [25].
Our derivation assumes that the total count rate is the same for all conformational states and that the distribution of the sum of acceptor and donor photons is Poissonian. When only the energy transfer rate depends on the conformation, this is equivalent to the requirement that the gamma-factor (which is the product of the ratios of the acceptor and donor quantum yields and detection efficiencies) is equal to one. [28] For arbitrary total count rates, the extension of the Gaussian approximation is a challenging problem that we are trying to solve.
In free diffusion experiments, even when the total count rate does not depend on conformation, it fluctuates because laser intensity changes as the molecule diffuses through the confocal volume. Nevertheless, our results can be applied to diffusing molecules when the bins or bursts are preselected to optimize the probability that the molecule is quasi-immobilized, i.e., during the observation time, it only explored a limited region of the observation volume where the intensity did not change significantly [22]. The parameters of the Gaussians in the case of free diffusion are still given by eqs 6, 13, and 14, but now 〈N−1〉 is the reciprocal of the sum of acceptor and donor photons averaged over the experimentally observed non-Poissonian distribution. This average can be obtained directly from the bins or bursts selected to construct the FRET efficiency histograms. When a photon trajectory is divided into time bins of the same duration, the approximation should be used only for high threshold to eliminate bins during which the molecule leaves and then reenters the laser spot. In other words, the bins selected for analysis should not contain significant gaps where only a few photons are detected. When bursts of photons of variable duration are selected using a burst search algorithm, the bursts should be trimmed into segments of the same duration T in such a way that intensity is fairly uniform. The best strategy for selecting bins or bursts of photons during which the molecule is quasi-immobilized still needs to be established. In this regard, the rates obtained by fitting the histograms constructed from trajectory fragments using different burst/bin selection criteria could be compared with those obtained using an alternative procedure that we have developed [25] that does not require the quasi-immobilization assumption.
Acknowledgments
This work was supported by the Intramural Research Program of the National Institutes of Health, NIDDK.
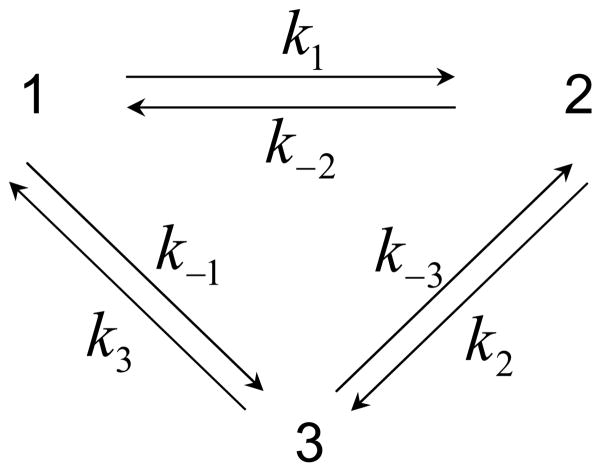
APPENDIX A: THREE-STATE SYSTEM
In this Appendix we present the formulas for the quantities that are required to calculate the 21 parameters of the 7 Gaussians (ij = 11, 22, 33, 12, 23, 13, 0) for a three-state system using eqs 6, 13 and 14. The rate matrix K for the three-state kinetic scheme shown in Fig. 4 is
FIG. 4.
Kinetic scheme for three interconverting conformational states.
| (A1) |
Detailed balance imposes the constraint that k1k2k3 = k−1k−2k−3.
The absolute values of the nonzero eigenvalues of this matrix are
| (A2) |
where
| (A3) |
The normalized equilibrium populations are
| (A4) |
By evaluating the matrix exponential in eq 4, it can be shown that 〈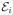 〉c is given by
〉c is given by
| (A5) |
where , X = (κ+φ− − κ−φ+)/(κ+ − κ−), Y = (φ− − φ+)/(κ+ − κ−), and φ± = φ(κ±T), where φ(τ) is given in eq 11. This is required to calculate using eq 14.
References
- 1.Jia Y, Talaga DS, Lau WL, Lu HSM, DeGrado WF, Hochstrasser RM. Chem Phys. 1999;247(1):69–83. [Google Scholar]
- 2.Deniz AA, Laurence TA, Beligere GS, Dahan M, Martin AB, Chemla DS, Dawson PE, Schultz P, Weiss S. Proc Natl Acad Sci USA. 2000;97(10):5179–5184. doi: 10.1073/pnas.090104997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schuler B, Lipman EA, Eaton WA. Nature. 2002;419(6908):743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 4.Rothwell PJ, Berger S, Kensch O, Felekyan S, Antonik M, Wöhrl BM, Restle T, Goody RS, Seidel CAM. Proc Natl Acad Sci USA. 2003;100(4):1655–1660. doi: 10.1073/pnas.0434003100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rhoades E, Cohen M, Schuler B, Haran G. J Am Chem Soc. 2004;126(45):14686– 14687. doi: 10.1021/ja046209k. [DOI] [PubMed] [Google Scholar]
- 6.Coban O, Lamb D, Zaychikov E, Heumann H, Nienhaus G. Biophys J. 2006;90(12):4605–4617. doi: 10.1529/biophysj.105.078840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moerner WE. Proc Natl Acad Sci USA. 2007;104(31):12596–12602. doi: 10.1073/pnas.0610081104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mukhopadhyay S, Krishnan R, Lemke EA, Lindquist S, Deniz AA. Proc Natl Acad Sci USA. 2007;104(8):2649–2654. doi: 10.1073/pnas.0611503104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kinoshita M, Kamagata K, Maeda A, Goto Y, Komatsuzaki T, Takahashi S. Proc Natl Acad Sci USA. 2007;104(25):10453. doi: 10.1073/pnas.0700267104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wozniak A, Schröder G, Grubmüller H, Seidel C, Oesterhelt F. Proc Natl Acad Sci USA. 2008;105(47):18337. doi: 10.1073/pnas.0800977105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roy R, Hohng S, Ha T. Nature methods. 2008;5(6):507–516. doi: 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chung HS, Louis JM, Eaton WA. Proc Natl Acad Sci USA. 2009;106(29):11837– 11844. doi: 10.1073/pnas.0901178106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Santoso Y, Joyce C, Potapova O, Le Reste L, Hohlbein J, Torella J, Grindley N, Kapanidis A. Proc Natl Acad Sci USA. 2010;107(2):715. doi: 10.1073/pnas.0910909107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hofmann H, Hillger F, Pfeil SH, Hoffmann A, Streich D, Haenni D, Nettels D, Lipman EA, Schuler B. Proc Natl Acad Sci USA. 2010;107(26):11793–11798. doi: 10.1073/pnas.1002356107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hanson J, Duderstadt K, Watkins L, Bhattacharyya S, Brokaw J, Chu J, Yang H. Proc Natl Acad Sci USA. 2007;104(46):18055. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pljevaljcic G, Millar DP, Deniz AA. Biophys J. 2004;87(1):457–467. doi: 10.1529/biophysj.103.036087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kalinin S, Valeri A, Antonik M, Felekyan S, Seidel CAM. J Phys Chem B. 2010;114(23):7983–7995. doi: 10.1021/jp102156t. [DOI] [PubMed] [Google Scholar]
- 18.Santoso Y, Torella JP, Kapanidis AN. Chem Phys Chem. 2010;11:2209–2219. doi: 10.1002/cphc.201000129. [DOI] [PubMed] [Google Scholar]
- 19.Chung HS, Gopich IV, McHale K, Cellmer T, Louis JM, Eaton WA. J Phys Chem A. 2010 doi: 10.1021/jp1009669. Articles ASAP. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gopich IV, Szabo A. J Phys Chem B. 2003;107(21):5058–5063. [Google Scholar]
- 21.Gopich I, Szabo A. J Chem Phys. 2005;122(1):14707-1–18. doi: 10.1063/1.1812746. [DOI] [PubMed] [Google Scholar]
- 22.Gopich IV, Szabo A. J Phys Chem B. 2007;111(44):12925–12932. doi: 10.1021/jp075255e. [DOI] [PubMed] [Google Scholar]
- 23.Wolfram Research, Inc. Mathematica Edition: Version 7.0. Wolfram Research, Inc; Champaign, Illinois: 2008. [Google Scholar]
- 24.Gopich IV, Szabo A. Adv Chem Phys. in press. [Google Scholar]
- 25.Gopich IV, Szabo A. J Phys Chem B. 2009;113(31):10965–10973. doi: 10.1021/jp903671p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Makarov DE, Plaxco KW. J Chem Phys. 2009;131:085105–1-6. doi: 10.1063/1.3212602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.The threshold is usually applied in free diffusion experiments, in order to minimize the number of bins where the molecule is not inside the spot during the entire bin time. However, even in the case of immobilized molecules, a threshold NT = 1 is obviously required to avoid division by zero in the FRET efficiency.
- 28.It is possible that the gamma-factor is not equal to one but the total count rate is the same for all states when some parameter, other than the energy transfer rate (e.g., the quantum yield [19]) also depends on conformation.