Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2010 Dec;20(12):1730–1739. doi: 10.1101/gr.108217.110

Gene expression profiling of human breast tissue samples using SAGE-Seq

Zhenhua Jeremy Wu 1,2, Clifford A Meyer 1,2,9, Sibgat Choudhury 3,4,5,9, Michail Shipitsin 3,4,5, Reo Maruyama 3,4,5, Marina Bessarabova 6, Tatiana Nikolskaya 6, Saraswati Sukumar 7, Armin Schwartzman 1,2, Jun S Liu 8,10, Kornelia Polyak 3,4,5,10, X Shirley Liu 1,2
PMCID: PMC2989999  PMID: 21045080

Abstract

We present a powerful application of ultra high-throughput sequencing, SAGE-Seq, for the accurate quantification of normal and neoplastic mammary epithelial cell transcriptomes. We develop data analysis pipelines that allow the mapping of sense and antisense strands of mitochondrial and RefSeq genes, the normalization between libraries, and the identification of differentially expressed genes. We find that the diversity of cancer transcriptomes is significantly higher than that of normal cells. Our analysis indicates that transcript discovery plateaus at 10 million reads/sample, and suggests a minimum desired sequencing depth around five million reads. Comparison of SAGE-Seq and traditional SAGE on normal and cancerous breast tissues reveals higher sensitivity of SAGE-Seq to detect less-abundant genes, including those encoding for known breast cancer-related transcription factors and G protein–coupled receptors (GPCRs). SAGE-Seq is able to identify genes and pathways abnormally activated in breast cancer that traditional SAGE failed to call. SAGE-Seq is a powerful method for the identification of biomarkers and therapeutic targets in human disease.

Microarrays and sequencing-based technologies have been widely used for gene expression profiling to create global pictures of cellular function (Adams et al. 1991; Schena et al. 1995; Velculescu et al. 1995). Early gene expression data analysis algorithms focused on biases and limitations introduced by each technology. For array-based technologies such as Affymetrix and NimbleGen microarrays, methods have been developed to overcome probe-specific behavior, GC content bias, dye bias, and cross-hybridization (Yang and Speed 2002; Johnson et al. 2006; Song et al. 2007). While traditional sequencing-based gene expression methods such as serial analysis of gene expression (SAGE) (Velculescu et al. 2000; Polyak and Riggins 2001) and expressed sequence tag (EST) (Adams et al. 1991) sequencing allow the identification and quantification of both known and novel genes, they were severely limited by sequencing throughput and cost (Adams et al. 1991; Velculescu et al. 1995). As next-generation sequencing platforms provide increased throughput at reduced cost (Johnson et al. 2007), their applications to SAGE become a natural choice for comprehensive analysis of gene expression (SAGE-Seq) or other applications (Bloushtain-Qimron et al. 2008) and promise greater sensitivity and specificity (Morrissy et al. 2009). However, SAGE-Seq poses its unique challenges with regard to data normalization, read alignment, identification of differentially expressed genes, and comparison to traditional SAGE.

To address the above questions, we describe data analysis pipelines to process SAGE-Seq data on mammary epithelial cells isolated from normal and cancerous human breast tissue samples deep sequenced on the Illumina platform (formerly known as Solexa). In order to normalize the SAGE-Seq raw data across different libraries, we utilize a nonparametric empirical Bayes method to reduce the sequence sampling bias (Robbins 1956; Gale and Sampson 1995). Appropriate global diversity measurements within and across data sets are evaluated and used to cluster the libraries. We propose a mapping strategy to align SAGE-Seq tags to the genome. We utilize the mapping information to minimize sequencing errors and obtain accurate quantification of sense and antisense transcripts corresponding to RefSeq and mitochondrial genes. We develop a method to identify differentially expressed genes with statistical significance and show its utility on differential gene detection between normal and neoplastic mammary epithelial cells. We also compare traditional SAGE and SAGE-Seq data sets and demonstrate the overwhelming power of SAGE-Seq to detect 20 times more differentially expressed genes with higher statistical confidence. Pathway analysis shows that the greater sequencing depth obtained by SAGE-Seq allows the identification of more than three times as many statistically significant Gene Ontology (GO) terms than by traditional SAGE and improves their statistical significance score. Many of these pathways are newly identified by SAGE-Seq and are completely missed by traditional SAGE.

Results

SAGE-Seq library generation

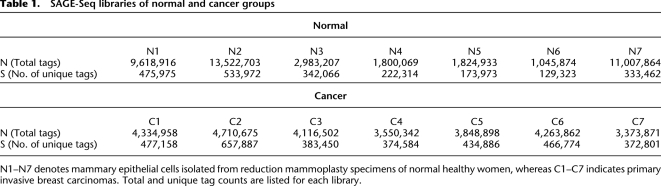
SAGE-Seq libraries in this study were generated from 50,000 to 100,000 uncultured mammary epithelial cells isolated from breast tissue of normal healthy women and from primary invasive ductal breast carcinomas (Table 1). Immunomagnetic bead purification of the cells and SAGE library generation was performed essentially as previously described (Shipitsin et al. 2007), except when modifications were necessary for sequencing on the Illumina platform (see Methods). The raw Illumina data consists of millions of sequence tags, but only the first 21 bp of each read is useful here. The first 4 bp are all “CATG,” which is the recognition site of the NlaIII-mapping restriction enzyme used during the construction of the SAGE libraries. MmeI is used as a tagging enzyme to cut 21 bp 3′ of its recognition site present in the linker immediately 5′ to the NlaIII site. Thus, a SAGE-Seq tag is composed of a 5′ “CATG” followed by a 17-bp unique transcript-specific sequence. The cross-lane correlation shows high reproducibility of the abundance measurement in SAGE-Seq libraries (Supplemental Fig. S1).

Table 1.

SAGE-Seq libraries of normal and cancer groups

graphic file with name 1730tbl1.jpg

Open in a new tab

N1–N7 denotes mammary epithelial cells isolated from reduction mammoplasty specimens of normal healthy women, whereas C1–C7 indicates primary invasive breast carcinomas. Total and unique tag counts are listed for each library.

Pipelines for tag mapping and sequencing error minimization

To analyze the expression of individual genes, we used SeqMap (Jiang and Wong 2008) and propose a mapping pipeline (Supplemental Fig. S3) to align tags to RefSeq genes. This mapping pipeline allows us to map tags to mitochondrial, sense, and antisense transcripts of RefSeq genes. If a transcript has multiple CATGs, then the one closest to the poly(A) tail (3′ end) is called the best tag (Fig. 1A). If a tag is mapped to multiple RefSeq locations with only one tag being a best tag, the best tag is considered as the uniquely mapped location. Otherwise, the tag is a nonunique tag, and its count is evenly divided among mapped locations. Sense tags are defined as tags that are mapped to the sense strand of exons of known transcripts. Antisense tags are defined as tags that cannot be mapped as sense tags, but are able to map against the antisense strand of known transcribed genes (He et al. 2008).

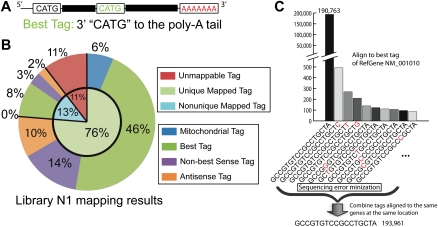
Figure 1.

Figure 1.

Open in a new tab

SAGE-Seq tag alignment and sequencing error minimization. (A) Best tag is defined as the tag next to the 3′-most NlaIII site (CATG) to the poly(A) tail. (B) Tag alignment statistics of sample N1 according to the tag alignment pipeline in Supplemental Figure S3. Detailed mapping of other data sets is shown in Supplemental spreadsheet 1. (C) Presumed sequencing errors revealed during tag mapping. All of the listed tags are best tags uniquely mapped to the same RefSeq gene “NM_001010.” (Not every tag uniquely mapped to this gene at the same location is listed.) X-axis is the tag sequences listed in descending order of tag count. The one-base difference in sequence most likely due to sequencing error is marked in red. Sequencing error minimization step for this particular example is done in the following way: sum up the count of all these tags and assign it to tag “CATGGCCGTGTCCGCCTGCTA” and remove all the other tags.

Mapping results can also be used to identify sequencing errors as shown in Figure 1C. We combined the counts of the tags that are uniquely mapped to the same genes at the same locations to reduce noise and sampling bias due to sequencing error (sequencing error minimization), which reduces the number of false positives in subsequent differentially expressed gene analysis. The tag in the reference genome is used as the consensus tag for sequencing error minimization. For example, suppose there are 190,793 occurrences of the tag “GCCGTGTCCGCCTGCTA,” which maps exactly to the reference genome. If there are 3198 tags that differ from this tag by a single base pair, combined together after sequencing error minimization there is a total of 193,961; therefore, the fraction of single base pair mismatches is 1.6% (3198/193,961). This is equivalent to a 0.1% sequencing error rate per base (17 × 0.001 × [1 − 0.001]16 = 1.7%). This is consistent with the estimation for high-quality reads of Illumina (Shendure and Ji 2008). Using library N1 as an example, we demonstrate that about 76% of the tags can be uniquely mapped using our pipeline; 6% of these tags are mitochondrial tags, 46% are unique RefSeq sense best tags, 14% are unique sense non-best tags, and 10% are unique antisense tags (Fig. 1B; Supplemental spreadsheet 1 for the mapping results of other libraries). All subsequent analyses are conducted on the 46% of unique sense best tags.

Overview of normal and cancer transcriptomes

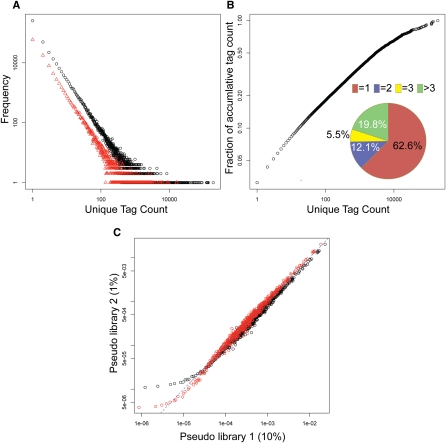
Gene expression patterns of cell populations in many ways resemble species populations of different species in an ecosystem, where an individual of a species is like a transcript in our study. In typical ecosystems some species are abundant, whereas the majority of species are rare (Magurran 2003). Similarly, SAGE-Seq profiling data shows that most of the genes are expressed at low levels (rare transcripts) and a few genes are expressed in large amounts (abundant transcripts) (Fig. 2A,B). Interestingly, although rarely expressed tags are the majority, highly expressed unique tags are still dominant when considering their population (expression level). By plotting the accumulative fraction of tag count out of total tag count as a function of unique tag count, we found that although the unique tags with one count are 63% of S (overall number of unique tags), they only account for 3% of N (the total tag count) (Fig. 2B). The question arises as to whether these low-count tags are spurious tags dominated by sequencing errors or true tags expressed at very low levels. As described above, after sequencing-error minimization, tags with one mismatch due to sequencing errors can be identified and corrected based on mapping information. Tags with more than two mismatches represent only 0.01% of all the reads (see Methods). Thus, these low-count tags cannot be explained by sequencing errors, as they are much more abundant than what could be explained by such errors. They are possibly a mixture of low-abundant transcripts and nucleic acid contamination (possibly genomic DNA), as the Sage-Seq preparation protocol does not include a step for the elimination of genomic DNA from the RNA samples.

Figure 2.

Figure 2.

Open in a new tab

Frequency plot of unique tag count and nonparametric empirical Bayes method. (A) Frequency of unique tag counts in libraries N1 (black) and N5 (red). X-axis is the observed tag count and y-axis is the frequency that shows the number of unique tags with a specific count. (B) Pie chart depicting the distribution of unique tags in library N1: 62.6% of unique tags has tag count 1, 12.1%, count 2, 5.5%, count 3, and 19.8% counts larger than 3. The outer plot shows the accumulative fraction of unique tag counts. Although 62.6% unique tags have count 1, they only account for 3% of total tag counts. (C) Scatter plot of tag proportion. X-axis is the proportion of tags in pseudo library 1 obtained by randomly sampling 10% of library N1. Y-axis is the average proportion of pseudo library 2 obtained by randomly sampling 1% of library N1. The data points are obtained in the following way. For example, find all of the tags in pseudo library 1 with proportion 1 × 10−6, then calculate the mean proportion of these tags in pseudo library 2, which gives for example 1 × 10−5. This gives a data point at (1 × 10−6, 1 × 10−5). The dashed line is y = x. Black symbols indicate the proportion using the maximum likelihood estimator, where overestimation in the low and intermediately expressed tags (<100/million) and underestimation in the highly expressed tags (>100/million) are observed. Red symbols mark the proportion calculated using nonparametric empirical Bayes method with improved, more comparable corrected proportions between two libraries with different sequencing depth in both low and highly abundant tags.

Nonparametric empirical Bayes normalization

If each SAGE library were sequenced to the same depth (i.e., the same N), tag counts in different libraries would be directly comparable. However, although most of the samples were subjected to one lane of Illumina sequencing, N varies from 1 million to 13 million in different libraries (Table 1). Thus, in order to accurately compare gene expression patterns of different libraries, normalization of tag counts is needed. One intuitive way for normalization is to use proportion p, defined as n/N, where n is the count of a unique tag. Known as the maximum likelihood (ML) estimator for population frequency (Fisher 1922). This approach has the drawback that the p of any tag that is missing from the sequencing data (undetected tags) is assigned to be zero, while it overestimates the p of low and intermediate abundance tags and underestimates highly abundant tags (Fig. 2C, black symbols). In addition, high-throughput quality reads from the Illumina Genome Analyzer provide a good estimate for the population frequency of tags at different enrichment levels (Fig. 2A). This heterogeneous population of tag frequency applied as a prior indicates that the best estimation of tag enrichment should be smaller than the observed count, because the population of less-abundant transcripts is larger than that of abundant ones (Fig. 2A). Thus, a more sophisticated approach for SAGE-Seq data normalization is needed.

We applied the nonparametric empirical Bayes (NEB) method (Good 1953; Robbins 1956; Orlitsky et al. 2003) to normalize libraries with different sequencing depths (see Methods). There are two advantages of NEB over ML. First, whereas ML simply considers the undetected tags as zero, NEB estimates the proportion of undetected tags as P0 = n1/N, where n1 is the frequency of unique tags with count one. To validate the accuracy of the NEB estimator of P0, we randomly sampled library N1 from 1% to 10% at a step of 1% to generate 10 pseudo libraries with different sequencing depths. We used NEB to estimate the P0 of the undetected tags in each pseudo library, compared them with their respective proportion in the original library, and found that they were in good agreement (Supplemental Fig. S2). Second, NEB adjusts tag counts based on both the observed count and the nature of the frequency distribution of unique tag counts (Fig. 2A), which is applied as the empirical prior to reduce the sequence sampling bias (Gale and Sampson 1995). It also renormalizes the adjusted proportion by the estimated total proportion of detected tags to 1 – P0 (See Supplemental material section “Algorithms comparison for differentially expressed genes” for comparison between NEB and ML normalization). To show the effect of sampling bias, we randomly sampled 10% (pseudo library 1) and 1% (pseudo library 2) tags from library N1 to generate two pseudo libraries with a 10-fold difference in sequencing depth. When comparing the proportion of tags in the two pseudo libraries, we found that the proportions are much more comparable after NEB normalization, whereas ML overestimates p for low-count tags and underestimates p for high-count tags in pseudo library 2 with lower sequencing depth (Fig. 2C).

Diversity of normal and cancer transcriptomes

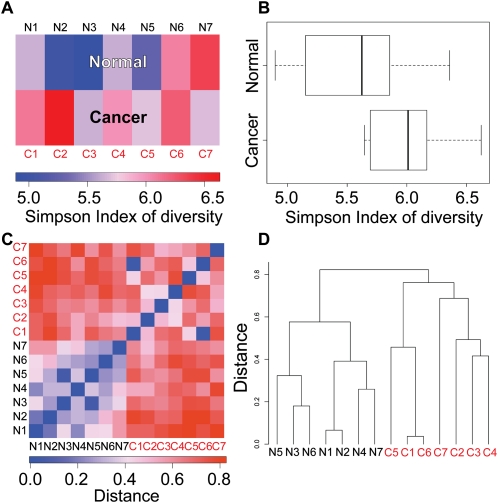
One advantage of sequence-based gene expression profiling is that it measures the absolute expression levels of many genes simultaneously. Thus, we can obtain a global view of transcript diversity within the cells and also among libraries. We used two different measures to compare transcript diversity in the libraries we analyzed. First, we used Simpson index of diversity (SID) (Simpson 1949) to characterize transcriptome diversity within each library. SID captures the variance of the tag count distribution and is independent of sequencing depth (see Methods). Higher values indicate higher diversity, which means the tag counts are more widely distributed among different genes. We found in our data sets that libraries from cancer samples, in general, have higher diversity than that from normal (Fig. 3A,B; Wilcoxon rank-sum test, P = 0.07284; the P-value is in the borderline of significance due to limited number of samples). This trend could be due to the fact that tumors express many more genes, either because they are composed of more diverse populations of cells or because they lost normal epigenetic controls that maintain tissue and cell type-specific gene expression patterns (Fig. 4D).

Figure 3.

Figure 3.

Open in a new tab

Diversity of normal and cancer transcriptomes. (A) Simpson index of diversity to measure within-library gene expression diversity. Libraries in the cancer group show higher within-library diversity compared with the normal group. (B) Box plot depicting Simpson index of diversity of normal and cancer samples. P = 0.07284 (Wilcoxon rank-sum test). (C) Distance defined as “1 – Morisita-Horn similarity index” is used to measure gene expression diversity across libraries. Libraries in the normal group are more similar to one another, whereas cancer libraries are more diverse. (D) Hierarchical clustering using “distance” defined in C separates normal and cancer libraries.

Figure 4.

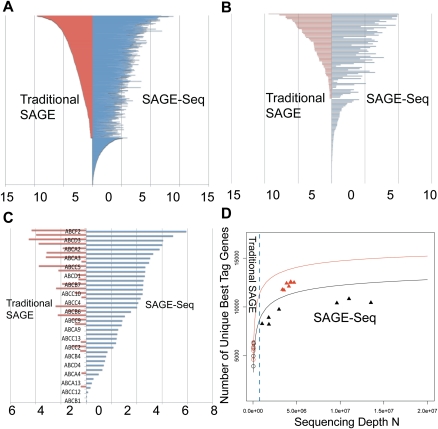
Figure 4.

Open in a new tab

SAGE-Seq tag mapping and sequencing depths saturation curve. (A–C) Differential coverage of expression profiles in three selected gene families: transcription factors (A), GPCRs (B), and ABC transporters (C). Y-axis lists the genes and x-axis is the mean gene expression index (logarithm of the normalized tag count). Red and blue colors mark traditional SAGE and SAGE-Seq, respectively. SAGE-Seq detects many more genes in these gene families than traditional SAGE does. (D) Number of unique best-tag genes (y-axis) in relation to sequencing depth (x-axis). The number of best-tag genes is the number of unique genes mapped by best tags, counted as one if multiple tags are mapped to the best tag of the same gene. Black and red colors indicate normal and cancer groups, respectively. Symbols “○” and “▴” mark traditional SAGE and SAGE-Seq, respectively. Solid curves (saturation curves) are from simulation by sampling the combination of all libraries in the normal (or cancer) group, which depict the trend with increasing sequencing depth. Traditional SAGE identifies much fewer best-tag genes than the SAGE-Seq. SAGE-Seq shows that cancer samples (red triangles) have a larger number of unique best-tag genes than normal samples (black triangles). This difference is not detected by traditional SAGE (red circles vs. black circles).

The second type of diversity is measured across libraries to study the gene expression diversity among libraries derived from different individuals. To ask how similar two libraries, A and B, are we used the Morisita-Horn (MH) similarity index CMH(A,B) (Wolda 1983) (see Methods), and calculated their distance as D ≡ 1 − CMH (A, B). The Morisita-Horn index has several advantages over other distance metric measurements. First, MH index is not strongly influenced by N and S, which is essential to ascertain that the difference of the measurement is not due to differences in sequencing depths. Second, compared with distance based on Pearson cross correlation, MH index has no singularity for data with standard deviation approaching zero.

We found that cancer samples are not only more diverse within each individual (Simpson index), but are also more diverse (MH index) across different individuals (Fig. 3C). This is not entirely surprising, since normal cells have a physiologic role that is essentially the same in different individuals, whereas tumors are genetically diverse and have no functional role in the body; thus, there is no selection pressure to keep their phenotype within certain limits. The hierarchical clustering of the libraries based on the MH index showed that cancer libraries are more different from each other (larger distance across libraries), and they are also very clearly separated from the normal libraries (Fig. 3D).

Data quality of SAGE-Seq compared with traditional SAGE

Following read alignment and sequencing error minimization, we further evaluated the ability of SAGE-Seq to profile genome-wide gene expression and compared it with traditional SAGE. With deeper sequencing coverage, SAGE-Seq gave much higher data correlation between different libraries within the same group (Supplemental Fig. S4). In addition, traditional SAGE can only detect genes with proportions from 10−5 to 10−3, whereas SAGE-Seq shows a much larger dynamic range (defined as the detected range of gene enrichment), covering about five orders of magnitude from 10−7 to 10−2. For example, genes encoding for transcription factors are often expressed at intermediate or low levels, and SAGE-Seq detected the expression of around 1300 transcription factors (out of 1658 total in the human genome) in our samples. Most of the transcription factors detected by traditional SAGE are also detected by SAGE-Seq, whereas 384 transcription factors are only detected by SAGE-Seq (Fig. 4A). We observed similar phenomena for genes encoding for GPCRs and ABC-transporters (Fig. 4B,C), which are known to be differentially expressed between normal and cancer cells and are expressed at relatively low levels (Li et al. 2005; Dean 2009).

To determine how far the sequenced SAGE-Seq libraries are from saturation, we calculated the number of unique best-tag genes (uniquely mapped best tags) detected in relation to the sequencing depth of each library. The number of uniquely mapped best tags is a good indicator of the number of genes detected. Deeper sequencing is expected to detect more genes until a plateau is reached when all of the genes are detected. To overcome the lack of data covering a broad range of sequencing depth, we combined all cancer (or normal) libraries and analytically calculated the number of detected unique tag genes at different sequencing depths to obtain the saturation curve (solid lines in Fig. 4D; see Methods for analytic calculation). For sequencing depths below 3 million reads, the number of genes detected increases dramatically with sequencing depth (fast-growth region). The rate continues to grow at a slower rate (slow-growth region) above 5 million reads, until it plateaus around 10 million reads for both normal and cancer samples (Fig. 4D). This suggests that the ideal sequencing depth for SAGE-Seq should be above 10 million reads, with a minimum desired sequence depth of 5 million per library. Sage-Seq data points (triangles) are all close to or in the slow-growth region, where most of the transcriptome is sequenced. Traditional SAGE data points (circles) are still in the fast-growth region, where more than half of the transcriptome is not detected due to low-sequencing depth. Figure 4D also indicates that more genes are expressed in cancer (red triangle) than in normal (black triangle) samples, which is consistent with our previous finding that cancer samples have higher transcript diversity within each library and across libraries.

Sampling noise and biological variability

To detect differentially expressed genes between two conditions, it is important to know the sources of gene expression variability. A major source of variability in SAGE-Seq or any techniques using sequencing techniques is sampling variation; and most algorithms analyzing traditional SAGE data tackled this using various approaches (Velculescu et al. 1995; Cai et al. 2004). Sequence-based transcriptome profiling can be modeled as a binomial sampling process with replacement that approximates a Poisson distribution, because using current technologies (Kharchenko et al. 2008), sequenced transcripts are a tiny minority of the total amount of cDNA loaded on the sequencers. If the same library is sequenced multiple times, Poisson model dictates that the variance in tag counts of a particular gene is equal to its abundance.

When examining the empirical variance of genes in the normal libraries versus their respective normalized count (normalized by NEB and scaled to the same sequencing depth of N = 1 million), the observed variance indeed depends on its gene expression level (count) (Fig. 5A; red dashed line with slope αobv ≈ 2.0 in log-log plot). However, if we denoted variance-to-mean slope for random binomial sampling as αrbs, which is expected to be 1.0 according to Poisson distribution (rbs stands for random binomial sampling, blue dashed line in Fig. 5A), we observed overdispersion (αobv ≈ 2αrbs > αrbs = 1), which means that the excess variability of the observed data is significantly larger than the variability expected in the random reference model (Poisson model in this case). This suggests a nonlinear dependency of gene expression variability on the mean expression level, which indicates that in our data sets overdispersion could be the result of variation from biological individuals in addition to the sampling variation (see Methods). We also observed overdispersion among a subset of housekeeping genes and subsets of uniquely mapped best tags both in normal and cancer groups (data not shown).

Figure 5.

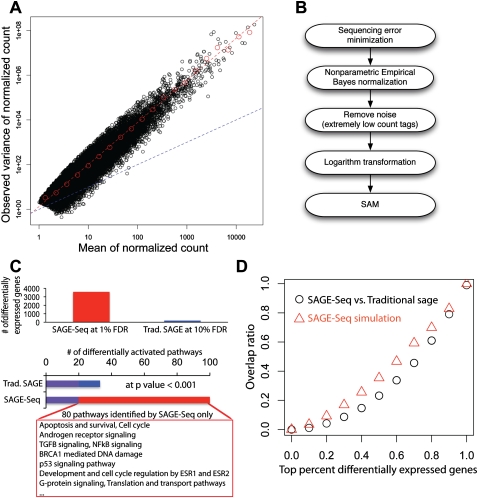
Figure 5.

Open in a new tab

Differentially expressed genes and their variance. (A) Mean-to-variance plot for the seven normal libraries after removing the noise and normalization. Red dashed line is the best linear fit in log-log plot. The slope gives the exponent αobv ≈ 1.9 Blue dashed line is the mean-to-variance line introduced by sampling. (B) Pipeline for the identification of differentially expressed genes: (1) Sequencing error minimization: After tag alignment, tags that are mapped to the same genes at the same locations are combined together; (2) NEB is used to normalize different libraries with different sequencing depth; (3) filtering to remove tags with counts ≥3 per million in less than two libraries followed by log2 transformation; (4) SAM is used for the detection of differentially expressed genes. (C) Detected differentially expressed genes (top) and activated pathways (bottom) in SAGE-Seq and traditional SAGE. SAGE-Seq identifies approximately 4000 differential genes at 1% FDR, while traditional SAGE identifies <200 at a much looser cut off (10% FDR). At P = 0.001, SAGE-Seq identifies 99 pathways significantly activated in breast cancer, while traditional SAGE only shows 32. The 80 pathways only identified by SAGE-Seq and missed by traditional SAGE are all breast cancer-related pathways. (D) The overlap ratio (defined as the number of overlapping genes divided by the gene number in traditional SAGE in the top x percent differentially expressed genes, where x changes between 0 and 1. The black symbols depict actual data (SAGE-Seq vs. traditional SAGE). It indicates that there is little overlap in the top differentially expressed genes list between SAGE-Seq and traditional SAGE. The red symbols indicate simulation (SAGE-Seq vs. sampled down SAGE-Seq). Sampled down SAGE-Seq means to binomially sample 50 k tags from each SAGE-Seq library; 50,000 is a typical sequencing depth for traditional SAGE. Simulation confirms the same conclusion as that drawn from the actual data: SAGE-Seq gives a different top differentially expressed gene list compared with traditional SAGE. Deeper sequencing reveals that traditional SAGE identifies different sets of top differentially expressed genes than that of SAGE-Seq, confirming our conclusion that traditional SAGE lacks sufficient sequencing depth.

Analysis of differentially expressed genes

One of the major applications of transcriptome profiling is the identification of genes differentially expressed between different samples. After tag alignment and sequencing error minimization, our analysis pipeline for the identification of differentially expressed genes (Fig. 5B) first applies the nonparametric empirical Bayes method as a normalization step to reduce sampling bias and to bring different libraries to the same sequencing depth (N = 1 million; Normalized sequencing depth has no influences on differential genes, which is different from sequencing depth of the library.). After normalization, tags with counts ≥3 per million in ≤2 out of all the libraries were discarded. This effectively removes a significant portion of noninformative tags, which either contain outliers or have too low counts to detect differential expression with statistical significance, and saves computational time and storage space during subsequent analysis.

The logarithmic transformation is then applied to obtain the expression index and decouple the correlation between the observed variance and the mean expression level of genes (Fig. 5A). Quantitatively, the observed variance in our libraries is proportional to the square of the expression level. According to the delta method in statistics, the logarithmic transformation is the right transformation to stabilize the variance (see Methods). An alternative transformation is arcsinh, which is also a logarithm-like transformation, but with the advantage of no singularity at zero (Huber et al. 2002). Supplemental Figure S5 shows that after applying a logarithmic transformation of base 2 on the normalized count, for intermediate and high abundance tags the variance of the expression index is almost independent of its mean. Finally, the SAM (significance analysis of microarray) algorithm is applied to the expression indices in the two groups of samples to identify differentially expressed genes (Fig. 5B; Tusher et al. 2001). We also tried the standard t-test and found many false positives resulting from the underestimated empirical standard deviation that gives rise to extreme t values. SAM algorithm stabilizes variance to reduce false positives. Other statistical tests could be used in this step instead of using SAM, such as Robinson and Smyth's moderated t-test or Baggerly's tw test (Baggerly et al. 2003, 2004; Lu et al. 2005; Robinson and Smyth 2007). Another alternative for the analysis of differentially expressed genes is to use overdispersed models such as overdispersed logistic regression or overdispersed log-linear model (Baggerly et al. 2004; Lu et al. 2005). However, whether these model-based methods can be scaled up to the deeper sequencing depths of SAGE-Seq data needs to be verified through systematic analysis with more data.

We compared the lists of differentially expressed genes between normal and cancer for both SAGE-Seq and traditional SAGE. The expression (i.e., presence) of 10,052 and 4953 best-tag genes is detected by SAGE-Seq and traditional SAGE, respectively (Supplemental spreadsheet 2), with 99% (4904) overlap. We calculated the false discovery rate (FDR) using the Q-value package of Storey and Tibshirani (2003). Traditional SAGE does not sequence deep enough to allow similar P-value or FDR cutoffs as SAGE-Seq. SAGE-Seq identifies about 4000 differentially expressed best tag genes at 1% FDR, whereas traditional SAGE detects less than 200 at 10% FDR (Fig. 5C). Deeper sequencing gives SAGE-Seq increased statistical power to detect more differentially expressed genes. To compare the two lists of differentially expressed genes, we examined the rank order of genes based on their t-scores. The top 10% of genes with the highest t-scores (495 genes for traditional SAGE and 1005 for SAGE-Seq) are used as differentially expressed gene lists for comparison between these two methods. SAGE-Seq detected all 26 genes known to be differentially expressed between normal and breast cancer samples based on prior studies, whereas traditional SAGE only identified four (Supplemental Table S1).

Surprisingly, we only identified 54 genes when comparing the overlap between the top 10% of genes identified as differentially expressed by the two methods. Further analysis confirmed that the top differentially expressed genes detected by traditional SAGE and SAGE-Seq is quite different (Fig. 5D; black symbols). Many factors could contribute to this discrepancy, such as differences in library preparation protocols and samples. Beside these factors, we observed that the top differentially expressed genes detected by SAGE-Seq are often expressed at moderate or low levels (∼100/million; see Supplemental Fig. S7), which traditional SAGE either completely fails to detect or has too low (two or three) a tag count to show differential expression with statistical power. These differentially expressed tags in SAGE-Seq are unlikely to be from sequencing errors based on the tag counts observed. These data imply that the increased sequencing depth of SAGE-Seq results in the detection of a different set of differentially expressed genes. To demonstrate this we resort to simulations, as the use of defined cell populations with limited numbers of cells isolated from primary breast tissues did not allow the generation of both SAGE-seq and traditional-SAGE libraries from the same sample. We took the 14 SAGE-Seq libraries and sampled them down (binomial sampling) to the sequencing-depth level of traditional SAGE (∼50,000). The top differentially expressed genes of these simulated libraries also show little overlap with the original SAGE-Seq libraries (Fig. 5D, red symbols).

Pathways and networks differentially activated between normal and cancer samples

To determine what signaling pathways are identified as differentially activated by SAGE-Seq and traditional SAGE, we applied a combination of gene ontology and pathway analyses for the differentially expressed gene sets using MetaCore (Nikolsky et al. 2009). However, SAGE-Seq identifies 3587 differentially expressed genes at 1% FDR cut off, whereas the most significantly differentially expressed gene identified by traditional SAGE has an FDR >9%. Thus, we decided to take the top 10% of differentially expressed genes identified by traditional SAGE genes (493) and SAGE-Seq genes at 1% FDR (3587), since an FDR cutoff gives too few differentially expressed genes in traditional SAGE (Supplemental spreadsheet 3). MetaCore provides a P-value for each tested GO term or pathway name. Using a P-value of 10−3 as the cutoff for significance, SAGE-Seq identifies 99 pathways to be significant, whereas with traditional SAGE only 32 have an overlap of 19 (Fig. 5C; Supplemental spreadsheet 4). The following pathways and GO processes are commonly enriched between SAGE-Seq and traditional SAGE: apoptosis, cell adhesion, cytoskeleton remodeling, development, immune response, G-protein signaling, signal transduction, and transcription. These are all pathways known to be relevant to breast cancer, and in each category SAGE-Seq identified the term with higher statistical significance. The 80 additional significant GO categories identified by SAGE-seq but not by traditional SAGE are all related to cancer, generally or specifically to breast cancer, based on published literature, especially categories such as Apoptosis and survival, Cell cycle, Androgen receptor signaling, TGFB signaling, NFKB signaling, BRCA1-mediated DNA damage, p53 signaling pathway, Development and cell cycle regulation by ESR1 and ESR2 (estrogen receptor), G-protein signaling, and translation and transport pathways. The genes in these pathways are typically expressed at low levels, and this is consistent with Figure 4, B and C, showing many genes in the GPCR- and ABC-transporter families as detected by SAGE-Seq, but missed by traditional SAGE (Li et al. 2005; Dean 2009). It is especially worth noting that the NFKB and TGFB pathways, which appeared in multiple GO and pathway branches and are known to be differentially regulated in breast cancer (Shipitsin et al. 2007), are found to be significant in SAGE-Seq, but insignificant in traditional SAGE.

Discussion

In this study, we systematically evaluated SAGE-Seq for transcriptome profiling and its ability to identify differentially expressed genes between normal and neoplastic mammary epithelial cells. We are the first to apply the NEB method to normalize different high-throughput SAGE-Seq libraries in order to correct the sampling bias due to incomplete sampling. NEB normalization can be applied to other types of techniques based on random sampling such as RNA-seq. We designed a pipeline to align SAGE tags to sense and antisense transcripts and minimize sequencing error through tag alignment and proposed an approach to detect differentially expressed genes by considering both sampling and biological variability. We compared SAGE-Seq and traditional SAGE to examine the effect of sequencing depth on gene coverage and differentially expressed gene detection. Comparison of SAGE-Seq data between normal and neoplastic mammary epithelial cells revealed that breast cancers have higher within- and across-library diversity than normal breast cells. SAGE-Seq identifies 20 times more differentially expressed genes at 10-fold more stringent cutoff (1% FDR) than traditional SAGE (10% FDR), and three times more pathways specifically activated in breast cancer, indicating its higher sensitivity and specificity.

Identifying changes in gene expression associated with physiologic processes is a central issue in biology, especially in the study of human diseases (Zhu et al. 2008). Commonly used methods include EST sequencing, cDNA microarray hybridization, subtractive cloning, differential display, and serial analysis of gene expression (traditional SAGE) (Adams et al. 1991; Schena et al. 1995; Velculescu et al. 1995). Compared with array-based hybridization methods, SAGE-Seq has many advantages. First, SAGE-Seq has higher sensitivity, which allows the detection of less-abundant genes with high-confidence levels. Second, SAGE-Seq is less subject to technical artifacts such as probe effects and hybridization bias (Yang and Speed 2002). Third, SAGE-Seq does not require the a priori knowledge of transcripts to be analyzed; thus, it allows a global analysis of transcriptome present in the cells.

Overdispersion of expression levels of highly expressed genes was observed in microarray data, and as a result, analyses were often conducted at the log intensity level (Irizarry et al. 2003). However, most people attribute the overdispersion to probe hybridization and scanning biases inherent to the microarray platform. We quantitatively identified the relationship between biological variability and mean expression level. The SAGE-Seq data presented here not only show that the Poisson distribution used in many SAGE analysis algorithms is insufficient to capture the biological variance, but also indicate that abundant genes have higher variability among biological samples (Fig. 5A). This suggests that cells tolerate variations in the levels of highly expressed genes much better. These findings also imply that efforts on disease marker and drug target discovery might be more fruitful if focused on intermediate or low-abundance transcripts, as these show less variation among samples within the same tissue type, and differences in their expression might play a more important role in the disease process.

SAGE-Seq with deeper sequencing depth is able to detect many more significant differentially expressed transcripts than traditional SAGE with higher significance. The top differentially expressed genes identified by SAGE-Seq are not the most abundant genes, but rather expressed at intermediate or low levels (∼100/million). For traditional SAGE, which is sequenced at 20 times less depth, these tags will be at the borderline of being detected. Thus, traditional SAGE has no power to differentiate these genes between different conditions. At the same time, these less-abundant genes often are transcription factors and receptors that play important roles of cell regulations, and in tumorigenesis (Fig. 4A–C). Thus, even small changes in the expression of these genes might have pronounced effects on the whole cellular environment. It seems that less-abundant genes also have less variability (Fig. 5A), which enables them to be detected as top differentially expressed genes despite the fact that the absolute change in their expression levels is not the largest. Thus, high-throughput sequencing technologies provide the opportunity to unveil subtle changes in gene expression in more detail and with improved statistical power.

In summary, we show here that SAGE-Seq is a powerful and cost-effective method for the gene expression profiling of small numbers of cells isolated from primary human tissue samples, and we present data analysis tools that enable researchers to decipher the physiological meaning of the immense SAGE-Seq data sets.

Methods

SAGE-Seq library construction

We posted our detailed protocol for SAGE-Seq library generation at http://research4.dfci.harvard.edu/polyaklab/protocols_linkpage.php.

All of the SAGE and SAGE-Seq libraries in this study were generated from immunomagnetic bead-purified cells freshly isolated from human breast tissue samples; thus, the cell numbers are estimates based on the microscopic examination of the number of captured cells in 10 uL of volume, and they are in the 50,000–100,000 cell range. However, based on FACS analyses and sorting of the same cell type we know their approximate abundance in the tissue sample. All of the cells are directly lysed and processed for poly(A) RNA selection, followed by library preparation. The amount of poly(A) RNA is either measured by Nanodrop or by SYBR green II, but if the number of cells is very limited, we just go straight to library preparation. Based on the estimate that one cell contains 10 pg of total RNA, 100,000 cells have ∼100 ng of total RNA and ∼1–10 ng of poly(A) RNA (depending on cell type, tumor cells in general have higher RNA content/cell). In addition, 10% of the poly(A) RNA is saved for semiquantitative RT-PCR testing of cell purity prior to proceeding with SAGE-Seq sample preparation, and this also gives an estimate of the transcribable mRNA present.

Sequencing error minimization

At 0.1% error rate per base, the population of tags with no error is (1 − 0.1%)17 = 0.9831353, and the population of tags with one error is 17 × 0.001 × (1 − 0.001)16 = 0.01673003. Thus, the population of tags with error in at least two bases is: 1 − 0.9831353 − 0.01673003 = 0.0001346471.

Simpson index of diversity

Simpson's measure of diversity (Simpson 1949) (SID) is defined as:

graphic file with name 1730equ1.jpg

where ni is the count of the ith tag and N is the total number of tag count. SID = 1 indicates that one tag dominates all of the tag counts of the system, which means that there is no diversity (highest dominance). The larger the value of SID is, the higher diversity is (less dominance). SID is not strongly influenced by the sequencing depth, which is confirmed by simulation.

Morisita-Horn similarity index

Morisita-Horn similarity index, CMH(A,B), between two libraries, A and B, is defined as:

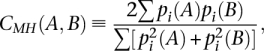graphic file with name 1730equ2.jpg

where pi(A) and pi(B) are the proportion of gene (or tag) i for library A and B, respectively. MH similarity index is independent of the sequencing depth N.

Sampling variance and biological variance

The high-throughput sequencing technology is modeled as a binomial sampling procedure with replacement. Mixing with the biological variability from different samples, another layer of variability is introduced due to sampling. Define pn, the proportion of tag with count n as, p = n/N, where N is the total number of tag count. From our hierarchical model, the mean proportion 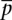Inline graphic of a gene is an unbiased estimator of the true abundance of genes. However, s2(xi), the observed variance of scaled count xi of gene i is an addition of the true biological variance from individuals and the sampling variance (Supplemental material for analytical proof),

graphic file with name 1730equ3.jpg

Normalization using nonparametric empirical Bayes correction

We implement the empirical Bayes using simple Good-Turing estimator (SGT) (Gale and Sampson 1995). Assume the total number of all unique tags in the mRNA is s, and pi is the true proportion of tag i, which is what we want to estimate from data. Empirical Bayes estimation of an observed tag count r is:

graphic file with name 1730equ4.jpg

where nr is the number of tags with count r. Thus, the expected total chance of all tags that are each represented r times (r ≥ 1) is: (r + 1) nr + 1/N, where N is the sequencing depth (N = n1 + 2n2 + 3n3 +…). Therefore, the expected total chance of all tags represented in the sample is: (2n2 + 3n3 +…)/N = 1 − n1/N. In SGT, the proportion of undetected tags, P0 is estimated as

graphic file with name 1730equ5.jpg

where n1 represents the number (frequency) of unique tags with count one. The corrected total tag count after SGT, N*, is N* = Σnr r*. The empirical Bayes estimator for proportion of a gene with count r, pr*, is renormalized by N* as

graphic file with name 1730equ6.jpg

Variance of Good-Turing estimator for unseen tags

The variance of P0 can be calculated in the following: Var(P0) = Var(n1)/N2. n1 = Σi Npi (1- pi)N − 1 under the assumption of binomial sampling approximation. Introducing a new random number xi : xi = 1 if the ith tag is sequenced with only one tag at sequencing depth N and xi = 0 otherwise. Then:

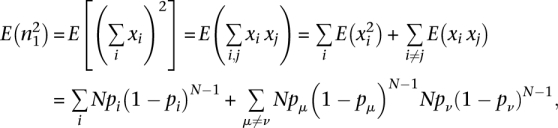graphic file with name 1730equ7.jpg

and

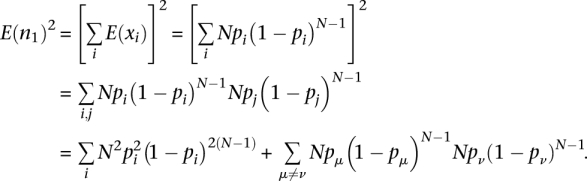graphic file with name 1730equ8.jpg

Thus,

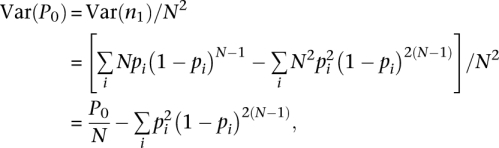graphic file with name 1730equ9.jpg

which gives:

graphic file with name 1730equ10.jpg

This indicates that the Good-Turing estimator for unseen tags is a stable estimator, which is shown in Supplemental Figure S2.

Saturation curve calculation

We define the total number of all unique tags in the mRNA as s and pi as the true proportion of tag i. pi is estimated from the data. Thus, the mean of unseen tags according to binomial sampling is:

graphic file with name 1730equ11.jpg

where the summation is overall the possible unique best tags and N is the sequencing depth. Thus, the number of detected unique best tag genes is the total number of unique best tag genes minus n0 (N) as shown in Figure 4D.

Variance stabilization

For the variance to mean relationship observed in our data, the correct transformation to stabilize variance is logarithm transformation based on the delta method. We provide the proof as follows. Suppose a random variable x follows a distribution with mean μ and variance σ2. Consider a transformation g (x). The Taylor expansion of g (x) around μ up to the first order is g(x) ≈ g (μ) + (x − μ) g′(μ). Thus, the transformed variable g (x) has approximate mean g (μ) and approximate variance Var[g(x)] ≈ σ2[ g′(μ)]2. In our data, μ and σ2 satisfies the observed dependency σ2 ∼ μ2, yielding Var[g(x)] ≈ μ2[g′(μ)]2. Assuming the transformation g stabilizes the variance, Var[g(x)] is a constant independent of μ, and thus g′(μ) = c/μ, where c is a constant. Integrating with respect to μ gives that the form of the stabilization transformation g should be:g (x) = log x.

Databases used

The transcription-factor gene list for humans is obtained from NCBI (http://www.ncbi.nlm.nih.gov). Go to Entrez Gene and search for human transcription factor. After filtering out nonhuman genes, 1658 human genes encoding for transcription factors are in this list. The seven normal and seven cancer raw SAGE-Seq data have been deposited in GEO (accession no. GSE24491).

Network and pathway analysis using METACORE

Network and pathway analysis using METACORE was performed essentially as previously described (Nikolsky et al. 2008). Specific details are in the Supplemental Methods.

Acknowledgments

We thank Andrea Richardson (Brigham and Women's Hospital) for her help with the acquisition of breast tumor samples; Haiyan Huang, Li Cai, Molin Wang, and David Harrington for valuable discussions; Love Nickerson for English proofreading. This work was supported by the Friends of Dana-Farber Women's Cancer Program (X.S.L.), NIH R01 1HG004069 (X.S.L.), NCI P50 CA89393 CA and R01 CA116235-04S1 (K.P.), the AVON Foundation (K.P.), Terri Brodeur Breast Cancer Research Foundation (S.C.), and the Susan G. Komen Foundation PDF0707996 (M.S., R.M.).

Author contributions: Z.W. did the computational analysis. Z.W., X.S.L., and K.P. designed the study and wrote the manuscript. Z.W., X.S.L., C.M., A.S., and J.L. developed the analytical methodology. S.C., M.S., R.M., M.B., and T.N. carried out experiments and analyzed data. S.S. provided normal tissue samples for the study.

Footnotes

[Supplemental material is available online at http://www.genome.org. The data from this study have been submitted to the NCBI Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo) under accession no. GSE24491. Software for SAGE-Seq data analysis is available at http://www.liulab.dfci.harvard.edu/sageExpress/.]

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.108217.110.

References

  1. Adams MD, Kelley JM, Gocayne JD, Dubnick M, Polymeropoulos MH, Xiao H, Merril CR, Wu A, Olde B, Moreno RF, et al. 1991. Complementary DNA sequencing: Expressed sequence tags and human genome project. Science 252: 1651–1656 [DOI] [PubMed] [Google Scholar]
  2. Baggerly KA, Deng L, Morris JS, Aldaz CM 2003. Differential expression in SAGE: Accounting for normal between-library variation. Bioinformatics 19: 1477–1483 [DOI] [PubMed] [Google Scholar]
  3. Baggerly KA, Deng L, Morris JS, Aldaz CM 2004. Overdispersed logistic regression for SAGE: Modelling multiple groups and covariates. BMC Bioinformatics 5: 144 doi: 10.1186/1471-2105-5-144 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bloushtain-Qimron N, Yao J, Snyder EL, Shipitsin M, Campbell LL, Mani SA, Hu M, Chen H, Ustyansky V, Antosiewicz JE, et al. 2008. Cell type-specific DNA methylation patterns in the human breast. Proc Natl Acad Sci 105: 14076–14081 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cai L, Huang H, Blackshaw S, Liu JS, Cepko C, Wong WH 2004. Clustering analysis of SAGE data using a Poisson approach. Genome Biol 5: R51 doi: 10.1186/gb-2004-5-7-51 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dean M 2009. ABC transporters, drug resistance, and cancer stem cells. J Mammary Gland Biol Neoplasia 14: 3–9 [DOI] [PubMed] [Google Scholar]
  7. Fisher RA 1922. On the mathematical foundations of theoretical statistics. Philos Trans R Soc Lond 222: 309–368 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gale WA, Sampson G 1995. Good-Turing frequency estimation without tears. J Quant Ling 2: 217–237 [Google Scholar]
  9. Good IJ 1953. The population frequencies of species and the estimation of population parameters. Biometrika 40: 237–264 [Google Scholar]
  10. He Y, Vogelstein B, Velculescu VE, Papadopoulos N, Kinzler KW 2008. The antisense transcriptomes of human cells. Science 322: 1855–1857 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Huber W, von Heydebreck A, Sültmann H, Poustka A, Vingron M 2002. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics 18: S96–S104 [DOI] [PubMed] [Google Scholar]
  12. Irizarry RA, Hobbs B, Collin F, Beazer-Barclay YD, Antonellis KJ, Scherf U, Speed TP 2003. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 4: 249–264 [DOI] [PubMed] [Google Scholar]
  13. Jiang H, Wong WH 2008. SeqMap: Mapping massive amount of oligonucleotides to the genome. Bioinformatics 24: 2395–2396 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Johnson WE, Li W, Meyer CA, Gottardo R, Carroll JS, Brown M, Liu XS 2006. Model-based analysis of tiling-arrays for ChIP-chip. Proc Natl Acad Sci 103: 12457–12462 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Johnson DS, Mortazavi A, Myers RM, Wold B 2007. Genome-wide mapping of in vivo protein-DNA interactions. Science 316: 1497–1502 [DOI] [PubMed] [Google Scholar]
  16. Kharchenko PV, Tolstorukov MY, Park PJ 2008. Design and analysis of ChIP-seq experiments for DNA-binding proteins. Nat Biotechnol 26: 1351–1359 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li S, Huang S, Peng SB 2005. Overexpression of G protein-coupled receptors in cancer cells: Involvement in tumor progression. Int J Oncol 27: 1329–1339 [PubMed] [Google Scholar]
  18. Lu J, Tomfohr JK, Kepler TB 2005. Identifying differential expression in multiple SAGE libraries: An overdispersed log-linear model approach. BMC Bioinformatics 6: 165 doi: 10.1186/1471-2105-6-165 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Magurran AE 2003. The commonness, and rarity, of species. In Measuring biological diveristy, p. 18, Wiley-Blackwell, Hoboken, NJ [Google Scholar]
  20. Morrissy AS, Morin RD, Delaney A, Zeng T, McDonald H, Jones S, Zhao Y, Hirst M, Marra MA 2009. Next-generation tag sequencing for cancer gene expression profiling. Genome Res 19: 1825–1835 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Nikolsky Y, Sviridov E, Yao J, Dosymbekov D, Ustyansky V, Kaznacheev V, Dezso Z, Mulvey L, Macconaill LE, Winckler W, et al. 2008. Genome-wide functional synergy between amplified and mutated genes in human breast cancer. Cancer Res 68: 9532–9540 [DOI] [PubMed] [Google Scholar]
  22. Nikolsky Y, Kirillov E, Zuev R, Rakhmatulin E, Nikolskaya T 2009. Functional analysis of OMICs data and small molecule compounds in an integrated “knowledge-based” platform. Methods Mol Biol 563: 177–196 [DOI] [PubMed] [Google Scholar]
  23. Orlitsky A, Santhanam NP, Zhang J 2003. Always Good Turing: Asymptotically optimal probability estimation. Science 302: 427–431 [DOI] [PubMed] [Google Scholar]
  24. Polyak K, Riggins GJ 2001. Gene discovery using the serial analysis of gene expression technique: Implications for cancer research. J Clin Oncol 19: 2948–2958 [DOI] [PubMed] [Google Scholar]
  25. Robbins H 1956. An empirical Bayes approach to statistics. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, pp. 157–163 University of California Press, Berkeley, CA [Google Scholar]
  26. Robinson MD, Smyth GK 2007. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics 23: 2881–2887 [DOI] [PubMed] [Google Scholar]
  27. Schena M, Shalon D, Davis RW, Brown PO 1995. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science 270: 467–470 [DOI] [PubMed] [Google Scholar]
  28. Shendure J, Ji H 2008. Next-generation DNA sequencing. Nat Biotechnol 26: 1135–1145 [DOI] [PubMed] [Google Scholar]
  29. Shipitsin M, Campbell LL, Argani P, Weremowicz S, Bloushtain-Qimron N, Yao J, Nikolskaya T, Serebryiskaya T, Beroukhim R, Hu M, et al. 2007. Molecular definition of breast tumor heterogeneity. Cancer Cell 11: 259–273 [DOI] [PubMed] [Google Scholar]
  30. Simpson EH 1949. Measurement of diversity. Nature 163: 688 [Google Scholar]
  31. Song JS, Johnson WE, Zhu X, Zhang X, Li W, Manrai AK, Liu JS, Chen R, Liu XS 2007. Model-based analysis of two-color arrays (MA2C). Genome Biol 8: R178 doi: 10.1186/gb-2007-8-8-r178 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Storey JD Tibshirani R 2003. Statistical significance for genome-wide studies. Proc Natl Acad Sci 100: 9440–9445 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Tusher VG, Tibshirani R, Chu G 2001. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci 98: 5116–5121 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Velculescu VE, Zhang L, Vogelstein B, Kinzler KW 1995. Serial analysis of gene expression. Science 270: 484–487 [DOI] [PubMed] [Google Scholar]
  35. Velculescu VE, Vogelstein B, Kinzler KW 2000. Analysing uncharted transcriptomes with SAGE. Trends Genet 16: 423–425 [DOI] [PubMed] [Google Scholar]
  36. Wolda H 1983. Diversity, diversity indices and tropical cockroaches. Oecologia 58: 290–298 [DOI] [PubMed] [Google Scholar]
  37. Yang YH, Speed T 2002. Design issues for cDNA microarray experiments. Nat Rev Genet 3: 579–588 [DOI] [PubMed] [Google Scholar]
  38. Zhu J, Zhang B, Schadt EE 2008. A systems biology approach to drug discovery. Adv Genet 60: 603–635 [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES