Nonexponential decay of internal rotational correlation functions of native proteins and self-similar structural fluctuations

Abstract

Structural fluctuations of a protein are essential for the function of native proteins and for protein folding. To understand how the main chain in the native state of a protein fluctuates on different time scales, we examined the rotational correlation functions (RCFs), C(t), of the backbone N-H bonds and of the dihedral angles γ built on four consecutive C^α atoms. Using molecular dynamics simulations of a model α/β protein (VA3) in its native state, we demonstrate that these RCFs decay as stretched exponentials, ln[C(t)] ≈ D_αt^α with a constant D_α and an exponent α (0 < α < 0.35) varying with the free-energy profiles (FEPs) along the amino acid sequence. The probability distributions of the fluctuations of the main chain computed at short time scale (1 ps) were identical to those computed at large time scale (1 ns) if the time is rescaled by a factor depending on α < 1. This self-similar property and the nonexponential decays (α ≠ 1) of the RCFs are described by a rotational diffusion equation with a time-dependent diffusion coefficient D(t) = αD_αt^α-1. The present findings agree with observations of subdiffusion (α < 1) of fluorescent probes within a protein molecule. The subdiffusion of ¹⁵N-H bonds did not affect the value of the order parameter S² extracted from the NMR relaxation data by assuming normal diffusion (α = 1) of ¹⁵N-H bonds on a nanosecond time scale. However, we found that the RCF does not converge to S² on the nanosecond time scale for residues with multiple-minima FEPs.

An important question for understanding protein dynamics, protein function, and protein folding is how the different segments of the backbone of a protein relax to a new conformation (1–3). On nanosecond and subnanosecond time scales, the dynamics of protein backbones can be probed in great detail experimentally by fluorescence (2) or by NMR relaxation studies (4–6), and theoretically by all-atom molecular dynamics (MD) simulations (7–12).

The orientation of the backbone of a protein around a residue n at any time t can be characterized by a unit vector u_n(t) representing the orientation of a local probe of the protein dynamics in a frame attached to the molecule. For example, the vector u_n(t) represents the orientation of a fluorophore linked to residue n in fluorescence anisotropy (2) or the orientation of a bond of the residue n in NMR (4–6). The local reorientation of a segment of the backbone of a protein moving from one conformation to another can be analyzed by recording the internal rotational correlation functions (RCFs) of u_n (2, 6, 13–15), which measure the average correlation of u_n with its initial orientation after a time t in the molecular frame. Different experimental techniques measure RCFs of different rank l, C_l(t), corresponding to averages of polynomials of u_n of different orders l. For example, dielectric spectroscopy measures the RCF C₁(t) of a rotating dipole and, in fluorescence anisotropy and NMR, the RCF C₂(t) for the fluctuations of a rotating dipole and of a bond, respectively, is obtained (2, 6). In experiments, the internal RCFs of u_n are extracted by assuming a model for the rotational diffusion of u_n. In the present work, we used all-atom MD simulations to establish the physical properties of the rotational diffusion of local probes u_n of the backbone dynamics. We address the following questions: How do the local probes u_n(t) diffuse on different time scales in a protein? How can a meaningful rotational diffusion constant of u_n be extracted from its RCF? How does the RCF of u_n reflect the free-energy profile (FEP) of the main chain of a protein along the sequence of the amino acids?

Two probes, u_n(t), of the backbone dynamics are considered here for each residue n (Fig. S1). First, u_n(t) represents the orientation of the main chain measured by a coarse-grained dihedral angle γ_n (16, 17) formed by the virtual bonds joining four consecutive C^α atoms (n - 1, n, n + 1, and n + 2) along the amino acid sequence; i.e., u_n(t) = { cos[γ_n(t)], sin[γ_n(t)]} with 2 < n < N - 2 and N being the number of residues. The dihedral angles γ_n (16) are coordinates used to describe (large) conformational changes of proteins (18) and are part of coarse-grained models of proteins (19, 20). The successive orientations of u_n(t) are represented by rotational diffusion on a circle (Fig. S1). Second, u_n(t) is a unit vector representing the orientation of the backbone amide (N-H)_n bond in a frame attached to the molecule. The successive orientations of u_n(t) are represented by rotational diffusion on a sphere centered on the N atom (Fig. S1). The rotational diffusion of these local probes was analyzed here by using all-atom MD simulations of a 46-residue α/β model protein VA3 (PDB ID code 1ED0) in its native state (21) (see details in Materials and Methods and SI Text). Protein VA3 was chosen because it is highly homologous to the well-studied protein crambin, but it is soluble in water whereas crambin is not (7). Because of the presence of three disulfide bonds (namely 3-40, 4-32, and 16-26), VA3 remains folded in all MD trajectories, which enables one to apply with confidence the separation of internal motions of the protein from its overall motion as required to compute the internal RCFs of N-H bonds (11) (see SI Materials and Methods).

The internal RCFs at short time scale contain valuable information about the mechanism of rotational diffusion of the local probe. We demonstrated that the internal RCFs are related to the angular mean-square displacement (MSD) of the rotating vector u_n at short time scale, i.e., for which MSD(t) ≪ 1,

[1]

where K₁ = 1/2, K₂ = 2 for diffusion on a circle (dihedral angle γ) and K₁ = 1/2, K₂ = 3/2 for a diffusion on a sphere (N-H bond) (see Eqs. S4, S5, S9, and S10 of SI Text Sec. 3). An analogous relation (Eq. 1) is found at long times (t → ∞) if the motion of u_n is restricted to small angular displacements (4). Eq. 1 is valid for any model of rotational diffusion of the vector u_n. For example, assuming a free-rotational diffusion on a circle (dihedral angles γ) [on a sphere (N-H bonds)], the RCF is C₂(t) = exp(-4Dt) [C₂(t) = exp(-6Dt)] with a relaxation time defined by τ_f = 1/4D (τ_f = 1/6D) (22). At short times, i.e., t ≪ τ_f, the exponential can be replaced by its first-order expansion, i.e., C₂(t) ≈ 1 - 4Dt [C₂(t) ≈ 1 - 6Dt]. Comparing this expansion of the RCF at short times with Eq. 1, we deduce correctly that the MSD for free diffusion on a circle (on a sphere) is MSD(t) = 2Dt [MSD(t) = 4Dt] (22).

Using Eq. 1 on a short time scale (t < 100 ps), we demonstrate that the RCFs of the dihedral angles γ and of the N-H bonds computed from MD decay approximately as power laws of time, which do not correspond to free diffusion of u_n. Indeed, the MSD of the dihedral angles γ and of the backbone N-H bonds are power laws of time; MSD(t) = 2D_αt^α (dihedral angles) (in agreement with ref. 17) and MSD(t) = 4D_αt^α (N-H bonds), with a constant D_α (deg² ps^-α) and an exponent α < 0.4 varying along the amino acid sequence (Fig. S2). For each dihedral angle γ_n [or (N-H)_n bond] along the amino acid sequence, the quantity 2D_α (4D_α) is by definition the variance of the distribution of the angular steps of a random walker on a circle (17) (on a sphere) moving each picosecond, whereas the exponent α is proportional to the speed of diffusion produced by these stochastic motions. An exponent α < 1 corresponds to a subdiffusive regime (23–26). The rotational subdiffusion found here agrees with translational subdiffusion found recently in proteins by fluorescence (27) and MD simulations (28). Subdiffusion was also found in the MD simulations of the dynamical structure factor of a protein (29).

We show that the RCFs computed from MD up to 1–2 ns are extremely well fitted by a stretched exponential (SE), ln[C(t)] ≈ D_αt^α with exponents (α < 0.4) and constants D_α close to the ones computed from the MSDs (Fig. 1). The parameters [α,D_α] for each residue reflect the variation of the free-energy profiles of the dihedral angles and of the backbone N-H bonds along the sequence of the amino acids. Residues existing in multiple substates have exponents larger than 0.2. We show that the motions of the N-H bonds and of the dihedral angles γ can be described at short time by an (approximate) free diffusion equation with an effective time-dependent diffusion coefficient D(t) = αD_αt^α-1 and that the fluctuations of the orientation of the N-H bonds and of the main-chain dihedral angles are self-similar at least up to 1 ns (as shown for the N-H bonds in Fig. 2). Finally, we discuss the consequences of the anomalous diffusion (α ≠ 1) of the backbone N-H bonds for the interpretation of the RCFs extracted from NMR data, and we compare the present results to the predictions of the model-free (MF) approach (13–15) (Fig. 3 and SI Text Sec. 9).

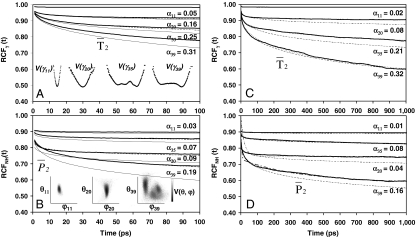
Fig. 1.

Typical results for RCFs of dihedral angles γ_n and of (N-H)_n bonds of VA3 computed from MD (thick lines) up to t < 100 ps (A and B) and up to t < 1 ns (C and D). Results are presented in A and C for dihedral angles γ₁₁, γ₂₀, γ₃₅, and γ₃₉ having free-energy profiles (shown schematically in A, Inset) representative of all V(γ) calculated in MD (Fig. S3), and in B and D for corresponding (N-H)_n amide bonds of residues n = 11, 20, 35, and 39 with typical free-energy profiles V(θ,φ) (shown schematically in B, Inset). For each dihedral angle γ_n (A) and each (N-H)_n bond (B), the RCFs computed from MD are compared to RCFs computed from Eq. 1 (thin lines) using a power-law MSD (see text) and with a SE (dashed lines) with an exponent α_n computed by fitting the RCF up to 50 ps (see text). The SE fit and the RCFs computed from MD are hardly distinguishable. For each dihedral angle γ_n (C) and each (N-H)_n bond (D), the RCFs are compared with a SE with an exponent α_n computed by fitting the RCF up to 50 ps (dashed lines) and by fitting the RCF up to 1 ns (dotted lines), respectively. The fit to a SE up to 1 ns is hardly distinguishable from the RCF computed from MD. In D, typical fits of the RCF up to 1 ns using the model-free approach (dot-dashed lines) for a monoexponential and biexponential function f₂(t), respectively, are shown for the bonds (N-H)₂₀ and (N-H)₃₉.

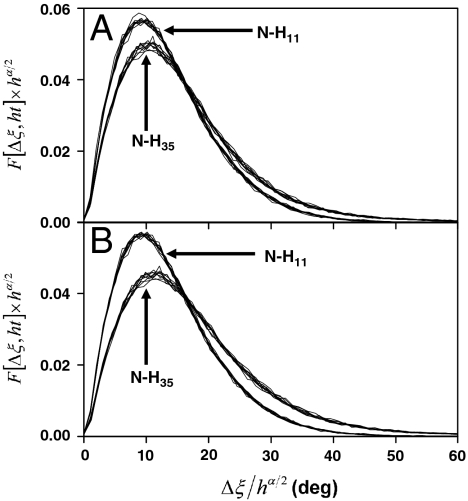
Fig. 2.

Typical results for the time evolution of the probability distribution function (PDF) of Δξ_n computed from the fluctuations of the (N-H)_n bonds extracted from MD trajectories of VA3. Results are presented for (N-H)₁₁ and (N-H)₃₅ with a typical harmonic FEP (Fig. 1B, Inset) and multiple-minima FEP, respectively. The superposed curves are the PDFs computed from MD and rescaled by using Eq. 4 at times t = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 300, 500, 600, 800, and 1,000 ps choosing h = 1 at t = 100 ps (A) and h = 1 at t = 1 ns (B). The PDFs are rescaled by using an exponent α ≠ 1 calculated from a fit to a SE of up to 50 ps (A) and up to 1 ns (B). The PDFs cannot be distinguished at the scale of the figure.

Fig. 3.

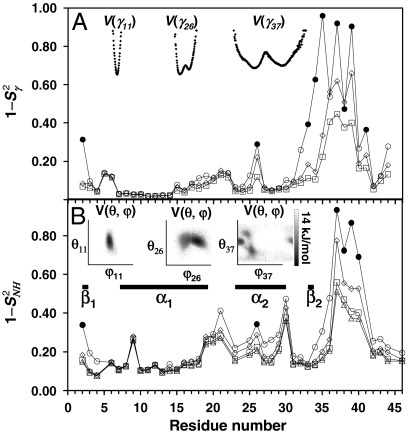
Convergence of RCF(t) to the generalized order parameter S² of dihedral angles γ_n (A) and (N-H)_n bonds (B) for each residue n along the amino acid sequence [values of 1 - RCF(t) and 1 - S² are shown]. (A) The 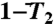(γ_n) at t = 1 ns (empty squares) and extrapolated at t = 10 ns (empty diamonds), computed by using a SE with an exponent α and diffusion constant D_α extracted from a fit of 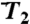up to 1 ns, are compared to 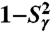(open and filled circles) computed by using Eq. S54 of SI Text. The filled circles represent the angles γ_n with multiple-minima FEP. (B) 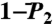(N-H)_n at t = 1 ns (empty squares) and extrapolated to t = 10 ns (empty diamonds), computed by using a SE with an exponent α and diffusion constant D_α extracted from a fit of 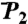up to 1 ns, are compared to 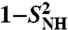(open and filled circles) computed by using Eq. S67 of SI Text. The filled circles represent the (N-H)_n amide bonds with multiple-minima 2D-free-energy landscapes. The values of 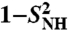computed by using the MF approach (see text) and a monoexponential or a biexponential function f₂(t) (empty triangles) are in excellent agreement with the values of 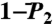at 1 ns computed using a SE model. Thick lines β₁, β₂ and α₁, α₂ are the locations of the two β-sheets and the two α-helices, respectively, of VA3. Typical FEP of angles γ_n (A) and (N-H)_n (B) bonds computed from MD are shown in Insets.

Results and Discussion

Computation of the RCFs for Diffusion on a Circle and on a Sphere.

The persistence of the orientation of u_n(t) is measured by computing the RCF C_l,n(t) of rank l = 1 and l = 2. For circular geometry, they are defined by

[2]

where T_l is a Tchebychev polynomial, namely T₁(x) = x and T₂(x) = 2x² - 1 (22). In Eq. 2, x_n ≡ u_n(t^′)•u_n(t^′ + t) is the cosine of the angular displacement Δγ_n of u_n between t^′ and t^′ + t (Fig. S1), and T_l is averaged over all possible initial orientations (at all times t^′).

For spherical geometry, the RCFs of rank l = 1 and l = 2 are computed (22) by using

[3]

where P_l is a Legendre polynomial, namely P₁(x) = x and P₂(x) = 3x²/2 - 1/2 (22). In Eq. 3, x_n ≡ u_n(t^′)•u_n(t^′ + t) is the cosine of the angular displacement Δξ_n of u_n between t^′ and t^′ + t (Fig. S1), and P_l is averaged over all possible initial orientations (at all times t^′).

The RCFs 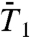and 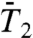of all 43 γ_n angles a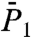nd and 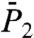of the 39 amide (N-H)_n bonds (excluding the nonexisting N-H bonds of PRO5, PRO22, PRO24, and PRO41) (a total of 820 RCFs) were computed by applying Eqs. 2 and 3, respectively, to five 80-ns MD trajectories of VA3 at 300 K in explicit solvent (see Materials and Methods). The 80-ns MD trajectories provide enough statistics to compute the RCFs accurately up to about 1–2 ns (30) (at large times, spurious oscillations in the RCFs of some residues are observed. See SI Text Sec. 1 and Fig. S4).

Relation Between RCF and MSD at Short Time (up to 100 ps).

The MSDs of the dihedral angles γ and of the N-H bonds were computed from the five MD trajectories by using Eqs. S6 and S11, respectively. The MSD of γ was shown previously (17) to be 2D_αt^α (with α < 1) by using all-atom MD. Therefore, the MSDs were fitted up to 50 ps by using MSD(t) = 2D_αt^α for the dihedral angles γ (diffusion on a circle) and MSD(t) = 4D_αt^α for the N-H bonds (diffusion on a sphere). All MSDs (a total of 410) were represented perfectly well by these power laws with α < 1 up to at least 100 ps (Fig. S2). We conclude that the diffusion of γ dihedral angles (17) and the diffusion of the N-H bonds are anomalous. Consequently, the RCFs should decay approximately as power laws at short time. The RCFs computed from MD were compared up to 100 ps to those computed by using the power-law MSD in Eq. 1; i.e., 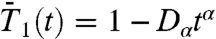(Fig. S5a), 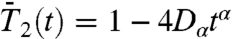(Fig. 1A), 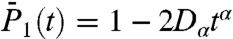(Fig. S6a), and 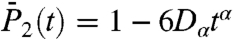(Fig. 1B). The RCFs computed from the MSD by using Eq. 1 are good approximations for most of the residues at least up to 100 ps with a maximum deviation of about 15% (as shown for 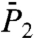of N-H₃₉ in Fig. 1B).

RCFs Decay as Stretched Exponentials.

The RCFs computed from MD were fitted to stretched exponentials, namely 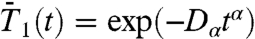, , 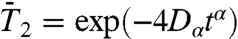, 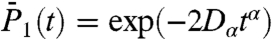and 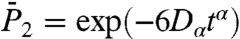, on two time scales: up to 50 ps [Fig. S5a (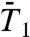), Fig. 1A (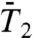), Fig. S6a (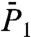), Fig. 1B (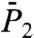)], and up to 1 ns [Fig. 1C (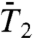) and Fig. 1D (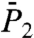)]. These SEs are hardly discernible from the RCFs computed from MD to which they were fitted.

The parameters D_α and α computed along the sequence of the amino acids from the SEs fitted to the RCFs up to 50 ps are very close to those extracted independently from the power laws fitted to the MSD up to 100 ps except for the exponents α of a few residues in loops (Figs. S5 b and c and S6 b and c). Therefore, we could, in principle, extract the constant D_α and the exponent α of the MSD of each N-H bond by fitting its RCF measured at short time (up to 50 ps) by a stretched exponential, keeping in mind that the exponent extracted from the RCF of an N-H bond within a loop might be slightly lower than the exponent of the MSD of the bond (Fig. S6).

The SEs fitted to the RCF up to 50 ps (Fig. 1 A and B) nicely reproduce the typical behavior of the RCFs up to 1 ns as shown in Fig. 1 C and D, but not their exact values (similar results are found for 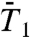and 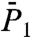). For most of the residues, the values of D_α computed from the RCFs up to 50 ps and up to 1 ns are nearly identical, and the exponents α computed from the RCFs up to 50 ps are larger than those calculated up to 1 ns (as illustrated in Fig. 1). The profiles of the variations of α and D_α along the sequence of the amino acids computed from the RCFs up to 50 ps and up to 1 ns are similar (see SI Text Sec. 2 and Figs. S5 and S6).

Variation of α and D_α Along the Amino Acid Sequence, FEP, and RCF.

The values of [α,D_α] of the RCF of a dihedral angle γ are governed by the shape of its effective 1D FEP, V(γ), as shown previously (17). The FEP was computed by using V(γ) = -kT ln[P(γ)], where k and T = 300 K are the Boltzmann constant and temperature, respectively, and where P(γ) is the PDF of each dihedral angle γ computed over the whole MD trajectory (17). The FEP, averaged over five trajectories, is represented along the primary sequence in Fig. S3. The FEPs are similar between the different trajectories, as shown by the comparison between the average FEP and the one computed from run 1 in Fig. S3. Typical FEPs, representative of all V(γ), are reproduced schematically in Fig. 1A, Inset: V(γ₁₁) is a stiff harmonic FEP, V(γ₂₀) is a single-minimum soft FEP, V(γ₃₅) is a triple-well FEP, and V(γ₃₉) is a double-well FEP.

The constant D_α has a tendency toward smaller values in stiffer (harmonic) FEPs [as V(γ₁₁)] (D_α ≈ 10 deg² ps^-α) and large values (D_α ≈ 50–110 deg² ps^-α) in wide FEPs [as V(γ₂₀)] and in multiple-minima FEPs [as V(γ₃₅) and V(γ₃₉)] (Figs. S3 and S5b). For each residue, the value of 2D_α is very close to the variance of the distribution of the displacements Δγ computed at 1 ps. All residues moving on multiple-minima FEPs [as V(γ₃₅) and V(γ₃₉) in Fig. 1A] have large exponents α (fast diffusion) (α≥0.2): They are generally found in loops but some (γ₁₇, γ₂₆, and γ₃₄) (see Fig. S3) are in secondary structures (Fig. S5c). Visual inspection of the structures produced by MD shows that the two minima of V(γ₂₆) are two possible orientations of the disulfide bond 16-26 corresponding to the formation or not of a hydrogen bond between the PRO24 and LYS28 both in the shortest helix of VA3. Rupture of the hydrogen bond implies a motion of ARG17 and of the two other disulfide bonds 4-32 and 3-40 and explains the multiple minima observed. This might be an artifact of the force field or an actual effect. Missing or nonnative hydrogen bonds in current force fields may be responsible for disagreements between the long-time limit of the RCFs computed by MD and the relaxation NMR data as illustrated in ref. 11. However, MD using current force fields (including the one used here) reproduce reasonably well most of the NMR data of proteins in the native state if electrostatic forces are fully taken into account (see Materials and Methods) and if the length of the MD trajectory is not too long (say up to 200 ns) (31).

As for the dihedral angles, the values of [α,D_α] of the N-H bonds are governed by the shape of the FEP V(θ,φ), where (θ,φ) are the polar coordinates of the N-H vector in a frame attached to the molecule (Fig. S1). The FEP V(θ,φ) was computed over the whole MD trajectory by using V(θ,φ) = -kT ln[P(θ,φ)], where P(θ,φ) is the 2D PDF of the vector u in the direction of the N-H bond (Fig. S1). Typical FEPs V(θ,φ) are shown in Fig. 1B, Inset. As for the dihedral angles γ_n, the constant D_α has a tendency toward smaller values in stiffer (harmonic) FEPs [as V(θ₁₁,φ₁₁)] (D_α ≈ 50 deg² ps^-α) and large values (D_α ≈ 90–100 deg² ps^-α) in wide FEPs [as V(θ₂₀,φ₂₀)] and in multiple-minima FEPs [as V(θ₃₉,φ₃₉)], which are located in loops except V(θ₂₆,φ₂₆) with two minima [as V(γ₂₆)] (see Fig. 3B, Inset) and in a helix. The largest exponents α are found for the N-H bonds within the loop between residues 37 and 40 (Fig. S7a), which possess both multiminima V(θ,φ) and V(γ) (Fig. S3) (see Fig. 1B, Inset, and Fig. 3B, Inset), and the lowest exponents α are found in helix (Fig. S7a).

The constant D_α of the (N-H)_n bond is generally larger than the one of the corresponding dihedral angle γ_n, which means that the amplitude of the displacement of the bond is larger than the one of the four virtual bonds C^α-C^α defining the dihedral angle, as expected (Fig. S7b). The exponents α of the N-H bonds at short time scale are in general lower than the ones of the dihedral angles because the RCFs 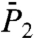in general converge more rapidly to a constant stationary value than the RCFs 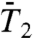. The profiles of [α,D_α] extracted from 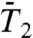and 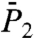are thus only qualitatively similar (Fig. S7). It is worth noting, for example, that (N-H)₉ and (N-H)₃₀, respectively, at the N and C terminals of a helix have large D_α (they move in soft FEP), whereas the constant D_α of γ₉ and γ₃₀ located in a helix pertains to the smallest D_α (they move in a stiff FEP shown in Fig. S3) (Fig. S7a).

Three different typical types of behaviors of the RCF 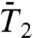and 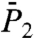at long time were observed, as shown in Fig. 1 C and D, respectively. Similar types were found in MD simulations of 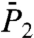of backbone N-H bonds of other proteins (11, 12). We found that they correspond to three different types of FEPs: for a single-minimum stiff FEP [γ₁₁ and (N-H)₁₁] and soft FEP [γ₂₀ and (N-H)₂₀ and (N-H)₃₅], 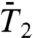and 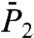exhibit a very fast drop at short times and converge to a constant value on the 1-ns time scale close to 1.0 for a stiff harmonic FEP and around 0.8–0.9 for a soft FEP. For multiple-minima FEP [γ₃₅, γ₃₉ and (N-H)₃₉], 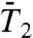and 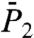have a strong decay with no convergence to a plateau up to 1 ns (Fig. 1 C and D and Fig. S4).

A Simple Model of the Nonexponential Decay of the RCF.

As demonstrated in SI Text Sec. 4, the stretched exponentials reproducing the RCF computed in MD (see Fig. 1), namely 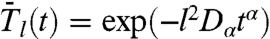for diffusion on a circle and 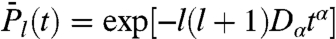for diffusion on a sphere, are RCFs of rank l of a free-diffusion equation with an effective time-dependent diffusion coefficient D(t) ≡ αD_αt^α-1 on both a circle and a sphere. The coefficient D(t) is the instantaneous diffusion constant at time t (26), i.e., nD(t) = ∂MSD(t)/∂t [n = 2 (4) for diffusion on a circle (sphere)]. A power-law time dependence of D(t) means that the velocity–velocity correlation function C_v(t) (32) decays slowly approximately as C_v(t) ≈ α²(α - 1)D_αt^α-2 (see details in SI Text Sec. 7).

The quantity F(Δγ; t)dγ is the probability that the vector u, representing a dihedral angle γ (Fig. S1), is rotated by an angle Δγ after a time t > 0 [with F(Δγ; 0) = δ(Δγ)]. For a free-diffusion equation on a circle (Eq. S15 in SI Text) with diffusion coefficient D(t), we find that the PDF F(Δγ; t) is a series of Tchebychev polynomials (see Eq. S17 in SI Text). The product F(Δξ; t)dξ is the probability that the vector u, representing an N-H bond (Fig. S1), is rotated by an angle Δξ after a time t > 0 [with F(Δξ; 0) = δ(Δξ)]. For a free-diffusion equation on a sphere (Eq. S25 in SI Text) with diffusion coefficient D(t), we show that F(Δξ; t) is a series of Legendre polynomials (see Eqs. S24 and S26 in SI Text). The analytical solutions F(Δγ; t) (Eq. S17 in SI Text] and F(Δξ; t) (Eqs. S24 and S26 in SI Text) agreed quite well with the PDF computed by MD, as shown in Fig. S8 a–f for different residues and typical values of [α,D_α]. This demonstrates that the internal motions of a protein can be interpreted (to a very good approximation) as free random walks with a diffusion coefficient D(t) ≡ αD_αt^α-1.

Self-Similarity of the PDF.

Replacing the time-independent diffusion constant by D(t) ≡ αD_αt^α-1 in the diffusion equations preserves the self-similarity property of the Brownian motion (26): The PDF solutions of the rotational diffusion equation on a circle (Eq. S17 in SI Text) and on a sphere (Eqs. S24 and S26 in SI Text) are indeed self-similar under the scaling transformations t → ht and ΔΦ → ΔΦ/h^α/2; i.e.,

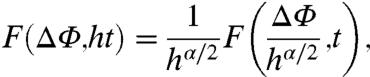[4]

where ΔΦ = Δγ (with F given by Eq. S17 in SI Text) or ΔΦ = Δξ (with F given by Eqs. S24 and S26 in SI Text). The PDFs computed from MD indeed obey the scaling property Eq. 4 very well, as shown in Fig. 2 for the N-H bond fluctuations and in Fig. S8 g–j for the dihedral angles γ fluctuations. In addition, Eq. 4 can be derived analytically from the PDF of the dihedral angles (see SI Text Sec. 5). Consequently, to a very good approximation from 1 ps to 1,000 ps studied here, the stochastic motions γ(t) and ξ(t) resemble each other in a statistical sense: The fluctuations of each of these angles at short time scales are similar to their fluctuations at large time scales. For example, choosing t = 10 ps and h = 100 in Eq. 4 provides the PDF at 1 ns (left-hand side of Eq. 4) from the scaled PDF observed at 10 ps (right-hand side of Eq. 4).

The self-similarity of F(Δξ_n,t) has been tested for all 195 PDFs computed for the 39 residues and 5 MD trajectories. Typical results, representative of all the data, are shown in Fig. 2 for residues 11 and 35. The PDFs were scaled according to Eq. 4 with ΔΦ = Δξ and t = 100 ps (Fig. 2A) and t = 1 ns (Fig. 2B) (see caption). There is a very good superposition of all the rescaled PDFs in all the panels in Fig. 2. Similar results were found for F(Δγ_n,t) as shown in SI Text Sec. 6.

Limits of 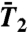and 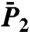as t → ∞ and the FEP.

In NMR relaxation studies, the RCF C₂(t) of each backbone ¹⁵N-H amide bond can be recorded by measuring the ¹⁵N spin relaxation of labeled proteins (4–6). The RCF is not measured in the time domain but is recorded as its Fourier transform in the frequency domain ω, instead, as the so-called spectral density J_NH(ω) (4–6, 33). Because J_NH(ω) is usually recorded at a few frequencies (4–6), the interpretation of the spectral density in terms of physically meaningful parameters requires a model for the rotational diffusion of the local probe u_n (15). The internal RCFs are extracted from the RCFs measured in the laboratory frame by assuming that the relaxation time of the overall tumbling of the whole protein [typically larger than 2 ns (15)] is much larger than the relaxation time of the motions of the N-H bonds (15). Under this assumption, the RCF is generally represented by the MF approach (13–15); i.e., 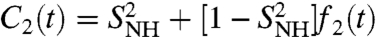, where f₂(t) describes the decay of the RCF toward its value at large times with f₂(0) = 1 and f₂(t → ∞) = 0 (1, 5, 11, 12). The limit 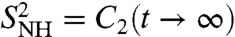, named the generalized order parameter (1, 5, 6, 11, 12), is an important parameter used to characterize protein dynamics along the sequence of the amino acids in NMR. Because it represents the equilibrium value reached by the RCFs, it is related to the FEPs (13, 34). The generalized order parameters 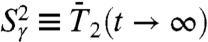and 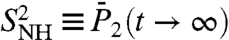were computed exactly from the FEP V(γ) and V(θ,φ), respectively (see Eqs. S54 and S67, SI Text Sec. 8). In order to evaluate the time necessary for the RCFs of each dihedral angle γ_n and each (N-H)_n bond to converge toward its equilibrium values at large times, in Fig. 3 we compared the values of 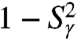(Fig. 3A) and 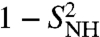(Fig. 3B), computed from the FEP (open circles for a single-minimum and filled circles for multiple-minima FEPs) to the values of the 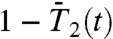and 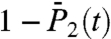computed by MD at t = 1 ns (time chosen arbitrarily) (open squares).

For most of the residues (mainly in helix), the RCFs 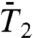at 1 ns have already converged to their limit values. However, the RCFs of the following dihedral angles γ_n did not clearly converge on the 1-ns time scale n = 2, 18, 19, 25, 26, 30, 32–41, and 44. The largest deviations from 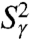at 1 ns are observed for γ₂, γ₂₆, γ₃₂-γ₄₁, and γ₄₄. All these dihedral angles have free-energy profiles with marked multiple minima (Fig. S3 and Fig. 3A, Inset) except γ₃₂, γ₃₆ (anharmonic FEP with no actual metastable minimum) and γ₄₀ and γ₄₄ (wide potentials). Approximation of the RCFs of the dihedral angles at larger time (t = 10 ns, chosen arbitrarily) (open diamonds in Fig. 3) using a stretched exponential fitted to the RCFs up to 1 ns (Fig. 1C) shows that only 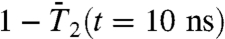for γ₃₆, γ₃₈ converges to 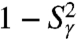on this longer time scale. As for γ_n, the RCFs of a series of (N-H)_n bonds, n = 2, 3, 4, 21–29, 34–45, did not converge to 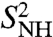on the 1-ns time scale. The FEPs of the (N-H)₂, (N-H)₂₆, (N-H)₃₀, and (N-H)₃₇-(N-H)₄₀ have clear multiple minima as shown, for example, for (N-H)₂₆ and (N-H)₃₇ in Fig. 3B, Inset. Only the RCF of (N-H)₄₄ converges to 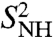on a 10-ns time scale as shown by extrapolating the RCFs of the N-H bonds up to 10 ns using a SE fitted to the RCFs up to 1 ns (Fig. 1D).

The two types of behavior found in Fig. 3, the convergence of the RCFs 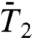and 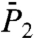towar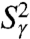d and 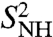on a 1-ns time scale for residues in a single-minimum stiff FEP (located in helix; see also ref. 34), and a slow convergence toward these limits for residues in multiple-minima and soft anharmonic FEPs (located mainly in loops), correspond very well to the two types of behavior observed at different time scales in helix and loops by NMR in protein G (35). We emphasize here that the convergence of the RCFs toward the order parameters depends on the anharmonicity of the FEP and on the existence of multiple substates (see Fig. 3 Insets) rather than by the type of secondary structure. The residues with multiple-minima free-energy profiles are mainly in loops but not necessarily, as for CYS26 of VA3 (Fig. 3) located in a helix.

Consequences of Anomalous Diffusion for the Interpretation of NMR Experimental Data.

Deviations of the time evolution of the RCFs from a simple exponential decay (free diffusion) were observed for a few residues along the sequence of proteins (14) (9 out 155 in Ribonuclease A in ref. 1). They were interpreted as due to slow conformational fluctuations, i.e., jumps of the N-H bonds between different orientations (14), which correlate with the bond orientation on a slower time scale τ_s. For these residues, the RCF is represented as a sum of a fast and a slow exponential decay; i.e., f₂(t) = a_f exp(-t/τ_f) + (1 - a_f) exp(-t/τ_s) with a_f a parameter weighting the fast motions in the MF approach (see SI Text Sec. 9). The MF approach with a monoexponential decay (a_f = 1) (Eq. S70 in SI Text) and biexponential decay (a_f ≠ 1) (Eq. S71 in SI Text) were fitted to the RCFs computed from MD up to 1 ns (see SI Text Sec. 9 and Table S1). The relaxation time τ_f (14) typically varies between about 30 ps to about 300–500 ps in the monoexponential model and τ_f < 12 ps in the biexponential model with 170 < τ_s < 580 ps (see Table S1). The generalized order parameter 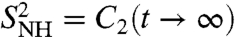computed by fitting the MF approach to the RCFs computed by MD up to 1 ns (SI Text Sec. 9 and Table S1) are compared to those computed using a SE in Fig. 3B. There is very good agreement between the two approaches for all the amide bonds with small differences for the residues in loop 37-40, which have multiple-minima FEPs. However, the values of the parameters 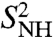in the MF approach are very close to the values of the RCFs at 1 ns (compare the values shown in Fig. 3 with the values in Fig. 1D) and, therefore, the MF approach fails to predict the nonconvergence of the RCFs to 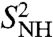observed for bonds having strong anharmonic FEP (filled circles in Fig. 3).

A (multi)exponential model is not easily interpreted. Even if a sum of exponentials could fit the RCF as well as a stretched exponential, a (multi)exponential model cannot explain anomalous diffusion. Because an exponential decay of an RCF corresponds to a diffusion equation with a time-independent diffusion constant, the probability distribution of the angular displacement solution of this diffusion equation is predicted to scale linearly with time (α = 1) according to Eq. 4, which is not the case as can be seen in Fig. 2. Therefore the (multi)exponential model, which assumes normal diffusion, cannot describe the SE decay (anomalous diffusion) found in MD at short time scale as can be seen in Fig. 1D. At short times (t ≪ τ_s), the RCFs of the (multi)exponential MF approach decay linearly as predicted by Eq. 1 with an effective diffusion constant D_MF proportional to (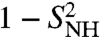) (Eq. S74 in SI) much lower than D_α (as shown by the comparison between Table S1 and Fig. S6b). It is, however, interesting to note that the quantity (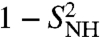) in the (multi)exponential MF approach can be interpreted as a diffusion constant that varies along the sequence of the amino acids as D_α (as shown by the comparison of Fig. 3B and Fig. S6b).

The diffusion equation with a time-dependent coefficient D(t) is a compact (approximate) model with only two parameters: D_α, which quantifies the width of the probability distribution of the angular displacements at 1 ps, and α, which quantifies the self-similarity of this distribution. It remains a challenge to extract from NMR relaxation data these parameters characterizing the angular MSD of the N-H bonds. The values [α,D_α] could be extracted by fitting the RCFs measured on a 100-ps time scale to a SE (Fig. 1 and Fig. S6 b and c) or by using a MF approach with a SE decay (Eq. S75 and Fig. S6 in SI Text). This objective will be pursued in the near future and will require accurate values of J_NH(ω) for a model protein.

Conclusions

By using MD, we demonstrated that the RCFs of two local probes of the backbone dynamics (coarse-grained dihedral angles and backbone N-H bonds) decay as stretched exponentials at least up to 1 ns (Fig. 1). They are characterized by a constant D_α and an exponent α varying along the amino acid sequence of the protein according to the anharmonicity of the FEP. Comparison with the MF approach used in NMR shows that the constant D_α of the local probes varies along the amino acid sequence like (1 - S²). The exponent α measures the “speed” of the exploration of the conformational space and was always found to be smaller than 1 (subdiffusion). Anomalous subdiffusion of the local probes was described by a rotational diffusion equation with a power-law diffusion coefficient that accounts for the self-similarity of the PDF of the angular displacements of the probes (Fig. 2). The larger exponents α of the local probes were found for residues moving on multiple-minima free-energy profiles for which the RCF converges slowly to the generalized order parameter S² (Fig. 3). Measurement of the parameters [α,D_α] for backbone ¹⁵N-H bonds at short time scale and of the P₂(t) on different time scales should enable one to detect multiple substates of the segments of the backbone of a protein. Such conformational substates may be related to protein function and protein folding, which involve both small reorganization of the backbone segments and large conformational changes occurring on different time scales.

Materials and Methods

Five MD simulations of VA3, each of a duration of 80 ns, were carried out at 300 K in explicit water (Simple Point Charge force field) with the GROMACS package (36) and the all-atom Optimized Potentials for Liquid Simulations force field (37) with no cutoff of the electrostatic interactions as this improves the accuracy of the force field compared to NMR data (31). The structure of VA3 was taken from the NMR model 1 of ref. 21. Details of all MD simulations are given in SI Materials and Methods. The coordinates of VA3 were saved every 1 ps. Consequently, the different initial times t^′ in Eqs. 2 and 3 were sampled every picosecond. For each t^′, the vector u_n(t^′) = { cos[γ_n(t^′)], sin[γ_n(t^′)]} was computed for each dihedral angle γ_n. For each time, the direction u_n(t^′) of each (N-H)_n bond (Fig. S1) was computed after the overall translation and rotation of the protein had been eliminated by aligning the structure at time t^′ on the initial structure. The averages in Eqs. 2 and 3 were calculated for the whole trajectory at different times t. The fits of the stretched exponentials to the RCFs computed from MD were made with a root-mean-square algorithm, and the PDFs shown in Fig. 2 and Fig. S8 were computed from MD by sampling Δγ and Δξ with a resolution of 1 °.