Pore opening and closing of a pentameric ligand-gated ion channel

Abstract

Nerve signaling in humans and chemical sensing in bacteria both rely on the controlled opening and closing of the ion-conducting pore in pentameric ligand-gated ion channels. With the help of a multiscale simulation approach that combines mixed elastic network model calculations with molecular dynamics simulations, we study the opening and closing of the pore in Gloeobacter violaceus channel GLIC at atomic resolution. In our simulations of the GLIC transmembrane domain, we first verify that the two endpoints of the transition are open and closed to sodium ion conduction, respectively. We then show that a two-stage tilting of the pore-lining helices induces cooperative drying and iris-like closing of the channel pore. From the free energy profile of the gating transition and from unrestrained simulations, we conclude that the pore of the isolated GLIC transmembrane domain closes spontaneously. The mechanical work of opening the pore is performed primarily on the M2-M3 loop. Strong interactions of this short and conserved loop with the extracellular domain are therefore crucial to couple ligand binding to channel opening.

Pentameric ligand-gated ion channels (1) (pLGICs) form a large family of membrane proteins with a central role in biological signal transduction. These channels transmit an external signal—the binding of a ligand—through the opening of their ion-conducting pore. With their important physiological roles, in particular in nerve signaling, pLGICs are major pharmaceutical targets. Accordingly, the gating transition, as an essential element of their function, has been studied extensively. At the structural level, advances came from ∼4-Å resolution electron microscopy structures of the nicotinic acetylcholine receptor (nAChR) (2), followed by a breakthrough based on crystallographic structures of two prokaryotic members of the family, ELIC and GLIC (3–5). The structures of the Erwinia chrysanthemi channel ELIC and the Gloeobacter violaceus channel GLIC, two homologous proteins with ∼18% sequence identity, appear to capture the conformations of the channel in closed and open states, respectively. Here, we use multiscale simulations to connect these two endpoints of the gating transition, providing a molecular pathway of channel gating and offering a window into the function of pLGICs at atomic resolution.

Complementary to experimental techniques, molecular dynamics (MD) simulation is a powerful tool to study ion channels (6–10), including the pLGICs nAChR (11–13), ELIC (14), and GLIC (5, 15). Remarkably, in a recent 1-μs MD simulation (15), pore closure could be induced in GLIC after the protonation states of 55 residues were simultaneously changed to mimic a pH jump from ∼4.6 to ∼7. However, even in this very long simulation under a strong driving force, the gating transition appeared to be only partial (15), without reaching a stable closed conformation. Furthermore, to obtain statistical properties such as the opening probability of the channel, one needs to observe multiple transitions between the open and closed states, requiring a simulation time far beyond those currently affordable. As an alternative to single long MD simulations, the string method (16, 17) has been developed to explore large-scale conformational changes, including complex molecular transitions in high-dimensional space (18, 19). Importantly, the free energy along the transition pathway can be obtained from this method. In this study, we characterize the atomistic pathway of the GLIC gating transition, together with its energetics and kinetics, by combining a mixed elastic network model (20), string method calculations, and unrestrained MD simulations.

pLGICs are composed of five subunits that assemble into an extracellular domain (ECD) and a transmembrane domain (TMD) whose ion conductivity is gated by signals (typically ligand binding) from the ECD. Given the challenges in studying the entire pLGIC complex, efforts have been made to dissect the pLGIC and investigate each domain separately. In particular, the crystal structure of isolated ECDs of GLIC has been determined recently (21). Here we focus on the function of an isolated TMD of GLIC with its conserved structure. Unlike most other pLGICs, GLIC is a pH-gated (22) channel, a characteristic reflected in unique features of its ECD. The TMD of GLIC, in contrast, fully reflects the common features of the family. Moreover, the sequence similarity in the TMDs of GLIC and ELIC allowed us to build a full transition pathway at a coarse-grained level (20) based on the respective crystal structures (3, 4), which in this study is refined at atomic detail using the string method (16, 17). In a series of restrained MD simulations (Table S1) of the membrane-embedded and solvated channel, we iteratively determine the minimum free energy pathway (string) between the open and closed states, mapped in the 1,240-dimensional space of the backbone C_α coordinates of the isolated TMD of GLIC. In addition to the large-scale rearrangements of the helices during the gating transition, we also study the important role of channel hydration and the transition to a dry state of the gate. From the reversible work performed on each of the residues during channel opening, we identify the key residues involved in the coupling between the TMD and the ECD.

Results

Ion Conductance in Open and Closed States.

Before studying the gating transition, we investigate the ion-conducting properties of the endpoint structures. To examine the ion permeability of the GLIC transmembrane pore, we calculate the one-dimensional free energy of a single Na⁺ ion and its mobility from umbrella-sampling simulations, as done similarly for the gramicidin channel (23). With the TMD in the open conformation (Fig. S1), a moderate free energy barrier of < 4 kcal/mol is located in the middle of the pore, whereas the intracellular entrance features an attractive well corroborating the “cation reservoir” observed in the 1-μs simulation (15). The position-dependent Na⁺ diffusion coefficients (Fig. S1, Inset), calculated by integrating the autocorrelation function of the ion coordinate (24), indicate that the ion mobility inside the pore is much lower than that in bulk water, with diffusion coefficients ∼20 times smaller. Based on a one-dimensional diffusion model incorporating the calculated free energy and diffusion coefficients (SI Text), the Na⁺ conductance at a concentration of 140 mM is estimated to be on the order of ∼1 pS, in good agreement with the single-channel measurement (8 pS) of GLIC (22) considering that our calculation ignores correlated ion motions. The GLIC pore in the crystal structures (4, 5) is thus in a conformation consistent with open-state ion-conduction rates. In contrast, an energetic barrier of more than 10 kcal/mol was found for the Na⁺ ion when the TMD is in the presumed closed conformation constructed from the backbone structure of ELIC (3). As a consequence, the conductance is reduced by at least 3 orders of magnitude, consistent with a closed state of the channel.

Gating Pathway.

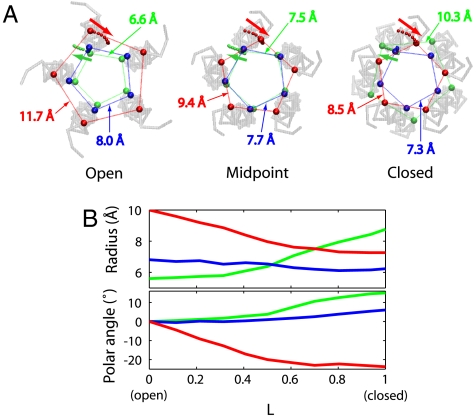
With the channel states confirmed, we now explore the gating transition. The protein structures obtained from the string method simulations show that the channel closes in a two-stage iris-like motion of the pore-lining helices. In pLGICs, the transmembrane helices M2 from each of the five subunits together form the ion-conducting pore. Along the pathway, the most prominent conformational change is a tilting motion of the M2 helices, with the two ends undergoing much larger displacements than the center of the helix (Fig. 1). The helix tilting axes do not intersect the pore axis. Consequently, the tilting results in an iris-like motion of the helix atoms, altering both their distance from the symmetry axis and their polar angles (Fig. 1B). Specifically, the extracellular end of the helix moves closer to the symmetry axis during the open-to-closed transition, along with a clockwise rotation consistent with the proposed global twisting between the ECD and TMD (5, 14, 15, 25). In contrast, the intracellular end moves in the opposite direction (Fig. 1). Furthermore, the tilting occurs in a stepwise fashion. As a result, the extracellular end of M2 has already moved almost to its position in the closed conformation at the midpoint of the transition, whereas the intracellular end remains near the open-state location (Fig. 1).

Fig. 1.

Closing transition of the GLIC pore. (A) M2 helices in the average symmetrized conformations of open, midpoint, and closed states, respectively, taken from the first, sixth, and last images along the pathway. Three C_α atoms (Top: red, Thr243; Middle: blue, Ile232; Bottom: green, Glu221) of the helix in each subunit are drawn as spheres, viewed from the extracellular side. The edge lengths of the regular pentagons formed by these atoms are marked. The trajectories of the three atoms in one of the subunits during the closing transition are shown as a series of smaller spheres, with arrows indicating the directions of motion. (B) Radii (distance to the symmetry axis) and changes in the polar angles of the three atoms in A as a function of the reduced path length L (see Methods).

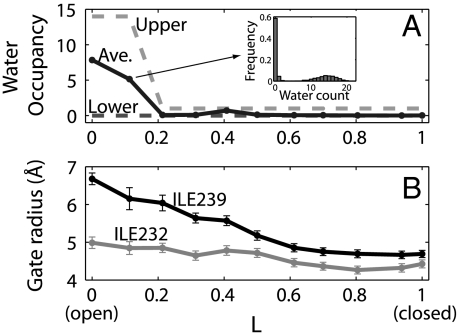
The gate in the GLIC channel is formed by the rings of residues Ile232 and Ile239 (15) (Fig. 2). Their hydrophobic and bulky side chains constrict the pore at the middle and near the extracellular entry, respectively. In the open state, the region between the isoleucine rings is fully hydrated; upon channel closure, a ∼15-Å long segment of the central pore becomes completely dry. Drying of the pore is induced by remarkably subtle changes in the pore width near the hydrophobic constriction. To quantify the width of the gate, we define a “gate radius” for each quintet of Ile residues by fitting a circle through the five centers of mass of their side chains in the xy plane parallel to the membrane. The average gate radii for each conformation (referred to as “image”; see Methods) along the string are shown in Fig. 3B. The gate radius at Ile239 undergoes a larger change during the transition than that at Ile232 and thus appears to play a more significant role in controlling the state of the pore. The pore radius near Ile239 decreases primarily during the first half of the open-to-closed transition and levels off when approaching the closed state. This two-stage process is a result of the nonuniform tilting motion of M2 described earlier. The average water count in the hydrophobic region between Ile232 and Ile239 is shown in Fig. 3A. In contrast to the gate radii, the water occupancy of the pore changes more abruptly along the pathway. Beyond a reduced path length of L = 0.2, the average occupancy is low and the hydrophobic region is rarely hydrated during the simulations, indicating an early drying and closure of the pore during the open-to-closed transition.

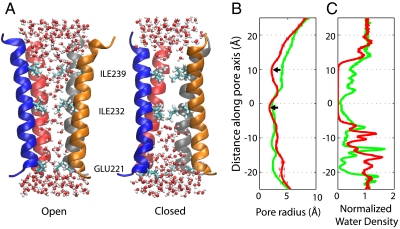
Fig. 2.

Structure and hydration of open (green lines) and closed (red lines) channels. (A) Snapshots of the M2 helices in the open and closed channels at the transition endpoints, with the extracellular side up. The subunit in the front is removed to reveal the water molecules inside the pore. The side chains of three residues forming constrictions are also shown. (B) Pore radius along the axis, calculated using the program HOLE (33) and averaged over all frames of the respective simulations. The two narrowest parts of the closed conformation are indicated by arrows. (C) Distribution of the water density within a 5-Å cylinder around the pore axis, relative to the bulk density.

Fig. 3.

Pore hydration and width along the closing transition. (A) Average water count (solid line) in a 10-Å long section of the pore between Ile232 and Ile239 for each image along the pathway. The dashed lines indicate the two modes in the bimodal occupancy distributions (see Inset for the histogram of the water count for the second image) for the open pore, corresponding to the filled and empty states. (B) Average gate radii at Ile232 and Ile239 for each image, determined from fits of circles in the xy plane through the centers of mass of the side chains.

A possible secondary gate, formed by a ring of glutamic acids at the intracellular entry, is open in simulations of both open and closed states. In the crystal structure solved at pH 4.0 (4), the Glu221 side chains from the five subunits are in close contact with each other near the pore axis, thus blocking the intracellular entry of the pore. At this low pH, the carboxylic groups are likely to be partially protonated. In our simulations, the unprotonated side chains repel each other and rapidly flip toward the bulk water on the intracellular side, adopting an orientation similar to that in a second GLIC crystal structure determined independently (5). Nonetheless, in the open state a constriction is present near the CH₂ moieties of Glu221 (Fig. 2 B and C). But despite the lower water occupancy on average, the hydrogen-bonded water chain in this region remains continuous during almost the entire simulation. Interestingly, in the closed state the intracellular entry of the pore is wider and does not form a constriction. We conclude from these results that the Glu221 ring is open at neutral pH, but the opening state of this region may be sensitive to intracellular pH and possibly ionic strength (SI Text). We note that ELIC and nAChR also feature Glu residues in adjacent locations, which are believed to account for the favored cation conduction in pLGICs (26).

Dehydration of Hydrophobic Gate.

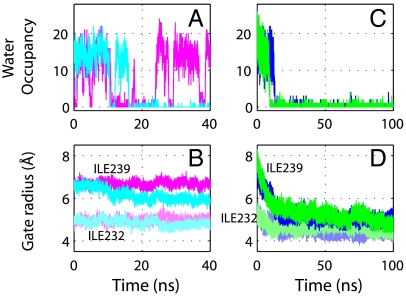
The water in the hydrophobic constriction of the channel exhibits cooperative emptying and filling transitions, with channel closure shifting the equilibrium toward the empty state. Fluctuations between water-filled and empty states of hydrophobic channels have been reported previously (9, 12, 27). Here we observe a similar behavior at the hydrophobic gate of the GLIC channel, as shown in Fig. 4A. When the protein is restrained in the open conformation (magenta), hydration and dehydration occur intermittently on the nanosecond time scale, associated with sharp transitions in the number of water molecules. Interestingly, the gate radii remain nearly constant during the simulation (Fig. 4B). For the next image along the string (cyan), the water occupancy in the gate exhibits similar fluctuations during the first half of the simulation, but then the gate remains empty during the second half, apparently caused by a decrease in the gate radius at Ile239 (Fig. 4 A and B). The hydration state of the pore thus seems to depend sensitively on the gate radius, as a small decrease in the radius can cause a dramatic drop in water occupancy (Figs. 3 and 4).

Fig. 4.

Time evolution of the water count (Top) and gate radii (Bottom), as defined in Fig. 3. (A and B) Simulations of the first image (i.e., the open state, magenta) and the second image in the string (cyan). (C and D) Two unrestrained simulations starting from the open conformation.

Energetics of Gating.

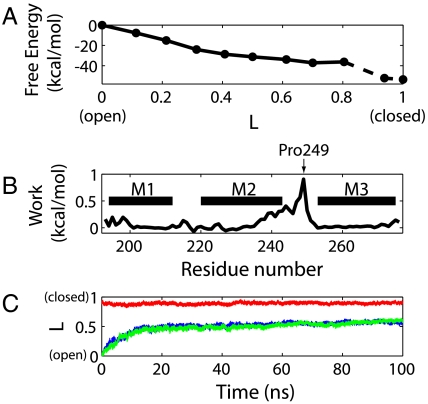
For an isolated TMD, the closed state is thermodynamically stable based on the simulations, and closing is driven by a large free energy gradient. By integrating the restraining forces along the string connecting the open and closed configurations, we can determine the free energy profile for the open-to-closed transition (Fig. 5A). Interestingly, the open conformation does not appear to be in a local free energy minimum. Instead, starting from the open conformation, the free energy decreases monotonically by a total of ∼35 kcal/mol during the first half of the transition. The free energy then levels off after the midpoint of the transition. The sharp drop in the free energy in the final two images is associated with a secondary structure rearrangement near the end of helix M1 and the beginning of the first intracellular loop. This local but abrupt conformational change results in a large discretization error of the calculated free energy profile near the end of the string. Despite this uncertainty, the closed state is clearly favored energetically.

Fig. 5.

Thermodynamics and kinetics of pore closing. (A) Free energy of each image along the pathway calculated using the string method. The last portion of the curve involves larger uncertainty in the calculation, as explained in the text, and is therefore denoted by a dashed line. (B) Mechanical work performed on each residue during the opening transition, integrated from the image at L ≈ 0.8 to L = 0. (C) Time evolution of the three unrestrained simulations (two starting from the open state and one from the closed state) along the pathway. The progression parameter is defined as the reduced path length L of the point on the pathway with the smallest root-mean-square distance to the instantaneous protein conformation.

Consistent with the free energy profile in Fig. 5A, which was obtained from the contour integral of the mean force along the pathway, initially open channels close spontaneously. As shown in Fig. 5C, the two unrestrained simulations (Table S2) starting from the open conformation of the GLIC TMD both undergo rapid closing transitions. In both simulations, the protein conformations approach the midpoint of the string (with a reduced path length of L ≈ 0.5) after ∼20 ns. Following this initial phase, the transition proceeds more slowly, and the conformations appear to be stabilized in intermediate states with reduced path lengths of L ≈ 0.5 to 0.6, fully consistent with the plateau in the free energy surface in Fig. 5A between reduced path lengths of L ≈ 0.5 and 0.8. In agreement with the string method results in Fig. 3A, drying of the pore occurs early in the transition, after ∼10 and ∼15 ns, respectively (Fig. 4C). As expected from the free energy, the unrestrained simulation starting from the closed state remains stable without any significant conformational change throughout the 100 ns (Fig. 5C). The free energy profile from the string method calculations is thus fully consistent with the spontaneous closure observed in unrestrained simulations here and in ref. 15.

Is channel closure driven by tension in the TMD, or by the removal of water and the resulting hydrophobic “collapse” of the pore gate? As shown in Fig. 4D, the gate radii decrease more or less gradually during the unrestrained simulations, even early in the transition with the pores still hydrated. Moreover, the water occupancy is already fluctuating between a dominant filled and a low-population empty state with the pore open (Figs. 3A, Inset, and 4A). These results indicate that water alone could not provide the large driving force for channel closure and suggest a dominant role of the protein. Nevertheless, water emptying appears to play a role in the closure dynamics. In the unrestrained simulations, the water occupancies exhibit a single sharp drop, and the pores remain empty thereafter (Fig. 4C). Just before emptying, the pore radii reach a slight plateau in one of the simulations. The time scales of water occupancy fluctuations (Fig. 4A) and pore closure (Fig. 4D) are comparable. Therefore, although the emptying of water is not driving the transition, it is a factor in the pore-closing dynamics. In recent simulations of a K⁺ channel, pore closure was also accompanied by a dewetting transition (10).

Symmetry.

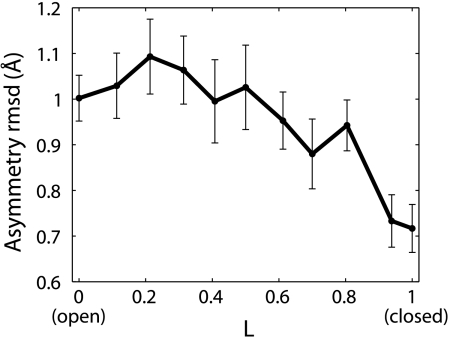
Despite the near perfect fivefold symmetry of both ELIC and GLIC crystal structures, individual conformations along the open-to-closed pathway do not have to be symmetric (but there will be other, symmetry-related pathways, resulting in a fully symmetric ensemble). In our string method calculations, we take care to permit asymmetry in the pathways by restraining only symmetric degrees of freedom (see Methods). Indeed, despite the identical sequence of the five GLIC subunits, the magnitude of asymmetry (Fig. 6), quantified by the rmsd between the structures along the pathway and their symmetrized conformations, is much larger than that (∼0.1 Å) present in the GLIC or ELIC crystal structures. Interestingly, we observe a trend of increasing symmetry (decreasing rmsd) during the open-to-closed transition, with the closed conformation being more symmetric. This high degree of symmetry in the closed state is consistent with a more compact and ordered structure. Overall, the asymmetry of the protein structures in both the string method and unrestrained simulations here does not appear to be as dramatic as that observed in the 1-μs simulation (15) of the entire GLIC.

Fig. 6.

Asymmetry in the protein conformation for the simulations of each image. The rmsd between the C_α coordinates 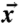and the symmetrized coordinates 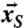(see SI Text) was calculated for each frame, and the average rmsd value over all simulation frames is plotted.

Coupling to Ligand Binding Domain.

Our simulations identify the M2-M3 loop as the main coupling element between ligand binding to the ECD and channel opening of the TMD. Fig. 5B shows the mechanical work of channel opening integrated individually for each residue along the pathway. More than 70% of the total work is done on the extracellular half of M2 and the M2-M3 loop, consistent with the 1-μs simulation in which the pore closure was initiated at the top of M2 (15). Remarkably, the peak of the work distribution occurs near Pro249 in the M2-M3 loop, in close contact with the β1-β2 loop from the ECD in the crystal structures (4, 5). We note that the M2-M3 loop is conservatively short and compact across the pLGIC family, and its critical role in the interdomain coupling has been established experimentally (28, 29). Therefore, although pLGICs achieve the conformational change in their ECDs through different mechanisms, they may consistently employ the M2-M3 loop in the TMD as a “handle” to pull open the pore.

Discussion

We have studied the gating transition of a pLGIC by constructing the transition pathway between open and closed structures of the GLIC TMD. Remarkably, the closed state of the isolated TMD is found to be considerably more stable than the open state. With the ECD removed, the TMD of GLIC alone does not actually have a metastable open state, as the simulations starting from the open conformation showed a spontaneous collapse of the pore into conformations with a narrow and dry hydrophobic gate. The associated free energy drop of more than 30 kcal/mol corresponds to an extremely low opening probability. The isolated TMD of GLIC should therefore remain closed in equilibrium, with virtually no constitutive activity.

An immediate concern is that in our calculations we have only a crystal structure of the open state. But, remarkably, our homology model of the closed state of the GLIC TMD, based on the crystal structure of the ELIC channel, turned out to be more stable than the open state (Fig. 5A). Consistent with the calculated free energy profile, unrestrained MD simulations starting from the open structure of the GLIC TMD are found to relax spontaneously toward the ELIC closed-state structure within 100 ns (Fig. S2). The observed stability of the closed structure and its low free energy thus support our homology model of the closed TMD.

For intact channels to have a significant constitutive activity, folding and assembly have to offset the free energy cost of opening the TMD. Single-channel currents through GLIC indicate a small but observable open-state population of ∼millisecond lifetime at pH 6 (22). Despite the extensive interface between the TMD and the ECD with substantial interaction energy, the calculated free energy drop of ∼35 kcal/mol (Fig. 5A) thus seems large. This value indeed has considerable uncertainties, beyond those arising from MD force field issues. The string method requires that the mean force varies smoothly along the transition pathway, which, given the typically rugged energy landscape in high-dimensional space and the relatively small number of images here, is a rough approximation. Furthermore, the changes in the free energy profile at different stages of the string calculation (Fig. S3) suggest that the 0.44-μs total simulation time in the last iteration may not be sufficient to sample, e.g., multiple side-chain conformations (Fig. 4B). Therefore although the overall shape of the obtained free energy profile is reasonable, and consistent with unrestrained simulations, the magnitude of the driving force may bear significant statistical and systematic errors.

The strong bias toward a closed state in isolated TMDs has possible physiological relevance. Although the exact function of GLIC has not been unambiguously established, its eukaryotic homolog, nAChR, triggers the contraction of muscle cells. After the nAChRs are opened, the resulting small change in the membrane potential can activate nearby voltage-gated ion channels, which then quickly depolarize the membrane. Once the latter channels are opened, too, the contraction of the muscle cell is inevitable even if the nAChRs return to the closed or inactivated state. Therefore, the risk of accidental damage would impose evolutionary pressure to have a low opening probability of TMDs uncoupled from their ECDs, as found here in the case of GLIC. Interestingly, for voltage-gated K⁺ channels, recent MD simulations (10) revealed that with the regulatory domain (the voltage sensor) removed, the pore domain also spontaneously underwent hydrophobic closure. It thus appears to be a common feature of gated ion channels that the pore domains alone would remain closed and can be opened only by a proper coupling to the regulatory domains.

Experimentally it is not known yet whether the GLIC TMDs alone could fold and form pentameric channels in the membrane. Therefore the validity of our model remains to be tested in experiments. We predict in particular that a lipid membrane should show no increase in ion permeability after incorporating GLIC mutants with the ECD deleted, without observable single-channel currents.

Another key result of our simulations, the timeline of gate closure, can be compared directly to experiment. Through careful analysis of the energetic and kinetic effects of point mutations in nAChR, interpreted in terms of Φ-values, Auerbach and coworkers developed a remarkably detailed picture of channel opening (30, 31). The small Φ-values of some pore-facing M2 residues in the gate region suggested a closed-like local environment at the transition barrier, and thus a late change in the hydration state during the opening of the channel (30, 31). This interpretation is in full agreement with the helix titling and early drying of the gate during the open-to-closed transition observed here in MD simulations. Our results also appear to be consistent with the kinetic modeling of channel gating by Auerbach (32) that was interpreted in terms of a broad and flat free energy profile across the transition region. Here, we find that early closure of the gate is followed by a slow drift on a free energy plateau toward the fully closed state of the channel (Fig. 5 A and C).

Despite this agreement, important questions remain inaccessible with the present model of an isolated TMD. Although shedding some light on the coupling between the ECD and the TMD by identifying the M2-M3 loop as a major factor in driving the gating transition, extracting details about the intramolecular signal transduction mechanism of pLGICs, from ligand binding at the ECD to opening of the TMD, will require additional simulations. String method calculations of the entire GLIC protein will become possible when the crystal structure of the closed state also becomes available. Notwithstanding these remaining challenges, an atomic picture of the gating transition of GLIC, and more generally the pLGIC family, is getting within sight.

Methods

The simulation system (Fig. S4) contains the TMD of GLIC embedded in a lipid bilayer and solvated by water molecules. In each iterative update of the string (17) representing the transition pathway between open and closed states, independent simulations are performed for each of its 11 images. In these simulations, 420 C_α atoms of the M1–M3 helices (84 in each monomer) are harmonically restrained to target positions. These positions are adjusted as the string converges toward the minimum free energy pathway in the space of the 3 × 420 = 1260 C_α Cartesian coordinates, with all other degrees of freedom integrated out. In the final string, the gradient of the free energy is everywhere tangential to the path, and the free energy along the string is then obtained by integrating the mean restraining forces.

To describe the fivefold symmetry of the GLIC homopentamer, we show that any conformation can be orthogonally decomposed into a perfectly symmetric component and an antisymmetric component. We develop a restraining scheme in which only the symmetric degrees of freedom are subject to the restraints, and the protein is otherwise free to deviate from symmetric structures. This allows us to restrain the overall conformation of the protein without artificially imposing any symmetry. See SI Text for the full methods.

Ion conduction is studied in umbrella-sampling simulations with 153 windows, covering a total distance of 76 Å for the Na⁺ ion. The position-dependent diffusion coefficients are obtained by integrating the autocorrelation function of the ion displacements in each umbrella window (24). The channel conductance is calculated by using the one-dimensional Smoluchowski equation within the linear-response range, ignoring the effects of correlated ion motions in multiply occupied channels. See SI Text for details.