Quantifying and Predicting the Promiscuity and Isoform Specificity of Small-Molecule Cytochrome P450 Inhibitors

Abstract

Drug promiscuity (i.e., inhibition of multiple enzymes by a single compound) is increasingly recognized as an important pharmacological consideration in the drug development process. However, systematic studies of functional or physicochemical characteristics that correlate with drug promiscuity are handicapped by the lack of a good way of quantifying promiscuity. In this article, we present a new entropy-based index of drug promiscuity. We apply this index to two high-throughput data sets describing inhibition of cytochrome P450 isoforms by small-molecule drugs and drug candidates, and we demonstrate how drug promiscuity or specificity can be quantified. For these drug-metabolizing enzymes, we find that there is essentially no correlation between a drug's potency and specificity. We also present an index to quantify the susceptibilities of different enzymes to inhibition by diverse substrates. Finally, we use partial least-squares regression to successfully predict isoform specificity and promiscuity of small molecules, using a set of fingerprint-based descriptors.

Introduction

In general terms, inhibitor promiscuity (i.e., a single compound affecting multiple protein targets) can lead to either adverse off-target effects (Peters et al., 2009) or enhanced therapeutic power (Roth et al., 2004; Keiser et al., 2009), depending on the nature and extent of promiscuity. In the context of drug metabolism by cytochrome P450 (P450) enzymes, drug promiscuity has potentially important effects on the occurrence of clinically significant drug-drug interactions (DDIs) (Atkins, 2004; Greenblatt and von Moltke, 2010). The P450 superfamily is responsible for phase I drug metabolism of the majority of pharmaceuticals and drug candidates (Nebert and Russell, 2002; Coon, 2005). The more P450 isoforms a given small molecule inhibits, the more likely it will be involved in DDIs with many different drugs. At the same time, metabolism of a compound by multiple isoforms provides redundancy in clearance and makes DDIs less likely. Thus, the relative promiscuity of a drug toward P450 inhibition versus P450 metabolism might be predictive of safety. Supporting this idea, Veith et al. (2009) found that the U.S. Food and Drug Administration (FDA)-approved drugs appeared qualitatively more specific with regard to P450 inhibition than a more general set of compounds (the NIH Molecular Libraries Small Molecular Repository). In contrast, several companies are making efforts to develop isoform-specific P450 inhibitors that would be administered as adjuvants to enhance the pharmacokinetic profile of drugs that are highly susceptible to P450 metabolism (Gilead Sciences, http://clinicaltrials.gov/show/NCT00892437 NLM Identifier: NCT00892437; Pfizer, http://clinicaltrials.gov/show/NCT00783484 NLM Identifier: NCT00783484; Tibotec Pharmaceuticals, http://clinicaltrials.gov/show/NCT00838760 NLM Identifier: NCT00838760).

Specificity in inhibition is thus an important functional parameter, but quantitative studies aimed at correlating this specificity with physicochemical properties of different compounds are handicapped by a very significant gap: there is currently no continuous measure of drug specificity with which to draw correlations, with respect to either inhibition or metabolism. In the first part of this article, we rectify this situation by introducing an index of inhibition promiscuity (or, equivalently, specificity) adapted from one developed to quantify catalytic promiscuity of enzymes. We apply this index to large-scale screens of P450 inhibition enabled by recent advances in automation and analytical protocols, with the goal of quantifying the specificity with which a given drug inhibits a particular P450 or P450s.

In the second part of this article, we use partial least-squares regression (PLSR), a powerful multivariate analysis technique, to identify chemical features that correlate with inhibitory activity toward particular P450s, as well as chemical features that correlate with nonspecific inhibition of several isoforms. We provide a template for how multivariate statistical techniques such as PLSR can be applied to large-scale screens of P450 inhibition, with the goals of predicting the specificity of new drugs, and predicting which isoforms are likely to be targeted by a new drug. Because P450 inhibition is a crucial contributor to clinically harmful DDIs, a more rigorous and global approach to inhibition studies will facilitate the identification of potentially problematic pharmacokinetic behavior early in the drug discovery process (Stoner et al., 2010).

We demonstrate these analytical approaches on two sets of P450 inhibition data. The first set (which we denote as “S₆₄”) consists of IC₅₀ values obtained for 64 commercially available pharmaceutical compounds and six P450 isoforms (1A2, 2C8, 2C9, 2C19, 2D6, 3A4). The second dataset (denoted as “S₄₆₉”) consists of percent inhibition values measured at a fixed inhibitor concentration measured for 469 proprietary compounds and 5 isoforms (1A2, 2C9, 2C19, 2D6, 3A4) in a cocktail format, a subset of a larger (∼10,000-compound) set (Zientek et al., 2008). To ensure that we efficiently sampled the full range of inhibitory patterns in the larger set, S₄₆₉ was designed to include 194 inhibitors chosen at random from the larger set, 116 compounds that showed no inhibition toward any isoform, 114 compounds that were qualitatively potent and specific (>90% inhibition of any one isoform and <20% inhibition of all others), and 45 inhibitors that were qualitatively potent and promiscuous (>80% inhibition of at least four isoforms).

I_inh: An Index of Inhibitor Specificity.

Shannon-Jaynes entropy is a fundamental concept in information theory that describes the amount of information in a dataset (Shannon, 1948) or equivalently in statistical mechanics describes the relative uniformity or “flatness” of a probability distribution (Jaynes, 1957). If there are N possible outcomes of a given process, each with probability p_i, the Shannon-Jaynes entropy of the process is given by the following:

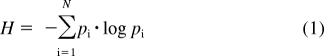If only one of the outcomes is certain (i.e., has p_i = 1) while all others have probability zero, then H takes the value 0. On the other hand, if all outcomes have equal probability, then H takes its maximum value of log N.

We previously proposed (Nath and Atkins, 2008a) an index to measure catalytic promiscuity based on Shannon entropy. Here, we derive an analogous index to describe the promiscuity with which a given drug inhibits a set of enzymes. Consider a set of N enzymes, such that a drug displays an inhibitory potency, denoted as x_i, toward enzyme i. The ratio

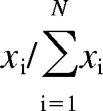can be thought of as approximating the probability that the drug will inhibit enzyme i out of all the enzymes in the set. Analogous to eq. 1, we can then define enzyme inhibitory promiscuity as follows:

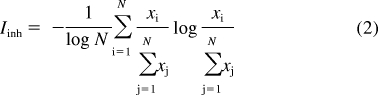If the drug inhibits all enzymes with equal potency (i.e., is completely promiscuous), I_inh = 1. If the drug inhibits only one enzyme but not any of the others (i.e., is completely specific), I_inh = 0. Two important points must be made about this proposed index. First, I_inh is dependent on the panel of enzymes included in the calculation: just as an IC₅₀ or a K_I is a functional parameter defined for a particular pair of enzymes and inhibitors, I_inh is defined for an inhibitor and a set of enzymes. Second, I_inh is completely independent of an inhibitor's absolute level of potency. This critical independence enables meaningful correlations to be drawn between potency and specificity for a series of inhibitors.

The I_inh index can be inverted to describe the promiscuity with which a particular isoform is inhibited by a panel of compounds or, in other words, the degree to which an isoform is susceptible to inhibition by a wide range of compounds. We will call this quantity the susceptibility index of an enzyme and denote it by using I_susc:

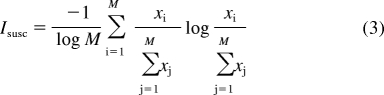Here, M is the number of compounds in the inhibitor panel, x_i is the inhibitory potency of compound i, and x_j is the inhibitory potency of compound j. We can extend I_susc to account for chemical similarities among the compounds in the inhibitor panel by weighting the index in a manner exactly analogous to our previous work (Nath and Atkins, 2008a). We performed weighting using the 166-bit MDL Key (Durant et al., 2002) feature-based fingerprints (also called MACCS keys) as chemical descriptors, because they are commonly used and easily implemented. The keys consist of 166 digits that take the values “1” or “0” depending on the presence or absence, respectively, of specific chemical moieties in a given inhibitor. We admit that fingerprint-based approaches have limitations in that they do not explicitly account for three-dimensional structural features as well as physicochemical characteristics such as molecular mass, hydrophobicity, and charge, but they are still capable of capturing important elements of chemical similarity.

We define a weighted enzyme susceptibility index, J_susc, as follows:

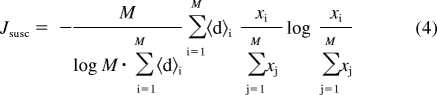Here, 〈d〉_i is the normalized mean chemical dissimilarity between compound i and all other members of the inhibitor panel, defined as follows. The Tanimoto distance between two compounds' descriptors is the number of exclusive features unique to either compound (i.e., present in exactly one of the descriptor bit strings), divided by the number of exclusive or shared features displayed by either compound (i.e., present in one or both of the descriptors bit strings). The Tanimoto distance is the complement of the Tanimoto similarity coefficient: if two compounds share all their features then the Tanimoto distance is 0, whereas if all features are exclusive to either compound then the distance is 1. As an upper bound on Tanimoto distance for a set of compounds, we can calculate an overall set dissimilarity as the number of features shared by at least one but not all of the descriptors, divided by the number of features shared by at least one of the descriptors in the set (i.e., the number of features in the numerator, plus the number of features shared by all the compounds in the set). Then, 〈d〉_i is defined as the mean of the Tanimoto distances calculated for compound i and each other compound in the panel, divided by the overall set dissimilarity for all compounds in the panel. This weighting strategy increases the susceptibility index for isoforms that are potently inhibited by chemically dissimilar compounds. For more details on the implementation of weighting, please see our earlier work (Nath and Atkins, 2008a).

PLSR.

PLSR (Abdi, 2003) is a multivariate statistical technique related to principal components analysis that seeks to explain the relationships between two matrices, one consisting of data and the other of predictors. In our context, the data matrix consists of inhibition data and the predictor matrix consists of chemical substructure fingerprints from the 166-bit MDL Keys. PLSR finds the vectors (called “latent vectors”) that maximize the covariance between the data and predictor matrices, under the assumption that such vectors represent the most significant trends relating the observed data and predictors. PLSR provides a regression matrix that shows how strongly each predictor (i.e., chemical substructure) influences the data (i.e., inhibitory potency toward a specific P450 isoform). PLSR differs from machine learning classifiers based on Bayes' theorem or support vector machines (Merkwirth et al., 2004; Arimoto et al., 2005) in that it can be used to reconstruct a continuous range of predicted values for the variable of interest, rather than simply binning it into one of two or more categories. Compared with support vector regression, PLSR is easier to implement and interpret, and it often provides similar results (Ustün et al., 2007; Shah et al., 2010).

We have previously found the related technique principal components analysis useful in understanding how individual probe substrates report on different regions of the functional space of single P450 isoforms (Nath and Atkins, 2008b) and also in the prediction of a compound's propensity to cause time-dependent inhibition of CYP3A4 (Zientek et al., 2010). In this study, we extend this approach from considering multiple probe substrates of a single enzyme to a panel of different enzymes, with the goal of understanding how P450s are distributed in functional space with respect to their susceptibility toward inhibition.

Materials and Methods

Reagents.

Acetonitrile (MeCN), acetaminophen, phenacetin, dehydrate amodiaquine dichloride, dextromethorphan hydrobromide monohydrate, diclofenac sodium salt, dimethyl sulfoxide (DMSO), dl-isocitric acid trisodium salt, isocitric dehydrogenase from porcine heart, 0.1 M magnesium chloride solution, miconazole, midazolam, β-nicotinamide adenine dinucleotide phosphate sodium salt hydrate (NADP⁺), β-nicotinamide adenine dinucleotide 2′-phosphate reduced tetrasodium salt hydrate (NADPH), 1 M potassium phosphate dibasic solution, 1 M potassium phosphate monobasic solution, tacrine hydrochloride, buspirone, along with all the compounds in Table 1 were purchased from Sigma-Aldrich (St. Louis, MO). Tacrine free-base, 1-OH midazolam, des-ethyl-S-amodiaquine, 4-OH-mephenytoin, and (S)-mephenytoin were synthesized and purified at Pfizer Global Research and Development. Human liver microsomes (HLM), pooled from 60 male and female donors, were obtained as a special order from BD Gentest (Woburn, MA). Stock solutions of diclofenac, dextromethorphan, (S)-mephenytoin, midazolam, and tacrine were prepared in water, 90% MeCN:10% methanol, MeCN, 66.7% methanol:33.3% MeCN, and DMSO, respectively, and at concentrations such that the total organic concentration in the assay was ≤0.2% (v/v). Assay buffer was 0.1 M potassium phosphate buffer (pH 7.4) containing 1 mM magnesium chloride. All reagents were diluted with assay buffer to the indicated concentrations.

TABLE 1.

Inhibitory potencies towards six P450 isoforms, and calculated specificity indices of compounds in S₆₄

	Potency a Towards P450 Isoform						Specificity b (1 − Iinh)
	2C8	3A4	2D6	2C9	1A2	2C19
Albendazole	0.19	0.00	0.12	0.07	0.30	0.10	0.17
Amiodarone	0.00	0.00	0.09	0.00	0.00	0.00	0.91
Amitriptyline	0.19	0.12	0.84	0.00	0.07	0.64	0.29
Artemisinin	0.11	0.25	0.04	0.00	2.08	0.18	0.56
Astemizole	0.28	0.97	0.86	0.00	0.00	0.19	0.33
Atenolol	0.12	0.00	0.00	0.00	0.00	0.00	0.94
Bepridil	0.02	0.17	3.00	0.00	0.00	0.11	0.78
Budesonide	0.52	1.35	0.21	0.73	0.07	0.12	0.22
Carbamazepine	0.06	0.11	0.00	0.08	0.04	0.19	0.18
Chloroquine	0.19	0.00	0.10	0.05	0.10	0.09	0.15
Chlorpheniramine	0.07	0.00	0.68	0.00	0.28	0.00	0.55
Chlorthalidone	0.06	0.00	0.00	0.03	0.02	0.18	0.41
Cimetidine	0.47	0.06	0.29	0.11	0.22	1.05	0.21
Cisapride	0.10	0.12	0.28	0.10	0.15	0.11	0.05
Clotrimazole	2.10	3.00	1.13	2.85	1.90	2.06	0.02
Clozapine	0.18	0.06	0.21	0.19	0.27	0.24	0.04
Cyclosporin	0.00	1.61	0.11	0.00	0.00	0.10	0.76
Danazol	1.76	0.18	1.66	1.95	0.28	1.70	0.12
Dexamethasone	0.12	0.02	0.00	0.07	0.00	0.00	0.47
Digoxin	0.10	0.06	0.00	0.09	0.05	0.09	0.12
Diltiazem	0.08	0.00	0.04	0.00	0.06	0.04	0.24
Diphenhydramine	0.09	0.04	0.68	0.03	0.00	0.06	0.52
Diphenylhydantoin	0.09	0.00	0.00	0.29	0.00	0.08	0.49
Disulfiram	2.33	1.59	0.46	2.03	1.92	1.35	0.05
Erythromycin	0.00	0.22	0.00	0.06	0.00	0.07	0.49
Felbamate	0.05	0.00	0.00	0.00	0.00	0.00	0.86
Fluconazole	0.31	0.97	0.28	0.74	0.24	1.23	0.10
Flurbiprofen	0.11	0.00	0.00	0.92	0.00	0.05	0.72
Fluvoxamine	0.22	0.11	0.85	1.03	3.00	2.42	0.21
Haloperidol	0.12	0.10	1.54	0.00	0.21	0.29	0.42
Indomethacin	0.00	0.00	0.00	0.60	0.11	0.14	0.55
Isradipine	1.30	1.09	0.16	1.44	0.55	1.32	0.08
Ivermectin	0.22	0.14	0.11	0.17	0.02	0.12	0.07
Ketoconazole	1.42	3.00	0.91	1.09	0.63	1.06	0.08
Ketoprofen	0.12	0.10	0.03	0.19	0.11	0.15	0.06
Lansoprazole	1.24	0.26	0.87	0.72	1.19	1.54	0.06
Loratadine	1.53	0.21	1.55	0.22	0.00	3.00	0.29
Lovastatin	0.82	1.47	0.17	0.12	0.00	0.10	0.37
Mefloquine	0.11	0.19	0.83	0.11	0.12	0.13	0.23
Methoxypsoralen	0.18	0.14	0.80	0.15	3.00	0.53	0.34
Naproxen	0.10	0.00	0.00	0.02	0.09	0.00	0.44
Nicardipine	1.81	2.17	1.48	2.42	0.12	1.80	0.08
Nifedipine	0.99	0.00	0.09	0.17	3.00	0.17	0.48
Norfloxacin	1.56	3.00	1.29	1.33	0.92	1.36	0.04
Omeprazole	0.89	0.22	0.06	0.17	0.79	0.29	0.17
Orphenadrine	0.22	0.09	0.62	0.00	0.02	0.07	0.38
Paclitaxel	0.10	0.15	0.06	0.13	0.13	0.13	0.02
Paroxetine	0.27	0.68	2.04	0.24	1.09	0.93	0.13
Perphenazine	0.26	0.26	2.68	0.24	2.13	0.63	0.25
Pimozide	0.17	0.14	0.18	0.11	0.17	0.10	0.01
Pravastatin	0.00	0.00	0.00	0.00	0.00	0.01	0.54
Promethazine	0.11	0.12	1.31	0.04	1.86	0.23	0.36
Propranolol	0.00	0.74	1.26	0.05	1.05	1.05	0.21
Quercetin	1.86	0.26	0.98	0.99	1.81	0.73	0.08
Quinapril	0.09	0.00	0.00	0.00	0.00	0.00	0.91
Quinidine	0.30	0.14	3.00	0.13	0.06	0.74	0.43
Ranolazine	0.00	0.22	0.00	0.00	0.00	0.00	0.96
Sertraline	0.26	0.70	1.48	0.24	0.85	1.21	0.10
Simvastatin	1.43	1.68	0.14	0.17	0.09	0.11	0.34
Tamoxifen	0.84	0.25	0.15	0.19	0.14	0.86	0.16
Terfenadine	0.28	1.19	1.19	0.18	0.12	0.19	0.21
Ticlopidine	0.22	0.00	0.73	0.17	0.76	1.60	0.25
Verapamil	0.17	0.83	0.15	0.15	0.06	0.10	0.25
Warfarin	0.15	0.00	0.02	1.08	0.03	0.04	0.64

^a Potency is defined as (−log(IC₅₀/100 μM)), so that a potency of 1 implies an IC₅₀ of 10 μM and a potency of 2 implies an IC₅₀ of 1 μM.

^b Specificity is defined in terms of the entropy-based I_inh metric (eq. 2), so that a value of 0 implies a completely promiscuous inhibitor and a value of 1 implies complete specificity of inhibition.

Assay Details.

IC₅₀ determinations for compounds in S₆₄ were conducted in polypropylene 96-well plates (Nalge Nunc International, Rochester, NY) using a Beckman Coulter Biomek FX (Fullerton, CA) automated system. Compounds were tested in triplicate at six concentrations of 0.1, 0.3, 1, 3, 10, and 30 μM. Miconazole, a broad spectrum P450 inhibitor, served as a quality control and was tested at 0.01, 0.03, 0.1, 0.3, 1, and 3 μM. Reactions were performed in a final volume of 300 μl/well using final concentrations of DMSO and acetonitrile organic solvents of 0.1 and 1.0% (v/v), respectively. Each well contained HLM (0.1 mg/ml protein), substrate cocktail (10 μM phenacetin, 40 μM S-mephenytoin, 5 μM dextromethorphan, 5 μM diclofenac, 2 μM midazolam, and 2 μM amodiaquine), and 1 mM NADPH in 100 mM potassium phosphate buffer (pH 7.4). Samples (compound, microsomes, and substrate cocktail) were preincubated for 5 min at 37°C on a Biomek FX recirculating water bath heating unit before the addition of the NADPH solution to start the reaction. After an 8-min incubation at 37°C, reactions were terminated by the addition of 600 μl/well chilled MeCN containing 0.2 μM buspirone, as an internal standard. P450 inhibition was quantitated by simultaneously analyzing the metabolites of S-mephenytoin, dextromethorphan, diclofenac, midazolam, phenacetin, and amodiaquine using a liquid chromatography/mass spectrometry method. The high-performance liquid chromatography-tandem mass spectrometry system consisted of Shimadzu LC-10AD vp pumps (Shimadzu, Kyoto, Japan), a CTC PAL autosampler (Leap Technologies, Carrboro, NC), and a PE Sciex API 4000 mass spectrometer (Applied Biosystems/MDS Sciex, Foster City, CA) fitted with a turbo ion spray interface in the positive ionization mode. A Phenomenex (Torrance, CA) Onyx Monolethic C18, 4.6 × 50-mm column was used. The analytes were eluted with a mobile phase comprising 0.1% formic acid (aqueous solvent A) and acetonitrile with 0.1% formic acid (solvent B). The primary gradient pumps flow rates were 0.2 ml/min (99% A:1% B), and the dilution pump's flow rate was 3.0 ml/min (100% A). After the analytes were focused onto the column, the dilution pump was stopped (minimal flow was maintained at 0.01 ml/min flow to prevent back flow) and the primary gradient pumps were ramped to 3.0 ml/min to initiate the gradient: 5 to 20% B from 0.0 to 0.5 min, 20 to 70% B from 0.5 to 1.2 min, 70% B from 1.2 to 1.4 min, and 70 to 5% B from 1.4 to 1.5 min. The compounds were monitored using the following multiple reaction monitoring transitions: 1-OH midazolam, 342.1 → 203.1; des-ethyl-S-amodiaquine, 328.2 → 283.2; acetaminophen, 152.0 → 110.0; 4-OH mephenytoin, 235.2 → 150.1; 4-OH diclofenac, 312.3 → 231.1; dextrorphan, 258.1→ 199.1; and internal standard, buspirone, 385.75 → 122.23. The compound concentrations were estimated based on standard curves that were calculated using a weighed linear regression (1/x²) of the concentration versus ratio of analyte to internal standard peak areas.

Inhibition values for compounds in S₄₆₉ were collected as previously described (Zientek et al., 2008) and similarly to the assay conducted for compounds in S₆₄. In brief, a single concentration inhibition assessment was conducted in polypropylene 384-well plates (Greiner Bio-One; Frickenhausen, Germany) using a Beckman Coulter Biomek FX. Compounds were tested in duplicate at a concentration of 3 μM. Miconazole, a broad spectrum P450 inhibitor that served as a quality control, was tested at 0.015, 0.15, and 3 μM. Reactions were performed in a final volume of 50 μl/well using final concentrations of DMSO and acetonitrile organic solvents of 0.1 and 1.0% (v/v), respectively. Each well contained HLM (0.1 mg/ml protein), substrate cocktail (40 μM S-mephenytoin, 5 μM dextromethorphan, 5 μM diclofenac, 2 μM midazolam, and 2 μM tacrine), and a NADPH regeneration system (5 mM isocitric acid, 1 mM NADP+, and 1 U/ml isocitrate dehydrogenase) in 100 mM potassium phosphate buffer (pH 7.4) containing 1 mM MgCl₂. Samples (compound, microsomes, and substrate cocktail) were preincubated for 5 min at 37°C on a Biomek FX Peltier heating unit before the addition of the NADPH regeneration system. After an 8-min incubation at 37°C, reactions were terminated by the addition of 50 μl/well chilled MeCN containing 0.2 μg/ml triazolam that was used as an internal standard. P450 inhibition was quantitated by simultaneously analyzing the metabolites of S-mephenytoin, dextromethorphan, diclofenac, midazolam, and tacrine using liquid chromatography/mass spectrometry as described by Smith et al. (2007).

Analytical Details.

Entropy-based metrics, such as I_inh, require the definition of inhibitory potency (x_i) values such that x_i is higher for more potent compounds, and always greater than zero. For compounds in set S₆₄, we define potency as x_i = −log(IC₅₀/100 μM), with 100 μM serving as a reference value to ensure that x_i > 0. Some compounds in S₆₄ did not display sufficiently potent inhibition for accurate IC₅₀ determinations with some isoforms. We used the percent activity remaining at 30 μM (the highest inhibitor concentration used) as an approximate upper bound on IC₅₀ for these compounds. If there was no detectable loss of activity at 30 μM, we used 99.9 μM as a universal upper bound on IC₅₀. As an example, we measured the IC₅₀ of artemisinin with respect to CYP1A2 to be 0.83 μM. Therefore, its potency toward CYP1A2 is −log(0.83/100) = 2.08. Furthermore, its IC₅₀ with respect to CYP3A4 could not be measured, but the percent activity remaining at 30 μM artemisinin was 56%. Therefore, its potency toward CYP3A4 is taken to be −log(56/100) = 0.11. For compounds in S₄₆₉, we simply define potency as percent inhibition achieved at an inhibitor concentration of 3 μM, with 0.01% as a lower bound on potency.

Specificity and susceptibility indices were calculated using scripts in Python and Scientific Python (Jones E, Oliphant T, and Peterson P, http://scipy.org). PLSR was performed using a Python script adapted from a Matlab program by Abdi (2003). All scripts are available upon request. Log D values were calculated using Pipeline Pilot (Accelrys, San Diego, CA).

Results

Inhibitor Specificity.

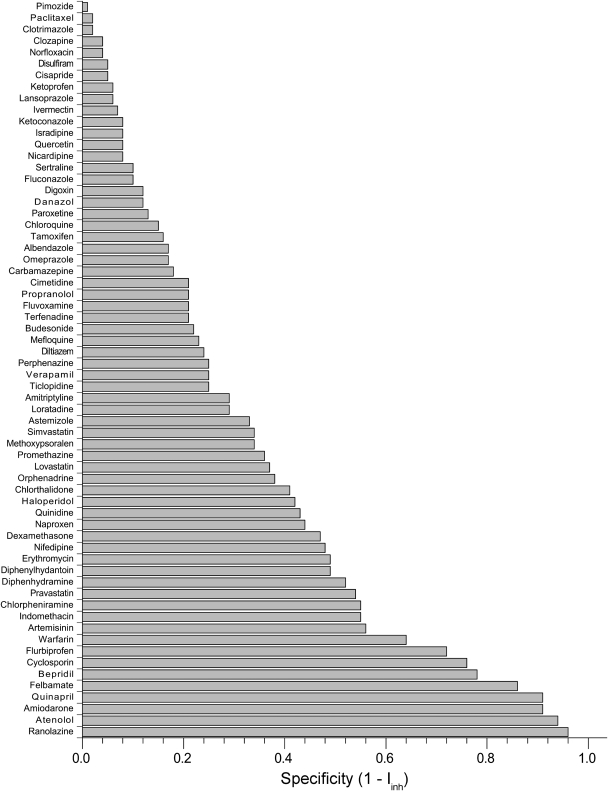
Table 1 shows potency values [i.e., −log(IC₅₀/100 μM)] obtained for the 64 inhibitors and six P450 isoforms that comprise S₆₄, along with calculated specificity values. A potency value of 1.0 in this table corresponds to an IC₅₀ of 10 μM; a potency of 2.0 corresponds to an IC₅₀ of 1 μM. As shown in Fig. 1, the inhibitors displayed a wide range of specificity, from specific inhibitors like ranolazine (which selectively inhibits 3A4) or atenolol (which selectively inhibits 2C8) to promiscuous inhibitors like clotrimazole and isradipine (which potently inhibit all six isoforms in S₆₄). Under our experimental conditions, some of the most specific compounds display weak inhibition toward a particular isoform and no detectable inhibition toward the five others; other specific inhibitors are much more potent, such as bepridil (2D6) and cyclosporin (3A4). Note that compounds displaying weak inhibition toward all six isoforms have low specificity as determined by the I_inh metric.

Fig. 1.

Specificity index values of the 64 drugs in S₆₄, ranked in order from most promiscuous (top) to most specific (bottom). I_inh is defined in eq. 2.

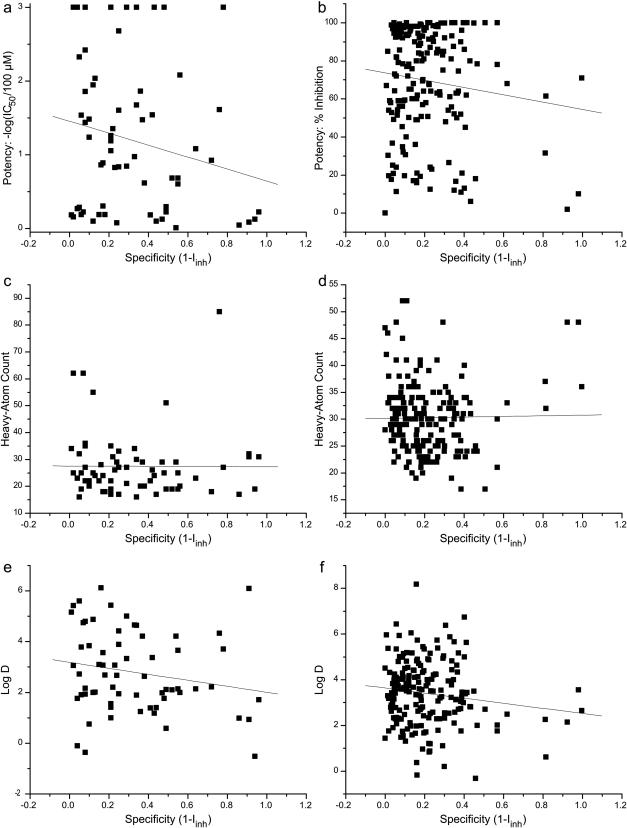
We found very low correlation between inhibitor potency and specificity (1 − I_inh) for either S₆₄ or the randomly chosen subset (194 compounds) of S₄₆₉, with R² values of 0.044 and 0.014, respectively (Fig. 2, a and b). To better understand the determinants of inhibitor specificity, we further correlated I_inh values with heavy-atom counts (a proxy for the molecular mass of a compound) and calculated log D values (a proxy for hydrophobicity). In the case of heavy-atom counts, we found no correlation for either S₆₄ or S₄₆₉ (R² of 3 × 10⁻⁵ and 3 × 10⁻⁴, respectively) (Fig. 2, c and d). Calculated log D values also showed no statistically significant correlation with specificity for either S₆₄ or S₄₆₉, with R² values of 0.036 and 0.019, respectively (Fig. 2, e and f).

Fig. 2.

Correlation between specificity and maximum inhibitory potency toward any P450 isoform (a and b), heavy-atom count (c and d), or calculated log D (e and f) for all 64 compounds in S₆₄ (a, c, and e) and 194 randomly selected compounds from S₄₆₉ (b, d, and f). Both datasets show low correlation between potency and specificity toward P450 isoforms (R² of 0.044 for S₆₄ and 0.014 for S₄₆₉), indicating that these are essentially independent quantities. Furthermore, the lack of correlation between specificity and molecular size (R² of 3 × 10⁻⁵ for S₆₄ and 3 × 10⁻⁴ for S₄₆₉) or hydrophobicity (R² of 0.036 for S₆₄ and 0.019 for S₄₆₉) indicates that these global physicochemical characteristics are not the primary determinants of inhibitor specificity.

P450 Susceptibility to Inhibition.

An important related question is the relative susceptibility of isoforms to inhibitors: i.e., how promiscuous or specific different P450s are in terms of how they are affected by diverse inhibitors. Table 2 shows I_susc (defined in eq. 3) and weighted J_susc (eq. 4) calculated for all six isoforms from S₆₄. The susceptibility index values for each isoform are fairly similar before and after weighting, indicating that S₆₄ represents a reasonably uniform sampling—i.e., the inhibitors in S₆₄ do not display a marked bias toward any subspace of the functional space spanned by the full set. All six isoforms have susceptibility indices within a narrow range from 0.75 to 0.85, indicating that drug-metabolizing P450s are generally inhibited by a broad range of compounds (as might be expected a priori for promiscuous detoxification enzymes). Within the range of observed susceptibility values, CYP3A4 has the lowest J_susc value, indicating that it is slightly more resistant to inhibition by diverse compounds. CYP2C8 has the highest J_susc value, meaning that it is (by a small margin) the most susceptible isoform to inhibition by diverse compounds. We performed a jackknife (leave-one-out) analysis to estimate uncertainties in the susceptibility indices. In general, two-tailed t tests indicated that the differences, while small, are meaningful: except for CYP1A2-CYP3A4 and CYP2C8-CYP2C19, the differences between each pair are significant to at least P < 0.001. In other words, susceptibility to inhibition follows the rank-order 3A4≈1A2 < 2C9 < 2D6 < 2C8≈2C19.

TABLE 2.

Inhibitory susceptibility indices for six P450 isoforms calculated from the inhibitory potencies displayed by compounds in S₆₄

Isoform	I susc a	J susc a
3A4	0.7734 ± 0.0034	0.7830 ± 0.0036
1A2	0.7616 ± 0.0035	0.7858 ± 0.0037
2C9	0.7741 ± 0.0034	0.8040 ± 0.0034
2D6	0.8268 ± 0.0031	0.8232 ± 0.0033
2C19	0.8253 ± 0.0027	0.8444 ± 0.0029
2C8	0.8278 ± 0.0022	0.8495 ± 0.0022

^a Higher values indicate inhibition by a wider range of compounds. J_susc values are weighted by the relative chemical similarities of the inhibitors, and I_susc values are unweighted. Error values represent S.D.s calculated by jackknife (leave-one-out) analysis of the compounds in S₆₄.

PLSR.

Because global physicochemical characteristics did not display informative correlations with specificity, we turned to PLS regression to gain additional insight. The results of regression on S₆₄, shown in Table 3, demonstrate the basic concepts of PLS and the prediction matrix. By simultaneously regressing the S₆₄ matrix against a matrix of chemical descriptors for each inhibitor, we identified how strongly the presence of each chemical feature correlates with inhibitory potency toward each isoform. For S₆₄, we limited the chemical descriptor to a 16-bit key to avoid overparametrizing the regression problem. Elements in the prediction matrix correspond to how much the presence of a particular chemical feature increases potency toward a corresponding P450 isoform. For example, the value of 0.43 in the “Azole” row and “3A4” column indicates that, on average, the presence of a triazole ring increases potency by 0.43: equivalent to a decrease in IC₅₀ for CYP3A4 by a factor of 10^0.43 = 2.7. From the S₆₄ prediction matrix, it is obvious that nitroaromatic and triazole moieties result in higher potency across the panel of P450 isoforms. This result agrees with the large body of data (Nivoix et al., 2008; Wen et al., 2008) collected with various members of these classes of compounds: the quantitative confirmation validates the PLSR method. Numbers in italics indicate negative values, i.e., a decrease in potency associated with the presence of the corresponding feature. For example, the presence of more than 45 nonhydrogen atoms in a compound was associated with a decreased potency toward all isoforms except CYP3A4; the presence of a tertiary amine moiety was associated with an increase in IC₅₀ for CYP1A2 by a factor of 10^0.46 = 2.9. However, regression with a 16-bit key can capture only a limited amount of information regarding the chemical characteristics of an inhibitor, and results are highly dependent on the choice of characteristics included in the key.

TABLE 3.

PLSR predictions of change in potency towards six P450 isoforms as a function of 16 chemical features, calculated for the compounds in S₆₄

Feature	2C8	3A4	2D6	2C9	1A2	2C19
<25 Heavy atoms	−0.03 a	−0.13	0.03	0.00	0.06	0.07
25–45 Heavy atoms	0.10	0.09	0.06	0.06	−0.04	0.01
>45 Heavy atoms	−0.14	0.07	−0.16	−0.10	−0.03	−0.14
Positive charge	−0.14	−0.14	−0.04	−0.12	−0.05	−0.05
Negative charge	0.12	−0.03	−0.25	0.18	−0.29	−0.21
1 Ring	0.02	−0.04	0.17	−0.02	−0.05	0.13
2 Fused rings	0.16	0.02	0.16	0.00	0.03	0.14
3 Fused rings	0.00	−0.11	0.30	−0.11	0.36	0.25
4 + Fused rings	0.11	−0.07	0.10	0.11	−0.27	0.09
Ester	−0.02	−0.06	−0.25	−0.10	−0.26	−0.10
Ether	−0.16	−0.09	0.03	−0.15	0.13	−0.05
Acid	−0.21	0.02	0.04	−0.12	0.02	0.01
Secondary amine	−0.08	0.18	0.06	−0.08	−0.02	−0.04
Tertiary amine	0.02	0.13	0.15	−0.08	−0.46	−0.06
Nitroaromatic	0.23	0.18	0.24	0.21	0.48	0.27
Azole	0.25	0.43	0.00	0.31	0.06	0.31

^a Italics indicate values <0, i.e., presence of a feature correlates with lower potency (higher IC₅₀) towards a particular isoform. A value of 0.5 corresponds to a 10^0.5 = 3.2-fold decrease in IC₅₀.

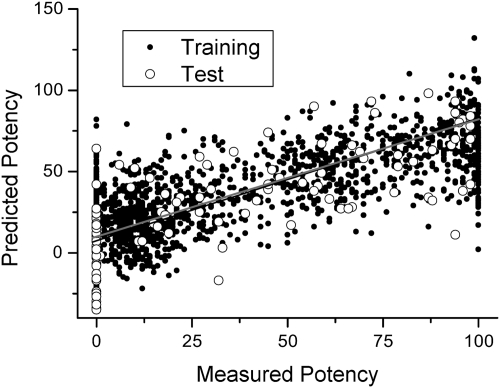
The larger number of compounds in S₄₆₉ instead allowed us to more rigorously evaluate the accuracy of PLSR and generate a more detailed prediction matrix without overparametrizing the regression problem. We regressed S₄₆₉ against a matrix derived from 166-bit MDL keys of each inhibitor and derived an average contribution for each feature, analogous to the S₆₄ feature contributions shown in Table 3. We found that the feature-based approach captured much of the functional diversity of S₄₆₉: there was reasonable correlation (R² = 0.60) between experimental percent inhibition values and those predicted by our regression (i.e., the product of the MDL-derived feature matrix and the prediction matrix obtained by PLSR). To validate the accuracy of regression, we randomly selected 23 compounds from S₄₆₉ to be a test set and performed PLSR on the remaining 95% of S₄₆₉. We then predicted percent inhibition values for the test set (open circles in Fig. 3) and again found a modest correlation (R² = 0.53) with the experimental values.

Fig. 3.

Correlation between measured inhibitory potency values and values predicted by PLSR from a training (closed circles) set of 95% of the compounds in S₄₆₉ (R² of 0.60). Open circles indicate values predicted by the PLSR model for a test set of the remaining 5% of the compounds (R² of 0.53, gray line), showing successful prediction of isoform-specific inhibition.

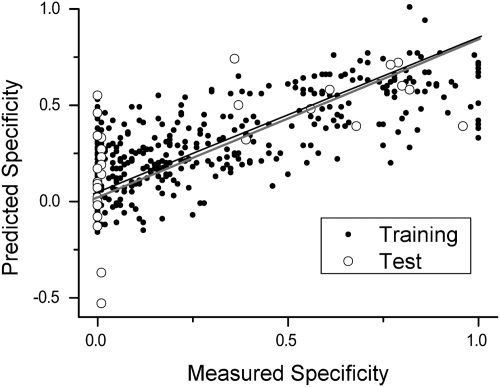
PLSR can also be used to predict specificity directly (rather than potency values for the individual isoforms), by using a data matrix of specificity values and the same MDL-derived descriptor matrix as before. Performing this procedure on all compounds from S₄₆₉ that showed detectable inhibition, we found again a good correlation (R² = 0.66) between measured and predicted specificity for compounds in the training set and an R² of 0.44 for compounds in the test set (open circles in Fig. 4) a level of correlation that should enable prediction of the specificity with which novel drug candidates will inhibit drug-metabolizing P450 isoforms.

Fig. 4.

Correlation between measured inhibition specificity (1 − I_inh) values and values predicted by PLSR from a training (closed circles) set of 95% of the S₄₆₉ compounds that showed detectable inhibition toward at least one isoform (R² of 0.66). Open circles indicate values predicted by the PLSR model for a test set of the remaining 5% of the compounds (R² of 0.44, gray line), showing successful prediction of inhibitor promiscuity.

Discussion

Quantitative specificity measurement may lead to better choices of prototypical specific inhibitors for in vitro and in vivo drug metabolism studies. For example, the FDA currently recommends (Food and Drug Administration, http://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm072101.pdf) that quinidine (I_inh = 0.57) be used as a 2D6 inhibitor; of the compounds in S₆₄, bepridil displays similar potency and is more specific (I_inh = 0.22), and therefore would be a better choice to selectively inhibit 2D6 in vitro. Even if other experimental considerations make the use of bepridil impractical, applying I_inh calculations to larger panels of potential inhibitors should identify other compounds that display similar high specificity and potency toward the major P450 isoforms. From S₆₄, the following compounds are relatively specific (I_inh < 0.5) and relatively potent (potency >1, i.e., IC₅₀ < 10 μM) toward the isoform in parentheses: bepridil (2D6); cyclosporine (3A4); warfarin (2C9); and artemisinin (1A2). Our data suggest that these compounds are perhaps good choices as prototypical inhibitors for their respective isoforms.

An important aspect of entropy-based metrics, such as I_inh, is that they are (by design) independent of overall potency, allowing us to test for a correlation between potency and specificity for both datasets. This finding is broadly important because, in different contexts, both positive (Maly et al., 2000) and negative (Ghoreschi et al., 2009) relationships between potency and specificity have been posited. We found essentially no correlation, indicating that under our experimental and analytical conditions, potency and specificity must essentially be considered independent quantities for drug-metabolizing P450s. Analogous I_inh-based experiments for other families of drug targets will enable a more rigorous understanding of the trade-offs between potency and specificity in different pharmacological contexts. Likewise, the lack of correlation between heavy-atom count and specificity indicates that for the compounds in our study (heavy-atom counts range from 16 to 85 for S₆₄ and from 17 to 52 for S₄₆₉), the size of a compound does not influence its propensity for promiscuous inhibition. Furthermore, the lack of correlation between calculated log D and specificity indicates that nonspecific hydrophobic interactions are neither necessary nor sufficient for promiscuous P450 inhibition. Although it has been shown that aggregate formation by hydrophobic compounds can lead to nonspecific interactions, promiscuous inhibition, and consequent false-positives in drug discovery contexts (Shoichet, 2006; Coan and Shoichet, 2008), the weak negative correlations we observe indicate that aggregate-based inhibition is probably not a major contributing factor under our assay conditions.

PLSR applied to feature-based chemical descriptors and P450 inhibition behavior provided much more predictive insight than the (univariate) linear regression results discussed above. It is quite probable that more complete descriptors of chemical features and structure, possibly combined with more advanced regression or machine learning techniques such as support vector machines (Merkwirth et al., 2004) or Bayesian classifiers (Arimoto et al., 2005), would lead to increases in accuracy. This type of analysis is made possible using a continuous, quantitative measure of specificity such as the one we have presented in this work, and the simpler approach demonstrated here as a proof of principle may itself prove useful in identifying potentially problematic P450 inhibitors early in the development process.

In an extremely comprehensive high-throughput study of P450 inhibition, Veith et al. (2009) recently studied the inhibition of five P450 isoforms by a panel of almost 17,000 compounds. They classified compounds as inhibitors, activators or inactive, and then used a fingerprint-based search to identify structural features that were under-represented in active compounds and over-represented in inactive compounds from a “biofocused” subset (i.e., drugs and drug-like molecules), compared to a more general subset of compounds. Such features are assumed to correlate with decreased potency toward P450s. Our analysis differs from that of Veith et al. (2009) in that we retain potency as a continuous value (rather than binning inhibitory behavior), enabling explicit predictions of inhibitory potency values for new compounds outside our training set. In addition, the PLSR approach effectively compares individual compounds to identify structural features correlated with increased or decreased potency, rather than comparing groups of compounds. This treatment eliminates any possibility of bias in the recovered structural features based on the assignment of compounds to the biofocused and general subsets.

Conclusions

Several aspects of drug metabolism are explored here, which concern the relative specificity of interaction between small molecules and several cytochrome P450s. It is clear that inhibitory metabolic drug interactions resulting from overlapping preferences of drugs for the various P450s can severely limit the use of some drug combinations, whereas specific P450 inhibitors could improve the therapeutic power of certain highly metabolized drugs. As a result, tools that aid in the prediction of the propensity of drugs to share metabolic or inhibitory overlap could facilitate the prediction and modulation of DDIs. In this study, we applied a novel metric for inhibitory specificity and partial least-squares regression to explore the range of specificities for P450 isoforms among 533 common drugs or proprietary drug candidates.

The strategy laid out here succeeds in that it agrees well with qualitatively “known” aspects of P450 inhibition: for instance, that the presence of certain functional groups on small molecules (such as triazoles and nitroaromatics) often increases inhibition for certain drug-metabolizing P450s. However, this strategy provides a more rigorous and systematic framework with which to understand and quantify these correlations. Fingerprint-based regression also succeeds quantitatively in that it predicts isoform-specific activity, or inhibitor promiscuity per se, with reasonable accuracy when performed with a sufficiently large training set.

The other major finding of this work is that there is essentially no correlation between inhibitory potency and specificity, at least for drug-metabolizing P450s. Understanding and quantifying the nature and strength of this correlation for other families of enzymes has important implications for drug design in general. Given the growing recognition of drug promiscuity (Roth et al., 2004; Keiser et al., 2009; Peters et al., 2009) in pharmacology, similar studies correlating drug potency and specificity and identifying the determinants of drug promiscuity may prove to be powerful tools for future drug design efforts.