Characterizing the regularity of tetrahedral packing motifs in protein tertiary structure

Abstract

Motivation: While protein secondary structure is well understood, representing the repetitive nature of tertiary packing in proteins remains difficult. We have developed a construct called the relative packing group (RPG) that applies the clique concept from graph theory as a natural basis for defining the packing motifs in proteins. An RPG is defined as a clique of residues, where every member contacts all others as determined by the Delaunay tessellation. Geometrically similar RPGs define a regular element of tertiary structure or tertiary motif (TerMo). This intuitive construct provides a simple approach to characterize general repetitive elements of tertiary structure.

Results: A dataset of over 4 million tetrahedral RPGs was clustered using different criteria to characterize the various aspects of regular tertiary structure in TerMos. Grouping this data within the SCOP classification levels of Family, Superfamily, Fold, Class and PDB showed that similar packing is shared across different folds. Classification of RPGs based on residue sequence locality reveals topological preferences according to protein sizes and secondary structure. We find that larger proteins favor RPGs with three local residues packed against a non-local residue. Classifying by secondary structure, helices prefer mostly local residues, sheets favor at least two local residues, while turns and coil populate with more local residues. To depict these TerMos, we have developed 2 complementary and intuitive representations: (i) Dirichlet process mixture density estimation of the torsion angle distributions and (ii) kernel density estimation of the Cartesian coordinate distribution. The TerMo library and representations software are available upon request.

Contact: jtsai@pacific.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The existence of common secondary structure motifs in proteins, as initially proposed by Pauling and Corey (1951a, b), is well known, and application of these backbone sequence preferences has proven successful in protein structure design (Kuhlman et al., 2003) and prediction (Bradley et al., 2005). As the packing of side-chains has been shown to be broadly regular and tetrahedral (Bagci et al., 2003), characterizing the recurring elements that make up protein tertiary structure would improve approaches to protein design and the refinement of predictive models toward their native structure. Our work investigates repetitive units of tertiary structure using an intuitive analysis of tetrahedral packing. Using an approach combining graph theory and the Delaunay tessellation (Delaunay, 1934), we can classify recurring patterns of side-chain packing that clearly describe motifs of tertiary structure.

Initial studies of protein tertiary structure (Kozitsyn and Ptitsyn, 1975; Nandi et al., 1993; Rustici and Lesk, 1994) were limited by the size of the Protein Data Bank (PDB) (Dutta et al., 2009). Currently, tertiary analyses are applied to improve structural alignment accuracy (Artymiuk et al., 1994; Berger, 1995; Berger and Singh, 1997; Dudev and Lim, 2007; Huan et al., 2004; Liu et al., 2009; Nebel et al., 2007; Ortiz et al., 2002; Roach et al., 2005; Shi et al., 2007; Sun et al., 1997), while classification of tertiary structure motifs has focused on side-chain packing within a fold family (Bandyopadhyay et al., 2009a, b; Bradley et al., 2002; Holmes and Tsai, 2005; Huan et al., 2005; Selvaraj and Gromiha, 2003). For example, Tropsha and co-workers (Bandyopadhyay et al., 2009a, b; Huan et al., 2005) used the Delaunay tessellation (Delaunay, 1934) and subgraph mining to identify tertiary packing motifs common to members of individual protein families, but no comparison of side-chain geometries were made. Comparison of the family subgraphs found no motifs in common between families. A number of studies have tried to identify tertiary motifs across protein fold families (Heringa and Argos, 1991; Kannan and Vishveshwara, 1999; Kleywegt, 1999; Nandi et al., 1993; Russell, 1998). Using an agglomerative clustering scheme, Heringa and Argos (1991) found clusters that involved large side-chains and tended to be on the surface of the protein. Limiting their search for conserved clusters to immunoglobulins and globins showed that aligned clusters were generally at aligned positions. Side-chain packing motifs have also been used to characterize binding or active sites (Bagley and Altman, 1995; Gregory et al., 1993; Gunasekaran et al., 2004; Pidcock and Moore, 2001; Russell, 1998; Russell et al., 1998; Shamim et al., 2007; Spriggs et al., 2003). Here, we are interested in the tertiary packing that defines a protein's global structure and build on these studies of tertiary structure to develop a new approach to classify the regular packing motifs across the PDB (Dutta et al., 2009).

Contact definitions based on radial distance cutoffs are ambiguous near their cutoff (see Section 2). The Delaunay tessellation (Delaunay, 1934) or its dual the (Voronoi polyhedra Voronoi, 1908) avoids this ambiguity by finding pairs of atoms satisfying an empty sphere criterion: if a sphere is drawn with the two atoms representing the endpoints of its diameter, no other atoms will fall within that sphere. Previously, our group applied this method to analyze tertiary structure in terms of pairwise contacts within the globin fold family and showed that ∼85% of the globin sequences fall into the volume delineated by these tertiary contacts (Holmes and Tsai, 2005). This result strongly suggested that further investigation using the Delaunay tessellation had the potential to characterize the regular elements of protein tertiary structure.

In this article, we have developed a simple construct to describe tertiary motifs: the TerMo. A TerMo is a clustered group of relative packing groups (RPGs). An RPG is a set of side-chain residues that are all in contact with each other when the Delaunay tessellation is used for contact identification. Analysis was performed on all tetrahedral RPGs from all folds in the PDB (Dutta et al., 2009). Geometric comparisons are made at the SCOP defined levels of Family, Superfamily, Fold and Class (Murzin et al., 1995), before comparing across the entire PDB. We also find clear correlations between relative sequence positions of residues and the types of secondary structure being packed. Finally, we apply statistical modeling to the TerMos that produces a simplified descriptions of tertiary packing based on torsion angles and Cartesian coordinates, which are similar in spirit to the Ramachandran plot's description of protein secondary structure (Ramachandran et al., 1963).

2 METHODS

2.1 Construct definitions

We define a tertiary motif (TerMo) as a set of clustered relative packing groups (RPG). A relative packing group is a set of residues that all are in contact with each other, i.e. a clique in the contact graph. The contact graph was defined by performing a Delaunay tessellation (Delaunay, 1934) on all non-bonded, protein heavy atoms and connecting residues (nodes) that had at least one atom in contact (Fig. S1). In addition to side-chain to side-chain contacts, we included main-chain to main-chain contacts for all non-neighboring residues and side-chain to main-chain contacts for all residues. RPGs were defined using the maximal clique detection method of Bron and Kerbosch 1973). We found RPGs for all 15 273 domains in the ASTRAL SCOP 1.73 set of structures filtered at 95% sequence identity (Chandonia et al., 2004) to permit comparisons of RPGs at the Domain and Family levels of SCOP. Also, the analysis considers the influence of redundancy added by such a high sequence cutoff. We focus our analysis on the tetrahedral RPGs defined by four residues. From our protein domain set, there are a total of 4 113 191 tetrahedral RPGs.

2.2 Tertiary motif: clustering of RPGs

We defined TerMos by clustering the RPGs described above using RMSD as a distance metric. RPGs were grouped and labeled based on the number of residues falling into helical (H), extended sheet (E), turn (T) and coil (C), where H is all helical DSSP defined residues (h, g, i), E includes sheets with their bulges (e, b), T are all turns (t, s), and C is everything else. Thus, an RPG with one residue from each DSSP class would be [H1 E1 T1 C1], whereas an all helical RPG would be labeled [H4 - - -]. These secondary structure groups were the subjects of a complete hierarchical clustering based on the minimum root mean square distance (RMSD) between their α-carbons and their side-chain centers of mass for all possible permutations of residue ordering. In a complete clustering, RPGs (or an RPG cluster) are added to growing clusters if the maximum RMSD between that RPG and any member of the growing cluster is the current minimum in the all vs. all RMSD matrix. This procedure yields a tree structure that can be pruned at an arbitrary RMSD cutoff. To produce the TerMos, we pruned our tree at 1.5 Å RMSD and 2.0 Å RMSD. These cutoffs were chosen based on the distribution of RMSD's for RPGs from different proteins that are completely aligned in a multiple sequence alignment (MSA) using MUSCLE (Edgar, 2004; Fig. S2). After an initial clustering within each sequence family, the member of each cluster with the lowest average RMSD to all others in the cluster and clustering of these representatives was repeated to identify TerMos at the SCOP (Murzin et al., 1995) defined levels superfamily, fold, class and PDB levels. A 2.0 Å RMSD cutoff was required for clustering at the class and PDB levels. Clustering with a 2.0 Å RMSD cutoff does not always preserve side-chain orientations (Fig. S3). However, a post hoc division of the cluster based on these subpopulations preserved common side-chain orientations.

Random TerMos were created to confirm that the observed clusters were meaningful. For each TerMo with at least 100 members, 1000 sets of randomly selected RPGs wer generated. Each of these randomly generated TerMos had the same number of members as the selected real TerMo. The radius of gyration and solvent accessible surface area were calculated for the real and random TerMos. The probability that a real TerMo could be formed at random was quantified by calculating the percentile of random TerMos with values as far or farther from the mean as the real TerMo.

2.3 Modeling tertiary motifs

2.3.1 Torsion angles

To calculate joint densities for angle pairs, we use a Dirichlet process mixture of bivariate von Mises distributions developed previously (Lennox et al., 2009). For a set of angle pairs (ϕ_i, ψ_i), i = 1,…, n, we consider the model:

(1)

(2)

(3)

where DP(τG₀) is a Dirichlet process with mass parameter τ and centering distribution H₁H₂. The distributions p and H₁ are bivariate von Mises sine models (Singh et al., 2002), which are defined as:

(4)

where a = κ₁ cos(ϕ−μ)+κ₂cos(ψ−ν)+λsin(ϕ−μ)sin(ψ−ν) with

(5)

and

(6)

and where I_m(x) is the modified Bessel function of the first kind of order m. The distribution H₂ is a 2-dimensional Wishart distribution with parameters α₀ and β₀, and mean α₀/(2β₀). Note that the definition of the angle pairs as (ϕ_i, ψ_i) is arbitrary, and these distributions are equally valid for the pairs (ϕ_i, χ_1,i) and (ψ_i, χ_1,i).

For all distributions of interest, we fit the aforementioned model using the sampling scheme described in Lennox et al. (2009). For H₁, we used prior parameters μ₀ = υ₀ = 0, and Ω was a diagonal matrix with elements 1/180². For H₂, we took α₀ = 2 and β₀ was a 2 × 2 diagonal matrix with elements equal to 400. For each model fit, we ran two independent chains for 11 000 iterations with the initial 1000 iterations discarded as burn in. Using 1-in-20 thinning gave 1000 total samples. We evaluated each distribution on a 360 × 360 grid of points for plotting.

2.3.2 Centroid-Cα cartesian coordinates

The side-chain centroid positions within a TerMo and the Cα positions, as Cartesian coordinates, lend themselves to a kernel density estimation approach. Let our data consist of a set {c_i}ⁿ_i=1 of n RPGs, where each observation c_i consists of the coordinates for the atoms from a clique of size m from the i-th RPG. That is c_ij = (x_ij, y_ij, z_ij) for j = 1,…, m. We propose to model the distribution c_i+1 through kernel density estimation:

(7)

where the unknown protein c_i+1 is distributed as an n-component mixture of 3m-variate normal distributions centered at observed RPG coordinate values and having a covariance matrix given by the ‘normal reference rule’ (Zhang et al., 2006). We define the above row vector h of length 3m as:

(8)

where s_i is the standard deviation of the observations in the i-th column of the data matrix. The vector h is then multiplied by I_3m, the 3m-dimensional identity matrix. A TerMos distribution of coordinate positions is a mixture of trivariate normal distributions, denoted as N, defined by the locations of the known RPGs.

3 RESULTS

3.1 RPG clustering to tertiary motifs

The results of clustering the RPGs to TerMos with a 2.0 Å RMSD cutoff across the SCOP categories (Murzin et al., 1995) are given in Figure 1 and Supplementary Table S1. Our analysis shows that clustering is not random. We calculated the average and sample standard deviations of radius of gyration and solvent accessible surface area for all TerMos and for random sets of RPGs of the same size as the true TerMos. We then calculated the percentiles of the true TerMo statistics relative to the distribution for random RPG clusters. If the clustering were random, the random and real TerMos would have the same values and the distribution of these percentiles would be uniform. As shown in Supplementary Figure S4, the distribution is not uniform, indicating that the clustering is not random.

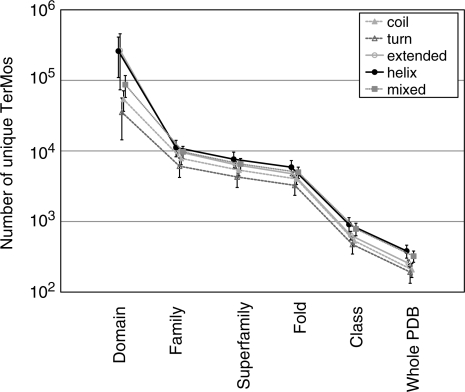
Fig. 1.

Clustering. RPG Clustering was carried out in a hierarchical fashion through the various levels of classification within SCOP. The number of unique TerMos (clusters) at each level is plotted (at the domain level, each RPG is considered a unique cluster), showing the efficiency of clustering at each level. All secondary structure classes cluster with similar efficiency. There were 15 273 total Domains, 3463 Families, 1776 Superfamilies, 1086 Folds, 7 Classes and Whole PDB represents the full dataset.

Clustering within the Family level results in a 5- to 50-fold reduction in the number of tertiary motifs (TerMos). TerMo classes with more residues in regular helical and/or sheet secondary structure cluster better than TerMo classes with more irregular coil secondary structure, indicating more ordered packing. The Superfamily level has a smaller decrease in clustering. Many Superfamilies contain only one family, so no further clustering is observed in these cases. This is also true at the Fold level, where there are 10 to 100 times fewer clusters of classification than there are starting RPGs. The next major reduction in the number of clusters occurs at the Class level. Here, 1086 folds are placed in one of seven classes based primarily on their secondary structure, though small proteins, disordered proteins, and membrane proteins have their own classes. This 100-fold reduction in SCOP classifications results in an approximately 7-fold reduction in clusters, indicating that TerMos are relatively dissimilar in different folds. The final level of clustering compares representative structural motifs from different classes and yields another 2.5-fold reduction in the number of clusters. Overall, this agglomerative clustering scheme yields ∼200 clusters per TerMo secondary structure type, with α-helical and β-sheet TerMo classes clustering significantly more consistently than TerMos involving residues from turns and loops. From this final clustering, histograms of TerMo populations along with radii of gyration and solvent accessible surface area are shown in Supplementary Figure S5. Of the over 4 million RPGs, <2% cluster in low populations of under 100 members, while the remaining 98% are 100 members of larger (Supplementary Fig. S5A). These well-populated TerMos display a smaller radius of gyration and solvent exposure with tighter distributions than the low populated TerMos (Supplementary Figs S5B and S5C, respectively).

The number of different TerMos in a protein domain depends on the size of the domain. On average, the average number of TerMos per residue is 0.27, and 95% of domains have fewer than 0.5 TerMos per residue. The set of TerMos that are common to all domains of a Family, Superfamily, or Fold can be used to distinguish between different Families, Superfamilies, or Folds. We compared the sets of TerMos that were present in at least 90% of the structures in all Families, Superfamilies and Folds with at least 40 members. This resulted in 1404 pairs of Families, 3740 pairs of Superfamilies and 2911 pairs of Folds. There was one pair of Families in this set with identical TerMos (SCOP classes: b.1.1.2 and b.1.1.4) and one pair of Families that share more than 80% of their TerMos (SCOP classes: c.1.8.1 and c.1.8.3). All Fold and Superfamily conserved TerMo sets are unique.

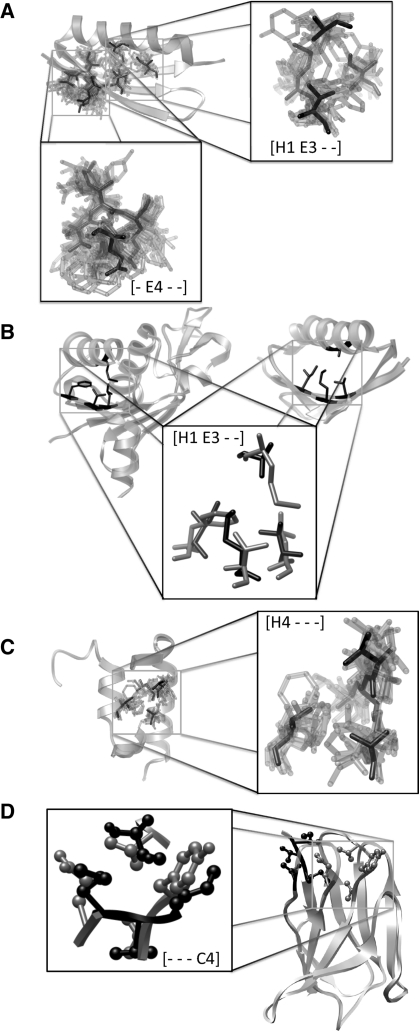
Comparing all the TerMo secondary structure classes individually provides the finer details of regular tertiary structure and is summarized in Table S1. To be clear in our discussion of TerMos, we will use a consistent notation, because the packing interactions are defined relative to each residue. Residues that are neighbors or near neighbors in the primary sequence will be referenced against an initial residue i, while non-local contacts will use j, k, & l. The all sheet [- E4 - -], helix contacting sheet [H1 E3 - -], and all helix [H4 - - -] TerMos ( Fig. 2A, B and C, respectively) produce the largest clusters with over 100 000 representatives within 2.0 Å RMSD of the representative RPG when clustering is carried across the full PDB. The largest [- E4 - -] TerMo describes the packing of three consecutive residues of one strand i, i+1, i+2 packing against one residue on the neighboring strand j (Fig. 2A). This TerMo involves side-chain to side-chain contacts between residues i, i+2, and j, as well as side-chain to main-chain contacts to residue i+1, and does not distinguish between parallel and anti-parallel strands. Similarly, the largest TerMo involving only helical residues describes the packing of one helix against another (Fig. 2C). This TerMo involves three residues from consecutive turns of one helix (i, i+1, i+4) packing with one residue from another helix (j) and is entirely defined by side-chain to side-chain contacts. The most populated TerMo in helix–sheet packing involves one residue from a helix packing against three residues from two strands of a sheet [H1 E3 - -], and as with the helix–helix packing motif described above, is entirely defined by side-chain to side-chain contacts (Fig. 2A and B). As an example of RPGs clustering from unaligned positions, Fig. 2B depicts 2 [H1 E3 - -] RPGs from topologically distinct protein folds.

Fig. 2.

Representative TerMos. The cluster center is shown in black, with all other members of the cluster overlaid. (A) Examples of the most populated [- E4 - -] all extended sheet residues (3+1) and [H1 E3 - -] one helical and three sheet residues (1+2+1) clusters. Members of these clusters found in the IG binding family are shown mapped to a reference structure protein L [1MHHa (Graille et al., 2002)]. (B) The previous [H1 E3 - -] TerMo shown from 2 different folds. (C) The most populated [H4 - - -] all helical (3+1) TerMo is shown overlaid on the protein A structure 1EDL (Starovasnik et al., 1996). The second helix of protein A has been removed for clarity. (D) Examples of the most populated all loop motif [- - - C4] from two loops in a single immunoglobulin light chain structure [1FAI (Lascombe et al., 1992)]. Their sequence locality is different, 3+1 in black and 1+2+1 in gray, but they are superimposable.

TerMos involving turns and loops are more difficult to describe in terms of sequence separation. In regular secondary structure (i.e. α-helices and β-sheets) the orientations of consecutive residues are strongly correlated, whereas in turns and loops the orientations of consecutive residues are not correlated. Thus, in motifs involving turns and loops, consecutive residues in different RPGs do not necessarily align with each other. As an example, Figure 2D shows two loop RPGs from different loops in one immunoglobulin light chain structure. Both loops cluster in the largest all loop ([- - - C4]) motif found in the immunoglobulin light chain structure. One of the RPGs is formed by three consecutive residues (i, i+1, i+2) from one loop packed against a residue (j) in another loop whereas the other loop is formed by three non-consecutive residues (i, i+3, i+4) in one loop packed against a residue (j) in a second loop. When the RPGs are aligned (Fig. 2D, inset), residue j from the first RPG aligns with residue i from the other, and the remaining residues i, i+1, and i+2 in the first RPG align with residues i+3, i+4 and j, respectively, in the other.

3.2 Dependency on sequence separation

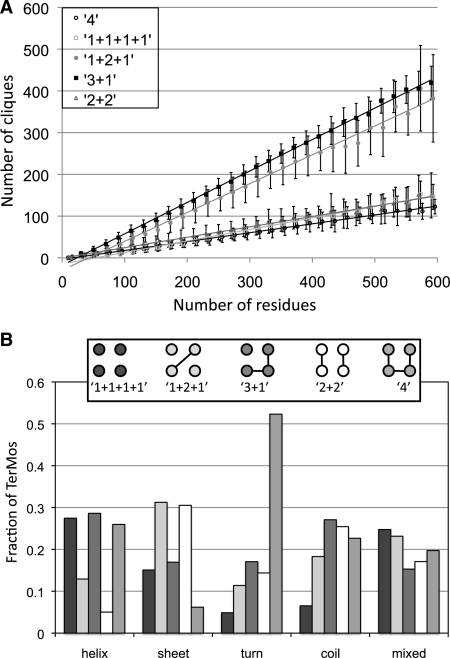
As introduced by Singh and coworkers (Singh et al., 1996), tetrahedral RPGs can be grouped into five classes based on the sequence locality of their contacts (Table 1). We consider residues in an RPG to be locally consecutive in sequence if they are separated by three or fewer positions. The average number of RPGs in each of these locality groups is a linear function of the protein's length as shown in Figure 3A. The slopes fall into two groups. The 1+1+1+1 (all non-local), 2+2 and 4 (all local) classes exhibit shallow slopes of 0.28, 0.25 and 0.21, respectively. The steeper slopes of 0.75 and 0.69 for the 3+1 and 1+2+1 classes, respectively, indicate that larger proteins' local contacts increase at a faster pace than non-local contacts. The rate at which a protein folds has been shown to be correlated with its contact order, a measure of the sequence locality of contacts (Plaxco et al., 1998), and these results corroborate the observation that larger proteins decrease in contact order.

Table 1.

Sequence locality classification of tertiary motifs

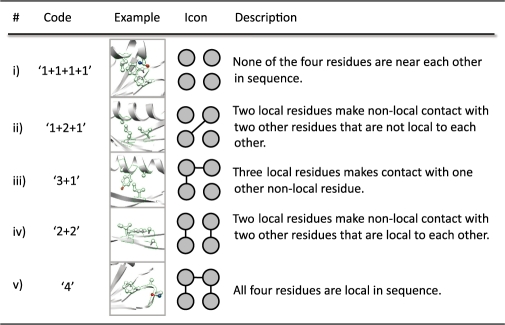Fig. 3.

Tertiary motif propensities. (A) Linear dependence of the number of RPGs having a given sequence locality on the number of residues in a protein. Errors bars represent one standard deviation. The lines are linear fits to the data with the following equations: 1+1+1+1 y = 0.28*x − 14, R² = 0.992; 1+2+1 y = 0.69*x − 27, R² = 0.991; 3+1 y = 0.75*x−20, R² = 0.999; 2+2 y = 0.25*x − 1, R² = 0.991; and 4 y = 0.21*x − 4, R² = 0.995. (B) Distribution of RPGs with different sequence locality as a function of secondary structural class. The helix, extended, turn, and coil classes represent RPGs in which a majority of the residues (3 or 4) are in the given secondary structure. The mixed class represents RPGs in which no secondary structure type dominates. Sequence localities are illustrated in the inset box and described in the text. Circles connected by lines represent residues that are close in sequence and unconnected circles represent residues that are not close in sequence.

By collapsing these secondary structure TerMos into their dominant classes of helix, extended, turn, coil and mixed (Fig. 3B), we discover some simple propensities favored by helices and sheets. More detail is provided by Supplementary Fig. S6, which shows the populations of each of the five types in Table 1 binned by the number of secondary structure types in the TerMo. Packing between and within helices favor RPGs with no local contacts (1+1+1+1 class), three local residues (3+1 class) and all local residues (4 class). In all helical residues [H4 - - -], the 1+1+1+1 TerMos do not generally indicate that four separate helices are interacting, but rather that four residues in separate turns from two helices pack against each other. The 3+1 TerMos of [H4 - - -] indicate packing of two helices against each other, where two locally packed residues from one helical turn pick up one local residue from the next turn and pack against a residue from another helix. Somewhat similar trends are shown for helical residues interacting with other types of secondary structure (Fig. S6). We find that these all non-local TerMos are most favored by two helical residues from consecutive turns packing with at least one sheet residue. The 3+1 class is dominated by the packing of three helical residues to any of the other secondary structure conformations ([H3 E1 - -], [H3 - T1 -], or [H3 - - C1]). In helices, the all local 4 class is always 2 or 3 helical residues with either turn or coil that are towards the ends of a helix and again exposed to solvent.

In direct complement to helical packing, extended sheets favor classes involving two local residues: 2+2 and 1+2+1 (Fig. 3B). The all sheet TerMos [- E4 - -] favor the 2+2 class, but not the 1+2+1 class. As detailed in Supplementary Figure S6, The 1+2+1 configuration is dominated by 3 sheet residues packing against a helix [H1 E3 - -], where the sheet residues consist of 2 local residues from 1 strand with the third coming from a neighboring strand. The 2+2 is primarily favored by 2 or more sheet residues packing with either coil or turn (no helix residues are favored). In contrast, secondary structure classes favored in the 1+2+1 arrangement involve at least one sheet residue with one helix residue packing against turn or coil, which includes the [H1 E3 - -] discussed above. A similar propensity is seen in the 1+1+1+1 all non-local class with the exception that [H1 E3 - -] does not favor this packing arrangement.

In general, turns and coils disfavor all non-local interactions 1+1+1+1. As expected, contacts in turns are dominated by the all local 4 interactions (Fig. 3B). Indeed, TerMos with four consecutive residues are found only in turns and TerMos with 2 or more turn residues display the highest frequencies in the all local 4 arrangement (see Supplementary Fig. S6). Similarly, packing between coil elements tends to involve relatively long stretches of local residues, though it is more likely to include one or more non-local residue. Coil has the highest frequency in 3+1 arrangement. This is due to favored contributions from all the predominantly coil classes and is also characteristic of any secondary structure TerMo that involves coil. The ‘mixed’ category includes situations where two residues or fewer from a secondary structure class pack against other secondary structure classes and shows no strong preferences for any type of primary structure arrangement. Our more detailed explanation of the previous classes encompassed many of the specific instances included in this category.

3.3 Representing TerMos

In a similar fashion that the planar backbone helped produce insightful predictions (Pauling and Corey, 1951a,b) and useful representations (Ramachandran et al., 1963) of secondary structure, any reduced representation of protein packing needs to allow an intuitive interpretation of tertiary structure without sacrificing the higher order, 3D nature of interactions. The RPG and its grouping into a TerMo allows simpler representations that retain the 3D network of tertiary interactions. To produce a simpler representation, we split the characterization of a TerMo into angular data and Cartesian data. For both, we provide clearer interpretation of the data by modeling continuous distributions of the data in Figure 4. We chose to model a well-populated [H1 E3 - -] TerMo as it demonstrated the general trends found between local and non-local residues.

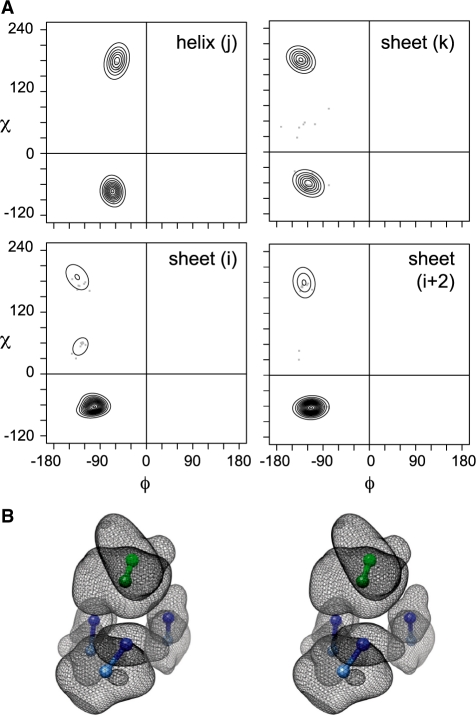
Fig. 4.

Representations of the [H1 E3 - -] TerMo. (A) Torsion angle density estimation of χ1 vs. ϕ for the [H1 E3 - -] TerMo shown in Figure 2A. Densities (solid lines) are based on 121 RPGs from the protein G family. Individual observations are given as points. Position 1 (a) is the helical position. Positions 2 (b), 3 (c) and 4 (d) are sheet residues. (B) Stereo view of atom backbone Cα and side-chain centroid position probability isosurfaces for [H1 E3 - -] TerMo. The displayed surface contains 95% of the probability density for each atom. Balls and sticks are the average Cα (lighter color) and centroid (darker color) positions for the four amino acid positions that make up the clique. Sheet residues are shaded blue and the helical residue is shaded green.

The angular data provides a representation of the conformational preferences for different TerMos and can be expressed in terms of the torsion angles (χ1, χ2, …) of their constitutive side chains. In order to relate backbone and side-chain conformational preferences, these χ angles can be related to the backbone ϕ, ψ angles through Ramachandran-like plots (Ramachandran et al., 1963). Estimating the density of the ϕ, χ1 torsion angle pairs (Lennox et al., 2009) produces the plots shown in Figure 4A for the helix–sheet ([H1 E3 - -]) TerMo shown in Figure 2A. This modeling should not be mistaken as individual plots of simple rotamer preferences,but all 4 plots in Figure 4A should be considered together as a description of tertiary structure. The 4 shown distributions correlate the rotamer preferences for the specific [H1 E3 - -] residues with each other and to their backbone conformations.

Because the angular data describes only residue conformations, a complete description of a TerMo also requires information about the positional relationship between the residues. We approximate the residues in a TerMo by considering the positions of the 4 side-chain centroids and 4 backbone Cα's. In this case, we have used a kernel density estimation to model the Cartesian space sampled by the TerMo (see Section 2) and the result is shown by Figure 4B. The modeling of the positional data has many advantages that can be seen by comparing Figure 2A with Figure 4B. The overlay of residues in Figure 2A provides a basic view of the TerMo residues, but the finer features of the data is obscured. The density in Figure 4B defines the orientation of the packing between the residues and their backbones in the TerMo and provides a clear depiction of the volume distribution occupied by the TerMo residues. The results illustrates that the 2 local residues vary much less (smaller volumes) than the 2 residues that are non-local in the TerMo (larger volumes).

4 DISCUSSION

Our goal in developing the RPG analysis of protein packing and the tertiary motif (TerMo) library of RPG clusters was to produce a construct that provided useful insight and an intuitive representation of the regular tetrahedral elements of protein tertiary structure. This is in contrast to sequence-structure motif finding algorithms, such as I-SITES (Bystroff and Baker, 1998) and TRILOGY (Bradley et al., 2002), which look for structurally similar motifs with well defined sequence patterns primarily within a sequence contiguous secondary/super-secondary structure class or within a maximal contact pattern in protein fold families, respectively. While these methods have been successful in describing specific motifs, we are looking for more general relationships in, for example, how helices pack with sheets. We also draw a distinction between our work and that of Russell and coworkers (Russell, 1998; Russell et al., 1998) and others who have found regular motifs in protein active sites. Solvent accessible surface area calculations indicate that some TerMos are preferentially found on the surface of proteins, but we do not correlate any of our TerMos with specific active sites. The TerMo classification based on sequence locality provides a simple yet general vocabulary to discuss and compare repetitive tertiary structure between proteins of similar or different folds. In the following sections, we discuss the general implications of our findings within the context of current views of protein structure and lastly provide a specific example where our two representations provide a characterization of the tertiary propensities of a TerMo.

4.1 Contact Order, packing and protein size

Protein folding is generally thought of in terms of a funnel, where each unit of structure formed has to gain enough contact energy to overcome the conformational entropy lost in ordering that unit (Bryngelson et al., 1995). This is why proteins with high contact order fold more slowly than those with low contact order (Plaxco et al., 1998). In high contact order proteins, long sections of chain must become ordered to form a unit of tertiary structure, leading to a greater loss of entropy and requiring a larger gain in contact energy to balance that loss. The residues in an RPG have maximized their contacts with the other residues; they all form contacts with all other members of the RPG. RPGs thus maximize their ability to overcome conformational entropy loss, making them natural packing units.

The distribution of RPGs having different sequence locality (e.g. all local 4, all non-local 1+1+1+1, and the three mixed local-non-local groups) suggests a limit on the possible packing topologies available to proteins. In a naïve random model, we would expect that the number of RPGs in each locality class would increase at the same rate with increasing protein size. As the protein size increases, however, the relative number of mixed local and non-local (i.e. 3+1, 1+2+1) RPGs increases (Fig. 3A). For every local RPG that is added, one 1+1+1+1, one 2+2, three 1+2+1 and three 3+1 RPGs will be added on average. There are three possible orderings of local and non-local residues in the 1+2+1 RPGs (1+2+1, 2+1+1, 1+1+2), so the increase in the number of 1+2+1 RPGs may still be described by a random model. There are only two possible ways to form a 3+1 RPG (3+1, 1+3), leaving us with the conclusion that packing arrangements in which one residue is packed against a cluster of three local residues are favored in larger proteins. The 3+1 class has the most local contacts of all of the mixed classes with 3 local contacts out of the 6 total contacts (2+2 has 2 of 6, 1+2+1 has 1 of 6). Only the all-local RPGs have more local contacts. Thus, the overall effect of these changes in packing is to decrease the relative contact order of longer proteins, consistent with earlier observations (Ivankov et al., 2003).

The detailed view of packing interactions provided by the TerMos also gives us insight into the differences between naturally occurring proteins and human designed proteins. For example, in most members of the protein G family, only one or two RPGs are within 1.5 Å RMSD of any other RPG from the same protein. In the designed protein L variant 1KH0 (Kuhlman et al., 2002), however, virtually all of the sheet only ([- E4 - -]) RPGs are within 1.5 Å RMSD of each other. The structure derives much of its packing arrangements from the same TerMo. This design did not use a limited amino acid alphabet, so it is likely that this homogeneity is due to certain packing arrangements being excessively favored by the simple energy function used in the design (Kuhlman and Baker, 2000).

4.2 Tertiary motif depiction

While we do not have space to go into detail for all the TerMos, we use the well-populated [H1 E3 - -] TerMo shown in Figure 2B as an example and discuss the insights provided by our two representations of TerMos shown in Figure 4. Both density plots are able to capture subtle features of the 1+2+1 packing arrangement that are not necessarily apparent by simple inspection. The gauche- side-chain conformation is favored by the two adjacent positions on the β-strand (i, i+2), whereas in the non-local sheet and the helical positions, both the gauche- and trans conformations are populated. Relating these data to backbone conformational preference, we find in this [H1 E3 - -] case that a more negative ϕ residue angle in sheet conformation tends to shift the side-chain population towards the trans conformation (compare the 3 sheet distributions in Fig. 4A).

The kernel density estimation in Figure 4B complements the torsion angle plots. The two adjacent positions on the β-strand are more constrained in their packing, as seen by their smaller volumes of density, while the non-local sheet and helical residues exhibit a much larger range of packing conformations. These data strongly suggests that the structural and sequence variation are largely accommodated by the non-local sheet and helical residues. Of particular interest is that the Cα atoms for the non-local sheet and helical positions exhibit the broadest range of spatial positions. The implication is that sequence changes in this TerMo cause larger backbone changes than side-chain rearrangements, but only for the non-local sheet and helix residues. The two local sheet residues remain more restrained in their backbone and side-chain positions. In this way, the TerMo construct in conjunction with our two representations is able to capture and depict the detailed tendencies for repetitive elements of tertiary structure. While the previous two representations provide a quantitative analysis of TerMo conformations, Figure 5 demonstrates how the sequence locality classification of RPGs simplifies, yet clearly describes tertiary structure. Corroborating our results from Figure 3, the core of Protein G possesses the dominant classes of locality RPGs (3+1 and 1+2+1) are the major RPGs for the core of Protein G, where the helix favors the 3+1 RPGs and the sheet 1+2+1 RPGs.

Fig. 5.

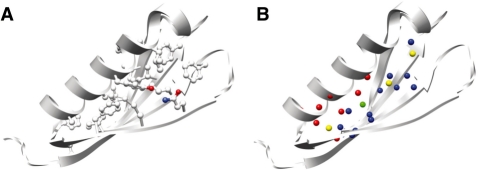
Tertiary structure simplified. (A) The core residues of Protein G [1pgb (Gallagher et al., 1994)] are shown in ball and stick representation, while the backbone is depicted in the classic cartoon ribbon. (B) For the same protein in A, the core residues are replaced with the centers of masses based on Cβ position of the RPGs. Each is color coded according to the sequence locality of interacting residues (see Table 1), where red: ‘3+1’; green: ‘2+2’; blue: ‘1+2+1’; and yellow: ‘1+1+1+1’. No all local or 4 RPGs exist in this structure.

Also, the 3+1 RPGs are concentrated in the densest area of the helix/sheet packing. Dotting the outside of the core are a single 2+2 and three non-local 1+1+1+1 RPGs. As highlighted by Figure 5, the tetrahedral clique construct of an RPG describes a basic packing unit of tertiary structure. In conjunction with the sequence locality classification, the RPG becomes an intuitive description of the packing within a protein core. The construct is simple enough for analyses within and between protein folds, but complex enough to capture the uniqueness of individual fold's tertiary structure. By providing a precise vocabulary to discuss tertiary structure, the sequence locality RPG classification has the potential to produce new insight and characterizations of protein tertiary structure.

Funding: National Institutes of Health (grant number NIH R01 GM81631).

Conflict of Interest: none declared.