Flexible mechanisms underlie the evaluation of visual confidence

Abstract

Visual processing is fraught with uncertainty: The visual system must attempt to estimate physical properties despite missing information and noisy mechanisms. Sometimes high visual uncertainty translates into lack of confidence in our visual perception: We are aware of not seeing well. The mechanism by which we achieve this awareness—how we assess our own visual uncertainty—is unknown, but its investigation is critical to our understanding of visual decision mechanisms. The simplest possibility is that the visual system relies on cues to uncertainty, stimulus features usually associated with visual uncertainty, like blurriness. Probabilistic models of the brain suggest a more sophisticated mechanism, in which visual uncertainty is explicitly represented as probability distributions. In two separate experiments, observers performed a visual discrimination task in which confidence could be determined by the cues available (contrast and crowding or eccentricity and masking) or by their actual performance, the latter requiring a more sophisticated mechanism than cue monitoring. Results show that observers’ confidence followed performance rather than cues, indicating that the mechanisms underlying the evaluation of visual confidence are relatively complex. This result supports probabilistic models, which imply the existence of sophisticated mechanisms for evaluating uncertainty.

Performance in a visual task cannot be perfect. When we try to infer some property of the physical world from visual data, there is always the chance that we will make a mistake. The possibility of error signals objective visual uncertainty: the more visual uncertainty, the higher the probability of an error. When asked how confident we feel in our visual judgment, we find it natural to estimate how strong that uncertainty is, if only by saying that we do not see well. Thus, the level of confidence actually reported by observers is a measure of subjective visual uncertainty.

It has been known for some time that performance and confidence usually correlate in human observers (1), and more recently this has also been observed in certain nonhuman species (2). If one asks observers to recognize blurry letters, both confidence and performance will decrease with the amount of blur. Although this fact seems intuitively obvious, the mechanisms involved in the correlation between performance and confidence have only recently begun to be investigated (3–6). A wide array of mechanisms could account for such a correlation, and finding out which one is actually at work could yield important insights into decision-making processes in the brain (7).

In any given visual task, such as letter recognition, performance is determined by a large number of factors: Some have to do with the stimulus (its level of blur, its size, etc.), some have to do with its context (surrounding letters), and some have to do with the internal constraints of the visual system (neural stochasticity, the shape of receptive fields, the availability of attentional resources, etc.). Some probabilistic models of the brain suggest that all these factors are taken into account in the decision and that uncertainty is represented explicitly (8–10), as in Barlow's suggestion that neurons fire in accordance with the probability that their target feature is present (11). In that view the brain operates directly in terms of probability distributions, updating them as information comes in. For our purposes we call these models uncertainty explicit: All of the probabilistic information is encoded explicitly in the system, so that there is no need for specific mechanisms to estimate uncertainty. Observers have all of the information they need to determine what their expected level of performance should be, simply by reading out the relevant probability distributions. If the visual system were uncertainty explicit, this would account naturally for the correlation between confidence and performance: Confidence follows performance, because uncertainty is kept track of throughout the decision process. This assumption is embedded in a lot of recent and influential work and has shown considerable empirical success (12–14).

A much simpler (and so far overlooked) mechanism could explain the classical finding that confidence follows performance: the visual system could simply monitor certain image properties, like blurriness. Everything else being equal, more blur always implies lower visual performance; blurriness is therefore a valid cue to visual uncertainty. Other valid cues include contrast, retinal size, eccentricity in the visual field, etc. In the context of a given visual task one cue often dominates the others—it accounts for much of the variation in performance. That dominance would be the case of blurriness in reading or contrast in detection. A radically simple way of determining confidence is therefore for the visual system to measure the dominant cue. This measurement would account for the correlation observed in previous experiments between performance and confidence: Difficulty varies along one obvious stimulus dimension (e.g., signal-to-noise ratio in an external noise task, blurriness) and so does confidence, because confidence is determined from that particular stimulus dimension. In this case the process of measuring confidence is separate from the perceptual process—both are based on physical attributes of the stimulus, but are otherwise independent.

Here we report the results of two experiments that aimed at testing the cue-monitoring hypothesis. In our tasks, performance was modulated by not one but two physical variables: contrast and crowdedness in the first experiment and eccentricity and the amount of masking in the second experiment. The cue-monitoring hypothesis implies that confidence should be determined by obvious cues to uncertainty like contrast in the first experiment or eccentricity in the second. The alternative is that, despite the joint manipulation of two physical variables, confidence should still follow performance, as suggested by uncertainty-explicit models. The results clearly refute the cue-monitoring hypothesis, which shows that confidence evaluation has to be sophisticated enough to keep track of at least two interacting sources of uncertainty. This result in turn favors probabilistic models of the brain, which directly implement such sophisticated mechanisms.

Results

Experiment 1.

Observers had to judge the orientation of a target [clockwise (CW) or counterclockwise (CCW) of the vertical] surrounded by four distractors. The stimulus was presented in the periphery of the visual field, to make the task challenging. The difficulty of the task depends on the orientation of the distractors: Vertical distractors, because their orientation is similar to that of the target, induce a crowding effect (15, 16); they reduce discrimination performance compared with horizontal distractors (Fig. 1).

Fig. 1.

Stimuli used in experiment 1. Stimuli consisted of five Gabor patches arranged on a cross. The central patch is the target, and the others are distractors. When viewed at high eccentricities, vertical distractors (B) induce a crowding effect on the target: The orientation of the target tends to assimilate with the similar orientation of the distractors, making small deviations from the vertical more difficult to discriminate. This effect does not occur with horizontal distractors (A), which are less similar in orientation. The crowding effect can be experienced by holding the figure at arms' length and fixating a few centimeters off the targets.

Another way to manipulate difficulty is to lower the contrast of the target patch: the lower the contrast, the lower the performance. Because of the crowding effect, at equal contrast levels, we expect performance to be higher with horizontal distractors than with vertical ones. This expectation implies that there are uncrowded stimuli that yield higher performance than crowded stimuli, despite having lower contrast (Fig. 2).

Fig. 2.

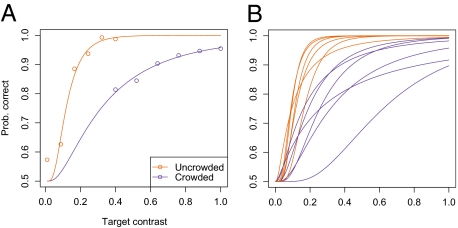
Crowding effect on performance. In the baseline condition observers chose between two stimuli with the same distractor orientation and the same target contrast (i.e., they were identical with the exception of target orientation, which was random). We varied the contrast of the stimulus and the orientation of the distractors across trials. (A) Data for observer AF. The blue and red circles represent measured frequency correct with horizontal and vertical distractors. Psychometric functions were fit to the data to summarize the effect of contrast on performance. (B) Psychometric functions for all six observers: Performance was systematically lower with vertical distractors than with horizontal ones (at equal contrast levels), showing that vertical distractors reliably induce a crowding effect.

In each trial of the experiment, two stimuli were displayed successively in different locations but at the same eccentricity. Observers were instructed to attend to the two stimuli and pick the one for which they felt more confident they could make a correct orientation judgment (a forced choice of confidence) (6). They then had to report the perceived orientation of the stimulus they picked and of that one alone.

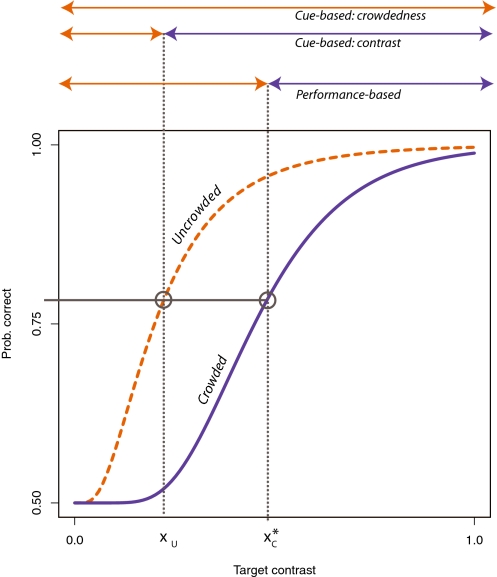
Suppose an observer is shown two stimuli, one crowded with contrast x_C and the other one uncrowded with contrast x_U. Which one will they choose as less uncertain? Three possible strategies are summarized in Fig. 3. According to the cue-based hypothesis, there are two valid cues to uncertainty that can be used in that context: crowdedness (crowded implies uncertainty) and contrast (low contrast implies uncertainty). Using the crowdedness cue, observers will always pick the uncrowded stimulus as less uncertain, whatever the contrasts of the two stimuli are. This result is suboptimal whenever the contrast of the crowded stimulus is high enough to induce higher performance than the uncrowded stimulus. When the contrast of the crowded stimulus is very high and the contrast of the uncrowded stimulus is very low, the sensible strategy is to choose the crowded stimulus and not the uncrowded one.

Fig. 3.

Principle of the experiment. The red and blue curves describe hypothetical psychometric functions: They give an observer's expected performance as a function of contrast in the crowded and uncrowded conditions, as in Fig. 2. Suppose we always give the choice between a fixed, uncrowded stimulus with contrast x_U and another, crowded stimulus with contrast x_C. How can we set x_C to make the observer feel more confident about the crowded stimulus? According to the cue-monitoring hypothesis, two cues to uncertainty are available: contrast and crowdedness. If the observer picks crowdedness as a cue, then he or she will always prefer the uncrowded stimulus, no matter what the value of x_C. If the observer uses contrast as a cue, then he or she should prefer the crowded stimulus as soon as 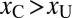. Alternatively, if confidence follows performance, what the observer should do is choose the crowded stimulus as soon as it yields a higher expected performance: here, any point beyond 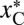. As shown above the plot, for any 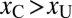, the predictions of the performance-based hypothesis differ from those of either of the two cue-based models.

If instead observers use the other available cue, contrast, then we expect them to pick the stimulus with higher physical contrast: i.e., the crowded one whenever x_C > x_U. However, if x_U is such that the uncrowded stimulus yields higher expected performance, then the best option is to go instead with the uncrowded stimulus, and this is what we expect observers to do if they are able to take into account the effect of crowding in their judgments of confidence. A performance-based strategy requires more flexibility than the use of cues.

Contrast levels in our experiment were chosen so that for certain contrast pairs it was more advantageous to choose the crowded stimulus and for other pairs it was the opposite. No cue (contrast or crowdedness) was able to predict the right choice for all possible pairs, so we set out to test whether observers followed one of the cues or were instead more flexible in their strategy, choosing according to expected performance.

To be able to interpret the data, we needed to know what choice observers ought to make to maximize performance when confronted with a particular pair of stimuli (x_C, x_U): As Fig. 3 shows, we needed to evaluate the probability of responding correctly at contrast x in the crowded and uncrowded conditions. This was done by inserting baseline trials in which the two stimuli displayed had the same crowdedness and the same contrast: i.e., the observers saw two crowded stimuli 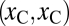or two uncrowded stimuli 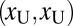. We measured observer's orientation discrimination performance as a function of contrast. The results are shown on Fig. 2. As expected, the data clearly display an effect of distractor orientation: thresholds are higher in the crowded condition for all observers. We fit psychometric functions 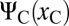and 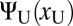to the data: They represent the expected performance of an observer if they are to make an orientation judgment for a crowded stimulus at contrast x_C or an uncrowded stimulus at contrast x_U. If the observer is presented with a pair 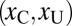, then it is advantageous to choose the crowded stimulus if 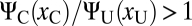. We call the ratio 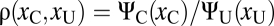the expected performance ratio.

We also ran control conditions in which the observer chose between two stimuli that were both crowded or both uncrowded, but with different contrast levels. In that condition the ideal strategy agrees with the contrast heuristic: The observer should pick the stimulus with more contrast, and this is what they did. We refer the reader to SI Materials and Methods (Figs. S1, S2, and S3) for details, but the data confirm that the larger the contrast difference was between the two stimuli, the more likely observers were to pick the stimulus with the higher contrast.

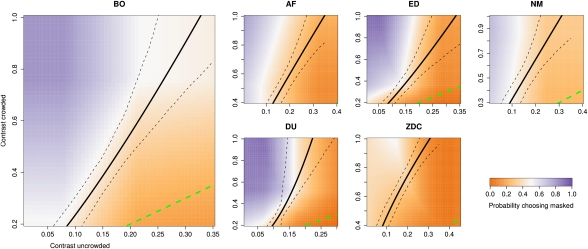
The most interesting condition pits an uncrowded stimulus against a crowded stimulus. These results appear in Fig. 4, where each section corresponds to the results for one individual observer. We plot response surfaces: For a stimulus pair 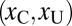the color of the corresponding point on the plot represents the probability of choosing the crowded stimulus. We smoothed the raw data using multivariate adaptive regression splines, a nonparametric technique that is neutral with respect to the different hypotheses tested (Materials and Methods).

Fig. 4.

Individual results for the uncrowded vs. crowded condition in experiment 1. The observer had to choose between two stimuli, one crowded and the other uncrowded, with target contrasts x_C and x_U. We plot the probability of choosing the crowded stimulus as a response surface. The solid black contours are contours of the expected performance ratio: 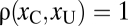means that the observer had equal probability of making a correct orientation judgment by picking either stimulus. The expected performance ratio is computed from the results of an independent baseline condition (Fig. 2) and shown along with 10–90% bootstrap quantiles (dashed lines) (SI Materials and Methods). The green dashed line is the line : Note that the contrast levels for crowded stimuli were on average higher, because the case 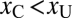is relatively uninteresting in the context of this experiment (all theories predict that the observer should choose the uncrowded stimulus). NM performed under different feedback conditions than the other five observers (Materials and Methods).

The thick line in each section of Fig. 4 represents the equal performance contour 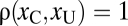of the observer. On the left-hand side of the equal performance contour observers could maximize performance by choosing the crowded stimulus, and on the right-hand side they could maximize performance by choosing the uncrowded stimulus. The green dashed line is the line of equal contrast 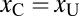: Above that line crowded stimuli have a higher contrast than uncrowded stimuli.

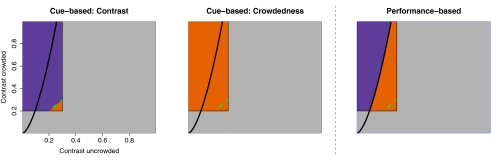
The model predictions are illustrated in Fig. 5. The cue-based hypothesis predicts that choice will be based on either contrast alone or crowdedness alone. The contrast heuristic predicts the observer will pick the crowded stimulus if 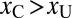. The crowdedness heuristic predicts the observer will always choose the uncrowded stimulus regardless of the values of x_C and x_U. An observer who is better aware of their true performance will choose stimuli in accordance with 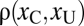: i.e., they will pick the crowded stimulus if 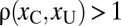and the uncrowded stimulus otherwise.

Fig. 5.

Idealized theoretical predictions for observer DU. We plot a response surface, as in Fig. 4. The Inset corresponds to the range of contrasts we tested the observer on (the exact range differed between observers). (Left) Contrast heuristic. The observer chooses the crowded stimulus whenever it has higher contrast than the uncrowded one. (Center) Crowdedness heuristic. The observer systematically chooses the uncrowded stimulus. (Right) Performance-based strategy. The observer chooses the crowded stimulus only if it affords higher expected performance.

As can be seen by comparing the individual results with the (idealized) model predictions, the results reject the two versions of the cue-based hypothesis. A bootstrap analysis shows that this conclusion is robust (SI Materials and Methods, Figs. S4 and S5). The cue-based hypothesis fails to predict observers’ choices in our task: Confidence cannot be determined by contrast or crowdedness alone. Qualitatively speaking, the results seem to better agree with the performance-based hypothesis—observers tend to choose the stimulus that brings the higher average performance, although deviations from ideal behavior are apparent in the response surfaces of at least some observers. There appears to be a tendency to go on choosing the uncrowded stimulus rather than the more advantageous crowded stimulus, at least when the difference between the two is small.

A possibility remains, however, that the cue that determines confidence is the perceived tilt of the target. A potential explanation could run as follows: Because of a pooling of orientation signals in the crowded condition, the distractors reduce the perceived tilt of the target, so that targets are perceived as more vertical than they are. Reducing the contrast could also reduce perceived tilt (for reasons that are less evident), and therefore the results could be due to a strategy of picking the stimulus with the higher perceived tilt: For stimuli with equal contrast, this would be the uncrowded stimulus. To gain further evidence that the evaluation of confidence was not cue based, we ran another experiment in which no such indirect mechanism could be posited.

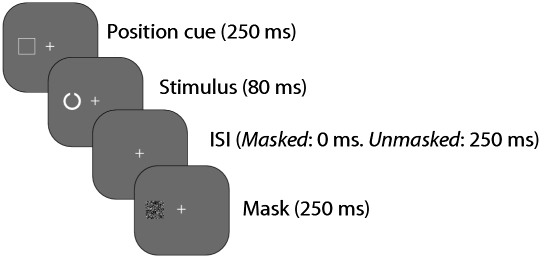
Experiment 2.

Experiment 2 is nearly identical in design to experiment 1, but replaces crowding with backward masking (17) and variations in contrast with variations in eccentricity. Observers were asked to make orientation judgments about “Landolt's C” stimuli that faced either upward or downward (Fig. 6). Stimuli were presented briefly and followed by a noise mask; the time interval between the stimulus and the mask (interstimulus interval, ISI) determines the strength of masking. The ISI could last either 250 or 0 ms. For simplicity we refer to the latter case as “masked stimuli” and to the former as “unmasked stimuli.”

Fig. 6.

Stimuli used in experiment 2. In experiment 2 the observer chose between masked and unmasked stimuli that differed in eccentricity. The underlying psychophysical task used Landolt's C stimuli is that the gap in the circle could be facing either up or down. Because stimuli were displayed at a random eccentricity, they were preceded by a cue that indicated the location the stimulus would appear in. The stimulus was flashed briefly immediately after the cue. In the masked condition, the stimulus was followed directly by a noise mask. In the unmasked condition, a blank interval (called the interstimulus interval, ISI), was inserted between the stimulus and the mask.

In experiment 1 we chose to vary contrast because of its plausibility as a universal cue to uncertainty: Lower contrast always means poorer performance. In experiment 2 we varied eccentricity, because like contrast it is highly plausible as a cue to uncertainty—generally speaking, the further objects are from the fovea, the less information is available about their features. If judgments of visual uncertainty were cue based, we would expect eccentricity to be used as a cue. In all other respects experiment 2 is identical to experiment 1: Two stimuli were displayed successively, and observers were asked to choose the one for which they felt more confident. None of the observers who took part in experiment 2 had previously taken part in experiment 1.

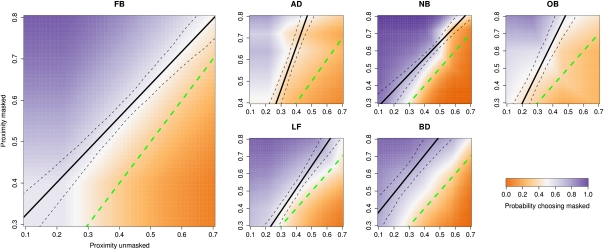
The results of the baseline condition confirm the presence of a masking effect for zero ISIs (Fig. S2), so that we can legitimately refer to these stimuli as masked. The results of the condition pitting a masked against an unmasked stimulus confirm that a cue-based mechanism cannot be at work (Fig. 7). Again, the data show that observers tend qualitatively to accord to a performance-based mechanism, although substantial biases are sometimes present: Observer BD, for example, has a strong bias in favor of masked stimuli. The results of experiment 2 confirm those of experiment 1: The evaluation of visual uncertainty must involve a process that is more complex than single-cue monitoring.

Fig. 7.

Results for the mixed condition in experiment 2. The same general format as in Fig. 4 is followed. The proximity of a stimulus is defined as the opposite of eccentricity. Stimuli with proximity 1 stand next to the fixation cross, and stimuli with proximity 0 are as far from the fixation cross as possible on the monitor used (corresponding to 17.9° of eccentricity). Eccentricity plays the same role here as contrast does in experiment 1. Observers chose between masked and unmasked stimuli, and we plot the probability of choosing the masked one. Again, we would expect that if observers followed the strategy of always picking the stimulus with lower eccentricity, the green dashed line should separate the blue and red regions. The black line represents the line of equal expected performance, with bootstrap 10% and 90% quantiles shown as dashed lines.

Discussion

In previous investigations of visual confidence, expected performance was tied to a unique, obvious physical variable. The reported correlation between performance and confidence could be explained by a cue-based strategy. Because we used a task in which performance depended on two physical variables, we were able to show that simple heuristics based on cues cannot account for observers’ confidence judgements when comparing crowded and uncrowded stimuli. Confidence seems to follow performance quite accurately. This result effectively rules out the most simple mechanism available, but leaves open a number of possibilities. Instead of using just one cue, it could be that the visual system keeps track of cue combinations (contrast and crowdedness, contrast and blurriness, blurriness and speed, …). The combinatorial explosion involved makes this difficult: The visual system would have to evaluate the impact on confidence of every two-way interaction, every three-way interaction, etc. A Bayesian mechanism (8–10) appears comparatively more likely, but there are difficulties with that hypothesis as well. Generally speaking, it is far from clear how realistic neural networks could implement the difficult computational problems arising in Bayesian inference. Even if we restrict the discussion to the relationship between confidence and performance, some outstanding issues remain.

There is a stark contrast between the accurate evaluation of uncertainty predicted by Bayesian models and the general outlook from the literature on decision making under uncertainty. Following the seminal work of Kahnemann and Tversky (18), innumerable biases have been found in human judgment. Some of them are errors of statistical reasoning, which are not at stake here. Others are deviations from optimal behavior under risk: At least as far as economic matters are concerned, humans rarely behave according to the prescriptions of statistical decision theory. Optimal behavior—maximization of expected utility—can be achieved only if one is able to evaluate probabilities, evaluate the expected utility of each possible line of action, and choose the action with the maximum expected utility. In our experiments we test only the first of these three abilities: the estimation of uncertainty. Observers judged comparative risk: No further computation was needed beyond judging which of two probabilities is larger. Yet some observers seem to display biases in their perception of risk: ZDC in the first experiment and BD in the second are distinctly suboptimal in their choice patterns. They show relative miscalibration, misjudging the effect of a certain manipulation on their performance. For example, in experiment 1 ZDC exhibits relative overconfidence in uncrowded stimuli: She favors uncrowded stimuli despite the fact that choosing crowded ones would yield a higher probability of responding correctly. Note that this can be equally well characterized as “overconfidence in uncrowded stimuli” or “underconfidence in crowded stimuli.” In experiment 2, BD displays a pattern of miscalibration favoring masked stimuli. This miscalibration may be related to the finding that in metacontrast masking (19), observers evaluate their level of awareness differently at equal performance levels but different asynchronies between target and mask.

The relative miscalibration found here should not be confused with an absolute miscalibration of probability judgments (20). Many studies have documented a widespread bias of absolute overconfidence: On average, people overestimate their probability of success in a task (21). Whereas the original experiments that uncovered overconfidence used general-knowledge tests, this finding holds in the motor and sensory domains as well (22, 23), although sometimes underconfidence is reported as well (24). The task used here sidesteps the issue by asking observers to choose the less uncertain of two stimuli. It does not matter if observers overestimate or underestimate their probability of success, because we require them to make comparative judgments. We expect an objective task such as the one used here to measure more robust effects than the ones obtained from confidence ratings, which are subject to uncontrollable variability between observers and over time (20, 25).

We set up a task that is drastically simple—from the observer's point of view—compared with most decision-making tasks. The cost is that we lose the ability to address significant issues of higher-level decision making, biases and heuristics. What we gain is direct access to the causes of visual uncertainty, letting us address the question of what makes observers perceive risk in visual decision making. As far as this study is concerned the Bayesian framework is qualitatively consistent with the data, but what of the cases when evaluation of visual uncertainty seems to break down completely?

Eyewitness testimony is a case in point: In experimental studies, the correlation between eyewitnesses’ confidence and their actual performance is found to be rather poor (26). However, to a large extent, this poor correlation seems to be attributable to memory biases rather than to poor evaluation of visual uncertainty (27). Potentially more troubling are cases of reported decorrelations between confidence and performance following visual manipulations. In change blindness tasks, observers overestimate their capacity to detect changes, in a phenomenon called “change-blindness blindness” (28). This result is a strong challenge to the Bayesian viewpoint, because to a Bayesian observer any factor that impacts performance in a significant way ought to be taken into account in the assessment of confidence.

One potentially important difference between the phenomena above and our experiment is that we use ecologically valid sources of uncertainty: The visual system has no choice but to cope with low contrast and eccentricity, whereas, for example, change blindness involves large objects suddenly going missing, a situation rarely encountered outside of the Bermuda triangle. A possibility is then that we learn only to deal appropriately with the uncertainty that matters (29).

However, a truly probabilistic system must show a considerable degree of sophistication. Here we ask observers to compare only two instances of the same visual task. But what if observers had to make judgments across modalities or across visual tasks? A probabilistic system knows when making, say, a visual judgment is more likely to be correct than an unrelated auditory judgment. But can observers do that? In other words, is there a single currency for uncertainty in the brain? Probabilistic systems also evolve over time, revising their estimation of uncertainty. Although a lot is now known about changes in performance during perceptual learning (30), there is a relative paucity of results on how these changes may interact with judgments of confidence, especially during rapid learning (31).

Our results provide a lower bound for the sophistication of confidence evaluation. The presence of sophisticated evaluation mechanisms lends only indirect support to the Bayesian hypothesis, and much more research is needed to determine to what extent the brain behaves as a probabilistic system. We believe nonetheless that a methodologically rigorous investigation of confidence judgments in perception will be essential to understanding the computational mechanisms at work in the visual system.

Materials and Methods

Experiment 1.

Stimuli.

The stimuli were composed of five Gabor patches arranged on a cross (Fig. 1). We refer to the central patch as the target and to the others as distractors. The orientation of the target was either 15° clockwise or 15° counterclockwise of the vertical. The distractors had vertical orientation in the crowded condition (C) and horizontal orientation in the uncrowded condition (U). The contrast of the distractors was set at 50%, and the contrast of the target was varied as described in SI Materials and Methods.

Stimuli were presented at an eccentricity of 12.5° of visual angle. They appeared left or right of the fixation cross at a random position along two semicircles of angular length 90° (Fig. S6). The individual patches in the stimuli subtended 0.4° of visual angle (SD of the Gaussian envelope).

Observers.

Six observers took part in the experiment. All observers had normal or corrected-to-normal eyesight and were completely naive to the purpose of the experiment. Observers were financially compensated for their participation.

Procedure.

Observers ran a total of five sessions. In the first session they were familiarized with the orientation discrimination task (SI Materials and Methods) and then ran a pretest designed to measure their performance in orientation discrimination (SI Materials and Methods). In the remaining four sessions they ran the main experiment. All sessions lasted <1 h.

In the main experiment two stimuli appeared successively in each trial. Observers were instructed to select the stimulus they felt they were more confident about (which one they were more comfortable with making an orientation judgment). They selected a stimulus using the keyboard and then indicated, again using the keyboard, the perceived orientation of the target patch in the stimulus they had selected.

One stimulus was displayed to the left of fixation and the other to the right. The order of appearance was randomized, and so was the orientation of the targets. We varied two factors: the contrast of the targets and the orientation of the distractors.

The baseline case occurred when the two stimuli displayed in one trial had identical distractor orientation and identical target contrast. In the baseline case there is no intrinsic value in picking one stimulus over the other. The contrast-only case occurred when the two stimuli had distractors with the same orientation but the targets had different levels of contrast. In the contrast-only case there is a benefit in choosing the stimulus with the higher contrast. In the mixed case, stimuli differed in both distractor orientation and target contrast. The probability of occurrence of those three trial types is given in Table 1. The contrast level of stimuli was chosen among 12 possible levels: 6 levels for crowded stimuli and 6 for uncrowded stimuli.

Table 1.

Probability of occurrence of the three trial types

Baseline, %	Contrast only, %	Mixed, %
37.5	37.5 (18.75 of CC trials + 18.75 of UU trials)	25 (12.5 CU, 12.5 UC)

CC, both stimuli crowded; CU, left-hand stimulus crowded, right-hand uncrowded; UC, left-hand stimulus uncrowded, right-hand crowded; UU, both stimuli uncrowded.

Feedback was given every 5 trials: Observers were told on how many trials they responded correctly (of the previous 5). Observers ran the experiment in four consecutive sessions of 800 trials. Sessions were divided into blocks of 100 trials, and observers were instructed to take short breaks between blocks (minimum duration 10 s).

To minimize the possibility that observers were simply learning over time how to choose appropriately between stimuli from the feedback they received (but still provide some motivation for them to maximize performance), we limited feedback to once every 5 trials. We also ran an additional observer, NM, who received feedback only every 20 trials, including in the training period. The results are essentially the same, as shown in Fig. 5, which excludes the possibility that feedback learning could explain our data.

Experiment 2.

The methods for experiment 2 are identical to those for experiment 1 (replacing “contrast” with “eccentricity” and “crowded” with “masked”), except where indicated otherwise.

Stimuli and mask.

We used Landolt's C as a stimulus (Fig. 6). We used up/down orientations instead of the more traditional left/right because of the potential confusion between choosing the less uncertain stimulus (which was a left/right judgment) and the orientation task. The stimulus subtended 2.6° of visual angle. Before the stimulus appeared, a cue was displayed at its future location. The cue was a square frame of width 2.9°.

Stimuli appeared within the area delimited by the frame. They were displayed for 80 ms and then followed immediately either by a noise mask or by a blank ISI (duration 250 ms) followed by a noise mask. The noise mask was a square region of white noise (width 2.9°). To eliminate variations in difficulty caused by variations in the mask, the mask was identical for the whole experiment and all observers.

The range of eccentricities used differed between participants (SI Materials and Methods). The maximum eccentricity displayable on the monitor was 17.9°.

Observers.

Six observers took part in the experiment. None had participated previously in experiment 1.

Procedure.

The overall procedure is identical to that of experiment 1. For details please refer to SI Materials and Methods and Table S1.