Chemically accurate coarse graining of double-stranded DNA

Abstract

Coarse-grained (CG) modeling approaches are widely used to simulate many important biological processes involving DNA, including chromatin folding and genomic packaging. The bending propensity of a semiflexible DNA molecule critically influences these processes. However, existing CG DNA models do not retain a sufficient fidelity of the important local chain motions, whose propagation at larger length scales would generate correct DNA persistent lengths, in particular when the solution’s ionic strength is widely varied. Here we report on a development of an accurate CG model for the double-stranded DNA chain, with explicit treatment of mobile ions, derived systematically from all-atom molecular dynamics simulations. Our model generates complex local motions of the DNA chain, similar to fully atomistic dynamics, leading also to a quantitative agreement of our simulation results with the experimental data on the dependence of the DNA persistence length on the solution ionic strength. We also predict a structural transition in a torsionally stressed DNA nanocircle as the buffer ionic strength is increased beyond a threshold value.

To successfully model many biological processes involving DNA, atomistic or coarse-grained (CG) DNA force fields should reproduce the bending rigidity of a semiflexible DNA chain, which is a large-scale polymer property of critical significance (1, 2). In particular, the response of the DNA persistence length to the change in the surrounding ionic environment is of major biological importance. For example, even a slight change in the persistence length of a linker DNA segment connecting adjacent nucleosomes in the chromatin fiber, induced by the variation of the ionic strength of the solution, may result in significant conformational changes of a chromatin in a compact state (3). Current structure-based DNA models (4, 5) do not generate DNA persistence length values that are fully consistent with those measured experimentally in a wide range of ionic concentrations, c ∼ [0.1–100] mM (6–8). These and other DNA models differ in resolution in terms of representing both the DNA structure and also the surrounding ionic environment.

The discrete nature of mobile ions and spatial correlations among them may significantly affect structure, dynamics, and the electrostatic atmosphere of many biomolecules, such as DNA and RNA (9–15). Thus, explicit inclusion of the monovalent mobile ions into the CG model of DNA is desirable from the physical standpoint. Another vital aspect of DNA modeling is a choice of the parametrization protocol. Many prior one-bead DNA models were based on use of the phenomenological worm-like chain Hamiltonian (16, 17). In more detailed structure-based models, parameters are often derived by combining the statistical information from the available crystal structures with some specific experimental data (4). However, this parametrization approach, which is focused on matching a small number of integral experimental characteristics (for example, the melting temperature or free energies of denaturation), does not guarantee the fidelity of specific local motions. On the other hand, large-scale polymer chain behavior is generated by propagation in the scale of local motions.

In our recent works on modeling double-stranded DNA, we used a different strategy of parameterizing a DNA potential, on the basis of coarse graining of high-resolution all-atom (AA) force field, in particular, using refined AMBER Parmbsc0 parameters for nucleic acids (18). A similar technique was applied to coarse-grain electrolyte solutions, where recently developed AMBER 10 ionic parameters were used (19). This method, which we called molecular renormalization group coarse graining (MRG-CG), is based on simultaneously matching the moments of all physical “observables” that enter the CG Hamiltonian, between the CG and AA systems. Each of these observables is associated with a specific type of CG effective interaction, such as DNA bond or bending angle potentials. In this approach, the transition from the detailed AA to simplified CG representation is seen as a one-step renormalization, which is further elaborated in Materials and Methods.

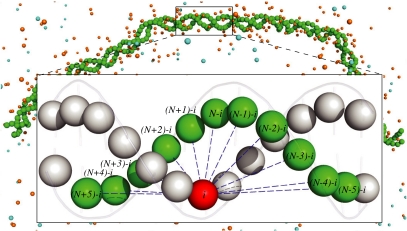
In the present work we merge our prior models for the double-stranded DNA and NaCl bulk solution, derived systematically from atomistic AMBER10 molecular dynamics (MD) simulations with the MRG-CG technique. Our goal is to accurately capture the local dynamics of both the DNA and mobile ions, including coupling between DNA motions and the ionic environment fluctuations. The model of the two-bead DNA chain surrounded by Na⁺ and Cl^- ions is depicted in Fig. 1. Although it is structurally similar to our previous DNA model (18), where electrostatic interactions were treated implicitly, by using simplified mean-field theory, here the force-field parameters need to be rederived because mobile ions are explicitly present. The procedure for estimating the initial parameters for all types of effective interactions, including structural DNA constraints, interionic interactions, and the interactions between DNA beads and mobile ions, is outlined in Materials and Methods. All trial interaction parameters were then subject to optimization with the MRG-CG technique. In contrast to many other CG models of DNA, where generic polymer chain Hamiltonians are used, our model is designed to reproduce complex, anharmonic motions of DNA, which emerge as a result of DNA’s chemical fine structural details. Hence, our Hamiltonian represents many important aspects of DNA’s stereochemical dynamics, albeit some other chemical details are omitted because of the particular resolution of two beads per base pair.

Fig. 1.

Our CG model for the DNA chain in the NaCl salt buffer is shown. Each DNA base pair is represented by two beads, each placed in the geometric center of the corresponding atomistic nucleotide. Blue dashed lines indicate the fan interactions, which represent a superposition of stacking and base pairing among two polynucleotides. Labels on beads indicate that fan interactions are between a given bead i located on one DNA strand and a number of beads [(N ± 0…5) - i] located on the other strand. N is the total number of particles. There are 11 fan interactions imposed on each CG bead.

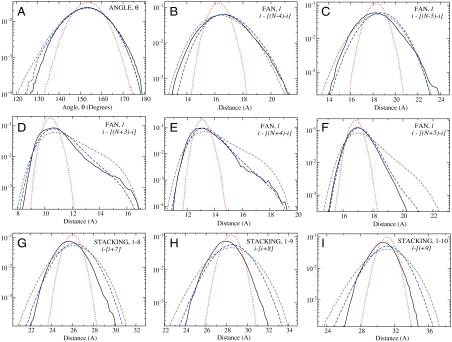
The quality of the CG model derived with the MRG-CG scheme is determined by the extent of equivalence between AA and CG partition functions, as determined by the matching between various moments of physical observables that enter the CG Hamiltonian (18, 19). In this and prior works, we required similarity of the first moments, which formally corresponds to the optimization problem being addressed on the mean-field level. However, as elaborated in the SI Appendix, the technique works beyond mean-field for “elementary” order parameters, such as bond lengths and angles, as evidenced by matching even rare fluctuations in these variables (see Fig. 2 below). In addition to evaluating the numerical differences between these averages obtained from AA and CG simulations (see the SI Appendix), the quality of the CG model may also be visualized by comparing various structural distribution functions generated for both CG and AA systems. The comparison among some of the DNA structural distributions is illustrated in Fig. 2, demonstrating how iterative adjustment of the Hamiltonian parameters with the MRG-CG technique results in a self-consistent widening of all initial distributions, morphing them into the desired atomistic results. In particular, the final CG distributions accurately follow the asymmetric shapes of the corresponding atomistic curves. Interestingly, structural DNA distributions that were not associated with any physical observables defining our CG Hamiltonian, thus, not optimized or biased in any way, turned out to be also well-reproduced (Fig. 2 G–I). These agreements indicate that our DNA Hamiltonian, elaborated in Materials and Methods, is composed of observables that form a nearly complete basis set.

Fig. 2.

Semilog plots for some of the DNA structural distributions: (A) bending angle; (B–F) several of the fan constraints (notations are explained in the caption of Fig. 1); (G–I) some of the intrastrand distances (1–8, 1–9, and 1–10 stacking interactions) between DNA particles separated by seven, eight, and nine nucleotides, respectively. Solid black (reference AA), red dotted (initial CG), and blue dashed lines (MRG-CG optimized) structural distributions were obtained from the corresponding simulations. Additionally, wider distributions that have been generated by uniformly rescaling the optimized CG Hamiltonian by 0.7 are shown as green dash-dotted lines (see the text). Note that there are no physical constraints imposed on the DNA chain that correspond to stacking interactions; i.e., they do not enter into the CG force field. However, the last three panels indicate that these (and other) structural distributions are still reasonably well-reproduced.

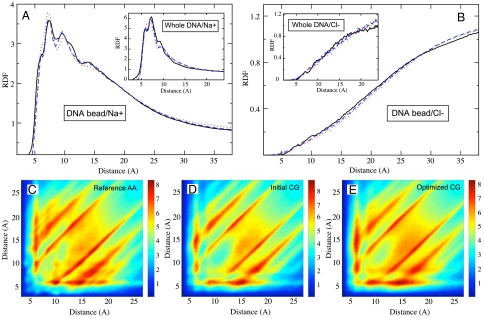
Analogous comparison for the interionic radial distribution functions (RDFs) also revealed a good agreement among Na⁺ and Cl^- distributions in AA and CG systems (see Fig. 1 in the SI Appendix). The DNA-bead–mobile-ion interactions were derived from a separate series of AA MD simulations of a system composed of a number of unconnected DNA backbone “monomers,” sodium dimethyl phosphate, and sodium chloride buffers (20). Interestingly, when those trial interaction potentials were used in the current model of DNA chain and NaCl salt, the generated DNA-bead–ion RDFs appeared to be very plausible and close to the atomistic results (see Fig. 3 A and B). However, subsequent parameter optimization with MRG-CG technique allowed achievement of even higher quality of these distributions.

Fig. 3.

Distributions of mobile ions around DNA are plotted. The Upper panels show one-dimensional RDFs for Na⁺ (A) and Cl^- (B) ions around a single DNA bead (main panels) and the whole DNA chain (Insets); line coloring is the same as in Fig. 2. (C–E) The Lower panels show two-dimensional RDFs for Na⁺ ions defined by two distances between the mobile ion and two different beads of DNA; it is seen that agreement with the reference AA distribution is improved after the MRG-CG optimization (see the text).

Two-body distributions shown in Fig. 3 A and B do not fully represent all aspects of the ionic atmosphere around DNA. Indeed, the tails of distributions shown in Fig. 3 A and B have contributions from two dissimilar sources: (i) the ions located far away from the DNA chain and (ii) the ions located in DNA proximity but far away from a particular DNA bead. Because the modulation of DNA dynamics by surrounding mobile ions is important, we explored finer details of ionic atmosphere around DNA by computing three-point correlation functions for ions with respect to two different beads of DNA chain. Such distributions for Na⁺ ions are shown in Fig. 3 C–E. They demonstrate that spatial correlations of the counterion atmosphere around DNA are well-reproduced in the CG system.

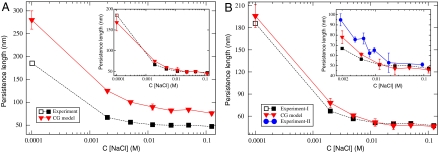
Having found close agreement among a multitude of CG and AA structural distributions, we investigated the dependence of DNA persistence length on the ionic strength of the solution. The central results of this study are presented in Fig. 4. It turned out that DNA persistence lengths generated by optimized Hamiltonian parameters were systematically larger than the corresponding experimental values (see Inset in Fig. 4A), producing a stiffer DNA at physiological conditions with a persistence length of l_p ∼ 75 nm. However, the success of the MRG-CG procedure is determined not by directly matching to experimental data but by fiducially reproducing the underlying reference atomistic Hamiltonian. Interestingly, Mazur used an independent technique based on elasticity theory to estimate persistence lengths of various DNA segments with alternating AT and GC sequences, finding values between 75 and 80 nm by using atomistic AMBER simulations (21). Hence, we found not only a close agreement between the CG structural distributions to those measured in the AA system, but also large-scale polymeric properties are accurately reproduced. Furthermore, a uniform rescaling of MD simulation results by a factor of ∼0.7 led to nearly exact agreement with the experimental data (see Inset in Fig. 4A), showing that the experimental trend is also well-reproduced.

Fig. 4.

Dependence of the DNA persistence length on the ionic strength of the solution are shown for various CG models. The main panel (A) shows the actual dependence produced by MRG-CG optimization of the AA AMBER Parmbcs0 force-field for the DNA (34) and the latest AMBER10 ionic parameters (35); this plot corresponds to the blue dashed DNA distributions of Fig. 2. The Inset of A is derived by a uniform rescaling of a red curve in the main panel by a factor of 0.7. (B) Response of the DNA persistence length to the change in ionic concentration generated by a CG Hamiltonian, which is uniformly scaled by a factor of 0.7, is shown; this plot corresponds to the green dash-dotted DNA distributions of Fig. 2. Experimental values are taken from ref. 6 (solid squares) and ref. 7 (open square). An additional set of experimental points (blue circles) derived by Baumann et al. (8) for a smaller range of ionic concentrations, c ∼ [2–100] mM, is shown in the Inset. Persistence lengths were calculated as elaborated in Materials and Methods. The error bars represent standard deviations.

However, in practical applications, such as modeling chromatin folding or genome packaging, it is desirable to have a structure-based DNA model that produces persistent lengths in nearly absolute agreement with the experiment. One such possibility is to soften the AMBER Parmbsc0 force field, which might require significant effort, and, subsequently, reoptimize the CG Hamiltonian. It is likely that tenths of k_BT per monomer error in the atomistic force field could propagate in scale, resulting in several tens of nanometers error in persistence length. Up to this step our CG force field was derived from the atomistic dynamics; however, the previous discussion motivates a physically plausible calibration on the basis of one experimental data point. Hence, we chose a simpler alternative strategy of uniformly rescaling all CG DNA structural parameters by 0.7, leaving the rest of the CG force field unchanged. Fig. 2 shows that such rescaling affected mostly the “fan” DNA distributions, making them slightly wider (i.e., increasing local fluctuations) but preserving the main features of atomistic results, such as asymmetric shapes of the curves. Using this new CG force field, we recomputed DNA persistence lengths for a wide range of NaCl concentrations, c ∼ [0.1–100] mM. These results agree well with experimental estimates without any further adjustment, as shown in Fig. 4B. It has to be noted that different experimental techniques lead to a noticeable scatter of DNA’s persistent length estimates, most likely because of systematic errors and model-dependent interpretation of raw data. Hence, our computational results agree with experiments within the experimental error.

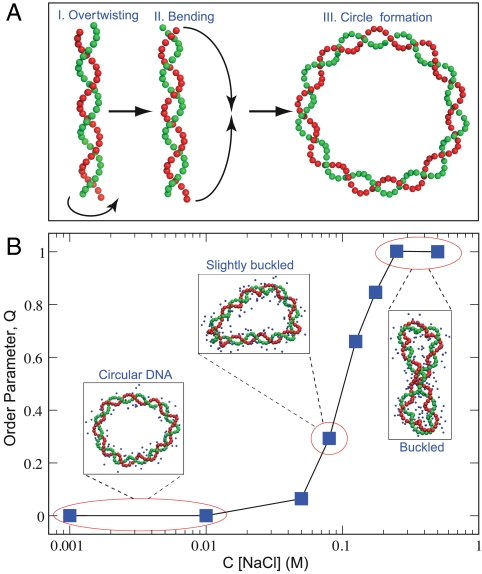
We further tested our CG model on yet another important class of systems, where a delicate balance between elastic and electrostatic interactions determines the chain’s structural behavior. Particularly, we have built and simulated a 90-base-pair nanocircular DNA, overtwisted by one helical turn (see Fig. 5A), to investigate whether such torsionally stressed DNA chain will undergo a structural transition upon changing the NaCl concentrations in the c ∼ [0.1–500] mM range. The importance of studying the topologically constrained DNA chains subject to torsional stress has been recently pointed out in the literature (22, 23). For example, it was experimentally shown that DNA supercoiling may inhibit the process of nucleosomal assembly (22). A recent computational work suggested that supercoiling of torsionally stressed DNA nanocircles depends strongly on the salt concentration, because intrachain electrostatic repulsion opposes elastically induced buckling (23). It should be noted, however, that because of very large system sizes used in explicit solvent atomistic simulations, the systems corresponding to the current work were studied for only 5 ns, which is less than sodium ion equilibration time around DNA, over 50 ns (10, 14). In addition, only a single Na⁺ concentration was investigated, corresponding to the DNA neutralization condition, with no additional salt. On the other hand, the DNA model developed in this work is well suited for interrogating the role of explicit mobile ions in modulating the DNA circle’s structural behavior as the salt concentration is broadly varied. Sufficiently long equilibration times, around 500 ns for each simulation, allows achievement of equilibration and prediction of the corresponding phase diagram.

Fig. 5.

Phase behavior of the overtwisted 90-base-pair circular DNA chain in explicit NaCl salt. (A) Steps of the initial structure preparation are shown. (B) The degree of the superhelical twisting at various NaCl concentrations is characterized by the structural order parameter Q. See Materials and Methods for details. Our CG model predicts a pronounced phase transition at physiological conditions, c ∼ [50–200] mM.

Next, we introduce a structural order parameter Q that characterizes DNA circle’s supercoiling (see Materials and Methods for its definition). The resulting dependence of Q on the ionic strength is shown in Fig. 5B. Our CG model predicts that a sharp phase transition occurs from a planar circular DNA to a strongly buckled DNA conformation with the transition midpoint located within a narrow physiological range of salt concentrations, c ∼ [50–200] mM (see Fig. 5B). Our predictions cannot be directly compared to the analogous AA simulations of the 90-base-pair DNA nanocircle investigated in ref. 23, because of the reasons outlined above. Nevertheless, Harris et al. found circle bending for d(GC)₉₀ and d(AT)₉₀, at approximately 140 mM of Na⁺ counterion concentration (no Cl^- coions were present). Their results are qualitatively consistent with the behavior of the DNA chain in the very beginning of our simulation at an equivalent salt concentration. However, we find that the DNA nanocircle buckles on longer time scales. On the other hand, it should be noted that the nanocircle becomes nearly planar in our CG simulations already at half of the concentration used in ref. 23, c ∼ 70 mM (see Fig. 5B). In light of significant differences between the corresponding simulation box sizes, ionic conditions, and time scales, these comparisons suggest that our simulation results might be broadly consistent with the fully atomistic models with explicit ions and water.

In summary, we applied the MRG-CG method to develop a two-bead model of DNA with explicit mobile ions. This DNA model, derived by matching molecular correlation functions with atomistic results and uniformly scaled, generates realistic local atomistic motions and, simultaneously, accurately reproduces the large-scale chain dynamics. In particular, quantitative agreement was found with the experimental data on the dependence of DNA persistence length on the solution ionic strength. In addition, we used our model to predict the structural transition of a DNA nanocircle consisting of 90 base pairs as the salt concentration is varied. Overall, the CG DNA model developed in this work may be directly used in various biomolecular simulations, when accessing large length and time scales is desirable, for example, to represent linker DNA in chromatin-folding simulations or to study genome packaging in viruses.

Materials and Methods

Foundation of MRG-CG Method.

There are a number of recognized coarse-graining strategies used to simulate many important biological processes (24–29). The optimization scheme used in this work closely follows the RG Monte Carlo method by Swendsen to compute critical exponents in a three-dimensional Ising model (30). This technique was later adapted by Lyubartsev and Laaksonen to simulate several molecular systems with simple pairwise interactions (31). Recently, we generalized the method (18, 19) by extending its applicability to complex systems, such as polymers, which are characterized by more sophisticated interactions (e.g., three-body bending angle interactions). The MRG-CG scheme relies on representing an effective Hamiltonian as a linear combination of N relevant dynamical observables, 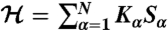, whose (various order) correlation functions 〈S_α…S_β〉 need to be reproduced in the CG system. Hence, a “conjugate field” K_α is prescribed to each observable, playing the role of a Hamiltonian force constant, whose numerical value has to be adjusted appropriately to generate the desired system dynamics. Because of Hamiltonian linearity, it is possible to establish a mathematical connection between these conjugate fields and expectation values of dynamical observables in terms of the covariance matrix of all observables:

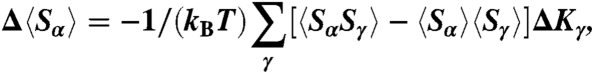[1]

where Δ〈S_α〉 ≡ 〈S_α〉_CG - 〈S_α〉_AA is the difference between the expectation values of an observable, S_α, averaged over CG and AA systems and the ΔK_γs are corrections to trial CG Hamiltonian parameters 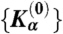. A similar-in-spirit formalism was used by Matysiak and Clementi to match protein free energy changes upon single point mutations with experimental measurements (32). A set of linear equations (Eq. 1) is solved at each CG iteration until the convergence is reached for all observables: Δ〈S_α〉 ≈ 0, α = 1…N. In this way, the process of parameter adjustment explicitly accounts for cross-correlations among various CG degrees of freedom—a key ingredient that is responsible for high fidelity of the local CG dynamics. For example, as we iteratively adjust Hamiltonian parameters for the DNA bending angle potential, we use the information of what impact that adjustment would have on all other CG structural degrees of freedom (for example, bond or stacking dynamical variables).

In a recent work (18), we interpreted the MRG-CG optimization technique in light of the field theory (33). Namely, Hamiltonian linearity allows us to interpret the CG partition function

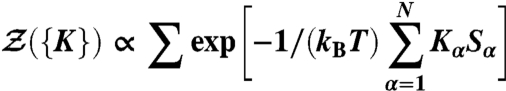as a generating functional, whose differentiation with respect to conjugate fields yields the corresponding auto- and cross-correlation functions of physical observables:

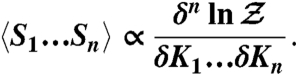[2]

Because the optimization is aimed at matching these various order correlation functions in AA and CG systems, the whole procedure is reminiscent of the central idea of RG theory. Indeed, matching the correlation functions of relevant physical observables ensures a significant equivalence of (restricted) AA and CG partition functions, by matching various order derivatives of the free energy. Additionally, an association with RG theory is strengthened by thinking of the parameter adjustment as a “flow” in space of Hamiltonians, spanned by a set of conjugate fields {K_α} coupled to the corresponding observables.

It follows from the last equation that the MRG-CG method can be straightforwardly generalized by demanding to reproduce not only average values but also higher-order correlation functions of observables. Particularly, if AA and CG partition functions generate identical sets of correlation functions of the order n and less, then the value of n may be seen as a quantitative “measure” of similarity between two systems. For example, in the case of n = 2 a set of linear equations 1 will be supplemented by N(N - 1)/2 additional (and still linear) equations aimed at matching second-order correlators Δ〈S_αS_γ〉 ≈ 0.

CG Model.

The model for DNA in the current study is structurally analogous to the model developed in our prior related work. The effective Hamiltonian for the double-stranded DNA is the following:

[3]

with the first two terms describing bond and bending angle potential energies (intrastrand interactions), and the third and the last terms representing interstrand (fan interactions; see Fig. 1) and Coulomb interactions, respectively. Functional forms for individual energetic contributions have been chosen to be quartic polynomials

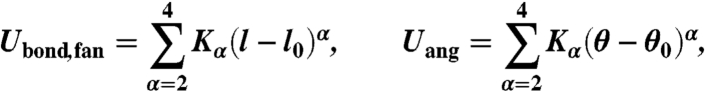[4]

to account for the asymmetric shape of DNA structural fluctuations (see Fig. 2). Here, l₀ and θ₀ are equilibrium interparticle separations for bond and fan interactions and the equilibrium angle for bending angle potential, respectively. These equilibrium interparticle separations, as well as the trial coefficients 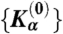, were extracted from the fit of the above polynomials to the corresponding potentials of mean forces obtained from AA MD simulations.

Interionic interaction potentials were taken from our prior work on coarse graining a bulk NaCl solution (19). Particularly, this part of CG Hamiltonian has the following functional form:

[5]

defined by the set of parameters {A,B^(k),C^(k)} and the positions of Gaussian peaks and minima, {R^(k)} (five Gaussian functions were introduced to account for short-range hydration effects and to accurately reproduce atomistic behavior of ions).

Finally, functional forms for interaction potentials among beads of DNA and the ions were derived from a separate series of AA MD simulations of a system comprised of unconnected DNA backbone monomers (sodium dimethylphosphate) and NaCl salt buffer (20). The latter system was chosen in an attempt to single out a “typical” DNA-bead–ion interaction by suppressing correlation effects caused by DNA connectivity (effects from neighboring DNA beads). These correlation effects were later accounted for by adjusting Hamiltonian parameters with the MRG-CG technique (see Fig. 3 A and B). The functional form for these types of effective interactions is similar to interionic potentials, however, with softer excluded volume interactions and a lesser number of Gaussian functions to describe hydration effects:

[6]

CG Hamiltonian as a Linear Combination of Dynamical Observables.

It follows from the structure of our CG Hamiltonian that the behavior of the system is described by a small number of observables, which may also be seen as structure-based collective order parameters. For example, according to polynomials (Eq. 4), DNA bond potential energy is described by three collective observables: , , and . Analogously, collective modes characterizing ion–DNA interactions (ionic “shells” around a DNA bead) are 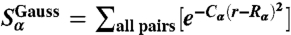, α = 1…3, whereas the corresponding parameters {K_α} are given by the set of constants {B^(k)}; see Eq. 6. As a result, DNA behavior is associated with N_DNA = 39 of structural observables (bond, angle, and fan interactions) coupled to the corresponding conjugate fields {K_α}, whereas the dynamics of the ionic atmosphere around DNA is described by a total of N_ions = 2 × 4 = 8 observables (four CG degrees of freedom per interaction of DNA with Na⁺ and Cl^-, respectively).

Calculation of the DNA Persistent Length.

Persistence length l_p was calculated by using the well-known formula for the semiflexible polymers

[7]

defining how a correlation function for tangent vectors decays with the chain length (1). We have chosen the average length of the segment, 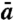, to be the distance between DNA beads separated by 10 nucleotides.

Preparation and Structural Analysis of the Overtwisted Circular DNA.

A 90-base-pair circular DNA chain, overtwisted by one helical turn, was prepared as shown in Fig. 5. The number of base pairs and the degree of the overtwisting were chosen to reproduce one of the DNA nanocircles studied recently with AA MD simulations in ref. 23. First, we imposed a homogeneous stress on the linear and torsionally relaxed DNA chain (Fig. 5A), which corresponded to the following excessive twisting angle per base pair:

[8]

Here, ϕ₀ and ϕ indicate the dihedral angle between consecutive base pairs in the torsionally relaxed DNA chain (in AMBER Parmbcs0 force field ϕ₀ ≈ 32°) and in the overtwisted DNA chain, respectively. This difference can be expressed in terms of the topological quantity known as the linking number, Lk, which is the number of helical repeats within a DNA chain of N_bp base pairs. The integer quantity ΔLk ≡ Lk₀ - Lk describes the deviation from the torsionally relaxed circular DNA and amounts to the degree of overtwisting (if positive) or undertwisting (if negative). For our model of interest the parameters in Eq. 8 were as follows: N_bp = 90 and ΔLk = 1 (overtwisting by one helical turn), which resulted in Δϕ = 4°. Subsequent bending of such an overtwisted DNA chain into the closed circle led to the desired initial structure (Fig. 5A).

To characterize structural rearrangements of the circular DNA as the concentration of NaCl varied, we introduced the following order parameter:

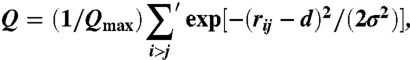[9]

which is reminiscent of the structural order parameters used for description of proteins and spin glasses. The Gaussian functional form is parametrized by the expectation value d for the distance r_ij between the DNA beads i and j and the variance σ. The prime on the sum indicates that only pairs of beads i and j separated along the chain by more than a certain number of base pairs are considered. From the structural analysis of the average buckled DNA conformations at high salt concentrations, we estimated these parameters to be d = 35 Å and σ = 5 Å, and the separation between beads along the chain was chosen to be 30 base pairs. This combination of parameters ensured a robust characterization of the structural DNA behavior. For example, it resulted in the zeroth value of Q at small ionic concentrations, as indicated in Fig. 5B. Note, finally, that the order parameter was normalized to unity by scaling with the maximum value Q_max attained at the highest salt concentration.