Contribution potential of glaciers to water availability in different climate regimes

Abstract

Although reliable figures are often missing, considerable detrimental changes due to shrinking glaciers are universally expected for water availability in river systems under the influence of ongoing global climate change. We estimate the contribution potential of seasonally delayed glacier melt water to total water availability in large river systems. We find that the seasonally delayed glacier contribution is largest where rivers enter seasonally arid regions and negligible in the lowlands of river basins governed by monsoon climates. By comparing monthly glacier melt contributions with population densities in different altitude bands within each river basin, we demonstrate that strong human dependence on glacier melt is not collocated with highest population densities in most basins.

Glaciers and seasonal snow cover are expected to change their water storage capacity under the ongoing warming of the global climate with major consequences for downriver water supply (1–4). Despite reliable observations and model results of projected changes in runoff from individual highly glacierized basins (5–13), a severe lack of appropriate data records and inadequately resolved model results (14–16) leave us with only vague ideas of the importance of glaciers and seasonal snow cover on regional scales.

Although reliable figures are often missing, considerable detrimental changes due to shrinking glaciers and snow cover are universally expected for water availability in river systems that originate from glacierized mountain regions. Approaches that compare glacier melt water production (obtained through measurements or modeling) with measurements of discharge volume somewhere downstream (e.g., ref. 17) are problematic because of the different nature of the two observed variables: Whereas glacier melt water can be considered as raw volume input into the runoff system, the discharge further downstream has been modified by, e.g., precipitation, evaporation, irrigation, damming, or exchange with subsurface flow regimes and groundwater. With increasing distance from the glaciers, modifications of runoff volume become more important, and the remaining fractional melt water contribution decreases. In a direct comparison between glacier melt water and runoff downriver, the volume contribution from glaciers is therefore overestimated by default with increasing distance from the glaciers. At the same time, the population that may depend on glacier melt as a resource typically increases downriver. A more detailed discussion of the shortcomings in the published literature is presented in ref. 18.

Here we quantify the importance of glacier melt for the availability of water in large river basins, on the basis of globally available datasets and fundamental considerations. We deliberately perform our analysis from a perspective of total water availability within the whole river basin, as opposed to estimating volume discharge rates of the main river within a basin.

Approaching the Problem

Glaciers produce melt water only during warm periods, i.e., periods with above-freezing temperatures over the lowest glacier tongues. Water storage in glaciers and seasonal snow cover increases only during wet periods, i.e., periods with precipitation over the accumulation region of the glaciers. If wet and warm periods in a region coincide, the production of melt water and the increase of water storage occur at the same time, reducing the effect of seasonally delayed water release from the glaciers. The relative impact of glacier melt during wet and warm periods is further decreased through the general increase in water availability from precipitation.* Therefore, melt water runoff matters most when it is both warm and dry and especially if a river flows into an arid area. Some regions of the world exhibit a combination of warm and dry conditions as part of their seasonal cycle, e.g., the western slopes of the tropical Andes, where seasonal temperature variability is small and extremely dry conditions persist from June to September (11). In other regions, these conditions may occur sporadically, e.g., in Europe during the 2003 heat wave (19). In Asia, many large river basins are dry and cold during winter and experience warm and wet conditions during summer (17, 20).

To achieve a first-order estimate of the importance of glacier melt water production to water availability, we compare the contribution potential of glaciers to the overall input of water into different large river basins by precipitation. We exclude the effects of seasonal snow cover from our analysis, and we assume the glaciers to be in equilibrium with climate. Potential effects of climate changes are discussed below.

Quantifying the Contributions

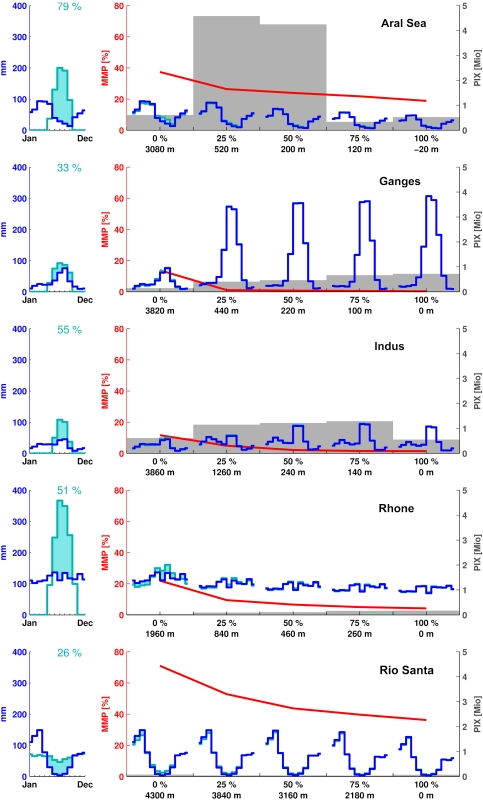
The left column of Fig. 1 shows the monthly mass budget of the glacierized area in each of five illustrative basins, derived from climatological data [21 referred to as CRU (Climatic Research Unit) data from here on]. Monthly accumulation (dark blue line) onto the glacier surface is calculated from CRU precipitation data. Monthly ablation (light blue line) is calculated by distributing the annual total accumulation over those months when the temperature at the area-weighted elevation of all the glaciers’ termini within the basin is above freezing.^† The amount of melt in each month is distributed proportional to the temperature. The elevation of the glaciers’ termini is obtained from the World Glacier Inventory (WGI)^‡; the temperature over the lowest glacier tongue is calculated from CRU data. A correction for any differences in altitude between the temperature dataset and the topographic dataset used in this study (GTOPO30^§) is applied by assuming a lapse rate of 0.0065 K m^-1. The shaded area between the two lines quantifies the seasonal modulation of runoff from the glaciers: When accumulation exceeds melt, the glacier increases its storage. When monthly melt exceeds accumulation, the glacier contributes seasonally delayed water to the river basin. The number in the upper center is the percentage of annual precipitation on the glacier that runs off as seasonally delayed melt water.

Fig. 1.

Left column: Monthly mass budget of the glacierized area, derived from CRU climatological data. Shown are monthly accumulation onto the glacier surface (dark blue), monthly ablation (light blue), and seasonally delayed runoff from glaciers (blue shading). Numbers at top center are the percentage of annual precipitation on the glacier that runs off as seasonally delayed melt water. Right column: Effect of seasonal delay on water input as a function of the altitude, starting at the altitude of the lowest glacier tongue and ending at the river’s estuary. Lower limits z_i of the altitude bands are given together with the percentage of total basin area (increasing from 0% at the altitude of the lowest glacier tongue to 100% at the river’s estuary). Shown are the climatological mean annual variation of precipitation above z_i (P_z, dark blue), seasonal modification of P_z by glacier storage and release (light blue), MMP (red), and PIX (gray bars).

In the right column of Fig. 1, the effect of seasonal delay on water input is shown as a function of the altitude in the respective basin, starting at the altitude of the lowest glacier tongue and ending at the river’s estuary. Lower limits z_i of the respective altitude bands are given together with the percentage of total basin area (increasing from 0% at the altitude of the lowermost glacier tongue, z₀, to 100% at the river’s estuary). The climatological mean annual variation of precipitation above z_i of the respective altitude band (P_i) is shown as a dark blue line centered on z_i. The light blue line shows the effect that glaciers have on total input of water into the basin: By storing precipitation during the cold months they decrease, and by releasing melt water during the warm months they increase, the total input of water into the basin. The red line shows the maximum of the monthly percentage of total water input into the basin that experiences seasonally delayed release by the glaciers (MMP).

To estimate the societal importance of seasonally delayed glacier melt, the MMP has to be set into relation with the potentially affected population. We therefore introduce a population impact index (PIX) as the product of the MMP and population in each altitude band. A small PIX thus indicates that either glaciers contribute little seasonally delayed melt water or few people are living in the respective altitude band. High values of the PIX will occur where both population and seasonally delayed glacier melt are high. The PIX is shown as a gray bar for each altitude band. Note that the absolute values of the PIX are not simple to interpret: If the entire water input into the basin was consumed by humans, the PIX indicates the number of people that would be left without water at least 1 mo during a year, if the glaciers were nonexistent and everybody else consumed the same amount as before. Because these conditions are rather unrealistic, the PIX is better to be understood as a way of comparing potential human dependence on seasonally delayed glacier melt between different basins and altitude bands. Another complication for the interpretation of the PIX arises if water is diverted from one river basin to another.^¶

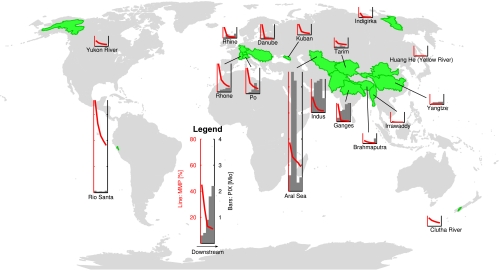
Fig. 2 shows the location, PIX, and MMP for all the basins considered in this study. Table 1 summarizes the climatological and geographical characteristics of the river basins shown in Figs. 1 and 2. The SI Appendix includes figures that show the detailed information from Fig. 1 for each of the river basins included in this study^∥ and a table that gives the numeric values of the annual percentage of precipitation affected by glacier storage, the MMP, and the month of occurrence of the MMP for each altitude band.

Fig. 2.

World map showing the location (shaded green), MMP (red lines), and PIX (gray bars) of each of the river basins considered in this study. The horizontal axis of the small plots is the same as in Fig. 1, Right column. The vertical scale of the small plots is held constant. Numeric values are provided in the SI Appendix.

Table 1.

Climatological and geographical characteristics of the river basins shown in Figs. 1 and 2, sorted by the PIX

Basin name	Basin area, km2	Glacier area, km2	Glacier area, %	Population, 106	PIX, 106
Aral Sea	1,234,075	11,319	0.92	41.01	10.29
Indus	1,139,814	20,325	1.78	211.28	4.82
Ganges	1,023,609	12,659	1.24	448.98	2.40
Po	73,297	818	1.12	16.55	0.81
Rhone	97,702	1,162	1.19	10.12	0.57
Rhine	190,713	459	0.24	59.07	0.52
Yangtze	1,746,593	1,895	0.11	383.04	0.37
Brahmaputra	527,666	16,118	3.05	62.43	0.31
Danube	794,133	617	0.08	81.38	0.31
Tarim	1,053,180	20,494	1.95	9.22	0.30
Rio Santa	11,901	503	4.23	0.57	0.27
Kuban	59,120	215	0.36	3.45	0.05
Huang He	988,702	172	0.02	162.70	0.02
Indigirka	341,577	338	0.10	0.04	0.00
Irrawaddy	410,376	25	0.01	35.26	0.00
Yukon River	830,257	9,070	1.09	0.13	0.00
Clutha River	17,182	147	0.86	0.03	0.00

Regional climate characteristics are reflected in the seasonally delayed runoff percentage of total precipitation onto the glacier surface, ranging from 79% in the Aral Sea basin to 17% for the Brahmaputra. The annual percentage (AP) of precipitation that experiences seasonally delayed release from the glaciers and the MMP depend on the extend of glaciers, temperature and precipitation seasonality, and the amount of precipitation received in the parts of the basin outside the glacierized area. The AP at z₀ nowhere exceeds 6.2% (Rhone), whereas the MMP at z₀ reaches 71% (Rio Santa in July; see SI Appendix). In the Himalaya-Hindu Kush region, the MMP at z₀ reaches a maximum of 14% for the Ganges in June. Downriver, the AP and MMP decrease rapidly, and only where glacier-fed rivers drain into arid lowlands does the AP exceed 1% and the MMP exceed 5%. Human dependence on seasonally delayed glacier melt is highest where a high MMP coincides with high population numbers.^** Because generally population numbers increase and the MMP decreases downriver, human dependence on glacier melt and, thus, the PIX often reach a maximum in an intermediate altitude band (e.g., Aral Sea, Indus, Tarim, Danube, and Po) of the river basin and not necessarily where the population numbers are highest.

Discussion

The results presented here assume the glaciers to be in equilibrium with a constant climate. During periods with strong glacier melt, e.g., in response to the ongoing warming of the global climate, the AP and possibly the MMP are expected to temporarily increase. Yet, with the glacier extent decreasing at the same time, this effect of the “deglaciation discharge dividend” (6) would soon get compensated (21). Furthermore, the generally low MMPs found in this study illustrate that, even with an assumed doubling of glacier melt water production over the equilibrium value during strong glacier volume loss, on the scale of a large river basin the impact would still be small and probably smaller than the interannual variability in precipitation. At the same time, the comparatively low estimates of human dependence on glacier melt obtained through our analysis do not contradict detrimental effects of potential changes in seasonally delayed glacier melt for numerous high-mountain communities.

A further limitation of our study is the omission of glacier mass loss by sublimation, which particularly in dry regions such as the tropical Andes or the inner Asian basins can reduce melt water production considerably (22–24). Consequently, our estimates provide an upper limit for the relative contribution of seasonally delayed glacier melt to the total water input into a basin. Storage of water in the seasonal snow cover is likely to be of more importance, but its runoff contribution cannot be estimated with the approach presented here. A modeling approach to partition different components of runoff contribution to large river basins that originate in the Himalayas yields numbers of glacier melt contributions that are similar to ours (18). It is, however, unclear to which degree the modeled estimates of the impact of future climate changes on food security are caused by changes in seasonal snow cover as opposed to changes in seasonally delayed glacier runoff.

The method presented here relies on glacier inventories, which are not complete everywhere (25). We therefore excluded North American river basins from our analysis, except for the Yukon, where data are available,^†† and we may slightly underestimate the effect of glaciers in central Asia.^‡‡ For more accurate and reliable estimates, a globally complete inventory of glaciers is therefore very important.

The first-order estimate presented here illustrates the importance of the differences in the climate regimes that govern the river basins. It shows that the glacier contribution to water availability is moderate in most midlatitude basins, minor in monsoon climates, and of major importance in very dry basins. The PIX allows for a regional subdivision for identification of those altitude bands in a given river basin in which the human dependence on glacier melt is strongest.

Materials and Methods

Monthly mean climatological values of precipitation P and temperature T are obtained from the CRU CL 2.0 dataset (26), which is based on the period 1961–1990, together with the altitude z_CRU of the data points. The horizontal resolution of this dataset is 10 arc min. The area-height distributions of the individual river basins are computed from the GTOPO30 digital elevation model with a resolution of approximately 1 km. River basin outlines are obtained as shape files from the Global Runoff Data Center.^§§

Information on glacier sizes, terminus elevations, and spatial distribution was derived from the WGI. Because the WGI is not complete in some regions, ref. 25 was used as glacier inventory for several Asian basins (Brahmaputra, Ganges, and Indus). Those three basins contain almost twice the glacier area that the WGI indicates, and another 6,000 km² (corresponding to approximately 5%) of glacier area in Central Asia are estimated to be missing even in ref. 25. For the Yukon basin, the total glacier area is taken from US Geological Survey, because no complete inventory for North America is available (25). Glacier terminus height information for the Yukon basin is obtained from WGI. The population within each elevation band is calculated from the CIESIN database.^¶¶

From the area-height distributions, the altitudes z_i limiting 0%, 25%, 50%, 75%, and 100% of the total basin area lower than the lowest glacier terminus (see below for a definition) are computed, starting from the altitude of the lowest glacier terminus (0%) and finishing at the river’s estuary (100%). In this way, a geographic mask of the upstream area A_i above the given altitude percentage i = 0,25,50,100 is created.

Individual glaciers are assigned to the river basins by using the “basin ID” field from WGI. Glacier areas are summed to calculate the total glacierized area A_G of each basin. In many basins there exist single glaciers that are highly uncharacteristic, in that they extend far below the mean altitude of the glacier termini in the respective basin. We therefore define the altitude of the lowest glacier terminus z₀ as the elevation of the lowest percentile of all the glacier termini in the basin. A reference height z_avg is defined as the average glacier terminus height, weighted by the area of each individual glacier, of all glaciers in the basin.

Melting on the glacier surface is assumed to take place when the monthly mean temperature T(z_avg) is above zero. T(z_avg) is computed from CRU, extrapolated to the height z obtained from WGI assuming a lapse rate of 0.0065 K m^-1, and averaged over the area A₀:

[1]

The extrapolation between z_CRU and z is needed because the CRU data, being delivered on a 10-arc min grid, do not have the spatial resolution necessary to capture the topography at the scale of the glaciers, whereas the heights from WGI are very accurate.

The monthly upstream precipitation P_z is taken from the CRU data, averaged over the upstream area A_i.

Monthly accumulation C_m (dark blue line in Fig. 1) onto the glacier surface is calculated as the mean monthly precipitation averaged over A₀.^∥∥ Because we assume the glaciers to be in equilibrium with climate, annual ablation (light blue line in Fig. 1) is set to equal annual accumulation:

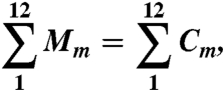[2]

where M_m denotes monthly ablation. Ablation is calculated to be proportional to the temperature T(z_avg) and is zero when T(z_avg) ≤ 0 °C. The monthly effect of the glacierized area on water availability in the basin ΔM_m is then the difference between C_m and M_m; if M_m > C_m during a given month (light blue shaded area in Fig. 1), the glaciers are reducing the amount of water they store, but if M_m < C_m, they are increasing the amount of water they store. Note that in this approach it is not necessary to distinguish between solid and liquid precipitation onto the glacier surface: If during a warm month the glacier receives part (or the whole) of C_m in liquid form, the instant runoff caused by this will be included in our estimate M_m.

The monthly water availability from precipitation and glacier runoff above the elevation z_i in a basin (light blue lines in Fig. 1, right) is then given by the mean precipitation in the basin above that elevation (dark blue lines in Fig. 1, right), plus the modification introduced by glacier ablation or accumulation in that basin, ΔM_m, scaled by the ratio of glacier area A_G to upstream area A_i. Finally, the MMP is calculated as the maximum of the monthly ratios of the scaled seasonally delayed glacier melt water contribution to the precipitation above each altitude band.