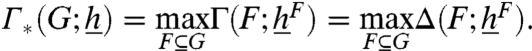The spread of innovations in social networks

Abstract

Which network structures favor the rapid spread of new ideas, behaviors, or technologies? This question has been studied extensively using epidemic models. Here we consider a complementary point of view and consider scenarios where the individuals’ behavior is the result of a strategic choice among competing alternatives. In particular, we study models that are based on the dynamics of coordination games. Classical results in game theory studying this model provide a simple condition for a new action or innovation to become widespread in the network. The present paper characterizes the rate of convergence as a function of the structure of the interaction network. The resulting predictions differ strongly from the ones provided by epidemic models. In particular, it appears that innovation spreads much more slowly on well-connected network structures dominated by long-range links than in low-dimensional ones dominated, for example, by geographic proximity.

A great variety of social or technological innovations spread in a population through the network of individual interactions. The dynamics of this process results in the formation of new norms and institutions and has been an important subject of study in sociology and economics (1, 2).

More recently, there has been a surge of interest in this subject because of the rapid growth and popularity of online social interaction. By providing new means for communication and interaction, the Internet has become a unique environment for the emergence and spread of innovations. At the same time, the Internet has changed the structure of the underlying network of interactions by allowing individuals to interact independently of their physical proximity.

Does the structure of online social networks favor the spread of all innovations? What is the impact of the structure of a social network on the spread of innovations? The present paper tries to address these questions.

Epidemic vs. Game-Theoretic Models

In the last few years, a considerable effort has been devoted to the study epidemic or independent cascade models on networks (3). The underlying assumption of these models is that people adopt a new behavior when they come in contact with others who have already adopted it. In other words, innovations spread much like epidemics.

The key predictions of such models are easy to grasp intuitively: (i) Innovations spread quickly in highly connected networks; (ii) long-range links are highly beneficial and facilitate such spreading; (iii) high-degree nodes (hubs) are the gateway for successful spreading.

The focus of this paper is on game-theoretic models that are based on the notion of utility maximization rather than exposure (2). The basic hypothesis here is that, when adopting a new behavior, each individual makes a rational choice to maximize his or her payoff in a coordination game. In these models, players adopt a new behavior when enough of their neighbors in the social network have adopted it; that is, innovations spread because there is an incentive to conform.

In this paper, we will show that the key predictions of game-theoretic models are antithetic to the ones of epidemic models: (i) Innovations spread quickly in locally connected networks; (ii) geographic (or more general finite-dimensional) structures favor such spreading; (iii) high-degree nodes slow down the diffusion process.

In summary, game-theoretic models lead to strikingly different conclusions from epidemic ones. This difference strongly suggests that assuming that diffusion of viruses, technologies, or new political or social beliefs have the same “viral” behavior may be misleading (4).

It also provides a rigorous evidence that the aggregate behavior of the diffusion is indeed very sensitive to the mechanism of interaction between individuals.^† This intuition can be quite important when it comes to making predictions about the success of new technologies or behaviors or developing algorithms for spreading or containing them.

Model and Description of the Results

We represent the social network by a graph in which each node represents an agent in the system. Each agent or player has to make a choice between two alternatives. The payoff of each of the two choices for the agent increases with the number of neighbors who are adopting the same choice.

The above model captures situations in which there is an incentive for individuals to make the same choices as their immediate friends or neighbors. This may happen when making a decision between two alternative operating systems (e.g., Windows versus Linux), choosing cell phone providers (AT&T versus Verizon), or even political parties (Republican versus Democratic).

We use a very simple dynamics for the evolution of play. Agents revise their strategies asynchronously. Each time they choose, with probability close to 1, the strategy with the best payoff, given the current behavior of their neighbors. Such noisy best-response dynamics have been studied extensively as a simple model for the emergence of technologies and social norms (2, 5–7). The main result in this line of work can be summarized as follows: The combination of random experimentation (noise) and the myopic attempts of players to increase their utility (best response) drives the system toward a particular equilibrium in which all players take the same action. The analysis also offers a simple condition (known as risk dominance) that determines whether an innovation introduced in the network will eventually become widespread.

The present paper characterizes the rate of convergence for such dynamics in terms of explicit graph-theoretic quantities. Suppose a superior (risk-dominant) technology is introduced as a new alternative. How long does it take until it becomes widespread in the network?

Our characterization is expressed in terms of quantities that we name tilted cutwidth and tilted cut of the graph. We refer the reader to the following sections for exact definition of these quantities. Roughly speaking, the two quantities are duals of each other: The former characterization is derived by calculating the most likely path to the equilibrium and implies an upper bound on the convergence time; the latter corresponds to a bottleneck in the space of configurations and provides a lower bound.

The proof uses an argument similar to (8–10) to relate hitting time to the spectrum of a suitable transition matrix. The convergence time is then estimated in terms of the most likely path from the worst-case initial configuration. A key contribution of this paper consists in proving that there exists a monotone increasing path with this property. This indicates that the risk-dominant strategy indeed spreads through the network, i.e., an increasing subset of players adopt it over time.

The above results allow us to estimate the convergence time for well-known models for the structure of social networks. This is done by relating the convergence time to the underlying dimension of the graph. For example, if the interaction graph can be embedded on a low-dimensional space, the dynamics converges in a very short time. On the other hand, random graphs or power-law networks are inherently high-dimensional objects, and the convergence may take a time as large as exponential in the number of nodes. As we mentioned earlier, epidemics have the opposite behavior. They spread much more rapidly on random or power-law networks.

Related Work

Kandori et al. (5) studied the noisy best-response dynamics and showed that it converges to an equilibrium in which every agent takes the same strategy. The strategy adopted by all the players was named by Harsanyi and Selten (7) as risk-dominant (see next section for a definition).

The role of graph structure and its interplay with convergence times was first emphasized by Ellison (11). In his pioneering work, Ellison considered two types of structures for the interaction network: a complete graph and a one-dimensional network obtained by placing individuals on a cycle and connecting all pairs of distance smaller than some given constant. Ellison proved that, on the first type of graph structure, convergence to the risk-dominant equilibrium is extremely slow (exponential in the number of players) and for practical purposes, not observable. On the contrary, convergence is relatively fast on linear network and the risk-dominant equilibrium is an important predictive concept in this case. Based on this observation, Ellison concludes that when the interaction is global, the outcome is determined by historic factors. In contrast, when players “interact with small sets of neighbors,” evolutionary forces may determine the outcome.

Even though this result has received a lot of attention in the economic theory [for example, see detailed expositions in books by Fudenberg and Levine (12) and by Young (2)], the conclusion of ref. 11 has remained rather imprecise. The contribution of the current paper is to precisely derive the graph quantity that captures the rate of convergence. Our results make a different prediction on models of social networks that are well-connected but sparse. We also show how to interpret Ellison’s result by defining a geometric embedding of graphs.

Most of our results are based on a reversible Markov chain model for the dynamics. Blume (13) already studied the same model, rederiving the results by Kandori et al. (5). In the last part of this paper, we will also consider generalizations to a broad family of nonreversible dynamics.

There is an extensive literature that motivates games and evolutionary dynamics as appropriate models for the formation of norms and social institutions. For example, see Young (6) for historic evidence about the evolution of the rules of the road as the dynamics of coordination games and to Skyrms (14) and Young (2) on the formation and evolution of social structures.

Finally, we refer to the next two sections for a comparison with related work within mathematical physics and Markov chain Monte Carlo (MCMC) theory.

Definitions

A game is played in periods t = 1,2,3,… among a set V of players, with |V| = n. The players interact on an undirected graph G = (V,E). Each player i∈V has two alternative strategies denoted by x_i∈{+1,-1}. The payoff matrix A is a 2 × 2-matrix illustrated in Fig. 1. Note that the game is symmetric. The payoff of player i is 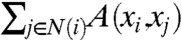, where N(i) is the set of neighbors of vertex i.

Fig. 1.

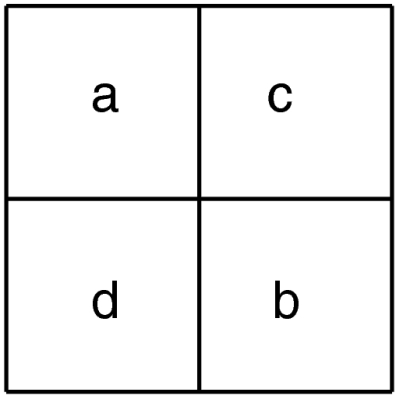
Payoff matrix of the coordination game.

We assume that the game defined by matrix A is a coordination game, i.e., the players obtain a higher payoff from adopting the same strategy as their opponents. More precisely, we have a > d and b > c. Let N₊(i) and N_-(i) be the set of neighbors of i adopting strategy +1 and -1, respectively. The best strategy for a node i is +1 if (a - d)N₊(i)≥(b - c)N_-(i) and it is -1 otherwise. For the convenience of notation, let us define 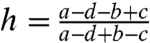and h_i = h|N(i)| where N(i) is the set of neighbors of i. In that case, every node i has a threshold value h_i such that the best strategy given the actions of others or the best-response strategy can be written as .

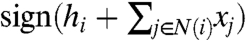We assume that a - b > d - c, so that h_i > 0 for all i∈V with nonzero degree. In other words, when the number of neighbors of node i taking action +1 is equal to the number of its neighbors taking action -1, the best response for i is +1. Harsanyi and Selten (7) named +1 the “risk-dominant” action because it seems to be the best strategy for a node that does not have any information about its neighbors. Notice that it is possible for h to be larger than 0 even though b > a. In other words, the risk-dominant equilibrium is in general distinct from the “payoff-dominant equilibrium,” the equilibrium in which all the players have the maximum possible payoff.

We study noisy best-response dynamics in this environment. In this dynamics, when the players revise their strategy they choose the best response action with probability close to 1. Still, there is a small chance that they choose the alternative strategy with inferior payoff.

More formally, a noisy best-response dynamics is specified by a one-parameter family of Markov chains P_β{⋯} indexed by β. The parameter β∈R₊ determines how noisy is the dynamics, with β = ∞ corresponding to the noise-free or best-response dynamics.

We assume that each node i updates its value at the arrival times of an independent Poisson clock of rate 1. The probability that node i takes action y_i is proportional to 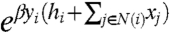. More precisely, the conditional distribution of the new strategy is

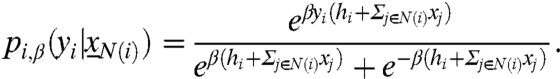[1]

Note that this is equivalent to the best-response dynamics 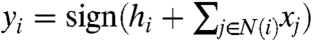for β = ∞. The above chain is called heat bath or Glauber dynamics for the Ising model. It is also known as logit update rule, which is the standard model in the discrete choice literature (16).

Let 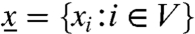. The corresponding Markov chain is reversible with the stationary distribution 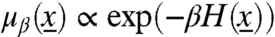where

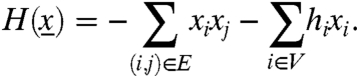[2]

For large β, the stationary distribution concentrates around the all-(+1) configuration. In other words, this dynamics predicts that the +1 equilibrium or the Harsanyi–Selten’s risk-dominant equilibrium is the likely outcome of the play in the long run.

The above was observed in by Kandori et al. (5) and Young (6) for a slightly different definition of noisy-best-response dynamics (see sections below and in SI Appendix). Their result has been studied and extended as a method for refining Nash equilibria in games. Also, it has been used as a simple model for studying formation of social norms and institutions and diffusion of technologies. See ref. 12 for the former and ref. 2 for an exposition of the latter.

Our aim is to determine whether the convergence to this equilibrium is fast. For example, suppose the behavior or technology corresponding to action -1 is the widespread action in the network. Now the technology or behavior +1 is offered as an alternative. Suppose a > b and c = d = 0 so the innovation corresponding to +1 is clearly superior. The above dynamics predict that the innovation corresponding to action +1 will eventually become widespread in the network. We are interested in characterizing the networks on which this innovation spreads in a reasonable time.

To this end, we let T₊ denote the hitting time or convergence time to the all-(+1) configuration and define the typical hitting time for 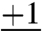as

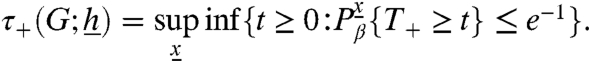[3]

For the sake of brevity, we will often refer to this as the hitting time and drop its arguments.

Notice that 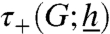conveys to a very strong notion of convergence: It is the typical time at which all the agents adopt the new strategy. In practice, the behavior of a vanishing fraction of agents is often unobservable. It is therefore important to consider weaker notions as well and ask what is the typical time 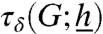such a fraction (1 - δ) of the agents (say, 90% of them) adopts the new strategy. Most of our results prove to be robust with respect to these modifications.

Relations with Markov Chain Monte Carlo Theory

The reversible Markov chain studied in this paper coincides with the Glauber dynamics for the Ising model and is arguably one of the most studied Markov chains of the same type. Among the few general results, Berger et al. (17) proved an upper bound on the mixing time for h = 0 in terms of the cutwidth of the graph. Their proof is based on a simple but elegant canonical path argument. Because of our very motivation, we must consider h > 0. It is important to stress that this seemingly innocuous modification leads to a dramatically different behavior. As an example, for a graph with a d-dimensional embedding (see below for definitions and analysis), the mixing time is exp{Θ(n^(d-1)/d)} for h = 0, while for any h > 0 is expected to be polynomial. This difference is not captured by the approach of ref. 17: Adapting the canonical path argument to the case h > 0 leads to an upper bound of order exp{Θ(n^(d-1)/d)}. We will see below that the correct behavior is instead captured by our approach.

There is another important difference with respect to the MCMC literature. As in ref. 5 and subsequent papers in the social science literature, we focus on the small-noise (β → ∞) limit. In particular, our estimates of the convergence time will take the form 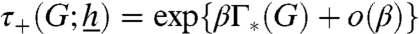. The constant Γ_∗(G) will then be estimated for large graphs. In particular, even if Γ_∗(G) is upper bounded by a constant, the o(β) term can hide n-dependent factors.

The same point of view (namely studying Glauber dynamics in the β → ∞ limit) has been explored within mathematical physics to understand “metastability.” This line of research has led to sharp estimates of the convergence time (more precisely, of the constant Γ_∗(G)) when the graph is a two- or three-dimensional grid (18–20).

Finally, Ising models with heterogeneous magnetic fields h_i have been intensively studied in statistical physics. However, in that context it is common to assume random h_is with symmetric distribution. This changes dramatically the model behavior with respect to our model, whereby h_i≥0 for all i.

Main Results: Specific Graph Families

The main result of this paper is the derivation of graph theoretical quantities that capture the low-noise behavior of the hitting time. In order to build intuition, we will start with some familiar and natural models of social networks:

Random graphs.

A random k-regular graph is a graph chosen uniformly at random from the set of graphs in which the degree of every vertex is k. A random graph with a fixed degree sequence is defined similarly. Random graphs with a given degree distribution (and in particular power-law) are standard models for the structure of social networks, World Wide Web, and the Internet.

Another popular class of models for the structure of social networks are preferential-attachment models. In this context, a graph is generated by adding the nodes sequentially. Every new node attaches to d existing vertices, and the probability of attaching to an existing vertex is proportional to its current degree. It has been shown that the degree distribution of graphs in this model converges to power-law.

d-dimensional networks.

We say that the graph G is embeddable in d dimensions or is a d-dimensional range-K graph if one can associate to each of its vertices i∈V a position ξ_i∈R^d such that, (i) (i,j)∈E implies d_Eucl(ξ_i,ξ_j) ≤ K (here d_Eucl(⋯) denotes Euclidean distance); (ii) any cube of volume v contains at most 2v vertices.

This is a simple model for networks in which social interaction is restricted by some underlying geometry such as physical proximity or closeness of interests.

Small-World Networks.

These network models are studied extensively, especially for understanding the small-world phenomenon. The vertices of this graph are those of a d-dimensional grid of side n^1/d. Two vertices i and j are connected by a “short-range” edge if they are nearest neighbors. Further, each vertex i is connected to k other vertices j(1),…,j(k) drawn independently with distribution P_i(j) = C(n)|i - j|^-r. We call these edges long-range links.

These networks can be seen as hybrid models with short and long-range links. Qualitatively, they are more similar to d-dimensional graphs when r is large. On the other hand, when r is close to zero the long-range edges form a random graph by themselves. The following theorem gives the rate of convergence to the equilibrium for the above network models:

Theorem 1.

As β → ∞, the convergence time is τ₊(G) = exp{2βΓ_∗(G) + o(β)} where

1. If G is a random k-regular graph with k≥3, a random graphs with a fixed degree sequence with minimum degree 3 or a preferential-attachment graph with minimum degree 2, then for h small enough, Γ_∗(G) = Ω(n).

2. If G is a d-dimensional graph with bounded range, then for all h > 0, Γ_∗(G) = O(1).

3. If G is a small-world network with r≥d, and h is such that , then with high probability Γ_∗(G) = Ω(log n/ log log n).

4. If G is a small-world network with r < d, and h is small enough, then with high probability Γ_∗(G) = Ω(n).

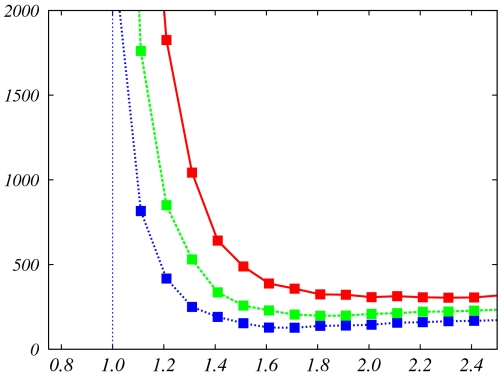
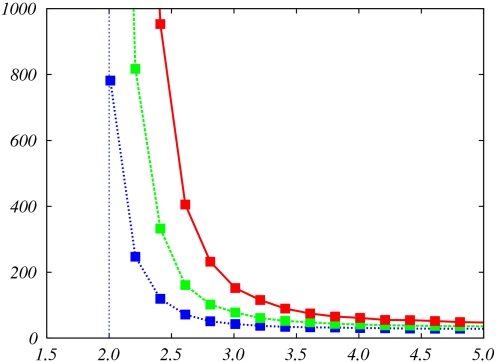
Figs. 2 and 3 illustrate points 3 and 4 by presenting numerical estimates of convergence times for small-world networks in d = 1 and d = 2 dimension. It is clear that τ₊ increases dramatically as r gets smaller and in particular when it crosses the threshold r = d. Also notice that the asymptotic (large β) characterization offers the right qualitative picture already at values as small as β ≈ 1.

Fig. 2.

Typical hitting time in a 1-dimensional small-world network as a function of the exponent r, determining the distribution of long-distance connections. Here n = 10³ and times are normalized by n. For each node we add k = 3 long distance connection. The payoff parameter is h = 0.5, and the three curves correspond, from bottom to top, to β = 1.3, 1.4, 1.5.

Fig. 3.

As in Fig. 2 but for a small-world network in d = 2 dimensions. Here n = 50², k = 3, h = 0.5 and, from bottom to top, β = 0.65, 0.70, 0.75.

Conclusions 1, 2, and 4 remain unchanged if the convergence time is replaced by τ_δ(G) [the typical time for a fraction (1 - δ) of the agents to switch to +1] provided δ is not too large. Conclusion 3 changes slightly: The exponent Γ_∗ is reduced from Ω(log n/ log log n) to Ω(1).

In order to better understand the above theorem, it is instructive to consider the isoperimetric function of the above networks. For a graph G = (V,E), and any integer ℓ∈{1,…,n} this quantity is defined as

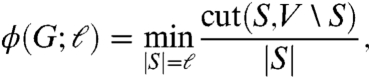[4]

where n = |V|. Random regular graphs of degree k≥3, random graphs with a fixed degree sequence with minimum degree 3, and random graphs in preferential-attachment model with minimum degree 2 are known to have isoperimetric numbers bounded away from 0 by a constant (21, 22) as long as ℓ ≤ n/2. In other words, it is known that there exists an α > 0 such that with high probability, for every set S with |S| ≤ n/2, cut(S,V∖S)≥α|S|. Such families of graphs are also called constant expanders or in short expanders.

Now consider a two-dimensional grid of side n^1/2 in which two vertices i and j are connected by an edge if they are nearest neighbors. In such a graph, a subset S defined by a subgrid of side k has k² vertices and only 4k edges in the cut between S and V∖S. In other words, .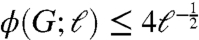

The basic intuition of the above theorem is that if the underlying interaction or social network is well-connected, i.e., it has high expansion, then the +1 action spreads very slowly in the network. On the other hand, if expansion is low because the interaction is restricted only to individuals that are geographically close, then convergence to +1 equilibrium is very fast. The next lemma makes this intuition more concrete (here G_U is the subgraph of G induced by the vertices in U⊆V):

Lemma 2.

Let G be a graph with maximum degree Δ. Assume that there exist constants α and γ < 1 such that for any subset of vertices U⊆V, and for any k∈{1,…,|U|}

[5]

Then there exists constant A = A(α,γ,h,Δ) such that Γ_∗(G) ≤ A.

Conversely, for a graph G with degree bounded by Δ, assume there exists a subset U⊆V(G), such that for i∈U, |N(i)∩(V∖U)| ≤ M, and the subgraph induced by U is a (δ,λ) expander, i.e., for every k ≤ δ|U|,

[6]

Then Γ_∗(G)≥(λ - hΔ - M)⌊δ|U|⌋.

In words, an upper bound on the isoperimetric function of the graph and its subgraphs leads to an upper bound on the hitting time. On the other hand, highly connected subgraphs that are loosely connected to the rest of the graph can slow down the convergence significantly.

Given the above intuition, one can easily derive the proof of Theorem 1, parts 1, 3, and 4, from the last lemma. As we said, random graphs described in the statement of the theorem have constant expansion with high probability (21, 22). This is also the case for small-world networks with r < d (23). Small-world networks with r≥d contain small, highly connected regions of size roughly O(log n). In fact, the proof of this part of the theorem is based on identifying an expander of this size in the graph.

For part 2 of Theorem 1 note that, roughly speaking, in networks with dimension d, the number of edges in the boundary of a ball that contains v vertices is of order O(v^1-1/d). Therefore the first part of Lemma 2 should give an intuition on why the convergence time is fast. The actual proof is significantly less straightforward because we must control the isoperimetric function of every subgraph of G (and there is no monotonicity with respect to the graph). The proof is presented in SI Appendix.

Results for General Graphs

In the previous section, we assumed that h_i = h|N(i)|. This choice simplifies the statements but is not technically needed. In this section, we will consider a generic graph G and generic values of h_i≥0.

Given 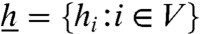and U⊆V, we let 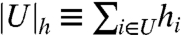. We define the tilted cutwidth of G as

[7]

Here the min is taken over all linear orderings of the vertices i(1),…,i(n), with S_t ≡ {i(1),…,i(t)}. Note that if for all i, h_i = 0, the above is equal to the cutwidth of the graph.

Given a collection of subsets of V, Ω⊆2^V such that ∅∈Ω, V∉Ω, we let ∂Ω be the collection of couples (S,S∪{i}) such that S∈Ω and S∪{i}∉Ω. We then define the tilted cut of G as

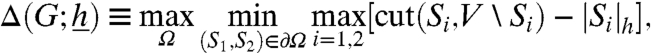[8]

the maximum being taken over monotone sets Ω (i.e., such that S∈Ω implies S^′∈Ω for all S^′⊆S).

Theorem 3.

Given an induced subgraph F⊆G, let be defined by , where |N(i)|_G∖F is the degree of i in G∖F. For reversible asynchronous dynamics we have , where

[9]

Note that tilted cutwidth and tilted cut are dual quantities. The former corresponds the maximum increase in the potential function 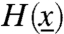along the lowest path to the +1 equilibrium. The latter is the lowest value of potential function along the highest separating set in the space of configurations. The above theorem shows that tilted cut and cutwidth coincide for the “slowest” subgraph of G provided that the h_is are nonnegative. This identity is highly nontrivial: For instance, the two expressions in Eq. 9 do not coincide for all subgraphs F. The hitting time is exponential in this graph parameter.

Monotonicity of the Optimal Path

The linear ordering in Eq. 7 corresponds to an evolution path leading to the risk-dominant (all +1) equilibrium from a worst-case starting point. Characterizing the optimal path provides insight on the typical process by which the network converges to the +1 equilibrium (20). For instance, if all optimal paths include a certain configuration , then the network will pass through the state on its way to the new equilibrium, with probability converging to 1 as β → ∞.

Remarkably in Eq. 7 it is sufficient to optimize over linear orderings instead of generic paths in {+1,-1}^V. This is suggestive of the fact that the convergence to the risk-dominant equilibrium is realized by a monotone process: The new +1 strategy effectively spreads as a new behavior is expected to spread. A similar phenomenon was indeed proved in the case of two- and three-dimensional grids (18, 24). Here we provide rigorous evidence that it is indeed generic.

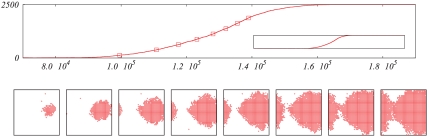
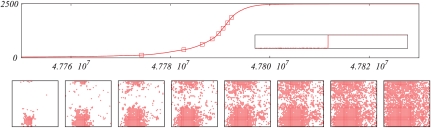
Figs. 4 and 5 illustrate the spread of the risk-dominant strategy in two-dimensional small-world networks. The evolution of the number of players adopting the new strategy is clearly monotone (although nonmonotonicities on small time scales are observable due to the modest value of β). Also, the qualitative behavior changes significantly with the density of long-range connections.

Fig. 4.

Diffusion of the risk-dominant strategy in a small-world network with d = 2, k = 3, n = 50² and mostly short-range connections, namely r = 5. We use β = 0.75 and h = 0.5. (Upper) Evolution of the number of nodes adopting the new strategy (in the inset, same curve with time axis starting at t = 0). (Lower) Configurations at times such that the number of nodes adopting the risk-dominant strategy is, from left to right, 125, 375, 625, 875, 1125, 1375, 1625, 1875 (indicated by squares in Upper).

Fig. 5.

As in Fig. 4 but for a small-world network with a larger number of long-range connections, namely r = 2.

Nonreversible and Synchronous Dynamics

So far, we have been focusing on asynchronous dynamics, and the noise was introduced in such a way that the resulting chain was reversible. Our next step is to demonstrate that our observations are applicable to a wide range of noisy best-response dynamics.

We consider a general class of Markovian dynamics over 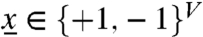. An element in this class is specified by 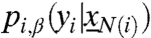, with 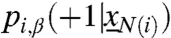a nondecreasing function of the number 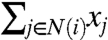. Further we assume that 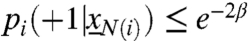when 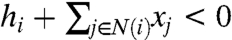. Note that the synchronous Markov chain studied in Kandori et al. (5) and Ellison (11) is a special case in this class.

Denote the hitting time of all (+1)-configuration in graph G with 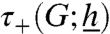as before.

Proposition 4.

Let G = (V,E) be a k-regular graph of size n such that for λ, δ > 0, every S⊂V, |S| ≤ δn has vertex expansion at least λ. Then for any noisy-best-response dynamics defined above, there exists a constant c = c(λ,δ,k) such that as long as .

Note that random regular graphs satisfy the condition of the above proposition as long as h_is are small enough. This proposition can be proved by considering the evolution of one-dimensional chain tracking the number of +1 vertices.

Proposition 5.

Let G be a d-dimensional grid of size n and constant d≥1. For any synchronous or asynchronous noisy-best-response dynamics defined above, there exists constant c such that .

The above proposition can be proved by a simple coupling argument very similar to that of Young (25).

Together, these two propositions show that for a large class of noisy-best-response dynamics including the one considered in (11), the isoperimetric constant of the network and more precisely its tilted cutwidth capture the rate of convergence.

Concluding Remarks

One of the weaknesses of the Nash equilibrium for predicting the outcome of a play is that even very simple games often have several equilibria. The coordination game studied in this paper is a very good example: Indeed, it is not hard to construct graphs with an exponential number of equilibria.

One of the standard ways for dealing with this problem is to use stability with respect to noise as a way to determine whether one equilibrium is more likely than another (7). In our opinion, the techniques developed for analyzing Markov chains in the last two decades are quite potent for advancing this area and achieving a deeper understanding of game dynamics and equilibrium selection.

The current paper focused on a particular game but presented a robust characterization of the rate and the likely path of convergence as a function of network structure. We see this as a first step in developing algorithms for making predictions of play for more generic games. Ideally, instead of singling out a particular equilibrium, such predictions would be a stochastic function of evolutionary dynamics, historic factors, and the length of the play.

As a final note, complete proofs of all the theorems and lemmas presented in this paper and a more extensive comparison with results in the economics literature are available in SI Appendix. A conference version of this paper was presented at FOCS 2009.