Abstract
High-frequency oscillations (HFOs) have been observed in animal and human intracranial recordings during both normal and aberrant brain states. It has been proposed that the relationship between subclasses of these oscillations can be used to identify epileptic brain. Studies of HFOs in epilepsy have been hampered by selection bias arising primarily out of the need to reduce the volume of data so that clinicians can manually review it. In this study, we introduce an algorithm for detecting and classifying these signals automatically and demonstrate the tractability of analyzing a data set of unprecedented size, over 31,000 channel-hours of intracranial electroencephalographic (iEEG) recordings from micro- and macroelectrodes in humans. Using an unsupervised approach that does not presuppose a specific number of clusters in the data, we show direct evidence for the existence of distinct classes of transient oscillations within the 100- to 500-Hz frequency range in a population of nine neocortical epilepsy patients and two controls. The number of classes we find, four (three plus one putative artifact class), is consistent with prior studies that identify “ripple” and “fast ripple” oscillations using human-intensive methods and, additionally, identifies a less examined class of mixed-frequency events.
INTRODUCTION
In the epilepsy research community, there is mounting interest in the idea that high-frequency oscillations (HFOs)—narrowband transients recorded on the intracranial electroencephalogram (iEEG), having predominant frequency between roughly 100 and 500 Hz and lasting on the order of tens of milliseconds—can be used to identify epileptogenic brain tissue. From a clinical perspective, the utility of HFOs as biomarkers lies in their potential to improve the outcomes of surgical resections in patients with medication-resistant epilepsy, either by augmenting or replacing signals currently used to delineate epileptogenic cortex. HFOs might also serve as input signals to controllers within implantable devices designed to deliver therapeutic intervention—for example, targeted electrical stimulation, drug delivery, or tissue cooling—in closed-loop fashion. Such devices, one of which is currently in clinical trials (Barkley et al. 2006), promise to help the large population of medically refractory epilepsy patients who are not candidates for resective surgery, either because their seizures appear to emanate from “eloquent” cortical areas with vital function or because epileptiform activity appears diffuse or multifocal within the brain.
To date, most studies of HFOs in epilepsy rely on highly human intensive methods to extract the signals of interest from multichannel iEEG. With the goals of increasing the tractability of labor-intensive marking and analysis tasks and improving the interpretability of results, investigators typically perform dramatic data reduction steps before committing the data to statistical analysis. Examples of common data-culling measures include preselecting: 1) subjects, electrodes, channels, and time epochs that, on visual preinspection, show prominent examples (e.g., high signal-to-noise ratio) of the activity to be analyzed; 2) electrodes or contacts that, according to magnetic resonance images, appear located in gray matter or specific brain structures; 3) data recorded during certain states of consciousness, typically slow-wave sleep; 4) data recorded during specific brain states such as interictal, preictal, or ictal periods; 5) data recorded from periods deemed artifact-free, typically by human reviewers; and 6) data—or a subsample thereof, such as a 10-min segment—that satisfy some combination of the above-cited criteria. A smaller number of studies use machine-based HFO detection in semiautomated procedures in which similar human screening occurs before the automatic detector is deployed, as well as after, in an attempt to reduce the number of spurious machine detections. Such quasi-automated methods are designed with the primary aim of reducing the workload for human reviewers.
In addition, based in large part on human observation, most studies of HFOs in epilepsy presuppose two discrete categories of these oscillations, distinguished by the subband between 100 and 500 Hz in which the majority of the transient signal's energy lies. The two types of high-frequency oscillations are termed “ripples” and “fast ripples,” and statistical analyses of HFO properties are typically preceded by the forced classification of all detected events as one of these two types.
Herein, we present a methodology for automatically detecting and classifying high-frequency oscillations in the human intracranial electroencephalogram. Differing from prior approaches to automated detection, we use no data preselection beyond our choice to study patients with epilepsy believed to be of neocortical origin and control patients, analyzing all recorded data from all available channels in all available patients. Furthermore, we do not presuppose the existence of two distinct subpopulations of HFOs. Instead, we treat this idea as a hypothesis, using it to inform the design of some of the features we use as inputs to our classifier. We develop an unsupervised, rather than supervised, scheme for event classification because 1) we believe ideas about what constitutes a physiologically or clinically meaningful HFO are still evolving and the former framework is more natural for exploratory analysis; and 2) prior studies in which “expert” human reviewers have been asked to mark HFO-like activity on the iEEG have shown poor interrater reliability and reproducibility (Gardner et al. 2007). In a similar vein, we find no good reason to constrain the categorization of events to two types. Thus the classification method we use requires no prespecification of the number of HFO classes present in the data and includes the possibility that the data do not cluster at all.
The primary purpose of this study was to present our method—both its rationale and the technical details to replicate it—along with results that support its utility as a tool for automatically processing and organizing large quantities of neurophysiologic data containing spontaneous, transient events, in a manner that minimizes not only selection bias but also human subjectivity and labor. Further, we show objective evidence for the existence of distinct classes of oscillations that have heretofore been taken largely for granted, strengthening the argument that “ripples” and “fast ripples” are meaningful physiologic labels (even if perhaps not the best terminology for avoiding confusion in the literature), and suggest that a third class of oscillations containing components of both frequencies should be investigated.
METHODS
Patient population and data acquisition
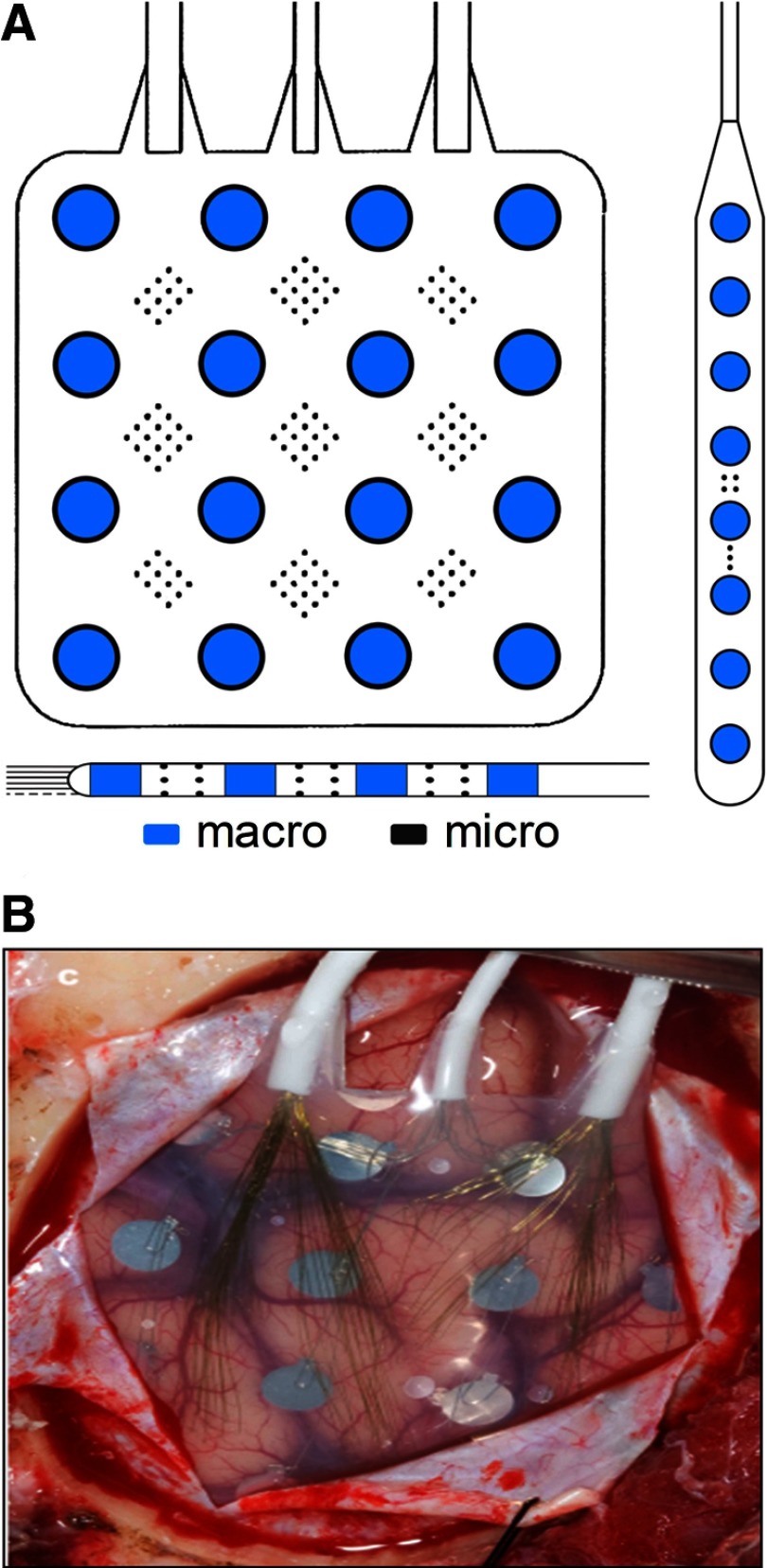
Nine patients with medically refractory partial epilepsy believed to be of neocortical origin underwent implantation of subdural electrodes (Ad Tech Medical Instruments, Racine, WI) to localize the seizure onset zone after noninvasive monitoring was indeterminate. The location, number, and type of intracranial electrodes (grid and/or strip and/or depth electrodes) were determined by a multidisciplinary team, including neurosurgeons, neurologists, neuroradiologists, and neuropsychologists, as part of routine clinical care. Standard clinical grid and strip electrodes were modified under an Institutional Review Board (IRB)–approved research protocol, by adding arrays of nonpenetrating platinum–iridium microwires (40-μm diameter, with intraarray spacing of 0.5–1 mm center-to-center) between the clinical, 4-mm diameter contacts (Van Gompel et al. 2008). Standard clinical depth leads were similarly modified, in two ways: 1) by embedding microwires around the circumference of the lead-body between the 2-mm long clinical contacts; and 2) by passing a bundle of microwires within the lumen of the lead, so that they protruded by about 7–8 mm from the distal tip (Worrell et al. 2008). Schematic depictions of the electrode modifications and an image of a typical implanted subdural grid are shown in Fig. 1, A and B, respectively.
Fig. 1.
A: example schematics for typical hybrid grid and strip (above) and depth (below) electrodes. Arrays of microwire contacts are located at regular intervals between the larger clinical contacts. Drawings are not to scale. B: image showing subdural placement of a hybrid grid electrode.
Two “control” patients, with chronic intractable facial pain but with no history of seizures, were similarly implanted, as part of an unrelated, IRB-approved research protocol investigating electrical stimulation of motor cortex as a potential treatment for their condition.
In addition to intracranial electrodes, a limited montage of standard gold scalp electrodes (EOM1, EOM2, Fp1, Fp2, Fpz, C3, and C4) was placed on all patients, as well as electrodes to record electromyographic signals from the chin and tibialis anterior surface. Two stainless steel surgical sutures (Ethicon, Somerville, NJ) were placed at the vertex region of the head at the time of surgery and used as reference and ground, respectively, for both intra- and extracranial electrodes.
Continuous, long-term data were acquired using the Digital Lynx Data Acquisition System (Neuralynx, Bozeman, MT) at 32,556 samples/s and 20 bits per sample (stored), from ≤144 channels in each patient (Brinkmann et al. 2009). The input dynamic range was ±132 mV and the noise level was ∼1.3 μV root-mean-square (RMS), yielding approximately 18 effective bits. Recordings were made using DC-capable amplifiers and a 9-kHz analog low-pass filter was used to minimize aliasing effects. The bandwidth of the raw recordings was thus approximately near–DC–9 kHz. Sleep staging was not part of the experimental protocol.
Overview of HFO detection and classification
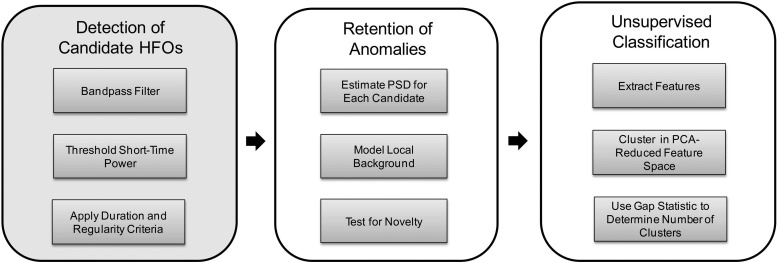
The automated HFO detection and classification algorithm is comprised of three major stages, depicted in Fig. 2. In the first stage, candidate HFO events are detected in the band-pass filtered iEEG using a method designed by Staba et al. (2002) to be sensitive, but which is highly nonspecific. This initial pass over the data set dramatically reduces its size. In the second stage, a statistical model of the local background iEEG surrounding each candidate event is built and events bearing too large a spectral similarity to the background activity according to the model are discarded from candidacy. In the final stage, computational features are extracted from the retained candidates (which we label simply “anomalies,” since they may or may not represent clinically meaningful events) and these features are used, after a dimensionality reduction step, as inputs to a classifier. Importantly, the classifier uses an automatic method of determining the number of clusters in the data and the possibility that the data do not cluster at all (i.e., there is a single cluster) is not excluded.
Fig. 2.
Block diagram showing the 3-stage detection and classification algorithm. The first stage was described in Staba et al. (2002). The second and third stages are the contributions of this work. PSD, power spectral density; PCA, principal components analysis.
In the following text, we describe the method in detail. All analyses were carried out using custom Matlab (The Mathworks, Natick, MA) scripts run on a computer with dual quad-core Intel Xeon E5430 CPUs at 2.66 GHz and 16 GB of RAM.
Stage 1: detection of candidate HFOs
HFOs are initially detected using methods closely adapted from those by Csicsvari et al. (1999a,b) and Staba et al. (2002). Raw, referential iEEG data are processed on a per-channel basis in 10-min nonoverlapping segments. Data are first decimated by a factor of 12 (8th-order low-pass Chebyshev type I filter, cutoff frequency of 1,085 Hz, forward and reverse filtered to eliminate phase distortion), to 2,713 Hz, before band-pass filtering between 100 and 500 Hz (20th order Cauer filter, forward and reverse filtered; specifications: 65 dB minimum lower/upper stop band attenuation, 0.5 dB maximum pass band ripple, 25 Hz lower/upper transition width). Filters were designed and tested for stability using Matlab's filter design toolbox.
Using a 3-ms sliding window, a running RMS signal is computed from the band-pass data. The RMS signal is then compared against a threshold (the mean of the RMS signal plus 5SDs) and successive samples exceeding this threshold for a minimum duration of 6 ms are delimited by their upward and downward threshold crossing times. Marked events are then subject to the additional criterion that they must have at least six peaks >3SDs from the mean of the rectified band-pass signal. Finally, retained events separated by <10 ms are merged to generate a candidate set of HFOs.
Stage 2: retention of anomalies
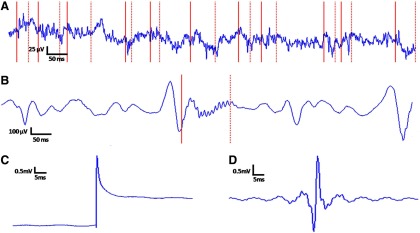
Staba et al. (2002) reported high sensitivity for their detector when compared with a ground truth set of human markings, but the method suffers high false-positive rates (Gardner et al. 2007), especially when no preselection of data is performed. In pilot studies, we observed that a common putative failure mode for the detector was retaining transients with amplitudes larger than the average global background signal (on which the algorithmic threshold is based) but similar in morphology to the local1 background iEEG. An example of these typical putative false positives is shown in Fig. 3A.
Fig. 3.
Macroelectrode (right frontal lobe) recording examples showing the lack of specificity of the stage 1 detector: partial motivation for the design of stages 2 and 3. A: a run of putative false positive stage 1 detections, none of which appears visually well distinguished from the surrounding intracranial electroencephalographic (iEEG) recording. Individual detections are delimited by solid (start) and dotted (stop) red lines. These detections should be contrasted with the single detection in B, a putatively valid high-frequency oscillation (HFO). C: typical sharp transient artifact detected by stage 1; unfiltered waveform. D: band-pass filtered version of C; this filter artifact is what the stage 1 detector actually “sees,” giving insight into why the event is flagged as an oscillation. The algorithm we present is designed to discard in stage 2 events like those in A and aggregate into a single cluster in stage 3 events like the one represented by C and D. More interesting events like those in B should group naturally into one or more clusters in stage 3.
The design of the second stage of the algorithm therefore assumed that a key aspect of an HFO's saliency for a human reading iEEG is not only its relative amplitude but also its spectral distinctiveness—the degree to which its morphology, as opposed to simply its size, “pops out” from the background.2 All stage 1 detections that fail to meet a spectral novelty criterion, as described in the following text, are eliminated.
Candidate HFOs passing through stage 1 are processed individually in stage 2,3 which operates on the decimated data. Twelve hundred milliseconds (after a 5-ms guard time) on either flank of a given candidate are used to build a model of the local background iEEG. Background data are segmented into clips of length equal to the candidate detection.4
For each background segment, as well as the candidate detection, the best linear fit is found using least-squares regression and removed by subtraction (i.e., the signal is detrended). Each segment is then energy-normalized by dividing by its Euclidean length and a power spectral density estimate is computed using a multitaper technique from Thomson (1982) (three tapers; 512-point Discrete Fourier Transform (DFT) (zero-padded); adaptive nonlinear combination method). The method in general involves multiplying the signal by n orthogonal data tapers having optimal spectral concentration properties—discrete prolate spheroidal sequences (Slepian and Pollak 1961)—before computing the squared magnitude of the DFT in each case. This produces n independent spectral estimates, which are then additively combined using weighting factors that are adaptively chosen depending on local characteristics of the spectrum.5
The nonstationary local background iEEG is modeled using a mixture of Gaussians, under the assumption that each background segment is an observation emitted from one of a small number (one to three) of multivariate Gaussian components. Thus the probability of observing any local background segment p(x), is represented by the density function6
| (1) |
where x is the D × 1 vector representing the background segment, K is the number of mixture components, πk is the weight of the kth mixture component, ∑k=1K πk = 1, πk ≥ 0 ∀ k ∈ {1, 2, … , K}), D is the dimensionality of the data, Σk is the D × D covariance matrix for the kth mixture component, uk is the D × 1 mean vector for the kth mixture component, and T is the transpose operator.
The objective is to maximize the (log) probability of the collection of background segments surrounding each candidate HFO, assuming the background segments are independent and identically distributed. This quantity viewed as a function of the model parameters—the component weights, mean vectors, and covariance matrices (unconstrained, in our case)—is known as the (log) likelihood function
| (2) |
where X is the N × D data matrix, N is the number of background segments, u is the D × K matrix of horizontally concatenated mean vectors, Σ is the D × (D·K) matrix of horizontally concatenated covariance matrices, π is the 1 × K vector of component weights, and 
 is the multivariate normal distribution (shown uncollapsed in Eq. 1, the expression to the right of πk).
is the multivariate normal distribution (shown uncollapsed in Eq. 1, the expression to the right of πk).
Maximization is performed using the Expectation-Maximization (EM) algorithm (Dempster et al. 1977), a two-stage iterative numerical procedure. We set initial component weights equal to each other (i.e., πk = 1/K) and initialized mean vectors and covariance matrices using the K-means algorithm (MacQueen 1967). The EM update steps, which guarantee an increase in the log-likelihood with each iteration, are then performed as described in appendix B.
Given the small number of background segments relative to the dimension of the data, to combat the curse of dimensionality (Bellman 1961) the number of dimensions of each background segment (and the candidate segment) is reduced to two (i.e., D = 2), prior to learning the Gaussian Mixture Model (GMM). This is done using principal components analysis (PCA) (Hotelling 1933; Pearson 1901) on the frequency-domain representations of the background segments discussed earlier, after removing the mean and dividing by the SD of the background segments.
Since there is no a priori reason to prefer a specific number of mixture components in the GMM, the parameters for 1, 2, and 3 component mixtures are learned and the Bayesian Information Criterion (BIC) (Schwarz 1978) is used to make the final model selection. A metric based on the Mahalanobis distances (McLachlan 1999) from the HFO candidate to each component of the mixture model is then used to decide whether to reject the candidate or to pass it on to stage 3 (see Supplemental Material for more detail).7
Stage 3: unsupervised classification
FEATURE EXTRACTION.
Before clustering, seven features are computed on the data corresponding to each event output from stage 2. All features were designed or chosen with one of two goals in mind: 1) to permit separation of “ripples” and “fast ripples,” should there indeed be evidence for such compartmentalization (and not otherwise); 2) to aggregate highly stereotypical, sharp transient recording artifacts that were observed in pilot studies (e.g., Fig. 3, C and D). Features in category 1 were conceived a priori (blinded to all patient data), whereas features in category 2 were developed and refined using labeled artifacts from two patients (CT01 and SZ05). The features used are described in detail in appendix A. The set of feature vectors {F1, … , ^FI}, where I is the total number of anomalies passing through stage 2 (across all patients and intracranial electrodes; in our case, I = 290,273), is the data set that is clustered.
K-MEDIODS CLUSTERING.
Clustering was accomplished using a variant of the k-means algorithm (MacQueen 1967). The k-means algorithm seeks to minimize the quantity
| (3) |
where K is the number of clusters, Ck denotes the set of indices of the observations in cluster k (with each observation assigned to a single cluster), and Nk denotes the number of observations in cluster k. dii′ is the squared Euclidean distance between P-dimensional observations xi and xi′
| (4) |
The quantity WK can be viewed as a modified version of the within-cluster point scatter (Hastie et al. 2001) in which each cluster's contribution is now weighted inversely by its membership. Thus diffuse clusters with few members are not counted as energetically favorably as compact clusters with many. Minimizing this metric is exactly equivalent to minimizing the pooled within-cluster sum of squared distances from the cluster means (centroids), so that WK can alternatively be written as8
| (5) |
where x̄k is the mean of the elements in cluster k. An iterative descent algorithm for minimizing the above-cited criterion can be obtained by first defining clusters via prototypes {uk}k=1K and attempting to minimize, over parameters u and Y, the error function
| (6) |
where u is the P × K matrix of prototypes and Y is a K × I indicator matrix of cluster assignments, with I the total number of data observations. That is, Yki = 1 whenever xi is assigned to cluster k, and 0 otherwise. The algorithm proceeds as shown in appendix B.
Instead of using the L2 norm (Euclidean distance), the classification scheme uses the L1 norm (Manhattan distance) as distance metric, which yields the k-mediods algorithm. In step 2 of the algorithm (Eq. B6 in appendix B), a given point is assigned to the prototype that is closest in the L1 sense, and in step three (Eq. B7 in appendix B) the appropriate minimization is obtained by computing the mediod, rather than the centroid, for each newly formed cluster. The k-mediods method is used to achieve a clustering that is more robust against outliers than k-means, albeit at computational expense (Hastie et al. 2001).
The gap statistic
In the preceding text, W has been subscripted with “K,” the number of clusters, to emphasize that the k-means and k-mediods algorithms require that the number of clusters in the data be prespecified. This is an obvious limitation in situations like the present study, in which the number of clusters (i.e., “types” of anomalous events passing through stage 2) is a priori unknown and is itself a major goal of the exploratory analysis.
Wk is a monotonically decreasing function of k; this can be intuited by considering the progression to the extreme case, in which each observation constitutes its own cluster and thus Wk is equal to zero. Plots of Wk versus k often show a characteristic “elbow point,” a value for k at which previously large decreases in the function become markedly flattened. Traditionally, this point has been taken to represent the transition between decreases that represent an evolution toward the data's true underlying structure and decreases that are simply attributable to the inevitably greater compactness of clusters that can be achieved by adding more cluster centroids. This elbow value of k is thus typically taken as the “optimal” number of clusters.
Tibshirani et al. (2001) addressed the issue of estimating the optimal number of clusters in a data set given a similarity metric and error measure, presenting a statistical procedure to formalize the above-cited elbow heuristic concept. Their idea was to compare the graph of log (Wk) versus k with its expectation, EI*[log (Wk)] , under a suitable null reference distribution of the data. They defined the “gap statistic” for sample size I, GI(k), as
| (7) |
and proposed to choose the optimal k as that for which the gap statistic is largest after taking its sampling distribution into account. The null model assumed is a single-component model and the statistical procedure is designed to reject it in favor of a k-component model (k > 1), if the strongest evidence for any such k under consideration merits it. The choice of the number of k values over which to probe is of course still up to the experimenter. As recommended by Tibshirani et al. (2001), a uniform distribution over a box aligned with the principal components of the data is used as the form of the single-component reference distribution.
The clustering procedure begins with the data set {^F1, … , ^FI}: the PCA-reduced feature-vector representations of anomalies 1 through I that have passed through stage 2 (see appendix A). For number-of-cluster values k = 1 through 20, the k-mediods algorithm is run using 10 random initializations and the run that yields the lowest log (Wk) is chosen. Then, again for each k, an expected value for log (Wk) under the null reference is computed, using 20 reference data sets for each value of k. A given reference set is created by performing a PCA rotation of the data, sampling I vectors uniformly over the range of values along each dimension, and then back-rotating the samples into the original coordinate frame. Each reference set is then clustered in an identical manner to the true data set and the expected value for each log (Wk) is taken as the average over the reference sets. In accordance with Tibshirani et al. (2001) a corrected SD sk, which accounts for the simulation error is then computed as
| (8) |
where sdk is the SD and B is the number of reference sets, in our case 20. Finally, again following Tibshirani et al. (2001), the optimal clustering of the data is taken as that which meets the following criterion
| (9) |
where k̂ is the estimated optimal number of clusters. (If the preceding set were empty, k̂ would be set equal to the largest value tested, which in our case is 20.)
RESULTS
The number of channels and total number of iEEG hours processed per subject are shown in Table 1, along with the number of events detected in stage 1 and retained after stage 2. Per-channel computation time, estimated using the data from subject SZ01, was about 1.94 s/min (1.2 s/min for stage 1, 0.7 s/min for stage 2, and 0.04 s/min for stage 3).
Table 1.
Raw data summary
| Subject | Number of Channels | Total iEEG Hours | Number of Stage 1 Events | Number of Stage 2 Events |
|---|---|---|---|---|
| CT01 | 144 | 1,176 | 44,819 | 14,768 |
| CT02 | 128 | 1,877 | 49,576 | 12,595 |
| SZ01 | 45 | 480 | 11,436 | 3,255 |
| SZ02 | 126 | 1,890 | 86,958 | 17,647 |
| SZ03 | 69 | 977 | 79,138 | 18,220 |
| SZ04 | 90 | 2,122 | 64,617 | 29,215 |
| SZ05 | 84 | 5,460 | 472,351 | 77,684 |
| SZ06 | 115 | 10,139 | 132,336 | 36,254 |
| SZ07 | 86 | 5,615 | 429,010 | 62,615 |
| SZ08 | 104 | 812 | 34,312 | 14,167 |
| SZ09 | 110 | 735 | 19,188 | 3,853 |
| All | 1,101 | 31,283 | 1,423,741 | 290,273 |
Total iEEG hours is the sum over all channels of the length of time recorded for each channel.
Across all 11 subjects, a total of 1,423,741 HFO candidates were detected in stage 1. The summed duration of all stage 1 detections was 13.7 h, or 0.04% of the total data processed, giving an indication of the rarity of stage 1 detections. Among these stage 1 candidates, 290,273 (∼20%) were flagged as anomalous events in stage 2 and passed on to stage 3 for clustering. To verify that the stage 2 anomaly detection algorithm was not performing the trivial task of taking a random subsample of post stage 1 events, we tested the null hypothesis that the proportion of events retained after stage 2 was the same for all patients, finding, as we expected, evidence to reject it [χ2(10, N = 1,423,741) = 57,088.23, P <<< 0.0001]. To examine whether electrode size influenced the per-channel event detection rate, we tested the null hypothesis that the cumulative distribution functions for event detection rate were identical for macro- and microelectrodes. There was a trend toward higher detection rates for macroelectrodes, but a two-sided test was not significant at the 0.05 level (Mann–Whitney U test, z = 1.84, nmacro = 479, nmicro = 622, P = 0.07). To examine whether electrode size influenced the proportion of retained events after stage 2, we tested the null hypothesis that the cumulative distribution functions for event retention fraction were identical for macro- and microelectrodes. Macroelectrodes tended to have lower event retention rates and a two-sided test was highly significant (Mann–Whitney U test, z = −6.05, nmacro = 479, nmicro = 622, P ≪ 0.001). (The latter two tests assume homogeneity across patients.)
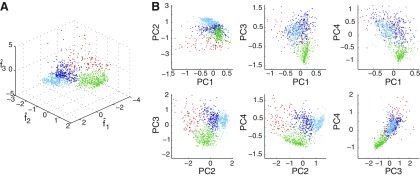
Four clusters were found in stage 3 by the k-mediods/gap-statistic method. The results of clustering are illustrated in Figs. 4 and 5. Figure 4A shows a clustering of 1,000 events selected randomly across all patients, plotted in the space defined by f̂1, f̂2, and f̂3 and colored according to class label. Figure 4B gives an alternative view of the clustering, projecting the points onto the planes defined by all possible pairs of principal components. Boundaries are apparent between the red, the green, and the two blue clusters taken together, while the separation between the light and dark blue clusters is less marked in these limited two- and three-dimensional representations of the four-dimensional clustering.
Fig. 4.
A: clustering of 1,000 randomly selected events (across all patients) passing through stage 2, in the 3-dimensional space defined by f̂1, f̂2, and f̂3. Each of the 4 clusters found by the algorithm is colored uniquely. B: the points on the left projected onto all possible pairs of principal components; axes are scaled to enable better visualization of cluster boundaries, so a small number of outlying points are not visible.
Fig. 5.
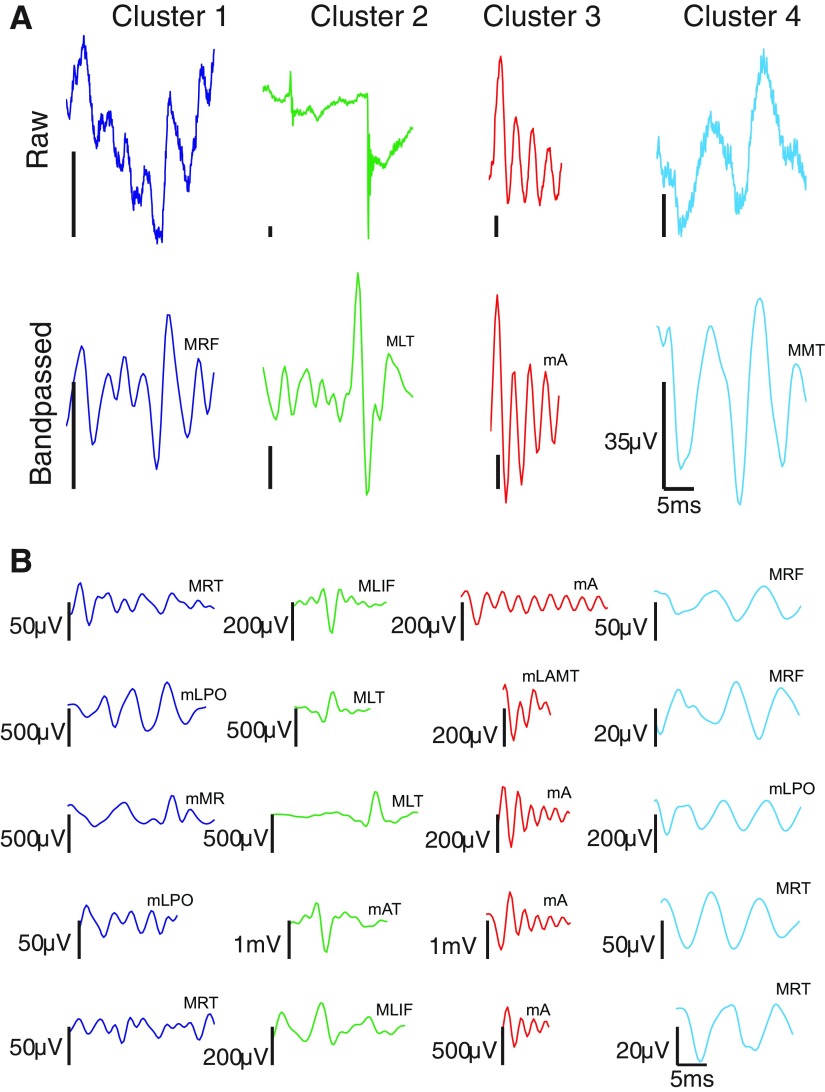
Characteristic waveforms derived from clustering all 290,273 events, across all patients, that passed through stage 2. A: cluster prototypes found by taking the cluster member nearest in the Mahalanobis sense to the cluster mediod in feature space. Top images are unfiltered waveforms; bottom images are the corresponding 100–500 Hz band-pass filtered waveforms [to facilitate comparison, events are plotted on identical time axes (0 to 25 ms; axes suppressed in individual plots), with events truncated to 25 ms if longer than this duration]. Vertical scale bar is 35 μV; horizontal scale bar is 5 ms. B: 5 randomly selected events from each cluster (band-passed waveforms only). In the abbreviations above each trace, the first letter indicates whether the recording comes from a macro- (M) or microelectrode (m). RF, right frontal; LT, left temporal; A, anterior; MT, middle temporal; RT, right temporal; LPO, left parietooccipital; MR, motor; LIF, left inferior frontal; AT, anterior temporal; LAMT, left anterior mesial temporal. Note that identical labels do not imply identical electrodes, only that the electrodes have the same lobar location.
Figure 5 shows the cluster prototypes for each of the four clusters found by applying our algorithm to all 290,273 events passing through stage 2. The prototypes are found by computing the class members nearest (in the Mahalanobis sense) to the cluster mediods in feature space. In Fig. 5A, both the raw (top) and the 100–500 Hz band-pass filtered (bottom) detection for each prototype are displayed. In Fig. 5B, we show five randomly selected members (band-passed version only) from each cluster. Supplemental Figs. S3–S6 show the latter events within the context of surrounding iEEG.
Qualitatively speaking, cluster 1 (n = 70,671; nmacro = 47,893, nmicro = 22,778) is comprised of irregular, mixed-frequency events; cluster 2 (n = 92,744; nmacro = 34,665, nmicro = 58,079) is comprised of sharp-rising transients that appear to be artifacts (i.e., whose oscillatory characteristics come from filtering the sharp rise); cluster 3 (n = 38,945; nmacro = 10,529, nmicro = 28,416) is comprised of fast, regular waveforms of relatively pure frequency; and cluster 4 (n = 87,913; nmacro = 48,190, nmicro = 39,723) is comprised of slow, regular waveforms of relatively pure frequency. We rejected the null hypothesis that the proportions of events detected by macro- and microelectrodes were the same across clusters [χ2(3, N = 290,273) = 23,678.65, P <<< 0.0001]. Supplemental Table S5 gives median event rates and amplitudes (excluding putative artifacts), broken down by subject and electrode type; Supplemental Table S6 gives event amplitudes broken down by cluster.
To investigate the stability of the clustering algorithm and test whether the aggregated clustering results we show in Figs. 4 and 5 were heavily influenced by individual subjects, we performed two additional experiments.
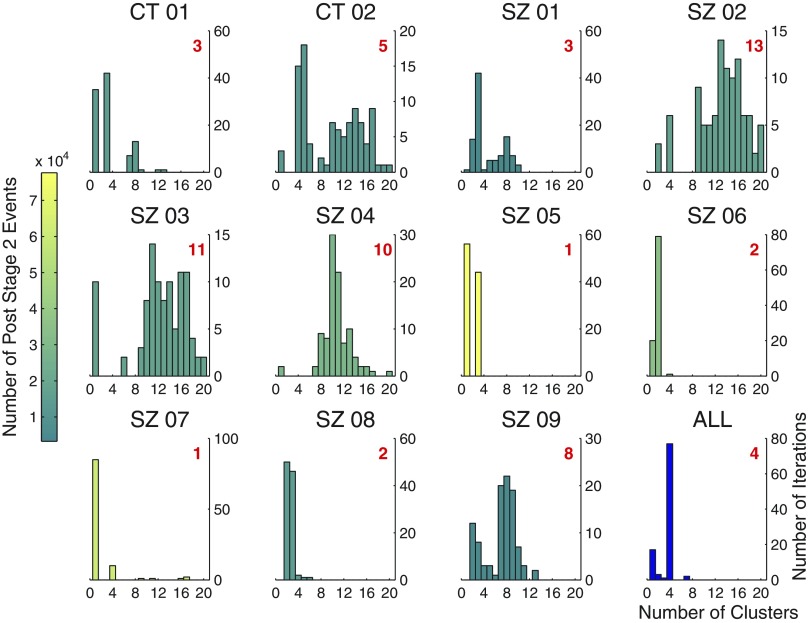
In the first, we applied the clustering algorithm to individual subjects, clustering 100 random samples drawn from the set of all events passing through stage 2 for each subject. The size of each of the 100 random samples was 25% of all the subject's post stage 2 events. Results are shown in Fig. 6, which contains one panel for each patient: a histogram summarizing the outcome of the 100-iteration sampling experiment. Figure 6, bottom right represents the results of a similar random sampling experiment performed on the data aggregated across subjects, with the only difference being that sample sizes of 5% (15,000 of all 290,273 events passing through stage 2 across all subjects) were used, due to the computational expense of clustering 25% 100 times. Each individual subject's histogram is colored in proportion to the relative number of events passing through stage 2 for that subject. Thus histogram color reflects the weight of the subject's contribution to each of the 100 random samples represented in the aggregate histogram in the bottom right panel. The number in red indicates the mode of the distribution, which can be interpreted as the number of clusters the algorithm yields for that patient. The degree of concentration of the distribution for a given individual reflects the stability of the algorithm for that subject, which is a function of the variability and shape of the subject's events in feature space, as well as the sample size clustered.
Fig. 6.
Individual subject clustering. Each panel (except the bottom rightmost panel) gives the results, for a single subject, of an experiment in which 100 random samples of size equal to 25% of all events passing through stage 2 for the subject were clustered. Number of clusters found by the algorithm is plotted on the x-axis. Number of iterations is plotted on the y-axis. Shown in red is the mode of each distribution, which can be interpreted as the number of clusters found by the algorithm for that subject. Histograms are colored in proportion to the relative number of events passing through stage 2 for each patient. The bottom rightmost panel gives the results of a similar sampling experiment performed on the aggregated data, the only difference being that random samples of size 5% of the total were used, instead of 25%, to ease the computational burden.
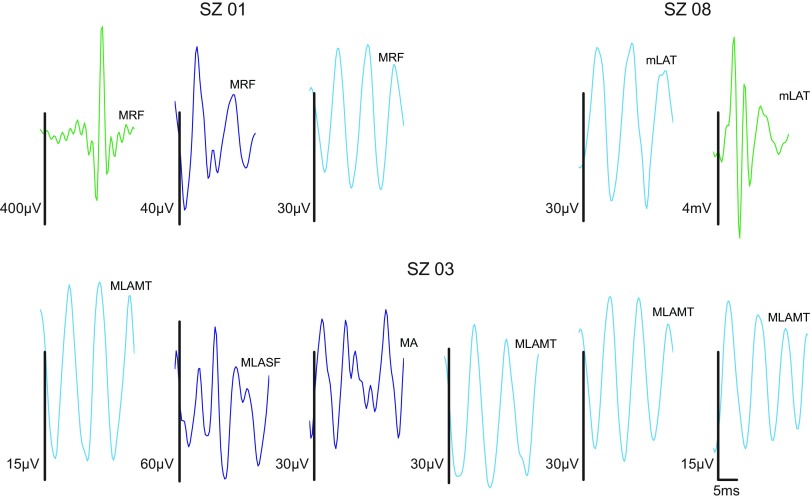
In the 6 of 11 subjects for whom the algorithm yielded 4 or fewer clusters, the clusters generally appeared to be subsets of those found in the aggregated data. In the remaining 5 subjects, for whom there were greater than 4 clusters, the additional clusters generally appeared to have resulted from oversplitting some combination of the 4 clusters found in the aggregated data. These trends are illustrated in Fig. 7, which shows examples of prototypes derived from clustering individual subject data. Prototypes in Fig. 7 are given a color corresponding to the aggregate prototype to which they bear the closest visual resemblance (cf. Fig. 5A, bottom set of waveforms). Subject SZ01, for whom the algorithm yields strong evidence for three clusters, appears to exhibit the artifact, mixed, and slower oscillation clusters, but not the faster oscillations of the aggregated clustering. Subject SZ08, for whom the algorithm weakly suggests two (over three) clusters, prominently exhibits the artifact and slower oscillation clusters. Subject SZ03, for whom the algorithm performs relatively poorly, also appears to have clusters that are a subset of those found in the aggregate—i.e., the mixed frequency and slower oscillation clusters—but they are often highly split by the algorithm. Figure 7 shows one particular iteration in which six clusters were obtained from what appears to be these two.
Fig. 7.
Example prototypes from individual patient clustering; 100–500 Hz band-passed waveforms only. Vertical scale bars are 35 μV; horizontal scale bar is 5 ms [to facilitate comparison, events are plotted on identical time axes (0 to 25 ms; axes suppressed in individual plots), with events truncated to 25 ms if longer than this duration]. Subjects SZ01 and SZ08 show clusters that appear to be subsets of the 4 clusters found in the aggregate. Subject SZ03 does as well, but in this case it appears that 2 groups have been oversplit by the algorithm, yielding 6 clusters. The latter type of cluster stability issue was not seen in the aggregate clustering. In the abbreviations above each trace, the first letter indicates whether the recording comes from a macro- (M) or microelectrode (m). RF, right frontal; LAMT, left anterior mesial temporal; A, anterior; LASF, left anterior subfrontal; LAT, left anterior temporal. Note that identical labels do not imply identical electrodes, only that the electrodes have the same lobar location.
To quantify these observations about the stability of the algorithm, we used Rand's C-statistic (Rand's index; Rand 1971), a common measure of agreement between two partitionings of a data set. Rand's index is simply the fraction of all pairs of observations that are treated similarly in both partitionings, where a “similarly treated” pair is one whose members either are in the same cluster or in different clusters in both partitionings (see appendix B). Being a proportion, Rand's index varies between zero, when no pairs are treated similarly by the two clusterings, and one, when the clusterings are identical.
We were interested in how similar one partitioning was to another, within a subject, for iterations on which the algorithm returned more than a single cluster. Because each of the 100 clusterings for a given subject was based on an independent random sample, the samples on which any two clusterings K and K′ were based almost always contained some nonoverlapping observations. Because the Rand index has nothing to say in regard to such unique observations, we considered only the intersection of the two clustered samples. For each individual subject, as well as for the aggregated clustering, we computed Rand's index for all pairs of clusterings in which both numbers of clusters were >1. Results are shown in Table 2. For completeness, we also show the results when the condition (K, K′) > 1 is removed.9
Table 2.
Rand's C-statistic
| Subject | c̄ | sd | n | s̄ | c̄(n=4,950) | sd(n=4,950) |
|---|---|---|---|---|---|---|
| CT01 | 0.843 | 0.114 | 2,080 | 923 | 0.610 | 0.314 |
| CT02 | 0.873 | 0.060 | 4,656 | 787 | 0.830 | 0.182 |
| SZ01 | 0.787 | 0.129 | 4,851 | 204 | 0.778 | 0.146 |
| SZ02 | 0.893 | 0.092 | 4,950 | 1,103 | 0.894 | 0.092 |
| SZ03 | 0.936 | 0.020 | 4,005 | 1,139 | 0.782 | 0.329 |
| SZ04 | 0.923 | 0.024 | 4,753 | 1,826 | 0.891 | 0.159 |
| SZ05 | 0.995 | 0.002 | 946 | 4,856 | 0.670 | 0.329 |
| SZ06 | 0.935 | 0.054 | 3,160 | 2,266 | 0.797 | 0.209 |
| SZ07 | 0.895 | 0.085 | 105 | 3,919 | 0.793 | 0.350 |
| SZ08 | 0.934 | 0.054 | 4,950 | 885 | 0.934 | 0.054 |
| SZ09 | 0.843 | 0.114 | 4,950 | 241 | 0.843 | 0.115 |
| All | 0.950 | 0.074 | 3,403 | 775 | 0.760 | 0.311 |
Rand's C-statistic (Rand's index) for all pairs of clusterings in which (K, K′) > 1 (columns 2–5). Shown for each subject are the mean c̄, SD sd, size of the sample (i.e., number of clustering pairs) on which the mean was based n, and the average number of overlapping data observations in each pair of samples s̄. A value of 1 for any given c̄ would indicate a perfect match between all n pairs of clusterings. Columns 6 and 7 included for reference, give the mean value for the Rand index when all 100-choose-2 (4,950) pairs of clusterings are considered and its SD, respectively. The average number of overlapping data observations in this case is so close to the value in column s̄ (i.e., ±1 observation, typically less) for all subjects that we have chosen not to replicate it.
The high values of c̄ in the second column of Table 2 (and the accompanying low SDs in column 3) indicate that in cases where the algorithm returns a number of clusters >1 on different iterations, the clusterings tend to have considerable agreement. This is consistent with the idea that the number-of-cluster variability for individual subjects comes largely from the bulk splitting and merging of the clusters that were found in the aggregate.10,11
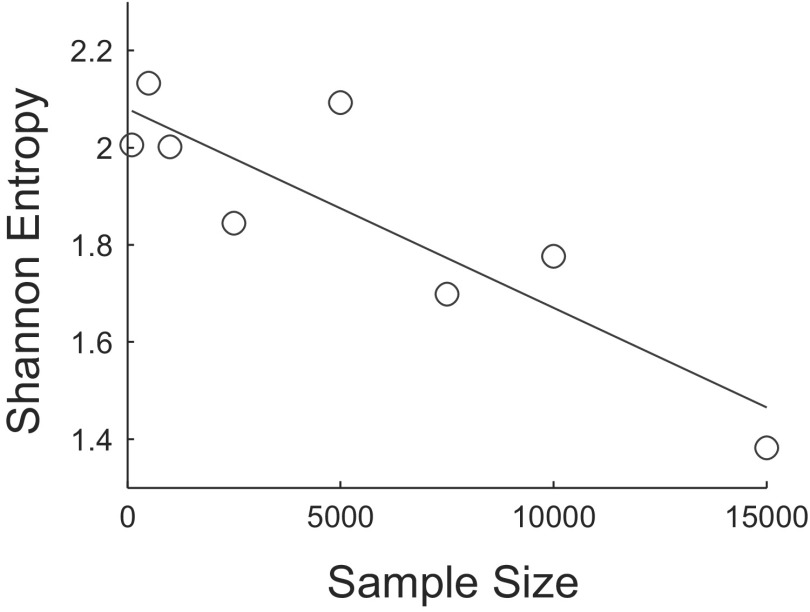
Despite the expected inconsistency on the individual subject data apparent in Fig. 6, the algorithm performs robustly on the aggregated data (bottom right panel), as well as on most patients for whom a relatively large number of events were clustered. Specifically, 77% of the clustering iterations performed on the aggregated data yielded four clusters; columns two and three of Table 2 (last row) show that, furthermore, these four-cluster partitionings were highly similar to one another. Figure 8 shows that Shannon entropy12 decreases with sample size for the aggregated data. There is a negative linear relationship (over the range of sample sizes considered) between the Shannon entropy of the distribution of number of clusters returned by the algorithm and sample size [β = −4.09 × 10−5, t(6) = −4.45, P = 0.004; r2 = 0.77]. Distributions were formed at each sample size by making 100 random draws from all post stage 2 detections. This result provides further quantitative evidence that the stability of the algorithm improves with the addition of data.
Fig. 8.
Scatterplot of sample size vs. the Shannon entropy of the distribution of the number of clusters returned by the algorithm for the aggregated data. Distributions were formed at each sample size by making 100 random draws from all post stage 2 detections. The equation for the regression line is y = −4.09 × 10−5x + 2.08.
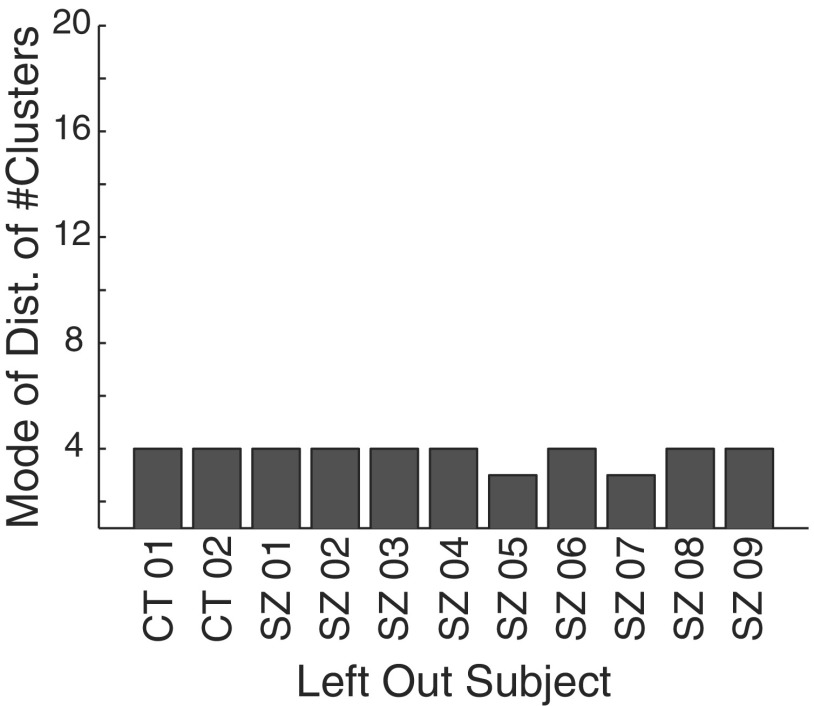
In the second experiment, to examine the influences of individual subjects on the aggregate result we performed “leave-one-out” clustering. Each subject, in turn, had his/her events removed from the pool available for clustering and 5,000 events were randomly drawn without replacement from the remaining events, in 25 iterations. Figure 9 shows that only subjects SZ05 and SZ07 alter the aggregate result of four clusters, suggesting that they were the predominant contributors to at least one cluster. Indeed, subjects SZ05 and SZ07 account for 73% of all events in cluster 3, whereas they make an average combined contribution of only 45% in clusters 1, 2, and 4 (and 48% to the total number of events clustered).
Fig. 9.
Results of an experiment in which each subject, in turn, was left out of the clustering. Five thousand randomly selected events from all events passing through stage 2 in the remaining patients were then clustered in 25 iterations. The x-axis shows the subject that was left out. The y-axis shows the mode of the distribution of number of clusters found in each of the 25 iterations.
Taken collectively, the results of both the individual patient and aggregated clustering experiments are objective evidence in support of the idea that human neocortex is capable of generating distinct classes of transient oscillations within the 100–500 Hz frequency band, and that there are three such classes (excluding the putative artifact class).
DISCUSSION
Main contributions
The first contribution of this work is automation. We have introduced a new methodology, based on prior work, for automatically detecting and clustering high-frequency oscillations on the human intracranial electroencephalogram. We believe this is significant for several reasons. Perhaps the most pedestrian, but nonetheless valuable, is the fact that it substantially decreases human labor. Researchers have reported that it can take up to 3 h to mark HFOs in a single channel of EEG that is just 1 min in duration (Urrestarazu et al. 2007). Assuming a generous per-channel marking rate of 1 h per 10 min of data, it would take a superhuman reviewer (who did nothing but mark EEG all day at the same rate for 8 continuous hours, never taking a weekend or holiday) over 64 yr to manually mark the quantity of data processed for this study.
Although the number of subjects in our sample is comparable to that of many previous studies of HFOs in epilepsy, the total amount of iEEG data we analyzed, to the best of our knowledge, is vastly larger. Analyzing similarly large databases of iEEG—ideally with an even greater number of subjects—will, in our opinion, be required to make definitive statistical statements about the relationship between HFOs and seizure generation going forward. We consider the present effort a step in the direction of such large-scale analyses.
Importantly, in our automated approach we have done away with all data preselection. One could argue that this is not as beneficial as we would like to believe. After all, reducing the human workload is not the only motivation for performing data preselection; one might claim, for example, that choosing channels in the appropriate brain regions or epochs during certain states of wakefulness is critical to the interpretability of findings, or that interesting results will be entirely masked in the absence of these steps. However, in fact, increasingly researchers are finding exactly the opposite: that many of the preselection steps previously thought to be critical are most likely not. In the following text, we list just a few examples of beliefs that have restricted past HFO analyses but are no longer as widely held (in parentheses, we list examples of studies that have cast doubt on the original belief): 1) that HFOs occur only in hippocampal and parahippocampal areas (they also are seen in neocortex; Grenier et al. 2001, 2003; Jirsch et al. 2006); 2) that HFOs occur only during periods of slow-wave sleep (they also are observed during the active states of waking and REM sleep; Bagshaw et al. 2009; Grenier et al. 2001); 3) that HFOs occur only interictally (they are observed ictally; Jirsch et al. 2006) and preictally (Jacobs et al. 2009) as well; and 4) that HFOs can be recorded only with microelectrodes [they can also be recorded with standard clinical macroelectrodes (Jirsch et al. 2006), albeit perhaps with less fidelity (Worrell et al. 2008)].
Moreover, our aim is precisely to investigate the generalizability of some of the enticing findings that have recently been reported in the study of HFOs in human epileptic brain. We are concerned with how, if at all, conclusions about the practical utility of HFOs for localization of epileptogenic regions are modified when the many conditions implied by stringent data preselection are removed. If the answer turns out to be “not much,” this will be particularly encouraging for the prospects of using HFOs as control signals on board implantable seizure therapy devices, for example, given that these devices, at least in early generations, will not have the same luxuries as human researchers when it comes to preidentifying optimal data for processing.
The second major contribution of this work is that we have provided objective evidence for the existence, in the neocortex of epilepsy and control patients, of distinct classes of transient oscillations in the range between 100 and 500 Hz. We do not think this is splitting hairs. Most studies of HFOs in epilepsy of which we are aware simply presuppose the existence of discrete entities typically termed “ripples” and “fast ripples” (albeit with experimental evidence, usually of the observational variety, for doing so). Moreover, at least one group has reported that their data did not clearly show distinct ripple and fast ripple modes (Worrell et al. 2008). One study that attempted to quantitatively verify the existence of discrete populations (Staba et al. 2002) did so by fitting functions to the distribution of peak frequency values of detected events, and arguing that the bimodality of the best-fitting function was telling. The authors acknowledged that their analysis ignored the possibility of events that themselves had bimodal or more complex frequency spectra. Here, we show evidence that there actually is a cluster of mixed-frequency events and, furthermore, that it appears to be separate from two other clusters that are comprised more purely of a single frequency.
Waveforms with similar time-domain characteristics to our mixed-frequency class prototype can be generated by applying a 100–500 Hz band-pass filter to a white Gaussian noise burst, and the features we use for classification will likely not disambiguate these types of broadband transients from truly bimodal ones. Having examined the spectra of these mixed-frequency events, often observing two prominent peaks, however, we feel confident suggesting that they should be further investigated as a legitimately hybrid class of oscillations. As for the other three clusters, we believe, as mentioned, that one is comprised largely of clinically uninteresting recording artifacts. The other two bear sufficient resemblance to what have been labeled ripples and fast ripples to persuade us that we are recording the oscillations that have been recognized by other researchers in the community.
In this work, we were interested in whether 100–500 Hz HFOs cluster in a frequency-based feature space. We focused on 100–500 Hz oscillations because the largest body of HFO research in epilepsy to date considers this range and our goal was to probe the generalizability of this prior research using automated techniques. We do not wish to suggest that 100–500 Hz is a definitive range; indeed, researchers are beginning to report HFOs of potential clinical interest >500 Hz and up to around 1,000 Hz (Kobayashi et al. 2010; Worrell et al. 2008) and a natural extension of the present work would be to broaden the analysis bandwidth. We also note that frequency alone may not distinguish pathological from physiological oscillations (Engel Jr et al. 2009); studies that seek to incorporate our method in correlating HFO activity with pathology will likely benefit from explicitly including other variables (e.g., anatomic coordinates, electrode size, presence of lesions, etc.) in postclustering analyses.
Conclusion
A flurry of recent studies suggests that the relationship between subclasses of high-frequency oscillations recorded using nonstandard, high bandwidth data acquisition systems could be a more reliable indicator of seizure-generating cortex than the waveform morphologies typically used by clinicians for seizure localization.13 In this study, we introduced an algorithm for detecting and classifying these signals in an automatic fashion and demonstrated the tractability of exploring a data set of unprecedented volume using the method. Using an unsupervised approach that did not presuppose a specific number of clusters in the data, we showed direct evidence for the existence of distinct classes of oscillations within the 100–500 Hz frequency range in a population of neocortical epilepsy patients and controls, addressing a current controversy in the field. The number of classes we found, four (three plus one artifact cluster), is consistent with prior studies that distinguish between ripple and fast ripple oscillations and, additionally, suggests that a class comprised of hybrid ripple/fast-ripple events exists.
By minimizing selection bias and other human judgment in detecting and classifying HFOs, we believe that it will be possible to answer the important question of whether they can practically be used to delineate epileptogenic brain. This work also demonstrates the tractability of using machine learning techniques to analyze large streams of high-resolution neurophysiologic data, which may become standard in the future as new devices and techniques for mapping and modulating function and dysfunction in neurological disorders, on multiple brain scales, evolve.
GRANTS
This work was supported by grants from the National Institute of Neurological Disorders and Stroke Grants R01 NS-041811 and R01 NS-48598 to B. Litt and R01 NS-630391 to G. A. Worrell; an Epilepsy Foundation grant to J. A. Blanco; and a Klingenstein Foundation grant to B. Litt and National Institute of Health Grant K08 NS-52232 and Mayo Foundation Research Early Career Development Award for Clinician Scientists to K. H. Lee.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
Supplementary Material
ACKNOWLEDGMENTS
We thank D. Maus for computing support and S. Isard and D. Maus for valuable technical discussions.
APPENDIX A
HFO distinguishing features
1. Power band ratio: (250–500 Hz)/(100–200 Hz).
Computed on the band-passed data; frequency-domain input. The ratio of estimated power in the hypothesized “fast-ripple” band to that in the hypothesized “ripple” band. If there are indeed two distinct populations of HFOs whose respective energy is concentrated in these two bands, one would expect the distribution of data along this feature to be strongly bimodal.
| (A1) |
where
| (A2) |
M[k] can be a multitaper power spectral density estimate. In our case, to lessen the computational burden we use the modified periodogram estimate, M[k] = ∑n=0N−1 w[n]x̃[n]e−j(2π/N)nk, k ∈ {0, 1, … , N − 1}, with an N-point Discrete Fourier Transfrom (DFT). {w[n]} is the Hanning window (Oppenheim et al. 1999) of length L and {x̃[n]} is the detrended signal, obtained by subtracting the least-squares fit of a line from the original length L signal, {x[n]}. Note the signal m[n] = w[n]x̃[n], n ∈ {0, 1, … , L − 1} is padded with N-L zeros before computing the DFT. ζ(u) = ⌊0.5 + NTu⌋, where T is the sampling period and ⌊·⌋ is the “floor” operator, which as used in this context accomplishes rounding to the nearest integer. This handles cases when a and b do not coincide precisely with the frequency values sampled by the DFT. Fs is the sampling frequency.
2. Spectral centroid.
Computed on the band-passed data; frequency-domain input. The frequency corresponding to the “center of mass” of the spectrum. This feature should distinguish events whose energy is relatively concentrated in either the ripple or fast ripple subband alone from those with narrow components in both bands, with relatively broadband spectra, or with predominant energy in an intermediate band
| (A3) |
3. Spectral peak.
Computed on the raw data; frequency-domain input. Frequency corresponding to the peak of the estimated power spectral density. This feature should capture some differences in the spectral characteristics of the background signal on which the detections are superimposed
| (A4) |
4. Line length.
Computed on the raw data, after first-order backward differencing (Gardner et al. 2007; Usui and Amidror 1982); time-domain input. Detections are first detrended and energy normalized by dividing by their Euclidean lengths. Because detections are also of different durations, we normalize by the signal length (i.e., number of samples) as well. This feature was included because it has proven broadly applicable in automatic EEG discrimination tasks, such as seizure (Esteller et al. 2001) and gamma oscillation (Gardner et al. 2007) detection.
| (A5) |
Artifact distinguishing features
1. Global/average-local peak ratio.
Computed on the band-passed data; time-domain input. Ratio of the global maximum value to the average of all other local maxima (i.e., excluding the global maximum). Detections are first detrended and smoothed using a three-point moving average filter.
| (A6) |
where G = {g1, … , gJ} is the set of all local maxima and g* = max G.
2. Entropy of the squared and normalized Teager Energy vector.
Computed on the band-passed data; time-domain input. Detections are first detrended and energy normalized by dividing by their Euclidean length. For a signal composed of a single time-varying (or not) frequency and sampled at a sufficiently high rate, the Teager Energy sequence has a value at any time that approximates, to within a constant, the energy required to “generate” the signal using a mechanical spring-and-mass analogy. It is given by (Kaiser 1990).
| (A7) |
where we have imposed our own definition by necessity at the endpoints. We square the signal, making it everywhere positive, and normalize by its sum to make it a pseudoprobability mass function before computing its entropy, so that
| (A8) |
| (A9) |
3. Wavelet packet-based energy feature.
Computed on the band-passed data; time-domain input. The signal is first made even length, if necessary, by appending a single sample equal in value to the last sample (sample L-1). It is then made length-512 by either truncation or periodized extension on both sides (Strang and Nguyen 1996) and energy-normalized by dividing by its Euclidean length. A four-level wavelet packet decomposition using the wavelet packet system generated from the Daubechies ϕD8 scaling function (Wickerhauser 1994) is performed. Finally, for each of the 31 nodes in the binary decomposition tree (i.e., each sequence of coefficients that is the output of high- or low-pass filtering followed by downsampling of the signal at the parent node), we compute the ratio of the node's total energy to the cumulative energy of all nodes at the same level. An energy vector E is then formed by concatenating these node relative energies, traversing the tree from top to bottom and left to right. The feature returned, f7, is the projection of this energy vector along a predetermined direction in 31-dimensional space, V1, found via PCA on a training set comprised of a subset of detections from two patients with putative artifacts labeled. An energy vector was formed for each detection using the method described earlier; the first principal component V1 was then found and stored for later use in computing f7
| (A10) |
Similar metrics have been used in developing features for the classification of acoustic transients (Learned and Willsky 1995). To ease the computational burden in the clustering stage, after forming the seven-dimensional feature vectors {F1, … , FI}, where I is the total number of detections (anomalies) that pass through stage 2, we form {F1, … , F̂I} by projecting onto the first four principal components. This set of four-dimensional feature vectors is the input to the clustering algorithm described in the main text.
APPENDIX B
Update equations for the Expectation-Maximization algorithm
E-STEP:
| (B1) |
M-STEP:
| (B2) |
| (B3) |
| (B4) |
where
| (B5) |
where z is a K-dimensional random variable (called a “latent” variable because it is not explicitly observed) having K possible states, such that whenever a particular element is equal to 1, all others are equal to zero. Its marginal distribution is defined in terms of the mixture component weights, such that p(zk = 1) = πk. It is introduced to achieve a formulation of the likelihood function that is amenable to maximization using EM. γ(znk) is then defined as the posterior probability that zk = 1, given that data segment xn has been observed; that is, the probability that mixture component k is “responsible” for generating observation xn. The EM algorithm allows us to learn the parameters of the model from the data. When it converges, it is guaranteed to converge to (at least) a local maximum of the likelihood function.14
K-means algorithm
Initialize u randomly.15
- For each xi, compute the nearest prototype
(B6) - Recompute cluster prototypes
(B7) Return to step 2. Repeat until convergence.
Because step 2 minimizes the error function with respect to Y and step 3 minimizes the error function with respect to u, ϵ is guaranteed to decrease with each iteration so that convergence, at least to a local minimum, is ensured.
Rand's C-statistic
| (B8) |
where K is the number of clusters in the first partitioning, K′ is the number of clusters in the second partitioning, and nkk′ is the number of observations that were simultaneously in cluster k in the first partitioning and cluster k′ in the second partitioning.
Footnotes
By “local” we mean the amount of time typically displayed when screening for HFOs in raw or modestly filtered data (e.g., 1 s/screen with ∼0.5 – 500 Hz bandwidth, ∼1.2-kHz sampling rate, and 7 μV/mm vertical scaling, on a monitor with 1,280 × 1,024 pixel resolution).
In the supplemental material (Figs. S1 and S2; Tables S1–S3) we compare the performance of the automated method with that of three expert human reviewers on an HFO verification task.
To simplify notation, in Eqs. 1, 2, and B1–B5, and supplemental material Eqs. S1–S7 that follow, we have suppressed the indexing subscripts that indicate that all functions and variables are specific to a particular candidate HFO, but we here emphasize that these subscripts are implicit.
Detections exceeding 50 ms (∼14%) are first truncated to 50 ms to place a lower limit on the number of background segments available.
Multitaper techniques are particularly well suited to the analysis of short duration signals, as well as signals with spectra having a large dynamic range of amplitudes (Mitra and Pesaran 1999; Percival and Walden 1993), making them an appropriate choice for our application.
In the Gaussian Mixture Model (GMM) discussion in the following text, we use the notation style of Bishop (2006).
The online version of this article contains supplemental data.
The technically inert factor of 2 in the denominator of Eq. 3 achieves this exact equivalence.
The latter result would be more interesting if, in cases where more than one cluster was found, the algorithm had a tendency to produce one very large cluster along with several very small clusters. However, since this was not our observation we felt the (K, K′) > 1 case was most relevant.
The results in Table 2 should not be overstated. For example, one would not take seriously any multicluster result for subject SZ05 despite its “high marks” in columns two and three of the table because the preponderance of its clustering results, as seen in Fig. 6, point toward a single cluster. (The low value for n in column four and the data in the last two columns of Table 2 serve as a reminder of this.)
As an alternative to the Rand index, which ranges from zero to one, one can compute the adjusted Rand index (Hubert and Arabie 1985). The latter can assume a larger range of values and is zero when the agreement between two partitionings is equal to its expectation under a chance model (i.e., each partitioning is picked at random from the set of all partitionings having the same number of clusters and members per cluster as the original). The average adjusted Rand indices for (K, K′) > 1 in our case take values from 0.5 to 0.9, from which it can be concluded that the similarities observed are substantially greater than would be expected by chance.
Shannon entropy S is defined as S = −∑i pi log2 pi, where pi is the probability of being in state i, and P log2 P := 0 when P = 0.
HFOs are not, by default, part of the classical armamentarium of electrographic signatures used for localization because they are difficult or impossible to visualize in standard clinical iEEG due to their short timescales, small relative amplitudes, and spectral contents that can exceed the bandwidth that is traditionally recorded.
We take the algorithm to have converged when successive computed values of the likelihood function differ by less than or equal to 1 × 10−5. In cases where numerical issues arise or where convergence is not achieved within a prespecified number of iterations (500)—either due to encountering singularities of the likelihood function or to otherwise slow rates of convergence—the algorithm returns an “indeterminate” flag, and the HFO candidate in question is passed to the third stage of processing without interruption of the program flow.
We use a randomly chosen k observations from the data set X.
REFERENCES
- Bagshaw et al., 2009. Bagshaw AP, Jacobs J, LeVan P, Dubeau F, Gotman J. Effect of sleep stage on interictal high-frequency oscillations recorded from depth macroelectrodes in patients with focal epilepsy. Epilepsia 50: 617–628, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barkley et al., 2006. Barkley GL, Smith B, Bergey G, Worrell G, Chabolla D, Drazkowski J, Labar D, Duckrow R, Murro A, Smith M, Gwinn R, Fisch B, Hirsch L, Morrell M. Safety and preliminary efficacy of the RNS responsive neurostimulator for the treatment of intractable epilepsy in adults (Abstract). Epilepsia 47, Suppl. 4: A12, 2006. [Google Scholar]
- Bellman, 1961. Bellman R. Adaptive Control Processes: A Guided Tour. Princeton, NJ: Princeton Univ. Press, 1961, p. 255. [Google Scholar]
- Bishop, 2006. Bishop CM. Pattern Recognition and Machine Learning. New York: Springer Science/Business Media, 2006, p. 738. [Google Scholar]
- Brinkmann et al., 2009. Brinkmann BH, Bower MR, Stengel KA, Worrell GA, Stead M. Large-scale electrophysiology: acquisition, compression, encryption, and storage of big data. J Neurosci Methods 180: 185–192, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari et al., 1999a. Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsáki G. Fast network oscillations in the hippocampal CA1 region of the freely behaving rat. J Neurosci 19: RC20 (1–4), 1999a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari et al., 1999b. Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsáki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving rat. J Neurosci 19: 274–287, 1999b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster et al., 1977. Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B Method 39: 1–38, 1977. [Google Scholar]
- Engel et al., 2009. Engel J, Jr, Bragin A, Staba R, Mody I. High-frequency oscillations: what is normal and what is not? Epilepsia 50: 598–604, 2009. [DOI] [PubMed] [Google Scholar]
- Esteller et al., 2001. Esteller R, Echauz J, Tcheng T, Litt B, Pless B. Line length: an efficient feature for seizure onset detection. Eng Med Biol Soc 2: 1707–1710, 2001. [Google Scholar]
- Gardner et al., 2007. Gardner AB, Worrell GA, Marsh E, Dlugos D, Litt B. Human and automated detection of high-frequency oscillations in clinical intracranial EEG recordings. Clin Neurophysiol 118: 1134–1143, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenier et al., 2001. Grenier F, Timofeev I, Steriade M. Focal synchronization of ripples (80–200 Hz) in neocortex and their neuronal correlates. J Neurophysiol 86: 1884–1898, 2001. [DOI] [PubMed] [Google Scholar]
- Grenier et al., 2003. Grenier F, Timofeev I, Steriade M. Neocortical very fast oscillations (ripples, 80–200 Hz) during seizures: intracellular correlates. J Neurophysiol 89: 841–852, 2003. [DOI] [PubMed] [Google Scholar]
- Hastie et al., 2001. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. New York: Springer-Verlag, 2001, p. 533. [Google Scholar]
- Hotelling, 1933. Hotelling H. Analysis of a complex of statistical variables into principal components. J Educ Psychol 24: 417–441, 1933. [Google Scholar]
- Hubert and Arabie, 1985. Hubert L, Arabie P. Comparing partitions. J Classification 2: 193–218, 1985. [Google Scholar]
- Jacobs et al., 2009. Jacobs J, Zelmann R, Jirsch J, Chander R, Chatillon C-E, Dubeau F, Gotman J. High frequency oscillations (80–500 Hz) in the preictal period in patients with focal seizures. Epilepsia 50: 1780–1792, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jirsch et al., 2006. Jirsch JD, Urrestarazu E, LeVan P, Olivier A, Dubeau F, Gotman J. High-frequency oscillations during human focal seizures. Brain 129: 1593–1608, 2006. [DOI] [PubMed] [Google Scholar]
- Kaiser, 1990. Kaiser JF. On a simple algorithm to calculate the energy of a signal. Proc ICASSP-90 1: 381–384, 1990. [Google Scholar]
- Kobayashi et al., 2010. Kobayashi K, Agari T, Oka M, Yoshinaga H, Date I, Ohtsuka Y, Gotman J. Detection of seizure-associated high-frequency oscillations above 500 Hz. Epilepsy Res 88: 139–144, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Learned and Willsky, 1995. Learned RE, Willsky AS. A wavelet packet approach to transient signal classification. Appl Comput Harmonic Anal 2: 265–278, 1995. [Google Scholar]
- MacQueen, 1967. MacQueen J. Some methods for classification and analysis of multivariate observations. In: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability Berkeley, CA: Univ. of California, 1967, p. 281–297. [Google Scholar]
- McLachlan, 1999. McLachlan GJ. Mahalanobis distance. Resonance 4: 20–26, 1999. [Google Scholar]
- Mitra and Pesaran, 1999. Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J 76: 691–708, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oppenheim et al., 1999. Oppenheim AV, Schafer RW, Buck JR. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, p. 870. [Google Scholar]
- Pearson, 1901. Pearson K. On lines and planes of closest fit to systems of points in space. Philosophical Magazine 2: 559–572, 1901. [Google Scholar]
- Percival and Walden, 1993. Percival DB, Walden AT. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge, UK: Cambridge Univ. Press, 1993. [Google Scholar]
- Rand, 1971. Rand WM. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66: 846–850, 1971. [Google Scholar]
- Schwarz, 1978. Schwarz G. Estimating the dimension of a model. Ann Stat 6: 461–464, 1978. [Google Scholar]
- Slepian and Pollak, 1961. Slepian D, Pollak HO. Prolate spheroidal wavefunctions, Fourier analysis and uncertainty. I. Bell System Tech J 40: 43–63, 1961. [Google Scholar]
- Staba et al., 2002. Staba RJ, Wilson CL, Bragin A, Fried I, Engel J., Jr Quantitative analysis of high-frequency oscillations (80–500 Hz) recorded in human epileptic hippocampus and entorhinal cortex. J Neurophysiol 88: 1743–1752, 2002. [DOI] [PubMed] [Google Scholar]
- Strang and Nguyen, 1996. Strang G, Nguyen T. Wavelets and Filter Banks. Wellesley, MA: Wellesley/Cambridge Press, 1996. [Google Scholar]
- Thomson, 1982. Thomson DJ. Spectrum estimation and harmonic analysis. Proc IEEE 9: 1055–1096, 1982. [Google Scholar]
- Tibshirani et al., 2001. Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic. J R Stat Soc B 63: 411–423, 2001. [Google Scholar]
- Urrestarazu et al., 2007. Urrestarazu E, Chander R, Dubeau F, Gotman J. Interictal high-frequency oscillations (100–500 Hz) in the intracerebral EEG of epileptic patients. Brain 130: 2354–2366, 2007. [DOI] [PubMed] [Google Scholar]
- Usui and Amidror, 1982. Usui S, Amidror I. Digital low-pass differentiation for biological signal processing. IEEE Trans Biomed Eng 29: 686–693, 1982. [DOI] [PubMed] [Google Scholar]
- Van Gompel et al., 2008. Van Gompel JJ, Stead SM, Giannini C, Meyer FB, Marsh WR, Fountain T, So E, Cohen-Gadol A, Lee KH, Worrell GA. Phase I trial: safety and feasibility of intracranial electroencephalography using hybrid subdural electrodes containing macro- and microelectrode arrays. Neurosurg Focus 25: 1–6, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickerhauser, 1994. Wickerhauser MV. Adapted Wavelet Analysis from Theory to Software. Wellesley, MA: A.K. Peters, 1994. [Google Scholar]
- Worrell et al., 2008. Worrell GA, Gardner AB, Stead SM, Hu S, Goerss S, Cascino GJ, Meyer FB, Marsh R, Litt B. High-frequency oscillations in human temporal lobe: simultaneous microwire and clinical macroelectrode recording. Brain 131: 928–937, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.