Real-Time Monitoring of Cell Elasticity Reveals Oscillating Myosin Activity

Abstract

The cytoskeleton is the physical and biochemical interface for a large variety of cellular processes. Its complex regulation machinery is involved upstream and downstream in various signaling pathways. The cytoskeleton determines the mechanical properties of a cell. Thus, cell elasticity could serve as a parameter reflecting the behavior of the system rather than reflecting the specific properties of isolated components. In this study, we used atomic force microscopy to perform real-time monitoring of cell elasticity unveiling cytoskeletal dynamics of living bronchial epithelial cells. In resting cells, we found a periodic activity of the cytoskeleton. Amplitude and frequency of this spontaneous oscillation were strongly affected by intracellular calcium. Experiments reveal that basal cell elasticity and superimposed elasticity oscillations are caused by the collective action of myosin motor proteins. We characterized the cell as a mechanically multilayered structure, and followed cytoskeletal dynamics in the different layers with high time resolution. In conclusion, the collective activities of the myosin motor proteins define overall mechanical cell dynamics, reflecting specific changes of the chemical and mechanical environment.

Introduction

Shape and surface architecture of cells are subjected to dynamical transformations as a response to changes of the chemical and mechanical environment. Such morphological changes are obligatory during many cell activities (e.g., cell motion, division, and transmembrane transport processes). The morphology of cells is determined by passive (structural) components which can be converted into active (dynamical) elements by a complex interplay of signaling molecules, gene expression, and protein-protein interaction. This induces ongoing rearrangements of the cytoskeleton and changes of the intracellular hydraulic pressure described as the morphodynamics of a cell. Obviously, such a complex behavior results from the dynamic architecture of the system rather than from specific properties of isolated components.

The cytoskeleton is a network that consists of actin filaments, microtubules, and intermediate filaments integrating a variety of cytoplasmic proteins, e.g., myosin motors (1). The function of the cytoskeleton is to arrange and maintain the integrity of intracellular compartments, connect the cell physically and biochemically to the external environment, and generate coordinated forces that enable the cell to move and change shape.

Mechanical stress, applied to a cell, is mediated mainly by the cytoskeleton (other components of stress dissipation are fluid displacement (2) and the change of plasma membrane tension (3)). The cytoskeleton can offer this wide spectrum of functions because it is not a static structure but a dynamic and adaptive system whose components such as biopolymers and regulatory proteins are in constant fluctuation (1). The status of the cytoskeleton determines primarily the cell's elasticity.

Elasticity (elastic modulus) or stiffness is used in the literature to describe a biophysical property of cells. Although both parameters provide information about the resistance of a material to deformation (the amount of deformation is called strain), they show significant differences (4). A material is said to be elastic if the relationship between stress and strain is linear and the deformation is completely reversible. Stiffness is the resistance of a solid body to deformation by an applied force. In general, elastic modulus is not the same as stiffness. Elastic modulus is a property of the constituent material; stiffness is a property of a solid body. The elastic modulus is an intensive property and therefore independent of size, shape, mass, and boundary conditions of the material; stiffness, on the other hand, is an extensive property which depends on the size, shape, mass and boundary conditions of the solid body. High elasticity is roughly equivalent to a low deformability. Elasticity is often referred as to the Young's modulus (E) given in Pascals (Pa). Here, elasticity was used to describe a biophysical property of the cells.

The filament networks of the cytoskeleton are described as semiflexible polymers (5) in which elasticity is composed of entropic (filament entanglement) and enthalpic (intramolecular interactions) components (6,7). In highly organized networks like the cytoskeleton, enthalpic elasticity dominates. For instance, when compressive forces are applied to growing actin filaments (e.g., at the leading edge of crawling cells), the cytoskeleton shows nonlinear stress stiffening, followed by stress softening at high stresses. Importantly, this softening behavior is completely reversible (8). Mechanical properties of highly organized, i.e., crosslinked, networks depend not only on bending and stretching of actin filaments but also on the properties of actin crosslinkers, like filamin, fascin, and α-actinin. Geometry and binding kinetics of crosslinkers determine the structural organization of the network and therefore affect its behavior during mechanical stress (9).

The described properties of the highly organized cytoskeletal network represent the passive components of cell elasticity, even though none of its components is static. Cells, however, represent not passive materials, but instead use molecular motors to convert chemical energy into mechanical work within the cytoskeleton. The active part affecting mechanical properties of cells is assigned to motor proteins, especially to myosins (10). These molecular motors have essential roles in organizing the cytoskeleton enabling the cells to contract and to sense their environment (11). Nonmuscle myosin II (hereafter, myosin II) is an actin-based motor protein that plays a crucial role in a variety of cellular processes, including cell migration, polarity formation, and cytokinesis (12). Myosin II plays a crucial role for the elasticity of the cytoskeleton (13,14) and is regulated downstream by a variety of biochemical signaling pathways through phosphorylation and dephosphorylation of its light chain (15).

Active cytoskeletal structures can undergo oscillating instabilities, where a nonoscillating state becomes unstable and is replaced by an oscillating one, if system parameters are changed. A prototype is the generation of oscillations by molecular motors (3). Oscillations of cytoskeletal structures driven by motor proteins were described as follows: A single motor, which generates a force along a filament, will attain a stably displaced state when acting on an elastic spring. If a large number of motors act together, this state can, under certain conditions, become unstable with respect to oscillatory motion. A collection of motors can suddenly lose the grip on the filaments on which they act, via a rupture process in which the initial detachment of a few motors induces the subsequent detachment of the remaining motors. If this collective detachment is followed by a renewed build-up of force, oscillatory motion is generated (16,17). Skinned skeletal and cardiac muscle fibers exhibit spontaneous oscillations in vitro under various conditions (18,19). Oscillating contractions of mesoderm cells during Drosophila morphogenesis result from cycles of myosin II activation/inactivation (20,21). Spontaneous oscillations have also been observed in the mitotic spindle during asymmetric cell division (22), in antennal hearing organs of insects (23) and in mechanosensory bundles of hair cells from the vertebrate ear (24). In addition, periodic myosin contractions are observed in the single cell Caenorhabditis elegans embryo and in anuclear cell fragments treated with nocodazole (25,26).

Oscillations are the simplest case of dynamical processes found in complex systems. The emergence of oscillations in a complex system is subtle, because it depends crucially on the dynamic properties of the interacting components and their collective behaviors. From this point of view, the widespread occurrence of oscillations in cell biology is therefore no surprise (16).

One of the primary body tissues in humans is the epithelium (the other ones being connective tissue, muscle tissue, and nervous tissue). Epithelial cells line the cavities and surfaces of structures throughout the body and present commonly extensive apical-basolateral polarity. Functions of epithelial cells include secretion, absorption, protection, and detection of sensation. The cell type used in this study is a human bronchial epithelial cell line, 16HBE14o⁻ (27). Bronchial epithelial cells lining the airways and protect the lung against inhaled particles and pathogens by a mechanical defense mechanism, the mucociliary clearance. A lot of work was done to characterize epithelium biochemically but the biomechanical characteristics of epithelial cells remains largely unknown.

In this work, we present an atomic force microscopy (AFM)-based method enabling real-time monitoring of cell elasticity to investigate the mechanical dynamics of human bronchial epithelial cells. The principle of an elasticity measurement is to indent a cell with a probe and measure the applied force. Fitting the force-indentation curve with an appropriate model allows the calculation of the Young's modulus. The AFM enables the detection of very small forces and therefore enables quantification of the interaction between a probe and a sample (28,29). An AFM equipped with either a sharp tip or a colloidal probe in which the tip is replaced by a sphere (30), has been widely used to measure the mechanical properties of soft materials (4,31). Elasticity of cells are not only determined by AFM techniques but also by optical (32,33) and magnetic (34,35) tweezers. Optical tweezers use a focused laser beam and magnetic tweezers use a magnetic field gradient to provide the attractive or repulsive forces (typically in the order of pN) required to hold and move a bead.

Our approach of real-time monitoring uses repetitive indentation of cells by a spherical AFM probe to characterize the cell's elasticity with a high time resolution. This allows us to follow the dynamics of cell's elasticity and subsequently the dynamics of the cytoskeletal activity under various conditions.

The aim of this study was to gain insights into the spontaneous activities of cell mechanics and its underlying mechanisms.

Materials and Methods

Cell culture

A human, wt-CFTR-expressing bronchial epithelial cell line, 16HBE14o⁻, was grown in Eagle's Minimal Essential Medium with 10% fetal bovine serum, 2 mM L-glutamine, 50 U/mL penicillin, and 50 mg/mL streptomycin. Cells were cultured at 37°C in a 5% CO₂ incubator. Cells were seeded at a density of 1.6 ×10⁵ on glass coverslips, then precoated overnight with a solution containing 0.01% collagen type I from calf skin and 1 mg/mL bovine plasma fibronectin (Invitrogen, Karlsruhe, Germany). The 16HBE14o⁻ cells were a generous gift from Dr. D. Gruenert (Cardiovascular Research Institute, University of California, San Francisco, CA).

Optical microscopy

Living 16HBE14o⁻ cells were imaged in HEPES buffered solution (140 mM NaCl; 5 mM KCl; 1 mM MgCl₂; 1 mM CaCl₂; 10 mM HEPES (n-2-hydroxyethylpiperazine-n′-2-ethanesulfonic acid); pH = 7.4) at room temperature using an Zeiss Axio Observer Z1 with a 40× oil immersion objective Ph3 Plan-NEOFLUAR (Carl Zeiss, Göttingen, Germany). Image acquisition was done with a back-illuminated electron-multiplying charge-coupled device camera Andor iXon^EM DU-888 (Andor, Belfast, Northern Ireland) and Metamorph software (Molecular Devices, Sunnyvale, CA).

Elasticity measurements

Elasticity measurements were performed as described before (4). Briefly, measurements were performed in HEPES buffered using a Nanoscope III Multimode-AFM (Veeco Instruments, Santa Barbara, CA). All measurements were carried out in a fluid cell at 37°C (MMFHTR-2 Air and Fluid Sample Heater, Veeco Instruments). Colloidal probe cantilevers with a sphere radius of 5 μm were used for this work, (PT.PS; Novascan Technologies, Ames, IA) Cantilevers were calibrated with a Nanoscope V controller (Veeco Instruments) by measuring the thermally induced motion of the unloaded cantilever. Spring constants of cantilevers used in this study ranged from 0.016 N/m to 0.024 N/m. Before the measurements, we calibrated the cantilever deflection sensitivity on a bare glass coverslip immersed in buffer solution. The sensitivity calibration corresponds to the position of the laser on the cantilever and allows calculating the force derived from cantilever deflection using the following equation:

$$\text{Force}\left[\text{N}\right]=\text{Spring}\text{constant}\left[\text{N}/\text{m}\right]\times \text{Cantilever}\text{sensitivity}\left[\text{m}/\text{V}\right]\times \text{Deflection}\left[\text{V}\right].$$ (1)

Once the sensitivity calibration had been performed, the AFM head was withdrawn and the samples prepared in the following way: Glass coverslips with cells were removed from the culture medium and washed two times with HEPES buffer. The coverslip was glued on metal disks with double-adhesive tape and mounted on the AFM. All elasticity measurements were carried out in HEPES buffer at 37°C. Probes were placed under optical control (OMV-PAL; Veeco Instruments) right above the center of the cells. Cells were indented repetitively with a frequency of 0.25 Hz, a ramp size of 2 μm and a loading force of 2 nN. The approach velocity was limited at 1 μm/s because larger velocities result in artificially high stiffnesses (36). Furthermore, cells behave in a viscoelastic manner, which means that energy is dissipated into the cell when they are indented by the AFM tip (hysteresis in the force-deformation curve). This hysteresis is minimized at probe velocities at 1 μm/s (37,38). Real-time monitoring of cell elasticity was performed for at least 10 min (150 force-indentation curves) and for maximally 37 min (550 force-indentation curves). Using the continuous ramping function and the relative trigger mode of the nanoscope software allows semiautomatic data acquisition while ramping parameters were kept constant. For each experiment, we analyzed 5–15 cells obtained from at least two separate cell samples.

Data processing

Force-indentation data were collected with a sampling frequency of 256 Hz (512 points per curve). Solely the approach curves were used to calculate Young's moduli. All force-indentation data were analyzed with protein unfolding and nanoindentation analysis software (PUNIAS; http://punias.voila.net/klmenu/punias0.htm), a custom-built semiautomatic processing and analysis software. Data were analyzed using our linear implementation of the Hertz model (4),

$$E=\frac{3}{4}{\left(\frac{\Delta {\left(f_{sphere}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{\Delta \delta }\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{1-{\nu }^2}{\sqrt{R}}=\frac{3}{4}slop{e}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{1-{\nu }^2}{\sqrt{R}}$$ (2)

(with Young's modulus (E), force (f), Poisson ratio of the sample (ν), and deformation (δ) radius of the sphere (R)). Cells were assumed to be linearly elastic and isotropic (39) and incompressible at small strains. Therefore, we used a Poisson ratio of 0.5. (For more detailed descriptions, see (40,41)). The Young's modulus of the cell is constant over linear ranges of the curve in plots of deformation data according to this linearized form of the Hertz model (f^2/3 vs. δ) (see Fig. 4 A). This linearized form of force-indentation curves simplifies the localization of the contact point, because it is indicated by the point of intersection between two straight lines (baseline, first slope). The first (initial) part of the curves with indentations of maximally 300 nm was analyzed, unless otherwise mentioned (boundary conditions: Δδ ≥ 100 nm with a regression coefficient of ≥0.95).

Figure 4.

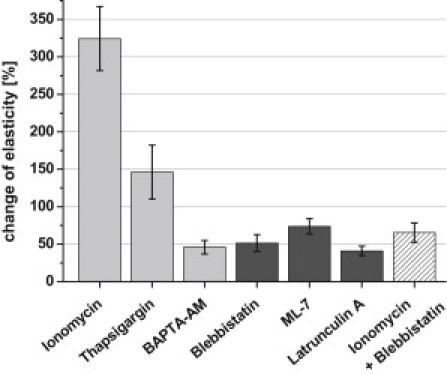
Relative elasticity changes observed 500 s after application of substances known to change intracellular calcium concentration (light shaded bars) and to influence cytoskeletal dynamics (dark shaded bars) (mean ± SE, n = 5–8).

Chemicals

All chemicals were purchased from Sigma (Deisenhofen, Germany), unless otherwise mentioned. Cell culture media and supplements were purchased from Invitrogen-Gibco (Karlsruhe, Germany).

Statistics

Data are presented as mean ± SE. Two-sided t-tests were performed to evaluate statistical significance. A P-value of <0.05 was accepted to indicate a significant difference between the compared data.

Results

Real-time monitoring of cell elasticity

The spherical AFM probe (sphere diameter 10 μm) was placed under optical control (40×) above the center of the cell located in a confluent cell layer. Epithelial cells form cell-cell contacts (adherens junctions, tight junctions) which are connected to the cytoskeleton, and therefore most likely influence the elasticity of a cell. Additionally, cell-cell contacts are a prerequisite to develop epithelium-specific properties. The optical control allows placing the probe always above the highest region of the cell (above the nucleus) to increase the comparability of different measurements. A phase micrograph of living 16HBE14o⁻ cells is shown in Fig. 1 (scale bar: 50 μm).

Figure 1.

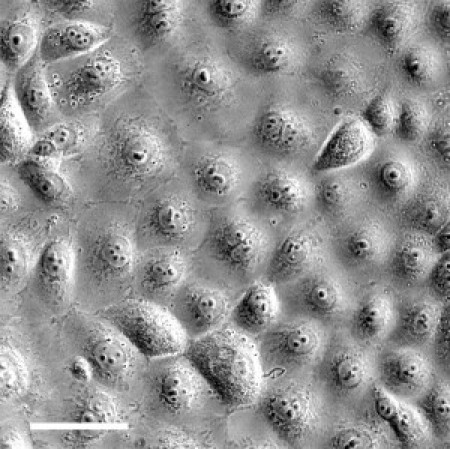
Phase micrograph of living 16HBE14o⁻ cells. Glass-cultured bronchial epithelial cells show an almost homogenous distribution of size and shape. Scale bar is 50 μm.

Real-time monitoring of cell elasticity of the untreated cell reveals elasticity oscillations (Fig. 2). Each point represents the result of a single force-indentation cycle. Adjacent-averaging with a 20-points window was performed to smooth out short-term fluctuations and highlight periodic elasticity changes. This oscillation can be described as a high amplitude/low frequency wave superimposed by a low amplitude/high frequency wave. The bronchial epithelial cells used in this study show a period of 200 s and a peak amplitude of ∼150 Pa. Elasticity oscillations were observed in virtually all cells, with a rather constant period of 200 s but considerable variations in amplitude.

Figure 2.

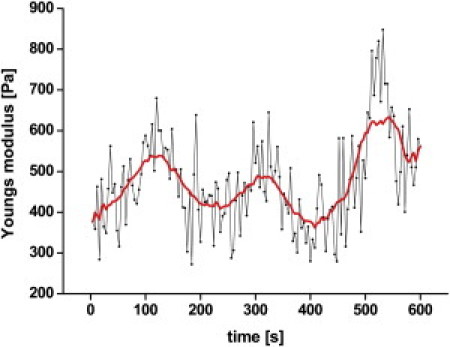
Real-time monitoring of cell elasticity reveals an oscillation with a period of 200 s. Each point represents the result calculated from a force-indentation cycle. Adjacent-averaging with a 20-points window was performed to smooth out short-term fluctuations and highlight periodic elasticity changes.

To test whether these oscillations originate from cytoskeletal activities, latrunculin A, an agent that disrupts specifically the actin cytoskeleton by sequestering monomeric G-actin, was added during experiments to destroy the integrity of the cytoskeleton. Fig. 3 A shows that it takes only ∼400 s to reduce the cell elasticity to half of its original value. Furthermore, oscillations, clearly visible before adding latrunculin A, disappear immediately after adding the actin polymerization inhibitor, indicating that oscillation depends on the integrity of the cytoskeleton. Note that the high amplitude/low frequency wave disappears, but not the high frequency/low amplitude oscillations. This indicates that the latter does not originate from the cytoskeleton but rather from measuring and data processing inaccuracies.

Figure 3.

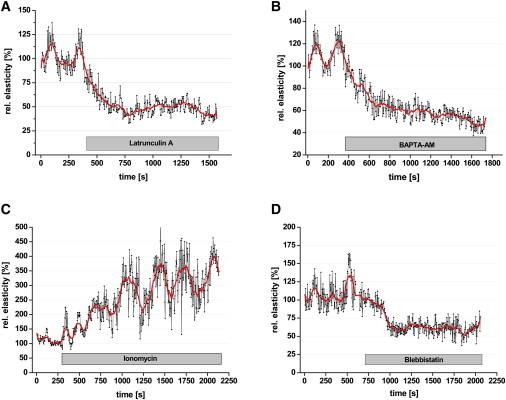
Time course of elasticity changes while blocking actin polymerization (A), lowering [Ca²⁺]_i (B), increasing [Ca²⁺]_i (C), and blocking myosin II activity (D). Adjacent-averaging with a 20-points window was performed to smooth out short-term fluctuations and highlight periodic elasticity changes.

Although the high amplitude/low frequency oscillations can be related to the actin cytoskeleton, the mechanisms are still unclear. Because calcium ions play an important role in cytoskeletal organization (42), any modification in intracellular calcium concentration could therefore affect the elasticity oscillations. Indeed, upon application of BAPTA-AM (a membrane-permeable calcium chelator), elasticity decreases within 5 min by 40% and the oscillatory activity disappears (Fig. 3 B). A completely different behavior of cell mechanics arises when the intracellular calcium concentration is increased by the application of the Ca²⁺-ionophore ionomycin (Fig. 3 C). Cell elasticity and oscillation amplitudes increase dramatically immediately after application of ionomycin. The timescale of the basal elasticity changes and the magnitude of the increase in the oscillation amplitude suggest an involvement of the motor protein nonmuscle myosin II. Therefore, blebbistatin, a specific blocker of myosin II (43), was used to test his hypothesis. Inhibition of the blebbistatin-sensitive myosin motor proteins results in a decrease of elasticity by 50% within 5 min and, as in BAPTA experiments, the oscillations also disappear (Fig. 3 D). All experiments displayed in Fig. 3 show oscillations in cell elasticity before applying any test substances. Furthermore, elasticity oscillations are strongly affected by cytoskeletal disintegration, inhibition of myosin motor proteins by blebbistatin, and changes of intracellular free calcium.

The results, summarized in Fig. 4, are expressed as relative values to allow appropriate comparisons between the different series of experiments. Data were complemented with experiments using thapsigargin and ML-7. Thapsigargin increases the concentration of intracellular free Ca²⁺ by inhibiting sarco/endoplasmic reticulum Ca²⁺-ATPases (44), and ML-7 (5-iodonaphthalene-1-sulphonyl-homopiperazine), a specific inhibitor of myosin light chain kinase, blocks myosin II activity (45). The elasticity measured 500 s after adding the respective substances is shown in relation to the initial control value (set as 100%). The error bars (standard error of the mean) include not only differences between individual experiments but also the oscillating behavior of cell elasticity. This is prominent in experiments where the amplitude of the elasticity oscillation increases, e.g., after application of ionomycin (324 ± 42.6%, n = 7) and thapsigargin (146 ± 35.9%, n = 5) (Fig. 4). In experiments where the elasticity change is paralleled by any decrease in the oscillation amplitude, the mean ± SE also clearly decreases (blebbistatin, 51 ± 11.2%, n = 8; ML-7, 73 ± 10.5%, n = 6; latrunculin A, 41 ± 6.3%, n = 5).

The experiments summarized in Fig. 4 show that an increase of free intracellular calcium induces a considerable increase in elasticity and oscillation amplitude whereas reducing intracellular calcium or blocking myosin II activity does the opposite. Oscillating contractions could result from cycles of actin filament turnover or myosin II activation/inactivation. To clarify further the role of myosin motor proteins for elasticity and the superimposed oscillations, ionomycin and blebbistatin were simultaneously applied. Both parameters, elasticity and amplitude, decrease (65 ± 12.8%, n = 5) (Fig. 4), indicating that myosin II activity determines cell elasticity rather than other processes induced by an increase of intracellular calcium.

Elasticity as a function of indentation depth?

Data were analyzed using the linear implementation of the Hertz model (4). Plotting the data of force-distance curves according to this model results in graphs displaying indentation against force to the power of 2/3 (δ vs. f^2/3) (Fig. 5 A). The Young's modulus (E) can be calculated from the linear slope of the force^2/3 deformation curve (Fig. 5 A). Linear regression (least-square fitting) reveals at least three linear slopes, i.e., Young's moduli of the cell, a behavior which is representative for all of our measurements. This means that the Young's modulus of the cell is not constant over the whole range of indentation, and is supposed to be a function of the indentation depth of the tip into the cell (46). The first slope, marked with a blue line (a), allows us to calculate the Young's modulus of the first 300 nm of indentation. The red line (b) indicates the slope at indentations between 800 and 1000 nm, allowing us to determine the elasticity of regions deep inside the cell. We compared the time courses of elasticity of this superficial region (<300 nm) with data obtained from deeper indentations (>500 nm) within the same experiments. This should provide information as to whether cellular structures underneath of the cortical actomyosin web contribute to the elasticity oscillations or the cortical actomyosin, as such, drives these oscillations. Fig. 5 B shows that the oscillating behavior is clearly detectable at small (<300 nm) as well as at large indentations (>500 nm). The period, the phase, and the relative amplitudes are nearly identical, whereas the basal elasticity is considerably higher at indentations >500 nm.

Figure 5.

Dependency of the elasticity from the indentation depth. (A) Force at the power 2/3 versus indentation curve. Line a represents elasticity below 300 nm and line b indicates elasticity measured at an indentation above 500 nm. (B) Comparison of elasticities calculated from indentations below 300 nm and above 500 nm from the same dataset. Adjacent-averaging with a 20-points window were shown for indentations of <300 nm and >500 nm.

We found that myosin II activity determines the elasticity of the cell in the superficial region (<300 nm) (Fig. 4). To test whether myosin II activity also dominates the elasticity measured at deeper indentations, we used the experimental data of blebbistatin experiments and calculated the Young's moduli from indentations above 500 nm. Fig. 6 shows the time course of elasticities calculated from indentations <300 nm and >500 nm obtained from the same experimental data. Before application of blebbistatin, similarities in frequency, phase, and amplitude of elasticity oscillations are visible. Again, higher Young's moduli are achieved at deeper indentations. After adding blebbistatin, elasticity decreases not only in the superficial region (<300 nm) but also at indentations above 500 nm. Interestingly, elasticity decreases in both regions to Young's moduli values of ∼300 Pa (Fig. 6) even though the Young's modulus directly before applying blebbistatin was 800 Pa and 400 Pa for indentations <300 nm and >500 nm, respectively. After blocking myosin II by blebbistatin, cells become more homogenous in terms of cell elasticity over a wide range of indentation depths.

Figure 6.

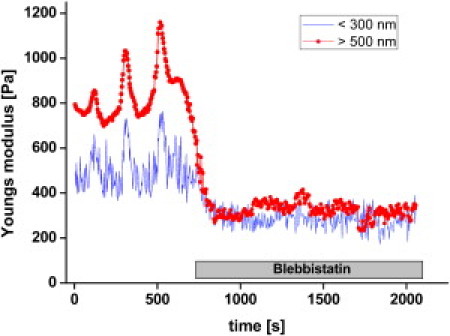
Effect of blocking myosin II on elasticities measured at indentations below 300 nm and above 500 nm.

Discussion

Oscillation of cell elasticity

In this article, elasticity oscillations of human bronchial epithelial cells were shown with a new experimental approach. The principle of this method is to indent a cell repetitively with a probe using a constant loading force. The resulting force-indentation data were fitted according to the implementation of the Hertz model (4), resulting in time-resolved sequences of cell elasticity. This approach discloses spontaneous oscillations of cell elasticity and allowed us to quantify its amplitude and period. Investigating the dynamics of complex systems that consist of many chemical, mechanical, and/or genetic networks readily leads to an oscillatory behavior as a consequence of self-organization. Experiments have shown that motor molecules collectively working within assemblies can generally power spontaneous oscillations (47,48). These oscillations are related to a wide range of functions, e.g., movement of cell organelles, cell length oscillation, and contraction. Oscillations can be spontaneous (self-induced) or induced by specific substances applied exogenously (49). Spontaneous oscillations in elasticity are potentially caused by oscillations of intracellular free calcium. Calcium oscillations serve fundamental cell signaling processes (49–51). One of these processes is the activity of myosin motor proteins. Activation of all types of vertebrate muscle involves calcium ions (52), but also the activity of many unconventional myosins dependent upon calcium (11).

We could show that, upon simultaneous application of ionomycin and blebbistatin, elasticity oscillations disappear despite the elevation of intracellular calcium by ionomycin. This shows that calcium-dependent and blebbistatin-sensitive motor proteins determine the dynamical behavior of the cell's elasticity. Calcium-induced polymerization and depolymerization, branching, crosslinking, and entanglement of cytoskeletal elements (entropic/enthalpic elasticity) are not primarily involved in the periodic elasticity changes. In agreement with our present findings, it has been reported that the myosin II motors show autooscillations, when the intracellular level of free Ca²⁺ is intermediate, between the high level during contraction and the low level during relaxation (19). Periodicity and amplitude Ca²⁺ oscillations can be varied over a wide range from 2 s up to 40 min (49).

The oscillations of bronchial epithelial cells observed in this work are driven by myosin motor proteins that strictly depend on calcium, and the period of 200 s fits well to the reported frequency range of Ca²⁺ oscillations. Thus, the observed elasticity changes are most likely a result of myosin II motor protein activity driven by spontaneous Ca²⁺ oscillations. Obviously, these oscillations represent a basal biomechanical activity of cells. The meaning of these oscillations as well as its effect on cell or tissue function is still unknown. It can be speculated that this basal biomechanical activity facilitates thixotropic gel-sol transition of the cytoplasm (53). It is also imaginable that the periodic elasticity changes in one cell are transmitted to the neighboring cells. Thus, elasticity oscillations could serve as a biomechanical signaling process. Possibly, cells within a monolayer oscillate synchronously to maintain mechanical homeostasis at the tissue, cellular, and subcellular levels. Further investigations are necessary to characterize these periodic mechanical activities and their meaning for cell and tissue function.

Cell elasticity is determined by the cortical actin cytoskeleton

Processing force-indentation data of bronchial epithelial cells relating to the indentation depth reveals that a cell is not homogenous in terms of elasticity. This has been also reported from elasticity measurements of COS cells (54) and human cervical epithelial cells (55) in which the cell was considered as a mechanically multilayered structure. The first layer (the most superficial one) is assumed to represent the cortical actin cytoskeleton. Therefore, any changes in the myosin activity should be most prominent at indentations between 0 and 300 nm.

Our data show that the Young's moduli at deep indentations (>500 nm) are approximately two-times higher than in the superficial region (<300 nm). Indenting a multilayered structure means that, at small indentations, mainly the first (superficial) layer is deformed. At deeper indentations, a second layer is also deformed but, due to the multilayered assembly, the first layer is certainly more severely deformed as compared to the second layer and thus, although less stiff than the second layer, will significantly contribute to the elasticity calculated from the force-indentation curves.

Additionally, stress stiffening of the cytoskeleton (56) could increase the elasticity calculated for deeper indentations. Obviously, the mechanical properties of the superficial region appear also in the deeper regions. Recently, a method called stiffness tomography was developed to show stiffness differences along the indentation path (46,54) by dividing a force-indentation curve into segments of 10 nm and applying the Hertz model to each segment. However, even when applying this elegant method, the influence of outer layers of a multilayered structure cannot be excluded when calculating elasticity from deeper indentations. Nevertheless, both the present method as well as stiffness tomography are suitable approaches for the detection of rather hard structures underneath soft superficial layers as a function of indentation depths.

The contribution of cortical myosin II to cell elasticity was shown by indentation depths depending upon data processing before and after application of blebbistatin. Blocking myosin II decreased elasticity not only in the superficial region but also at indentations beyond 500 nm. Although cells exhibit two-times' higher Young's moduli at deep indentations, blebbistatin induces a decrease of elasticity in both regions down to the same value. This indicates that the elasticity of a cell is determined by the elastic properties of the bulky cytosol (passive component) superimposed by myosin II activity (active component). After blocking the active component (myosin II) by blebbistatin, the mechanical properties of the passive component (bulky cytosol) dominates and cells become more homogenous in terms of cell elasticity over a wide range of indentation depths. This indicates that elasticity of the cortical actomyosin dominates the mechanical properties of the cell at all indentation depths.

Conclusions

Our approach of real-time monitoring of cell elasticity allows following the dynamics of the cytoskeleton with high time resolution. This discloses oscillations of cell elasticity in bronchial epithelial cells which were driven by periodic activities of Ca²⁺-dependent myosin II motor proteins. The cell elasticity reflects the status of the cytoskeleton, which is determined by active and passive components. Because the status of the cytoskeleton is the result of a complex regulatory machinery, elasticity is a parameter that reflects the behavior of the system rather than the specific properties of individual components. Thus, a time-resolved elasticity measurement could provide deep insight into cellular dynamics in response to changes of the chemical and mechanical environment.