Abstract
Between 1994 and 2006, the ratio of foreign-born scientists and engineers (FSE) to native scientists and engineers (NSE) doubled. I decompose this change into a migration effect (which accounts for migration in general), a proportional college effect (which accounts for the relative proportions of college graduates among migrant and native workers), and a proportional science and engineering (S&E) effect (which accounts for the relative proportions of S&Es among migrant and native college-educated workers). Results show that the migration effect explains about three-quarters of the increase in FSE/NSE during the entire period under study. The proportional S&E effect, which captures changes in the ratio as a result of immigration of S&Es in excess of what would be expected from general migration alone, was largest in 1995–1998, which were years of sustained economic growth. Conversely, a slower economy coincided with a declining proportional S&E effect after 2000. Increases in the annual cap on H-1B visas, an important avenue of entry for foreign-born S&Es, had little effect on the ratio. In short, during 1994–2006, the association between economic swings and the specific, more than proportional migration of S&Es was much stronger than the association between the latter and changes in the H-1B cap.
While the international movement of unskilled labor normally confronts obstacles and barriers to entry, virtually all developed countries, as well as the leading emerging economies, compete to attract highly skilled workers (Economist 2006; Hawthorne 2005; Iredale 2000; Regets 2001). This competition spans across all fields of knowledge and is certainly noticeable in science and engineering (S&E1). In the United States, the immigration of S&E workers has been the subject of debate, especially when predicated upon claimed shortages of skilled labor in the Information, Communications, and Technology (ICT) industry (North 1995; Teitelbaum 2003) and facilitated by the H-1B visa program. The immigration of S&E workers to meet employers’ genuine needs, however, is often considered a matter of national economic and strategic interest (Jorgenson and Wessner 2007; Lowell 1999; Regets 2001). Under the perception that the domestic labor supply of S&Es was insufficient to meet U.S. demand, Congress took specific measures to attract foreign-born S&Es toward the end of the previous century and early in the present one.
Accepting the strategic and economic importance of a sizable S&E workforce but avoiding judgment on the actual size of the S&E supply, I examine changes in the composition of the U.S. S&E employed workforce by nativity in the 1994–2006 period. Specifically, I analyze year-to-year changes in the ratio of foreign-born2 S&Es (FSE) to native S&Es (NSE) and relate these changes to immigration policy—specifically, variations in the H-1B visa cap—and overall economic growth. The analysis is meaningful because the so-called “new economy” was predicated upon the productivity boost fueled by the ICT industry, an important employer of S&Es and a major lobbyist for pro-immigration measures (Jorgenson and Wessner 2007). For example, a scenario in which pro-immigration policy measures were followed by an increase in the foreign-born component of the S&E workforce, followed in turn by strong economic growth, would cast an aura of success on such policies even if solid causality claims would demand more nuanced analysis.
My methodological tool is a well-known decomposition technique proposed by Das Gupta (1993). I decompose the change in the ratio in question into a migration effect, a proportional college effect, and a proportional S&E effect. My focus is on the latter, which accounts for the relative proportions of S&Es among migrant and native college-educated workers, or a measure of the relative concentration of foreign-born and native skilled3 workers in S&E occupations. A positive and large proportional S&E effect would signal migration of S&Es of a larger magnitude than what would be expected from given levels of migration and given levels of migration of college-educated workers.
In this article, I report that the largest proportional S&E effects have mostly been associated with years of economic growth and have not been associated with increases in the H-1B visa cap, a policy measure specifically intended to increase the supply of foreign-born S&Es. In other words, a dynamic economy created jobs and opportunities that attracted all kinds of foreign-born workers, including S&Es, but immigration policy designed to attract foreign-born S&Es was of limited consequence when the economy was not on a growing track. This is not to say that immigrant S&Es do not contribute to economic dynamism—the present analysis cannot address that question—but that in the absence of a positive economic outlook, immigration policies to attract skilled workers would probably be ineffective. The current slowdown in applications for H-1B visas seems to confirm this conclusion.
THE SCIENCE AND ENGINEERING WORKFORCE
Estimates of the size of the S&E workforce as well as of any subgroup within it, such as the foreign-born, naturally depend on the criteria used to define who is a scientist or an engineer. This definition can be based on occupation, highest degree earned, or job requirements. All three criteria have advantages and disadvantages, and preference for any of them depends on the purpose of the analysis. They lead to divergent estimates, with those based on degrees tripling those based on occupations, a result of a loose fit between occupations and degrees. Using 2006 data, degree-based definitions produce estimates ranging from 14.5 to 21.4 million S&Es, and occupational definitions lead to estimates in the 3.9–5.4 million range, depending on the data source (National Science Foundation 2008). The research presented here relies on an occupational definition, the rationale for which will be provided in the Data section of this article.
Foreign-born graduates accounted for most of the growth in S&E doctoral degrees awarded by U.S. universities in the period 1985–2005: “During this period, the number of S&E doctorates earned by U.S. citizens fluctuated from approximately 14,000 to about 17,000, while the number earned by temporary residents rose from 4,200 to a peak of 10,800 in 2005. The temporary resident share of S&E doctorates rose from 21% in 1985 to 36% in 2005” (National Science Foundation 2008:2–31). Among S&E master’s degree recipients, the same share rose from 19% to 28%, while it remained low (close to 4%) among recipients of bachelor’s degrees in S&E (National Science Foundation 2008:2–27 and 2–29).
Many foreign-born S&E graduates from American universities secure jobs upon graduation and eventually settle in the United States. They represent a sizable share of the S&E immigration flow (Lowell 2001; North 1995). Migration researchers as well as those who track developments in the S&E workforce have paid close attention to foreign-born S&Es. They have addressed questions concerning measurement, productivity, wages, immigrant entrepreneurship, alleged shortages of skilled ICT workers, outsourcing of ICT jobs, and immigration policy (Bean and Brown 2005; Espenshade 2001; Espenshade, Usdansky, and Chung 2001; Freeman 2005; National Science Foundation 2008; North 1995; Regets 2001; Saxenian 1999; Saxenian, Motoyama, and Quan 2002; Stephan and Levin 2001; Teitelbaum 2003; Wadhwa et al. 2007; Watts 2001).
IMMIGRANT S&ES AND THE H-1B PROGRAM
To work legally in the United States, a foreign-born individual must hold a student visa or a work visa, or be a lawful permanent resident (LPR) or a United States naturalized citizen. Students are the most constrained because they can work only for the educational institutions in which they are enrolled, and this work must be part of their training program. A work visa holder may work only for the employer that sponsored the visa. These constraints do not apply to LPRs and citizens. Except for eligibility for most federal—and some state—government jobs, there is no work-related difference between them.
There are S&Es, of course, in all four situations. Graduate students typically work as research assistants, thus participating in the S&E workforce. Foreign-born professionals trained abroad as well as foreign-born graduates from U.S. universities join the S&E workforce every year on work visas. In turn, sponsored by their employers, many adjust their status from a work visa (or, less frequently, a student visa) to LPR. In addition, large numbers of skilled immigrants reach LPR status through family ties rather than employment (Kannankutty and Burrelli 2007). After a number of years in LPR status (in most cases, five years), immigrants become eligible for citizenship.
The United States issues work visas to skilled individuals under various classifications, of which the H-1B is the one that most directly targets S&Es. Legislation regulating work visas is more malleable and subject to change on a more regular basis than legislation on lawful permanent residency, and the H-1B visa has been one of the avenues of admission into the United States most significantly affected by immigration policy since Congress introduced it in 1990. Under the H-1B program, employers wishing to hire a foreign-born professional must file a labor condition application with the Department of Labor, attesting to posting the application at the job site, a lack of a strike or lockout, working conditions consistent with those of comparable workers, and payment of the prevailing wage for the position requested (Meyers 2006). Foreign workers can be on H-1B status for up to six years unless they have applied for adjustment of status to LPR, in which case their H-1B visas are extended until their cases are adjudicated.
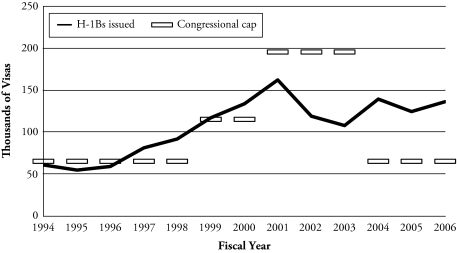
Work visas, whether H-1B or other classifications, require shorter processing and adjudication time than employment-based lawful permanent residency. Because of this, and because work visa holders are legally bound to their sponsors, employers wishing to hire skilled foreigners have made extensive use of “nonimmigrant” visa categories. Of these visas, the H-1B is the only one subject to an annual cap set by Congress. With data from the Immigrant Visa Control and Reporting Division of the Department of State,4 Figure 1 shows the number of H-1B visas issued5 annually during fiscal years6 (FY) 1994–2006, as well as the respective congressional caps.7
Figure 1.
H-1B Visas Issued and Congressional H-1B Cap, 1994–2006
Toward the end of last century, claims of a shortage of talented ICT labor persuaded Congress to raise the annual cap on H-1B visas from 65,000 to 115,000 in FY 1999. As the economy roared and the ICT industry overheated, the new cap was quickly reached, and Congress raised it again to 195,000 effective in FY 2001. However, almost simultaneously, the economic boom came to an end. The new cap proved unneeded, and it was never reached. In FY 2004, Congress returned the cap to its pre-1999 level. Exemptions to the cap were introduced in 2000, benefiting skilled foreign workers hired by universities, nonprofit organizations, and government research laboratories; and again in 2005, assigning 20,000 extra visas to foreigners who earn a graduate degree from a U.S. university. These exemptions explain the number of H-1B visas issued over the cap since 2000.
ECONOMIC TRENDS
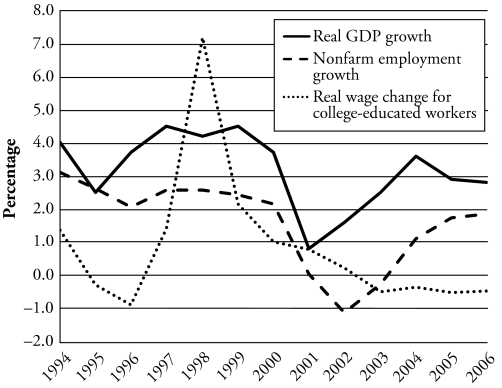
Figure 2 depicts growth in real gross domestic product (GDP), nonfarm employment, and mean wages of college graduates during the period under study, 1994–2006. The figure shows high GDP growth rates during the late 1990s, followed by an economic slowdown in 2000–2001, and a gradual recovery since. Nonfarm employment trends follow GDP trends with a one-year lag at the 1995–1996 and 2001–2002 turns. Real wages of college-educated workers show a dramatic spike during the economic boom of the late 1990s, followed by some years of more moderate growth and losses after 2002 despite the economic recovery.
Figure 2.
Growth in Real GDP, Nonfarm Employment, and Mean Wages Among College-Educated Workers, 1994–2006
Sources: For GDP, data are from the Bureau of Economic Analysis (http://www.bea.gov). Data for nonfarm employment are from the Bureau of Labor Statistics (http://www.bls.gov). Wage figures are from author’s calculations using the Merged Outgoing Rotation Groups (MORG) extracts of the Current Population Survey.
The late 1990s were characterized by sustained economic growth associated with a rapid increase in productivity, low inflation despite low unemployment, a high rate of investment in new technology, and a booming stock market, among other features of what came to be called the “new economy” (Council of Economic Advisers 2001; Temple 2002). The roaring stock market was largely led by the price of ICT shares associated with what was dubbed the “dot-com boom,” conventionally dated between August 9, 1995 (the day of the Netscape initial public offering) and March 10, 2000 (the day the NASDAQ index peaked). While the extremely high prices of ICT stocks at the peak of the boom reflected a financial bubble (Cassidy 2002), the leading role of the ICT sector during the economic boom was real. Specifically, the increase in production of semiconductors, computer hardware and peripherals, and software—together with the dramatic decline in the cost of telecommunications and data transmission—was at the core of the productivity boost of the late 1990s (Jorgenson and Wessner 2007; Oliner and Sichel 2000). These are sectors with high concentration of skilled labor and, in particular, S&Es. The importance of skilled labor in the productivity boost of the late 1990s is suggested by positive growth rates in the real wages of college graduates, with a remarkable spike in 1998.
After the slowdown, the economy began to recover, supported by a new “productivity growth explosion” in 2001–2004 (Gordon 2006), although slower rates of productivity growth were recorded in 2005 and 2006, consistent with the lower rates of real GDP growth shown in Figure 2 for those years. In the new century, increases in productivity seem only loosely associated with skilled labor. Industry restructuring and cost-cutting in response to profit pressures appear to be the major contributors to the post-2001 productivity explosion (Oliner, Sichel, and Stiroh 2007), an explanation that is consistent with the declining real wages of college graduates shown in Figure 2. It follows that prospects for S&Es since the beginning of the present century have not matched those of the late 1990s.
THE RATIO OF FOREIGN-BORN TO NATIVE S&ES
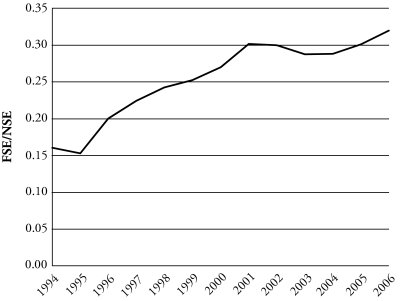
The following analysis focuses on annual changes in the ratio of foreign-born to native S&Es. Defining scientists and engineers as college-educated individuals in S&E occupations, the ratio between foreign-born and native S&Es doubled from 0.16 in 1994 to 0.32 in 2006. Or, equivalently, there were 6.2 natives per migrant in S&E occupations in 1994, but only 3.1 in 2006 (estimation details are given later in the article). The evolution of the ratio during the period under study, 1994–2006, is displayed in Figure 3, which shows steady increases between 1995 and 2001, and since 2004. As discussed earlier, these periods were characterized by high rates of economic growth. It also appears that growth in the ratio accelerated between 1999 and 2001, after the first increase in the H-1B visa cap, but then stagnated and even reversed after the second cap raise in 2001.
Figure 3.
Ratio of Foreign-born to Native S&Es (FSE/NSE), 1994–2006
DATA
As described in the Method section, six data series are needed: total number of workers, college-educated workers, and college-educated workers in S&E occupations, each of these for U.S. natives and for the foreign-born, for each year of the period 1994–2006. I use the Merged Outgoing Rotation Groups (MORG) extracts from the Current Population Survey (CPS). The CPS, which is conducted monthly by the U.S. Census Bureau for the Bureau of Labor Statistics (BLS), collects data on nativity since 1994, which sets the first year of the analysis. Every household that enters the CPS is interviewed each month for 4 months, ignored for 8 months, and then interviewed again for 4 more months. The MORG data sets, available from the National Bureau of Economic Research,8 are annual data files that include only those households in their fourth and eighth interview each month. Because the fourth and eighth interviews are one year apart, in the MORG extracts, no household is recorded twice in the same survey year. By comparison with any monthly CPS, the MORG extracts contain households interviewed throughout the year, reducing the effect of occasional large sampling errors in any given month (Schmidley and Robinson 2003:3). Because each month covers one-fourth of all CPS households surveyed that month, each MORG annual data set has about three times as many households as the average monthly CPS. Therefore, after weights are adjusted (simply using one-third of the CPS final weight variable), my estimated counts of a given subpopulation in any given year produced with the MORG extracts may differ very slightly from published counts computed as averages of the 12 monthly estimates.
Comparability Issues
Comparability between estimates from different years of the survey is affected by a change in the population controls used to produce the sample weights and by a revision of the U.S. Standard Occupational Classification (SOC) used to code occupations.
CPS data are weighted to produce population totals. The weights depend on “population controls” derived from population projections benchmarked to the last census and adjusted for various factors that do not include nativity (U.S. Census Bureau 2006: appendix C). In other words, estimates of population totals that can be obtained from the CPS ultimately depend on population projections prepared by the Census Bureau. The 2000 census revealed that the projections based on the 1990 census were low. Using 2000 census results, the CPS population controls were corrected. Schmidley and Robinson (2003) showed that the percent increase in the estimate of the foreign-born that results from the new weights is significantly larger than the increase recorded for natives.
The MORG data files provide both the 1990-based weights and the 2000-based weights for the years 2000–2002. The new weights do result in a larger estimate for all six data series, and the increases are proportionally much higher for the three foreign-born subpopulations. The largest percentage increase among natives is 0.70% (for the college-educated in 2002), while percentage increases among the foreign-born range from 6.82% (college-educated in 2000) to 8.69% (S&Es in 2002). Increases of such magnitudes in the foreign-born population because of the revision of weights in the year 2000 are almost certainly artificial if one attributes them entirely to 1999–2000, but they are most likely genuine for the period between the two censuses: 1990–2000. I chose to smooth the effect of the revision of weights, for all six populations under study, by distributing percentage increases evenly throughout the 1990–2000 period.9
The SOC was introduced in 1977, revised in 1980, and revised again in 2000 (Bureau of Labor Statistics 1999). In the MORG data sets, occupations are coded using the 1980 SOC through 1999, and the 2000 SOC afterward. However, to allow comparability and for evaluation purposes, the 1980 codes are also available in 2000, 2001, and 2002. Given that an important share of the substantial changes in the U.S. occupational structure between 1980 and 2000 relates to the dramatic growth of the ICT industry, it is not surprising that the effect of the new classification is to increase the number of workers in S&E occupations (Ellis 2007). The effect is much larger among the foreign-born than among natives. Comparing estimates by using the 2000 SOC with those obtained using the 1980 SOC results in an increase of 15% (for 2000 and 2001) and 19% (2002) of foreign-born S&Es, more than doubling the increase among natives of 7% (in 2000) and 6% (in 2001 and 2002).
In response to this problem, I conducted two separate analyses.10 In one analysis, I used 1980 SOC codes for 1994–1999 and 2000 SOC codes since 2000; in the other analysis, I used 1980 SOC codes through 2002 and 2000 SOC codes starting in 2003. In both cases, it is important to keep in mind that the annual increase in S&E occupations recorded when the 2000 SOC codes are adopted should not be interpreted as a genuine sudden spike. The dual exercise is useful because changes up to 2000, 2001, or 2002 can be considered using the analysis that preserves 1980 SOC codes through 2002; for changes beginning in 2000, I can focus on the analysis that uses 2000 SOC codes since 2000.
Definition of Scientists and Engineers
I define scientists and engineers as employed college-educated workers in S&E occupations. This operational definition leaves aside those not in the labor force; the unemployed; those without college degrees; and, more importantly, people with training in S&E but with jobs that are not classified as S&E jobs.
My preference for an occupational definition is both data related and conceptual. The alternative data set to study the S&E population is the National Survey of College Graduates (NSCG) sponsored by the National Science Foundation. In addition to the occupational data available from the CPS, the NSCG has information on degree field that can be used for a degree-based definition of S&Es. An advantage of the NSCG is that it makes it possible to count graduate research assistants (as long as their college-level degrees are in S&E fields) who perform S&E work but are coded as full-time students in the CPS. The CPS, however, has two key advantages: first, its regularity allows for a full decomposition analysis that makes it possible to associate changes to events that took place in specific years. The NSCG, by contrast, has produced six surveys between 1993 and 2006. Second, CPS response rates have hovered around 93%–94% since 1994 (U.S. Census Bureau 2006: chap. 16). For the NSCG, the weighted response rate was comparatively low in 1993 (80%) and in 2003 (73%).11
Conceptually, an occupational definition is useful for two reasons. First, occupations are more responsive than educational credentials to short-term changes, such as those produced by economic swings or immigration policy. Because the present study aims at precisely identifying such changes, an occupational definition is in order. Second, the H-1B program does not sponsor the migration of professionals in general, but rather the migration of specific individuals to work specific jobs. It prioritizes jobs over degree field while virtually restricting entry to those with higher education credentials—altogether, a good match with the occupational definition that I use.
The appendix lists my selection of S&E occupations using 1980 SOC codes and using 2000 SOC codes. My list includes professional but not technical occupations. A downside from the reclassification of occupations in 2000 stems from the grouping of all post-secondary teachers into a single code (Ellis 2007; National Science Foundation 2008:3–10). Had the discrimination by discipline (present in the 1980 SOC) been maintained, I would have been able to include postsecondary teachers of S&E specialties. Because this is impossible using the 2000 SOC, I did not include them when I used the 1980 SOC, either. Another limitation is that full-time graduate research assistants, even when performing S&E work, are coded as students.
ANALYTICAL APPROACH
Rationale
The dramatic increase in the ratio of foreign-born to native S&Es described earlier resulted from the interplay of changes in six populations or subpopulations: employed natives, employed college-educated natives, college-educated natives in S&E occupations, and their foreign-born counterparts in all three cases. Using a technique proposed by Das Gupta (1993), outlined in the next section, I decompose the change in the ratio in question into a migration effect (which accounts for migration in general), a proportional college effect (which accounts for the relative proportions of college graduates among migrant and native workers), and a proportional S&E effect (which accounts for the relative proportions of S&Es among migrant and native college-educated workers). These effects can be pinpointed to specific subperiods within the time span under analysis, which makes them informative in light of the immigration policy measures and economic trends reviewed earlier. The key effect of interest is the proportional S&E effect, which in essence is a measure of the relative concentration of foreign-born and native skilled workers in S&E occupations.
For example, how do the three effects listed earlier relate to the timing of immigration policy measures aimed at increasing the number of visas for ICT workers? Recall that the cap on H-1B visas was increased in 1999 and in 2001, returning to its pre-1999 level in 2004. Presumably, these measures should have resulted in a large proportional S&E effect: that is, a sizable increase in the proportion of S&Es among foreign-born college-educated workers, far larger than the same increase among their native counterparts. This is just to say that a large proportion of the growth in the ratio of foreign-born to native S&Es after raises in the H-1B cap would have been a consequence of the specifically supported immigration of S&Es.
Further interest is elicited by focusing on the peak years of the “new economy” of the late 1990s, which preceded H-1B cap increases. If a booming economy, even in the absence of specific immigration policy measures, strongly attracts immigrant S&Es, one should observe a large proportional S&E effect in the years that preceded increases in the H-1B cap. Otherwise, a booming economy will simply attract all sorts of migrants, explaining increases in the ratio of interest via a large migration effect.
Method
The initial formula for the decomposition analysis is
| (1) |
where, for any given year, F indexes the foreign-born, N indexes natives, SE stands for scientists & engineers, and C indicates college degree or higher. The equation refers to the employed workforce only. I can rewrite it as
| (2) |
In words, in any given year, the ratio of foreign-born to native S&Es is the product of the ratio of migrant to native workers (m); the ratio of the proportion of college-educated workers among the foreign-born to that among the native workforce, or proportional college ratio (c); and the ratio of the proportion of S&Es among foreign-born college-educated workers to that among native-born college-educated workers, or proportional S&E ratio (se). With data for each year of the period 1994–2006, using a technique developed by Das Gupta (1993), I decompose the change in FSE/NSE between any pair of years in the series into effects attributable to m, c, and se, which I label the migration effect, the proportional college effect, and the proportional S&E effect, respectively. Each effect reports how the FSE/NSE ratio would have changed if only the factor in question had changed while the other two remained constant.
For example, the migration effect shows the change in FSE/NSE that would have still happened even if c and se had not changed. Conceptually, this subsumes the effect of migration12 alone. To clarify what this means, imagine the scenario in which migration alone explained 100% of the increase in FSE/NSE with the other effects being zero: a larger percentage increase in the migrant workforce than in the native workforce (i.e., m increases), with no change in the ratio between the proportions of workers with college degrees in the two populations (c is constant), and no change in the ratio between the proportions of these college-educated workers in S&E occupations (se is constant), again in both populations. In this case, the growth in the ratio of foreign-born to native S&Es is no more than the normal consequence of overall migration growth.
The second effect, the proportional college effect, refers to the change in FSE/NSE that would have been recorded if only the relative proportions of college graduates among migrants and natives had changed. In essence, this is a simplified skills effect that does not take into account the distribution of these skills among fields. In the presentation of results, I make only occasional references to this effect because of its limited empirical significance.
As I defined them, only college graduates can be scientists or engineers; thus, the last effect is attributable to changes in the proportions of S&Es among eligible workers only. This is the proportional S&E effect, which represents the change in FSE/NSE that would have occurred if only the ratio of the proportion of college-graduate S&Es among migrants to that among natives had changed. To interpret this effect, consider the scenario in which it alone explains 100% of the change in FSE/NSE and the migration and the proportional college effects are both zero. This scenario results from FC growing at the same rate as NC, and also F growing at the same rate as N, so that m and c do not change between Time 1 and Time 2. (Notice that because I am assuming that FSE/NSE does change, change in at least F and FC, or in N and NC, is implied.) In short, the proportional S&E ratio signals change in FSE/NSE as a result of a “genuine” (or disproportionate) growing presence of migrants in S&E occupations, over and above what one would expect from overall migration alone and from changes in the proportions of natives and migrants with college degrees.
A decomposition analysis begins with a standardization technique. In this case, I standardize the ratio in question (FSE/NSE) for all factors except (one at a time) m, c, and se. For example, the series for FSE/NSE standardized for all factors except m shows what FSE/ NSE would have been, in each year of the period under study, if only m had varied, while c and se remained constant. After this is done, the effects introduced earlier are simply calculated as differences between standardized ratios. For example, the migration effect for the subperiod 2000–2006 is calculated as FSE/NSE standardized for all factors except m in 2006 minus FSE/NSE standardized for all factors except m in 2000. Two consistency conditions must be met. First, the sum of all three effects for any given pair of years must equal the difference between the two observed values of FSE/NSE for those same years. Second, the sum of the effects for subperiods within a period must equal the effect for the total period; for example, the migration effect for 2000–2006 must equal the sum of the migration effects for 2000–2004 and 2004–2006.
In formulas, for any given number of years, one must first calculate all the pairwise standardized FSE/NSE, ignoring the other years (Das Gupta 1993:8). For example, for Years 1 and 2, FSE/NSE standardized for all factors except m is
| (3) |
| (4) |
Afterward, the standardization formula that meets the two consistency conditions is (Das Gupta 1993:106)
| (5) |
where α i.j represents FSE/NSE standardized for all factors except α for the comparison between year i with year j, ignoring the other years. If α is, for example, the migrant-to-native worker ratio m, the standardization refers to FSE/NSE standardized for c and se (as in formulas 3 and 4). α 1.23…N refers to FSE/NSE standardized for all factors except α in Year 1, in the presence of the other years, given N years.
Unlike regression, a decomposition technique neither addresses causality nor is affected by random error. Instead, it provides a nuanced description of the trend under study.
RESULTS
Basic Trends and Input Data
Table 1 shows workers, college-educated workers, and S&Es among both the foreign-born and natives. The 2.63 million U.S.-born S&Es (rightmost column) in 1994 outnumbered their foreign-born counterparts (423,000) by a factor of 6.2. In 2006, there were only 3.1 U.S.-born S&Es per foreign-born peer (3.55 million vs. 1.14 million).
Table 1.
Workers, College-Educated Workers, and College-Educated Workers in S&E Occupations, Foreign-born and Native, 1994–2006 (in thousands)
| Foreign-born |
Native |
|||||
|---|---|---|---|---|---|---|
| Year | All Workers | College+ | S&E | All Workers | College+ | S&E |
| 1994 | 12,185 | 3,039 | 423 | 111,271 | 28,111 | 2,633 |
| 1995 | 12,332 | 3,025 | 409 | 113,046 | 29,052 | 2,675 |
| 1996 | 13,938 | 3,635 | 541 | 113,400 | 29,627 | 2,699 |
| 1997 | 15,129 | 3,971 | 641 | 115,229 | 30,433 | 2,861 |
| 1998 | 16,037 | 4,270 | 713 | 116,757 | 31,426 | 2,945 |
| 1999 | 16,653 | 4,602 | 771 | 118,218 | 32,293 | 3,053 |
| 2000 (1980 SOC) | 18,143 | 4,938 | 814 | 118,737 | 32,740 | 3,225 |
| 2000 (2000 SOC) | 18,143 | 4,938 | 933 | 118,737 | 32,740 | 3,459 |
| 2001 (1980 SOC) | 18,870 | 5,241 | 874 | 118,300 | 33,118 | 3,139 |
| 2001 (2000 SOC) | 18,870 | 5,241 | 1,003 | 118,300 | 33,118 | 3,329 |
| 2002 (1980 SOC) | 18,986 | 5,390 | 794 | 117,464 | 33,828 | 2,983 |
| 2002 (2000 SOC) | 18,986 | 5,390 | 947 | 117,464 | 33,828 | 3,163 |
| 2003 | 19,680 | 5,581 | 979 | 118,050 | 34,723 | 3,408 |
| 2004 | 20,261 | 5,690 | 984 | 119,108 | 35,583 | 3,418 |
| 2005 | 21,008 | 5,995 | 1,063 | 120,921 | 36,201 | 3,535 |
| 2006 | 22,179 | 6,423 | 1,135 | 122,339 | 37,168 | 3,554 |
Notes: Figures shown are point estimates from CPS-MORG files. College+ stands for college degree or higher. S&E is short for science and engineering occupations. Each column category is fully included into the previous one, so that all college+ are workers, and all S&Es are college-educated workers. See the text for treatment of weights.
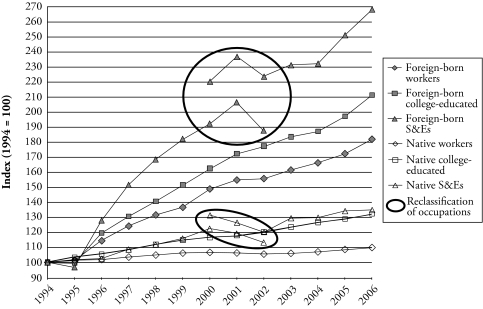
The growth of each of the six subpopulations can be better appreciated in Figure 4, which shows indices based in 1994. The figure also shows the effect of the reclassification of occupations: for the two series on S&Es, estimates from data coded using the 1980 SOC are shown through 2002; estimates from data coded using the 2000 SOC are shown from 2000 onward. The second series clearly produces higher estimates than the first one for the overlapping years 2000–2002. Figure 4 shows that all three foreign-born subpopulations grew much more rapidly than all three U.S.-born subpopulations. In addition, for both the foreign-born and natives, it is clear that the subpopulation of S&Es grew faster than the subpopulation of college graduates, which in turn grew faster than the overall working population.
Figure 4.
Working Population: Total, College Graduates, and College Graduates in Science and Engineering Occupations, Foreign-born and Native, 1994–2006 (1994 = 100)
Table 2 shows the series of ratios needed for the decomposition analysis, calculated from Table 1. The goal is to decompose the change in FSE/NSE, the ratio between foreign-born and native S&Es. As defined earlier, this ratio is the product of the other three ratios shown: the migrant-to-native worker ratio (m), the migrant-to-native proportional college ratio (c), and the migrant-to-native proportional S&E ratio (se).
Table 2.
Ratios Used in the Decomposition
| Year | FSE/NSEa | mb | cc | sed | se With 1980 SOCe |
|---|---|---|---|---|---|
| 1994 | 0.161 | 0.110 | 0.987 | 1.487 | |
| 1995 | 0.153 | 0.109 | 0.955 | 1.469 | |
| 1996 | 0.200 | 0.123 | 0.998 | 1.634 | |
| 1997 | 0.224 | 0.131 | 0.994 | 1.718 | |
| 1998 | 0.242 | 0.137 | 0.989 | 1.782 | |
| 1999 | 0.253 | 0.141 | 1.012 | 1.772 | |
| 2000 | 0.270 | 0.153 | 0.987 | 1.788 | 1.674 |
| 2001 | 0.301 | 0.160 | 0.992 | 1.903 | 1.760 |
| 2002 | 0.299 | 0.162 | 0.986 | 1.879 | 1.671 |
| 2003 | 0.287 | 0.167 | 0.964 | 1.788 | |
| 2004 | 0.288 | 0.170 | 0.940 | 1.800 | |
| 2005 | 0.301 | 0.174 | 0.953 | 1.816 | |
| 2006 | 0.319 | 0.181 | 0.953 | 1.849 |
FSE/NSE: Ratio of foreign-born to native S&Es.
m: Ratio of foreign-born to native workers.
c: Foreign-born-to-native proportional college ratio.
se: Foreign-born-to-native proportional S&E ratio. 1980 SOC codes for 1994–1999, and 2000 SOC codes for 2000–2006.
The last column shows the foreign-born-to-native proportional S&E ratio when the 1980 SOC codes are used for 2000–2002.
Decomposition
Table 3 presents observed and standardized ratios of foreign-born to native S&Es for each year of the period 1994–2006. The left panel uses the 1980 SOC for the classification of S&Es through 2002, and the 2000 SOC from 2003 on. The right panel uses the 1980 SOC through 1999, and applies the 2000 SOC from 2000 on. To obtain the effects, consider the figures on the left panel for 1994 and 2006. In 1994, the observed FSE/NSE was 0.161; in 2006, it was 0.319, for an increase equal to 0.158. The difference between the ratio standardized for all factors except m (that is, standardized for c and se) for those same years is 0.304 – 0.187 = 0.117.13 This figure is the migration effect for 1994–2006. Similar calculations lead to the other two effects.
Table 3.
Ratio of Foreign-born to Native S&Es, Observed and Standardized, 1994–2006
| Year | With 1980 SOC Through 2002 |
With 1980 SOC Through 1999 |
||||||
|---|---|---|---|---|---|---|---|---|
| Observed FSE/NSE | FSE/NSE Standardized for All Factors Except: |
Observed FSE/NSE | FSE/NSE Standardized for All Factors Except: |
|||||
| m | c | se | m | c | se | |||
| 1994 | 0.161 | 0.187 | 0.250 | 0.218 | 0.161 | 0.191 | 0.255 | 0.219 |
| 1995 | 0.153 | 0.187 | 0.243 | 0.216 | 0.153 | 0.192 | 0.248 | 0.217 |
| 1996 | 0.200 | 0.206 | 0.252 | 0.236 | 0.200 | 0.211 | 0.258 | 0.236 |
| 1997 | 0.224 | 0.219 | 0.252 | 0.247 | 0.224 | 0.224 | 0.257 | 0.248 |
| 1998 | 0.242 | 0.229 | 0.251 | 0.256 | 0.242 | 0.234 | 0.256 | 0.256 |
| 1999 | 0.253 | 0.235 | 0.256 | 0.255 | 0.253 | 0.240 | 0.262 | 0.255 |
| 2000 | 0.252 | 0.255 | 0.250 | 0.241 | 0.270 | 0.261 | 0.256 | 0.258 |
| 2001 | 0.278 | 0.267 | 0.252 | 0.254 | 0.301 | 0.273 | 0.257 | 0.275 |
| 2002 | 0.266 | 0.270 | 0.250 | 0.240 | 0.299 | 0.277 | 0.255 | 0.272 |
| 2003 | 0.287 | 0.279 | 0.244 | 0.258 | 0.287 | 0.285 | 0.249 | 0.258 |
| 2004 | 0.288 | 0.284 | 0.237 | 0.260 | 0.288 | 0.290 | 0.243 | 0.260 |
| 2005 | 0.301 | 0.291 | 0.241 | 0.263 | 0.301 | 0.297 | 0.246 | 0.262 |
| 2006 | 0.319 | 0.304 | 0.241 | 0.268 | 0.319 | 0.310 | 0.246 | 0.268 |
Note: FSE/NSE: Ratio of foreign-born to native S&Es.
Table 4 presents the computed effects, and the distribution of total change among them, for a selection of pairs of years within the period under study. Except for that corresponding to the whole period (1994–2006), the top panel presents pairs of years in which only the 1980 SOC codes were used to identify S&Es. With the same exception as in the top panel, the bottom panel shows pairs of years in which the 2000 SOC codes were used.
Table 4.
Selected Decomposition Pairs for the Change in the Ratio of Foreign-born to Native S&Es, 1994–2006
| Period | Total Change in FSE/NSE | Migration Effect | Proportional College Effect | Proportional S&E Effect |
|---|---|---|---|---|
| Using 1980 SOC Through 2002 | ||||
| Effects, selected years | ||||
| 1994–2006 | 0.159 | 0.118 | –0.009 | 0.050 |
| 1994–1999 | 0.092 | 0.048 | 0.007 | 0.037 |
| 1995–1998 | 0.089 | 0.042 | 0.008 | 0.040 |
| 1995–2000 | 0.099 | 0.068 | 0.007 | 0.025 |
| 1998–2002 | 0.024 | 0.041 | –0.001 | –0.016 |
| 1998–2001 | 0.036 | 0.038 | 0.001 | –0.003 |
| Effects, selected years (%) | ||||
| 1994–2006 | 100 | 74 | –6 | 32 |
| 1994–1999 | 100 | 52 | 7 | 40 |
| 1995–1998 | 100 | 47 | 9 | 45 |
| 1995–2000 | 100 | 68 | 7 | 25 |
| 1998–2002 | 100 | 169 | –3 | –66 |
| 1998–2001 | 100 | 104 | 3 | –7 |
| Using 2000 SOC From 2000 on | ||||
| Effects, selected years | ||||
| 1994–2006 | 0.159 | 0.119 | –0.009 | 0.049 |
| 2000–2006 | 0.050 | 0.049 | –0.010 | 0.010 |
| 2003–2006 | 0.032 | 0.026 | –0.003 | 0.010 |
| 2000–2003 | 0.018 | 0.024 | –0.006 | 0.000 |
| Effects, selected years (%) | ||||
| 1994–2006 | 100 | 75 | –6 | 31 |
| 2000–2006 | 100 | 99 | –20 | 20 |
| 2003–2006 | 100 | 80 | –11 | 31 |
| 2000–2003 | 100 | 135 | –36 | 1 |
Note: FSE/NSE: Ratio of foreign-born to native S&Es.
The results are instructive. The effects recorded for the whole period tell a clear story: about 75% of the observed increase in the ratio of interest corresponds to the migration effect. As stated earlier, this means that 75% of the observed change results from general migration growth alone. Slightly more than 30% of the increase in the ratio throughout the period is explained by the proportional S&E effect: that is, by more than proportional growth of the foreign-born S&E population.
During the 1990s (see 1994–1999 in the top panel), the increase in FSE/NSE is also mostly explained by the migration effect (52%), but not as dramatically as for the whole period, followed again by the proportional S&E effect, which explains 40% of the change. If one considers the period 1995–1998, the migration effect (47%) is nearly matched by the proportional S&E effect (45%). If the whole period of the dot-com boom (1995–2000) is considered, the migration effect explains 68% of the observed change in FSE/NSE, and the proportional S&E effect accounts for 25% of it. Focusing on the period 1998–2002, which includes the two increases in the H-1B cap, reveals that the proportional S&E effect is actually negative, mostly as a consequence of S&E job losses recorded in 2001–2002 (see Table 1). Looking instead at 1998–2001 still reveals a slightly negative proportional S&E effect.
In the new century (see 2000–2006, bottom panel of Table 4), virtually the entire observed change in FSE/NSE would still have happened as a consequence of migration alone even if the proportional college ratio and the proportional S&E ratio had not changed. Twenty percent of it would have taken place if only the proportional S&E ratio had changed, and the ratio would have shrunk (by 20% of the observed positive change) if only the proportional college ratio had changed.14 Most of the increase in FSE/NSE between 2000 and 2006 occurred in the second half of this period. In 2003–2006, the proportional S&E effect explains 31% of the observed increase in the ratio. In 2000–2003, because the change in the ratio was very small, the percentage change attributable to each effect becomes a little too volatile in that period.
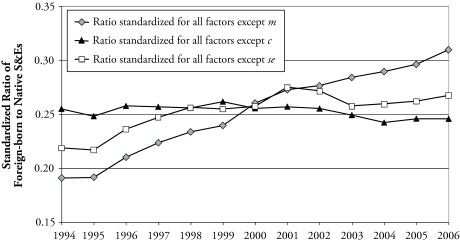
A chart of standardized ratios offers the full view of what happened during the period under study. Figure 5, constructed with the results from Table 3, shows the three series of standardized FSE/NSE, where 2000 SOC codes are used for the classification of S&Es in 2000–2002. Displacements along the vertical axis show the migration, proportional college, and proportional S&E effects that correspond to subperiods along the horizontal axis (as in Smith, Morgan, and Koropeckyj-Cox 1996). Recall that the effect from one factor is computed from the series of FSE/NSE standardized for the other two factors, so that the slopes of the curves show the periods in which each factor by itself would have produced an increase or a decrease in the ratio.
Figure 5.
Standardized Ratios of Foreign-born to Native S&Es, 1994–2006
The most obvious result is that the migration effect was positive throughout the whole period. In contrast, the proportional S&E effect was slightly negative in the first year of the series, in 1998–1999 (just as the H-1B cap was raised for the first time), and in 2001–2003.15 The proportional college effect, in turn, was generally moderate, and it was negative more often than positive. Focusing on the slopes reveals two subperiods during which the proportional S&E effect roughly matched the migration effect: 1995–1998 and 2000–2001.16
DISCUSSION
Defining S&Es as college-educated workers in S&E occupations, the ratio of foreign-born to native S&Es (FSE/NSE) doubled between 1994 and 2006, from 0.16 to 0.32. The analysis presented in this article takes a close look at this ratio and how it came to change during the period under study. The most salient finding is that the migration effect explains about three-quarters of the increase in FSE/NSE during the entire period. Thus, I can attribute 75% of the increase in this ratio during 1994–2006 to overall migration alone. In short, given a large number of migrants, it is to be expected that many of them will be skilled and will take S&E jobs. The proportional S&E effect accounted for about one-third of the growth in the ratio during the same period. The proportional college effect was small and slightly negative, and in the interest of brevity, it is left out of this discussion. As shown earlier, the proportional S&E effect is attributable to an increase in the number of college-educated migrants in S&E occupations over and above what one would expect from overall migration growth or migration of college-educated workers alone.
As shown in Figure 5, the proportional S&E effect roughly matched the migration effect in two periods: 1995–1998 and 2000–2001. I speculate that the latter might be a reflection of the relative flexibility (from the point of view of natives) or rigidity (from the point of view of work visa holders) of labor contracts. The year 2001 marked both the demise of the dot-com boom and a sudden economic slowdown. Although foreign-born workers on nonimmigrant visas such as the H-1B are bound to sponsoring employers, native workers can rapidly switch employers and even industries. At the end of the dot-com boom and ICT-propelled economic growth, native S&E workers may have quit earlier, or may have been dismissed earlier, than their foreign-born counterparts. As shown in Table 1, the number of college-educated natives in S&E occupations did indeed decline in 2000–2001, and the number of foreigners increased for one more year, until job loss (or job turnover) reached the foreign-born as well.
More substantial is the finding of a large proportional S&E effect in 1995–1998. Those were years of impressive economic growth and high rates of productivity growth driven by developments in the ICT industry. Furthermore, mean real wages for skilled workers were on the rise, reaching a peak 7% increase in 1998. It appears that this economic background created auspicious conditions for the specific immigration of S&Es—just as much as what would be expected from large migration alone.
Results change when considering a different economic background: real growth slowed in 2000–2001; between 2001 and 2003, the economy destroyed more jobs than it created; and the growth rate of real wages declined until becoming negative since 2003. The years 2001–2003 mark the only subperiod of this analysis during which the ratio of foreign-born to native S&Es actually declined (Figure 3). In the last few years of the series, the economy grew in real terms and created jobs. However, economic growth in this period was no longer predicated on an ever-expanding ICT sector, and real skilled wages continued to fall. By far, most of the increase in FSE/NSE was again explained by the migration effect alone.
Can the results be linked to changes in the H-1B visa cap? Congress raised the annual cap on H-1B visas in 1999 and again in 2001. The latter was inconsequential. The reversal of economic conditions in the new century meant that the new cap was never reached. As for the 1999 cap increase, it cannot be associated with a large proportional S&E effect. If, for consistency, one uses 1980 SOC codes through 2002, then the proportional S&E effect was negative between 1998 and either 2001 or 2002 (Table 4). Switching to 2000 SOC codes in 2000 produces a more important proportional S&E effect (Figure 5), but this may well be the result of the change in occupational coding. In other words, as Congress took action to specifically promote the migration of S&Es, this type of migration had already peaked, apparently as a by-product of a booming economy.
For the period under analysis, then, economic growth is the key to understanding changes in the composition of the S&E workforce by nativity. A growing economy created jobs for all types of workers, including large numbers of foreign-born S&Es. On the other hand, when the economy slowed down, immigration policy implemented to attract foreign-born S&Es had little to no effect. The corollary is that current debates on the H-1B visa cap, at the time of the present recession, are likely unwarranted. In the current economic climate, an increase in the cap would be politically controversial, but it would probably be of limited consequence. The volume and timing of H-1B petitions received by the United States Citizenship and Immigration Services (USCIS) seems to support this conclusion. Each April 1st USCIS begins to accept petitions toward the next fiscal year’s cap. In recent years, petitions largely exceeded the cap already in the first week of April: 133,000 received by April 7, 2007 (for FY 2008) and 163,000 received by April 3, 2008 (for FY 2009). Petitions for FY 2010, however, only reached the 65,000 cap in December of 2009. Not surprisingly, as of this writing (early June, 2010), USCIS has not received enough petitions to reach the cap for FY 2011.
I have described the correspondence between, on one hand, the timing of changes in the ratio of foreign-born to native S&Es and of its components and, on the other hand, the timing of economic swings and legislation on H-1B visas. A decomposition analysis precludes causality claims, but I shall at least note that the association between economic swings and the specific, more than proportional, migration of S&Es during 1994–2006 was much stronger than the association between the latter and changes in the H-1B cap. For the whole period under study, however, overall migration explains most of the story. Large numbers of immigrants implied large numbers of immigrant S&Es.
Acknowledgments
The research reported in this article was funded by a grant from the Alfred P. Sloan Foundation. The author wishes to thank Katharine Donato, Frederick Weil, Michael S. Teitelbaum, and three anonymous reviewers for their helpful comments. An earlier version of the manuscript was presented at the 73rd annual meeting of the Population Association of America, New Orleans, LA, April 16–19, 2008.
APPENDIX: SCIENCE AND ENGINEERING OCCUPATIONS
The S&E occupations in the 1980 Standard Classification of Occupations, with MORG codes in parentheses, are as follows: aerospace engineers (44), metallurgical and materials engineers (45), mining engineers (46), petroleum engineers (47), chemical engineers (48), nuclear engineers (49), civil engineers (53), agricultural engineers (54), engineers, electrical and electronic (55), engineers, industrial (56), engineers, mechanical (57), marine and naval architects (58), engineers, n.e.c. (not elsewhere classified) (59), surveyors and mapping scientists (63), computer systems analysts and scientists (64), operations and systems researchers and analysts (65), actuaries (66), statisticians (67), mathematical scientists, n.e.c. (68), physicists and astronomers (69), chemists, except biochemists (73), atmospheric and space scientists (74), geologists and geodesists (75), physical scientists, n.e.c. (76), agricultural and food scientists (77), biological and life scientists (78), forestry and conservation scientists (79), medical scientists (83), economists (166), psychologists (167), sociologists (168), social scientists, n.e.c. (169), urban planners (173).
The S&E occupations in the 2000 Standard Classification of Occupations, with MORG codes in parentheses, are as follows: computer scientists and systems analysts (1000), computer programmers (1010), computer software engineers (1020), computer support specialists (1040), database administrators (1060), network and computer systems administrators (1100), network systems and data communications analysts (1110), actuaries (1200), mathematicians (1210), operations research analysts (1220), statisticians (1230), miscellaneous mathematical science occupations (1240), surveyors, cartographers, and photogrammetrists (1310), aerospace engineers (1320), agricultural engineers (1330), biomedical engineers (1340), chemical engineers (1350), civil engineers (1360), computer hardware engineers (1400), electrical and electronic engineers (1410), environmental engineers (1420), industrial engineers, including health and safety (1430), marine engineers and naval architects (1440), materials engineers (1450), mechanical engineers (1460), mining and geological engineers, including mining safety engineers (1500), nuclear engineers (1510), petroleum engineers (1520), engineers, all other (1530), agricultural and food scientists (1600), biological scientists (1610), conservation scientists and foresters (1640), medical scientists (1650), astronomers and physicists (1700), atmospheric and space scientists (1710), chemists and materials scientists (1720), environmental scientists and geoscientists (1740), physical scientists, all other (1760), economists (1800), market and survey researchers (1810), psychologists (1820), sociologists (1830), urban and regional planners (1840), miscellaneous social scientists and related workers (1860).
Footnotes
I use “S&E” as short for “science and engineering” and “S&Es” as short for “scientists and engineers.”
I use the terms “foreign-born” and “immigrant” interchangeably.
Throughout this article, “skilled” is understood to mean college educated.
Data were downloaded from the Web site of the Immigrant Visa Control and Reporting Division of the Department of State (http://travel.state.gov/visa/statistics/statistics_1476.html).
A common mistake, the use of admission statistics from the Department of Homeland Security rather than visas issued by the Department of State, pervades references to the H-1B program on the part of both lay persons and migration specialists. Statistics on admissions refer to entries and are therefore susceptible to multiple counting of the same individuals. As an estimate of persons admitted into the country on H-1B visas, admissions exceed the actual figure by an unknown factor.
Fiscal year (FY) x begins on October 1 of year x − 1 and ends on September 30 of year x.
The apparent excess of visas issued in 1997 and 1998 results from the standard official procedure to count visas, based on approved petitions, and not on visas actually issued. Reciprocity schedules with various countries can also result in mismatches between the total number of visas issued in a given fiscal year and the cap (Stephen Fischel, former Director of the Office of Legislation, Regulations and Advisory Assistance in the Visa Office of the U.S. Department of State, e-mail communication, August 14, 2007). For mismatches from 2000 onward, see the text.
Data are available online at http://www.nber.org/data/morg.html.
For example, a 10% increase as a result of the revision of weights in 2000 would translate into a 4% increase over the figure estimated for 1994, a 5% increase over the 1995 figure, and so on.
Unlike the choice I made for the adjustment of weights backward through 1994, I did not make any adjustments on estimates of S&E workers produced with the 1980 SOC because, first, the period involved is longer (1980–2000) and the necessary assumptions are likely to be unsound; and, second, it is uncertain which share of the change is genuine and which is only a result of reclassification of occupations.
I use the word “migration” to refer to the foreign-born component of the workforce. Because the decomposition technique focuses on population stock, and not on migration flows, this use of the word is somewhat liberal. Yet, referring to “migration” seems practical because changes in the nativity composition of the workforce can ultimately be tracked to migration trends, and because alternative terms, such as “entry/exit of immigrants into/from the workforce,” are inevitably too wordy.
Because of rounding to the third decimal place, some of the numbers shown in this manual calculation do not exactly match the numbers shown in Table 4.
This reflects two trends shown in Table 2: a lower proportional college ratio in 2006 than in 2000 indicates that the rate of growth of the subpopulation of college-educated workers was higher among natives than among the foreign-born, but a higher proportional S&E ratio in 2006 than in 2000 shows that the proportion of these college-educated workers holding S&E jobs grew faster among the foreign-born than among natives.
When 1980 SOC codes are used through 2002, the FSE/NSE ratio standardized for all factors except se shifts downward earlier, in 2000–2002 (alternative chart available from the author). This results from the underestimation of S&E occupations by the 1980 SOC classification. Consequently, the proportional S&E effect becomes strongly negative in 1999–2000 and sharply positive in 2002–2003.
The latter is the case regardless of the choice of SOC codes for 2000–2002.
REFERENCES
- Bean FD, Brown SK. A Canary in the Mineshaft? International Graduate Enrollments in Science and Engineering in the United States. Paper prepared for the Forum on the Impact of Foreign Graduate Student Enrollment on the Economy, Universities, and Security; Irvine: University of California; 2005. [Google Scholar]
- Bureau of Labor Statistics. Report No. 929. U.S. Department of Labor; Washington, DC: 1999. Revising the Standard Occupational Classification System. [Google Scholar]
- Cassidy J. Dot.con: The Greatest Story Ever Sold. New York: Harper-Collins; 2002. [Google Scholar]
- Council of Economic Advisers. Economic Report of the President. Washington, DC: U.S. Government Printing Office; 2001. [Google Scholar]
- Das Gupta P. Standardization and Decomposition of Rates: A User’s Manual. Current Population Reports. U.S. Government Printing Office; Washington, DC: 1993. pp. P23–186. [Google Scholar]
- The Economist. The Battle for Brainpower. 2006. Oct 5, Print Edition. [Google Scholar]
- Ellis RA. STEM Workforce Data Project: White Paper No. 3. Commission on Professionals in Science and Technology; Washington, DC: 2007. Effects of Recent Revisions in Federal Standard Occupational Classification (SOC) Categories on Counts of the Employment of STEM Professionals. [Google Scholar]
- Espenshade TJ. High-end Immigrants and the Shortage of Skilled Labor. Population Research and Policy Review. 2001;20:135–41. [Google Scholar]
- Espenshade TJ, Usdansky ML, Chung CY. Employment and Earnings of Foreign-born Scientists and Engineers. Population Research and Policy Review. 2001;20:81–105. [Google Scholar]
- Freeman RB. NBER Working Paper No. 11457. National Bureau of Economic Research; Cambridge, MA: 2005. Does Globalization of the Scientific/Engineering Workforce Threaten U.S. Economic Leadership? [Google Scholar]
- Gordon RJ. Future U.S. Productivity Growth: Looking Ahead by Looking Back. Paper presented at “Workshop on the Occasion of Angus Maddison’s 80th Birthday, World Economic Performance: Past, Present, and Future.” University of Groningen; the Netherlands. October 27.2006. [Google Scholar]
- Hawthorne L. ‘Picking Winners’: The Recent Transformation of Australia’s Skilled Migration Policy. International Migration Review. 2005;39:663–96. [Google Scholar]
- Iredale R. Migration Policies for the Highly Skilled in the Asia-Pacific Region. International Migration Review. 2000;34:882–906. [Google Scholar]
- Jorgenson DW, Wessner CW, editors. Enhancing Productivity Growth in the Information Age. Washington, DC: National Academies Press; 2007. [Google Scholar]
- Kannankutty N, Burrelli J. InfoBrief NSF07-324. National Science Foundation, Directorate for Social, Behavioral, and Economic Sciences; Arlington, VA: 2007. Why Did They Come to the United States? A Profile of Immigrant Scientists and Engineers. [Google Scholar]
- Lowell BL, editor. Foreign Temporary Workers in America: Policies that Benefit the U.S. Economy. Westport, CT: Quorum; 1999. [Google Scholar]
- Lowell BL. Skilled Temporary and Permanent Immigrants in the United States. Population Research and Policy Review. 2001;20:33–58. [Google Scholar]
- Meyers DW. Insight. 12. Migration Policy Institute; Washington, DC: 2006. Temporary Worker Programs: A Patchwork Policy Response. [Google Scholar]
- National Science Foundation. Science and Engineering Indicators 2008. NSB 08-01; NSB 08-01A. National Science Foundation; Arlington, VA: 2008. [Google Scholar]
- North DS. Soothing the Establishment: The Impact of Foreign Born Scientists and Engineers on America. Lanham, MD: University Press of America; 1995. [Google Scholar]
- Oliner SD, Sichel DE. The Resurgence of Growth in the Late 1990s: Is Information Technology the Story? Journal of Economic Perspectives. 2000;14(4):3–22. [Google Scholar]
- Oliner SD, Sichel DE, Stiroh K. Explaining a Productive Decade. Brookings Papers on Economic Activity. 2007;38:81–152. [Google Scholar]
- Regets MC. IZA Discussion Paper No. 366. Institute for the Study of Labor; Bonn, Germany: 2001. Research and Policy Issues in High-Skilled International Migration: A Perspective With Data From the United States. [Google Scholar]
- Saxenian A. Local and Global Networks of Immigrants in Silicon Valley. San Francisco: Public Policy Institute of California; 1999. [Google Scholar]
- Saxenian A, Motoyama Y, Quan X. Silicon Valley’s New Immigrant Entrepreneurs. San Francisco: Public Policy Institute of California; 2002. [Google Scholar]
- Schmidley AD, Robinson JG. Working Paper No. 73. Population Division, U.S. Census Bureau; Washington, DC: 2003. Measuring the Foreign-born Population in the United States With the Current Population Survey: 1994–2002. [Google Scholar]
- Smith HL, Morgan SP, Koropeckyj-Cox T. A Decomposition of Trends in the Nonmarital Fertility Ratios of Blacks and Whites in the United States, 1960–1992. Demography. 1996;33:141–51. [PubMed] [Google Scholar]
- Stephan PE, Levin SG. Exceptional Contributions to US Science by the Foreign-born and Foreign-Educated. Population Research and Policy Review. 2001;20:59–79. [Google Scholar]
- Teitelbaum MS. Do We Need More Scientists? The Public Interest. 2003 Fall;153:40–53. [Google Scholar]
- Temple J. The Assessment: The New Economy. Oxford Review of Economic Policy. 2002;18:241–64. [Google Scholar]
- U.S. Census Bureau. Technical Paper 66. U.S. Census Bureau; Washington, DC: 2006. Current Population Survey: Design and Methodology. [Google Scholar]
- Wadhwa V, Gereffi G, Rissing B, Ong R. Where the Engineers Are. Issues in Science and Technology. 2007;23(3):73–84. [Google Scholar]
- Watts JR. The H-1B Visa: Free Market Solutions for Business and Labor. Population Research and Policy Review. 2001;20:143–56. [Google Scholar]