Major Antiparallel and Minor Parallel β Sheet Populations Detected in the Membrane-Associated Human Immunodeficiency Virus Fusion Peptide

Abstract

The HIV gp41 protein catalyzes fusion between viral and host cell membranes and its apolar N-terminal region or “fusion peptide” binds to the host cell membrane and plays a key role in fusion. “HFP” is a construct containing the fusion peptide sequence, induces membrane vesicle fusion, and is an important fusion model system. Earlier solid-state NMR (SSNMR) studies showed that when HFP is associated with membranes with ~30 mol% cholesterol, the first sixteen residues have predominant β strand secondary structure and a fraction of the strands form antiparallel β sheet structure with residue 16→1/1→16 or 17→1/1→17 registries of adjacent strands. In some contrast, other SSNMR and infrared studies have been interpreted to support a large fraction of approximately in-register parallel registry of adjacent strands. However, the samples had extensive isotopic labeling and other structural models were also consistent with the data. The present SSNMR study uses sparse labeling schemes that reduce ambiguity in the determination of the fraction of HFP molecules with parallel β registry. Quantitative analysis of the data shows that the parallel fraction is at most 0.15 with a much greater fraction of antiparallel 16→1/1→16 and 17→1/1→17 registries. These data strongly support a model of HFP-induced vesicle fusion caused by antiparallel rather than parallel registries and provide insight into the arrangement of gp41 molecules during HIV/host cell fusion. This study is an example of quantitative determination of a complex structural distribution by SSNMR including experimentally-validated inclusion of natural abundance contributions to the SSNMR data.

AIDS is caused by membrane-enveloped human immunodeficiency virus (HIV) which infects host cells by fusion, i.e. joining of viral and host cell membranes (1). Fusion is facilitated by gp41 which is an integral HIV membrane protein. The N-terminal ~175-residue gp41 ectodomain lies outside the virus and X-ray crystal and liquid-state nuclear magnetic resonance (LSNMR) structures of soluble regions of the ectodomain have shown molecular trimers (1–5). These structures lacked the ~25-residue N-terminal “fusion peptide” region which plays a key role in fusion and infection as evidenced by inhibition of fusion and infection when gp41 had mutations within the fusion peptide region (1, 6, 7). Peptides with the fusion peptide sequence are denoted HFPs and have been studied as model fusion systems because they induce vesicle fusion and because their mutation-fusion activity relationships are similar to those of in vivo fusion and infection (1, 8–10).

The HFP structure-function literature includes NMR data showing random coil structure for HFP in aqueous solution (11, 12). Solid-state nuclear magnetic resonance (SSNMR) has shown predominant β sheet structure for residues 1–16 of membrane-associated HFP where the membranes contained ~30 mol% cholesterol which is comparable to the mol% cholesterol of membranes of HIV and host cells of HIV (13–16). A fluorescence and infrared (IR) study reported the time-resolved courses of HFP structural changes and the intervesicle lipid mixing function following addition of a HFP solution to a membrane vesicle solution (17). The experimental rates (Rs) were ordered R_{HFP membrane binding} > R_{HFP β sheet formation} > R_{lipid mixing} and were consistent with the sequence: (1) random coil HFPs bind to a membrane vesicle; (2) HFP structure changes to oligomeric β sheet; and finally (3) vesicle fusion.

The biological relevance of HFP oligomers is further supported by the molecular trimer structure of soluble regions of the gp41 ectodomain (3–5). The region between residues T25 and G85 of each molecule was a continuous helix and the helices of the different molecules formed a parallel coiled-coil. The fusion peptide region was not included in the protein constructs for these structures but would be N-terminal of residue T25. A C-terminally cross-linked HFP trimer (HFPtr) was therefore synthesized to mimic the close proximity of the three T25 residues in the coiled-coil. Relative to HFP monomer, HFPtr induced membrane vesicle fusion with ~40-fold faster rate which supported the functional significance of the trimer (18). Although both the monomer and trimer formed β sheet oligomers in membranes with cholesterol, HFPtr is more deeply inserted which correlates with greater membrane perturbation and a reduction of the vesicle fusion activation energy (19). The in vivo importance of fusion peptide oligomers was also demonstrated by dominant inhibition of fusion and infection in viruses and cells for which a small fraction of the gp41 had the V2E point mutation in the fusion peptide region (7, 20). Analyses of these data supported the involvement of multiple gp41 trimers and fusion peptides in fusion (21). Electron micrographs of virus-cell contacts have also been interpreted to show multiple gp41 trimers at the contact site (22). Functional importance of fusion peptide trimers has also been demonstrated for fusion peptides of other viruses (23, 24).

Because of the aforementioned functional significance of HIV fusion peptide oligomers, there has been effort to elucidate the distribution of structures of membrane-associated HFP oligomers. SSNMR has played a key role in this effort in particular for samples prepared in a manner similar to that of fusion assays with addition of an aqueous fusion peptide solution to a membrane vesicle solution (14). Appendage of a C-terminal lysine tag to HFP greatly reduced HFP aggregation in aqueous solution and allowed separation of pelleted fused vesicles with bound HFP from unbound HFP in the supernatant (12, 18, 25). HFP/lipid binding was supported by SSNMR detection of a HFP A1 ¹³CO(carbonyl)-lipid ³¹P distance of ~5 Å (19). For membrane-associated HFP, the ¹³C chemical shifts derived from an unambiguous assignment were consistent with a fully extended β strand conformation for residues between A1 and G16 (15). Detection of intermolecular ¹³C-¹³C and ¹³C-¹⁵N distances of ~5 Å supported β sheet oligomer/aggregate structure and the A1 ¹³CO-lipid ³¹P contact and other data suggest that the number of molecules in the oligomer is small (15, 19, 26).

The present work focuses on quantitative determination of populations of specific β sheet registries. The clearest information to-date on this topic has been a SSNMR experiment on membrane-associated HFP with an A14 ¹³CO label and a G3 ¹⁵N label whose separation (r_CN) was >20 Å along a single β strand (15). SSNMR can detect labeled ¹³CO-¹⁵N dipolar coupling (d_CN) where d_CN = 3109/r_CN³ with d in Hz and r in Å. The minimum detectable d_CN≈ 10 Hz correlates with r_CN ≈ 7 Å so that detectable d_CN in this sample were necessarily ascribed to interrather than intramolecular ¹³CO-¹⁵N proximity. SSNMR detection of d > 30 Hz strongly supported a significant fraction of molecules with intermolecular A14-G3 hydrogen bonding and labeled r_CN of 4.1 and 5.5 Å, i.e. 16→1/1→16 antiparallel β sheet registry. Fig. 1c displays this registry with isotopic labeling from the present study and not the earlier study. Detection of similarly large d in an A14 ¹³CO/I4 ¹⁵N HFP sample supported a fraction of 17→1/1→17 antiparallel registry.

Figure 1.

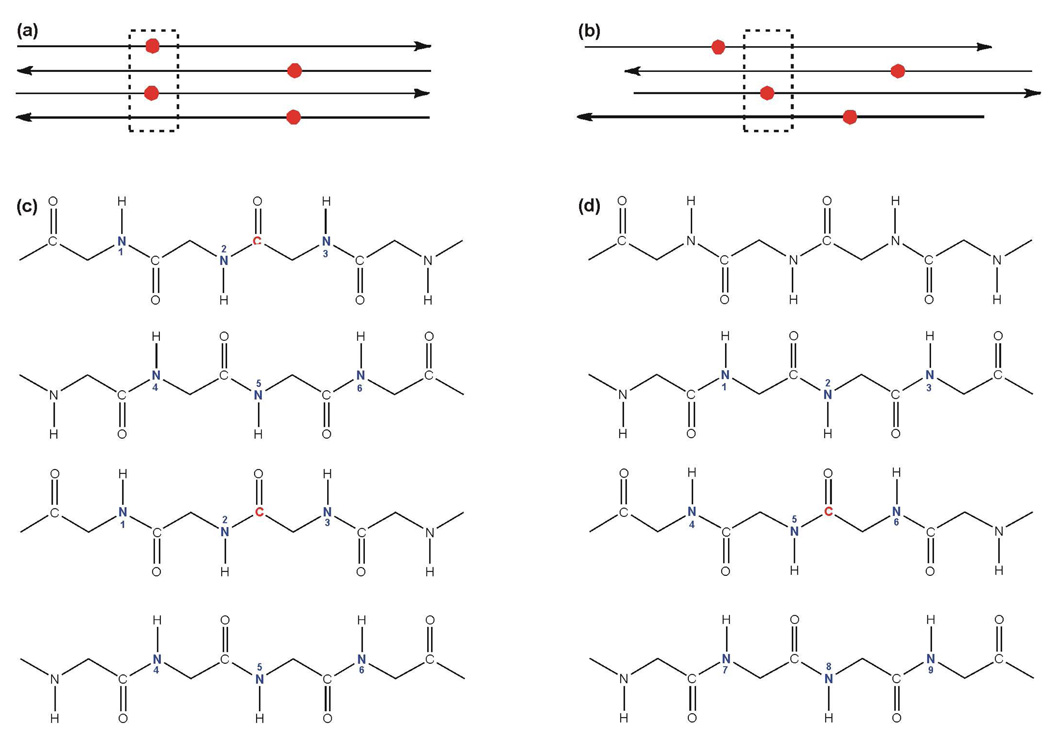
(a) HFPs where red and blue correspond to ¹³CO and ¹⁵N labeled residues, respectively. (b) HFP-NC, HFP-P, HFP-A, and HFP-AP were SSNMR samples which each contained a mixture of ¹³CO and ¹⁵N labeled peptides in a 1:2 mol ratio. The HFP-NC sample was a mixture of HFP-F8 and HFP-A6L7 that had been lyophilized separately. The other samples were membrane-associated HFPs that formed β sheet structure with a molecular mixture of ¹³CO and ¹⁵N labeled peptides in the sample. (c) Registries probed by the SSNMR REDOR experiments and labeled ¹³CO/labeled ¹⁵N proximities for the membrane-associated HFPs in these registries. Consideration of residue 1→16 or 1→17 registries is based on the fully extended conformation of this HFP region. For parallel sheets, there is CO(residue i) – HN(residue i+1) hydrogen bonding of adjacent strands.

At most half of the membrane-associated HFP molecules were in the 16→1/1→16 or 17→1/1→17 registries, i.e. a large fraction of the molecules were in registries not detected in either the A14 ¹³CO/G3 ¹⁵N or A14 ¹³CO/I4 ¹⁵N labeled samples. Because of the close proximity of the T25 residues of the three molecules of the gp41 trimer, a reasonable hypothesis for a populated HFP registry is in-register parallel β sheet, i.e. 1→17/1→17 in Fig. 1c. An earlier SSNMR study attempted to test this hypothesis using samples each containing an equimolar mixture of two labeled HFPs, one with three sequential backbone ¹³CO labels and the other with three sequential backbone ¹⁵N labels (27). Detection of an average d_CN > 10 Hz for a G5-L7 ¹³CO/G5-L7 ¹⁵N sample and a F11-G13 ¹³CO/F11-G13 ¹⁵N sample were consistent with a fraction of in-register parallel HFP molecules. However, because the samples were extensively labeled, the data were also consistent with other parallel or antiparallel registries. In addition, the data reflected an average of many intermolecular d_CNs so it was not possible to determine the fraction of molecules with a particular registry. There have also been efforts to detect in-register parallel structure using SSNMR measurement of intermolecular ¹³C-¹³C dipolar couplings (d_CCs) where d_CC = 7710/r_CC³ with d_CC in Hz and r_CC in Å. For HFP with a single ¹³CO label and inregister parallel structure, the labeled interstrand r_CC ≈ 5 Å with d_CC ≈ 70 Hz (28, 29). These parameters will be independent of the residue that is ¹³CO labeled. For membrane-associated HFP with F8 ¹³CO, a best-fit d_CC ≈ 70 Hz was detected whereas for membrane-associated HFPtr, d_CC depended on the position of the labeled ¹³CO residue with a range of 10–60 Hz (30, 31). This residue dependence argued against a major fraction of in-register parallel structure in HFPtr.

There was also an IR spectroscopy effort to distinguish between the 1→17/1→17 parallel and 16→1/1→16 antiparallel registries using samples that contained backbone ¹³CO labeling at either: (1) A1 to V3, G5 to I9; (2) F8 to G16; or (3) A1 to V3, G5 to G16 (32). The IR wavenumbers and intensities of different samples were interpreted to support a large fraction of parallel structure and little antiparallel structure. However, in our view, the extensive labeling of the IR samples precluded quantitation of specific registries and greater support for this argument is provided in the Discussion section.

The present paper reports a determination of the fraction of parallel structure in membrane-associated HFP oligomers. We were motivated to study this question because of: (1) the functional significance of HIV fusion peptide oligomers; and (2) the existing undefinitive and conflicting data and interpretations relevant to this question. As part of this effort, we developed a model to quantify effects of natural abundance ¹³C and ¹⁵N nuclei on SSNMR measurements of d_CN and experimentally validated this model.

MATERIALS AND METHODS

Materials

9-fluorenylmethoxycarbonyl (FMOC) protected amino acids and FMOC-Ala-Wang resin were purchased from Peptides International (Louisville, KY). Isotopically labeled amino acids were purchased from Cambridge Isotopes (Andover, MA) and were FMOC-protected using literature methods (33). Fig. 1a shows the labeled HFPs. The 23 N-terminal residues (AVGIGALFLGFLGAAGSTMGARS) are a consensus sequence of the gp41 fusion peptide, non-native W24 is an A₂₈₀ chromophore and the non-native lysines greatly reduced HFP aggregation in aqueous solution prior to membrane binding (12, 18). This ensured that membrane-associated β sheet oligomers/aggregates were formed after membrane binding.

HFP was manually synthesized and then cleaved from the resin for three hours in a solution of trifluoroacetic acid (TFA):water:anisole:thioanisole:ethanedithiol in a 90:5:2:2:2 volume ratio. After precipitation with cold diethyl ether, centrifugation, and dissolution of the pellet in water, crude HFP was purified by reversed-phase high-performance liquid chromatography with a semi-preparative C₄ column and a water-acetonitrile gradient containing 0.1% TFA. Acetonitrile and TFA were removed with nitrogen gas and water was then removed by lyophilization. HFP purity was >95% as determined by mass spectrometry. HFP amounts were quantified using A₂₈₀ of aqueous solutions of HFP with ε = 5600 M⁻¹cm⁻¹.

SSNMR samples

As shown in Fig. 1b, each sample contained a ¹³CO and a ¹⁵N labeled peptide in a 1:2 mol ratio. Three samples contained membrane-associated HFP β sheet oligomers/aggregates that were each a statistical mixture of ¹³CO and ¹⁵N labeled HFPs. Detection of substantial d_CN by SSNMR indicated proximity of the labeled ¹³CO and ¹⁵N nuclei on adjacent strands and was used to estimate the fractional populations of specific registries as detailed below. As shown in Fig. 1c, the HFP-P sample was designed to detect parallel 1→17/1→17 and 2→17/1→16 registries, the HFP-A sample was designed to detect previously observed antiparallel 16→1/1→16 and 17→1/1→17 registries, and the HFP-AP sample was designed to detect both parallel 1→17/1→17 and 2→17/1→16 registries as well as antiparallel 16→1/1→16 and 17→1/1→17 registries.

In addition to the potential proximity of labeled ¹³CO and ¹⁵N nuclei, there will always be proximity between labeled ¹³CO and some natural abundance (n.a.) ¹⁵N nuclei as well as proximity between some n.a. ¹³CO and labeled ¹⁵N nuclei. These proximities will contribute to the d_CN detected in the SSNMR experiment and should be included in the data modeling. Quantitative understanding of these proximities required a negative control (HFP-NC) sample with: (1) the same relative fractions of labeled ¹³CO, ¹⁵N, and n.a. sites as the HFP-P, HFP-A, and HFP-AP samples; and (2) labeled ¹³CO – labeled ¹⁵N r_CN that are much greater than the REDOR detection limit of ~7 Å. One possibility was a sample made like HFP-P, HFP-A, and HFP-AP but with labels at sites that do not form intermolecular hydrogen bonds. This possibility was not pursued because the distribution of registries of membrane-associated HFP is not yet well-defined. Instead, the HFP-NC sample was a physical mixture of lyophilized HFP-F8 (5.0 mg) and HFP-A6L7 (10.0 mg) without any membrane. Each peptide was lyophilized separately and the two peptides were then mixed in the solid phase to form a uniform physical mixture. Water and membrane were not added to the physical mixture so that the labeled ¹³COs and ¹⁵Ns remained much farther apart than the 7 Å REDOR detection limit. Although there were populations of β sheet as well as α helical lyophilized peptides in the HFP-NC sample, each population yielded very similar (ΔS/S₀) – see Results section for further details.

For the HFP-P, HFP-A, and HFP-AP samples, the membrane composition was 1,2-di-O-tetradecyl-sn-glycero-3-phosphocholine (DTPC) lipid, 1,2-di-O-tetradecyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (DTPG) lipid, and cholesterol in a 8:2:5 mol ratio. This composition reflected the large amount of choline lipid and fractions of negatively charged lipid and cholesterol in membranes of host cells of HIV (16). Ether- rather than more physiologically abundant ester-linked lipids were used because the latter have two COs/molecule that would contribute substantial n.a. ¹³CO signal. Bilayer phase is retained for ether-linked lipids with cholesterol and with HFP (34–36). In addition, membrane-associated HFP has predominant β sheet structure in either ester-linked lipid + cholesterol or ether-linked lipid + cholesterol compositions (30).

Samples were prepared by first dissolving DTPC (40 µmol), DTPG (10 µmol), and cholesterol (25 µmol) in chloroform and removing the chloroform with nitrogen gas and vacuum. The lipid film was suspended in 2 mL of 5 mM HEPES buffer at pH 7.0 with 0.01% NaN₃ preservative. The suspension was homogenized with ten freeze-thaw cycles and large unilamellar vesicles were formed by extrusion through a 100 nm diameter polycarbonate filter (Avestin, Ottawa, ON). A separate solution was prepared with ¹³CO-labeled HFP (3.0 mg) and ¹⁵N labeled HFP (6.0 mg) in HEPES buffer (32 mL). The HFP solution was added drop-wise to the vesicle solution and the combined solution was gently stirred overnight. Ultracentrifugation at ~150000g for four hours pelleted membranes with bound HFP while unbound HFP remained in the supernatant (14). The pellet was lyophilized, transferred to the SSNMR rotor, and rehydrated with 30 µL H₂O (37). The validity of the lyophilization/rehydration approach was evidenced by peak ¹³CO chemical shifts that were within 0.6 ppm of those of samples that were not lyophilized (15).

SSNMR experiments

Data were collected on a 9.4 T spectrometer (Varian Infinity Plus, Palo Alto, CA) using a triple resonance MAS probe equipped for 4.0 mm rotors and tuned to ¹³C, ¹H, and ¹⁵N nuclei at respective frequencies of 100.8, 400.8, and 40.6 MHz. The ¹³C chemical shift was externally referenced to the methylene resonance of adamantane at 40.5 ppm and the ¹³C transmitter was set to 153 ppm. The ¹³CO-¹⁵N dipolar coupling (d_CN) was probed with the rotational-echo double-resonance (REDOR) experiment with typical parameters: (1) 52 kHz ¹H π/2 pulse; (2) 2.2 ms cross-polarization with 74 kHz ¹H field and 83–98 kHz ramped ¹³C field; (3) dephasing period of duration τ for which the “S₀” and “S₁” acquisitions had 60 kHz ¹³C π pulses at the end of each rotor cycle except the last cycle, and the S₁ acquisitions additionally had 59 kHz ¹⁵N π pulses in the middle of each rotor cycle; and (4) ¹³C detection (30, 38). The MAS frequency was 10 kHz, the recycle delay was 2 s, 88 kHz TPPM ¹H decoupling was applied during the dephasing and detection periods, and XY-8 phase cycling was applied to the ¹³C π pulses and to the ¹⁵N π pulses (39, 40). Experiments were calibrated using a lyophilized helical peptide with sequence AEAAAKEAAAKEAAAKA, N-terminal acetylation and C-terminal amidation, and A9 ¹³CO and A13 ¹⁵N labels (30, 41). The labeled r_CN ≈ 4.1 Å corresponds to d_CN ≈ 45 Hz. Samples were typically cooled by nitrogen gas at −50 °C to enhance ¹³CO signal and reduce motional averaging of d_CN (42). The typical difference between ¹³C shift in cooled and uncooled membrane-associated HFP samples is ≤ 0.5 ppm and indicates little variation in secondary structure with temperature (26). For each sample, data were collected for τ = 2.2, 8.2, 16.2, 24.2, 32.2, 40.2, and 48.2 ms.

The ¹³CO-¹⁵N dipolar coupling, d_CN, is detected by reduction of ¹³CO signal intensity in the S₁ spectrum relative to the S₀ spectrum with greater reduction at increased τ. These intensities were also denoted S₁ and S₀ and were determined from integration over a shift range that encompassed most of the ¹³CO signal. A range of 8 ppm was used for HFP-NC spectra and a range of 5 ppm was used for HFP-P, HFP-A, and HFP-AP spectra. The normalized dephasing:

$${\left(\frac{\mathrm{\Delta }S}{S_0}\right)}^{\mathit{\text{exp}}}=\frac{{S_0}^{\mathit{\text{exp}}}-{S_1}^{\mathit{\text{exp}}}}{{S_0}^{\mathit{\text{exp}}}}=1-\frac{{S_1}^{\mathit{\text{exp}}}}{{S_0}^{\mathit{\text{exp}}}}$$ (1)

and its standard deviation:

$${\sigma }^{\mathit{\text{exp}}}=\sqrt{\frac{({S_0}^2\times {{\sigma }_{S_0}}^2)+({S_1}^2\times {{\sigma }_{S_1}}^2)}{{S_0}^2}}$$ (2)

where σS₀ and σS₁ were the experimental root-mean-squared deviations of the spectral intensities derived from 12 regions of the spectrum that did not include spectral features (43).

Experimental dephasing of a membrane-associated HFP sample was modeled as a sum of S₀ and a sum of S₁ signals of different spin geometries of ¹³CO and ¹⁵N nuclei where the geometries reflected statistical distributions of n.a. ¹³CO and ¹⁵N nuclei as well as geometries of (1) 1→17/1→17 and 2→17/1→16 parallel adjacent strand registries; (2) 16→1/1→16 and 17→1/1→17 antiparallel registries; and (3) other “X” registries where all labeled r_CN > 7 Å and S₁ = S₀. The notation (ΔS/S₀)^sim will be generally used for simulated (ΔS/S₀) and can refer to a particular spin geometry or to the population weighted sum using calculations from different spin geometries. For the former case, the (S₁/S₀)^sim ≡ γ were calculated using the SIMPSON program with input parameters that included d_CNs as well as Euler angles in a fixed crystal frame for each ¹³CO-¹⁵N vector and for the ¹³CO chemical shift anisotropy (CSA) principal axis system (44, 45). These input parameters were calculated by the SIMMOL program using ¹³CO and ¹⁵N coordinates from a region of a high-resolution crystal structure with the appropriate structural motif, e.g. parallel β sheet (46). Coordinates were obtained from the following Protein Data Bank (PDB) files: 1JK3, 1IGD, 1NKI, 2E4T, 1CEX, 1MNZ, and 2IWW. For each spin geometry, (S₁/S₀)^sim was the average of ten different SIMPSON calculations and each calculation was based on input parameters from a different set of atomic coordinates. The ¹³CO CSA principal values of 247, 176, and 99 ppm were inputs to the SIMPSON calculations and ¹Hs and relaxation were not considered.

RESULTS

Chemical shift and conformational distributions

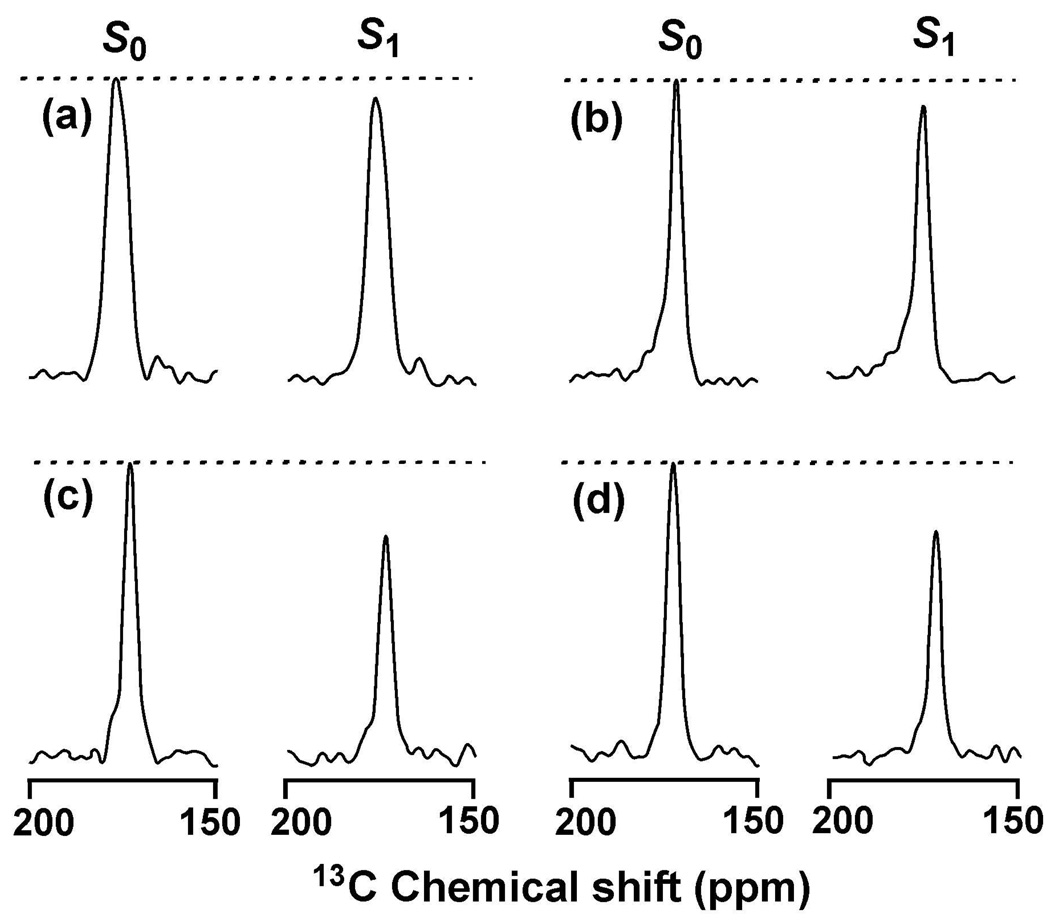
Fig. 2 displays REDOR S₀ and S₁ ¹³C SSNMR spectra for τ = 32.2 ms. Each S₀ spectrum has a ~50% contribution from the labeled ¹³CO and ~50% contribution from n.a. ¹³COs of the unlabeled residues. The full-width at half-maximum linewidths of the membrane-associated HFP samples in Fig. 2b–d are 3–4 ppm and indicate a distinct secondary structure. For the HFP-AP sample with F8 ¹³CO label, the peak ¹³CO shift of 173 ppm is the same as was observed for F8 ¹³CO of HFP in known β strand conformation and is very different from the 178 ppm shift observed in α helical conformation (15, 30). For the HFP-P and HFP-A samples with L12 ¹³CO label, the 174 ppm peak shift is also the same as β strand HFP and different from the 179 ppm shift of Leu in helical HFP (30, 47). Overall, the shifts and linewidths are consistent with the fully extended conformation that has been observed for the first sixteen residues of HFP associated with membranes with biologically relevant cholesterol content (15).

Figure 2.

REDOR S₀ and S₁ ¹³C SSNMR spectra at 32.2 ms dephasing time for (a) HFP-NC, (b) HFP-P, (c) HFP-A, or (d) HFP-AP. Each spectrum was processed with 200 Hz line broadening and baseline correction and was the sum of: (a) 38624; (b) 23488; (c) 24914; or (d) 14240 scans. Relatively narrow ¹³CO signals were observed in the HFP-P, HFP-A, and HFP-AP samples because the HFPs were membrane-associated with predominant β sheet conformation at the labeled ¹³CO site. A broader ¹³CO signal was observed in the HFP-NC sample because there was no membrane and there were populations of lyophilized HFP with either α helical or β sheet conformation at the labeled ¹³CO site.

The linewidth of the lyophilized HFP-NC sample with F8 ¹³CO label is ~7 ppm and correlates with a broad distribution of secondary structures that is also evidenced by a 176 ppm peak ¹³CO shift that is midway between typical Phe helical and β strand shifts (48).

Qualitative analysis of REDOR data

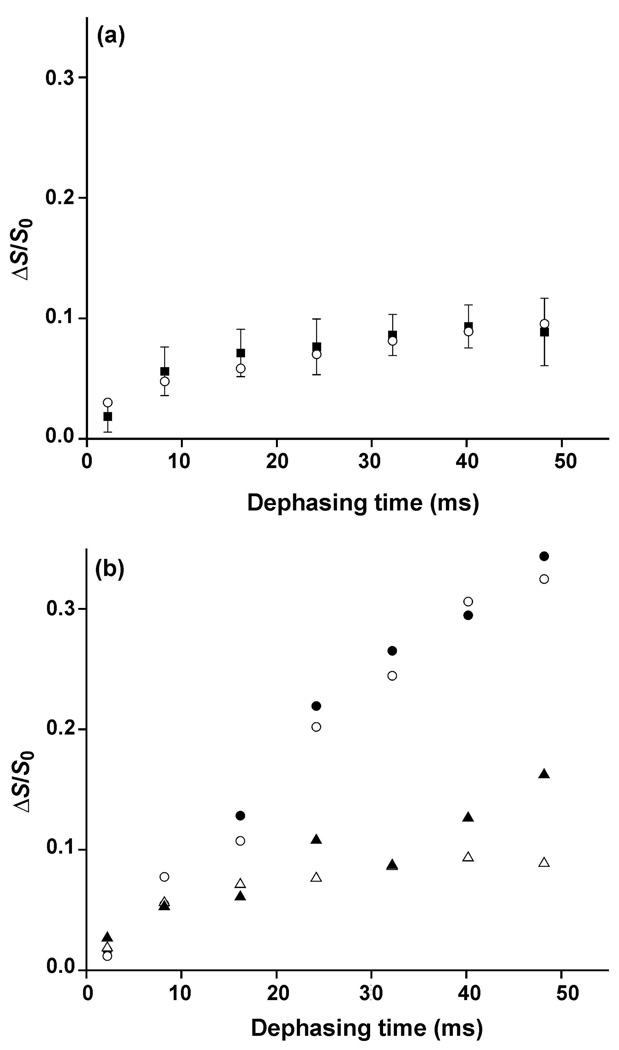
Relative to the S₀ signals, there is attenuation in the S₁ signals of ¹³COs within ~7 Å of ¹⁵Ns and the associated ΔS/S₀ normalized dephasing increased with dephasing time, Fig. 2 and Fig. 3. Because of the physical separation of the ¹³CO and ¹⁵N labeled HFPs in HFP-NC, the S₁ attenuation and (ΔS/S₀)^exp of this sample reflected F8 ¹³CO-n.a. ¹⁵N and n.a. ¹³CO-A6,L7 ¹⁵N proximities but not F8 ¹³CO-A6,L7 ¹⁵N proximity, Figs. 2a and 3a. There was similar S₁ attenuation and (ΔS/S₀)^exp in HFP-P, Figs. 2b and 3b, which demonstrated that there was little L12 ¹³CO-G13,A14 ¹⁵N proximity in HFP-P and only a small fraction of parallel 1→17/1→17 and 2→17/1→16 registries. There was much larger S₁ attenuation and (ΔS/S₀)^exp for the HFP-A sample, Figs. 2c and 3b, which indicated significant L12 ¹³CO-G5,A6 ¹⁵N proximity and therefore a substantial fraction of antiparallel 16→1/1→16 and 17→17/1→17 registries. Comparably large S₁ attenuation and (ΔS/S₀)^exp were observed for the HFP-AP sample, Figs. 2d and 3b. The similarity of the HFP-NC and HFP-P data and the similarity of the HFP-A and HFP-AP data were consistent with ascribing F8 ¹³CO-L9,G10 ¹⁵N proximity in HFP-AP to antiparallel 16→1/1→16 and 17→1/1→17 registries rather than parallel 1→17/1→17 and 2→17/1→16 registries. Detection of a substantial fraction of these antiparallel registries is consistent with earlier SSNMR data for sparsely labeled HFP (15). Detection of only a small fraction of parallel registries is a new result and disagrees with previous interpretations of SSNMR and IR data for samples with extensive labeling (27, 32). These new data highlight the importance of sparse labeling to reduce interpretational ambiguity for systems with a structural distribution like membrane-associated HFP.

Figure 3.

(a) Plot of REDOR (ΔS/S₀)^exp (filled squares with error bars) and (ΔS/S₀)^sim(open circles) vs dephasing time for the lyophilized HFP-NC sample. The (ΔS/S₀)^sim were calculated using a mixture of n.a.d. models with fractional populations: α helical, 0.5; min β sheet, 0.25; max β sheet, 0.25. (b) Plots of (ΔS/S₀)^exp vs dephasing time for: HFP-NC, open triangles; HFP-P, filled triangles; HFP-A, open circles; HFP-AP, filled circles. The typical σ^exp is ±0.02. Variation of ±0.02 in (ΔS/S₀)^exp was also observed between two different preparations of the same sample type, e.g. HFP-A.

Natural abundance models

Quantitative analysis of the (ΔS/S₀)^exp to yield the fraction of parallel and antiparallel HFP registries requires an accurate natural abundance dephasing (n.a.d.) model, i.e. a model that accounts for effects of labeled ¹³CO-n.a. ¹⁵N and n.a. ¹³CO-labeled ¹⁵N proximities. Both types of proximities were considered but for conciseness of presentation, the discussion in this paper focuses on labeled ¹³CO-n.a. ¹⁵N. One measure of validity of a n.a.d. model was agreement within experimental error between (ΔS/S₀)^exp of HFP-NC and (ΔS/S₀)^sim of the model. Consideration was first given to the HFP-F8 regions of HFP-NC including the spin geometries of one or two labeled ¹³COs and one n.a. ¹⁵N. Geometries with two or more n.a. ¹⁵Ns were not considered because the fractional isotopic abundance of ¹⁵N is only 0.0037. For each geometry, the SIMPSON program was used to calculate (S₁/S₀)^sim as a function of the dephasing time τ. Only geometries with r_CN < 7 Å were considered because those with r_CN > 7 Å do not affect (S₁/S₀)^sim within our experimental signal-to-noise. We consider this a “long-range” n.a.d. model which is distinguished from a “short-range” model of earlier studies that only considered n.a. nuclei separated by one or two bonds from a labeled nucleus, i.e. r_CN < 3 Å (15, 30). The broad spectral linewidth of HFP-NC indicated both helical and β strand conformational populations and coordinates of spin geometries for both α helical and β sheet structures were obtained from corresponding regions of high-resolution structure PDB files. For α helical structure, the r_CN < 7 Å criterion resulted in geometries with a single labeled ¹³CO at residue i and a single n.a. ¹⁵N at a residue between i − 3 and i + 5. These nine geometries are one aspect of the α n.a.d. model.

Fig. 4 illustrates relevant labeled ¹³COs and n.a. ¹⁵Ns for antiparallel β sheet structure. The strands in panels a and c are “fully constrained” to a single registry with resultant six unique spin geometries. Three geometries had one labeled ¹³CO and one n.a. ¹⁵N within the same strand and three geometries had two labeled ¹³COs on vicinal strands and one n.a. ¹⁵N in the intervening strand. In panels b and d, the strands have different registries so that the labeled ¹³CO in the top strand was >7 Å from the nine n.a. ¹⁵N sites of the ¹³CO of the third strand. The structure of panels b and d has nine unique spin geometries and is denoted a maximum β sheet n.a.d. (max β n.a.d.) model while the structure of panels a and c has six geometries and is denoted a minimum β sheet n.a.d. (min β n.a.d.) model. In either structure there are nine n.a. ¹⁵N sites within 7 Å of each labeled ¹³CO but in the min n.a.d. model, some sites (e.g. 4–6 in Fig. 4c) are “shared” between two ¹³COs, i.e. within 7 Å of two ¹³COs. This reduces the average number of n.a. ¹⁵N sites per ¹³CO and the overall n.a.d.

Figure 4.

(a, b) Schematic diagrams of the HFP-F8 region of the HFP-NC sample in antiparallel β sheet structure with labeled ¹³COs represented as red circles. Panel a shows a model that is fully constrained to a single registry while panel b shows multiple registries. (c, d) β sheet backbone representations of the respective boxed regions of panels a and b with labeled ¹³COs in red and possible n.a. ¹⁵N sites in blue, i.e. sites for which a n.a. ¹⁵N is within 7 Å of a labeled ¹³CO. A particular spin geometry will have only one ¹⁵N. The min n.a.d. model is shown in panel c and each spin geometry will have either one labeled ¹³CO and one n.a. ¹⁵N (#1, 2 or 3) or two labeled ¹³COs and one n.a. ¹⁵N (#4, 5, or 6). The max n.a.d model is shown in panel d and each spin geometry will have one labeled ¹³CO and one n.a. ¹⁵N.

There are many indices and parameters in the quantitative modeling and descriptions and possible values for them are compiled in Table 1. For the α, min β, or max β n.a.d. models, the average γ = (S₁/S₀) for the relevant spin geometries:

$${\gamma }_{\mathit{\text{lN}}}^{\mathit{\text{na}}}(\tau )={(J)}^{-1}{\displaystyle \sum _{j=1}^J{\left[\frac{S_{\mathit{\text{lj}}}(\tau )}{S_{0j}(\tau )}\right]}^{\mathit{\text{sim}}}}$$ (3)

where “ na ” refers to natural abundance, l = 0 or 1, “N ” refers to n.a. ¹⁵N, j is the index of a particular spin geometry, and J is the number of unique spin geometries of the model (J = 9 for α or max β n.a.d. and J = 6 for min β n.a.d.). The γ_0N^na(τ) = 1 for all τ while γ_1N^na(τ) were calculated using [S_1j (τ)/S_0j (τ)] ^sim from the SIMPSON program and generally decreased with increasing τ. After setting a total labeled ¹³CO population of 1.0 for HFP-F8 in HFP-NC, the relative population affected by n.a. ¹⁵N is J × 0.0037 while the remainder population, [1 − (J × 0.0037)], has S₁ = S₀. There is also an n.a. ¹³CO contribution from unlabeled residues in HFP-F8 with a relative population 30 × 0.011 and with S₁ = S₀. Similar analysis for ¹⁵N labeled HFP-A6L7 in HFP-NC results in:

$${\gamma }_{\mathit{\text{lC}}}^{\mathit{\text{na}}}(\tau )={(K)}^{-1}{\displaystyle \sum _{k=1}^K{\left[\frac{S_{\mathit{\text{lk}}}(\tau )}{S_{0k}(\tau )}\right]}^{\mathit{\text{sim}}}}$$ (4)

where l = 0 or 1, “C” refers to n.a. ¹³CO, k is the index of a particular spin geometry, K is the number of unique n.a. ¹³CO-labeled ¹⁵N spin geometries of the model (K = 10, 8, or 12, respectively, for α, min β, or max β n.a.d. models), and γ_0C^na(τ) = 1. Accounting for the 1:2 ratio of HFP-F8:HFP-A6L7, the total n.a. ¹³CO population of HFP-A6L7 is 2 × 31 × 0.011 with population 2K × 0.011 affected by labeled ¹⁵N and the remainder having S₁ = S₀. For HFP-NC in total:

$$S_{\mathit{\text{l,tot}}}^{\mathit{\text{sim}}}(\tau )=\{[J\times 0.0037\times {\gamma }_{\mathit{\text{lN}}}^{\mathit{\text{na}}}(\tau )]+[2K\times 0.011\times {\gamma }_{\mathit{\text{lC}}}^{\mathit{\text{na}}}(\tau )]\}+\{2.0-[J\times 0.0037]-[2K\times 0.011]\}$$ (5)

where l = 0 or 1 and the terms in the first braces are τ- and l-dependent.

Table 1.

Indices and parameters

Index/parameter	Description	Values
ft	fractional population of structure t	for membr. assoc. samples, determined by fitting
j, k	index for n.a. site <7 Å from a labeled site: j, n.a. 15N near labeled 13CO; k, n.a 13CO near labeled 15N
J, K	number of n.a. sites <7 Å from a labeled site: J, n.a. 15Ns near labeled 13CO; K, n.a 13COs near labeled 15N	α helical structure, J = 9, K = 10; min β sheet structure, J = 6, K = 8; max β sheet structure, J = 9, K = 12
l	REDOR data type index	0 ≡ no dipolar evolution 1 ≡ dipolar evolution
m	datum index	1, 2, 3, 4, 5, 6, or 7
Sl, Slj, Slk, Slu	REDOR signal intensity	determined by experiment or calculation
t, t1, t2	structural population index; for unconstrained model of membr. assoc. samples, t1 indexes the top/middle registry and t2 indexes the middle/bottom registry	for membr. assoc. samples: 1 ≡ parallel registry 2 ≡ antiparallel registry 3 ≡ other “X” registry
u	membr. assoc. sample index	1 ≡ HFP-P 2 ≡ HFP-A 3 ≡ HFP-AP
v	index for arrangement of three adjacent labeled HFPs in membr. assoc. samples – middle HFP has 13CO labeling and the 13CO is hydrogen bonded to HN of top HFP	1 ≡ 13CO HFP (top), 13CO HFP (bottom) 2 ≡ 15N HFP (top), 13CO HFP (bottom) 3 ≡ 13CO HFP (top), 15N HFP (bottom) 4 ≡ 15N HFP(top),15N HFP(bottom)
wv	fractional population of arrangement of three adjacent labeled HFPs in membr. assoc. samples	fully constrained model: w1 = 1/9, w2 = 2/9, w3 = 2/9, w4 = 4/9; unconstrained model: w1 = 1/81, w2 = 2/81, w3 = 2/81, w4 = 4/81
γlNna(τ), γlCna(τ)	Sl(τ)/S0: γlN(τ), labeled 13CO-n.a. 15N; γlC(τ), n.a. 13CO-labeled 15N	γ0N(τ) = 1; γ0C(τ) = 1; γ1N(τ) and γ1C(τ) determined by calculation
γltuvlab(τ), γlt1t2uvlab(τ)	Slulab(τ)/S0lab for arrangement of labeled 13CO and 15N nuclei: γ1tuvlab(τ), fully constrained model; γ1t1t2uvlab(τ), unconstrained model	γ0tuvlab(τ) = 1; γ0t1t2uvlab(τ) = 1; γ1tuvlab(τ) and γ1t1t2uvlab(τ) determined by calculation
τ	REDOR dephasing time	2.2, 8.2, 16.2, 24.2, 32.2, 40.2, or 48.2 ms

For each n.a.d. model (α, min β, and max β), (ΔS/S₀)^sim for each τ was calculated with Eq. 5 and statistical comparison was then made to (ΔS/S₀)^exp:

$${\chi }^2={\displaystyle \sum _{m=1}^7{\left\{\frac{{\left(\raisebox{1ex}{$\mathrm{\Delta }S$}\!\left/ \!\raisebox{-1ex}{$S_0$}\right.\right)}_m^{\mathit{\text{sim}}}-{\left(\raisebox{1ex}{$\mathrm{\Delta }S$}\!\left/ \!\raisebox{-1ex}{$S_0$}\right.\right)}_m^{\mathit{\text{exp}}}}{{\sigma }_m^{\mathit{\text{exp}}}}\right\}}^2}$$ (6)

where m is the index for an experimental datum, i.e. a particular τ. The respective χ² for the α, min β, and max β n.a.d. models were 1.2, 3.8, and 2.0 which were all less than the number of degrees of fitting, 7, i.e. the number of data, 7, minus the number of independent fitting parameters, 0. The validity of the approach to n.a.d. calculation was supported by good fits for all models (43).

The broad ¹³CO linewidth of HFP-NC in Fig. 2a was consistent with two HFP populations, one with helical and one with β strand secondary structure. It was therefore reasonable to calculate (ΔS/S₀)^sim for “mixtures” with contributions from multiple models:

$$S_{\mathit{\text{l, mix}}}^{\mathit{\text{sim}}}(\tau )={\displaystyle \sum _{t=1}^3\left[f_t\times S_{\mathit{\text{lt}}}^{\mathit{\text{sim}}}(\tau )\right]}$$ (7)

where l = 0 or 1, t was the index that referred to the α, min β, or max β model, f_t was fractional population with Σf_t = 1, and each S_lt^sim(τ) was calculated using Eq. 5. The HFP-NC distribution of ¹³CO shifts indicated f_α ≈ 0.5 and f_minβ + f_maxβ ≈ 0.5 but did not provide information about individual f_minβ or f_maxβ Fitting using f_α = 0.5 and f_minβ = 0.5, f_maxβ = 0.0 yielded χ² = 1.5 while fitting using either f_α = 0.5, f_minβ = 0.0, f_maxβ = 0.5 or f_α = 0.5, f_minβ = 0.25, f_maxβ = 0.25 yielded χ² = 1.2 and (ΔS/S₀)^sim in Fig. 3a were calculated with the latter distribution. The (ΔS/S₀)^sim from all three conformational distributions fit well to the (ΔS/S₀)^exp and these models are statistically similar. Together with previously described good fitting for different secondary structure models show that n.a.d. is accurately calculated with these models and only weakly dependent on secondary and tertiary structure. The key feature of all these well-fitting long-range models was consideration of the multiple n.a. sites within 7 Å of a labeled site which led to continually increasing (ΔS/S₀) with τ, Fig. 3a. The (ΔS/S₀)^sim were also calculated using a short-range model that only considered n.a. sites separated by one or two bonds from each labeled site. The (ΔS/S₀)^sim were systematically less than the (ΔS/S₀)^exp with resultant poor fit and χ² = 29.

Quantitative analysis of registry populations – fully constrained model

For membrane-associated HFP, there is a single distribution of registries which we model as fractions of: (1) 1→17/1→17 and 2→17/1→16 parallel registries; (2) 16→1/1→16 and 17→1/1→17 antiparallel registries; and (3) X registries not detected by any of our labeling schemes, Fig. 1c. Fraction 1 contributed to the (ΔS/S₀)^exp of HFP-P, fraction 2 contributed to the (ΔS/S₀)^exp of HFP-A, and fractions 1 and 2 contributed to (ΔS/S₀)^exp of HFP-AP. The overall goal was best-fit determination of these fractions based on the (ΔS/S₀)^exp of the three samples, Fig. 3b, and this analysis required calculation of the n.a.d. contribution to (ΔS/S₀)^exp. Because a 1:2 ¹³CO-HFP:¹⁵N-HFP ratio was used for all samples, this contribution was calculated using models developed for HFP-NC and resulted in a modified Eq. 5 appropriate for HFP-P, HFP-A, and HFP-AP:

$$S_{\mathit{\text{lu, tot}}}^{\mathit{\text{sim}}}(\tau )=\left\{\left[J\times 0.0037\times {\gamma }_{\mathit{\text{ln}}}^{\mathit{\text{na}}}(\tau )\right]+\left[2K\times 0.011\times {\gamma }_{\mathit{\text{lc}}}^{\mathit{\text{na}}}(\tau )\right]\right\}+\{1.0-(2K\times 0.011)\}+\{[1.0-(J\times 0.0037)]\times {\gamma }_{\mathit{\text{ltuv}}}^{\mathit{\text{lab}}}(\tau )\}$$ (8)

$$=S_l^{\mathit{\text{na}}}(\tau )+S_{\mathit{\text{lu}}}^{\mathit{\text{lab}}}(\tau )$$ (9)

where S_l^na is the sum of the first two braced terms in Eq. 8 and S_lu^lab is the third braced term. Each membrane-associated sample is labeled by the index u where u = 1, 2, or 3 respectively refers to HFP-P, HFP-A, or HFP-AP, Table 1 and Fig. 1b. The first braced term in Eq. 8 corresponds to labeled and n.a. ¹³CO that experience n.a.d., the second braced term corresponds to n.a. ¹³COs that do not experience n.a.d., and the third braced term corresponds to labeled ¹³COs that do not experience n.a.d. but may experience dephasing from labeled ¹⁵Ns. The secondary structure of membrane-associated HFP was predominantly β sheet, Fig. 2b–d, and the best estimates of the n.a.d. terms in the first braced term were taken to be the average of the max β and min β calculated values. In the second and third braced terms, K and J were estimated to be their respective average values of 10 and 7.5. S_0u^lab(τ) was calculated using γ_0tuv^lab(τ) = 1 while γ_1tuv^lab(τ) and therefore S_1u^lab(τ) were first calculated with a “fully constrained” model, Fig. 4a,c, in which a β sheet region contained either: (1) 1→17/1→17 or 2→17/1→16 parallel registries; or (2) 16→1/16→1 or 17→1/1→17 antiparallel registries; or (3) X registries not directly detected by any of our labeling schemes, Fig. 1c. A sample was considered to be a mixture of the three registry types each denoted by index t = 1, 2, or 3 and fractional population f_t, Table 1. The S_1u^lab(τ) was calculated by modified Eq. 7:

$$S_{1u}^{\mathit{\text{lab}}}(\tau )={\displaystyle \sum _{t=1}^3\left[f_t\times {\gamma }_{1\mathit{\text{tuv}}}^{\mathit{\text{lab}}}(\tau )\right]\times S_0^{\mathit{\text{lab}}}(\tau )}$$ (10)

The γ_1tuv^lab(τ) values depended on the labeled d_CNs and therefore r_CNs which in turn depended on registry type t and sample labeling u, Fig. 1c. For some combinations of t and u, all labeled r_CN > 7 Å with consequent d_CN ≈ 0 and γ_1tuv^lab(τ) = 1. Specific examples are t = 1 and u = 2, t = 2 and u = 1, and t = 3 and u = 1, 2, or 3. For other combinations of t and u, γ_1tuv^lab(τ) were determined from SIMPSON calculations and Fig. 5a–d displays schematic examples for t = 2, u = 2 with numerical values of γ_1tuv^lab(τ) and more details in the Supporting Information. Column a, b, c, or d corresponds to particular arrangements of ¹³CO and ¹⁵N labeled HFPs that are respectively denoted by the index v = 1, 2, 3, or 4. For each v, the typical difference between the calculated γ_122v^lab(τ) for the 16→1/1→16 or 17→1/1→17 registry was ≤ 0.01 and the final γ_122v^lab(τ) were the average for the two registries. The antiparallel γ_123v^lab(τ) of HFP-AP were analogously calculated and the parallel γ_111v^lab(τ) of HFP-P and parallel γ_113v^lab(τ) of HFP-AP were calculated using the 1→17/1→17 registry and had similar values to γs calculated using the 2→17/1→16 registry. Fractional weightings w_v were based on the 1:2 ratio of ¹³CO HFP:¹⁵N HFP with w₁ = 1/9, w₂ = 2/9, w₃ = 2/9, and w₄ = 4/9. A more complete version of Eq. 10:

$$S_{1u}^{\mathit{\text{lab}}}(\tau )={\displaystyle \sum _{t=1}^3\left\{f_t\times {\displaystyle \sum _{\nu =1}^4\left[w_{\nu }\times {\gamma }_{1\mathit{\text{tuv}}}^{\mathit{\text{lab}}}(\tau )\right]}\right\}\times S_0^{\mathit{\text{lab}}}(\tau )}$$ (11)

with indices and parameters summarized in Table 1.

Figure 5.

Schematics of three adjacent HFPs for HFP-A, i.e. u = 2, in (a–d) fully constrained or (e–h) unconstrained models. Red and blue correspond to ¹³CO and ¹⁵N labeled residues, respectively, and the labeled ¹³CO in the middle strand was hydrogen bonded to the HN group of the residue in the top strand. Panels a–d display antiparallel 16→1/1→16 (top) or 17→1/1→17 (bottom) registries while panels e–h display parallel 1→17/1→17, antiparallel 16→1/1→16, and X registries where X refers to a registry for which the labeled r_CN > 7 Å, i.e. beyond the approximate detection limit of the SSNMR experiment, and which is not 1→17/1→17, 2→17/1→16, 16→1/1→16, or 17→1/1→17. Correspondence between columns and the index v are: a and e, v = 1; b and f, v = 2; c and g; v = 3; d and h; v = 4. Both rows of three-strand arrangements in panels a–d correspond to t = 2 and the row, t₁, t₂ correspondence in panels e–h is: row 1, t₁ = 1, t₂ = 1; row 2, t₁ = 1, t₂ = 2; row 3, t₁ = 1, t₂ = 3; row 4, t₁ = 2, t₂ = 1; row 5, t₁ = 2, t₂ = 2; row 6, t₁ = 2, t₂ = 3; row 7, t₁ = 3, t₂ = 1; row 8, t₁ = 3, t₂ = 2; row 9, t₁ = 3, t₂ = 3. For each three-strand arrangement enclosed by a box, the γ_1tuv^lab(τ) or γ_1t1t2uv^lab(τ) were calculated by SIMPSON simulation. For arrangements with t, t₁, or t₂= 2, fitting to experiment was based on γs that were the average of those calculated with 16→1/1→16 and 17→1/1→17 registries although the latter registry is not displayed in panels e–h. For any arrangement not enclosed by a box, γ_1tuv^lab(τ) = 1 or γ_1t1t2uv^lab(τ) = 1.

The values of f₁, f₂, and f₃ were the same for the HFP-P, HFP-A, and HFP-AP samples with f₃ = 1 – f₁ – f₂. Best-fit values of f₁ and f₂ were obtained by calculating χ²(f₁, f₂) using an expression analogous to Eq. 6:

$${\chi }^2(f_1,f_2)={\displaystyle \sum _{u=1}^3{\displaystyle \sum _{m=1}^7{\left\{\frac{{\left[\raisebox{1ex}{$\mathrm{\Delta }S(f_1,f_2)$}\!\left/ \!\raisebox{-1ex}{$S_0$}\right.\right]}_{\mathit{\text{um}}}^{\mathit{\text{sim}}}-{\left[\raisebox{1ex}{$\mathrm{\Delta }S$}\!\left/ \!\raisebox{-1ex}{$S_0$}\right.\right]}_{\mathit{\text{um}}}^{\mathit{\text{exp}}}}{{\sigma }_{\mathit{\text{um}}}^{\mathit{\text{exp}}}}\right\}}^2}}$$ (12)

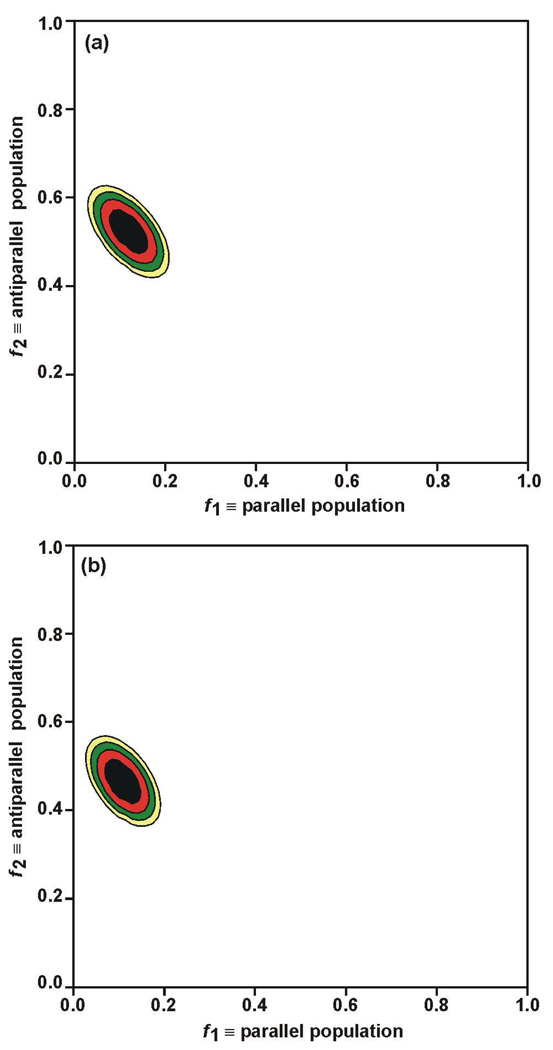
and then selecting the f₁ and f₂ values which corresponded to minimum χ², i.e. χ²_min. In Eq. 12, m is the index for each τ, and [ΔS(f₁, f₂)/S₀]_um^sim was determined using Eqs. 8–11. For this fully constrained model, Fig. 6a displays a plot of χ² vs f₁ and f₂ with best-fit f₁ = 0.12 and f₂ = 0.52 and χ²_min = 11. The model was reasonable as evidenced by χ²_min which was smaller than the number of degrees of fitting, 19, i.e. the number of data, 21, minus the number of fitting parameters, 2. The f₁ fractional parallel population, Fig. 1c, was small which was consistent with qualitative analysis of the data, Fig. 3b. The f₂ antiparallel population was substantially larger and also consistent with Fig. 3b. The f₃ ≈ 0.35 indicated a substantial population of X registries not detected by the labeling of the three samples.

Figure 6.

Contour plots of χ² vs f₁ parallel and f₂ antiparallel fractional populations for (a) fully constrained and (b) unconstrained models. In each plot, f₁ is the sum of populations of 1→17/1→17 and 2→17/1→16 parallel registries and f₂ is the sum of populations of 16→1/1→16 and 17→1/1→17 antiparallel registries. For plot a, the best-fit values were f₁ = 0.12 ± 0.03 and f₂ = 0.52 ± 0.04 with χ²_min = 11, and for plot b, f₁ = 0.11 ± 0.03, f₂ = 0.46 ± 0.04, and χ²_min = 8. Parameter uncertainties were determined by the region of χ² within about three units of χ²_min. In plot a, the black, red, green, yellow, and white regions correspond to χ² < 14, 14 < χ² < 17, 17 < χ²< 20, 20 < χ²< 23, and χ² > 23 and in plot b, the regions correspond to χ² < 11, 11 < χ² < 14, 14 < χ² < 17, 17 < χ² < 20, and χ² > 20.

The above fitting was done using a long-range n.a.d. model that considered effects of n.a. sites within 7 Å of each labeled nucleus. Fitting displayed in Fig. 6a was based on n.a.d. calculated from half min β and half max β sheet structure, Fig. 4, but the best-fit f₁ and f₂ and χ²_min were not sensitive to the structural composition of the long-range n.a.d. model. For example, fitting done using n.a.d. for half α helical and half max β sheet structure yielded best-fit f₁ and f₂ and χ²_min respectively within 0.01, 0.01, and 1 of the corresponding Fig. 6a values. For HFP-NC fitting, n.a.d. was underestimated by a short-range model that only considered n.a. sites separated by one or two bonds from each labeled site. This effect was also observed when fitting membrane-associated HFP data with the short-range n.a.d. model and led to best-fit f₁ = 0.22 and f₂ = 0.57 which were significantly higher than the Fig. 6a values. The χ²_min = 20 using the short-range model was also higher than the χ²_min in Fig. 6a.

Quantitative analysis of registry populations – unconstrained model

In addition to the fully constrained model for strand registries, an alternate “unconstrained” fitting model was also considered for which there was local mixing of: (1) 1→17/1→17 parallel registries; (2) 16→1/1→16 and 17→1/1→17 antiparallel registries; and (3) X registries not directly detected by any of our labeling schemes, Fig. 1c. Each pairwise registry type was labeled by t =1, 2, or 3 with fractional population f_t. For this unconstrained model, Fig. 5e–h displays schematics of three-strand registries with ¹³CO labeled HFP in the middle strand. Each e–h row has three-strand registries that were each a combination of two registries labeled by specific t₁ and t₂ which denote the respective t of the top/middle and middle/bottom strands. As with the fully constrained models, the registries in each e–h column corresponded to a particular ¹³CO HFP/¹⁵N HFP arrangement which respective label v = 1, 2, 3, or 4. The ¹³CO HFP:¹⁵N HFP population ratio of 1:2 correlated with a sum weighting of 1/9 for the v = 1 registries with individual registry weighting w₁ = 1/(9×9) = 1/81. The sum weightings for v = 2, 3, or 4 were respectively 2/9, 2/9, or 4/9 with respective individual weightings w₂ = 2/81, w₃ = 2/81, and w₄ = 4/81. Eq. 11 was modified for the unconstrained model:

$$S_{1u}^{\mathit{\text{lab}}}(\tau )={\displaystyle \sum _{t_1=1}^3{\displaystyle \sum _{t_2=1}^3\left\{f_{t_1}\times f_{t_2}\times {\displaystyle \sum _{\nu =1}^4\left[w_{\nu }\times {\gamma }_{1t_1{t}_2\mathit{\text{uv}}}^{\mathit{\text{lab}}}(\tau )\right]}\right\}\times S_0^{\mathit{\text{lab}}}(\tau )}}$$ (13)

Similar to the fully constrained model, many combinations of t₁, t₂, u, and v have r_CN > 7 Å with consequent d_CN ≈ 0 and γ_1t1t2uv^lab(τ) = 1. In Fig. 5e–g, such registries are not enclosed by a box. Similar to results for the fully constrained model, the γ_1t1t2uv^lab(τ) were similar for the two antiparallel registries and an average value was used.

The values of f₁, f₂, and f₃ in the unconstrained model were the same for the HFP-P, HFP-A, and HFP-AP samples with f₃ = 1 – f₁ – f₂. Best-fit values of f₁ and f₂ were obtained with Eq. 12 and Fig. 6b displays a plot of χ² vs f₁ and f₂ with best-fit f₁ = 0.11 and f₂ = 0.46 and corresponding χ²_min = 8. The unconstrained model was reasonable as evidenced by a best-fit χ² which was smaller than the number of degrees of fitting, 19. Similar to the results of the fully constrained model, the f₁ fractional parallel population was small and the f₂ antiparallel population and f₃ ≈ 0.4 other population were significant.

This unconstrained model fitting was done with n.a.d. calculated with a long-range model and half min β and half max β structure. Similar to the fully constrained model, best-fit f₁, f₂, and χ² for the unconstrained model were: (1) negligibly affected by the structural distribution of the long-range n.a.d. model; and (2) significantly increased by use of a short-range n.a.d. model.

DISCUSSION

This paper sets an upper limit of ~0.15 on the fraction of membrane-associated HFP in in-register parallel β sheet structure and this result is supported by both qualitative analysis of the data, Fig. 3b, as well as quantitative analyses with fully constrained and unconstrained models, Fig. 6. Both models fit the data well and yielded similar best-fit fractional population of parallel registries and similar populations of antiparallel registries. The small fractional parallel population agrees with some earlier SSNMR studies but differs from interpretations of other SSNMR and IR data which respectively reported ~0.5 and ~1.0 fractions of in-register parallel structure (27, 30–32). The present study used samples with sparse isotopic labeling while the earlier studies interpreted to support a large fraction of parallel structure used samples with extensive labeling. We think that there was ambiguity of interpretation in the studies of extensively labeled samples and that the data could also be reasonably interpreted in terms of small in-register parallel population. For example, the earlier SSNMR study also used the REDOR technique but with only a single τ (24 ms) and with samples containing equimolar amounts of HFP ¹³CO labeled on three sequential residues and HFP ¹⁵N labeled on three sequential residues. The typical (ΔS/S₀)^exp was ~0.1 and was approximately independent of the positions of the labeled residues and also had some contribution from n.a.d. It was not possible to do unambiguous quantitative analysis of registry distributions because: (1) each sample was extensively labeled so that non-zero (ΔS/S₀) was expected for many different registries; (2) (ΔS/S₀)^exp were only measured for a single τ; and (3) a “HFP-NC”-type sample was not studied and n.a.d. was therefore not quantitatively modeled.

The samples for the IR study were also extensively labeled with backbone ¹³CO labeling at either: (1) A1 to V3, G5 to L9; (2) F8 to G16; or (3) A1 to V3, G5 to G16. The authors’ interpretation of their spectra to support predominant in-register parallel structure was based in part on expected effects of (¹³C=¹⁶O electric dipole)^…(¹³C=¹⁶O electric dipole) coupling on ¹³C=O vibrational wavenumber and intensity. However, their interpretation appeared to neglect the substantial intramolecular coupling between ¹³C=Os on adjacent residues and we note that this coupling is independent of registry. In addition to these “undiluted” samples, three “diluted” samples were studied that had an equimolar mixture of a labeled and unlabeled peptide. The wavenumber (v) of a ¹³C=¹⁶O vibration is sensitive to nearby (~5 Å away) C=O vibrations and is higher with ¹²C=¹⁶O neighbors than with ¹³C=¹⁶O neighbors. If there is hydrogen bonding between ¹³CO labeled residues of adjacent strands in an undiluted sample, the corresponding diluted sample should have an increased fraction of ¹³C=O/¹²C=O proximities, decreased fraction of ¹³C=O/¹³C=O proximities, and Δv = v_diluted − v_undiluted > 0. If there were a major fraction of parallel 1→17/1→17 structure (as claimed by the authors), dilution of (1) A1-V3, G5-L9; (2) F8-G16; or (3) A1-V3, G5-G16 labeled HFPs would have had comparable effect on proximities and resulted in similar Δv. However, the experimental Δv_A1-V3,G5-L9 ≈ Δv_F8-G16 ≈ (Δv_A1-V3,G5-G16)/2 which is inconsistent with a large fraction of in-register parallel structure. Like the earlier SSNMR study on extensively labeled samples, extensive labeling of the IR samples also meant that the IR data were consistent with many registry distributions and precluded more quantitative analysis of the distribution. Overall, the sparse labeling of the present SSNMR study allowed for much more unambiguous and quantitative determination of the populations of specific registries. This general approach can be applied in the future to determine the registry distributions of HFP constructs with very high or low fusogenicity such as HFPtr or V2E mutant, respectively.

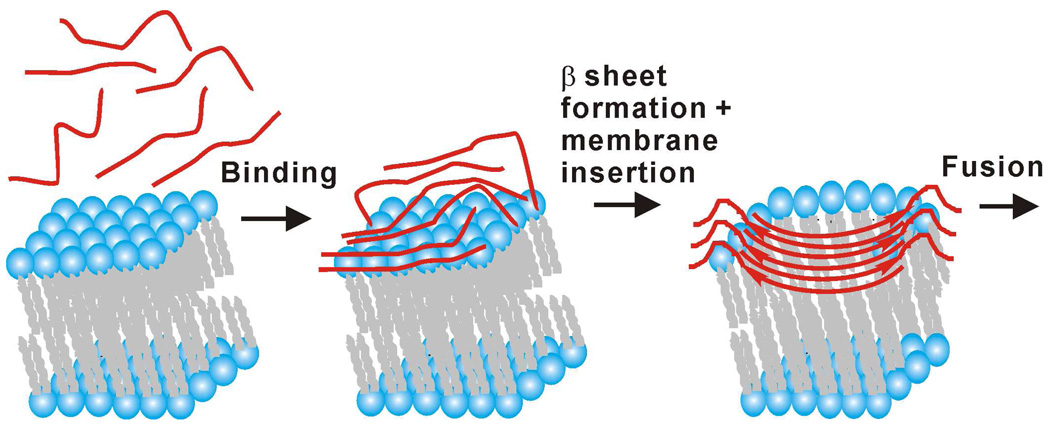
Fig. 7 displays a structure/function model for HFP based on results from this and earlier studies. Prior to membrane binding, HFP is monomeric in aqueous solution and has random coil structure (11, 12, 18). HFP sequentially: (1) binds to membranes; (2) forms β sheet oligomers with a significant fraction of 16→1/1→16 and 17→1/1→17 antiparallel registries; and (3) induces membrane fusion as monitored by intervesicle lipid mixing (12, 14, 17, 18). It is also known that the A6 and L9 residues of β sheet HFP insert shallowly into the membrane with correlation between membrane insertion depth and both membrane perturbation and fusion rate (19, 36, 49). A global structure-function model is non-transmembrane HFP insertion perturbs bilayer structure and moves the membrane on the fusion reaction coordinate towards the highly perturbed transition state with consequent reduction in fusion activation energy and increase in fusion rate.

Figure 7.

Pictorial model of HFP (red lines) binding to membranes followed by antiparallel β sheet formation and membrane insertion and then fusion. Time increases from left-to-right. For reasons of clarity, some lipids are not shown in the right-most picture. Although there are no data yet on fusion peptide structure during HIV/host cell fusion, the antiparallel β sheet structure of the right-most picture is plausible because: (1) the structure is consistent with multiple trimers at the fusion site; and (2) the structure is membrane-inserted with deeper insertion positively correlated with increased membrane perturbation and vesicle fusion rate.

There is functional and electron microscopic evidence that multiple gp41 trimers are required for fusion and Fig. 7(right) shows a β sheet HFP hexamer as would be reasonable for interleaved antiparallel fusion peptides from two gp41 trimers. While there are no data specifically supporting a HFP hexamer, HFP β sheet oligomers likely contain a small number of molecules because: (1) for ~90% of HFP molecules, there is an A1 ¹³CO-lipid ³¹P distance of ~5 Å, i.e. close contact of most HFPs with the membrane; and (2) significant temperature dependence of intensities of SSNMR spectra (19, 26). Interleaved antiparallel fusion peptides from multiple gp41 trimers may also be the fusogenic structure of HIV/host cell fusion. As noted above, this structure can insert into and perturb membranes which are likely requirements for HIV/host cell fusion.

The experimentally observed membrane insertion of the central β sheet region (e.g. A6 to L12) of HFP is consistent with ΔG^insertion ≈ −6 kJ/mol for the fully constrained 17→1/1→17 registry as calculated by summing individual residue insertion energies for L12→A6/A6→L12, Fig. 1c (50). A similar calculation yielded ΔG^insertion ≈ −3 kJ/mol for L12→G5/G5→L12 of the 16→1/1→16 registry. The ΔG^insertion ≈ −6 kJ/mol for A6→L12/A6→L12 of the 1→17/1→17 parallel registry suggests that ΔG^insertion does not underlie the preference for antiparallel over parallel structure. This preference may instead be due to ΔG^{electrostatic} as the HFP N-terminus is located in the high water content lipid headgroup region and is therefore likely protonated. Closest intermolecular NH₃⁺−NH₃⁺ distance is ~5 Å for the low population 1→17/1→17 registry and ~10 Å for the significantly populated 17→1/1→17 registry. For ε_dielectric = 78 and hexameric HFP, ΔG^{electrostatic} ≈ +5.1 kJ/mol for the 1→17/1→17 registry and +1.5 kJ/mol for the 17→1/1→17 registry.

We expect that inclusion of the non-native C-terminal W(K)₆A tag does not contribute to the preference for antiparallel over parallel registry because either registry would have similar minimized electrostatic repulsion energy. Such repulsion would be minimized by: (1) extensive solvation of the tag; and (2) large inter-tag distances that are possible because of random coil tag structure. Tag solvation is supported by the previously observed lack of membrane insertion of HFP beyond residue L12 and random coil tag structure is supported by broad NMR linewidths in the C-terminal region of HFP (14, 19). We also note that inclusion of the tag has minor effect on fusion activity and that similar REDOR ΔS/S₀ were observed for mixtures of triply ¹³CO and ¹⁵N labeled HFPs with or without the tag (12, 27).

In contrast to the reasonably large distribution of membrane-associated HFP registries, i.e. significant 16→1/1→16, 17→1/1→17, and X registries, SSNMR studies of β sheet registries of protein in amyloid fibrils have typically shown a single registry which is usually in-register parallel, e.g. 1→17/1→17 (28, 29). The width of a fibril is at most a few protein molecules and the length is >200 molecules and along the intermolecular β sheet hydrogen bonding direction. The amyloid fibrils are grown in aqueous solution (without lipid) and their greater registry homogeneity may reflect ordered fibril growth from seeds (51).

One distinctive feature of the present study is the development of a quantitative n.a.d. model that was experimentally validated. Accurate fitting of the HFP-NC data and fitting of the membrane-associated HFP data relied on a long-range n.a.d. model which included effects of n.a. nuclei <7 Å from each labeled nucleus. For this model, the n.a.d. was approximately independent of secondary and tertiary structure. The n.a.d. was systematically underestimated by a short-range model which only considered n.a. nuclei separated by one or two bonds from each labeled nucleus.

ABBREVIATIONS

CO

carbonyl

d

magnetic dipole-dipole coupling

DTPC

1,2-di-O-tetradecyl-sn-glycero-3-phosphocholine

DTPG

1,2-di-O-tetradecyl-sn-glycero-3-phosp-rac-(1-glycerol) sodium salt

FMOC

9-fluorenylmethoxycarbonyl

HEPES

N-(2-hydroxyethyl)piperazine-N'-2-ethanesulfonic acid

HFP

HIV fusion peptide

HFPtr

HIV fusion peptide trimer

HIV

human immunodeficiency virus

IR

infrared

MAS

magic angle spinning

max n.a.d.

maximum natural abundance dephasing

min n.a.d.

minimum natural abundance dephasing

n.a.

natural abundance

n.a.d.

natural abundance dephasing

NMR

nuclear magnetic resonance

PDB

Protein Data Bank

r

internuclear distance

REDOR

rotational-echo double resonance

SIMPSON

simulation program for solid-state NMR spectroscopy

SSNMR

solid-state NMR

TFA

trifluoroacetic acid

TPPM

two-pulse phase-modulation